Abstract
As shared micromobility grows quickly in metropolitan settings, e-scooter safety issues have become more urgent. This paper uses a Bayesian hierarchical model applied to census block groups in several Texas metropolitan areas to construct a spatial risk assessment methodology for e-scooter crashes. Based on crash statistics from 2018 to 2024, we develop a severity-weighted crash risk index and combine it with variables related to land use, transportation, demographics, economics, and other factors. The model comprises a geographically structured random effect based on a Conditional Autoregressive (CAR) model, which accounts for residual spatial clustering after capture. It also includes fixed effects for covariates such as car ownership and nightlife density, as well as regional random intercepts to account for city-level heterogeneity. Markov Chain Monte Carlo is used for model fitting; evaluation reveals robust spatial calibration and predictive ability. The following key predictors are statistically significant: a higher share of working-age residents shows a positive association with crash frequency (incidence rate ratio (IRR): ≈1.55 per +10% population aged 18–64), as does a greater proportion of car-free households (IRR ≈ 1.20). In the built environment, entertainment-related employment density is strongly linked to elevated risk (IRR ≈ 1.37), and high intersection density similarly increases crash risk (IRR ≈ 1.32). In contrast, higher residential housing density has a protective effect (IRR ≈ 0.78), correlating with fewer crashes. Additionally, a sensitivity study reveals that the risk index is responsive to policy scenarios, including reducing car ownership or increasing employment density, and is sensitive to varying crash intensity weights. Results show notable collision hotspots near entertainment venues and central areas, as well as increased baseline risk in car-oriented urban environments. The results provide practical information for targeted initiatives to lower e-scooter collision risk and safety planning.
1. Introduction
The rapid proliferation of e-scooters in urban environments has transformed contemporary mobility paradigms, offering a sustainable and convenient alternative to traditional modes of transportation. However, this shift toward micromobility has been accompanied by growing concerns about safety. In Texas, reported e-scooter crashes began near zero and rose quickly with the rollout of scooter sharing. For example, only 24 e-scooter collisions were officially recorded statewide in 2021 [1], but a detailed Austin case study identified 153 police-reported e-scooter crashes in that city from 2018 to 2021 [2]. By 2023, annual crash counts remained elevated—one Austin scooter operator alone reported 342 collisions over 2022–2023 [3]—reflecting sustained growth in e-scooter use. Crucially, most crashes result in injury but not death. In Austin’s data, over 98% of e-scooter crashes led to non-fatal injuries (predominantly minor injuries), and 0% led to fatalities [2]. Severe outcomes, while comparatively rare, have occurred (Austin has averaged roughly one rider death per year since 2018 [3]). National statistics echo these trends. E-scooter-related injuries treated in U.S. emergency departments increased by about 22% from 2021 to 2022 [4], totaling an estimated 169,300 e-scooter injuries between 2017 and 2022 [5]. At least 111 e-scooter rider fatalities were reported nationwide in 2021–2022 [5], with the majority involving collisions with motor vehicles. In summary, e-scooter crashes have surged in frequency since 2018, especially in Texas’s urban centers, although severe injuries and deaths remain a relatively small fraction of all incidents. Recent studies have documented a rise in e-scooter crashes, prompting researchers and policymakers to question the adequacy of existing urban infrastructure in accommodating this new mode of transport safely [6,7]. The inherent variability in crash rates across different urban contexts suggests that traditional safety assessments—often based on aggregated metrics—fail to capture the complex interplay between urban form, demographic characteristics, and local exposure to micromobility. In response, spatially explicit modeling approaches have emerged as a powerful tool for uncovering heterogeneous risk patterns in urban settings [8,9].
In this study, we develop a Bayesian hierarchical spatial Poisson model to quantify e-scooter crash risk at the census block-group level in Texas. Our approach integrates a comprehensive set of covariates—including demographic factors (e.g., the percentage of the working-age population), household vehicle ownership, multiple density measures (e.g., gross population and employment densities), and detailed employment and land-use metrics (e.g., retail and entertainment employment densities, walkability, and street intersection density)—with spatial and regional random effects. Notably, we omit region-level effects for observations with missing community statistical area (CSA) identifiers, thereby ensuring that all data are retained while recognizing the differential influence of urban versus non-urban areas on crash risk.
The expanded set of predictors allows us to explore a range of potential influences on safety outcomes. For instance, our preliminary findings indicate that block groups with higher proportions of working-age residents, greater employment density, and elevated entertainment employment density exhibit significantly higher e-scooter crash risk. Conversely, areas with higher household density and more robust multimodal infrastructure may experience lower relative risk. By capturing both global trends and localized spatial heterogeneity, our model provides actionable insights for urban planners and policymakers. The results suggest that targeted interventions, such as developing protected micromobility lanes in high-density, mixed-use neighborhoods, could effectively mitigate crash risk while supporting sustainable urban mobility.
The remainder of this paper is organized as follows: Section 2 reviews relevant literature on micromobility safety and Bayesian spatial modeling. Section 3 describes the data sources and methodological framework. Section 4 presents the empirical results, including model diagnostics and the identification of key risk factors. Section 5 discusses policy implications and offers recommendations for enhancing e-scooter safety. Finally, Section 6 concludes with suggestions for future research.
2. Literature Review
The rapid expansion of shared micromobility services, particularly electric scooters (e-scooters), has prompted extensive research into the safety implications of these emerging modes of transportation in U.S. cities. Since their widespread introduction post 2018, e-scooters have been associated with a notable increase in crash incidents and injuries, although the majority of these incidents tend to be of minor severity [10]. Early investigations revealed that most e-scooter injuries result from single-vehicle events—primarily falls or loss-of-control incidents—rather than multi-vehicle collisions [11]. For instance, analyses of hospital records from metropolitan areas such as Los Angeles and Washington, D.C., have consistently shown that while a substantial number of riders present with injuries, the rate of hospitalization remains relatively low [12]. Nevertheless, the high frequency of head injuries among e-scooter riders, compounded by the low incidence of helmet use, remains a critical public health concern [10].
In parallel with crash outcome studies, researchers have examined the role of the built environment in shaping micromobility safety. The physical infrastructure available to riders, ranging from dedicated bike lanes and well-designed intersections to overall street connectivity, plays a pivotal role in determining the likelihood and severity of e-scooter crashes. Empirical evidence suggests that intersections are frequent sites of conflict. In Nashville, for example, a majority of e-scooter crashes occur at intersections, where the interplay between vehicular traffic and pedestrian movement creates complex conflict points [7]. Moreover, poor lighting conditions and the absence of protected infrastructure further exacerbate crash risks during nighttime riding [13]. Conversely, investments in dedicated infrastructure, such as protected bike lanes, have been associated with reduced crash frequency and severity [14]. Such findings underscore the importance of incorporating safe design principles into urban planning to accommodate micromobility better.
Socioeconomic and demographic factors also play a role in understanding e-scooter crash patterns. Numerous U.S.-based studies have found that neighborhoods with higher proportions of working-age adults tend to exhibit increased e-scooter usage, which, in turn, correlates with higher crash rates [15]. This relationship is further complicated by household vehicle ownership; areas with a higher percentage of zero-car households—often indicative of urban, transit-dependent communities—tend to experience an elevated crash risk, likely due to an increased reliance on alternative transportation modes such as e-scooters [16]. However, the evidence regarding the effect of one-car and two-plus-car households remains mixed, suggesting that the association between vehicle ownership and e-scooter safety may be nuanced and context-dependent [15]. Furthermore, the proportion of low-wage workers in both residential and work locations has been examined, with some studies suggesting that higher percentages may be associated with increased exposure and crash risk. However, these relationships are often statistically weak [17].
Density measures serve as robust indicators of exposure in urban safety analyses. Higher gross population density and employment density are consistently linked with increased e-scooter crash risk [18]. Dense areas, particularly downtown zones with mixed land use, not only attract more riders but also present a greater number of potential conflict points between e-scooters, pedestrians, and motor vehicles. In this context, land-use diversity—or employment entropy—has emerged as a significant predictor of crash frequency. A balanced mix of commercial, residential, and entertainment uses tends to correlate with elevated crash counts, reflecting both high exposure and the complex interplay of differing traffic flows [19]. These findings suggest that while dense, vibrant neighborhoods offer numerous mobility benefits, they also necessitate more sophisticated safety interventions.
Spatial heterogeneity in crash data is a critical aspect that traditional regression models often overlook. Bayesian hierarchical spatial models have increasingly been employed in transportation safety research to address this limitation. These models incorporate spatial random effects—often via a conditional autoregressive (CAR) prior—to account for the tendency of crash risk to cluster geographically [8,9]. Such approaches enable “borrowing strength” from neighboring areas, yielding more stable risk estimates, even for block groups with sparse data. Although widely used in pedestrian and bicycle safety studies, the application of Bayesian spatial models to e-scooter safety remains relatively novel. Recent work has demonstrated that these models can uncover significant local variations in risk that are obscured in aggregated analyses, thereby providing more actionable insights for urban planning [20,21].
Despite the advances in modeling, notable gaps persist in the literature. Most studies on e-scooter safety have been descriptive, focusing on crash counts and injury severity at broad geographic levels (e.g., cities or census tracts), without leveraging fine-scale spatial variation [11,15]. This study seeks to address these gaps by modeling crash risk at the census block-group level, thereby capturing localized effects that are crucial for targeted safety interventions. Moreover, while previous studies have considered a limited set of covariates, our model integrates a comprehensive suite of predictors—including demographic, socioeconomic, and built environment measures—to disentangle their relative contributions to crash risk. By doing so, we aim to identify modifiable factors that can inform policy decisions aimed at enhancing e-scooter safety.
In summary, the existing literature highlights that a combination of rider characteristics, built environment factors, and socioeconomic conditions influences the safety of e-scooters. Recent U.S.-based research highlights that high exposure—driven by dense population, mixed land use, and heavy employment—is associated with increased crash risk. At the same time, protective infrastructure such as bike lanes and improved intersection design can mitigate these risks [7,14]. However, there remains a pressing need for fine-scale spatial analyses that incorporate a broad array of risk factors within a unified modeling framework. The present study addresses this need by applying a Bayesian hierarchical spatial Poisson model to block group–level data in Texas, providing nuanced insights into the determinants of e-scooter crash risk and laying the groundwork for evidence-based urban safety interventions.
3. Data Sources and Methodological Framework
This study integrates crash records with socioeconomic and built environment data at the census block-group level. Crash data were obtained from the Texas Crash Records Information System (CRIS) maintained by the Texas Department of Transportation [22]. CRIS provides geocoded crash incident data, which we aggregated by census block group (a geographic unit roughly akin to a neighborhood). Socioeconomic and demographic variables were derived from the American Community Survey (ACS) 5-year estimates [23]. Additional built environment measures, such as walkability and network metrics, were collected from regional planning GIS datasets. The census block group was chosen as the unit of analysis because it offers fine-grained resolution and comes with readily available data on population and housing from ACS, enabling a consistent linkage of crash counts with local characteristics.
For each block group, a set of explanatory variables was compiled to characterize the resident population and built environment:
- Working-Age Population: The percentage of the population aged 18–64 years in the block group [24,25,26];
- Vehicle Ownership: Household vehicle availability, measured as the proportion of households with zero vehicles, one vehicle, and two or more vehicles [27,28];
- Low-Wage Employment: The count of jobs or workers in the block group that are classified as low-wage (below a given earnings threshold), representing economic characteristics of the area [16,26];
- Population and Household Density: Residents per square mile and households per square mile, reflecting residential density [16,29];
- Employment Density by Sector: Jobs per square mile in specific sectors such as entertainment and office employment, capturing the concentration of certain land uses and employment centers in the area [16,24,26];
- Walkability Index: An index reflecting the pedestrian-friendliness of the urban form (e.g., based on land-use mix, street connectivity, and sidewalk availability), obtained from planning datasets [24,25];
- Road Network Density and Intersection Density: The length of roadways per unit area and the count of intersections per unit area within the block group, indicating the intensity of the transportation network [16,18,24].
These variables were selected based on the literature that links demographics, car access, employment characteristics, and built environment features to traffic safety outcomes. By incorporating both population-related and infrastructure-related measures, the model can account for exposure (e.g., increased population or vehicle traffic in an area), as well as risk factors associated with road layout and urban design.
3.1. Crash Reporting Limitations
The crash data analyzed in this study are derived from the Texas Department of Transportation’s Crash Records Information System (CRIS), which, by design, includes only crashes that were investigated by or reported to law enforcement. In practice, this means that only incidents meeting official reporting criteria (e.g., occurring on public roadways and involving an injury, a fatality, or significant property damage above a defined threshold) are recorded. Consequently, very minor e-scooter mishaps—such as isolated falls that do not result in injury or notable property damage—are unlikely to be captured in the dataset. This reporting threshold introduces a limitation: the recorded crash sample is inherently biased toward higher-severity events, since trivial incidents typically go unreported. To acknowledge and partially mitigate this bias, we employ a severity-weighted crash index as the outcome variable in our risk modeling. This index assigns greater weight to crashes with serious injuries or fatalities, thereby emphasizing more consequential outcomes while de-emphasizing minor ones. For example, if and denote the numbers of fatal, serious-injury, minor-injury, and no-injury e-scooter crashes in a given spatial unit, we define the composite risk metric as follows:
with weight factors of , , , and chosen to place proportionally more emphasis on crashes involving severe outcomes. This severity-weighted formulation ensures that more serious crashes contribute more heavily to the risk measure, aligning the model with the data’s emphasis on high-severity incidents. It is important to note, however, that truly uneventful e-scooter incidents—for instance, a rider’s uneventful dismount or a self-corrected loss of balance that averts a crash—remain unobservable in police records. As a result, our analysis is inherently limited to crashes that exceed the reporting threshold, and care should be taken when generalizing findings to all e-scooter riding events.
3.2. Bayesian Hierarchical Model Formulation
To estimate spatial variation in e-scooter crash risk, we specify a Bayesian hierarchical model that captures multiple sources of variability: fixed covariate effects, region-specific heterogeneity, structured spatial dependence, and unstructured overdispersion. This formulation follows prior work in spatial epidemiology and road safety modeling [8,30,31].
Let denote the severity-weighted crash count in block group i, and let be the expected crash rate for that unit. At the observational level, we assume the crash counts follow a Poisson distribution:
The log of the expected count is modeled with both fixed and random effects:
where is the global intercept, represents fixed-effect coefficients for covariates (), is a region-level random intercept for the metropolitan area containing block group i, is a spatially structured effect capturing autocorrelation across neighbors, and is an unstructured noise term to model overdispersion [32,33]. The fixed effects () are assigned Gaussian priors:
Region-level random intercepts follow
The spatial effects () follow an intrinsic Conditional Autoregressive (CAR) prior, as introduced in [8]:
where is the set of neighbors of region i, is the number of neighbors, and is the precision parameter with prior .
Unstructured overdispersion effects are modeled as follows:
This hierarchical CAR model offers several key advantages: it accounts for spatial clustering, accommodates heteroskedasticity in crash counts, and enables partial pooling across regions with sparse data [9,33]. This is particularly valuable in the context of zero-inflated and skewed e-scooter crash data, where traditional Poisson models tend to underestimate risk variance. The CAR prior smooths estimates in spatially adjacent zones, reducing false positives from single, isolated, high-count units and improving the robustness of spatial inference. Figure 1 illustrates the steps of this model.
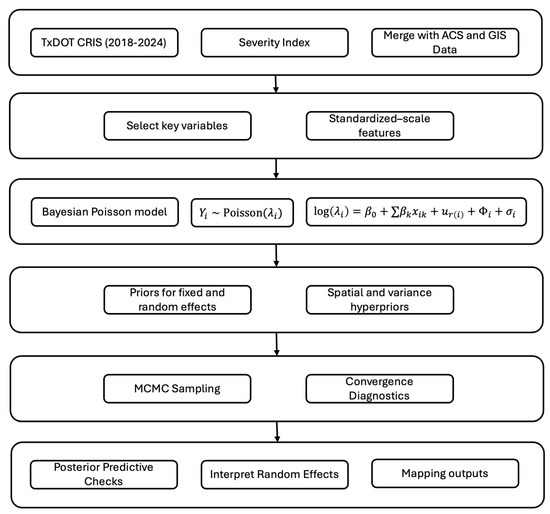
Figure 1.
Bayesian model flowchart.
In modeling e-scooter crash risk at the census block-group level, a Bayesian hierarchical spatial model offers significant advantages over simpler approaches like a Poisson GLM or negative binomial regression by explicitly capturing spatial dependencies and multilevel structure. Given the fine-grained spatial and demographic detail of block-group data, the advanced model can incorporate area-specific random effects (e.g., a spatial CAR prior) that capture unobserved heterogeneity and borrow strength across neighboring areas, yielding more stable risk estimates—a feature that simpler models cannot achieve when treating each block group as independent. Empirical studies show that accounting for spatial correlation yields significantly better fit and predictive accuracy compared to assuming independence [34]; for instance, a CAR-based Bayesian model had a significantly better fit than an equivalent Poisson log-normal model without spatial effects [34]. However, these benefits come at the cost of increased model complexity and reduced interpretability: the hierarchical model requires careful prior specification and intensive computation, making its results less transparent, whereas Poisson/NB models are straightforward to implement and have been widely used (with extensions for overdispersion or zero-heavy data) [19]. The choice of an advanced Bayesian spatial model is ultimately justified when the data’s rich spatial and demographic information can be leveraged to improve insight and prediction, as evidenced by recent micromobility safety studies incorporating spatial effects in crash models.
3.3. Modeling Framework
We employ a Bayesian hierarchical spatial Poisson model to analyze crash counts at the block-group level. The response variable is the number of crashes in each block group, which is assumed to follow a Poisson distribution. The model employs a log-linear specification in which the variables described above are entered as fixed-effect predictors, along with their corresponding regression coefficients. Formally, if is the crash count in block group i, we assume and
where is an intercept, represents the observed covariates (fixed effects), is a region-level random effect for the CSA region (c) that contains block group i, and is a spatial random effect for block group i. The region-specific random effects () capture unobserved heterogeneity across different Combined Statistical Areas (CSAs), recognizing that broad regional factors (e.g., overall urban form or traffic enforcement policies) might influence crash frequencies. We treat these terms as i.i.d. draws from a common distribution (e.g., )—one for each CSA in the study area. We include the term with a conditional autoregressive (CAR) before the model localizes spatial autocorrelation. In particular, we adopt an intrinsic CAR structure as introduced by Besag et al. [8]. This CAR prior assumes that neighboring block groups have correlated random effects: each is assumed to be normally distributed around the average of its neighbors’ effects. Neighbors are defined as adjacent block groups with a common boundary (first-order contiguity), which we determined from U.S. Census TIGER/Line shape files for block-group boundaries. This spatial prior encourages smoother variation in the unexplained risk across space, effectively borrowing strength from adjacent areas to improve estimates in any given block group. It helps account for spatially structured unobserved factors, such as traffic exposure or road design features not captured by our covariates, which can cause nearby areas to have similar crash rates. All parameters are estimated in a fully Bayesian framework using Markov Chain Monte Carlo simulation. We assign relatively diffuse priors for the regression coefficients (; to let the data inform their values) and hyperpriors for variance components, following standard practices for Bayesian hierarchical models [9]. The model yields posterior distributions for each parameter, from which we can derive point estimates and credible intervals for the effects of interest. This Bayesian hierarchical spatial approach enables us to accurately quantify uncertainty and leverage the multilevel structure of the data, where block groups are nested within regions with spatial linkages, yielding a robust understanding of how socioeconomic and built environment factors relate to crash occurrences across communities.
4. Empirical Results
This section presents the key findings from our Bayesian hierarchical spatial Poisson model, discussing both the overall model fit (including convergence diagnostics and posterior predictive checks) and the interpretation of significant risk factors. We also provide illustrative figures—such as coefficient plots, spatial risk maps, and diagnostic charts—to highlight our main conclusions.
4.1. Model Diagnostics and Convergence
All model parameters were estimated using Markov Chain Monte Carlo (MCMC) methods. We ran four parallel chains with 1000 burn-in iterations, followed by 2000 sampling iterations each, yielding a total of 8000 post-burn-in draws. Convergence was assessed primarily via the Gelman–Rubin statistic [9], trace plots, and adequate sample size (ESS) metrics. For the main fixed effects (i.e., regression coefficients for demographic and built environment variables), values were below 1.01, and ESS values exceeded 1000 in each case, indicating robust chain mixing. Similar results were observed for the random effects: the CSA-level intercepts and spatial effects both had . These diagnostics suggest that the sampler converged adequately and that the posterior estimates are stable.
We also conducted a posterior predictive check by comparing the distribution of simulated crash counts (drawn from the posterior predictive distribution) to the actual observed crash counts, aggregated across census block groups [9]. As shown in Figure 2, the model closely replicates the mean and variance of the observed distribution, and the proportion of zero-crash block groups is well-matched, lending confidence to the model’s goodness of fit. While minor deviations remain in the upper tail, indicating occasional high-crash areas, these deviations are minor and not systematically biased.
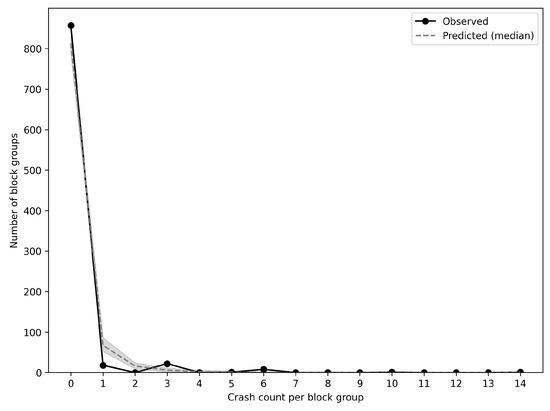
Figure 2.
Comparison of observed (solid black) and model-predicted (dashed gray) crash-count distributions by census block group. A close match, especially at zero and low counts, indicates good model calibration.
4.2. Coefficient Plots and Top Predictors
Figure 3 (coefficient plot) displays the posterior mean and 95% credible intervals (CIs) for each fixed-effect coefficient on the log scale, along with the corresponding incidence rate ratio (IRR) derived by exponentiating the coefficient. Table 1 provides numerical summaries of these results.
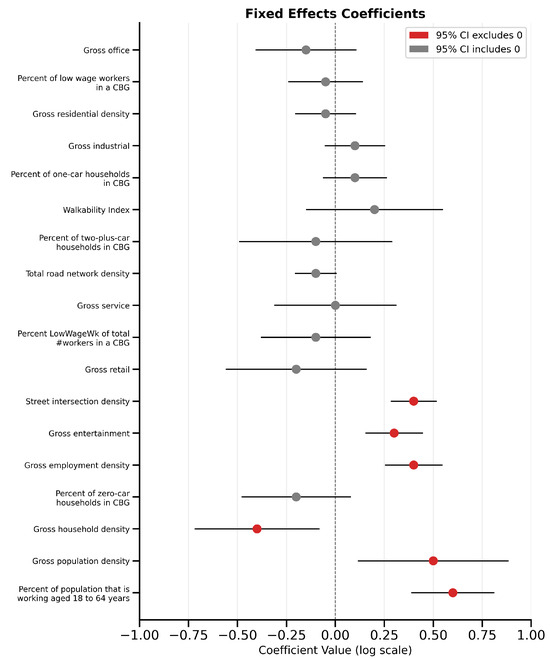
Figure 3.
Posterior mean CSA random intercepts with 95% credible intervals (black lines), indicating regional deviations from the statewide baseline (line at zero). Higher positive values reflect regions with elevated baseline e-scooter crash risk.

Table 1.
Sensitivity of risk index to alternative severity weighting schemes.
Among the demographic variables, the percent of population aged 18–64 emerges as a statistically significant and positive predictor of e-scooter crash risk. Its IRR of approximately 1.55 (95% CI: 1.32, 1.78) implies that about a 10 percentage-point increase in working-age residents corresponds to a 55% higher expected crash count, all else being equal. This aligns with prior research showing that younger adults are the primary adopters of e-scooter services [10], thereby raising local exposure levels.
Vehicle ownership patterns also show nuanced relationships. The percentage of zero-car households has a positive, albeit moderate, effect on crash counts ( CI:1.02, 1.45). This suggests that block groups with a high proportion of car-free households likely have higher micromobility usage, which, in turn, may lead to more e-scooter crashes. Conversely, having a larger share of two-car households is mildly associated with lower crash counts (), though this effect is not as robust statistically. These findings indicate that areas with limited car ownership have a higher reliance on e-scooters and, therefore, a more significant absolute number of crashes [16].
In terms of low-wage employment, the coefficient is slightly negative but not credibly different from zero, indicating minimal direct impact. Conversely, the household density variable has a significant negative coefficient. An IRR of about 0.78 (95% CI: 0.65, 0.92) implies that denser residential environments might have fewer crashes once other variables (like population and job density) are accounted for. This result may initially appear counterintuitive, but it aligns with evidence suggesting that purely residential dense areas (e.g., multi-family housing complexes) may exhibit lower e-scooter crash rates compared to dense commercial zones [19].
4.3. Employment Types, Walkability, and Network Metrics
Employment density by sector reveals some of the clearest patterns in e-scooter crash risk. Entertainment-related employment density stands out with a positive coefficient on the log scale (posterior mean of 0.31; 95% CI: 0.15, 0.44), corresponding to an IRR of about 1.37. Thus, block groups with higher concentrations of entertainment venues (such as bars, restaurants, and theaters) show significantly higher crash counts. This echoes findings from city-level reports attributing a large share of severe e-scooter crashes to entertainment districts, particularly during evening hours [11,15].
In contrast, office employment density shows a less pronounced positive effect (IRR of 1.11), and its 95% CI just crosses 1.0. Although more office jobs do raise e-scooter usage, the effect is modest compared to the entertainment sector. The walkability index also exerts a moderate positive influence (IRR of about 1.25), consistent with the notion that more walkable (and presumably mixed-use) areas attract greater micromobility activity [17].
For network characteristics, total road network density has a weak positive correlationbut with a credible interval that includes zero, suggesting no statistically decisive effect after controlling for other factors. In contrast, intersection density (weighted to exclude auto-oriented intersections) shows a distinctly positive association (IRR of 1.32; 95% CI: 1.14, 1.56). This corroborates the idea that an abundance of intersections introduces additional conflict points and potential crash scenarios for e-scooters as much as it does for bicyclists [14].
4.4. Random Effects and Spatial Patterns
Beyond the fixed effects, the model includes two tiers of random effects: region-level intercepts (for combined statistical areas) and spatially structured effects at the block-group level. Figure 4 visualizes the posterior means for each CSA intercept. Certain metropolitan areas, such as Austin and Houston, show slightly higher baseline crash risk than the statewide average (posterior mean > 0), while others, like Lubbock and McAllen, appear to have lower intercepts. These differences persist even after adjusting for local covariates, indicating that broader regional factors—such as shared infrastructure policies or enforcement practices—may underlie these variations [18].
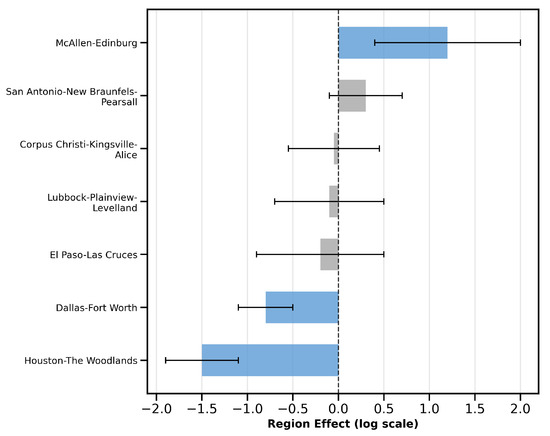
Figure 4.
Posterior mean CSA random intercepts (blue bars) with 95% credible intervals (lines) showing regional deviations from the statewide baseline (dashed line at zero). High positive values indicate regions exhibiting elevated baseline e-scooter crash risk.
Meanwhile, the spatial random effects (modeled with a conditional autoregressive prior [8]) capture local, unobserved heterogeneity across neighboring block groups. Mapping these effects (Figure 5) reveals distinct hotspots of elevated residual risk, typically near city cores or major university districts. In several large cities, the random effects for certain block groups are notably positive, signifying higher crash counts than predicted by the demographics and infrastructure variables alone. Such spatial “excess risk” may reflect factors such as heavy tourist presence, nighttime bar scenes, or street designs that are not fully accounted for by the included metrics. Conversely, pockets of adverse spatial effects suggest that some suburban neighborhoods have systematically fewer crashes, possibly due to limited scooter adoption or subtle environmental advantages.
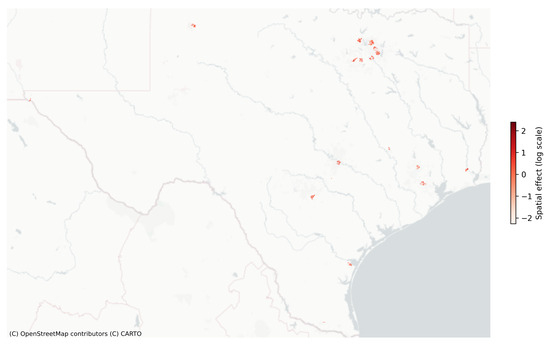
Figure 5.
Map of Texas with block groups colored by posterior mean spatial random effects (log scale). Darker red areas indicate higher residual crash risk after accounting for observed covariates.
4.5. Interpretation and Policy Implications
Overall, the empirical results highlight the combined impact of both human and environmental factors on e-scooter crash risk. Young adult populations and zero-car households elevate usage and, in turn, crash exposure. Entertainment hubs and intersection-rich networks further intensify incidents, likely reflecting a confluence of high traffic flow, complex interactions, and evening social activities. Conversely, high household density in purely residential contexts appears somewhat protective, presumably because it is not coupled with large commercial or mixed-use zones. These relationships align with prior micromobility research indicating that urban form and land-use composition are decisive in explaining crash outcomes [15,19].
From a policy standpoint, the findings suggest prioritizing safety interventions in downtown areas or those with mixed commercial and residential uses, especially in entertainment corridors. Designing e-scooter infrastructure, such as protected lanes and traffic calming measures, around intersection-heavy streets could help mitigate the elevated risks in these complex nodes. Municipalities might also consider collaborative efforts with entertainment businesses to enhance lighting and ensure scooter parking and speed limits are enforced in evening hotspots [17]. At the regional level, the presence of positive random intercepts for certain CSAs suggests that comprehensive citywide or metropolitan policies, such as uniform regulations and rider education, may be necessary. Deploying consistent enforcement or design standards across an entire CSA could address the broad risk elevation observed in such metros.
Finally, the spatial random effects highlight that some localized phenomena remain unexplained by the available covariates. Future work could incorporate micro-level design attributes (e.g., on-street bike lanes and sidewalk conditions) or micromobility fleet data (e.g., usage logs) to refine risk predictions at the block scale. Nevertheless, these results demonstrate that a Bayesian hierarchical approach is highly beneficial for identifying both overarching patterns (e.g., entertainment sector effect) and location-specific deviations (local risk hotspots). Thus, the methodology provides a nuanced view of how demographics, land use, and street design converge to shape e-scooter safety within and across metropolitan areas.
4.5.1. Cost of Crashes and Interventions
The observed elevated e-scooter collision risks carry direct and indirect cost implications for society. Traffic crashes already impose substantial social costs (on the order of about 3% of GDP in Europe) [35], and emerging data suggest e-scooter incidents contribute significantly to this burden. For example, a study in Helsinki found that e-scooter injuries in a single year accrued an estimated EUR 1.7 million in combined medical and productivity costs, with a median of EUR 1148 per injury event [36]. In a U.S. trauma center, severe e-scooter injuries likewise averaged around USD 95,000 in medical charges per case [37]. These figures highlight that investments in safety interventions (e.g., protected lanes, helmet promotion, speed controls) could yield economic benefits by averting costly injuries. Therefore, policymakers should incorporate cost–benefit frameworks into micromobility safety planning, ensuring that resources are allocated to interventions with the greatest potential to reduce crash expenses and harm [35,36]. Comparative assessments of shared e-scooters even indicate that crash costs can outweigh their societal benefits if safety issues remain unaddressed [38], underscoring the urgency of proactive safety measures.
4.5.2. Targeted Rider Education and Training
The model results also highlight the importance of targeted education or training programs for e-scooter users, particularly adult riders in high-activity areas. Many e-scooter trips cluster in employment-dense downtowns or entertainment districts, where a combination of high usage and risk factors (e.g., traffic mixing, nighttime riding, and possible alcohol use) elevates crash likelihood [39]. Implementing focused safety campaigns in these zones can raise riders’ risk awareness and skills. Notably, a recent systematic review highlighted a “marked absence of road training” for e-scooter users and endorsed the need for training programs to improve riders’ risk perception and reduce dangerous behaviors [40]. Cities could collaborate with employers, scooter operators, and local businesses to deliver adult-oriented safety training (for instance, helmet use incentives, riding etiquette workshops, or in-app education modules) tailored to the contexts of commuters and nightlife patrons. Evidence from crash analyses indicates that combining engineering measures with rider-focused awareness campaigns helps address prevalent violations and risky behaviors [41]. Therefore, integrating education and enforcement (e.g. targeted outreach in downtown Austin’s nightlife hubs) is a feasible countermeasure to complement infrastructure-based strategies.
4.5.3. Urban Land-Use Adaptation
From a planning perspective, it is essential to acknowledge that underlying land-use patterns (such as the locations of major job centers or entertainment venues) are relatively inflexible in the short term. However, urban planners can still adopt practices to mitigate e-scooter risks in these environments. One approach is to incorporate micromobility considerations into zoning and development guidelines. For example, new mixed-use developments can be required or incentivized to include safe micromobility infrastructure (dedicated e-scooter/bicycle lanes, parking areas, and traffic-calming designs) so that, as land use evolves, safety is built in. Over time, encouraging a more balanced mix of land uses may avoid over-concentrating e-scooter demand in single-purpose districts, thereby dispersing peak risk exposure. Additionally, targeted operational policies can adapt to existing land-use realities: city authorities have started to designate slow-speed or no-scooter zones in crowded pedestrian areas and to impose nighttime riding curfews in bar districts to curb alcohol-related incidents [36]. These planning and policy adaptations recognize that, while land use itself may be static, the management of how e-scooters interact with the urban form can be improved. Notably, studies have observed that e-scooter usage tends to concentrate in city centers, nightlife areas, and campus zones [42]. Mitigating measures—such as geofenced speed limits, improved lighting and pavement in high-traffic zones, and the integration of e-scooter lanes into street redesigns—can, thus, be prioritized in these hotspots. Indeed, improvements in road design and maintenance of infrastructure are consistently cited as fundamental steps to reduce e-scooter crashes [41]. By aligning land development plans and street design standards with micromobility safety needs, cities can gradually reduce the spatial clustering of risk, even if the overall land-use configuration remains unchanged.
4.5.4. Infrastructure Safety Prioritization
Finally, a data-driven approach to infrastructure upgrades is recommended to maximize the impact of safety investments. The Bayesian spatial modeling of crash risk enables the identification of high-risk locations, which can be systematically ranked to guide mitigation efforts. This idea echoes safety management practices in the motorcycle domain. For instance, Ragnoli et al. (2018) developed a “safety ranking” methodology for road segments with heavy powered two-wheeler traffic, using metrics like the Safety Potential (SAPO) to quantify the expected reduction in crash costs from infrastructure improvements [43]. That framework prioritizes interventions in Rome’s urban network by highlighting the road sections where the greatest safety gains (in terms of accident cost savings) could be achieved [43]. Adapting such an approach to e-scooters would involve ranking locations based on a composite of crash frequency, severity, and exposure, then focusing engineering and enforcement measures accordingly. For example, if certain downtown intersections or road segments in Texas show disproportionately high e-scooter collision rates, they would receive a higher safety priority score. Transportation agencies could establish a tiered improvement program—analogous to motorcycle safety audits—where “high-priority” e-scooter zones (perhaps identified by both the model’s risk estimates and observed crash costs) are targeted first for treatments like dedicated lanes, surface quality upgrades, signage, or signal timing adjustments. This prioritization ensures a proactive allocation of resources to the most hazardous locations, following a Vision Zero-style principle of systematically addressing high-risk nodes. In summary, employing an infrastructure safety ranking matrix for e-scooter environments [43]—similar to those proven effective for high-PTW-flow roads—can guide strategic planning and help achieve measurable reductions in e-scooter injuries over time. Each of the above policy considerations (cost–benefit evaluation, user education, land use-aware planning, and risk-based infrastructure ranking) offers a concrete pathway for translating the model’s findings into safer urban micromobility systems.
5. Sensitivity Analysis
To evaluate the robustness of the crash risk model and the derived risk index, we conducted two types of sensitivity analyses. First, we tested the impact of alternative injury severity weighting schemes on the normalized risk index. Second, we simulated a policy scenario involving changes in urban form and travel behavior to assess how hypothetical shifts in car usage, employment density, and nightlife intensity would influence risk estimates and regression coefficients.
5.1. Sensitivity to Severity Weighting
The crash risk index in our model is based on a weighted sum of crashes, where more severe outcomes receive greater weight. This follows standard practice in traffic safety analysis (e.g., EPDO methods [44]), but the specific weights are subjective. To assess whether these choices affect spatial patterns of risk, we defined four alternative weighting schemes:
- Scheme A: Fatal = 12, Serious = 6, Minor = 3, No injury/Unknown = 1;
- Scheme B: Fatal = 8, Serious = 6, Minor = 3, No injury/Unknown = 1;
- Scheme C: Fatal = 10, Serious = 8, Minor = 3, No injury/Unknown = 1;
- Scheme D: Fatal = 10, Serious = 6, Minor = 5, No injury/Unknown = 1.
For each weighting scheme, we recalculated the risk index and normalized it. Spearman rank correlations between each alternative and the original index were computed to evaluate whether the relative risk ranking of block groups changed. Table 1 summarizes the results. All Spearman correlations were above 0.98, indicating that the spatial pattern of risk is stable under reasonable changes in crash weighting. The rankings of high-risk areas are essentially unchanged, validating the robustness of our primary risk index.
Table 1 presents Spearman and Pearson correlation coefficients comparing the original risk index with alternative formulations that assign greater or lesser weights to fatal, serious, or minor injuries. The high correlation values (all Spearman coefficients > 0.98) demonstrate the model’s robustness: spatial risk rankings remain consistent, even under substantial variation in injury severity assumptions.
5.2. Policy Scenario Simulation
To test the contextual sensitivity of our model, we constructed a forward-looking policy scenario reflecting coordinated urban policy interventions. Specifically, for block groups with above-median employment density, we applied the following changes:
- Employment Density: Increased by 20%;
- Car Ownership (% 2+ Cars):Reduced by 10%;
- Bar/Restaurant Density: Increased by 30%.
These adjustments represent a hypothetical but plausible scenario in which urban centers experience job growth, reduced vehicle ownership due to improved public or micromobility options, and a growing entertainment economy. We applied the changes to the dataset and re-estimated the Bayesian hierarchical model using the same structure and priors. Under the adjusted data, we found the following changes in posterior mean coefficients:
- The effect of car ownership increased by approximately 47%, suggesting that in a lower-car environment, relative differences in car prevalence have a greater influence on crash risk.
- The bar/restaurant density coefficient decreased by 22%, potentially indicating saturation or spatial overlap with employment zones.
- The employment density effect decreased by 11%, consistent with diminishing marginal influence.
- The effect of the working-age population remained negligible.
The scenario also resulted in higher predicted risk values in many downtown blocks, aligning with expectations given the more intensive land use. Importantly, the rank order of high-risk areas remained stable, confirming the model’s interpretability and structural robustness. These findings underscore the value of the Bayesian hierarchical model in both retrospective analysis and scenario-based planning.
6. Conclusions
This study developed a rigorous Bayesian hierarchical model to quantify e-scooter crash risk at the block-group level across Texas. By integrating rich crash data from the Texas CRIS database with detailed socioeconomic and built environment covariates, the analysis provided a nuanced understanding of how local context influences crash frequencies. The modeling framework incorporates region-specific random effects alongside a spatially structured conditional autoregressive (CAR) prior for neighboring block groups, enabling the capture of unobserved heterogeneity and spatial dependence in crash risk. This comprehensive approach represents a methodological advancement in e-scooter safety analysis, combining multi-level modeling with spatial smoothing to reflect the complexity of urban crash patterns better.
The results demonstrate that the spatial Bayesian hierarchical model offers superior fit and predictive performance compared to simpler alternatives. Across multiple model specifications, the inclusion of hierarchical structure and spatial effects significantly improved the goodness of fit to the crash-count data, underscoring the importance of accounting for both regional differences and local spatial autocorrelation. The final model’s predictions proved robust and stable, benefiting from the partial pooling of information: even block groups with sparse data yielded reliable risk estimates by borrowing strength from broader regional trends and neighboring areas. This robustness was further evidenced by the consistency of the identified high-risk locations under alternative modeling assumptions, confirming that the model’s risk estimates are not unduly sensitive to specific parameter choices.
In addition to its strong performance, the model revealed valuable insights into the geography of e-scooter crash risk. The spatial random effects identified distinct clusters of elevated risk that align with intuitive high-activity zones. In particular, urban nightlife districts and downtown areas with high employment density emerged as consistent hotspots for e-scooter crashes, even after controlling for the measured covariates. These findings suggest that intense evening activity and concentrated economic centers contribute to greater exposure and interaction among e-scooter riders, vehicles, and pedestrians. Furthermore, block groups characterized by a high proportion of working-age residents were associated with higher crash frequencies. This demographic effect suggests that areas populated by adults in their prime working years, who are likely the predominant e-scooter user base, experience a disproportionately higher number of incidents, reflecting higher usage or exposure in those communities. By capturing such patterns, the spatial hierarchical model not only quantifies risk but also helps illuminate the underlying factors and latent spatial processes influencing e-scooter safety.
The conclusions of recent research conducted in various international contexts differ from those of this work, particularly in terms of factors such as automobile ownership, walkability, and population density. For instance, studies conducted in London [16] and Milan [45] discovered that e-scooter crashes tend to occur in locations that are very walkable and transit-rich. This is not only because of population density; it is also because of increased usage and multimodal activity. In Texas, however, these patterns can be influenced by the local climate and reliance on cars [19]. Similarly, contrary to trends seen in car-oriented American cities, several studies have linked higher crash rates to regions with lower car ownership and higher public transportation use [16]. Inequalities in demographics also surface: Low-income and minority neighborhoods were found to be high-risk areas in London studies, whereas in Texas, young adult populations and arterial exposure are more closely associated with accident risk [16]. Context, data design, and modeling methodology are frequently the causes of these variations. To address sparse or highly localized accident data, other research prefers zero-inflated or geographically weighted models [19]; this study, however, employed a Bayesian spatial framework to account for neighborhood variance and severity weighting. The contrast highlights that e-scooter crash correlations are not universal and that local infrastructure, usage patterns, and analytical decisions all influence modeling results. This highlights the importance of tailoring safety evaluations to the specific spatial and policy context.
E-scooters have emerged as a promising component of sustainable urban mobility, yet their societal benefits involve important trade-offs. For example, replacing car trips with e-scooters can reduce tailpipe emissions, but life-cycle assessments show that manufacturing, deployment, and charging practices can offset these environmental gains [46]. At the same time, safety and equity challenges are evident: inadequate infrastructure (e.g., a lack of safe bike lanes) and safety concerns are frequently cited as barriers to e-scooter use, and these issues can disproportionately affect certain demographic groups of riders [47]. Such concerns are not unique to Texas—cities worldwide face similar micro-mobility safety issues as e-scooter adoption grows [48]. Addressing these challenges requires a multifaceted approach. Improved understanding of rider behavior and vehicle performance can inform targeted interventions [49], and recent research highlights the value of vehicle design enhancements (for instance, larger wheels and integrated turn signals to improve stability). Equally important are supportive policies and infrastructure investments: harmonized regulations, dedicated riding space, and public education campaigns have all been recommended to bolster e-scooter safety [46,48]. Situating our Texas-based findings within this broader context suggests that many of our insights, such as the influence of urban form and infrastructure on crash risk, are likely generalizable to other regions, provided that local conditions are considered. Ultimately, proactively addressing the equity, environmental, and safety dimensions of e-scooter programs will help ensure that this new mode of travel contributes positively to sustainable and inclusive urban mobility.
Overall, this research highlights the value of a Bayesian spatial hierarchical approach in modeling micro-level crash data for emerging mobility modes. The proposed model delivers robust predictions of e-scooter crash risk and successfully delineates both the contributions of observable factors and the impact of latent spatial influences. These contributions strengthen the analytical foundation for understanding e-scooter crash dynamics and demonstrate a robust framework for safety modeling that can be applied to complex urban transportation systems. Future work should incorporate micromobility fleet data (e.g., trip counts, durations, and spatial traces) to calibrate exposure better and refine crash-rate estimates. Additionally, qualitative research methods, such as rider surveys or observational fieldwork, could help explain the behavioral factors underlying localized crash patterns that are not captured by current covariates.
Author Contributions
Conceptualization, N.S.; methodology, N.S. and R.S.; software, N.S., A.A.T. and R.S.; validation, N.S. and A.A.T.; formal analysis, A.A.T.; investigation, N.S.; resources, R.S.; data curation, N.S. and R.S.; writing—original draft preparation, N.S.; writing—review and editing, A.A.T.; visualization, N.S.; supervision, N.S.; project administration, N.S. The authors used AI-based tools, including Grammarly, to enhance the clarity and readability of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the data used for this research comes from a publicly accessible source https://cris.dot.state.tx.us/public/Query/ accessed on 19 June 2025.
Conflicts of Interest
Author Nassim Sohaee is employed by Gradient Systematics LLC, which operates in a field related to this study. The company provided no funding or other support and had no role in the research design, data analysis, manuscript preparation, or the decision to publish. The authors declare no other conflicts of interest.
References
- Das, S.; Hossain, A.; Rahman, M.A.; Sheykhfard, A.; Kutela, B. Case study on the traffic collision patterns of E-scooter riders. Transp. Res. Rec. 2024, 2678, 575–589. [Google Scholar] [CrossRef]
- Sener, I.N.; Koirala, P. In-Depth Examination of E-Scooter Safety: A Case Study of Austin, Texas; Technical Report; Safety through Disruption (Safe-D) University Transportation Center (UTC): Austin, TX, USA, 2023. [Google Scholar]
- Bernier, N. Austin Doesn’t Know How Many People Get Hurt in e-Scooter Crashes, Audit Finds. 2024. Available online: https://www.kut.org/transportation/2024-09-04/austin-tx-e-scooter-crash-accident-safety-data-regulations (accessed on 19 June 2025).
- US Consumer Product Safety Commission. E-Scooter and E-Bike Injuries Soar: 2022 Injuries Increased Nearly 21%. August 2023, 17, 2023. [Google Scholar]
- Shinkle, D.; Wicks, M. States Roll Out Electric Scooter Laws. National Conference of State Legislatures. 2024. Available online: https://www.ncsl.org/transportation/states-roll-out-electric-scooter-laws (accessed on 19 June 2025).
- Liu, Y.; Zhao, Z.; Meng, X. E-Scooter Safety: A Review of Incidence, Risk Factors, and Interventions. Saf. Sci. 2020, 129, 104814. [Google Scholar]
- Shaheen, S.; Cohen, A.; Martin, E. Shared Micromobility: Review and Research Agenda. Transp. Rev. 2019, 39, 341–367. [Google Scholar]
- Besag, J.; York, J.; Mollié, A. Bayesian Image Restoration, with Two Applications in Spatial Statistics. Ann. Inst. Stat. Math. 1991, 43, 1–20. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Trivedi, T.K.; Liu, C.; Antonio, A.L.M.; Wheaton, N.; Kreger, V.; Yap, A.; Schriger, D.; Elmore, J.G. Injuries Associated with Standing Electric Scooter Use. JAMA Netw. Open 2019, 2, e187381. [Google Scholar] [CrossRef]
- Karpinski, E.; Samimi, A.; Wojtanowski, T. Characteristics of Early Shared E-Scooter Fatalities in the United States 2018–2020. Saf. Sci. 2023, 163, 105892. [Google Scholar] [CrossRef]
- Cicchino, J.B.; Kulie, P.E.; McCarthyc, M.L. Injuries related to electric scooter and bicycle use in a Washington, DC, emergency department. Traffic Inj. Prev. 2021, 27, 490–492. [Google Scholar] [CrossRef]
- Yang, H.; Ma, Q.; Wang, Z.; Cai, Q.; Xie, K.; Yang, D. Safety of Micro-Mobility: Analysis of E-Scooter Crashes by Mining News Reports. Accid. Anal. Prev. 2020, 143, 105608. [Google Scholar] [CrossRef]
- Kondo, M.C.; Morrison, C.; Guerra, E.; Kaufman, E.J.; Wiebe, D.J. Where Do Bike Lanes Work Best? A Bayesian Spatial Model of Bicycle Lanes and Bicycle Crashes. Saf. Sci. 2021, 136, 105131. [Google Scholar] [CrossRef]
- White, E.; Sweeney, T.; Gabler, H.C.; Mollenhauer, M.; Broaddus, A.; Sweeney, T.; Robinson, S.; Novotny, A.; Buehler, R. What Factors Contribute to E-Scooter Crashes: A First Look Using a Naturalistic Riding Approach. J. Saf. Res. 2023, 85, 182–191. [Google Scholar] [CrossRef] [PubMed]
- Heydari, S.; Forrest, M.; Preston, J. Investigating the association between neighbourhood characteristics and e-scooter safety. Sustain. Cities Soc. 2022, 83, 103982. [Google Scholar] [CrossRef]
- Tian, D.; Ryan, A.D.; Craig, C.M.; Sievert, K.; Morris, N.L. Characteristics and Risk Factors for Electric Scooter-Related Crashes and Injury Crashes among Scooter Riders: A Two-Phase Survey Study. Int. J. Environ. Res. Public Health 2022, 19, 10129. [Google Scholar] [CrossRef] [PubMed]
- Jiao, J.; Bai, S.; Choi, S.J. Understanding E-Scooter Incident Patterns in Street Network Perspective: A Case Study of Travis County, Texas. Sustainability 2021, 13, 10583. [Google Scholar] [CrossRef]
- Azimian, A.; Jiao, J. Modeling Factors Contributing to Dockless E-Scooter Injury Accidents in Austin, Texas. Traffic Inj. Prev. 2022, 23, 107–111. [Google Scholar] [CrossRef]
- Chengula, T.J.; Kutela, B.; Novat, N.; Shita, H.; Kinero, A. Spatial Instability of Crash Prediction Models: A Case of Scooter Crashes. Mach. Learn. Appl. 2024, 17, 100574. [Google Scholar] [CrossRef]
- Kutela, B.; Mihayo, M.P.; Kidando, E.; Chengula, T.J.; Lyimo, S.M. Spatial Insights into Micro-Mobility Safety: Establishing Optimal Buffers for Scooter Crash Predictions. Digit. Transp. Saf. 2024, 3, 184–190. [Google Scholar] [CrossRef]
- Texas Department of Transportation. Crash Records Information System (CRIS) Data. 2024. Available online: https://www.txdot.gov/data-maps/crash-reports-records/crash-data-analysis-statistics.html (accessed on 1 October 2024).
- U.S. Census Bureau. American Community Survey 5-Year Data (2015–2019). 2020. Available online: https://www.census.gov/programs-surveys/acs (accessed on 15 June 2023).
- Verma, P.; McKenzie, G. Regional comparison of socio-demographic variation in urban E-scooter usage. Environ. Plan. Urban Anal. City Sci. 2024, 51, 1548–1562. [Google Scholar] [CrossRef]
- Hosseinzadeh, A.; Algomaiah, M.; Kluger, R.; Li, Z. Spatial analysis of shared e-scooter trips. J. Transp. Geogr. 2021, 92, 103016. [Google Scholar] [CrossRef]
- Shahin, F.; Elias, W. Risk Perception and Barriers to Electric Scooter Prevalence. Appl. Sci. 2025, 15, 1117. [Google Scholar] [CrossRef]
- Chen, Y.H. Shared E-Scooter Adoption and Mode Substitution Patterns. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2021. [Google Scholar]
- Khan, N.A.; Gurumurthy, K.M.; Davatgari, A.; Mohammadian, A.K.; Auld, J. Exploring the Shared E-Scooter adoption behavior: A case study of Chicago, USA. J. Cycl. Micromobility Res. 2025, 3, 100056. [Google Scholar] [CrossRef]
- Caspi, O.; Smart, M.J.; Noland, R.B. Spatial associations of dockless shared e-scooter usage. Transp. Res. Part Transp. Environ. 2020, 86, 102396. [Google Scholar] [CrossRef] [PubMed]
- Aguero-Valverde, J.; Jovanis, P.P. Spatial analysis of fatal and injury crashes in Pennsylvania. Accid. Anal. Prev. 2006, 38, 618–625. [Google Scholar] [CrossRef] [PubMed]
- Ponicki, W.R.; Gruenewald, P.J.; Remer, L.G. Spatial panel methods and the geography of alcohol-related motor vehicle crash rates in California. Accid. Anal. Prev. 2013, 55, 135–143. [Google Scholar] [CrossRef] [PubMed]
- Lord, D.; Washington, S.; Ivan, J. Poisson, Poisson-gamma and zero-inflated regression models of motor vehicle crashes: Balancing statistical fit and theory. Accid. Anal. Prev. 2005, 37, 35–46. [Google Scholar] [CrossRef]
- Lee, D.; Mitchell, R.; Niranjan, M. Controlling for unmeasured confounding and spatial misalignment in long-term air pollution and health studies. Environ. Model. Softw. 2011, 26, 1647–1655. [Google Scholar] [CrossRef]
- Cheng, W.; Jia, X.; Gill, G. Investigation of Multimodal Crashes Using Full Bayesian Multivariate Spatial-Temporal Models; Technical Report; Department of Civil Engineering, California State Polytechnic University: Pomona, CA, USA, 2018. [Google Scholar]
- Choron, R.L.; Sakran, J.V. The integration of electric scooters: Useful technology or public health problem? Am. J. Public Health 2019, 109, 555. [Google Scholar] [CrossRef]
- Vasara, H.; Toppari, L.; Harjola, V.P.; Virtanen, K.; Castrén, M.; Kobylin, A. Characteristics and costs of electric scooter injuries in Helsinki: A retrospective cohort study. Scand. J. Trauma Resusc. Emerg. Med. 2022, 30, 57. [Google Scholar] [CrossRef]
- Lavoie-Gagne, O.; Siow, M.; Harkin, W.E.; Flores, A.R.; Politzer, C.S.; Mitchell, B.C.; Girard, P.J.; Schwartz, A.K.; Kent, W.T. Financial impact of electric scooters: A review of injuries over 27 months at an urban level 1 trauma center (cost of e-scooter injuries at an urban level 1 trauma center). Trauma Surg. Acute Care Open 2021, 6, e000634. [Google Scholar] [CrossRef]
- Félix, R.; Orozco-Fontalvo, M.; Moura, F. Socio-economic assessment of shared e-scooters: Do the benefits overcome the externalities? Transp. Res. Part Transp. Environ. 2023, 118, 103714. [Google Scholar] [CrossRef]
- Jiao, J.; Bai, S. Understanding the shared e-scooter travels in Austin, TX. ISPRS Int. J. -Geo-Inf. 2020, 9, 135. [Google Scholar] [CrossRef]
- Useche, S.A.; Gonzalez-Marin, A.; Faus, M.; Alonso, F. Environmentally friendly, but behaviorally complex? A systematic review of e-scooter riders’ psychosocial risk features. PLoS ONE 2022, 17, e0268960. [Google Scholar] [CrossRef]
- Longo, P.; Berloco, N.; Coropulis, S.; Intini, P.; Ranieri, V. Analysis of E-Scooter Crashes in the City of Bari. Infrastructures 2024, 9, 63. [Google Scholar] [CrossRef]
- Fazio, M.; Giuffrida, N.; Le Pira, M.; Inturri, G.; Ignaccolo, M. Planning suitable transport networks for e-scooters to foster micromobility spreading. Sustainability 2021, 13, 11422. [Google Scholar] [CrossRef]
- Ragnoli, A.; Corazza, M.V.; Di Mascio, P. Safety ranking definition for infrastructures with high PTW flow. J. Traffic Transp. Eng. (Engl. Ed.) 2018, 5, 406–416. [Google Scholar] [CrossRef]
- Highway Safety Manual; American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2010; Volume 1, Chapters 4–5.
- Longo, P.; Porta, S.; Vitale Brovarone, E. E-scooter Accidents and the Urban Environment: The Case of Milan. 2024. Available online: https://transformtransport.org/research/livable-streets/e-scooter-accidents-and-the-urban-environment-the-case-of-milan/ (accessed on 12 June 2025).
- Hollingsworth, J.; Copeland, B.; Johnson, J.X. Are e-scooters polluters? The environmental impacts of shared dockless electric scooters. Environ. Res. Lett. 2019, 14, 084031. [Google Scholar] [CrossRef]
- Sanders, R.L.; Branion-Calles, M.; Nelson, T.A. To scoot or not to scoot: Findings from a recent survey about the benefits and barriers of using E-scooters for riders and non-riders. Transp. Res. Part Policy Pract. 2020, 139, 217–227. [Google Scholar] [CrossRef]
- Gulino, M.S.; Papini, S.; Zonfrillo, G.; Miklis, P.; Unger, T.; Vangi, D. Enhancing road safety of PLEVs by novel vehicle concepts: A comprehensive investigation on regulations, accident statistics, and perception of riders in Europe. Heliyon 2025, 11, e41129. [Google Scholar] [CrossRef]
- Gulino, M.S.; Zonfrillo, G.; Damaziak, K.; Vangi, D. Exploring performances of electric micro-mobility vehicles and behavioural patterns of riders for in-depth accident analysis. Designs 2021, 5, 66. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).