Abstract
This study investigates fire separation distances as essential means of passive fire protection in building design. The focus is on the inner corner configuration of building exterior walls, which represents the worst-case scenario for façade fire spread outside of a building. The inner-corner configuration appears to increase the intensity of the radiative heat flux due to reflection and reradiation of heat. Comprehensive approaches for determining fire separation distances around the various façade geometries can be found, but none of them is focused on detailed descriptions of the unprotected area in an inner corner. A medium-scale scenario was chosen and was experimentally validated with a radiant panel for a better understanding of heat flux spread. This paper compares the experiment with analytical and numerical models. The analytical model is based on the Stefan–Boltzmann law and the calculated configuration factor as per Eurocode 1. The numerical model combines radiative and convective components of the heat flux because convection is non-negligible near the heat source. Experimental data confirm the prediction based on the numerical and analytical model and show agreement. The final increase in heat flux due to the corner configuration investigated at the medium scale reaches up to 29%.
1. Introduction
Determining fire separation distances is a preventive measure for limiting the spread of fire from the affected fire compartment to another compartment or to an adjacent building. Fire separation distances are usually determined for all unprotected (radiating) areas in facades, which can be a wall without fire resistance, a wall with combustible cladding or openings such as windows and doors. This is covered by national standards with precalculated tabulated values or by more or less advanced calculations [1,2,3,4]. Fire spread between buildings is driven by radiative heat transfer, which reaches a greater distance than direct flame or convection [5]. The detailed calculations for determining fire separation distances for a straight facade were described by Law in the 1960s [6]. The calculations were experimentally confirmed by Law [7] and in subsequent studies (e.g., Reichel [8], Webster and Smith [9], etc.) and they remain valid [1,2,3,4].
The detailed calculation [1,2,3,4] neglects the influence of flame radiation. The influence of flame radiation was experimentally evaluated by Law [7] and by Webster and Smith, who observed that the influence could be 20% for small windows and, for larger windows, only 2% of the total amount of received radiation. Convective heat transfer is neglected because its influence is limited to the nearby surroundings of the radiating façade. Ignition by radiation can occur at substantially greater distances [3].
Law described two calculation methods for recessed and set-back facades [6], which are still in use according to the British building regulations [4]. The Enclosing Rectangles method uses the equivalent radiator (the plane of reference) where unprotected areas are projected. A similar solution was presented by Collier in 1996 [5] and by Reichel in 1979 [10]. The Enclosing Rectangles method may cause significant overestimation in a corner area of the building. The second method, the Aggregate National Area method, considers individual view factors on the relevant boundaries. This method can provide more accurate results for unprotected areas in the inner corner of buildings, but it may still be conservative at some locations. Oversizing, as a result of complex methods for determining the fire separation distance, can limit the design of a building or can exclude the placement of unprotected areas.
This paper is focused on a specific configuration of the building façade—an inner corner area—which is potentially the worst-case scenario for fire spread [11]. The side wall effect, which occurs in the corner, has been investigated in recent studies and changes the behaviour of external heat transfer. Lu et al. [12] investigated window flame projection in a wide vertical channel formed by two side walls with different widths of the side walls and changing heat release rates (HRR). The room with a heat source had a square window with a side of 0.15 m and 0.20 m. The study found the effect of side walls on the flame height and the room temperature. The change in heat flux was not investigated. The study was compared with numerical calculations carried out by Duny et al. [13] and found good agreement. Another study was carried out by Fang et al. [14]. This study had a similar setup as Lu et al. [12]. The window was square with a side of 0.15 m and rectangular with 0.10 m width and 0.20 m height. The study confirmed the effect of flame height projection with changing HRR, wind conditions and side wall distance. Heat fluxes were not measured. Another study, by Tang et al. [15], focused on the influence of two parallel (side) walls on the geometric parameters of the flame and the radiative heat flux measured in one of two parallel walls. The heat fluxes were measured with eight Smidt Boelter radiometers placed in a tree. The changing parameters were the distance between parallel walls, the burner size, the mass flow rate and HRR. The results show increased heat flux with decreasing distance between parallel walls. Similar results were discovered by Lee et al. [16], which tested the changing distance between opposite building walls. The heat fluxes were measured by steel plate gauges at both walls. When the distance between walls decreases, the heat fluxes increase.
Previous studies show the influence of changed boundary conditions, e.g., the side wall. However, none of the presented literature describes changes in heat flux in a horizontal plane caused by the presence of side walls, i.e., the inner corner configuration, which is crucial for determining fire separation distances. Calculations of fire separation distances for corner areas can be conducted utilising complex methods. These methods do not cover the problem in detail, making the final fire separation distance too conservative. The impact of the inner corner configuration is also not well understood. Therefore, this paper focuses on one unprotected area in an inner corner, thereby examining the impact of these specific boundary conditions. This configuration can be essential for position verification of two adjacent windows of different fire compartments or restrictions on combustible exterior constructions and claddings. It is expected that the presence of the side wall will contribute to the overall radiation intensity and, therefore, increase the required separation distances. The objective of the presented research is to quantify this contribution and evaluate how accurately the available calculation approaches cope with this phenomenon. This study is closely related to the design of buildings, which can ensure higher safety conditions.
This medium-scale study compares the straight wall configuration (SC) as a reference model with the corner configuration (CC). The side wall creating the corner configuration is placed at the jamb of the unprotected area, representing a window. The experiment serves as a crucial component of this study, with subsequent sections—the analytical solution and the numerical solution—building directly upon the methodologies and configurations established in the experimental phase. This study conducts a comparative analysis of the results obtained from each approach to verify their accuracy and additionally evaluates both configurations (SC and CC) against each other under steady-state conditions.
2. Materials and Methods
The investigation of the described phenomena was reflected in the experimental setup. The SC configuration was represented by a non-combustible wall with one unprotected area. The CC configuration was represented by two abutting perpendicular non-combustible walls, with the unprotected area identical to the SC configuration. Both configurations are illustrated in Figure 1. The investigation was directly focused on one changed condition performed by a non-combustible board placed in the jamb of a radiant panel representing an unprotected area. Only non-combustible materials were used for the walls to prevent them undergoing thermal degradation, deterioration or burning during the experiments.
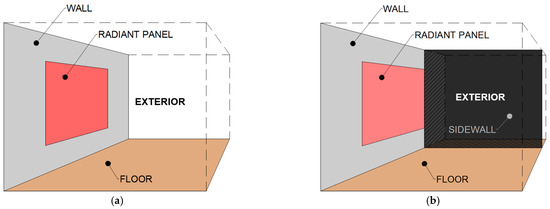
Figure 1.
Two compared configurations (axonometry): (a) straight wall configuration (SC); (b) corner configuration (CC).
2.1. Experimental Setup
The measurements were taken under laboratory conditions under the exhaust hood of the Room Corner Test (RCT, ISO 9705-1 [17]) in its centre. Ventilation was set to the minimum required for safe operation (0.8 m3·s−1) without affecting the experiment by forced convection. The laboratory temperature during tests rose from 20 °C to 24 °C up to 28 °C during the tests. Humidity varied between 36 and 44%. Fire conditions were considered as fully developed, with the radiant panel temperature fixed at approx. 900 °C.
Due to the complexity of the studied area, simplifications had to be applied. The heat source (unprotected opening—window) was represented by a radiant panel, which offers more steady-state conditions than a gas burner and, similarly to the prescriptive design, represents the unprotected area as a single rectangular area with constant temperature conditions throughout the entire area. The heat source was a Kaspo K30 radiant gas panel (Kaspo Praha s.r.o., Sulice-Kamenice, Czech Republic) with an input power of 30 kW. The radiant panel was set to its maximum power to achieve temperature uniformity at the surface. The radiant panel was divided into 12 elements. Each of them was measured to assure identical experimental and numerical evaluation inputs. The radiant panel and its simplification for the numerical calculation are illustrated in Figure 2. The percentage difference between the real and simulated radiant panel surfaces is 1%.
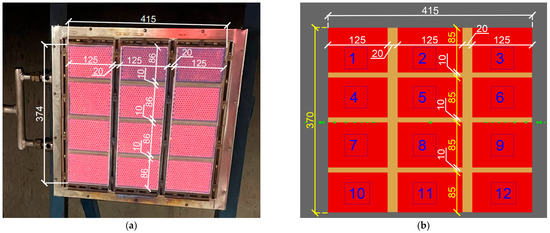
Figure 2.
Radiant panel (all dimensions in mm): (a) real radiant panel; (b) simulated radiant panel (yellow-coloured dimensions = difference between real and simulated panel; blue numbers = positions on the radiant panel).
The walls representing the exterior side of a building facade were constructed from cement-bonded lightweight concrete board with alkali-resistant glass fabric, specifically Fermacell Powerpanel H2O boards (James Hardie Europe GmbH, Düsseldorf, Germany) with a thickness of 12.5 mm. The thermal properties of these boards were [18]:
- Bulk density ρ = 1000 kg·m−3;
- Thermal conductivity λ = 0.17 W·m−1·K−1;
- Thermal capacity c = 1000 J·kg−1·K−1.
The building facade was created as follows:
- The main wall 1250 mm in width and 1000 mm in height in both SC and CC configurations;
- The side wall 1250 mm in width and 1000 mm in height in CC configuration;
- The heat source was placed in the centre of the main wall in both SC and CC configurations.
The floor was made of wooden board due to the ease of drilling and cutting. The floor board served only as a spacing grid for a heat flux sensor holder.
2.2. Technical Equipment
Mavis MTC 10 type K (MAVIS Nový Bor s.r.o., Nový Bor, Czech Republic) sheathed thermocouples (3 mm in diameter) were used to measure the temperatures on the surface of the radiant panel. The differences in radiant panel surface temperatures are shown in Table 1. The surface temperature measurement was performed in advance to eliminate shading of the heat flux sensor. Only one specific surface temperature was checked (Figure 3) during the following tests to verify identical radiant panel conditions. Thermocouples were also used to measure the side wall surface temperature in order to ensure constant thermal conditions in the studied area. Side wall surface temperatures were recorded only at distances of 100 mm at a height corresponding to the centre height of the radiant panel by cable thermocouples with a copper disc end (Mavis AP07543-1, MAVIS Nový Bor s.r.o., Nový Bor, Czech Republic) with a diameter of 10 mm. The thermocouples were covered by 3 mm thick Nefalit fibre boards with dimensions of 30 mm × 30 mm to eliminate the effect of the surrounding gas temperature.

Table 1.
Average temperature on the radiant panel.

Figure 3.
Photo of the real model in CC configuration with an illustration of the measuring grid (red dots = heat flux meter at specific location; blue dots = fixed thermocouples).
Temperatures were also measured by FLIR technology (Forward Looking InfraRed, camera FLIR T1030SC, FLIR Systems, Inc., Wilsonville, OR, USA). The results were used as input for the analytical solution of the CC configuration.
The heat fluxes were measured by a single water-cooled heat flux sensor, Hukseflux SBG01 (Hukseflux Thermal Sensors B.V., XJ Delft, The Netherlands), in the range of 0 to 20 kW·m−2 (the physical limit is 30 kW·m−2). It was not possible to use more than one specific heat flux sensor because they would shadow each other. Also, each heat flux sensor has a measurement uncertainty that contributes to the inaccuracy of the results when multiple sensors measure different positions, especially when the comparison is crucial.
The presented heat flux values were measured at the mid height of the radiant panel, which imposes the highest heat flux according to the Stefan–Boltzmann Law. The floor measuring grid for positioning the heat flux sensor holder was 100 mm × 100 mm. The floor plan and the cross-section are presented in Figure 4. The real model with an insulated heat flux sensor is shown in Figure 3, where the red dot represents the location of the currently measured heat flux. Blue dots represent the locations of the thermocouples—in the centre of the radiant panel, there is a thermocouple for checking the temperature of a specific element and, on the side wall, there are thermocouples for checking the side wall conditions.
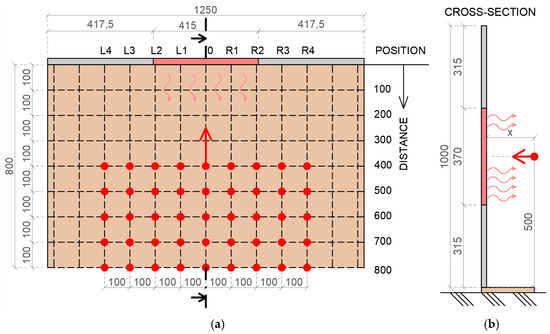
Figure 4.
Drawings of the real model with measuring positions (all dimensions in mm): (a) floor plan; (b) cross-section (red dots = heat flux measuring locations; red arrow = heat flux sensor orientation (normal)).
2.3. Experimental Uncertainties
According to the user manual [19], the SBG01-20 heat flux sensor (Hukseflux Thermal Sensors B.V., XJ Delft, The Netherlands) has a nonlinearity specification of ±2% of the rated measurement range, or 0.4 kW·m−2 in absolute units. The calibration uncertainty is 6.5%, which could cause a maximum deviation of ±1.3 kW·m−2.
The heat flux sensor was placed 500 mm above the wooden floor. The floor temperature rose by about 80 °C at a distance of 400 mm in front of the panel after two hours of measurements. Closer to the heat source, the temperature grew even more. Its effect was calculated by considering this area as a square of 0.4 m × 0.4 m with a temperature of 200 °C (by FLIR analysis, 200 °C was the maximum temperature in this area). This, according to the analytical calculation, could make a 0.2 kW·m−2 difference in the maximum. This influence was neglected in the subsequent comparison.
The thermocouple measurement error is max. 9 °C according to its manufacturer Mavis.
According to the CFD model, heat convection contributed only 0.05 kW·m−2. For further analysis, this impact was neglected.
2.4. Experimentally Measured Data as Inputs into the Subsequent Calculations
The measured temperature values were essential inputs for numerical and analytical solutions to replicate the experiments. The numerical solution depends on the radiant panel temperature. Due to temperature imbalances in the radiant panel, the temperature of each element had to be measured. Each of the 12 radiant panel elements was set as an input to the FDS model for identical repetition.
Based on the studies presented in the Introduction section that pointed to an effect of the presence of the side wall on the room temperature, the measurements were conducted without and with a side wall. Results are presented in Table 1.
The average of the radiant panel temperatures was also used in the analytical solution. For the numerical solution, the side wall temperatures were calculated by the computer model but, for the analytical solution, it was crucial to know the side wall temperatures and their distribution. Throughout the experiments, measurements of the side wall temperature were obtained using FLIR technology in combination with cable thermocouples with copper disc ends. The outcomes established the parameters for subsequent calculations. The side wall temperatures were input to the calculations by the simplification of making rectangles with specific dimensions and temperatures—see Figure 5.
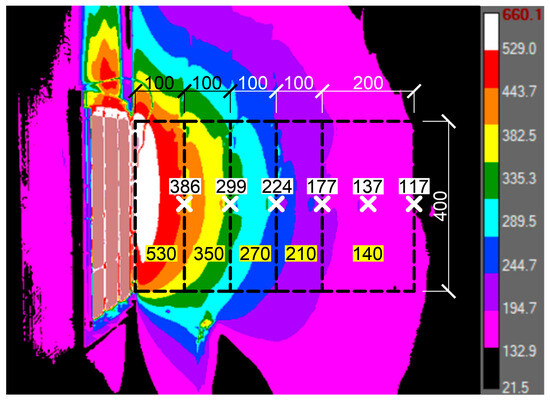
Figure 5.
FLIR output with specification of heated areas at the side wall (white = position of surface disc thermocouples with the measured temperature; yellow = temperature estimation used in the calculations).
2.5. Experimental Procedure
Measurements of both configurations—with the side wall (CC) and without the side wall (SC)—were carried out twice in order to minimise errors. All values were measured at mid height of the radiant panel. Because of the measuring range of the heat flux sensor, the heat flux sensor was placed at distances from 400 mm to 800 mm.
To avoid errors during the measurements, uniform steady-state conditions were set at the start of each experiment. This was achieved by a 1 h preheat period, during which all surfaces achieved a stable temperature and no further fluctuations in measurements were observed. Heat fluxes were measured using the grid (Figure 4) from the farthest to the nearest point in front of the radiant panel. Each position of the heat flux sensor was maintained during the tests for 100 s.
FLIR analysis was conducted with emissivity estimated at 0.9. Cable thermocouples with copper disc ends were used to correct potential discrepancies.
2.6. Numerical Solution
For the numerical solution, the CFD model was employed, namely the Fire Dynamics Simulator (FDS, version 6.8.0). According to a previous case study focused on a sensitivity analysis of the simulation parameters, differences up to 20% were found in comparison to the analytical solution [20]. The selected options for this model based on the previous study and time consumption were set by the following commands:
- NUMBER_RADIATION_ANGLES = 512;
- PATH_LENGTH = 0.4.
Increasing the number of radiation angles is imperative to enhance accuracy when comparing results with experimental data. While the default value in FDS offers greater time efficiency, it leads to the formation of a ray (star-like) effect, which is inappropriate for more accurate comparisons [21,22]. Although the setting of the number of solid angles is five times higher than the default, the ray effect still occurs, and this affects the resulting heat flux values (see Figure 6).
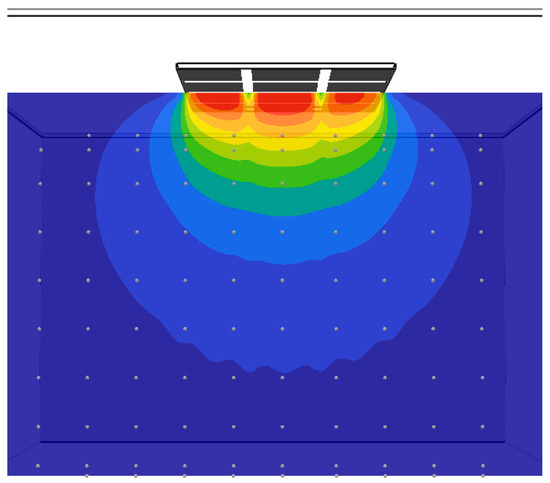
Figure 6.
Visualisation of the ray effect.
FDS was also set up, taking the cell size of the simulation into consideration. The final dimensions of the cells were 10 mm × 10 mm × 10 mm and, compared to 5 mm × 5 mm × 5 mm, this resulted in an average difference of 0.09 kW·m−2. The minimum deviation was −0.54 kW·m−2 and the maximum was 0.12 kW·m−2.
The heat source (a radiant panel) was simulated by the command TMP_FRONT, similarly to the approach used in the FDS Verification Guide [23]. The heat source was created identically with the real radiant panel that was used. It was divided into 12 areas with different temperatures, according to Table 1.
The quantity measured by the heat flux sensor is irradiance (W·m−2) [19], which is defined by EN ISO 13943 as the ratio of the radiant flux incident on a small but measurable element of the surface containing the point, by the area of the element [24]. The heat flux sensor was unshielded during the experiments, which makes it sensitive to the convective heat flux. Numerically, according to the FDS User’s guide, this device can be simulated by command GAUGE HEAT FLUX given by the following equation, where the convective part of the heat flux is taken into account [22]:
where σ is the Stefan–Boltzmann constant (W∙m−2∙K−4) = 5.67∙10−8 W∙m−2∙K−4, εgauge is the sensor emissivity (-), is the incident radiative heat flux (W∙m−2), Tgauge is sensor temperature (set to 20 °C) (°C), and hc is the heat transfer coefficient (W∙m−2∙K−1) (calculated automatically as a function of the local gas temperature and velocity). The GAUGE HEAT FLUX GAS command was used because it measures the same quantity and can be placed freely in space, i.e., represents the real heat flux sensor behaviour.
The second device used for comparing analytical with numerical solutions is set by a command of the RADIATIVE HEAT FLUX GAS, which can also be placed in space without a solid backing. The convective part is calculated as the difference between GAUGE HEAT FLUX GAS and RADIATIVE HEAT FLUX GAS. The equation for RADIATIVE HEAT FLUX GAS is [22]:
where Ts represents the ambient temperature (20 °C) (°C), identical with Tgauge in the GAUGE HEAT FLUX GAS command.
According to the sensitivity analysis, the emissivity of the radiant panel was determined to be 0.94, which corresponds with the experimentally measured data close to the maximum range of the heat flux sensor. The emissivity of the receiver was set to its minimum value of 0.95 [19]. The emissivity of the Fermacell Powerpanel H2O was arbitrarily set at 0.9. In case of other physical properties such as the density, the specific heat capacity and the thermal conductivity, the real values given by the manufacturer were set.
The preheating phase was also necessary in numerical analysis to achieve constant thermal conditions of the gas phase, which was influenced by the radiant panel and heated side wall. Due to time efficiency, nearly steady-state conditions were achieved after 1200 s. At this time the temperature of the side wall was stable for the first half of measured positions. The second half showed the maximum temperature increase of 0.02 °C·s−1 in the last 100 s of the calculation. These conditions ensured that the main attributes—side wall temperature and received heat flux—were stable.
2.7. Analytical Solution
The analytical solution uses standard calculations for radiative heat transfer. The radiative heat flux I in a specific position is calculated using the Stefan–Boltzmann law (Equation (3)) combined with a detailed prediction of the configuration factor (Equation (4)) according to Eurocode 1 [25,26].
where σ is the Stefan–Boltzmann constant (W∙m−2∙K−4) = 5.67∙10−8 W∙m−2∙K−4; ε is emissivity (-); ϕ is the configuration factor (-); TN is the temperature of the burning gases (K) and T0 is the initial ambient temperature (usually 20 °C) (K).
where a = h/s; b = w/s; s is the (separation) distance between the radiating and receiving surfaces (m); h is the height of the segment of the radiating surface (m); w is the width of the segment of the radiating surface (m); and θ is the angle between the emitting and receiving surface.
For the perpendicular configuration of the facade, the CC in this study, the reflected heat flux needs to be solved. The calculation of CC is expanded with Kirchhoff’s law for a diffuse-grey surface, which replaces absorption by emissivity and describes the outgoing heat flux as the sum of the emitted and reflected heat flux. The radiative energy balance of the energy added to the surface is completed when the outgoing heat flux is decreased by the incident heat flux (also called irradiance). If multiple emitting surfaces exist, the sum of the radiation from each surface in the facade represents the incident heat flux to the controlled surface with the corresponding configuration factor [27,28]. Simplified calculations were made using Python programming language (version 3.10.7).
The calculation inputs are based on the experiment. The dimensions and the side wall temperature of each rectangle are specified in Figure 5. The heat source (radiant panel) was simplified to one unprotected area with one temperature and dimensions of 0.4 m × 0.4 m. To compensate the difference of the assumed and the full dimensions (0.415 m × 0.374 m) of the radiant panel area (Figure 2), the percentage of the radiating surface was decreased to 80%. This reduction also accounted for the presence of nonheated structural parts in the panel. The heat source temperatures are based on the experimental measurements of each element of the radiant panel (Table 1). An average temperature of 886 °C was used for SC and 913 °C was used for CC. It is assumed that the steady-state temperature profile of the radiant panel and side wall included mutually reflected heat.
The emissivity values were set identically with the numerical solutions. The calculation grid was established with dimensions of 100 mm × 100 mm. Calculations were performed at the height corresponding to the centre of the heat source (radiant panel).
3. Results
This part is focused on an evaluation of the results produced by the approaches. The complete results of our study can be found in Appendix A (Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11, Table A12, Table A13, Table A14, Table A15, Table A16, Table A17, Table A18, Table A19, Table A20, Table A21 and Table A22). The comparison between the two configurations takes the form of graphs for specific positions—see Figure 7. The chosen positions were the jambs of the radiant panel (positions L2 and R2), its centre (position 0), and position R1, which was the experimentally measured position that was closest to the side wall. With the side wall in place, it was not possible to position a radiometer at the right jamb (position R2). The numerical solution and the experiment comparison are therefore conducted solely for position R1.
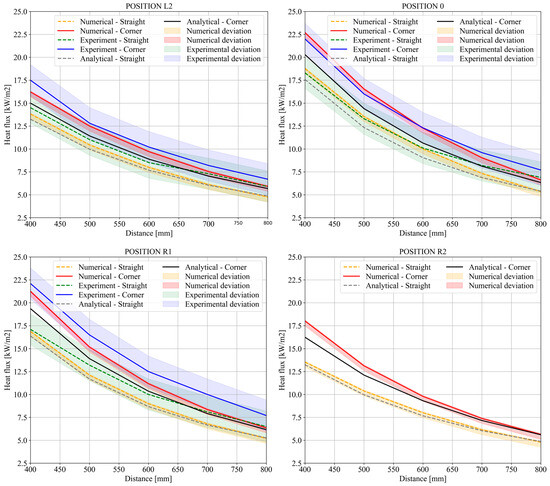
Figure 7.
Comparison of all approaches in selected positions.
Table 2 illustrates the similarity, where especially the analytical approach demonstrates strong agreement with the numerical approach. The statistics describe the whole monitored area, not individual measurement points. Greater differences can be observed in the comparison between the experimental approach and the numerical approach. For the SC configuration, only three measured values are outside the heat flux sensor deviation (positions L4|400 mm, L4|700 mm, and L3|700 mm). In these positions, lower heat fluxes were measured farthest from the corner. For the CC configuration, none of the measured values are outside the heat flux sensor deviation.

Table 2.
A comparison of the approaches (SC = straight wall configuration, CC = corner configuration).
Heat fluxes in the CC configuration are influenced by the side wall temperature. During the experiment, the temperatures were measured by cable thermocouples with a copper disc end at a distance of 100 mm in front of the radiant panel. The FLIR camera also measured the side wall temperature, which was used for temperature estimation in the analytical solution. In the numerical model, the side wall temperature was calculated. The comparison is illustrated in Figure 8.
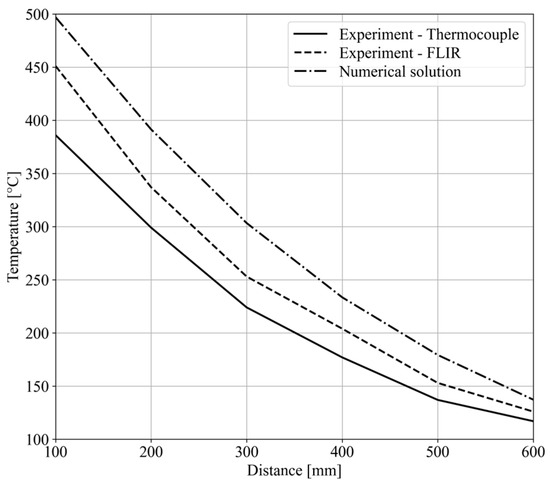
Figure 8.
Temperatures measured on the side wall.
The occurrence of convection was initially numerically investigated. In both configurations, minimal convective heat flux was observed. In the SC configuration, the maximum convective heat flux was calculated at 400 mm from the radiant panel, registering a value of 0.007 kW·m−2, and it decreased further. By contrast, the highest convection heat flux in the CC configuration was noted at position R2, nearer to the side wall. The maximum convective heat flux at position R2|400 mm was 0.038 kW·m−2. In comparison to the SC configuration, a maximum of 0.007 kW·m−2 was observed at 400 mm. With the exception of position R2, the difference between the SC configuration and the CC configuration was lower than 0.002 kW·m−2. The results in the monitored position are almost negligible, and convection is therefore neglected for the following evaluation.
The heat flux increase of the side wall was evaluated using the analytical solution. The simplified model with the estimated temperature distribution (by the rectangles specified in Figure 5) shows a 1.73 kW·m−2 maximum increase and an average 0.59 kW·m−2 increase with 0.35 kW·m−2 of standard deviation in the studied area. This implies that the presence of the side wall, which increases the temperature of the radiant panel, makes a smaller contribution than the radiant panel to the increase in the heat flux. The heat flux from the side wall represents an average of 6% of the total heat flux in the corner configuration, with a 2% standard deviation. The statistics describe the whole monitored area, not individual measurement points.
For all approaches, the greatest increase in the heat fluxes caused by a changed configuration is observed close to the side wall. All values in all approaches decrease exponentially with increasing distance from the radiant panel, which follows the trend of the Stefan–Boltzmann law. The curve shape depends on the distance from the centre of the radiant panel. For the analytical calculation, the maximum increase is 3.0 kW·m−2 in position R1|400 mm and R2|400 mm. The numerical calculation has the maximum increase in the R2|400 mm position and the value is 4.52 kW·m−2. The greatest increase is experimentally measured by the heat flux sensor again in position R1|400 mm, with a 5 kW·m−2 increase.
Generally, in the whole monitored area, the heat flux grows by about 17% with a 2% standard deviation for the analytical solution and by about 22% with a 3% standard deviation for the numerical solution. Experimental validation shows a 17% average growth with a 6% standard deviation. The maximum growth occurs at R2|400 mm, with 23% for the analytical solution and 33% for the numerical solution. The maximum experimentally measured growth is observed in R1|400 mm position with a 29% increase. The minimum growth in the analytical and numerical solutions is observed in L2 and L3 in the 400 mm and R2|800 mm positions, where the increase is only 16–18%. In the experimental solution, the minimum is 5% growth, which is observed at L4|700 mm.
4. Discussion
The difference between the approaches is only indicative and supports correct behaviour of each model. In this section, a comparison between the SC and CC approaches shows the effect of the added side wall and also the drawbacks of each solution.
The heat flux growth was confirmed by three approaches: the analytical, numerical and experimental solutions at all measured points. On average, the heat flux rises by about 20%. All solutions show similar trends in behaviour. However, the observed increase in the percentage configurations differs between the analytical solutions, the numerical solutions and the experimental solutions—see MATLAB R2024b visualisation in Figure 9.
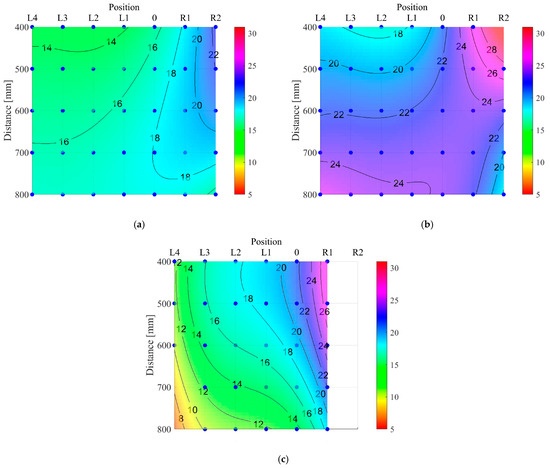
Figure 9.
Percentage increase caused by the side wall and visualisation of the ray effect: (a) analytical solution, (b) numerical solution, (c) experimental solution.
The experimental solution presents smaller growth on the side without the side wall. Compared to the analytical and numerical solutions, the experimentally measured heat flux is higher in position R1. It is assumed that the heat fluxes in position R2 will be even higher.
The observed increase in heat fluxes is caused primarily by the non-combustible side wall placed at the jamb of the radiant panel. The increase is influenced by the temperatures of the radiant panel and the side wall. The mere presence of the side wall also increases the surface radiant panel temperature up to 26.5 °C on average. The surface of the side wall heats to 450 °C in the closest measured point. The side wall also limits the cooling airflow effect from one side.
The configuration and the temperature distribution of the radiating surfaces in each solution were set differently. Analytical solutions represent a simplified, easy-to-use and rapid calculation. The radiant panel represents one area with one temperature. Based on the experimental measurement, the side wall was divided into five rectangles with specified average temperatures. The differences between the analytical evaluation and the experimental evaluation can be caused by simplification and also by inaccurate estimates of the surface temperatures. The difference is 19% on average for the SC configuration and 19% for the CC configuration, but the calculation was made within seconds.
In the numerical solution, the radiant surface temperatures were set according to the experiment, and the side wall temperature was calculated by the model. The difference between the numerical solution and the experimental solution is lower. It is 17% on average for the SC configuration and 16% on average for the CC configuration. Because of the precise radiation solver set, the calculation lasted for weeks.
In contrast, the analytical and numerical calculations show great similarity. For this specific study, convection is minimal and can be neglected. If the surface temperature of the side wall is known, the analytical model provides fast results with minimal deviation.
In the fire safety design of buildings, the radiative heat flux is calculated to determine fire separation distances, which are limited by the critical heat flux. This can range from 12.5 kW·m−2 to 18.5 kW·m−2 depending on national requirements [29]. If the fire separation distances are calculated only according to Equations (3) and (4), without any corner compensation, the underestimation can be significantly greater.
The difference in distances between straight and corner configurations is also significant in all approaches. The increase depends on the investigated line of measurement positions—see Table 3. The chosen critical heat fluxes are 12.5 and 15 kW·m−2. Heat fluxes equal to 18.5 kW m−2 occurred only in the CC configuration. The comparison is made only for the investigated range by reading the values from Figure 7. The maximum increase of 18% on average is observed in position R2 for 12.5 kW·m−2. On average, a minimum increase of 12% is observed in position 0 and L2.

Table 3.
Difference in the configurations for each approach.
5. Conclusions
This study is focused on the change in heat flux in the horizontal plane caused by changed boundary conditions on one side. Heat flux was measured only in the direction perpendicular to the heat source represented by the radiation panel. The boundary conditions were varied by the presence of a wall made from a non-combustible material. All other parameters were the same for straight and corner configurations. Heat radiation intensity was investigated analytically, numerically and experimentally. A medium-scale model was utilised, due to the size of the available radiant panel. This study was based on one window in an inner corner. The numerical model indicated minimal convection contribution to the overall heat flux in measured points. The convection was therefore neglected for the subsequent evaluation. The influence of multiple windows and scaling was not investigated.
Experimental, analytical and numerical approaches show a similar trend and confirm the hypothesis of increasing heat flux in an inner corner of the facade. Each approach has its limitations. Simplification of the radiant panel and the side wall surface temperature progression was used for the analytical solution. The numerical model was set similarly to the experiment, but the calculation was computationally very demanding and time-consuming.
The main conclusions from this study are:
- In all investigated positions, an increase in heat flux caused by the presence of a side wall was observed.
- The surface temperature of the radiant panel rose when the side wall was placed at its side (jamb), due to heat reflection or reradiation.
- The analytical model indicated that the heat flux from the side wall accounts for 6% of the total heat flux in the corner configuration on average, with a 2% standard deviation through all measured positions.
- The analytical and numerical solutions have different heat flux progression shapes compared to the experimental solution. The greatest increase occurred diagonally, starting from the corner of the walls out to the open space. The experimental solution, in contrast, shows maximum growth in the corner, with values decreasing directly towards the open space. This is due to the nature—underlying mathematical models—and the limitations of the calculation approaches used.
- Comparing the SC and CC configurations, the average heat flux increase was about 20%. The maximum growth was observed in the R2|400 mm position, where the analytical solution was an increase of 23% and the numerical solution was 33%. An experimentally measured maximum increase of 29% was observed in position R1|400 mm.
- Ignoring the corner configuration when determining the fire separation distance can generate significant errors. This underestimation generates up to 20% error in the scale studied here.
- Calculating heat reflection from the side wall is a complex problem due to the variability of its temperature. The analytical solution was simplified. The reflection from the side wall is accounted for through a fixed temperature profile of the side wall. Due to the configuration factor, however, the additional heat reflection is minimal and was neglected for the subsequent calculations.
For practical application in determining fire separation distances in the corner area in opposing positions to unprotected areas, the authors do not recommend reducing the configuration factor below 1.0. Furthermore, they note that disregarding the corner configuration leads to underestimation of fire separation distances. Based on the findings, it appears appropriate to increase these distances by 20%. However, scaling was not conducted, so the actual full-scale conditions still need to be confirmed.
This study was limited to the use of non-combustible materials and a radiant panel instead of a burner. It did not evaluate other receiver (heat flux sensor) orientations and changing to the position of the side wall. It would be beneficial to expand the work to include receiver orientation, more accurate determination of material emissivity, measuring the heat flux on the side wall, and further scaling.
Author Contributions
Conceptualisation, D.Š.P., P.H. and V.M.; Methodology, D.Š.P., P.H. and V.M.; Validation, D.Š.P.; Analysis, D.Š.P.; Investigation, D.Š.P.; Resources, D.Š.P. and V.M.; Data Curation, D.Š.P. and P.H.; Writing—Original Draft Preparation, D.Š.P.; Writing—Review and Editing, P.H. and V.M.; Visualisation, D.Š.P. and P.H.; Supervision, P.H. and V.M.; Project Administration, D.Š.P. and V.M.; Funding Acquisition, D.Š.P. and V.M. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented in this paper has been supported by the Grant Agency of CTU in Prague, project no. SGS22/009/OHK1/1T/11.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All results of this study are presented in Appendix A. Source codes are available from the authors on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Complete results are presented in the following tables. Orange colour represents the position of the radiant panel. Grey colour represents the position of the non-combustible Fermacell Powerpanel H2O board.

Table A1.
Analytical solution—straight configuration.
Table A1.
Analytical solution—straight configuration.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 6.19 | 9.45 | 13.24 | 16.36 | 17.57 | 16.36 | 13.24 |
| 500 | 5.61 | 7.74 | 9.96 | 11.69 | 12.34 | 11.69 | 9.96 |
| 600 | 4.91 | 6.31 | 7.67 | 8.68 | 9.05 | 8.68 | 7.67 |
| 700 | 4.23 | 5.18 | 6.04 | 6.66 | 6.88 | 6.66 | 6.04 |
| 800 | 3.63 | 4.29 | 4.86 | 5.25 | 5.39 | 5.25 | 4.86 |

Table A2.
Numerical solution—straight configuration—RADIATIVE HEAT FLUX GAS.
Table A2.
Numerical solution—straight configuration—RADIATIVE HEAT FLUX GAS.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 6.19 | 9.56 | 13.80 | 17.02 | 18.76 | 16.86 | 13.53 |
| 500 | 5.63 | 7.92 | 10.42 | 12.29 | 13.53 | 12.10 | 10.38 |
| 600 | 4.83 | 6.39 | 7.97 | 9.18 | 9.99 | 8.99 | 8.00 |
| 700 | 4.01 | 5.02 | 6.11 | 6.94 | 7.33 | 6.79 | 6.15 |
| 800 | 3.34 | 3.93 | 4.76 | 5.33 | 5.34 | 5.20 | 4.79 |

Table A3.
Numerical solution—straight configuration—GAUGE HEAT FLUX GAS.
Table A3.
Numerical solution—straight configuration—GAUGE HEAT FLUX GAS.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 6.20 | 9.57 | 13.81 | 17.03 | 18.76 | 16.87 | 13.53 |
| 500 | 5.63 | 7.93 | 10.42 | 12.29 | 13.54 | 12.10 | 10.38 |
| 600 | 4.83 | 6.39 | 7.97 | 9.19 | 9.99 | 8.99 | 8.00 |
| 700 | 4.01 | 5.02 | 6.12 | 6.94 | 7.33 | 6.79 | 6.15 |
| 800 | 3.34 | 3.93 | 4.76 | 5.33 | 5.34 | 5.20 | 4.79 |

Table A4.
Experiment—straight configuration.
Table A4.
Experiment—straight configuration.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 8.00 | 10.60 | 14.50 | 16.80 | 18.30 | 17.10 | 14.80 |
| 500 | 7.10 | 9.30 | 11.00 | 13.00 | 13.30 | 13.20 | 11.60 |
| 600 | 6.50 | 7.60 | 8.50 | 9.90 | 10.10 | 10.00 | 9.20 |
| 700 | 6.20 | 6.80 | 7.30 | 8.00 | 8.20 | 8.10 | 7.60 |
| 800 | 4.30 1) | 5.60 | 5.90 | 6.60 | 6.90 | 6.50 | 6.30 |
1) The value is probably incorrectly measured.

Table A5.
Straight configuration—difference between the analytical solution and the numerical solution.
Table A5.
Straight configuration—difference between the analytical solution and the numerical solution.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 0.05 | 0.06 | −0.84 | −0.81 | −1.02 | −0.59 | 0.06 |
| 500 | 0.00 | −0.11 | −0.57 | −0.66 | −1.18 | −0.50 | −0.29 |
| 600 | −0.02 | −0.18 | −0.46 | −0.60 | −1.19 | −0.41 | −0.42 |
| 700 | 0.08 | −0.07 | −0.30 | −0.51 | −0.94 | −0.31 | −0.33 |
| 800 | 0.22 | 0.16 | −0.07 | −0.28 | −0.44 | −0.13 | −0.11 |

Table A6.
Straight configuration—difference between experiment and the numerical solution.
Table A6.
Straight configuration—difference between experiment and the numerical solution.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 1.80 1) | 1.03 | 0.69 | −0.23 | −0.46 | 0.23 | 1.27 |
| 500 | 1.47 | 1.37 | 0.58 | 0.71 | −0.24 | 1.10 | 1.22 |
| 600 | 1.67 | 1.21 | 0.53 | 0.71 | 0.11 | 1.01 | 1.20 |
| 700 | 2.19 1) | 1.78 1) | 1.18 | 1.06 | 0.87 | 1.31 | 1.45 |
| 800 | 0.96 | 1.67 | 1.14 | 1.27 | 1.56 | 1.30 | 1.51 |
1) The value is outside the heat flux sensor maximum deviation (±1.7 kW·m−2).

Table A7.
Straight configuration—numerical solution—convective heat flux.
Table A7.
Straight configuration—numerical solution—convective heat flux.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 0.003 | 0.004 | 0.006 | 0.007 | 0.006 | 0.007 | 0.005 |
| 500 | 0.003 | 0.004 | 0.005 | 0.004 | 0.005 | 0.004 | 0.005 |
| 600 | 0.002 | 0.002 | 0.003 | 0.003 | 0.003 | 0.003 | 0.003 |
| 700 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| 800 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |

Table A8.
Analytical solution—corner configuration.
Table A8.
Analytical solution—corner configuration.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 7.03 | 10.70 | 15.00 | 18.64 | 20.29 | 19.36 | 16.24 |
| 500 | 6.42 | 8.85 | 11.41 | 13.48 | 14.41 | 13.91 | 12.11 |
| 600 | 5.66 | 7.28 | 8.88 | 10.10 | 10.65 | 10.36 | 9.32 |
| 700 | 4.91 | 6.02 | 7.04 | 7.80 | 8.12 | 7.91 | 7.16 |
| 800 | 4.24 | 5.00 | 5.68 | 6.16 | 6.34 | 6.16 | 5.60 |

Table A9.
Numerical solution—corner configuration—RADIATIVE HEAT FLUX GAS.
Table A9.
Numerical solution—corner configuration—RADIATIVE HEAT FLUX GAS.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 7.35 | 11.25 | 16.21 | 20.19 | 22.67 | 21.23 | 18.01 |
| 500 | 6.77 | 9.48 | 12.48 | 14.85 | 16.53 | 15.17 | 13.12 |
| 600 | 5.89 | 7.76 | 9.69 | 11.22 | 12.26 | 11.17 | 9.79 |
| 700 | 4.97 | 6.20 | 7.53 | 8.56 | 9.03 | 8.35 | 7.38 |
| 800 | 4.18 | 4.92 | 5.91 | 6.61 | 6.62 | 6.34 | 5.64 |

Table A10.
Numerical solution—corner configuration—GAUGE HEAT FLUX GAS.
Table A10.
Numerical solution—corner configuration—GAUGE HEAT FLUX GAS.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 7.35 | 11.26 | 16.22 | 20.20 | 22.68 | 21.24 | 18.05 |
| 500 | 6.77 | 9.49 | 12.48 | 14.85 | 16.54 | 15.17 | 13.15 |
| 600 | 5.90 | 7.76 | 9.69 | 11.23 | 12.26 | 11.17 | 9.81 |
| 700 | 4.97 | 6.20 | 7.53 | 8.56 | 9.03 | 8.35 | 7.41 |
| 800 | 4.18 | 4.92 | 5.91 | 6.61 | 6.62 | 6.34 | 5.64 |

Table A11.
Experiment—corner configuration.
Table A11.
Experiment—corner configuration.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 8.60 | 12.40 | 17.50 | 20.20 | 22.00 | 22.10 | X 1) |
| 500 | 8.30 | 10.60 | 12.80 | 14.80 | 16.00 | 16.50 | X 1) |
| 600 | 7.40 | 8.30 | 10.20 | 11.80 | 12.30 | 12.50 | X 1) |
| 700 | 6.50 | 7.50 | 8.20 | 9.20 | 9.60 | 10.00 | X 1) |
| 800 | 5.70 | 6.30 | 6.70 | 7.30 | 7.70 | 7.70 | X 1) |
1) The R2 position could not be measured because of the side wall position.

Table A12.
Corner configuration—difference between the analytical solution and the numerical solution.
Table A12.
Corner configuration—difference between the analytical solution and the numerical solution.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | −0.32 | −0.55 | −1.22 | −1.54 | −2.38 | −1.87 | −1.77 |
| 500 | −0.34 | −0.63 | −1.06 | −1.37 | −2.12 | −1.26 | −1.01 |
| 600 | −0.23 | −0.48 | −0.82 | −1.12 | −1.62 | −0.82 | −0.47 |
| 700 | −0.05 | −0.18 | −0.49 | −0.76 | −0.91 | −0.44 | −0.22 |
| 800 | 0.06 | 0.08 | −0.23 | −0.45 | −0.28 | −0.18 | −0.04 |

Table A13.
Corner configuration—difference between the experiment and the numerical solution.
Table A13.
Corner configuration—difference between the experiment and the numerical solution.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 1.25 | 1.14 | 1.28 | 0.00 1) | −0.68 | 0.86 | X |
| 500 | 1.53 | 1.11 | 0.32 | −0.05 | −0.54 | 1.33 | X |
| 600 | 1.50 | 0.54 | 0.51 | 0.57 | 0.04 | 1.33 | X |
| 700 | 1.53 | 1.30 | 0.67 | 0.64 | 0.57 | 1.65 | X |
| 800 | 1.52 | 1.38 | 0.79 | 0.69 | 1.08 | 1.36 | X |
1) The value represents the accuracy of the chosen emissivity values in FDS.

Table A14.
Corner configuration—numerical solution—convective heat flux.
Table A14.
Corner configuration—numerical solution—convective heat flux.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 0.003 | 0.006 | 0.007 | 0.008 | 0.008 | 0.005 | 0.038 |
| 500 | 0.003 | 0.004 | 0.005 | 0.004 | 0.004 | 0.002 | 0.025 |
| 600 | 0.003 | 0.002 | 0.002 | 0.002 | 0.002 | 0.001 | 0.021 |
| 700 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.000 | 0.027 |
| 800 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |

Table A15.
Difference between configurations—analytical solution.
Table A15.
Difference between configurations—analytical solution.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 0.84 | 1.25 | 1.76 | 2.28 | 2.72 | 3.00 | 3.00 |
| 500 | 0.81 | 1.11 | 1.45 | 1.79 | 2.07 | 2.22 | 2.15 |
| 600 | 0.76 | 0.97 | 1.20 | 1.42 | 1.60 | 1.68 | 1.64 |
| 700 | 0.68 | 0.84 | 1.00 | 1.14 | 1.24 | 1.26 | 1.12 |
| 800 | 0.61 | 0.72 | 0.82 | 0.90 | 0.94 | 0.91 | 0.74 |

Table A16.
Difference between configurations—numerical solution—RADIATIVE HEAT FLUX GAS.
Table A16.
Difference between configurations—numerical solution—RADIATIVE HEAT FLUX GAS.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 1.15 | 1.69 | 2.41 | 3.17 | 3.92 | 4.37 | 4.48 |
| 500 | 1.14 | 1.56 | 2.06 | 2.56 | 3.00 | 3.07 | 2.74 |
| 600 | 1.06 | 1.38 | 1.72 | 2.04 | 2.27 | 2.18 | 1.79 |
| 700 | 0.96 | 1.18 | 1.42 | 1.61 | 1.71 | 1.57 | 1.23 |
| 800 | 0.84 | 0.99 | 1.16 | 1.28 | 1.28 | 1.15 | 0.85 |

Table A17.
Difference between configurations—numerical solution—GAUGE HEAT FLUX GAS.
Table A17.
Difference between configurations—numerical solution—GAUGE HEAT FLUX GAS.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 1.15 | 1.69 | 2.41 | 3.17 | 3.92 | 4.37 | 4.52 |
| 500 | 1.14 | 1.56 | 2.06 | 2.56 | 3.00 | 3.07 | 2.76 |
| 600 | 1.07 | 1.38 | 1.72 | 2.04 | 2.27 | 2.18 | 1.81 |
| 700 | 0.96 | 1.18 | 1.42 | 1.61 | 1.71 | 1.57 | 1.25 |
| 800 | 0.84 | 0.99 | 1.16 | 1.28 | 1.28 | 1.15 | 0.85 |

Table A18.
Difference between configurations—experiment.
Table A18.
Difference between configurations—experiment.
| Distance | Position (kW·m−2) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 0.60 | 1.80 | 3.00 | 3.40 | 3.70 | 5.00 | x |
| 500 | 1.20 | 1.30 | 1.80 | 1.80 | 2.70 | 3.30 | x |
| 600 | 0.90 | 0.70 | 1.70 | 1.90 | 2.20 | 2.50 | x |
| 700 | 0.30 | 0.70 | 0.90 | 1.20 | 1.40 | 1.90 | x |
| 800 | 1.40 1) | 0.70 | 0.80 | 0.70 | 0.80 | 1.20 | x |
1) The value is probably incorrectly measured.

Table A19.
Increase caused by side wall—analytical solution.
Table A19.
Increase caused by side wall—analytical solution.
| Distance | Position (%) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 11 | 13 | 13 | 14 | 15 | 18 | 23 |
| 500 | 15 | 14 | 15 | 15 | 17 | 19 | 22 |
| 600 | 15 | 15 | 16 | 16 | 18 | 19 | 21 |
| 700 | 16 | 16 | 17 | 17 | 18 | 19 | 18 |
| 800 | 17 | 17 | 17 | 17 | 18 | 17 | 15 |

Table A20.
Increase caused by the side wall—numerical solution—RADIATIVE HEAT FLUX GAS.
Table A20.
Increase caused by the side wall—numerical solution—RADIATIVE HEAT FLUX GAS.
| Distance | Position (%) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 19 | 18 | 17 | 19 | 21 | 26 | 33 |
| 500 | 20 | 20 | 20 | 21 | 22 | 25 | 26 |
| 600 | 22 | 22 | 22 | 22 | 23 | 24 | 22 |
| 700 | 24 | 23 | 23 | 23 | 23 | 23 | 20 |
| 800 | 25 | 25 | 24 | 24 | 24 | 22 | 18 |

Table A21.
Increase caused by the side wall—numerical solution—GAUGE HEAT FLUX GAS.
Table A21.
Increase caused by the side wall—numerical solution—GAUGE HEAT FLUX GAS.
| Distance | Position (%) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 19 | 18 | 17 | 19 | 21 | 26 | 33 |
| 500 | 20 | 20 | 20 | 21 | 22 | 25 | 27 |
| 600 | 22 | 22 | 22 | 22 | 23 | 24 | 23 |
| 700 | 24 | 23 | 23 | 23 | 23 | 23 | 20 |
| 800 | 25 | 25 | 24 | 24 | 24 | 22 | 18 |

Table A22.
Increase caused by the side wall—experimental solution.
Table A22.
Increase caused by the side wall—experimental solution.
| Distance | Position (%) | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | L4 | L3 | L2 | L1 | 0 | R1 | R2 |
| 400 | 8 | 17 | 21 | 20 | 20 | 29 | x |
| 500 | 17 | 14 | 16 | 14 | 20 | 25 | x |
| 600 | 14 | 9 | 20 | 19 | 22 | 25 | x |
| 700 | 5 | 10 | 12 | 15 | 17 | 23 | x |
| 800 | 33 1) | 13 | 14 | 11 | 12 | 18 | x |
1) Outlier is not counted into the overall statistics.
References
- ČSN 73 0802; Požární Bezpečnost Staveb—Nevýrobní Objekty ed.2. ÚNMZ: Prague, Czech Republic, 2023.
- STN 92 0201-4:2000 + Z1:2002 + Z2:2006 + Z3:2020 + O1:2020; Požiarna Bezpečnosť Stavieb. Spoločné Ustanovenia. Časť 4: Odstupové Vzdialenosti. ÚNMS SR: Bratislava, Slovakia, 2000.
- National Fire Protection Association NFPA. NFPA 80A. Recommended Practice for Protection of Buildings from Exterior Fire Exposures; National Fire Protection Association: Quincy, MA, USA, 2022. [Google Scholar]
- Chitty, R. External Fire Spread: Building Separation and Boundary Distances, 2nd ed.; IHS BRE Press: Bracknell, UK, 2014. [Google Scholar]
- Carlsson, E. EXTERNAL FIRE SPREAD TO ADJOINING BUILDINGS—A Review of Fire Safety Design Guidance and Related Research; Lunds Tekniska Högskola, Lunds Universitet: Lund, Sweden, 1999. [Google Scholar]
- Law, M. Heat Radiation from Fires and Building Separation; Her Majesty’s Stationery Office: London, UK, 1963. [Google Scholar]
- Law, M. Radiation from Fires in a Compartment; Her Majesty’s Stationery Office: London, UK, 1968. [Google Scholar]
- Reichel, V. Zabraňujeme Škodám—Navrhování Požární Bezpečnosti Staveb—Odstupové Vzdálenosti, 1st ed.; Česká Státní Pojišťovna: Prague, Czech Republic, 1984. [Google Scholar]
- Webster, C.T.; Smith, P.G. The Burning of Well Ventilated Compartment Fires. Part IV. Brick Compartment, 2.4 m Cube; Fire Safety Science: London, UK, 1964; Fire Research Notes 578; Available online: https://publications.iafss.org/publications/frn/578/-1 (accessed on 6 July 2024).
- Reichel, V. Zabraňujeme Škodám—Navrhování Požární Bezpečnosti Staveb—Díl II; Česká Státní Pojišťovna: Prague, Czech Republic, 1979. [Google Scholar]
- ČSN ISO 13785-1; Zkoušky Reakce na Oheň pro Fasády—Část 1: Zkouška Středního Rozměru. ÚNMZ: Prague, Czech Republic, 2010.
- Lu, K.H.; Hu, L.H.; Tang, F.; He, L.H.; Zhang, X.C.; Qiu, Z.W. Experimental investigation on window ejected facade flame heights with different constraint side wall lengths and global correlation. Int. J. Heat Mass Transf. 2014, 78, 17–24. [Google Scholar] [CrossRef]
- Duny, M.; Dhima, D.; Garo, J.P.; Wang, H.Y. Numerical investigation on window ejected facade flames. J. Build. Eng. 2016, 8, 305–312. [Google Scholar] [CrossRef]
- Fang, X.; Ren, F.; Zhang, X.; Sun, X.; Yang, Y.; Hu, L. Facade flame height ejected from opening of a compartment under the coupling effect of side walls and ambient wind. Fire Saf. J. 2020, 112, 102966. [Google Scholar] [CrossRef]
- Tang, F.; Hu, P.; Wen, J.X. Flame evolution and radiation hazards of rectangular fires between two parallel walls. Proc. Combust. Inst. 2023, 39, 3683–3693. [Google Scholar] [CrossRef]
- Lee, Y.-P.; Delichatsios, M.A.; Ohmiya, Y.; Wakatsuki, K.; Yanagisawa, A.; Goto, D. Heat fluxes on opposite building wall by flames emerging from an enclosure. Proc. Combust. Inst. 2009, 32, 2551–2558. [Google Scholar] [CrossRef]
- ISO 9705-1; Reaction to Fire Tests—Room Corner Test for Wall and Ceiling Lining Products—Part 1: Test Method for a Small Room Configuration. ISO: Geneva, Switzerland, 2016.
- James Hardie Europe GmbH Technický List Fermacell Powerpanel H2O. 2016. Available online: https://www.fermacell.cz/cz/ke-stazeni-cs?documentTypeId=48 (accessed on 20 March 2024).
- Hukseflux Thermal Sensors User Manual SBG Series Water-Cooled Heat Flux Sensors. 2023. Available online: https://www.hukseflux.com/uploads/product-documents/SBG_series_manual_v2302_0.pdf (accessed on 2 March 2023).
- Pitelková, D.; Mózer, V.; Hejtmánek, P. Využití CFD při Predikci Požárně Nebezpečného Prostoru. TZB-Info. 2021. Available online: https://www.tzb-info.cz/pozarni-bezpecnost-staveb/23115-vyuziti-cfd-pri-predikci-pozarne-nebezpecneho-prostoru (accessed on 24 January 2022).
- Hostikka, S. Development of Fire Simulation Models for Radiative Heat Transfer and Probabilistic Risk Assessment; VTT Publications: Espoo, Finland, 2008; Volume 683, 103p. [Google Scholar]
- McGrattan, K.; Hostikka, S.; Floyd, J.; McDermott, R.; Vanella, M.; Mueller, E. Fire Dynamics Simulator—User’s Guide, 6th ed.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2023. [Google Scholar]
- McGrattan, K.; Hostikka, S.; Floyd, J.; McDermott, R.; Vanella, M.; Mueller, E. Fire Dynamics Simulator—Technical Reference Guide Volume 2: Verification, 6th ed.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2023. [Google Scholar]
- EN ISO 13943; Fire Safety—Vocabulary. CEN: Brussels, Belgium, 2017.
- ČSN EN 1991-1-2; Eurokód 1: Zatížení Konstrukcí—Část 1-2: Obecná Zatížení—Zatížení Konstrukcí Vystavených Účinkům Požáru. Český Normalizační Institut: Prague, Czech Republic, 2004.
- Kučera, P.; Kaiser, R.; Pavlík, T.; Pokorný, J. Požární Inženýrství: Dynamika Požáru; Sdružení Požárního a Bezpečnostního Inženýrství: Ostrava, Czech Republic, 2009. [Google Scholar]
- Howell, J.R. Net radiation method in radiative transfer. In Thermopedia; Begell House Inc.: Danbury, CT, USA, 2011. [Google Scholar]
- Siegel, R.; Howell, J.R. Thermal Radiation Heat Transfer, 4th ed.; Taylor & Francis: New York, NY, USA, 2002. [Google Scholar]
- Pitelková, D.; Hejtmánek, P.; Mózer, V.; Vorlíčková, E. Degradation of OSB exposed to the critical heat flux for determination of fire separation distances. AIP Conf. Proc. 2023, 2887, 020040. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).