Super-Resolved Dynamic 3D Reconstruction of the Vocal Tract during Natural Speech
Abstract
:1. Introduction
2. Materials and Methods
2.1. Volunteers and Speech Task
2.2. Data Acquisition
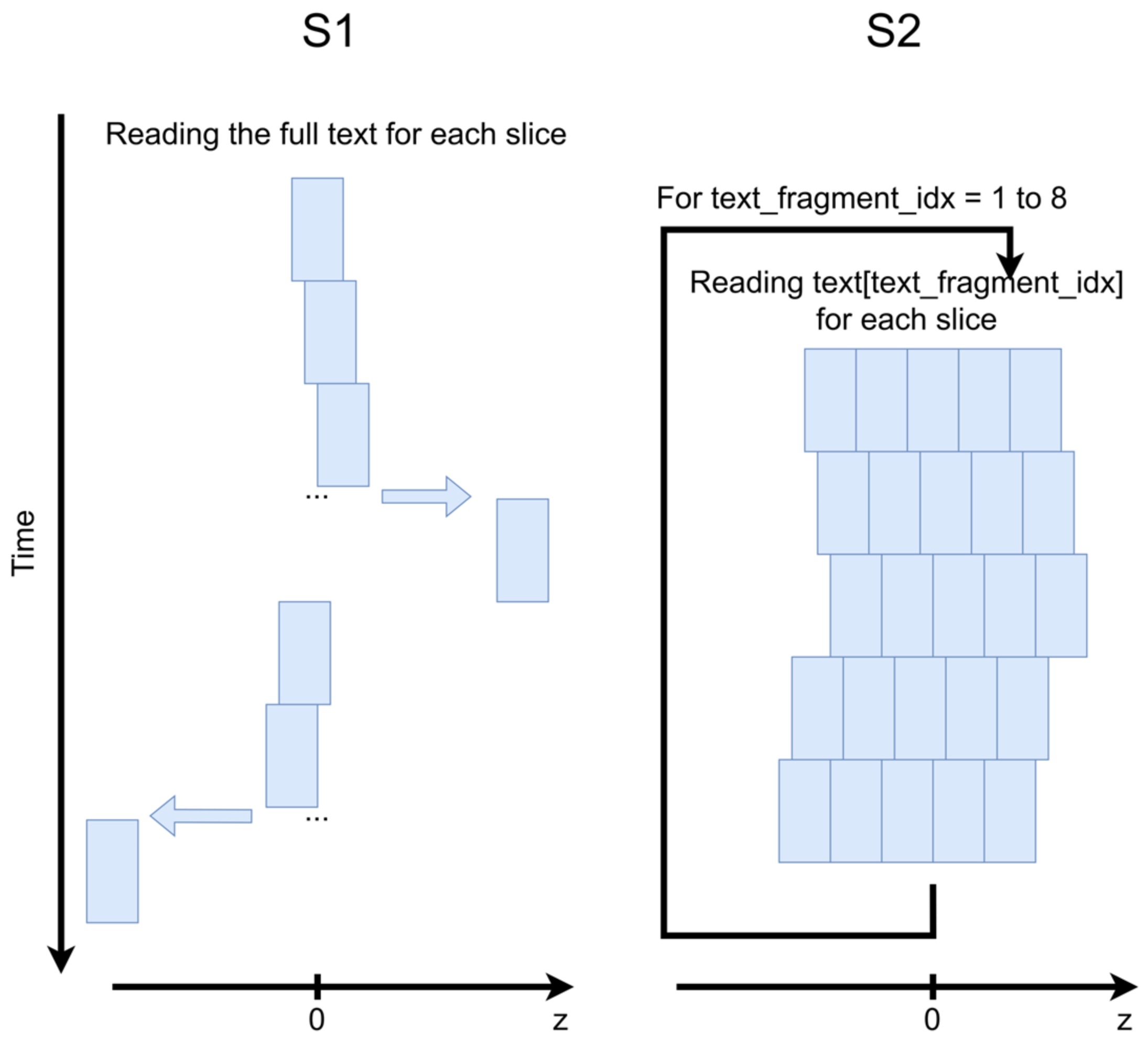
- S1 was reading the integrality of the text repeatedly 25 times. Each repetition covered one slice and lasted approximately 1 min. The acquisition started from the mid-sagittal slice, then all slices on the right from the mid-sagittal slice were acquired, and finally all slices on the left were acquired. The slice placement order was central to lateral for both sides and the shift between the slices was 1.6 mm. The total acquisition duration was 1 h 20 min and 4000 images were acquired for each slice.
- S2 was reading 25 repetitions of a small text fragment and then passed to the next one. The repetitions were divided into 5 groups of 5 slices. Each slice group represented a volume of 5 slices (without any distance between them) which were acquired one after one without temporal breaks. The slice groups had a shift of 1.6 mm in the slice direction between them. S2 had a teleprompting visual support forcing her to keep a similar speech rate during each repetition. The teleprompter was launched manually with sequence start. It should be noted that the acquisition of each data slice required 100 pre-scans. Thus, the acquisition protocol used for S2 introduced a longer dead time between acquisitions. Therefore, only fragments 1 to 5 (which correspond to approximately 60% of the text) could be read by S2 due to the ethical protocol restrictions. In total, 1627 images were acquired for each slice.
2.3. Pre-Processing
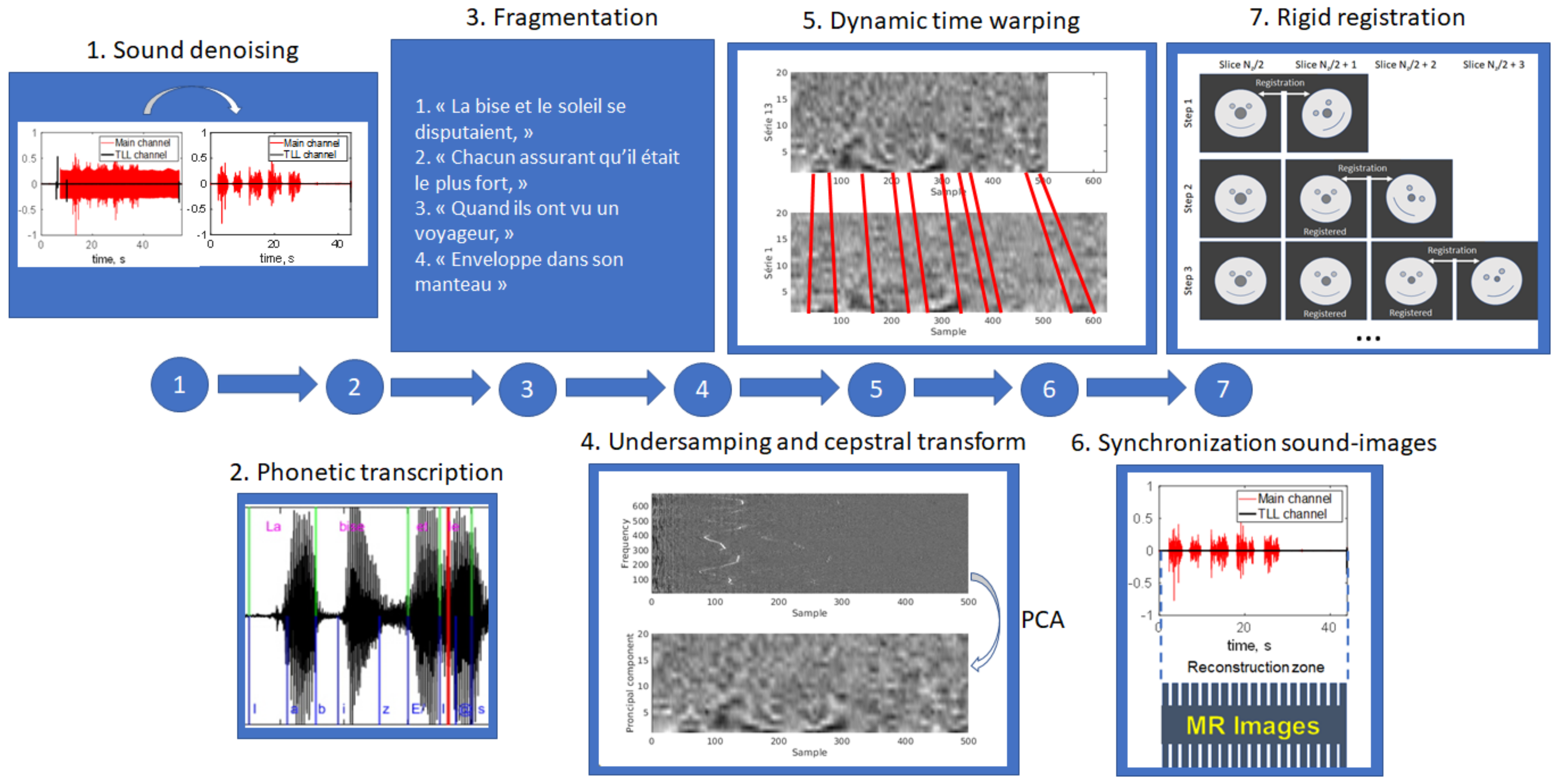
- 1.
- Sound denoising. In order to suppress the MRI acoustic noise, we used a source-separation algorithm described in [27]. The Gaussian-mixture model was trained on the speech sample with MRI noise and on the clear speech sample recorded at the end of the protocol.
- 2.
- Phonetic transcription (applied only to S1). The text and the audio signal were synchronized by a forced alignment automatic French speech recognition system Astali (https://astali.loria.fr/en/ accessed on 8 September 2023).
- 3.
- Text fragmentation. In order to simplify further processing, the text and the corresponding audio recordings of S1 were manually divided on smaller parts which had punctuation or logical pauses between them (“La bise et le soleil se disputaient”, “chaqun assurant qu’il était le plus fort”, “alors qu’ils ont vu on voyageur”, etc.). The resulting fragments are presented in Table S1. The audio recordings corresponding to each volume of S2 were automatically divided into five parts, with each belonging to each separate slice. This was achieved using the TTL signals emitted at the beginning and at the end of each slice and recorded by the SAEC system.
- 4.
- Sound feature extraction. We adopted a strategy similar to that proposed in [20]. Firstly, a MATLAB implementation of cepstral transform [28] was applied to the sound recordings. The cepstrum was then 64-times undersampled to facilitate further processing. Oppositely to Zhu et al. [20] who proposed to keep only some fixed cepstrum frequencies, we selected to reduce the feature number by applying the principal component analysis (PCA). The number of principal components to keep was selected to be 20 based on audial and visual comparison of the synchronization quality.
- 5.
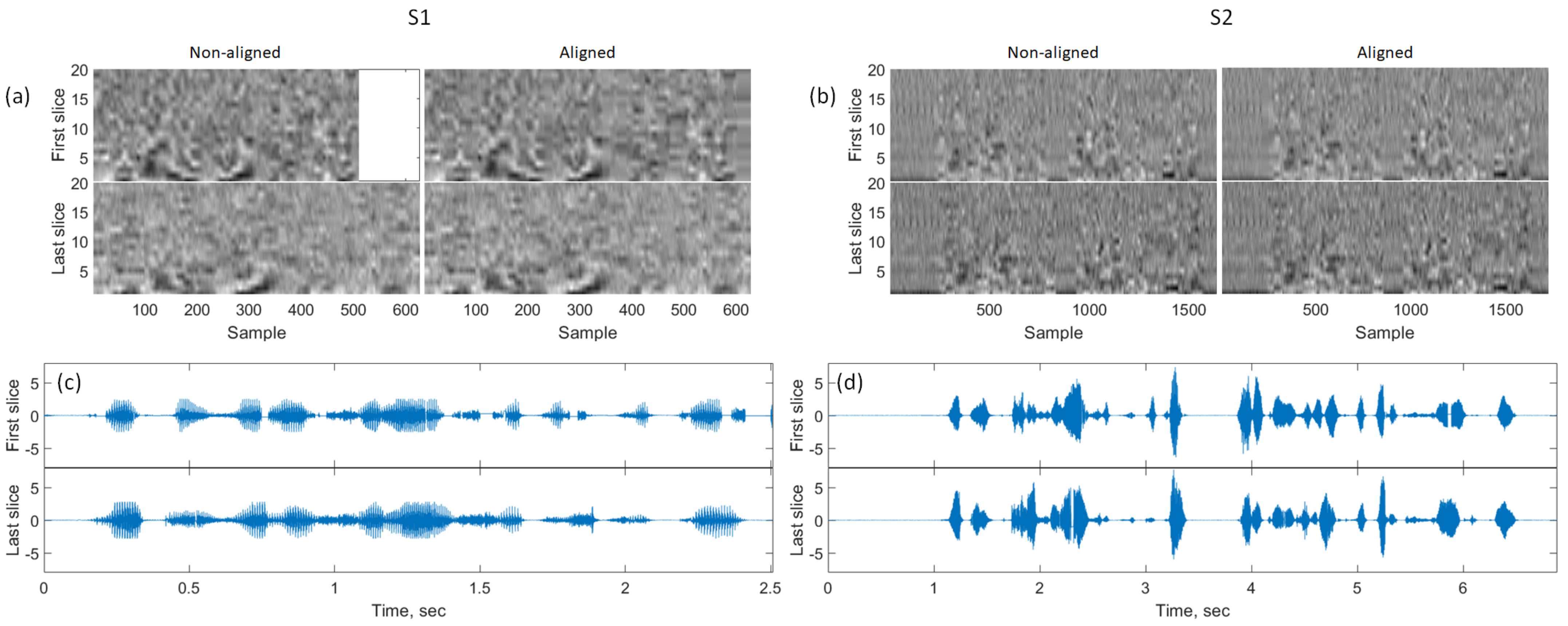
- Dynamic time warping (DTW). Sound recordings of lateral slices were aligned to that of the mid-sagittal slice using dynamic time warping implementation dtw from the MATLAB Signal Processing Toolbox. The DTW algorithm was applied to the undersampled cepstrum. The fully sampled recordings were aligned using a piece-wise approach: the pieces were warped and the sound samples within each piece remained unchanged.
- 6.
- Image-sound alignment. The alignment was performed based on TTL signals recorded by the SAEC system, taking into account the DTW applied to the lateral slices.
- 7.
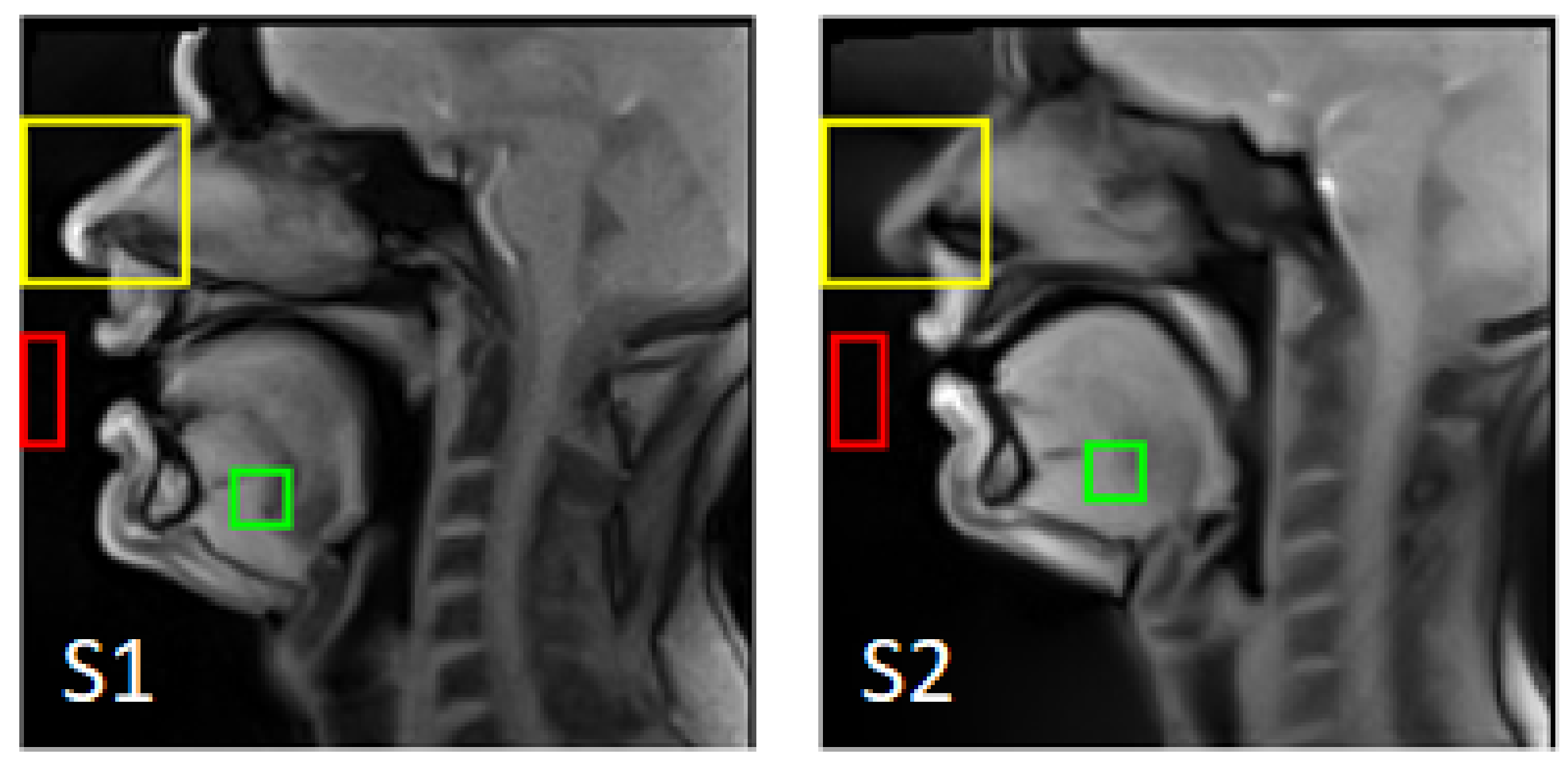
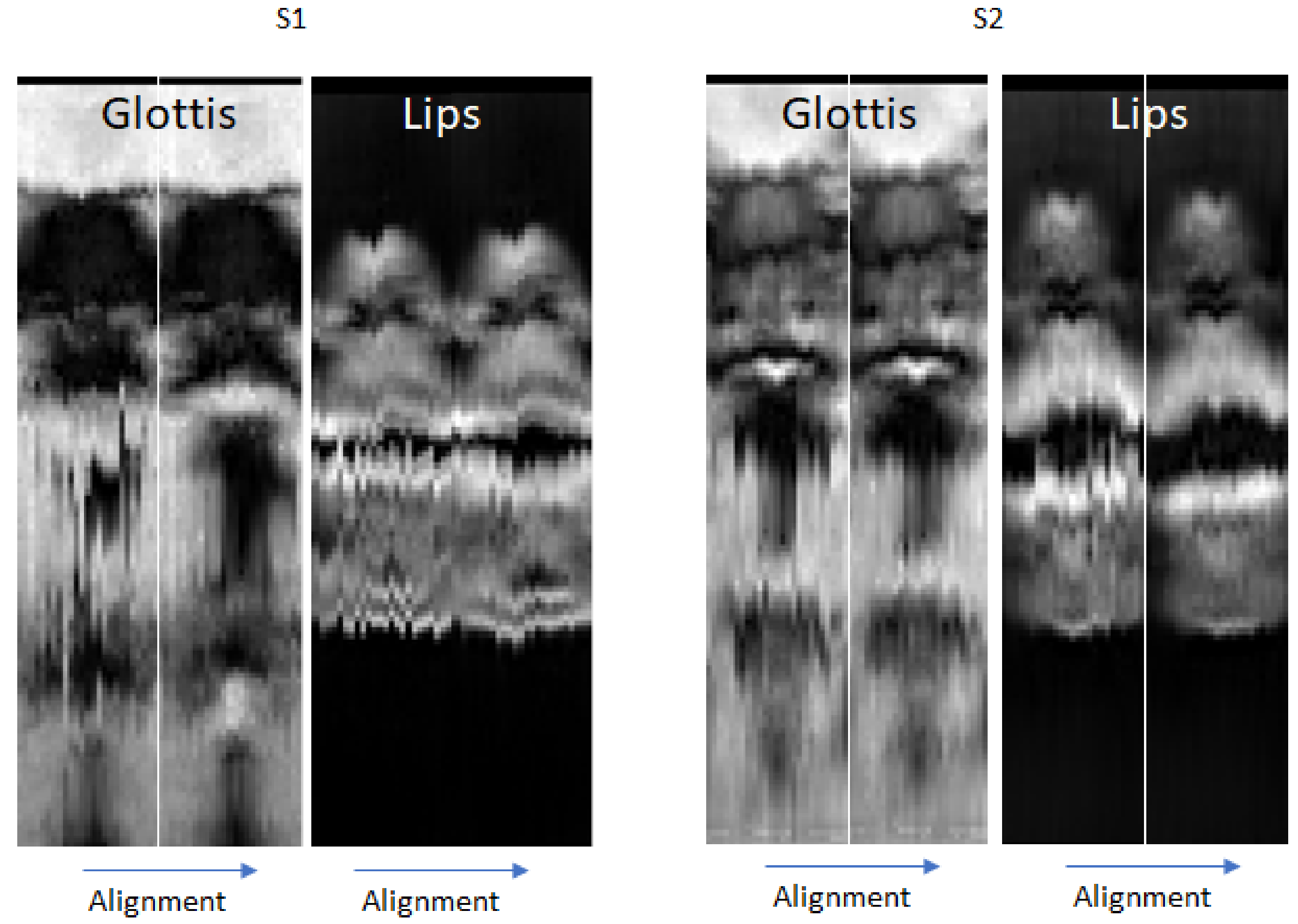
- Rigid registration. Considering the long acquisition time, one can suppose the presence of involuntary head motion. The out-of-plane motion cannot be corrected within the selected multi-slice strategy; however, the in-plane motion can be handled. A region of interest (ROI) including only the subject’s nose (which does not move during speech) was manually selected on the first mid-sagittal image for each subject (see Figure 3). Each lateral slice was registered to the adjacent slice located closer to the center by its translation and rotation:
| For slice = 1 to (N − 1)/2 | |
| Right slices: | , |
| Left slices: | , , |
| end | |
2.4. Super-Resolution
2.5. Validation
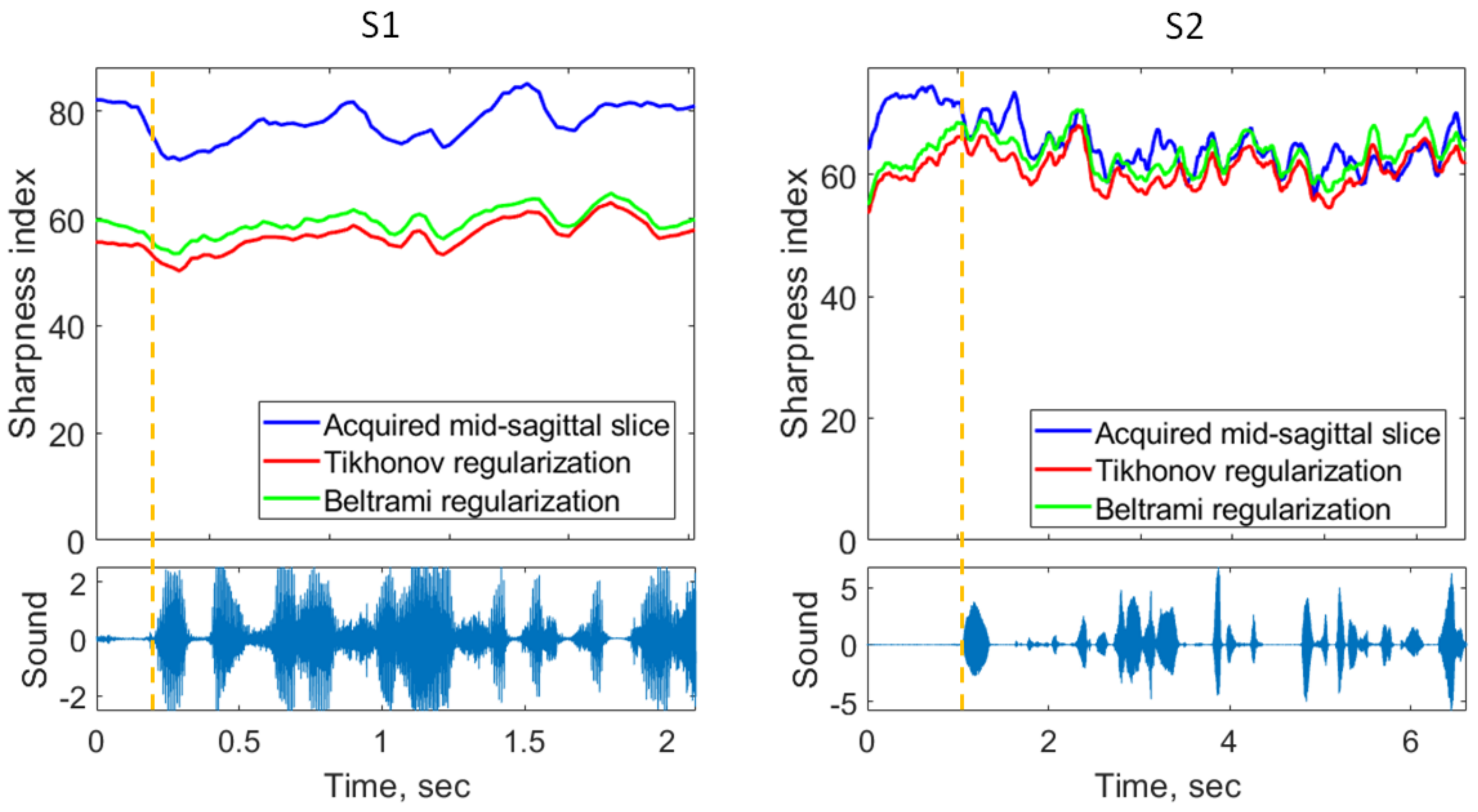
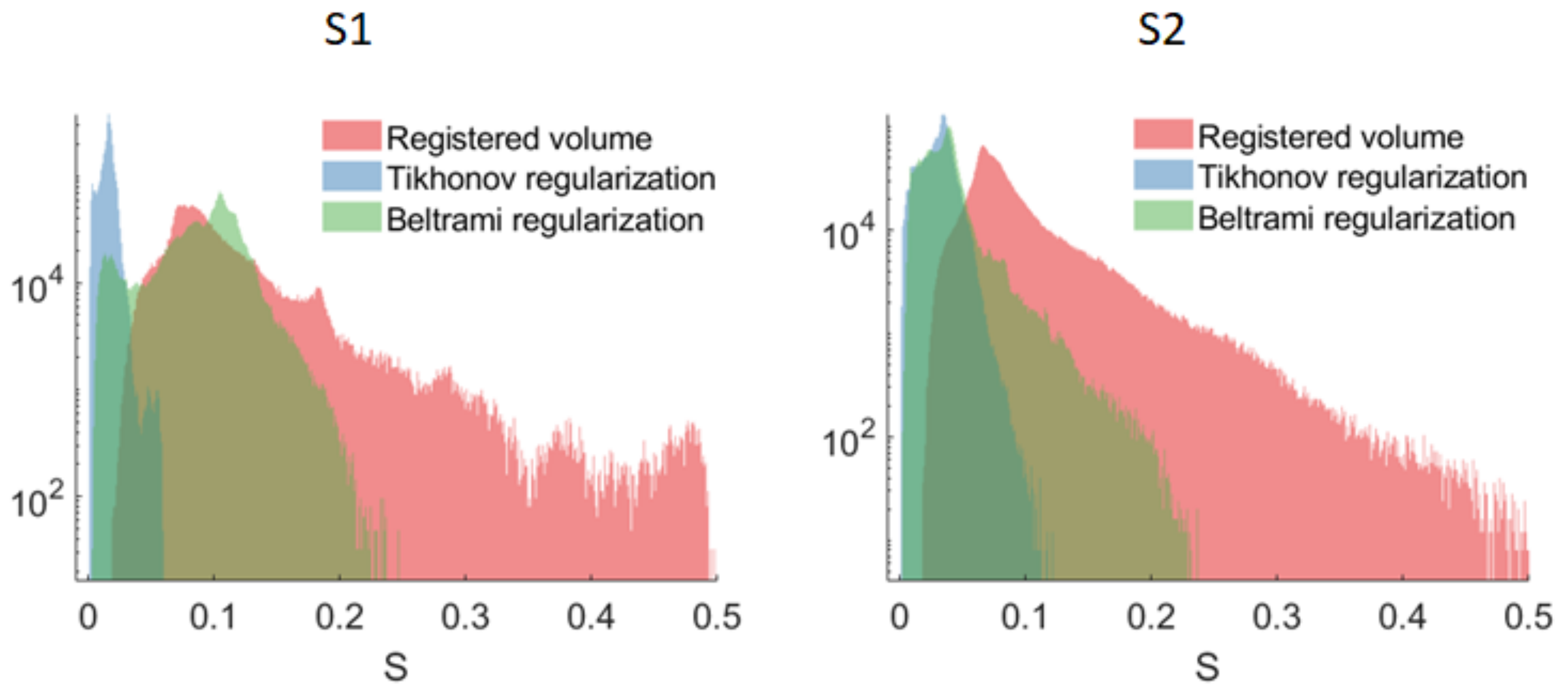
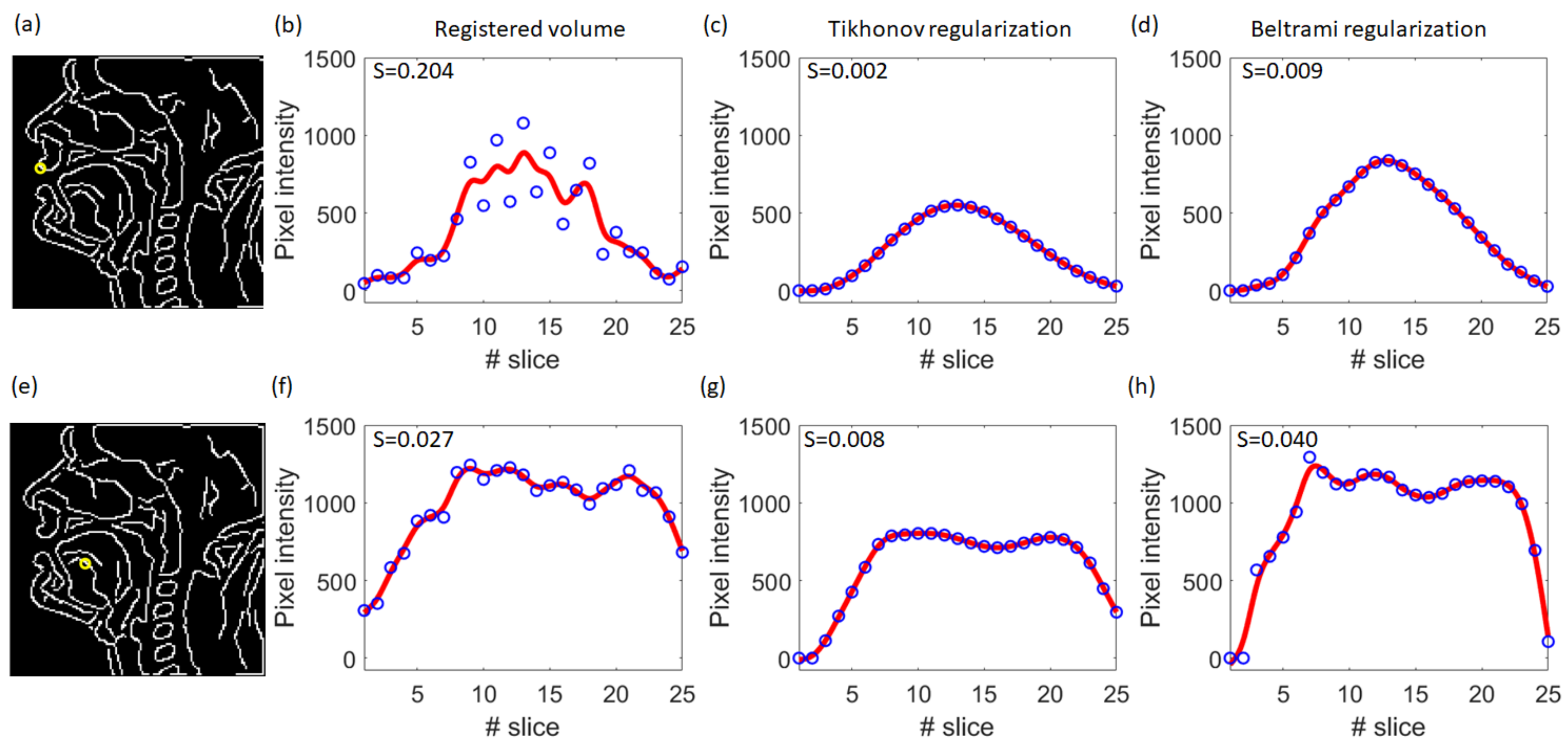
3. Results
3.1. Pre-Processing
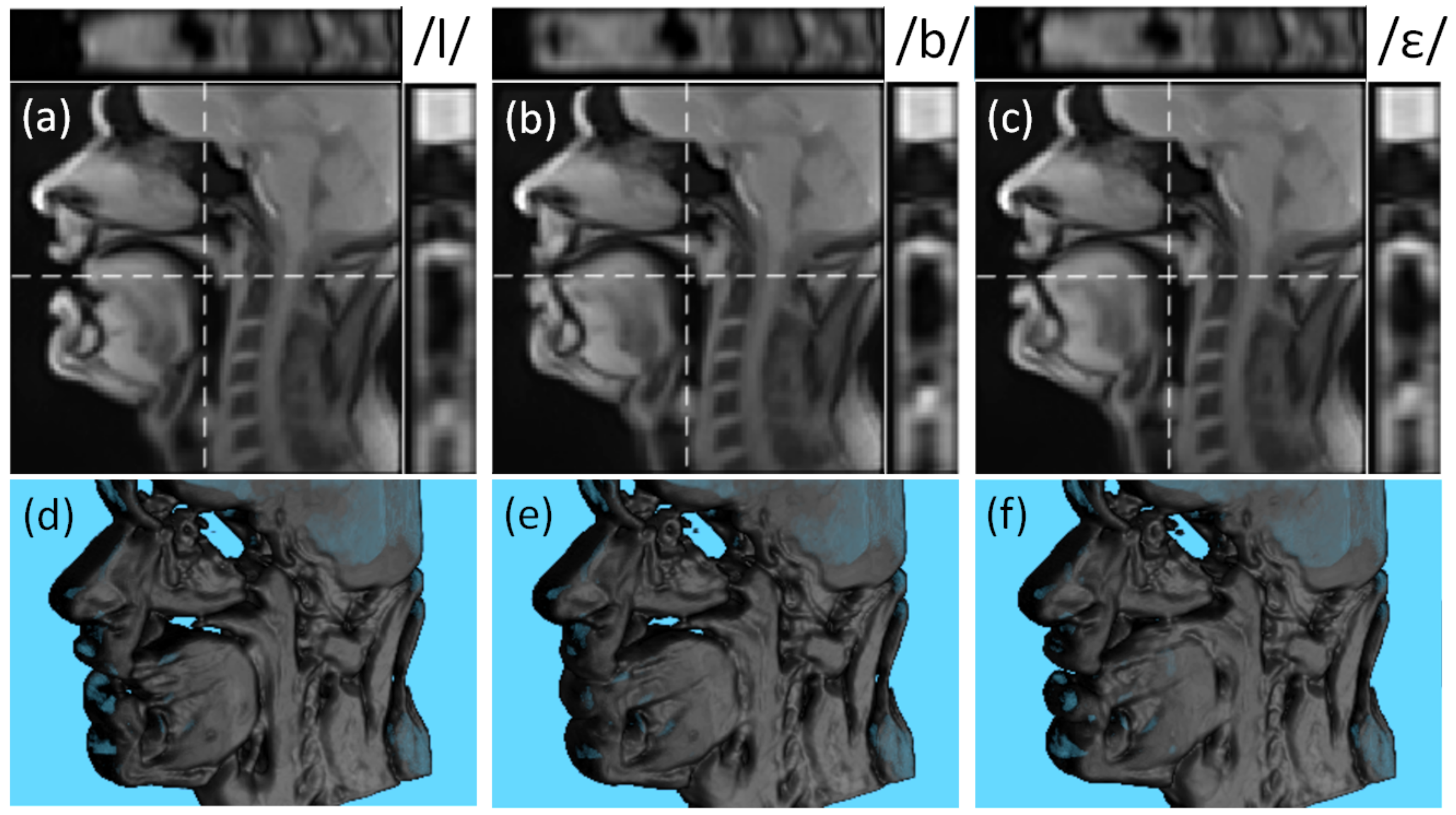
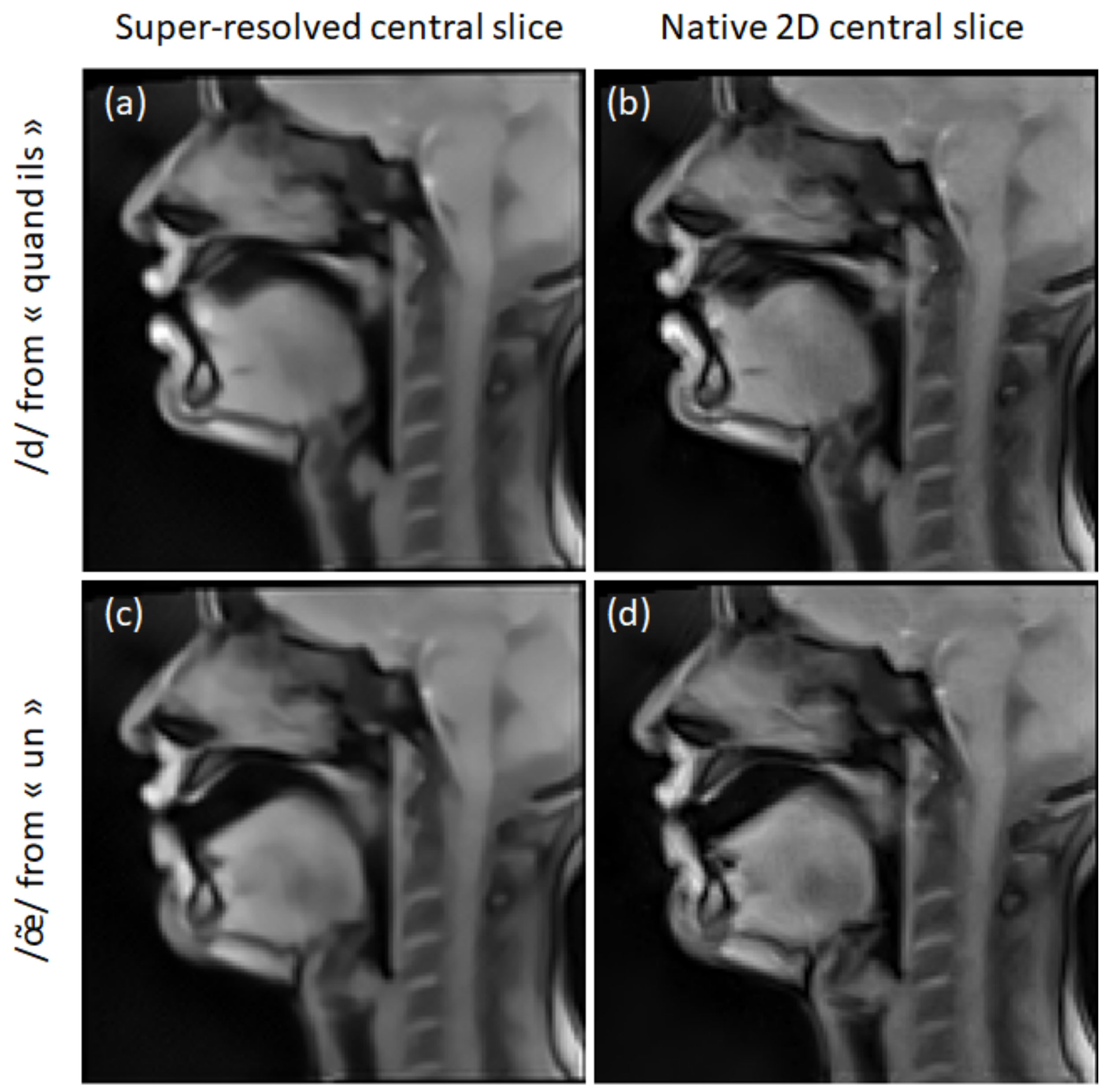
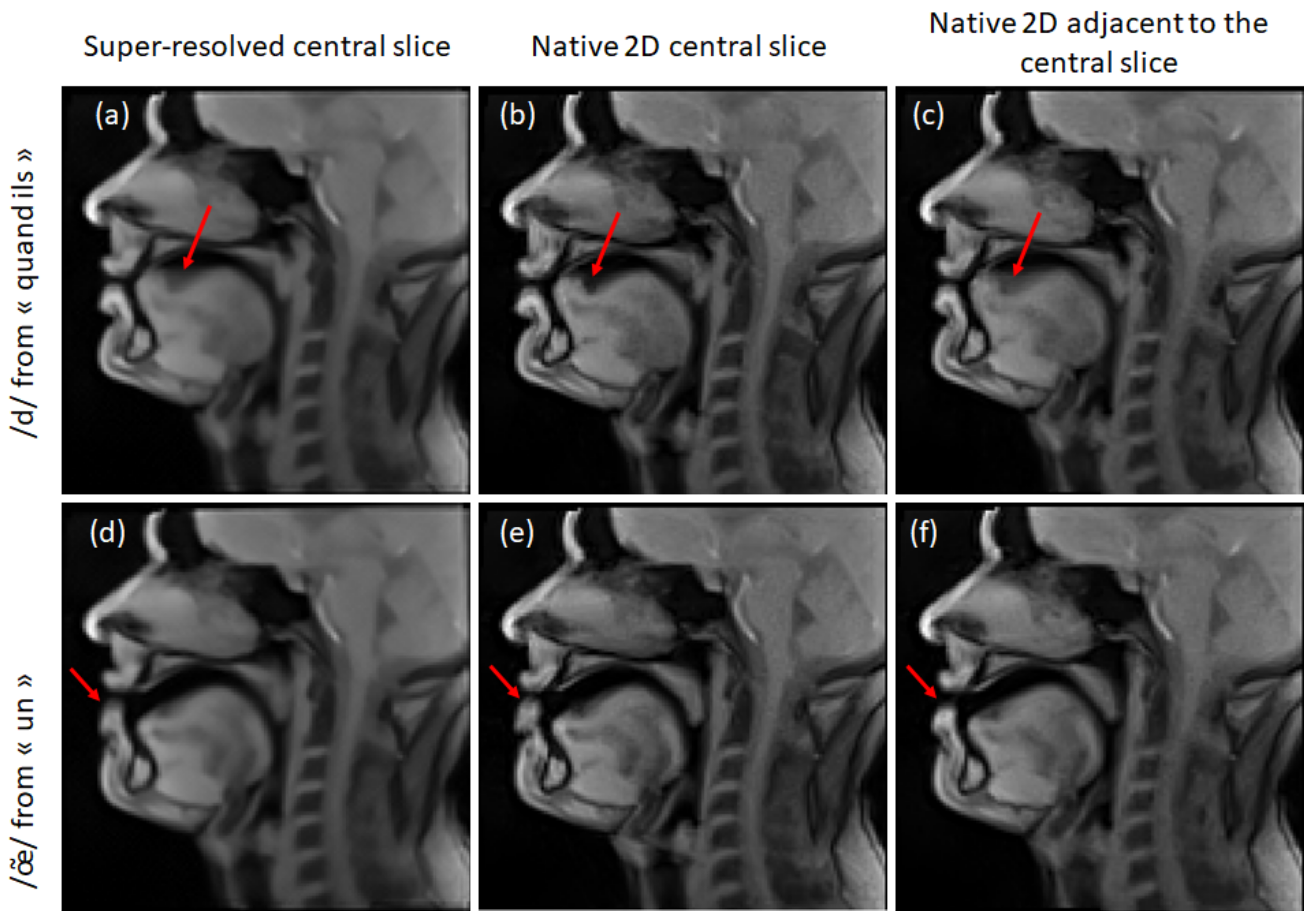
3.2. Super-Resolution
3.3. Comfort
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lingala, S.G.; Sutton, B.P.; Miquel, M.E.; Nayak, K.S. Recommendations for Real-Time Speech MRI. J. Magn. Reson. Imaging 2016, 43, 28–44. [Google Scholar] [CrossRef] [PubMed]
- Katz, W.F.; Mehta, S.; Wood, M.; Wang, J. Using Electromagnetic Articulography with a Tongue Lateral Sensor to Discriminate Manner of Articulation. J. Acoust. Soc. Am. 2017, 141, EL57–EL63. [Google Scholar] [CrossRef] [PubMed]
- Badin, P. Fricative Consonants: Acoustic and X-Ray Measurements. J. Phon. 1991, 19, 397–408. [Google Scholar] [CrossRef]
- Al-hammuri, K.; Gebali, F.; Thirumarai Chelvan, I.; Kanan, A. Tongue Contour Tracking and Segmentation in Lingual Ultrasound for Speech Recognition: A Review. Diagnostics 2022, 12, 2811. [Google Scholar] [CrossRef]
- Fabre, D.; Hueber, T.; Girin, L.; Alameda-Pineda, X.; Badin, P. Automatic Animation of an Articulatory Tongue Model from Ultrasound Images of the Vocal Tract. Speech Commun. 2017, 93, 63–75. [Google Scholar] [CrossRef]
- Masaki, S.; Tiede, M.K.; Honda, K.; Shimada, Y.; Fujimoto, I.; Nakamura, Y.; Ninomiya, N. MRI-Based Speech Production Study Using a Synchronized Sampling Method. J. Acoust. Soc. Jpn. (E) 1999, 20, 375–379. [Google Scholar] [CrossRef]
- Woo, J.; Xing, F.; Lee, J.; Stone, M.; Prince, J.L. A Spatio-Temporal Atlas and Statistical Model of the Tongue During Speech from Cine-MRI. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 520–531. [Google Scholar] [CrossRef] [PubMed]
- Bresch, E.; Yoon-Chul, K.; Nayak, K.; Byrd, D.; Narayanan, S. Seeing Speech: Capturing Vocal Tract Shaping Using Real-Time Magnetic Resonance Imaging [Exploratory DSP]. IEEE Signal Process. Mag. 2008, 25, 123–132. [Google Scholar] [CrossRef]
- Fu, M.; Zhao, B.; Carignan, C.; Shosted, R.K.; Perry, J.L.; Kuehn, D.P.; Liang, Z.-P.; Sutton, B.P. High-Resolution Dynamic Speech Imaging with Joint Low-Rank and Sparsity Constraints. Magn. Reson. Med. 2015, 73, 1820–1832. [Google Scholar] [CrossRef]
- Lingala, S.G.; Toutios, A.; Töger, J.; Lim, Y.; Zhu, Y.; Kim, Y.-C.; Vaz, C.; Narayanan, S.S.; Nayak, K.S. State-of-the-Art MRI Protocol for Comprehensive Assessment of Vocal Tract Structure and Function. In Proceedings of the Interspeech 2016, San Francisco, CA, USA, 8–16 September 2016; pp. 475–479. [Google Scholar]
- Burdumy, M.; Traser, L.; Richter, B.; Echternach, M.; Korvink, J.G.; Hennig, J.; Zaitsev, M. Acceleration of MRI of the Vocal Tract Provides Additional Insight into Articulator Modifications. J. Magn. Reson. Imaging 2015, 42, 925–935. [Google Scholar] [CrossRef]
- Niebergall, A.; Zhang, S.; Kunay, E.; Keydana, G.; Job, M.; Uecker, M.; Frahm, J. Real-Time MRI of Speaking at a Resolution of 33 Ms: Undersampled Radial FLASH with Nonlinear Inverse Reconstruction. Magn. Reson. Med. 2013, 69, 477–485. [Google Scholar] [CrossRef]
- Isaieva, K.; Laprie, Y.; Leclère, J.; Douros, I.K.; Felblinger, J.; Vuissoz, P.-A. Multimodal Dataset of Real-Time 2D and Static 3D MRI of Healthy French Speakers. Sci. Data 2021, 8, 258. [Google Scholar] [CrossRef]
- Lim, Y.; Toutios, A.; Bliesener, Y.; Tian, Y.; Lingala, S.G.; Vaz, C.; Sorensen, T.; Oh, M.; Harper, S.; Chen, W.; et al. A Multispeaker Dataset of Raw and Reconstructed Speech Production Real-Time MRI Video and 3D Volumetric Images. Sci. Data 2021, 8, 187. [Google Scholar] [CrossRef] [PubMed]
- Tsukanova, A.; Douros, I.K.; Shimorina, A.; Laprie, Y. Can Static Vocal Tract Positions Represent Articulatory Targets in Continuous Speech? Matching Static MRI Captures against Real-Time MRI for the French Language. In Proceedings of the ICPhS 2019-International Congress of Phonetic Sciences, Melbourne, Australia, 5–9 August 2019. [Google Scholar]
- Fu, M.; Barlaz, M.S.; Holtrop, J.L.; Perry, J.L.; Kuehn, D.P.; Shosted, R.K.; Liang, Z.-P.; Sutton, B.P. High-Frame-Rate Full-Vocal-Tract 3D Dynamic Speech Imaging. Magn. Reson. Med. 2017, 77, 1619–1629. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Lim, Y.; Byrd, D.; Narayanan, S.; Nayak, K.S. Improved 3D Real-Time MRI of Speech Production. Magn. Reson. Med. 2021, 85, 3182–3195. [Google Scholar] [CrossRef] [PubMed]
- Jin, R.; Shosted, R.K.; Xing, F.; Gilbert, I.R.; Perry, J.L.; Woo, J.; Liang, Z.; Sutton, B.P. Enhancing Linguistic Research through 2-mm Isotropic 3D Dynamic Speech MRI Optimized by Sparse Temporal Sampling and Low-rank Reconstruction. Magn. Reson. Med. 2023, 89, 652–664. [Google Scholar] [CrossRef] [PubMed]
- Douros, I.K.; Xie, Y.; Dourou, C.; Isaieva, K.; Vuissoz, P.-A.; Felblinger, J.; Laprie, Y. 3D Dynamic Spatiotemporal Atlas of the Vocal Tract during Consonant–Vowel Production from 2D Real Time MRI. J. Imaging 2022, 8, 227. [Google Scholar] [CrossRef]
- Zhu, Y.; Kim, Y.-C.; Proctor, M.I.; Narayanan, S.S.; Nayak, K.S. Dynamic 3D Visualization of Vocal Tract Shaping During Speech. IEEE Trans. Med. Imaging 2013, 32, 838–848. [Google Scholar] [CrossRef]
- Rusho, R.Z.; Zou, Q.; Alam, W.; Erattakulangara, S.; Jacob, M.; Lingala, S.G. Accelerated Pseudo 3D Dynamic Speech MR Imaging at 3T Using Unsupervised Deep Variational Manifold Learning; Springer Nature: Cham, Switzerland, 2022; pp. 697–706. [Google Scholar]
- Van Reeth, E.; Tham, I.W.K.; Tan, C.H.; Poh, C.L. Super-Resolution in Magnetic Resonance Imaging: A Review. Concepts Magn. Reson. Part A 2012, 40A, 306–325. [Google Scholar] [CrossRef]
- Delbany, M.; Bustin, A.; Poujol, J.; Thomassin-Naggara, I.; Felblinger, J.; Vuissoz, P.-A.; Odille, F. One-millimeter Isotropic Breast Diffusion-weighted Imaging: Evaluation of a Superresolution Strategy in Terms of Signal-to-noise Ratio, Sharpness and Apparent Diffusion Coefficient. Magn. Reson. Med. 2019, 81, 2588–2599. [Google Scholar] [CrossRef]
- International Phonetic Association. Handbook of the International Phonetic Association: A Guide to the Use of the International Phonetic Alphabet; Cambridge University Press: Cambridge, MA, USA, 1999; ISBN 978-0-521-63751-0. [Google Scholar]
- Uecker, M.; Zhang, S.; Voit, D.; Karaus, A.; Merboldt, K.-D.; Frahm, J. Real-Time MRI at a Resolution of 20 Ms. NMR Biomed. 2010, 23, 986–994. [Google Scholar] [CrossRef] [PubMed]
- Isaieva, K.; Fauvel, M.; Weber, N.; Vuissoz, P.-A.; Felblinger, J.; Oster, J.; Odille, F. A Hardware and Software System for MRI Applications Requiring External Device Data. Magn. Reson. Med. 2022, 88, 1406–1418. [Google Scholar] [CrossRef] [PubMed]
- Ozerov, A.; Vincent, E.; Bimbot, F. A General Flexible Framework for the Handling of Prior Information in Audio Source Separation. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1118–1133. [Google Scholar] [CrossRef]
- Zhivomirov, H. Short-Time Cepstrum (Cepstrogram) with Matlab. 2016. Available online: https://mathworks.com/matlabcentral/fileexchange/59694-Short-Time-Cepstrum-Cepstrogram-with-Matlab (accessed on 8 September 2023).
- Odille, F.; Bustin, A.; Liu, S.; Chen, B.; Vuissoz, P.-A.; Felblinger, J.; Bonnemains, L. Isotropic 3D Cardiac Cine MRI Allows Efficient Sparse Segmentation Strategies Based on 3D Surface Reconstruction: Isotropic Cardiac Cine MRI and Sparse Segmentation. Magn. Reson. Med. 2018, 79, 2665–2675. [Google Scholar] [CrossRef] [PubMed]
- Zosso, D.; Bustin, A. A Primal-Dual Projected Gradient Algorithm for Efficient Beltrami Regularization. Comput. Vis. Image Underst. 2014, 14–52. [Google Scholar]


| Method | S1 | S2 |
|---|---|---|
| Native 2D | 76.3 ± 10.4 | 47.1 ± 7.8 |
| Tikhonov | 95.0 ± 14.1 | 58.5 ± 8.1 |
| Beltrami | 81.0 ± 7.7 | 55.7 ± 6.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isaieva, K.; Odille, F.; Laprie, Y.; Drouot, G.; Felblinger, J.; Vuissoz, P.-A. Super-Resolved Dynamic 3D Reconstruction of the Vocal Tract during Natural Speech. J. Imaging 2023, 9, 233. https://doi.org/10.3390/jimaging9100233
Isaieva K, Odille F, Laprie Y, Drouot G, Felblinger J, Vuissoz P-A. Super-Resolved Dynamic 3D Reconstruction of the Vocal Tract during Natural Speech. Journal of Imaging. 2023; 9(10):233. https://doi.org/10.3390/jimaging9100233
Chicago/Turabian StyleIsaieva, Karyna, Freddy Odille, Yves Laprie, Guillaume Drouot, Jacques Felblinger, and Pierre-André Vuissoz. 2023. "Super-Resolved Dynamic 3D Reconstruction of the Vocal Tract during Natural Speech" Journal of Imaging 9, no. 10: 233. https://doi.org/10.3390/jimaging9100233
APA StyleIsaieva, K., Odille, F., Laprie, Y., Drouot, G., Felblinger, J., & Vuissoz, P.-A. (2023). Super-Resolved Dynamic 3D Reconstruction of the Vocal Tract during Natural Speech. Journal of Imaging, 9(10), 233. https://doi.org/10.3390/jimaging9100233






