A Spatially Guided Machine-Learning Method to Classify and Quantify Glomerular Patterns of Injury in Histology Images
Abstract
:1. Introduction
2. Material and Methods
2.1. Patient Specimens, Digital Image Acquisition and Image Preprocessing
2.2. Ethics Declarations
2.3. Defining Glomerular Injury Patterns and Datasets for Classification
2.4. Workflow of the Study
2.4.1. Multiclass Classification of Glomerular Injury Patterns by a Single Artificial Neural Network-Based Classifier
2.4.2. One-vs-Rest Classification of Glomerular Injury Patterns by Multiple Binary Classifiers
2.4.3. Spatially Guided Multiclass Classification of Glomerular Injury Patterns
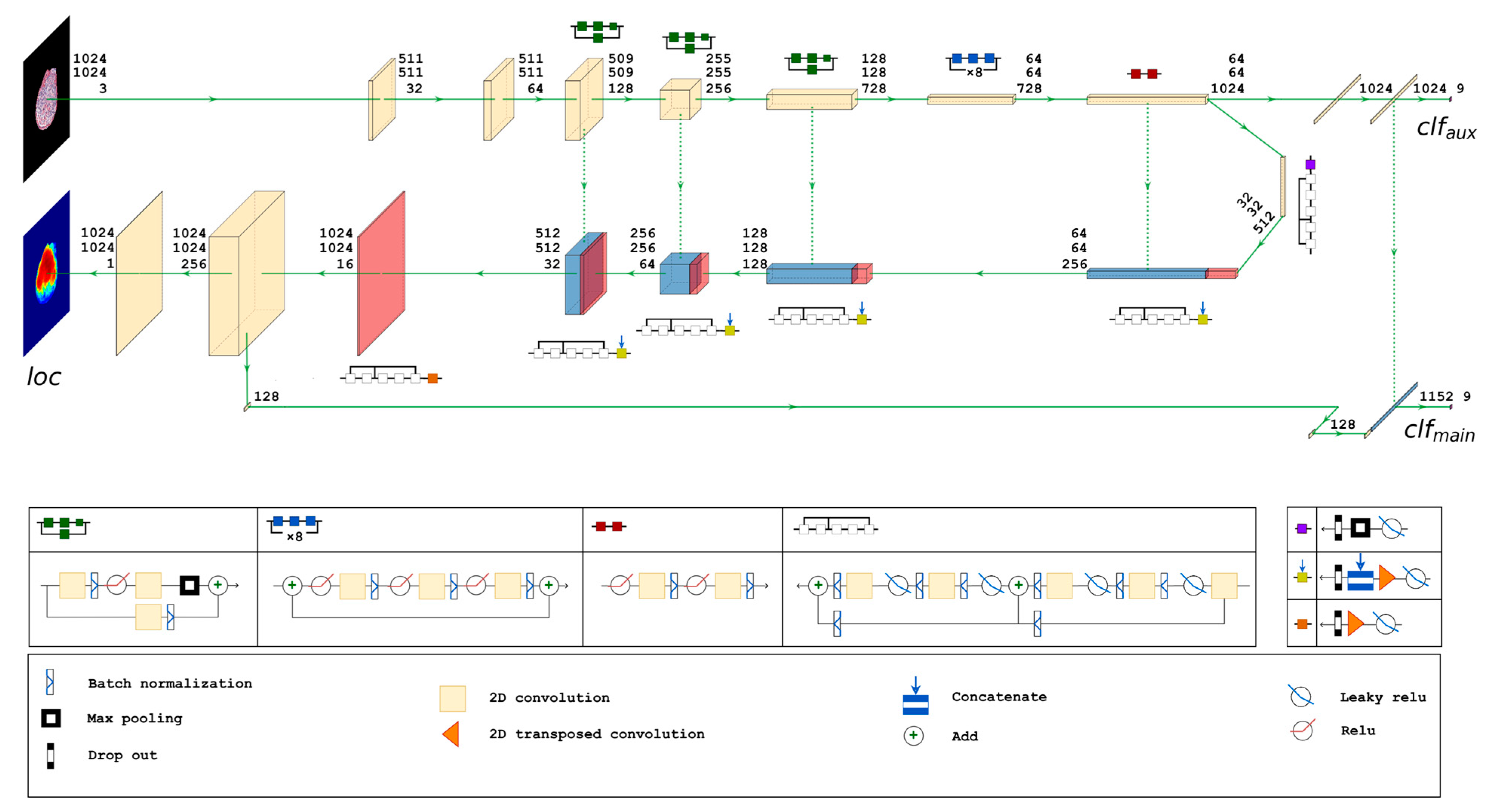
2.4.4. Proposed Neural Network Architecture
2.4.5. Ground Truth Localization Heatmaps
2.4.6. The Cross-Validation Scheme
2.5. Metrics
2.6. Implementation
3. Results
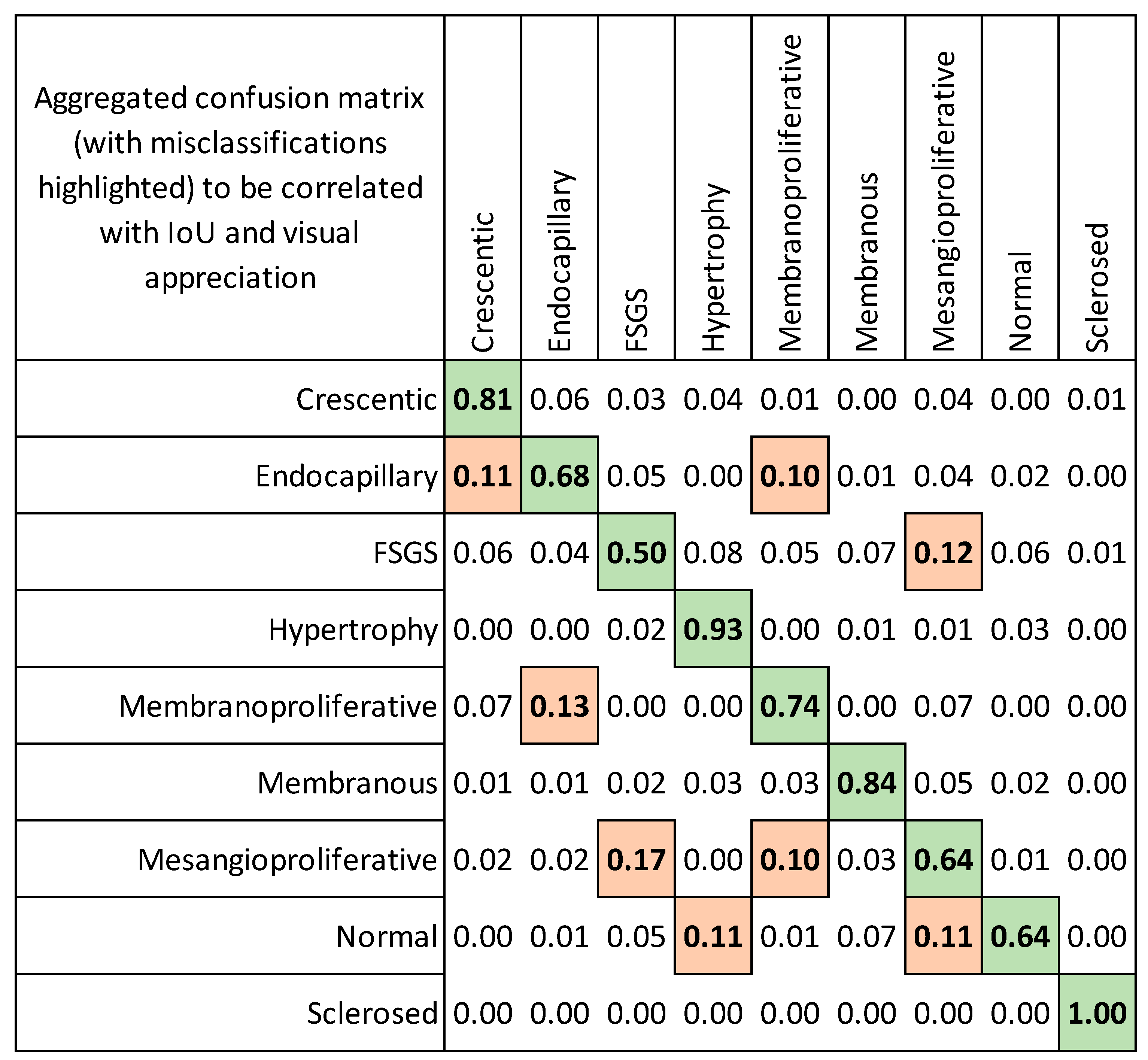
3.1. Classification of Glomeruli Patterns
| Classifier Experiment | Crescentic | Endocapillary | FSGS | Mesangioproliferative | Membranoproliferative | Membranous | Hypertrophy | Normal | Sclerosed | Generalized Multiclass |
|---|---|---|---|---|---|---|---|---|---|---|
| Segmental Injury | Diffuse | |||||||||
| Mean Classification Accuracy (Standard Deviation) | ||||||||||
| Single-multiclass | 0.841 (0.046) | 0.730 (0.118) | 0.478 (0.076) | 0.586 (0.148) | 0.765 (0.060) | 0.817 (0.066) | 0.879 (0.057) | 0.640 (0.025) | 0.978 (0.000) | 0.719 (0.010) |
| Multiple-binary | 0.745 (0.072) | 0.573 (0.147) | 0.437 (0.025) | 0.486 (0.080) | 0.757 (0.082) | 0.840 (0.048) | 0.830 (0.051) | 0.625 (0.039) | 0.978 (0.000) | 0.677 (0.006) |
| Spatially guided | 0.814 (0.076) | 0.676 (0.128) | 0.504 (0.072) | 0.643 (0.154) | 0.739 (0.063) | 0.840 (0.082) | 0.927 (0.046) | 0.644 (0.120) | 1.000 (0.000) | 0.728 (0.028) |
| Mean AUC (standard deviation) | ||||||||||
| Single-multiclass | 0.971 (0.005) | 0.964 (0.006) | 0.840 (0.014) | 0.920 (0.010) | 0.965 (0.005) | 0.970 (0.004) | 0.970 (0.005) | 0.943 (0.007) | 0.995 (0.000) | 0.949 (0.002) |
| Multiple-binary | 0.935 (0.013) | 0.919 (0.006) | 0.767 (0.006) | 0.886 (0.012) | 0.948 (0.003) | 0.953 (0.001) | 0.970 (0.003) | 0.935 (0.006) | 0.991 (0.000) | 0.923 (0.003) |
| Spatially guided | 0.971 (0.003) | 0.971 (0.003) | 0.863 (0.020) | 0.915 (0.010) | 0.956 (0.005) | 0.972 (0.003) | 0.981 (0.003) | 0.964 (0.003) | 0.995 (0.000) | 0.954 (0.004) |
| Mean IoU (standard deviation) | ||||||||||
| Single-multiclass | 0.061 (0.012) | 0.050 (0.006) | 0.042 (0.003) | 0.041 (0.003) | n/a | n/a | n/a | n/a | n/a | 0.049 (0.003) |
| Multiple-binary | 0.060 (0.006) | 0.052 (0.007) | 0.034 (0.012) | 0.049 (0.016) | n/a | n/a | n/a | n/a | n/a | 0.048 (0.007) |
| Spatially guided | 0.404 (0.174) | 0.379 (0.138) | 0.263 (0.116) | 0.235 (0.114) | n/a | n/a | n/a | n/a | n/a | 0.320 (0.133) |
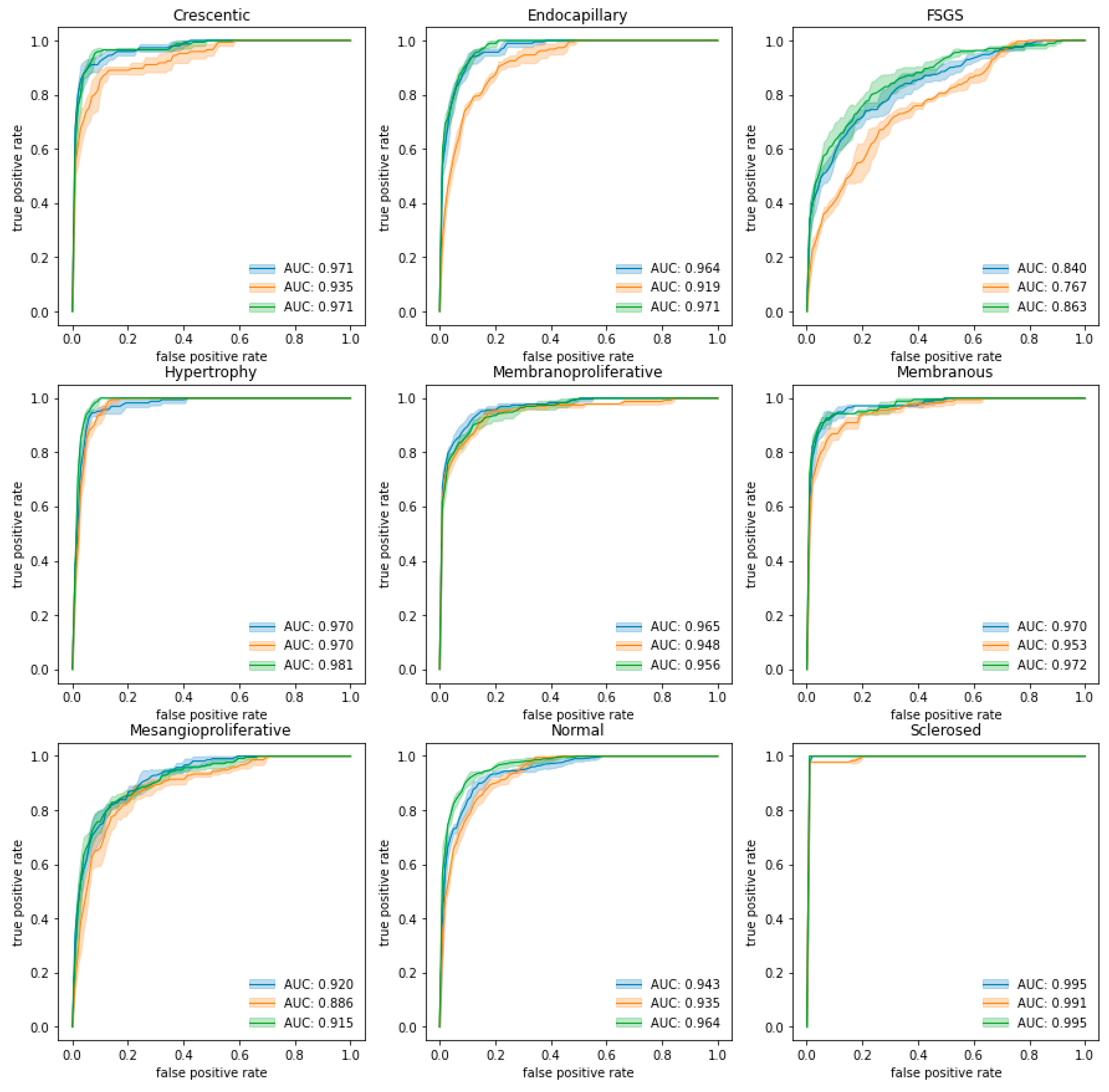
3.2. Evaluation of Localization Heatmaps and Pattern Quantification
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | convolutional neural network |
| IoU | intersection over union metrics |
| GN | glomerulonephritis |
| Grad-CAM gradient | weighted class activation mapping technique |
| WSI | whole slide images |
| FSGS | focal segmental glomerular sclerosis |
| SGD | stochastic gradient descent |
References
- Weening, J.J.; D’Agati, V.D.; Schwartz, M.M.; Seshan, S.V.; Alpers, C.E.; Appel, G.B.; Balow, J.E.; Bruijn, J.A.; Cook, T.; Ferrario, F.; et al. The classification of glomerulonephritis in systemic lupus erythematosus revisited. Kidney Int. 2004, 65, 521–530. [Google Scholar] [CrossRef]
- Tervaert, T.W.; Mooyaart, A.L.; Amann, K.; Cohen, A.H.; Cook, H.T.; Drachenberg, C.B.; Ferrario, F.; Fogo, A.B.; Haas, M.; de Heer, E.; et al. Pathologic classification of diabetic nephropathy. J. Am. Soc. Nephrol. 2010, 21, 556–563. [Google Scholar] [CrossRef] [PubMed]
- D’Agati, V.D.; Fogo, A.B.; Bruijn, J.A.; Jennette, J.C. Pathologic classification of focal segmental glomerulosclerosis: A working proposal. Am. J. Kidney Dis. 2004, 43, 368–382. [Google Scholar] [CrossRef] [PubMed]
- Berden, A.E.; Ferrario, F.; Hagen, E.C.; Jayne, D.R.; Jennette, J.C.; Joh, K.; Neumann, I.; Noel, L.H.; Pusey, C.D.; Waldherr, R.; et al. Histopathologic classification of ANCA-associated glomerulonephritis. J. Am. Soc. Nephrol. 2010, 21, 1628–1636. [Google Scholar] [CrossRef] [PubMed]
- Sethi, S.; Haas, M.; Markowitz, G.S.; D’Agati, V.D.; Rennke, H.G.; Jennette, J.C.; Bajema, I.M.; Alpers, C.E.; Chang, A.; Cornell, L.D.; et al. Mayo Clinic/Renal Pathology Society Consensus Report on Pathologic Classification, Diagnosis, and Reporting of GN. J. Am. Soc. Nephrol. 2016, 27, 1278–1287. [Google Scholar] [CrossRef] [PubMed]
- Trimarchi, H.; Barratt, J.; Cattran, D.C.; Cook, H.T.; Coppo, R.; Haas, M.; Liu, Z.H.; Roberts, I.S.; Yuzawa, Y.; Zhang, H.; et al. Oxford Classification of IgA nephropathy 2016: An update from the IgA Nephropathy Classification Working Group. Kidney Int. 2017, 91, 1014–1021. [Google Scholar] [CrossRef] [PubMed]
- Haas, M.; Seshan, S.V.; Barisoni, L.; Amann, K.; Bajema, I.M.; Becker, J.U.; Joh, K.; Ljubanovic, D.; Roberts, I.S.D.; Roelofs, J.J.; et al. Consensus definitions for glomerular lesions by light and electron microscopy: Recommendations from a working group of the Renal Pathology Society. Kidney Int. 2020, 98, 1120–1134. [Google Scholar] [CrossRef]
- Bertsias, G.K.; Tektonidou, M.; Amoura, Z.; Aringer, M.; Bajema, I.; Berden, J.H.; Boletis, J.; Cervera, R.; Dorner, T.; Doria, A.; et al. Joint European League Against Rheumatism and European Renal Association-European Dialysis and Transplant Association (EULAR/ERA-EDTA) recommendations for the management of adult and paediatric lupus nephritis. Ann. Rheum. Dis. 2012, 71, 1771–1782. [Google Scholar] [CrossRef]
- Rovin, B.H.; Adler, S.G.; Barratt, J.; Bridoux, F.; Burdge, K.A.; Chan, T.M.; Cook, H.T.; Fervenza, F.C.; Gibson, K.L.; Glassock, R.J.; et al. Executive summary of the KDIGO 2021 Guideline for the Management of Glomerular Diseases. Kidney Int. 2021, 100, 753–779. [Google Scholar] [CrossRef]
- Bajema, I.M.; Wilhelmus, S.; Alpers, C.E.; Bruijn, J.A.; Colvin, R.B.; Cook, H.T.; D’Agati, V.D.; Ferrario, F.; Haas, M.; Jennette, J.C.; et al. Revision of the International Society of Nephrology/Renal Pathology Society classification for lupus nephritis: Clarification of definitions, and modified National Institutes of Health activity and chronicity indices. Kidney Int. 2018, 93, 789–796. [Google Scholar] [CrossRef]
- Gasparotto, M.; Gatto, M.; Binda, V.; Doria, A.; Moroni, G. Lupus nephritis: Clinical presentations and outcomes in the 21st century. Rheumatology 2020, 59 (Suppl. S5), v39–v51. [Google Scholar] [CrossRef]
- Bellur, S.S.; Roberts, I.S.D.; Troyanov, S.; Royal, V.; Coppo, R.; Cook, H.T.; Cattran, D.; Arce Terroba, Y.; Asunis, A.M.; Bajema, I.; et al. Reproducibility of the Oxford classification of immunoglobulin A nephropathy, impact of biopsy scoring on treatment allocation and clinical relevance of disagreements: Evidence from the VALidation of IGA study cohort. Nephrol. Dial. Transpl. 2019, 34, 1681–1690. [Google Scholar] [CrossRef]
- Restrepo-Escobar, M.; Granda-Carvajal, P.A.; Jaimes, F. Systematic review of the literature on reproducibility of the interpretation of renal biopsy in lupus nephritis. Lupus 2017, 26, 1502–1512. [Google Scholar] [CrossRef]
- Dasari, S.; Chakraborty, A.; Truong, L.; Mohan, C. A Systematic Review of Interpathologist Agreement in Histologic Classification of Lupus Nephritis. Kidney Int. Rep. 2019, 4, 1420–1425. [Google Scholar] [CrossRef]
- Haas, M.; Mirocha, J.; Amann, K.; Bajema, I.M.; Barisoni, L.; Becker, J.U.; Jennette, J.C.; Joh, K.; Ljubanovic, D.G.; Roberts, I.S.D.; et al. Impact of Consensus Definitions on Identification of Glomerular Lesions by Light and Electron Microscopy. Kidney Int. Rep. 2022, 7, 78–86. [Google Scholar] [CrossRef]
- Hermsen, M.; de Bel, T.; den Boer, M.; Steenbergen, E.J.; Kers, J.; Florquin, S.; Roelofs, J.J.T.H.; Stegall, M.D.; Alexander, M.P.; Smith, B.H.; et al. Deep Learning-Based Histopathologic Assessment of Kidney Tissue. J. Am. Soc. Nephrol. 2019, 30, 1968–1979. [Google Scholar] [CrossRef]
- Hara, S.; Haneda, E.; Kawakami, M.; Morita, K.; Nishioka, R.; Zoshima, T.; Kometani, M.; Yoneda, T.; Kawano, M.; Karashima, S.; et al. Evaluating tubulointerstitial compartments in renal biopsy specimens using a deep learning-based approach for classifying normal and abnormal tubules. PLoS ONE 2022, 17, e0271161. [Google Scholar] [CrossRef]
- Sheehan, S.M.; Korstanje, R. Automatic glomerular identification and quantification of histological phenotypes using image analysis and machine learning. Am. J. Physiol. Ren. Physiol. 2018, 315, F1644–F1651. [Google Scholar] [CrossRef]
- Wilbur, D.C.; Pettus, J.R.; Smith, M.L.; Cornell, L.D.; Andryushkin, A.; Wingard, R.; Wirch, E. Using Image Registration and Machine Learning to Develop a Workstation Tool for Rapid Analysis of Glomeruli in Medical Renal Biopsies. J. Pathol. Inf. 2020, 11, 37. [Google Scholar] [CrossRef]
- Bouteldja, N.; Klinkhammer, B.M.; Bulow, R.D.; Droste, P.; Otten, S.W.; Freifrau von Stillfried, S.; Moellmann, J.; Sheehan, S.M.; Korstanje, R.; Menzel, S.; et al. Deep Learning-Based Segmentation and Quantification in Experimental Kidney Histopathology. J. Am. Soc. Nephrol. 2021, 32, 52–68. [Google Scholar] [CrossRef]
- Jiang, L.; Chen, W.; Dong, B.; Mei, K.; Zhu, C.; Liu, J.; Cai, M.; Yan, Y.; Wang, G.; Zuo, L.; et al. A Deep Learning-Based Approach for Glomeruli Instance Segmentation from Multistained Renal Biopsy Pathologic Images. Am. J. Pathol. 2021, 191, 1431–1441. [Google Scholar] [CrossRef] [PubMed]
- Kannan, S.; Morgan, L.A.; Liang, B.; Cheung, M.G.; Lin, C.Q.; Mun, D.; Nader, R.G.; Belghasem, M.E.; Henderson, J.M.; Francis, J.M.; et al. Segmentation of Glomeruli Within Trichrome Images Using Deep Learning. Kidney Int. Rep. 2019, 4, 955–962. [Google Scholar] [CrossRef]
- Kawazoe, Y.; Shimamoto, K.; Yamaguchi, R.; Shintani-Domoto, Y.; Uozaki, H.; Fukayama, M.; Ohe, K. Faster R-CNN-Based Glomerular Detection in Multistained Human Whole Slide Images. J. Imaging 2018, 4, 91. [Google Scholar] [CrossRef]
- Li, X.; Davis, R.C.; Xu, Y.; Wang, Z.; Souma, N.; Sotolongo, G.; Bell, J.; Ellis, M.; Howell, D.; Shen, X.; et al. Deep learning segmentation of glomeruli on kidney donor frozen sections. J. Med. Imaging 2021, 8, 067501. [Google Scholar] [CrossRef] [PubMed]
- Marsh, J.N.; Matlock, M.K.; Kudose, S.; Liu, T.C.; Stappenbeck, T.S.; Gaut, J.P.; Swamidass, S.J. Deep Learning Global Glomerulosclerosis in Transplant Kidney Frozen Sections. IEEE Trans. Med. Imaging 2018, 37, 2718–2728. [Google Scholar] [CrossRef] [PubMed]
- Bukowy, J.D.; Dayton, A.; Cloutier, D.; Manis, A.D.; Staruschenko, A.; Lombard, J.H.; Solberg Woods, L.C.; Beard, D.A.; Cowley, A.W., Jr. Region-Based Convolutional Neural Nets for Localization of Glomeruli in Trichrome-Stained Whole Kidney Sections. J. Am. Soc. Nephrol. 2018, 29, 2081–2088. [Google Scholar] [CrossRef]
- Bueno, G.; Fernandez-Carrobles, M.M.; Gonzalez-Lopez, L.; Deniz, O. Glomerulosclerosis identification in whole slide images using semantic segmentation. Comput. Methods Programs Biomed. 2020, 184, 105273. [Google Scholar] [CrossRef]
- Barros, G.O.; Navarro, B.; Duarte, A.; Dos-Santos, W.L.C. PathoSpotter-K: A computational tool for the automatic identification of glomerular lesions in histological images of kidneys. Sci. Rep. 2017, 7, 46769. [Google Scholar] [CrossRef]
- Jayapandian, C.P.; Chen, Y.; Janowczyk, A.R.; Palmer, M.B.; Cassol, C.A.; Sekulic, M.; Hodgin, J.B.; Zee, J.; Hewitt, S.M.; O’Toole, J.; et al. Development and evaluation of deep learning-based segmentation of histologic structures in the kidney cortex with multiple histologic stains. Kidney Int. 2021, 99, 86–101. [Google Scholar] [CrossRef]
- Sato, N.; Uchino, E.; Kojima, R.; Sakuragi, M.; Hiragi, S.; Minamiguchi, S.; Haga, H.; Yokoi, H.; Yanagita, M.; Okuno, Y. Evaluation of Kidney Histological Images Using Unsupervised Deep Learning. Kidney Int. Rep. 2021, 6, 2445–2454. [Google Scholar] [CrossRef]
- Yang, C.K.; Lee, C.Y.; Wang, H.S.; Huang, S.C.; Liang, P.I.; Chen, J.S.; Kuo, C.F.; Tu, K.H.; Yeh, C.Y.; Chen, T.D. Glomerular disease classification and lesion identification by machine learning. Biomed. J. 2022, 45, 675–685. [Google Scholar] [CrossRef]
- Altini, N.; Cascarano, G.D.; Brunetti, A.; Marino, F.; Rocchetti, M.T.; Matino, S.; Venere, U.; Rossini, M.; Pesce, F.; Gesualdo, L.; et al. Semantic Segmentation Framework for Glomeruli Detection and Classification in Kidney Histological Sections. Electronics 2020, 9, 503. [Google Scholar] [CrossRef]
- Weis, C.A.; Bindzus, J.N.; Voigt, J.; Runz, M.; Hertjens, S.; Gaida, M.M.; Popovic, Z.V.; Porubsky, S. Assessment of glomerular morphological patterns by deep learning algorithms. J. Nephrol. 2022, 35, 417–427. [Google Scholar] [CrossRef]
- Altini, N.; Cascarano, G.D.; Brunetti, A.; De Feudis, I.; Buongiorno, D.; Rossini, M.; Pesce, F.; Gesualdo, L.; Bevilacqua, V. A Deep Learning Instance Segmentation Approach for Global Glomerulosclerosis Assessment in Donor Kidney Biopsies. Electronics 2020, 9, 1768. [Google Scholar] [CrossRef]
- Ginley, B.; Jen, K.Y.; Han, S.S.; Rodrigues, L.; Jain, S.; Fogo, A.B.; Zuckerman, J.; Walavalkar, V.; Miecznikowski, J.C.; Wen, Y.; et al. Automated Computational Detection of Interstitial Fibrosis, Tubular Atrophy, and Glomerulosclerosis. J. Am. Soc. Nephrol. 2021, 32, 837–850. [Google Scholar] [CrossRef] [PubMed]
- Bullow, R.D.; Marsh, J.N.; Swamidass, S.J.; Gaut, J.P.; Boor, P. The potential of artificial intelligence-based applications in kidney pathology. Curr. Opin. Nephrol. Hypertens. 2022, 31, 251–257. [Google Scholar] [CrossRef] [PubMed]
- Gallego, J.; Swiderska-Chadaj, Z.; Markiewicz, T.; Yamashita, M.; Gabaldon, M.A.; Gertych, A. A U-Net based framework to quantify glomerulosclerosis in digitized PAS and H&E stained human tissues. Comput. Med. Imaging Graph. 2021, 89, 101865. [Google Scholar]
- Ginley, B.; Lutnick, B.; Jen, K.Y.; Fogo, A.B.; Jain, S.; Rosenberg, A.; Walavalkar, V.; Wilding, G.; Tomaszewski, J.E.; Yacoub, R.; et al. Computational Segmentation and Classification of Diabetic Glomerulosclerosis. J. Am. Soc. Nephrol. 2019, 30, 1953–1967. [Google Scholar] [CrossRef]
- Zeng, C.; Nan, Y.; Xu, F.; Lei, Q.; Li, F.; Chen, T.; Liang, S.; Hou, X.; Lv, B.; Liang, D.; et al. Identification of glomerular lesions and intrinsic glomerular cell types in kidney diseases via deep learning. J. Pathol. 2020, 252, 53–64. [Google Scholar] [CrossRef]
- Yamaguchi, R.; Kawazoe, Y.; Shimamoto, K.; Shinohara, E.; Tsukamoto, T.; Shintani-Domoto, Y.; Nagasu, H.; Uozaki, H.; Ushiku, T.; Nangaku, M.; et al. Glomerular Classification Using Convolutional Neural Networks Based on Defined Annotation Criteria and Concordance Evaluation Among Clinicians. Kidney Int. Rep. 2021, 6, 716–726. [Google Scholar] [CrossRef] [PubMed]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. Int. J. Comput. Vis. 2020, 128, 336–359. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition (Cvpr 2017), Honolulu, HI, USA, 21–26 July 2016; pp. 1800–1807. [Google Scholar]
- Oksuz, K.; Cam, B.C.; Kalkan, S.; Akbas, E. Imbalance Problems in Object Detection: A Review. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3388–3415. [Google Scholar] [CrossRef] [PubMed]
- Lateef, F.; Ruichek, Y. Survey on semantic segmentation using deep learning techniques. Neurocomputing 2019, 338, 321–348. [Google Scholar] [CrossRef]


| Glomerular Injury Pattern | Testing Set | Training Set | Total Original Glomeruli | |
|---|---|---|---|---|
| Original | Original | Augmented | ||
| Crescentic | 29 | 81 | 81 | 110 |
| Endocapillary | 37 | 81 | 81 | 118 |
| FSGS | 54 | 81 | 81 | 135 |
| Hypertrophy | 33 | 81 | 81 | 114 |
| Membranoproliferative | 46 | 81 | 81 | 127 |
| Membranous | 35 | 81 | 81 | 116 |
| Mesangioproliferative | 42 | 81 | 81 | 123 |
| Normal | 96 | 81 | 81 | 177 |
| Sclerosed | 45 | 81 | 81 | 126 |
| Total | 417 | 1458 | 1146 | |
| Original | Annotation | Single Multiclass | Multiple Binary | Spatially Guided | |
|---|---|---|---|---|---|
| True label: Crescentic | 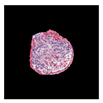 | 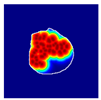 | 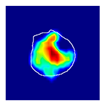 | 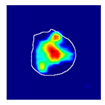 |  |
| single-multiclass: Crescentic p = 0.999, IoU = 0.154 | |||||
| multiple-binary: Crescentic p = 1.000, IoU = 0.128 | |||||
| Spatially guided: Crescentic p = 0.979, IoU = 0.740 | |||||
| True label: Endocapillary | 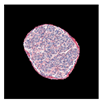 |  | 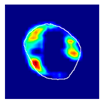 |  | 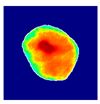 |
| single-multiclass: Endocapillary p = 1.000, IoU = 0.055 | |||||
| multiple-binary: Endocapillary p = 0.993, IoU = 0.029 | |||||
| spatially guided: Endocapillary p = 0.976, IoU = 0.710 | |||||
| True label: FSGS | 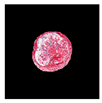 |  | 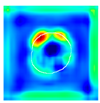 | 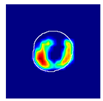 | 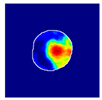 |
| single-multiclass: FSGS p = 0.964, IoU = 0.063 | |||||
| multiple-binary: FSGS p = 0.999, IoU = 0.076 | |||||
| spatially guided: FSGS p = 0.862, IoU = 0.390 | |||||
| True label: Mesangioproliferative | 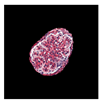 |  |  | 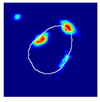 |  |
| single-multiclass: Mesangioproliferative p = 0.935, IoU = 0.029 | |||||
| multiple-binary: Mesangioproliferative p = 0.988, IoU = 0.032 | |||||
| spatially guided: Mesangioproliferative p = 0.873, IoU = 0.201 |
| Original | Annotation | Single Multiclass | Multiple Binary | Spatially Guided | |
|---|---|---|---|---|---|
| True label: Crescentic | 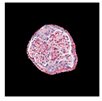 |  | 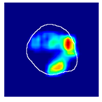 | 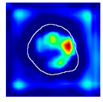 |  |
| single-multiclass: Crescentic p = 0.940, IoU = 0.058 | |||||
| multiple-binary: Crescentic p = 0.959, IoU = 0.048 | |||||
| spatially guided: Crescentic p = 0.983, IoU = 0.163 | |||||
| True label: FSGS |  |  | 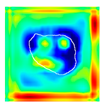 |  |  |
| single-multiclass: FSGS p = 0.960, IoU = 0.058 | |||||
| multiple-binary: FSGS p = 0.986, IoU = 0.041 | |||||
| spatially guided: FSGS p = 0.774, IoU = 0.015 | |||||
| True label: Mesangioproliferative |  | 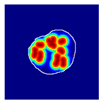 |  |  | 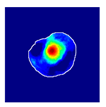 |
| single-multiclass: Mesangioproliferative p = 0.868, IoU = 0.047 | |||||
| multiple-binary: Mesangioproliferative p = 0.956, IoU = 0.031 | |||||
| spatially guided: Mesangioproliferative p = 0.840, IoU = 0.141 |
| Original | Annotation | Single Multiclass | Multiple Binary | Spatially Guided | |
|---|---|---|---|---|---|
| True label: FSGS |  |  | 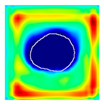 | 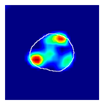 |  |
| single-multiclass: FSGS p = 0.672, IoU = 0.056 | |||||
| multiple-binary: Crescentic p = 0.938, IoU = 0.047 | |||||
| spatially guided: Crescentic p = 0.715, IoU = 0.568 | |||||
| True label: FSGS | 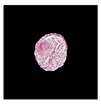 | 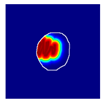 |  |  |  |
| single-multiclass: Crescentic p = 0.949, IoU = 0.102 | |||||
| multiple-binary: Crescentic p = 0.990, IoU = 0.118 | |||||
| spatially guided: Crescentic p = 0.966, IoU = 0.449 | |||||
| True label: FSGS | 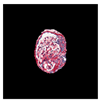 | 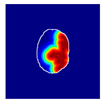 |  | 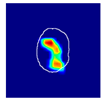 | 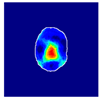 |
| single-multiclass: Normal p = 0.529, IoU = 0.067 | |||||
| multiple-binary: FSGS p = 0.752, IoU = 0.070 | |||||
| spatially guided: Mesangioproliferative p = 0.588, IoU = 0.121 | |||||
| True label: FSGS |  | 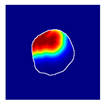 |  |  |  |
| single-multiclass: Normal p = 0.917, IoU = 0.052 | |||||
| multiple-binary: FSGS p = 0.414, IoU = 0.000 | |||||
| spatially guided: Normal p = 0.817, IoU = 0.199 | |||||
| True label: Endocapillary | 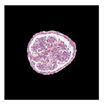 | 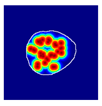 | 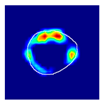 |  |  |
| single-multiclass: Endocapillary p = 0.447, IoU = 0.057 | |||||
| multiple-binary: Crescentic p = 0.766, IoU = 0.081 | |||||
| spatially guided: Membranoproliferative p = 0.833, IoU = 0.484 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Besusparis, J.; Morkunas, M.; Laurinavicius, A. A Spatially Guided Machine-Learning Method to Classify and Quantify Glomerular Patterns of Injury in Histology Images. J. Imaging 2023, 9, 220. https://doi.org/10.3390/jimaging9100220
Besusparis J, Morkunas M, Laurinavicius A. A Spatially Guided Machine-Learning Method to Classify and Quantify Glomerular Patterns of Injury in Histology Images. Journal of Imaging. 2023; 9(10):220. https://doi.org/10.3390/jimaging9100220
Chicago/Turabian StyleBesusparis, Justinas, Mindaugas Morkunas, and Arvydas Laurinavicius. 2023. "A Spatially Guided Machine-Learning Method to Classify and Quantify Glomerular Patterns of Injury in Histology Images" Journal of Imaging 9, no. 10: 220. https://doi.org/10.3390/jimaging9100220
APA StyleBesusparis, J., Morkunas, M., & Laurinavicius, A. (2023). A Spatially Guided Machine-Learning Method to Classify and Quantify Glomerular Patterns of Injury in Histology Images. Journal of Imaging, 9(10), 220. https://doi.org/10.3390/jimaging9100220






