Local Contrast-Based Pixel Ordering for Exact Histogram Specification
Abstract
:1. Introduction
2. Related Work
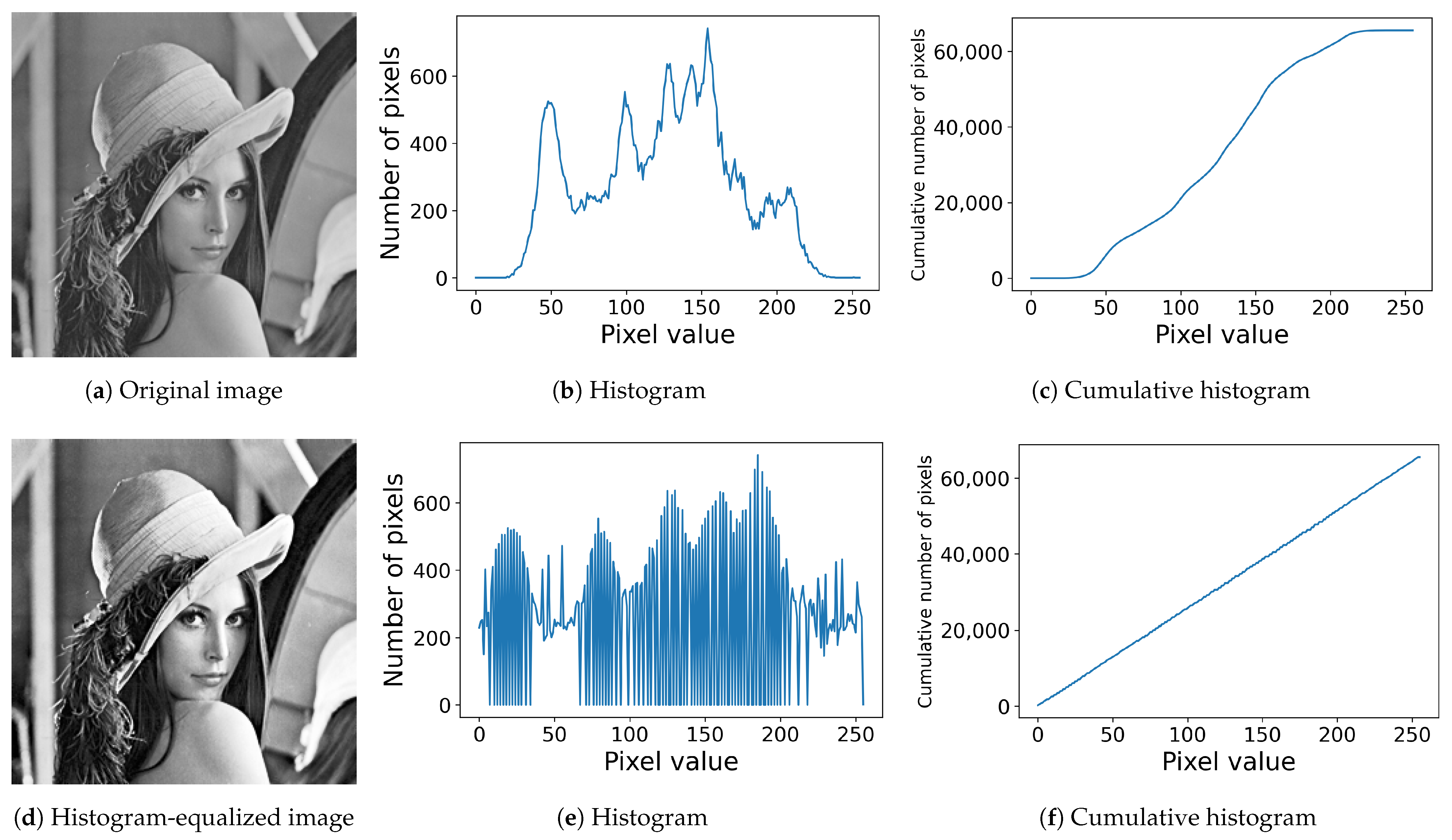
3. Histogram Equalization
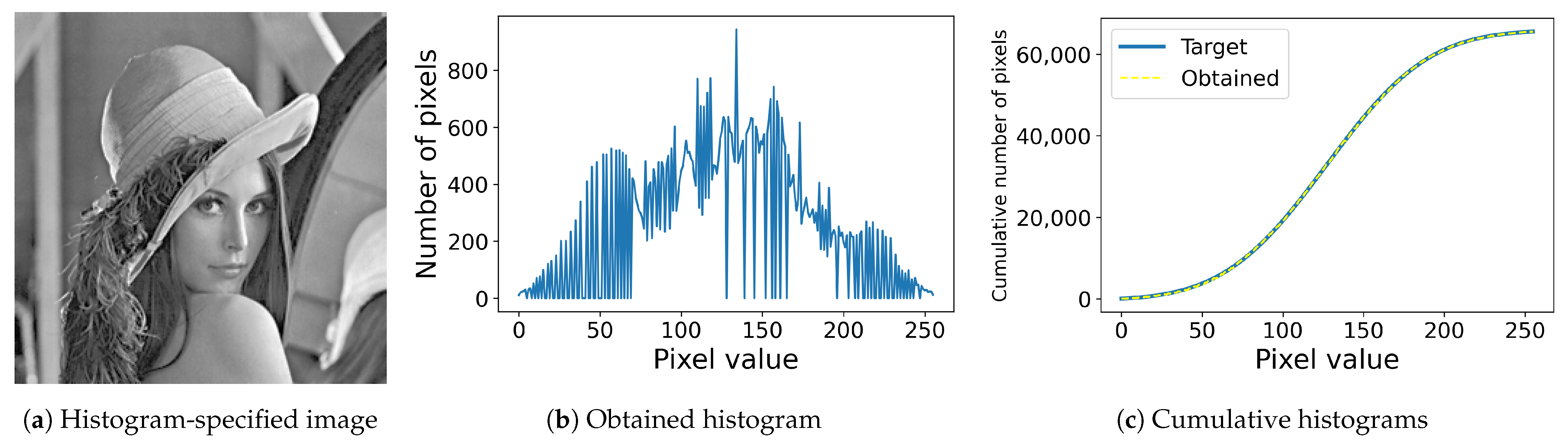
4. Histogram Specification
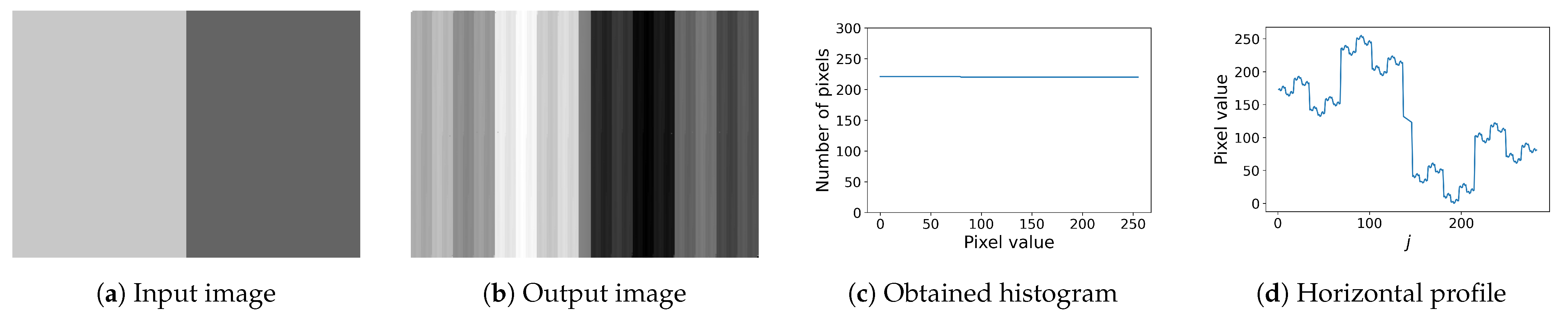
4.1. Conventional Histogram Specification
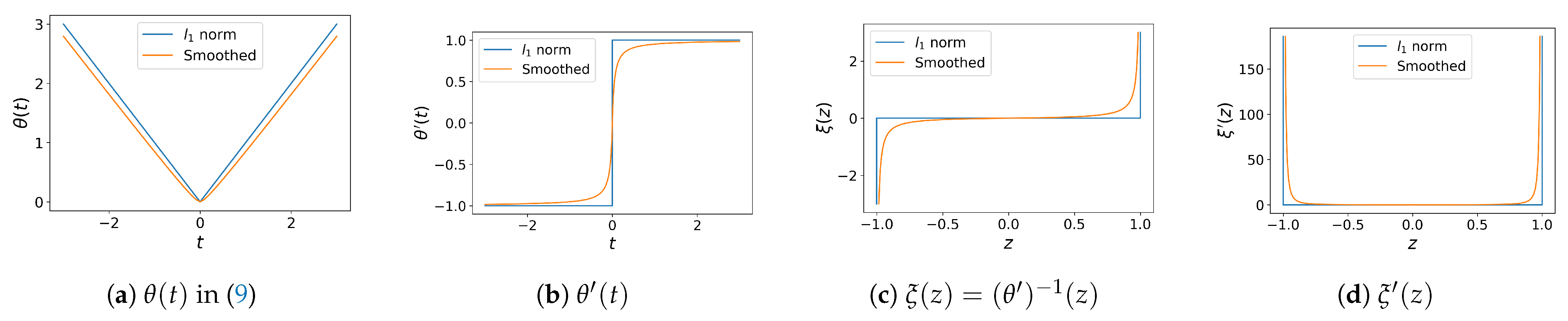
4.2. Nikolova and Steidl’s Method
| Algorithm 1 Fully smoothed -TV minimization algorithm [13] |
|
5. Proposed Method
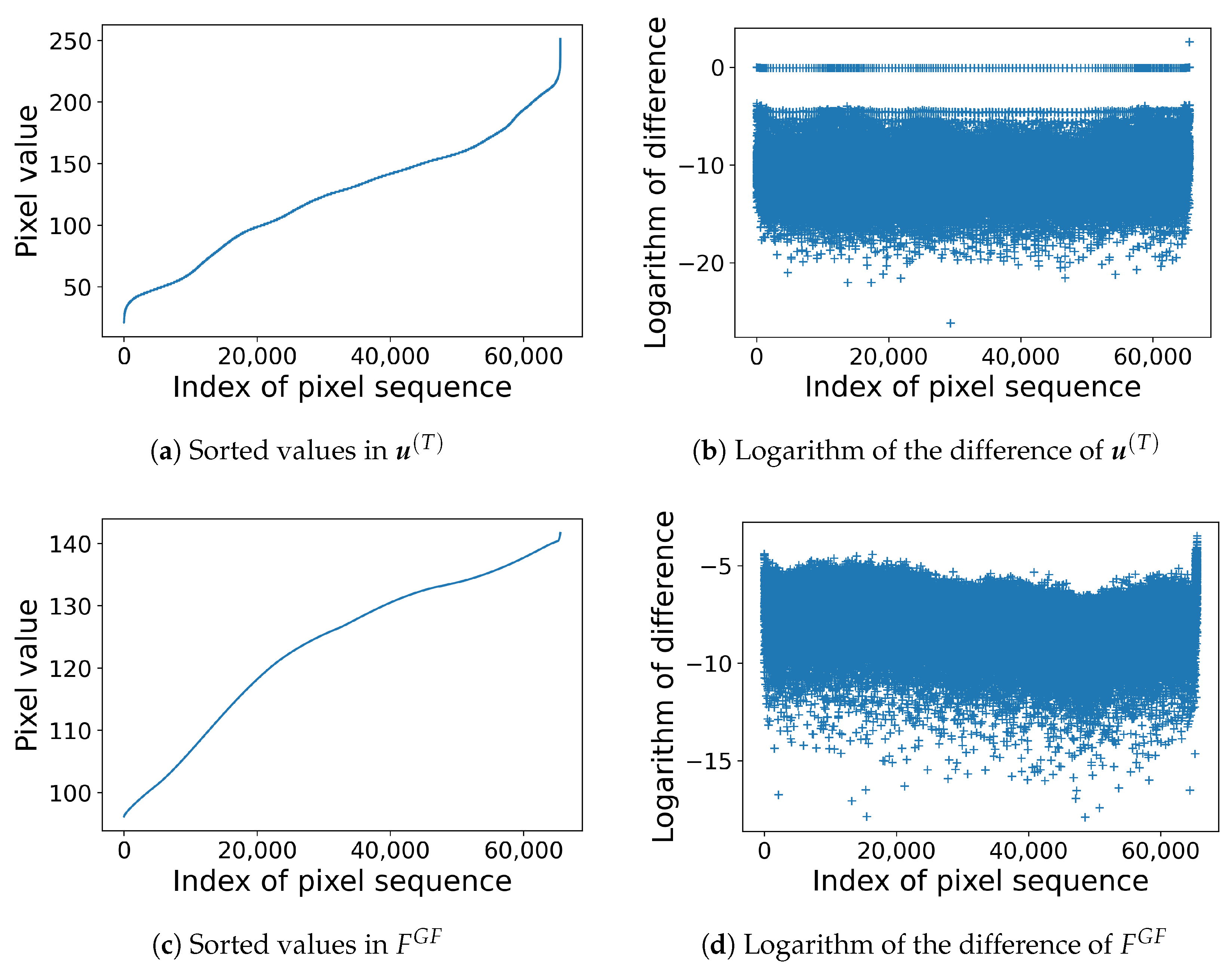
5.1. Local Contrast-Based Exact Histogram Specification for Grayscale Images
| Algorithm 2 Local contrast-based exact histogram specification |
|
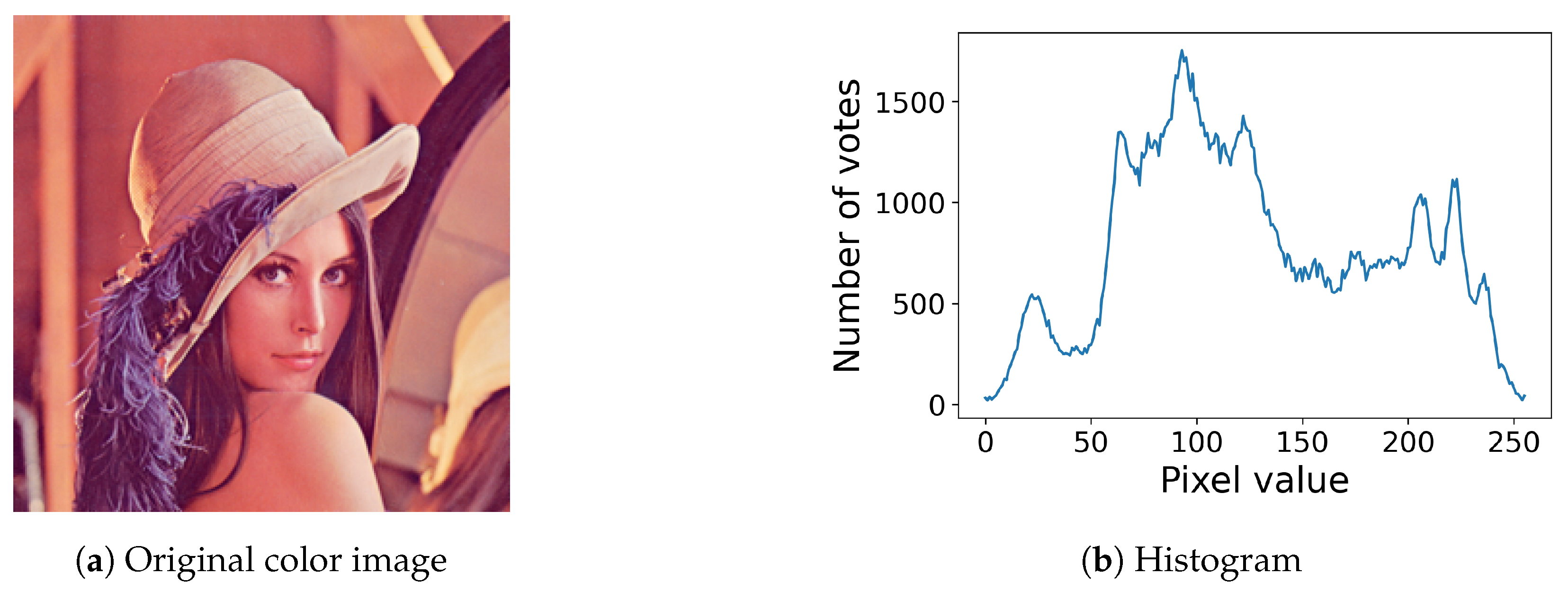
5.2. Extension to Color Images
| Algorithm 3 Local contrast-based exact histogram specification for color images |
|
5.3. Complexity Analysis
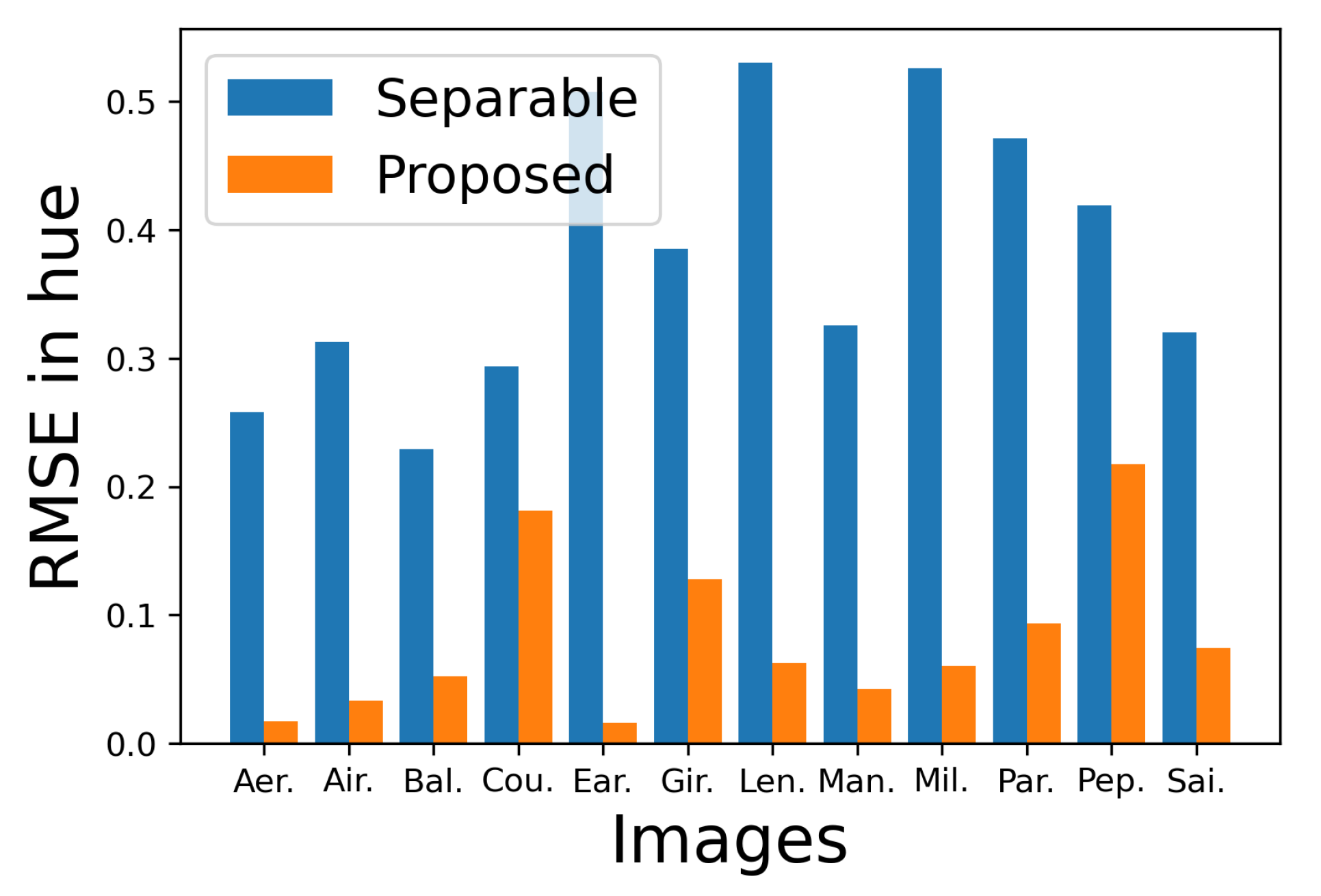
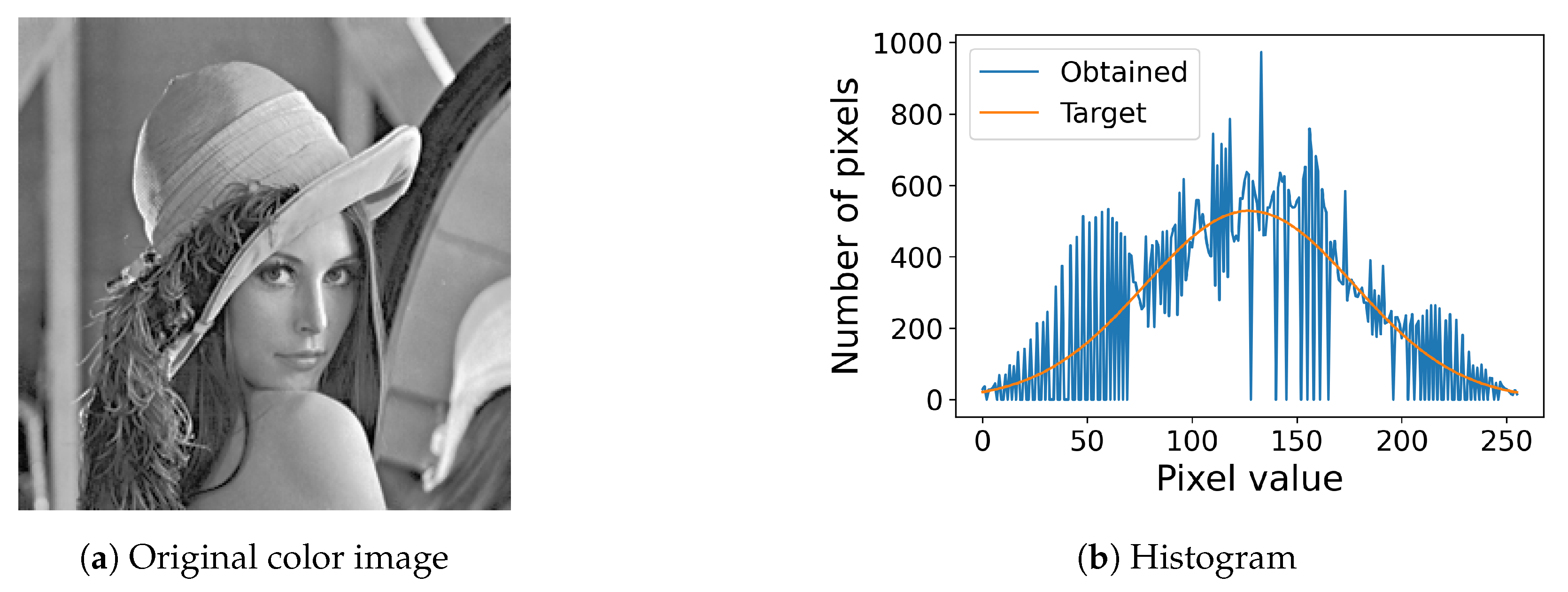
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LM | Local mean method |
| WA | Wavelet-based exact pixel ordering algorithm |
| TV | Total variation |
| SIDBA | The Standard Image Data-BAse |
| RMSE | Root mean squared error |
References
- Pouli, T.; Reinhard, E.; Cunningham, D.W. Image Statistics in Visual Computing, 1st ed.; A. K. Peters, Ltd.: Natick, MA, USA, 2013. [Google Scholar]
- Naik, S.K.; Murthy, C.A. Hue-preserving color image enhancement without gamut problem. IEEE Trans. Image Process. 2003, 12, 1591–1598. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.A.; Fazle Rabbi, M.M.; Rahman, M.M.; Islam, M.M.; Islam, M.R. Histogram modification based lossy image compression scheme using Huffman coding. In Proceedings of the 2018 4th International Conference on Electrical Engineering and Information & Communication Technology (iCEEiCT), Dhaka, Bangladesh, 13–15 September 2018; pp. 279–284. [Google Scholar] [CrossRef]
- Qin, K.; Xu, K.; Liu, F.; Li, D. Image segmentation based on histogram analysis utilizing the cloud model. Comput. Math. Appl. 2011, 62, 2824–2833. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2008; pp. 150–161. [Google Scholar]
- Gonzalez, R.C.; Fittes, B.A. Gray-level transformations for interactive image enhancement. Mech. Mach. Theory 1977, 12, 111–122. [Google Scholar] [CrossRef]
- Raheja, A.; Chawla, R.; Gupta, S.; Vashist, A. Controlling Over Enhancement of Images Using Histogram Equalization Technique. IOP Conf. Ser. Mater. Sci. Eng. 2020, 804, 012055. Available online: https://iopscience.iop.org/article/10.1088/1757-899X/804/1/012055 (accessed on 28 June 2022). [CrossRef]
- Nikolova, M.; Wen, Y.W.; Chan, R. Exact Histogram Specification for Digital Images Using a Variational Approach. J. Math. Imaging Vis. 2013, 46, 309–325. [Google Scholar] [CrossRef]
- Hall, E.L. Almost Uniform Distributions for Computer Image Enhancement. IEEE Trans. Comput. 1974, C-23, 207–208. [Google Scholar] [CrossRef]
- Rosenfeld, A.; Kak, A.C. Digital Picture Processing: Volume 1 and 2; Academic Press: Orlando, FL, USA, 1982; ISBN 0-12-597301-2/0-12-597302-0. [Google Scholar]
- Coltuc, D.; Bolon, P.; Chassery, J.-M. Exact histogram specification. IEEE Trans. Image Process. 2006, 15, 1143–1152. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Shi, D. Joint Exact Histogram Specification and Image Enhancement Through the Wavelet Transform. IEEE Trans. Image Process. 2007, 16, 2245–2250. [Google Scholar] [CrossRef] [PubMed]
- Nikolova, M.; Steidl, G. Fast Ordering Algorithm for Exact Histogram Specification. IEEE Trans. Image Process. 2014, 23, 5274–5283. [Google Scholar] [CrossRef] [Green Version]
- Nikolova, M.; Steidl, G. Fast Hue and Range Preserving Histogram Specification: Theory and New Algorithms for Color Image Enhancement. IEEE Trans. Image Process. 2014, 23, 4087–4100. [Google Scholar] [CrossRef]
- Lindeberg, T. Scale-space for discrete signals. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 234–254. [Google Scholar] [CrossRef]
- Ramos, V.S.; Silveira, L.F.d.Q.; Silveira Júnior, L.G.d.Q. Histogram Specification by Assignment of Optimal Unique Values. arXiv 2021, arXiv:2102.02378. [Google Scholar]
- Pallavi, S.; Sannidhan, M.S.; Abhir Bhandary. A Comprehensive Review on Various State-of-the-Art Techniques for Image Enhancement. Int. J. Eng. Technol. 2018, 7, 86–864. Available online: https://www.sciencepubco.com/index.php/ijet/article/view/19576 (accessed on 28 June 2022).
- Yadav, G.; Maheshwari, S.; Agarwal, A. Contrast limited adaptive histogram equalization based enhancement for real time video system. In Proceedings of the 2014 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Delhi, India, 24–27 September 2014; pp. 2392–2397. [Google Scholar] [CrossRef]
- Kim, Y.-T. Contrast enhancement using brightness preserving bi-histogram equalization. IEEE Trans. Consum. Electron. 1997, 43, 1–8. [Google Scholar] [CrossRef]
- Trongtirakul, T.; Agaian, S. Weighted Histogram Equalization Using Entropy of Probability Density Function. In Proceedings of the 44th Electrical Engineering Conference (EECON 44), Nan, Thailand, 17–19 November 2021; Volume 1, pp. 461–464. Available online: https://arxiv.org/ftp/arxiv/papers/2111/2111.08578.pdf (accessed on 28 June 2022).
- Ren, X.; Yang, W.; Cheng, W.-H.; Liu, J. LR3M: Robust Low-Light Enhancement via Low-Rank Regularized Retinex Model. IEEE Trans. Image Process. 2020, 29, 5862–5876. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Shao, Y.; Sun, Y.; Zhu, K.; Gao, C.; Sang, N. Unsupervised Low-Light Image Enhancement via Histogram Equalization Prior. arXiv 2021, arXiv:2112.01766. [Google Scholar]
- Hussain, K.; Rahman, S.; Rahman, M.; Khaled, S.M.; Wadud, A.A.; Hossain Khan, M.A.; Shoyaib, M. A histogram specification technique for dark image enhancement using a local transformation method. IPSJ Trans. Comput. Vis. Appl. 2018, 10, 3. [Google Scholar] [CrossRef]
- Balado, F. Optimum Exact Histogram Specification. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 1413–1417. [Google Scholar] [CrossRef] [Green Version]
- Vectorization (Mathematics) From Wikipedia, the Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/Vectorization_(mathematics) (accessed on 28 June 2022).
- Weisstein, E.W. “Transpose.” From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/Transpose.html (accessed on 29 May 2022).
- Weisstein, E.W. “Floor Function.” From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/FloorFunction.html (accessed on 13 June 2022).
- The Standard Image Data-BAse (SIDBA). Available online: http://www.ess.ic.kanagawa-it.ac.jp/app_images_j.html (accessed on 21 June 2022).



















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inoue, K.; Ono, N.; Hara, K. Local Contrast-Based Pixel Ordering for Exact Histogram Specification. J. Imaging 2022, 8, 247. https://doi.org/10.3390/jimaging8090247
Inoue K, Ono N, Hara K. Local Contrast-Based Pixel Ordering for Exact Histogram Specification. Journal of Imaging. 2022; 8(9):247. https://doi.org/10.3390/jimaging8090247
Chicago/Turabian StyleInoue, Kohei, Naoki Ono, and Kenji Hara. 2022. "Local Contrast-Based Pixel Ordering for Exact Histogram Specification" Journal of Imaging 8, no. 9: 247. https://doi.org/10.3390/jimaging8090247
APA StyleInoue, K., Ono, N., & Hara, K. (2022). Local Contrast-Based Pixel Ordering for Exact Histogram Specification. Journal of Imaging, 8(9), 247. https://doi.org/10.3390/jimaging8090247






