Extra Proximal-Gradient Network with Learned Regularization for Image Compressive Sensing Reconstruction
Abstract
:1. Introduction
2. Related Work
3. Extra Proximal Gradient Network
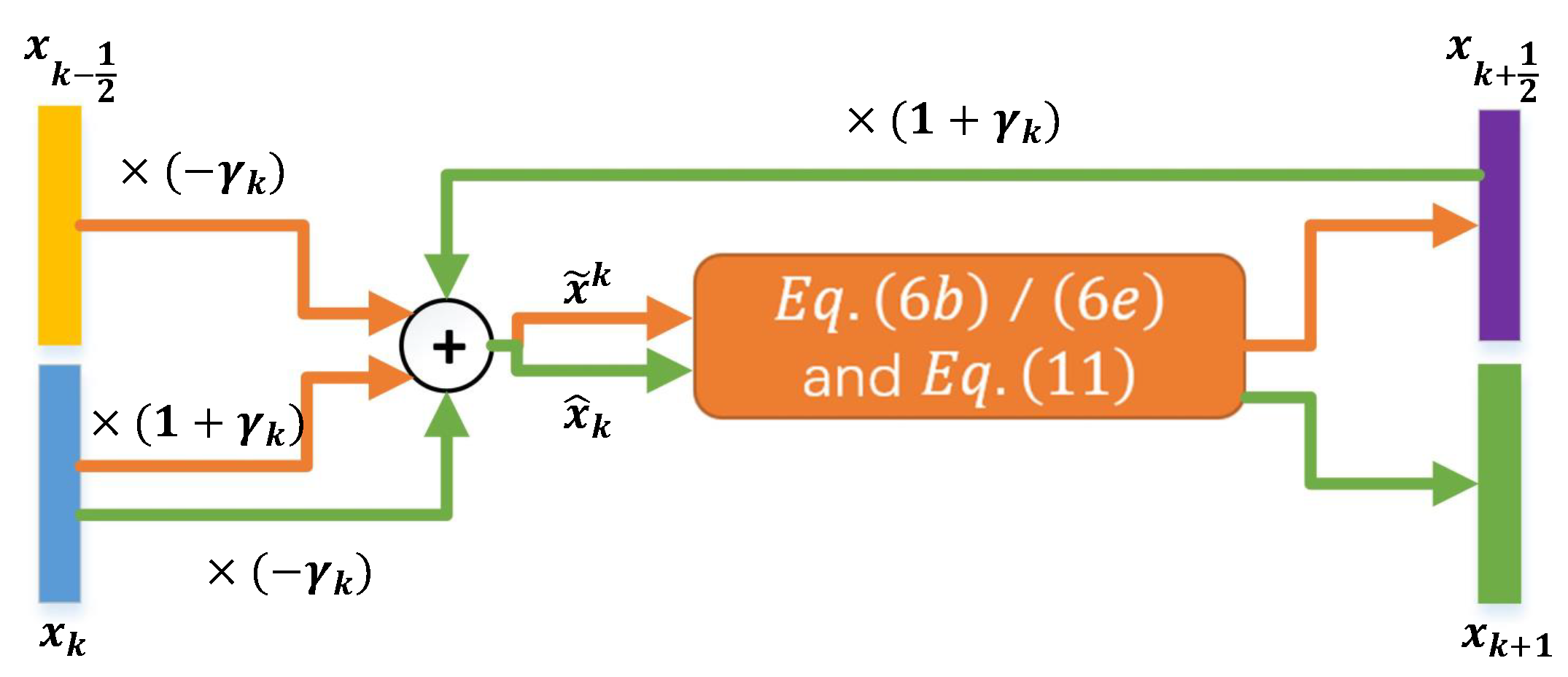
3.1. Extra Proximal Gradient Algorithm
| Algorithm 1: Accelerated Extra Proximal Gradient Algorithm. |
|
3.2. Extra Proximal Gradient Network (EPGN)
3.2.1. Nonlinear Feature Extraction Operator
3.2.2. Nonlinear Residual Resembling Operator
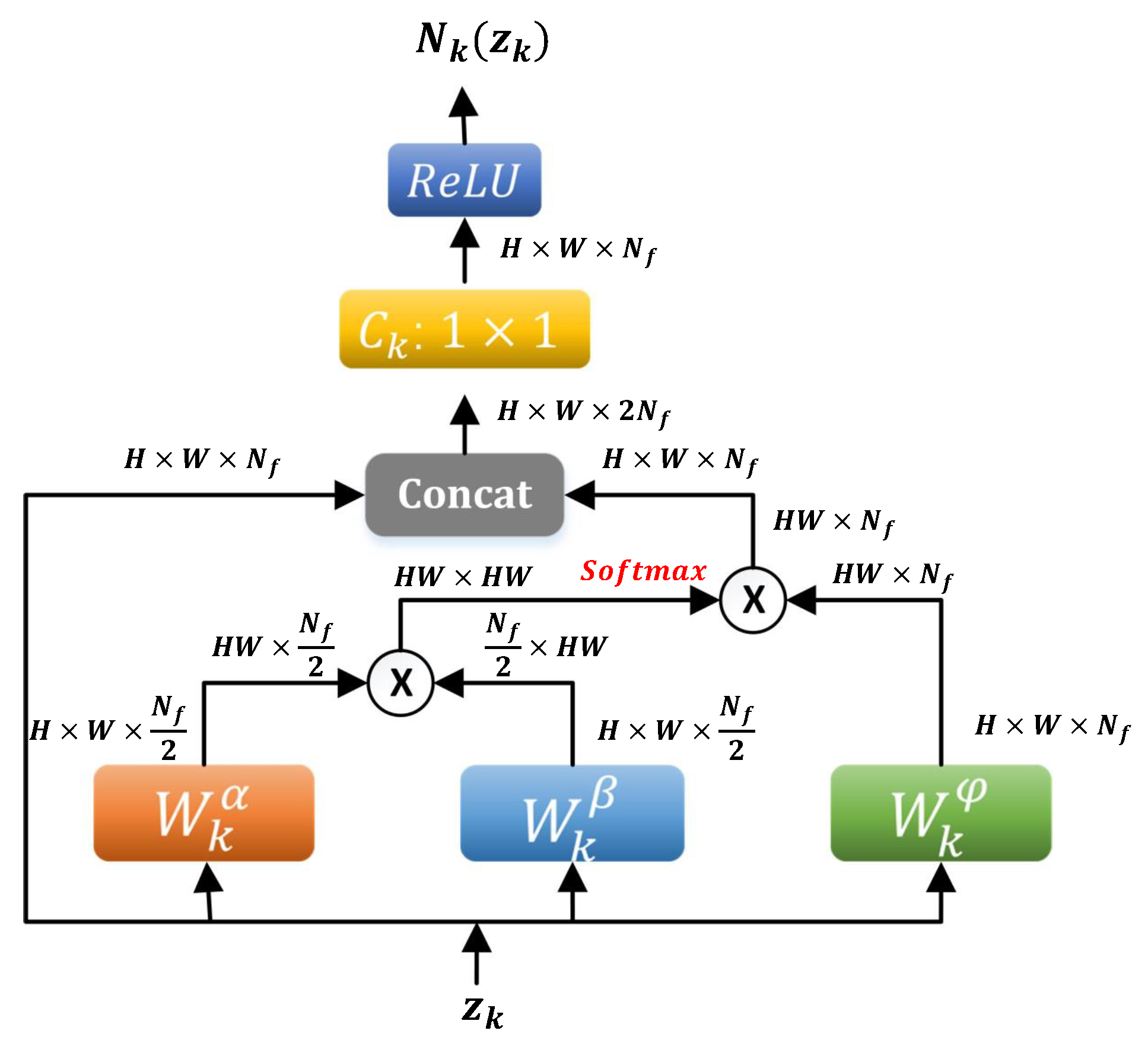
3.3. EPGN with Nonlocal Operator (NL-EPGN)
3.3.1. Nonlocal Feature Extraction Block
3.3.2. Local and Nonlocal Combination Layer
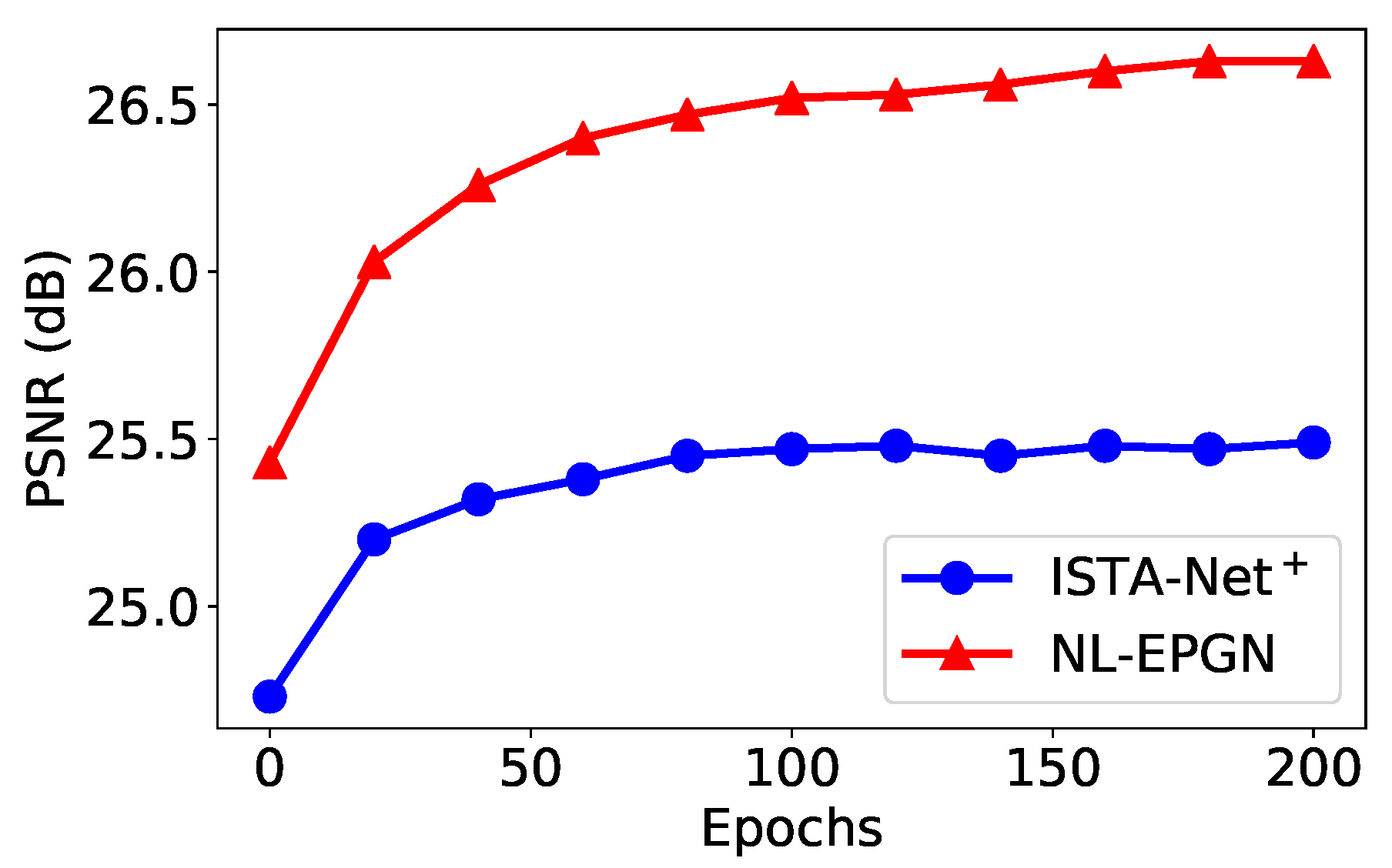
3.4. Network Training
4. Numerical Experiments
4.1. Nature Images Compressive Sensing
4.1.1. Comparison with Existing Methods
4.1.2. Reconstruction Quality Assessment
4.1.3. Parameter Efficiency
4.2. MR Images Compressive Sensing
5. Concluding Remarks
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 26th Annual Conference on Neural Information Processing Systems 2012, Lake Tahoe, NV, USA, 3–6 December 2012. Advances in Neural Information Processing Systems 25. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Yang, W.; Zhang, X.; Tian, Y.; Wang, W.; Xue, J.H.; Liao, Q. Deep learning for single image super-resolution: A brief review. IEEE Trans. Multimed. 2019, 21, 3106–3121. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Ye, X.; Zhang, Q. Variational Model-Based Deep Neural Networks for Image Reconstruction. In Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging: Mathematical Imaging and Vision; Chen, K., Schönlieb, C.B., Tai, X.C., Younces, L., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 1–29. [Google Scholar] [CrossRef]
- Wan, M.; Zha, D.; Liu, N.; Zou, N. Modeling Techniques for Machine Learning Fairness: A Survey. arXiv 2021, arXiv:2111.03015. [Google Scholar]
- Young, T.; Hazarika, D.; Poria, S.; Cambria, E. Recent trends in deep learning based natural language processing. IEEE Comput. Intell. Mag. 2018, 13, 55–75. [Google Scholar] [CrossRef]
- Tian, H.; Jiang, X.; Trozzi, F.; Xiao, S.; Larson, E.C.; Tao, P. Explore Protein Conformational Space With Variational Autoencoder. Front. Mol. Biosci. 2021, 8, 781635. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Van Der Laak, J.A.; Van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [Green Version]
- Hesamian, M.H.; Jia, W.; He, X.; Kennedy, P. Deep learning techniques for medical image segmentation: Achievements and challenges. J. Digit. Imaging 2019, 32, 582–596. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.; Pu, H.; Wang, F. The expressive power of neural networks: A view from the width. In Proceedings of the Thirty-First Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6231–6239. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zhang, B.; Fu, Y.; Lu, Y.; Zhang, Z.; Clarke, R.; Van Eyk, J.E.; Herrington, D.M.; Wang, Y. DDN2.0: R and Python packages for differential dependency network analysis of biological systems. bioRxiv 2021. [Google Scholar] [CrossRef]
- Bao, R.; Gu, B.; Huang, H. Efficient Approximate Solution Path Algorithm for Order Weight L1-Norm with Accuracy Guarantee. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 958–963. [Google Scholar] [CrossRef]
- Gregor, K.; LeCun, Y. Learning Fast Approximations of Sparse Coding. In Proceedings of the 27th International Conference on Machine Learning (ICML 2010), Haifa, Israel, 21–24 June 2010; pp. 399–406. [Google Scholar]
- Chen, X.; Liu, J.; Wang, Z.; Yin, W. Theoretical linear convergence of unfolded ISTA and its practical weights and thresholds. In Proceedings of the Thirty-second Annual Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 3–8 December 2018; pp. 9061–9071. [Google Scholar]
- Liu, J.; Chen, X.; Wang, Z.; Yin, W. ALISTA: Analytic weights are as good as learned weights in LISTA. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Sprechmann, P.; Bronstein, A.M.; Sapiro, G. Learning efficient sparse and low rank models. TPAMI 2015, 37, 1821–1833. [Google Scholar] [CrossRef]
- Xin, B.; Wang, Y.; Gao, W.; Wipf, D.; Wang, B. Maximal sparsity with deep networks? In Proceedings of the Thirtieth Conference on Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016; pp. 4340–4348. [Google Scholar]
- Borgerding, M.; Schniter, P.; Rangan, S. AMP-inspired deep networks for sparse linear inverse problems. IEEE Trans. Signal Process. 2017, 65, 4293–4308. [Google Scholar] [CrossRef]
- Xie, X.; Wu, J.; Zhong, Z.; Liu, G.; Lin, Z. Differentiable Linearized ADMM. arXiv 2019, arXiv:1905.06179. [Google Scholar]
- Bao, R.; Gu, B.; Huang, H. Fast OSCAR and OWL Regression via Safe Screening Rules. In Proceedings of the 37th International Conference on Machine Learning, Virtual Event, 12–18 July 2020; pp. 653–663. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26–30 June 2016; pp. 770–778. [Google Scholar]
- Zhang, K.; Zuo, W.; Gu, S.; Zhang, L. Learning deep CNN denoiser prior for image restoration. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 22–25 July 2017; pp. 3929–3938. [Google Scholar]
- Chang, J.R.; Li, C.L.; Poczos, B.; Kumar, B.V. One network to solve them all: Solving linear inverse problems using deep projection models. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 5889–5898. [Google Scholar]
- Meinhardt, T.; Moller, M.; Hazirbas, C. Learning proximal operators: Using denoising networks for regularizing inverse imaging problems. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1781–1790. [Google Scholar]
- Yang, Y.; Sun, J.; Li, H.; Xu, Z. Deep ADMM-Net for Compressive Sensing MRI. In Proceedings of the Thirtieth Conference on Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016; pp. 10–18. [Google Scholar]
- Zhang, J.; Ghanem, B. ISTA-Net: Interpretable Optimization-Inspired Deep Network for Image Compressive Sensing. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Korpelevi, G.M. An extragradient method for finding saddle points and for other problems. Ekon. Mate. Metody 1976, 12, 747–756. [Google Scholar]
- Censor, Y.; Gibali, A.; Reich, S. The subgradient extragradient method for solving variational inequalities in Hilbert space. J. Optim. Theory Appl. 2011, 148, 318–335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, T.P.; Pauwels, E.; Richard, E.; Suter, B.W. Extragradient method in optimization: Convergence and complexity. J. Optim. Theory Appl. 2018, 176, 137–162. [Google Scholar] [CrossRef] [Green Version]
- Diakonikolas, J.; Orecchia, L. Accelerated Extra-Gradient Descent: A Novel Accelerated First-Order Method. In Proceedings of the 9th Annual Innovations in Theoretical Computer Science (ITCS) Conference, Cambridge, MA, USA, 11–14 January 2018; pp. 23:1–23:19. [Google Scholar] [CrossRef]
- Nesterov, Y. Introductory Lectures on Convex Optimization: A Basic Course, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Li, H.; Lin, Z. Accelerated proximal gradient methods for nonconvex programming. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS 2015), Montréal, QC, Canada, 7–12 December 2015; pp. 379–387. [Google Scholar]
- Le, H.; Borji, A. What are the Receptive, Effective Receptive, and Projective Fields of Neurons in Convolutional Neural Networks? arXiv 2017, arXiv:abs/1705.07049. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–26 June 2005; pp. 60–65. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Lefkimmiatis, S. Non-local color image denoising with convolutional neural networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 22–25 July 2017; pp. 3587–3596. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 7794–7803. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the 13th International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Kulkarni, K.; Lohit, S.; Turaga, P. Reconnet: Non-iterative reconstruction of images from compressively sensed measurements. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26–30 June 2016; pp. 449–458. [Google Scholar]
- Li, C.; Yin, W.; Jiang, H. An efficient augmented Lagrangian method with applications to total variation minimization. Comput. Optim. Appl. 2013, 56, 507–530. [Google Scholar] [CrossRef] [Green Version]
- Metzler, C.; Maleki, A.; Baraniuk, R. From denoising to compressed sensing. IEEE Trans. Inf. Theory 2016, 62, 5117–5144. [Google Scholar] [CrossRef]
- Yao, H.; Dai, F.; Zhang, S.; Zhang, Y.; Tian, Q.; Xu, C. DR2-Net: Deep residual reconstruction network for image compressive sensing. Neurocomputing 2019, 359, 483–493. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Chen, J.; Liu, Q.; Liu, B.; Guo, G. Dual-Path Attention Network for Compressed Sensing Image Reconstruction. IEEE Trans. Image Process. 2020, 29, 9482–9495. [Google Scholar] [CrossRef] [PubMed]
- Landman, B.; Warfield, S. (Eds.) 2013 Diencephalon Free Challenge; Sage Bionetworks: Seattle, WA, USA, 2013. [Google Scholar] [CrossRef]





| Method | 10% | 25% | ||
|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | |
| TVAL3 [43] | 22.99 | 0.3758 | 27.92 | 0.6238 |
| D-AMP [44] | 22.64 | - | 28.46 | - |
| IRCNN [23] | 24.02 | - | 30.07 | - |
| ReconNet [42] | 24.28 | 0.6406 | 25.60 | 0.7589 |
| DR-Net [45] | 24.32 | 0.7175 | 28.66 | 0.8432 |
| ISTA-Net+ [27] | 26.64 | 0.8036 | 32.57 | 0.9237 |
| DPA-Net [46] | 26.99 | 0.8354 | 31.74 | 0.9238 |
| EPGN (9-phase) | 27.12 | 0.8893 | 32.87 | 0.9611 |
| NL-EPGN (7-phase) | 27.33 | 0.8956 | 33.02 | 0.9623 |
| Network (# Phase) | # PARM | PSNR (dB) | Time (s) |
|---|---|---|---|
| ISTA-Net (9) | 336,978 | 32.57 ± 2.20 | 0.084 |
| ISTA-Net (15) | 561,630 | 32.60 ± 2.19 | 0.103 |
| EPGN (9) | 337,275 | 32.87 ± 2.24 | 0.110 |
| NL-EPGN (7) | 290,997 | 33.02 ± 2.05 | 0.802 |
| Method | 10% | 20% | 30% |
|---|---|---|---|
| ISTA-Net | 33.49 | 40.66 | 44.70 |
| EPGN | 33.70 | 40.94 | 45.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Ye, X.; Chen, Y. Extra Proximal-Gradient Network with Learned Regularization for Image Compressive Sensing Reconstruction. J. Imaging 2022, 8, 178. https://doi.org/10.3390/jimaging8070178
Zhang Q, Ye X, Chen Y. Extra Proximal-Gradient Network with Learned Regularization for Image Compressive Sensing Reconstruction. Journal of Imaging. 2022; 8(7):178. https://doi.org/10.3390/jimaging8070178
Chicago/Turabian StyleZhang, Qingchao, Xiaojing Ye, and Yunmei Chen. 2022. "Extra Proximal-Gradient Network with Learned Regularization for Image Compressive Sensing Reconstruction" Journal of Imaging 8, no. 7: 178. https://doi.org/10.3390/jimaging8070178
APA StyleZhang, Q., Ye, X., & Chen, Y. (2022). Extra Proximal-Gradient Network with Learned Regularization for Image Compressive Sensing Reconstruction. Journal of Imaging, 8(7), 178. https://doi.org/10.3390/jimaging8070178





