Metal Artifact Reduction in Spectral X-ray CT Using Spectral Deep Learning
Abstract
:1. Introduction
2. Methods and Techniques
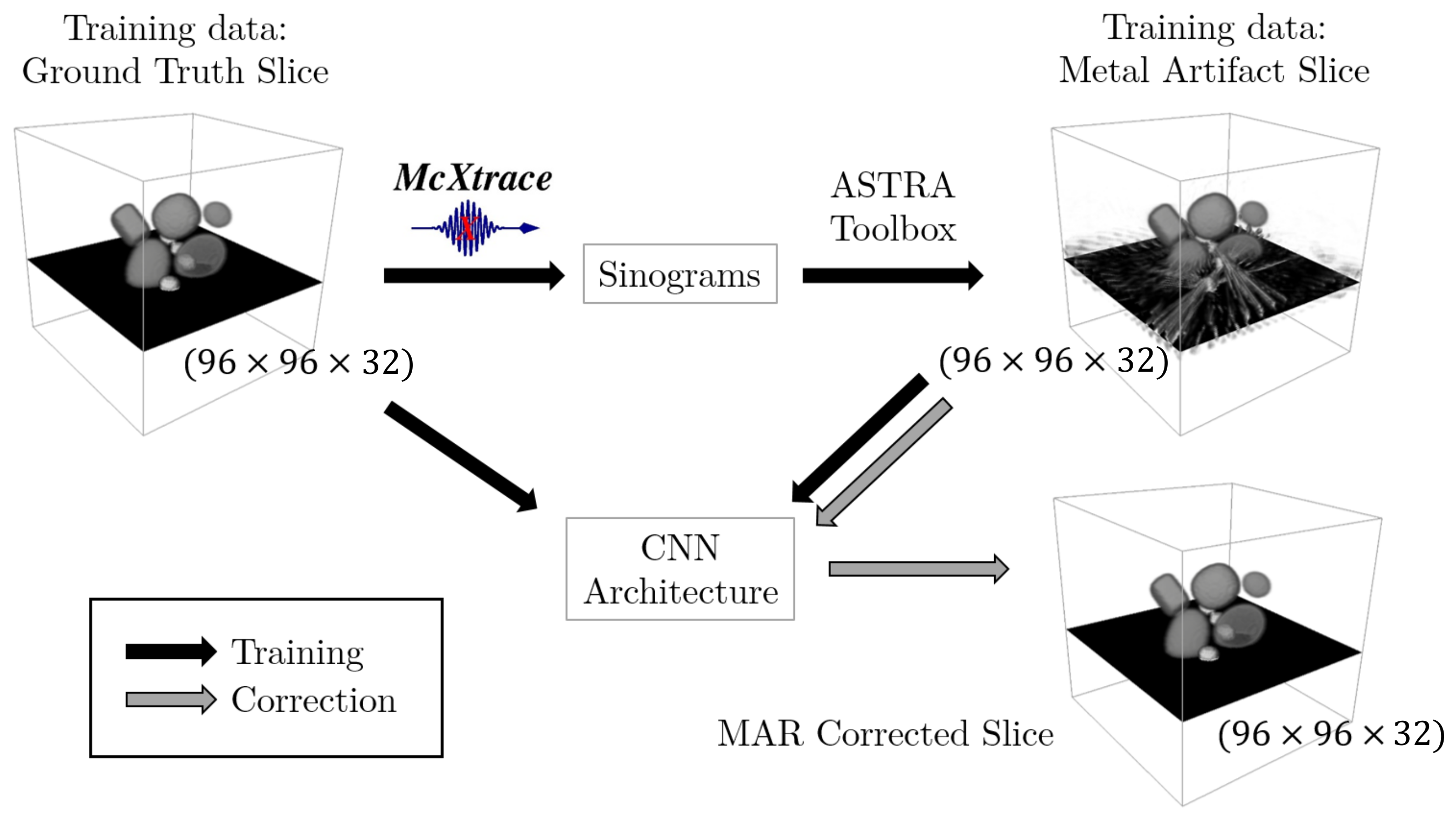
2.1. Training Data
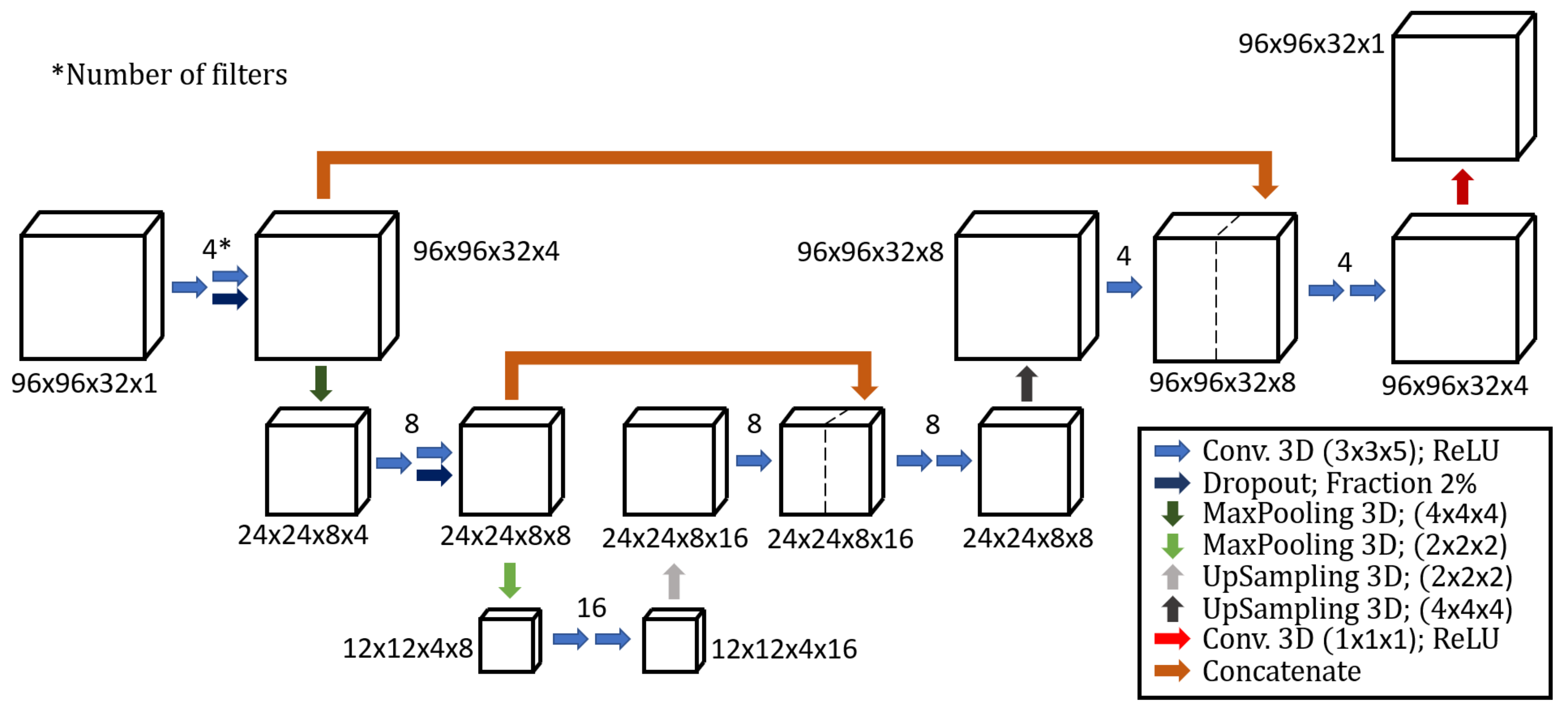
2.2. Spectral CNN Architecture
- Conv. 3D: These are layers of the network consisting of a defined number of 3D convolutional filters with defined size. These filters are the main units (or neurons) of the network as they contain all the coefficients being tuned during the training process. Note that the number of filters at each step defines the fourth dimension of the incoming dataset in Figure 3. The Rectified Linear Units (ReLU) apply the function to all the values in the input volume, which replaces all the negative activation with zeros. ReLU is applied after each convolutional layer to introduce non-linearity.
- Dropout: During training, some training entities (i.e., pixels) are randomly chosen and ignored or, in other terms, dropped. This step is introduced to avoid overfitting, as suggested by Srivastava et al. [36].
- MaxPooling: Max pooling refers to the step of applying a maximum filter to (usually) non-overlapping sub-regions of the initial representation, and it is necessary to reduce the dimension of the data while preserving the features. For example, a 3D MaxPooling with size halves the size data in each of the three dimensions.
- UpSampling: Works as opposite of the MaxPooling operation. By default, this is conducted by padding the matrix cells with zero values. Alternatively, the upsampling can be carried out with interpolation.
- Concatenate: This step concatenates datasets along a chosen dimension. For example, the concatenation in the first layer of the CNN architecture concatenates the data preceding the MaxPooling and the data connected to the 4 filters convolutional layers, both with a size of , into a single data with size .
2.3. Issues Faced in MAR Development
3. Experiments
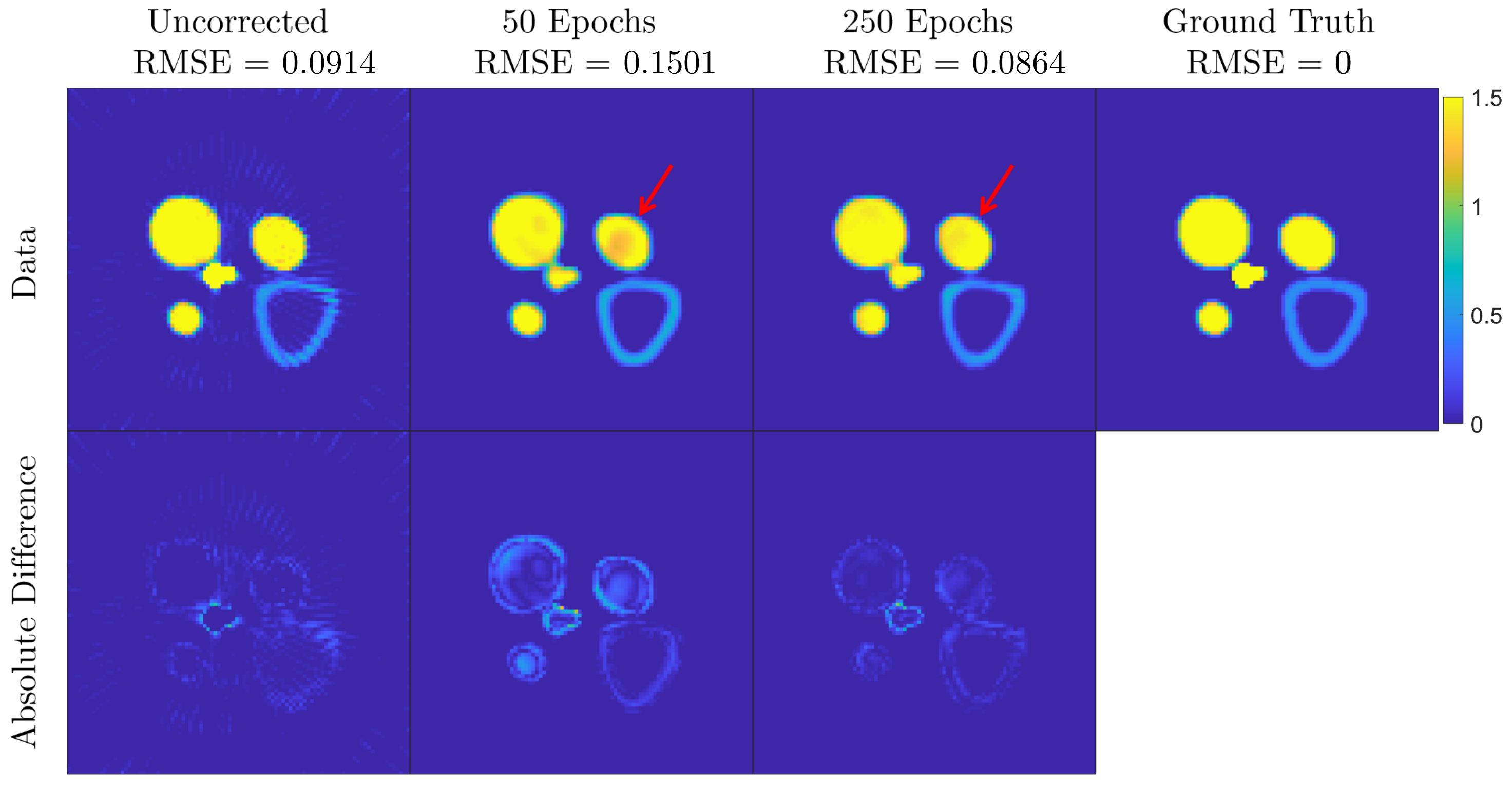
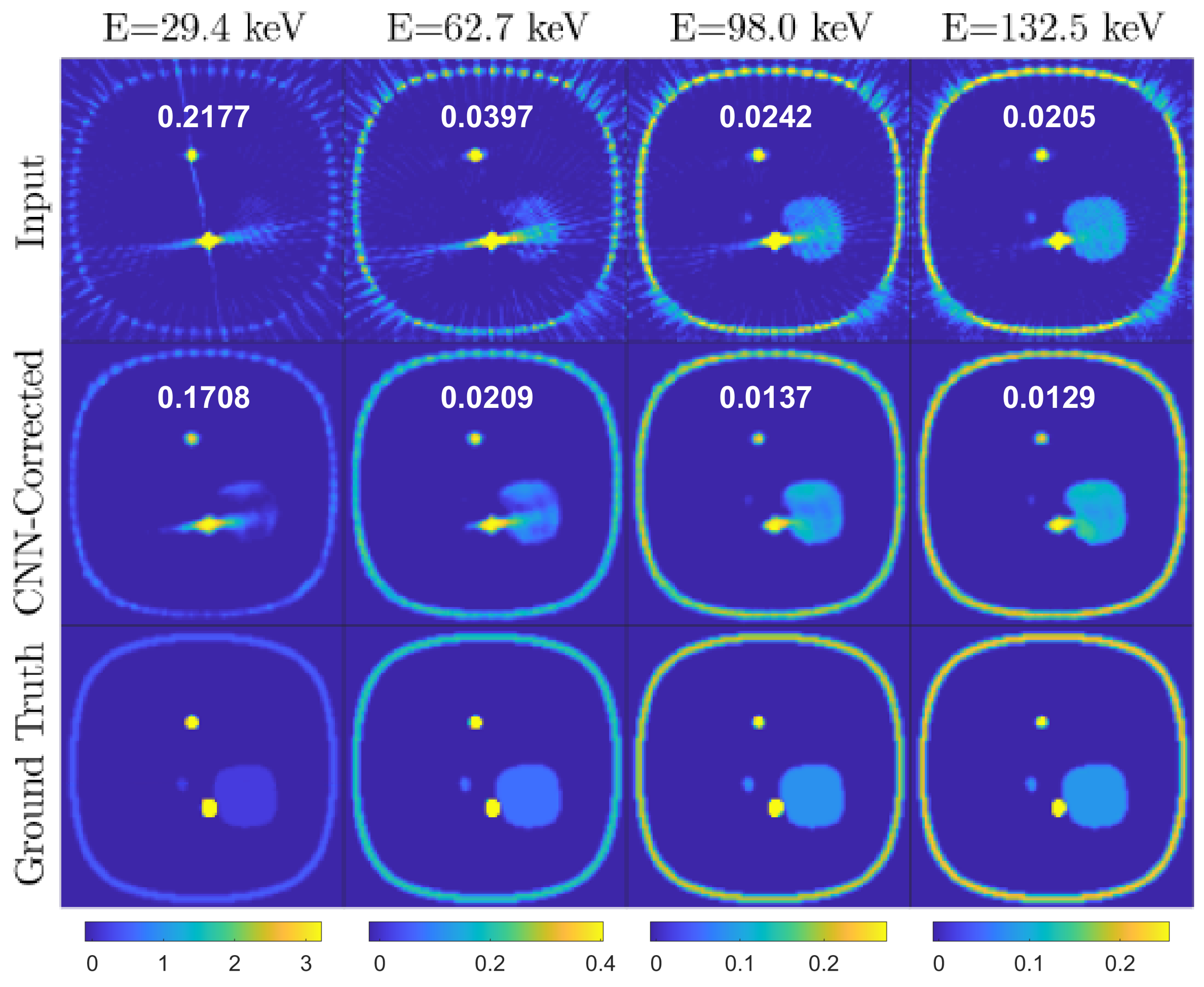
3.1. Simulation Test Data
- Root Mean Squared Error ():where is the number of pixels in the ground truth () and CNN corrected () energy resolved reconstructions.
- Normalized Root Mean Squared Error ():which is RMSE divided by the mean of the ground truth pixel values.
- Mean Structural Similarity (MSSIM). Structural Similarity (SSIM) is a method for measuring the similarity between two images presented by Wang et al. [38]. This method returns an image with the same size as the input images, with values ranging from −1 to 1 taking maximum value when the two images are identical. In the MSSIM, a single index value is calculated as the mean value over the SSIM image.
Results and Discussion
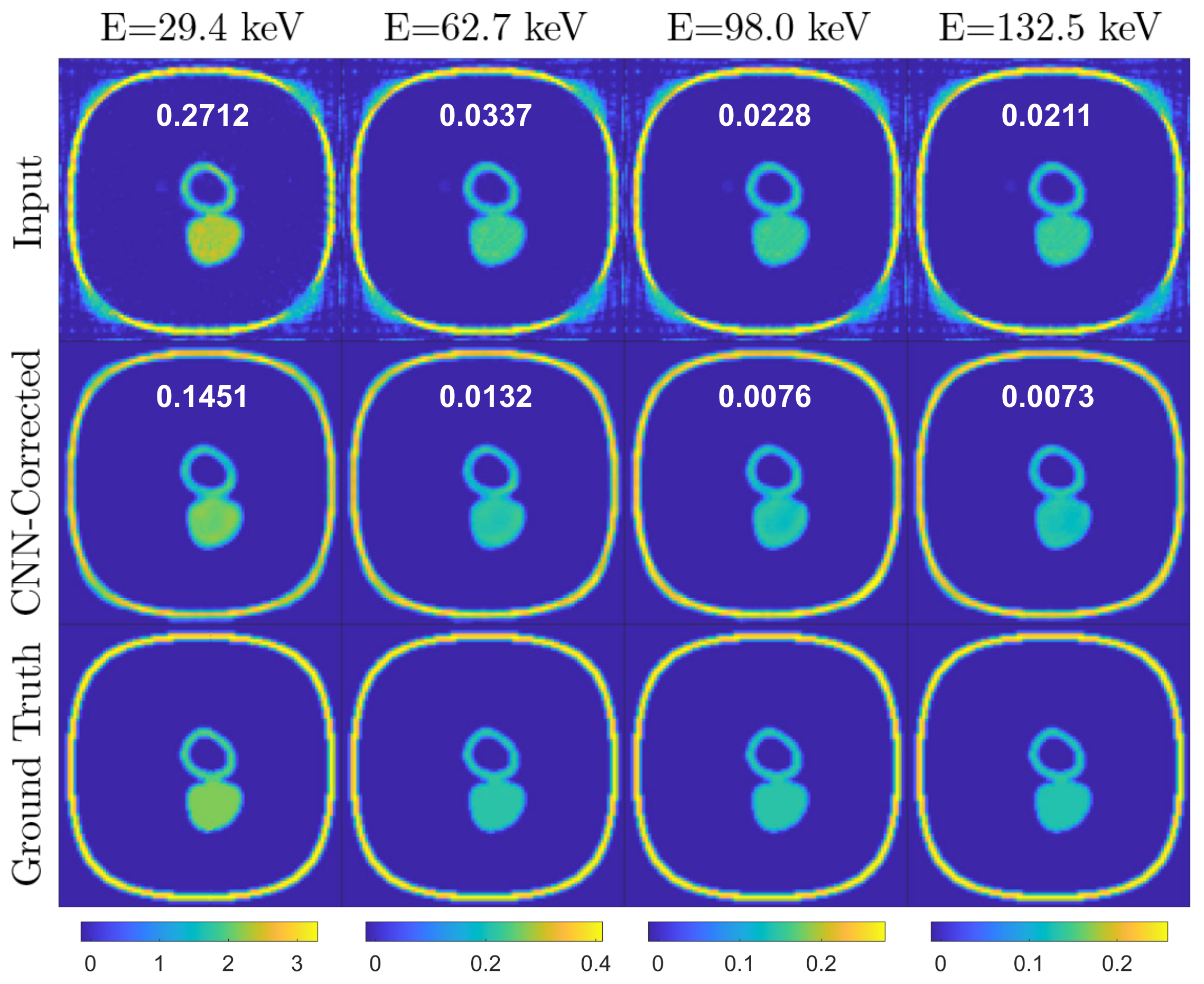
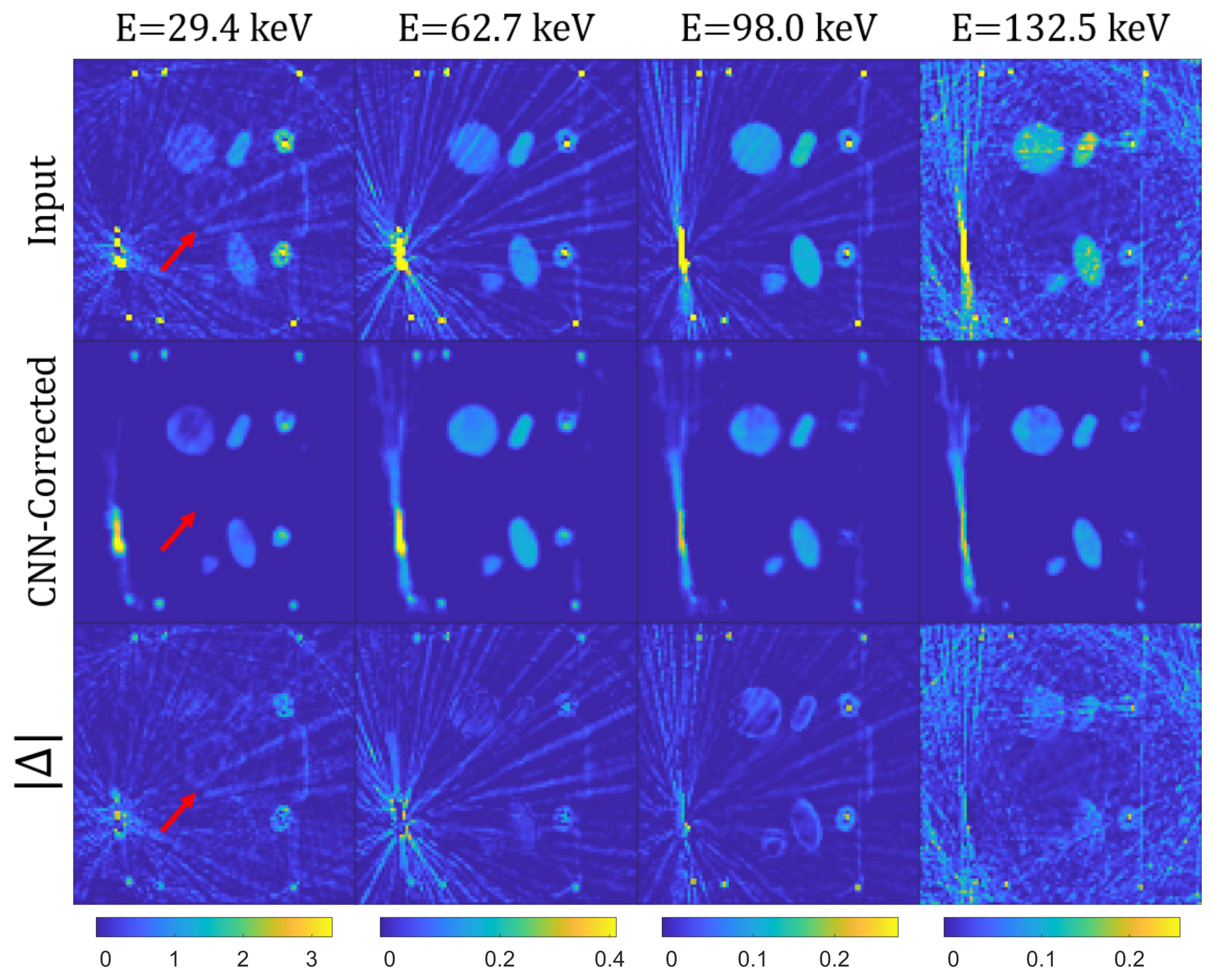
3.2. Experimental Test Data
Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shikhaliev, P.M. Energy-resolved computed tomography: First experimental results. Phys. Med. Biol. 2008, 53, 5595. [Google Scholar] [CrossRef] [PubMed]
- Anderson, N.; Butler, A.; Scott, N.; Cook, N.; Butzer, J.; Schleich, N.; Firsching, M.; Grasset, R.; De Ruiter, N.; Campbell, M.; et al. Spectroscopic (multi-energy) CT distinguishes iodine and barium contrast material in MICE. Eur. Radiol. 2010, 20, 2126–2134. [Google Scholar] [CrossRef] [PubMed]
- Fornaro, J.; Leschka, S.; Hibbeln, D.; Butler, A.; Anderson, N.; Pache, G.; Scheffel, H.; Wildermuth, S.; Alkadhi, H.; Stolzmann, P. Dual-and multi-energy CT: Approach to functional imaging. Insights Imaging 2011, 2, 149–159. [Google Scholar] [CrossRef] [Green Version]
- Rebuffel, V.; Rinkel, J.; Tabary, J.; Verger, L. New perspectives of X-ray techniques for explosive detection based on CdTe/CdZnTe spectrometric detectors. In Proceedings of the International Symposium on Digital Industrial Radiology and Computed Tomography, Berlin, Germany, 20–22 June 2011; Volume 2. [Google Scholar]
- Wang, X.; Meier, D.; Taguchi, K.; Wagenaar, D.J.; Patt, B.E.; Frey, E.C. Material separation in X-ray CT with energy resolved photon-counting detectors. Med. Phys. 2011, 38, 1534–1546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Busi, M.; Mohan, K.A.; Dooraghi, A.A.; Champley, K.M.; Martz, H.E.; Olsen, U.L. Method for system-independent material characterization from spectral X-ray CT. NDT E Int. 2019, 107, 102136. [Google Scholar] [CrossRef]
- Busi, M.; Kehres, J.; Khalil, M.; Olsen, U.L. Effective atomic number and electron density determination using spectral X-ray CT. In Anomaly Detection and Imaging with X-rays (ADIX) IV; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 10999, p. 1099903. [Google Scholar]
- Jumanazarov, D.; Koo, J.; Busi, M.; Poulsen, H.F.; Olsen, U.L.; Iovea, M. System-independent material classification through X-ray attenuation decomposition from spectral X-ray CT. NDT E Int. 2020, 116, 102336. [Google Scholar] [CrossRef]
- Wang, G.; Frei, T.; Vannier, M.W. Fast iterative algorithm for metal artifact reduction in X-ray CT. Acad. Radiol. 2000, 7, 607–614. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Xing, L. Metal artifact reduction in X-ray computed tomography (CT) by constrained optimization. Med. Phys. 2011, 38, 701–711. [Google Scholar] [CrossRef] [Green Version]
- Karimi, S.; Martz, H.; Cosman, P. Metal artifact reduction for CT-based luggage screening. J. X-ray Sci. Technol. 2015, 23, 435–451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mouton, A.; Megherbi, N.; Flitton, G.T.; Bizot, S.; Breckon, T.P. A novel intensity limiting approach to metal artefact reduction in 3D CT baggage imagery. In Proceedings of the 2012 19th IEEE International Conference on Image Processing, Orlando, FL, USA, 30 September–3 October 2012; pp. 2057–2060. [Google Scholar]
- Cai, L.; Gao, J.; Zhao, D. A review of the application of deep learning in medical image classification and segmentation. Ann. Transl. Med. 2020, 8, 713. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.; Zeng, H.; Li, A.; Ngai, E.W.T. Deep learning in computer vision: A critical review of emerging techniques and application scenarios. Mach. Learn. Appl. 2021, 6, 100134. [Google Scholar] [CrossRef]
- Minaee, S.; Boykov, Y.Y.; Porikli, F.; Plaza, A.J.; Kehtarnavaz, N.; Terzopoulos, D. Image Segmentation Using Deep Learning: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022. [Google Scholar] [CrossRef] [PubMed]
- Gjesteby, L.; Yang, Q.; Xi, Y.; Shan, H.; Claus, B.; Jin, Y.; De Man, B.; Wang, G. Deep learning methods for CT image-domain metal artifact reduction. In Developments in X-ray Tomography XI; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 10391, p. 103910W. [Google Scholar]
- Ghani, M.U.; Karl, W.C. Deep learning based sinogram correction for metal artifact reduction. Electron. Imaging 2018, 2018, 472-1–472-8. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, H. Convolutional neural network based metal artifact reduction in X-ray computed tomography. IEEE Trans. Med. Imaging 2018, 37, 1370–1381. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Prinsen, P.; Wiegert, J.; Manjeshwar, R. Deep residual learning in CT physics: Scatter correction for spectral CT. In Proceedings of the 2017 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), Atlanta, GA, USA, 21–28 October 2017; pp. 1–3. [Google Scholar]
- Maier, J.; Sawall, S.; Knaup, M.; Kachelrieß, M. Deep Scatter Estimation (DSE): Accurate Real-Time Scatter Estimation for X-ray CT Using a Deep Convolutional Neural Network. J. Nondestruct. Eval. 2018, 37, 57. [Google Scholar] [CrossRef] [Green Version]
- Fang, W.; Li, L.; Chen, Z. Removing Ring Artefacts for Photon-Counting Detectors Using Neural Networks in Different Domains. IEEE Access 2020, 8, 42447–42457. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y.; Zhang, W.; Liao, P.; Li, K.; Zhou, J.; Wang, G. Low-dose CT via convolutional neural network. Biomed. Opt. Express 2017, 8, 679–694. [Google Scholar] [CrossRef] [PubMed]
- Kang, E.; Min, J.; Ye, J.C. A deep convolutional neural network using directional wavelets for low-dose X-ray CT reconstruction. Med. Phys. 2017, 44, e360–e375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning dense volumetric segmentation from sparse annotation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2016; pp. 424–432. [Google Scholar]
- Wu, W.; Hu, D.; Niu, C.; Broeke, L.V.; Butler, A.P.; Cao, P.; Atlas, J.; Chernoglazov, A.; Vardhanabhuti, V.; Wang, G. Deep learning based spectral CT imaging. Neural Netw. 2021, 144, 342–358. [Google Scholar] [CrossRef]
- Lai, Z.; Li, L.; Cao, W. Metal artifact reduction with deep learning based spectral CT. In Proceedings of the International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI 2021), Beijing, China, 17–19 October 2021. [Google Scholar]
- Kong, F.; Cheng, M.; Wang, N.; Cao, H.; Shi, Z. Metal Artifact Reduction by Using Dual-Energy Raw Data Constraint Learning. In Proceedings of the International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI 2021), Beijing, China, 17–19 October 2021. [Google Scholar]
- Van Aarle, W.; Palenstijn, W.J.; De Beenhouwer, J.; Altantzis, T.; Bals, S.; Batenburg, K.J.; Sijbers, J. The ASTRA Toolbox: A platform for advanced algorithm development in electron tomography. Ultramicroscopy 2015, 157, 35–47. [Google Scholar] [CrossRef] [Green Version]
- Kazantsev, D.; Pickalov, V.; Nagella, S.; Pasca, E.; Withers, P.J. TomoPhantom, a software package to generate 2D–4D analytical phantoms for CT image reconstruction algorithm benchmarks. SoftwareX 2018, 7, 150–155. [Google Scholar] [CrossRef]
- Berger, M.J.; Hubbell, J. XCOM: Photon Cross Sections on a Personal Computer; Technical Report; Center for Radiation, National Bureau of Standards: Washington, DC, USA, 1987. [Google Scholar]
- Busi, M.; Olsen, U.L.; Knudsen, E.B.; Frisvad, J.R.; Kehres, J.; Dreier, E.S.; Khalil, M.; Haldrup, K. Simulation tools for scattering corrections in spectrally resolved X-ray computed tomography using McXtrace. Opt. Eng. 2018, 57, 037105. [Google Scholar] [CrossRef] [Green Version]
- Bergbäck Knudsen, E.; Prodi, A.; Baltser, J.; Thomsen, M.; Kjær Willendrup, P.; Sanchez del Rio, M.; Ferrero, C.; Farhi, E.; Haldrup, K.; Vickery, A.; et al. McXtrace: A Monte Carlo software package for simulating X-ray optics, beamlines and experiments. J. Appl. Crystallogr. 2013, 46, 679–696. [Google Scholar] [CrossRef]
- Ng, A. Machine Learning. Available online: https://www.coursera.org/learn/machine-learning (accessed on 1 May 2018).
- KerasTeam. Keras: Deep Learning for Humans. 2019. Available online: https://github.com/keras-team/keras (accessed on 1 May 2018).
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sidky, E.Y.; Kao, C.M.; Pan, X. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT. J. X-ray Sci. Technol. 2006, 14, 119–139. [Google Scholar]



| Data | RMSE | NRMSE | MSSIM |
|---|---|---|---|
| Uncorrected | 0.0035 | 0.12 | 0.926 |
| 50 epochs | 0.0031 | 0.13 | 0.978 |
| 250 epochs | 0.0020 | 0.09 | 0.990 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Busi, M.; Kehl, C.; Frisvad, J.R.; Olsen, U.L. Metal Artifact Reduction in Spectral X-ray CT Using Spectral Deep Learning. J. Imaging 2022, 8, 77. https://doi.org/10.3390/jimaging8030077
Busi M, Kehl C, Frisvad JR, Olsen UL. Metal Artifact Reduction in Spectral X-ray CT Using Spectral Deep Learning. Journal of Imaging. 2022; 8(3):77. https://doi.org/10.3390/jimaging8030077
Chicago/Turabian StyleBusi, Matteo, Christian Kehl, Jeppe R. Frisvad, and Ulrik L. Olsen. 2022. "Metal Artifact Reduction in Spectral X-ray CT Using Spectral Deep Learning" Journal of Imaging 8, no. 3: 77. https://doi.org/10.3390/jimaging8030077
APA StyleBusi, M., Kehl, C., Frisvad, J. R., & Olsen, U. L. (2022). Metal Artifact Reduction in Spectral X-ray CT Using Spectral Deep Learning. Journal of Imaging, 8(3), 77. https://doi.org/10.3390/jimaging8030077







