Fabrication of a Human Skin Mockup with a Multilayered Concentration Map of Pigment Components Using a UV Printer
Abstract
:1. Introduction
2. Previous Works
2.1. Skin Pigment Separation
2.2. Estimation of the Layered Ink Layout
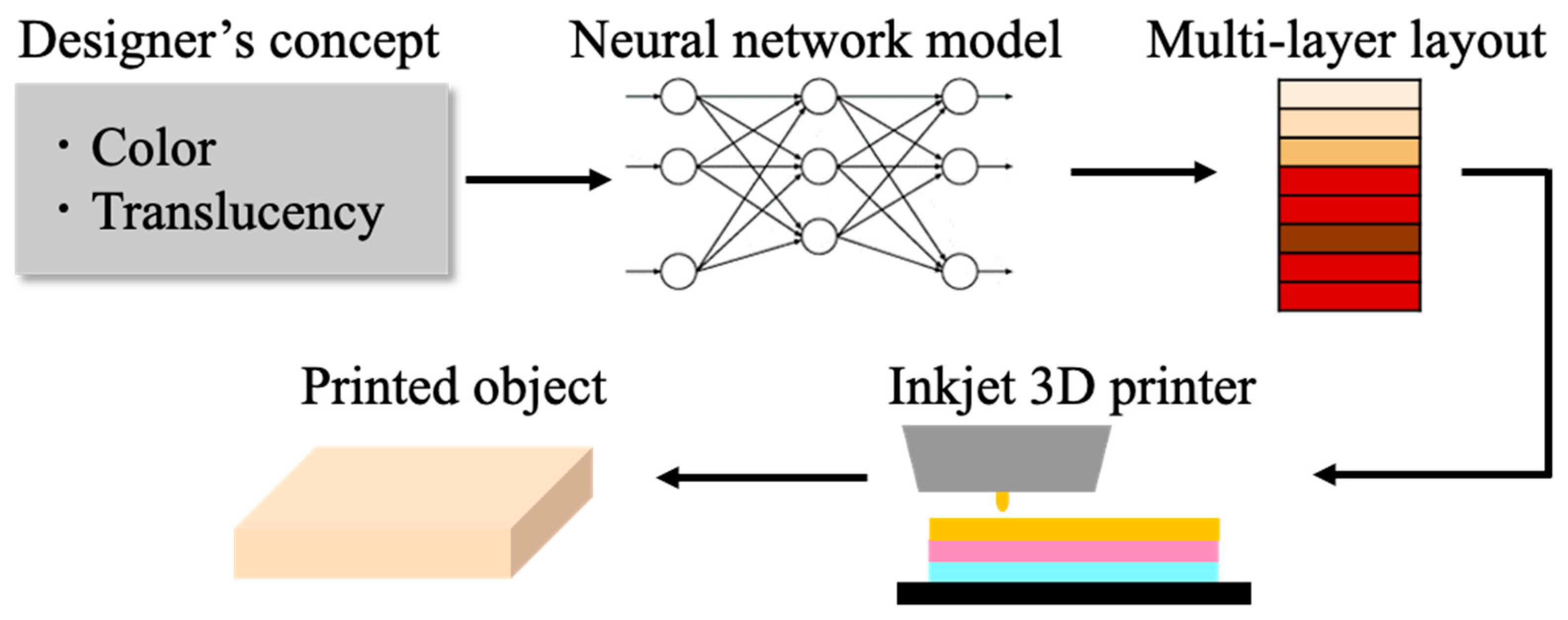
3. Overview of the Proposed Method
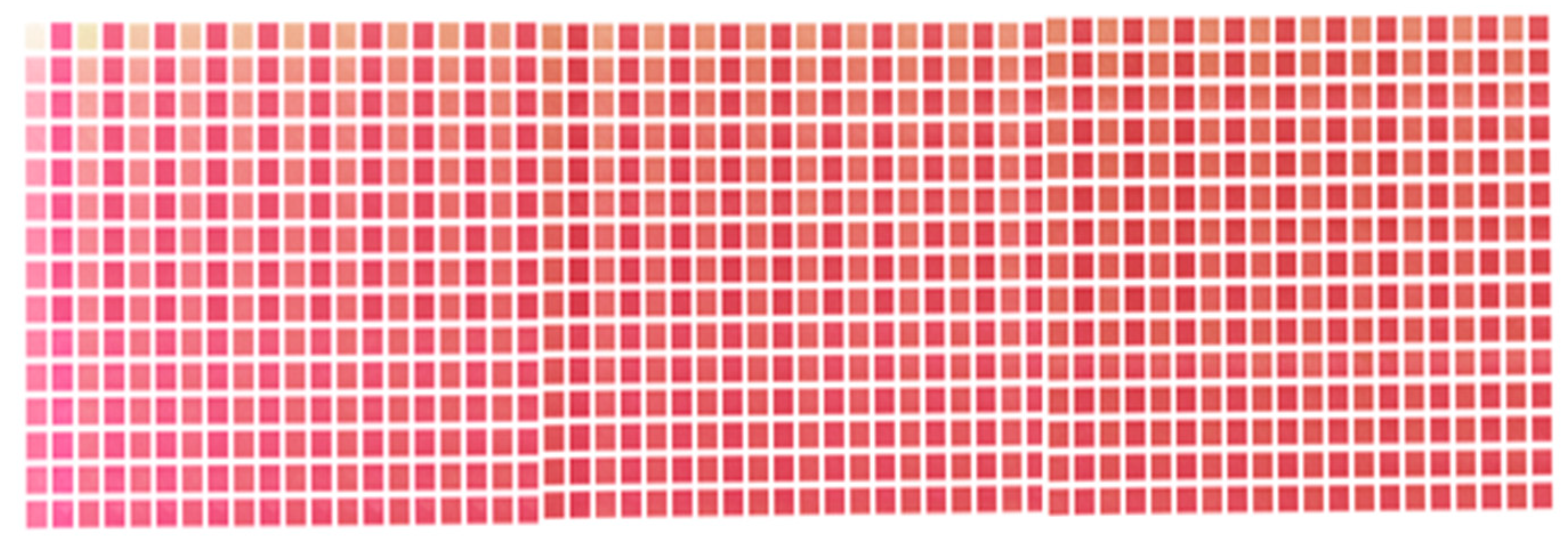
4. Color Patches for Human Skin
4.1. Condition of Color Patches
4.2. Modeling of Color Patches
5. Conversion of Pigment Concentration to CMYK
5.1. Lookup Table
5.2. Multiple Regression Analysis
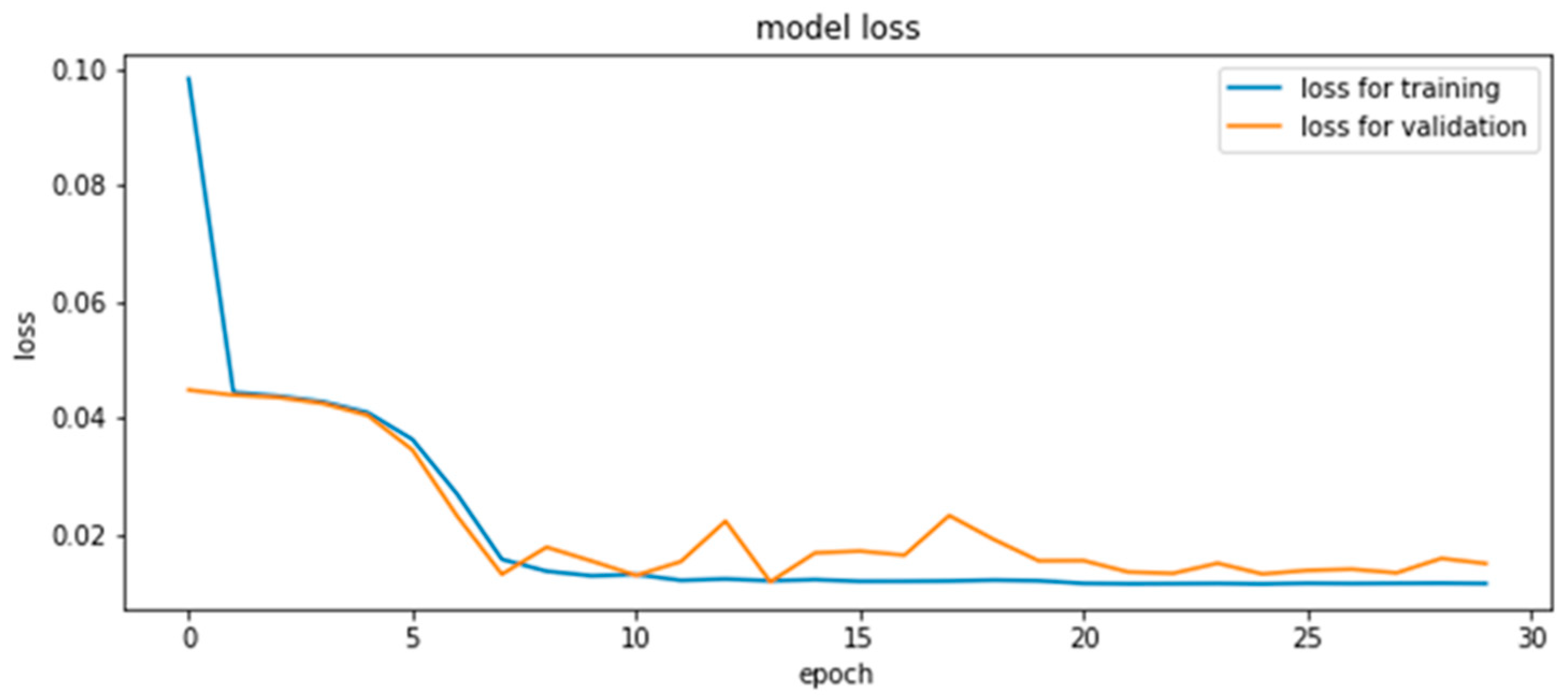
5.3. Neural Network
6. Fabrication of Human Skin
6.1. Comparison of Methods
6.2. Number of Clear Layers
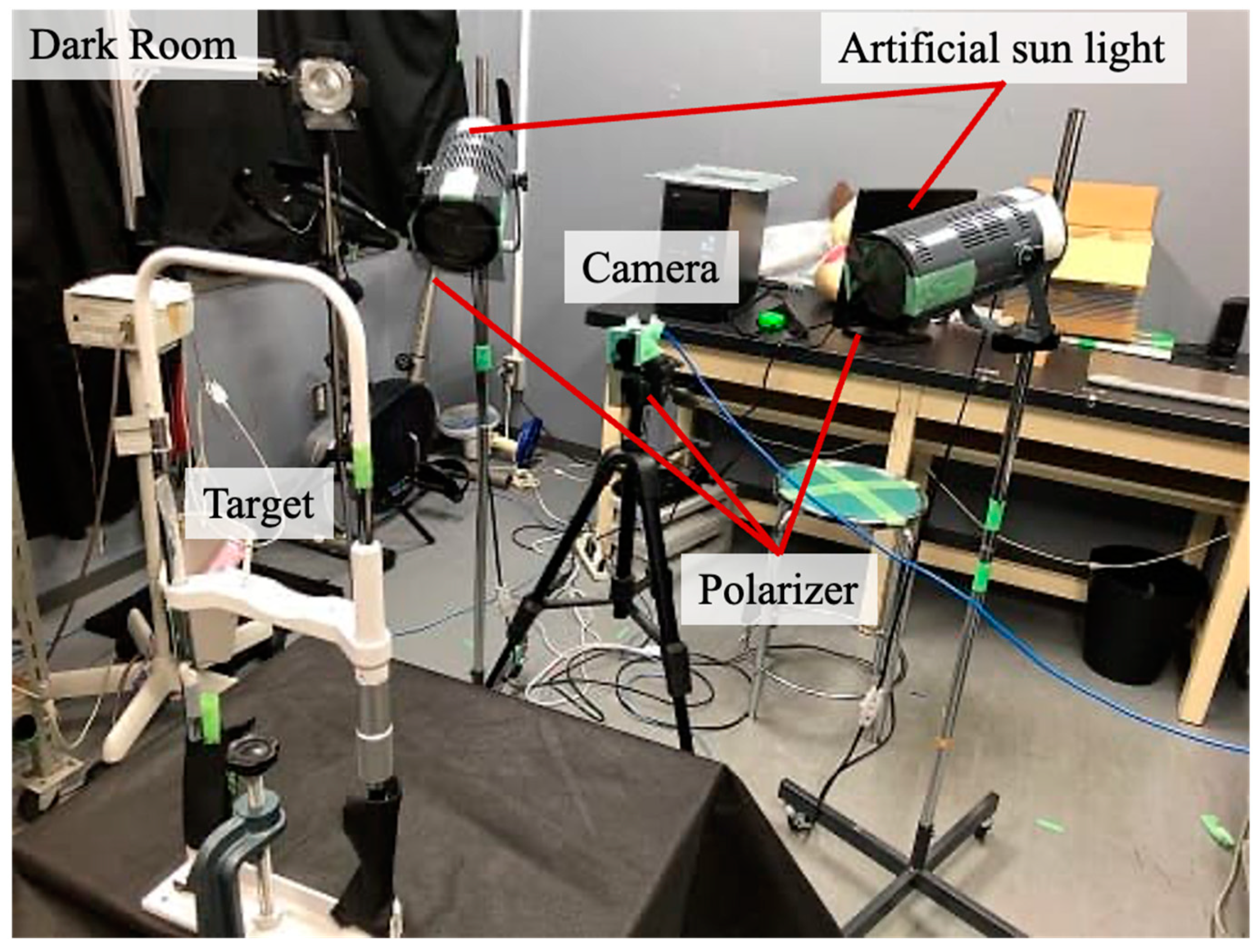
7. Subjective Evaluation
7.1. Evaluation Method
7.2. Evaluation Results
8. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Lee, V.C. Medical applications for 3D printing: Current and projected uses. Pharm. Ther. 2014, 39, 704. [Google Scholar]
- Dawood, A.B.; Marti, M.; Sauret-Jackson, V.; Darwood, A. 3D printing in dentistry. Br. Dent. J. 2015, 219, 521. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Q.; Cai, X.; Zhou, S.; Kobe, B.; Yang, J. Initiator-Integrated 3D Printing Enables the Formation of Complex Metallic Architectures. ACS Appl. Mater. Interfaces 2013, 6, 2583–2587. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Chen, G.; Li, H.; Prautzsch, H.; Xiao, K. Accurate and Computational: A review of color reproduction in Full-color 3D printing. Mater. Des. 2021, 209, 109943. [Google Scholar] [CrossRef]
- Brunton, A.; Arikan, C.A.; Urban, P. Pushing the limits of 3D color printing: Error diffusion with translucent materials. ACM Trans. Graph. (TOG) 2015, 35, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Sun, P.-L.; Sie, Y.-P. Color Uniformity Improvement for an Inkjet Color 3D Printing System. Electron. Imaging 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- Babaei, V.; Vidimče, K.; Foshey, M.; Kaspar, A.; Didyk, P.; Matusik, W. Color contoning for 3D printing. ACM Trans. Graph. (TOG) 2017, 36, 1–15. [Google Scholar] [CrossRef]
- Shi, L.; Babaei, V.; Kim, C.; Foshey, M.; Hu, Y.; Sitthi-Amorn, P.; Rusinkiewicz, S.; Matusik, W. Deep multispectral painting reproduction via multi-layer, custom-ink printing. ACM Trans. Graph. 2018, 37, 271. [Google Scholar] [CrossRef]
- Baar, T.; Brettel, H.; Segovia, M.V.O. Towards gloss control in fine art reproduction. In Measuring, Modeling, and Reproducing Material Appearance; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9398, p. 93980T. [Google Scholar]
- Piovarči, M.; Foshey, M.; Babaei, V.; Rusinkiewicz, S.; Matusik, W.; Didyk, P. Towards spatially varying gloss reproduction for 3D printing. ACM Trans. Graph. 2020, 39, 206. [Google Scholar] [CrossRef]
- Hašan, M.; Fuchs, M.; Matusik, W.; Pfister, H.; Rusinkiewicz, S. Physical reproduction of materials with specified subsurface scattering. In Proceedings of the ACM SIGGRAPH 2010, Los Angeles, CA, USA, 26–30 July 2010; Voulme 2010, p. 61. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, J.; Pellacini, F.; Tong, X.; Guo, B. Fabricating spatially-varying subsurface scattering. In Proceedings of the ACM SIGGRAPH 2010, Los Angeles, CA, USA, 26–30 July 2010; Voulem 2010, p. 62. [Google Scholar]
- Elek, O.; Sumin, D.; Zhang, R.; Weyrich, T.; Myszkowski, K.; Bickel, B.; Wilkie, A.; Křivánek, J. Scattering-aware texture reproduction for 3D printing. ACM Trans. Graph. 2017, 36, 241. [Google Scholar] [CrossRef] [Green Version]
- Papas, M.; Regg, C.; Jarosz, W.; Bickel, B.; Jackson, P.; Matusik, W.; Marschner, S.; Gross, M. Fabricating translucent materials using continuous pigment mixtures. ACM Trans. Graph. 2013, 32, 146. [Google Scholar] [CrossRef]
- Brunton, A.; Arikan, C.A.; Tanksale, T.M.; Urban, P. 3D printing spatially varying color and translucency. ACM Trans. Graph. 2018, 37, 157. [Google Scholar] [CrossRef] [Green Version]
- Urban, P.; Tanksale, T.M.; Brunton, A.; Vu, B.M.; Nakauchi, S. Redefining a in rgba: Towards a standard for graphical 3d printing. ACM Trans. Graph. (TOG) 2019, 38, 21. [Google Scholar] [CrossRef] [Green Version]
- Takatani, T.; Fujita, K.; Tanaka, K.; Funatomi, T.; Mukaigawa, Y. Controlling translucency by UV printing on a translucent object. IPSJ Trans. Comput. Vis. Appl. 2018, 10, 7. [Google Scholar] [CrossRef]
- Donner, C.; Weyrich, T.; D’Eon, E.; Ramamoorthi, R.; Rusinkiewicz, S. A layered, heterogeneous reflectance model for acquiring and rendering human skin. ACM Trans. Graph. 2008, 27, 140. [Google Scholar] [CrossRef]
- Donner, C.; Jensen, H.W. Light diffusion in multi-layered translucent materials. ACM Trans. Graph. 2005, 24, 1032–1039. [Google Scholar] [CrossRef]
- Tsumura, N.; Kawabuchi, M.; Haneishi, H.; Miyake, Y. Mapping pigmentation in human skin from a multi-channel visible spectrum image by inverse optical scattering technique. J. Imaging Sci. Technol. 2001, 45, 444–450. [Google Scholar]
- Lin, M.; Iuchi, K.; Ono, K.; Ogawa-Ochiai, K.; Tsumura, N. Estimation of blood concentration at different skin depths using a spectroscopic camera. Artif. Life Robot. 2022, 27, 80–89. [Google Scholar] [CrossRef]
- Iuchi, K.; Igarashi, T.; Ojima, N.; Ogawa-Ochiai, K.; Tsumura, N. Spectral-based estimation of components concentration in skin tissue layers with independence of shading via optical modeling of skin tissue. Artif. Life Robot. 2022, 27, 9–18. [Google Scholar] [CrossRef]
- Tsumura, N.; Ojima, N.; Nakaguchi, T.; Miyake, Y. Skin Color Separation and Synthesis for E-Cosmetics. In Signal Processing Techniques for Knowledge Extraction and Information Fusion; Springer: Boston, MA, USA, 2008; pp. 201–220. [Google Scholar]
- Nagasawa, K.; Yoshii, J.; Yamamoto, S.; Arai, W.; Kaneko, S.; Hirai, K.; Tsumura, N. Prediction of the layered ink layout for 3D printers considering a desired skin color and line spread function. Opt. Rev. 2021, 28, 449–461. [Google Scholar] [CrossRef]
- Nagasawa, K.; Fukumoto, K.; Arai, W.; Hakkaku, K.; Kaneko, S.; Hirai, K.; Tsumura, N. Layout Estimation for Layered Ink of 3D Printer to Reproduce the Desired Line Spread Function of Skin using Simulated Data1. J. Imaging Sci. Technol. 2021, 65, 50501-1–50501-12. [Google Scholar] [CrossRef]
- Tsumura, N.; Ojima, N.; Sato, K.; Shiraishi, M.; Shimizu, H.; Nabeshima, H.; Akazaki, S.; Hori, K.; Miyake, Y. Image-based skin color and texture analysis/synthesis by extracting hemoglobin and melanin information in the skin. ACM Trans. Graph. 2003, 22, 770–779. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Tsumura, N.; Haneishi, H.; Miyake, Y. Independent-component analysis of skin color image. J. Opt. Soc. Am. A 1999, 16, 2169–2176. [Google Scholar] [CrossRef] [PubMed]
- Shimada, M.; Masuda, Y.; Yamada, Y.; Itoh, M.; Takahashi, M.; Yatagai, T. Explanation of Human Skin Color by Multiple Linear Regression Analysis Based on the Modified Lambert-Beer Law. Opt. Rev. 2000, 7, 348–352. [Google Scholar] [CrossRef]
- Tominaga, S. Color control using neural networks and its application. In Color Imaging: Device-Independent Color, Color Hard Copy, and Graphic Arts; International Society for Optics and Photonics: Bellingham, WA, USA, 1996; Volume 2658, pp. 253–260. [Google Scholar] [CrossRef]
- Meglinsky, I.V.; Matcher, S.J. Modelling the sampling volume for skin blood oxygenation measurements. Med. Biol. Eng. Comput. 2001, 39, 44–50. [Google Scholar] [CrossRef]
- Kearns, M.; Ron, D. Algorithmic Stability and Sanity-Check Bounds for Leave-One-Out Cross-Validation. Neural Comput. 1999, 11, 1427–1453. [Google Scholar] [CrossRef]
- Patterson, J.; Gibson, A. Deep Learning: A Practitioner’s Approach; O’Reilly Media: Newton, MA, USA, 2017. [Google Scholar]
- Mimaki Engineering. 3DUJ-553. 2021. Available online: https://japan.mimaki.com/product/3d/3d-inkjet/3duj-553/ (accessed on 9 March 2022).
- Stratasys. 2021. Available online: https://www.stratasys.com/3d-printers/ (accessed on 9 March 2022).
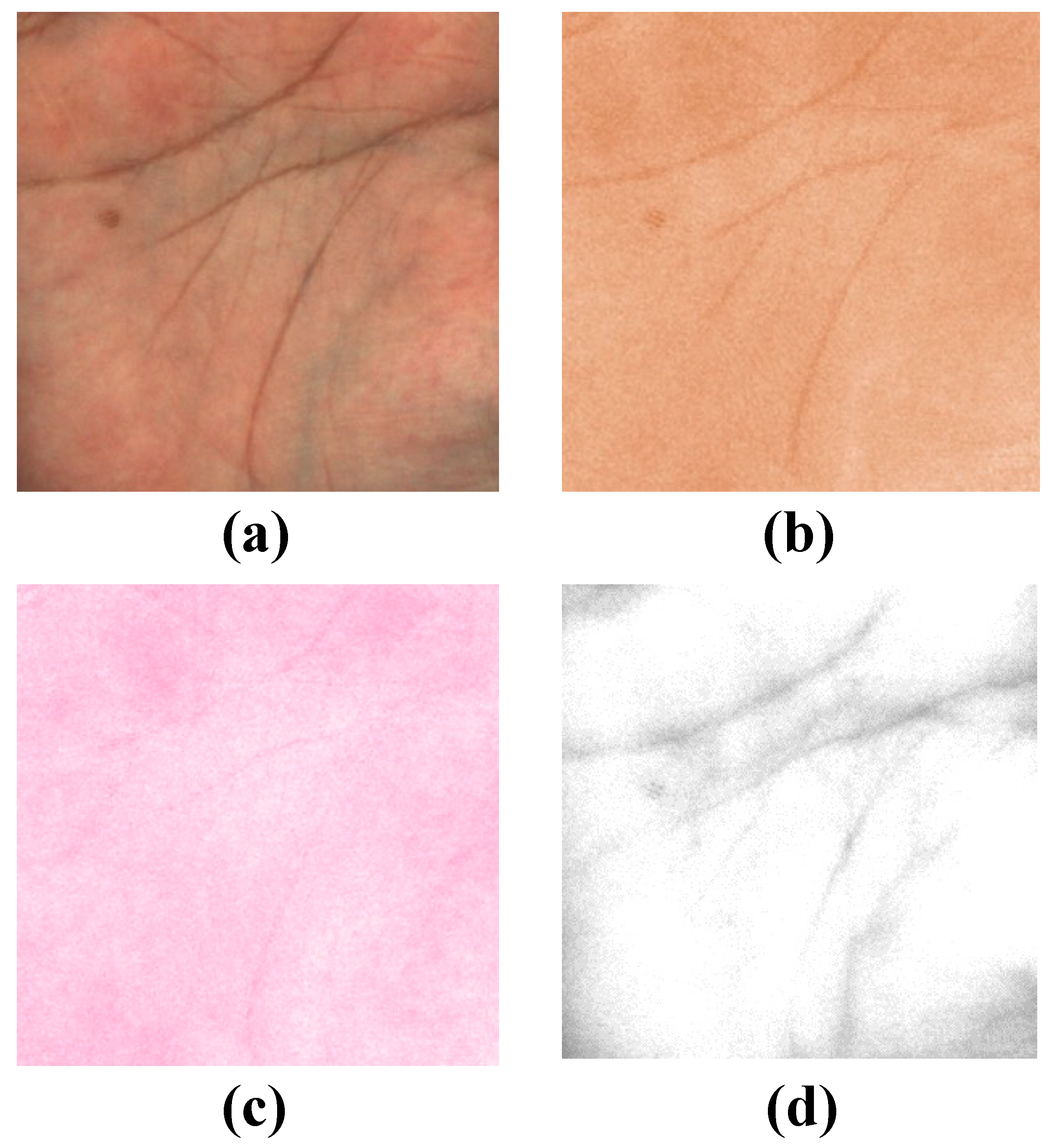
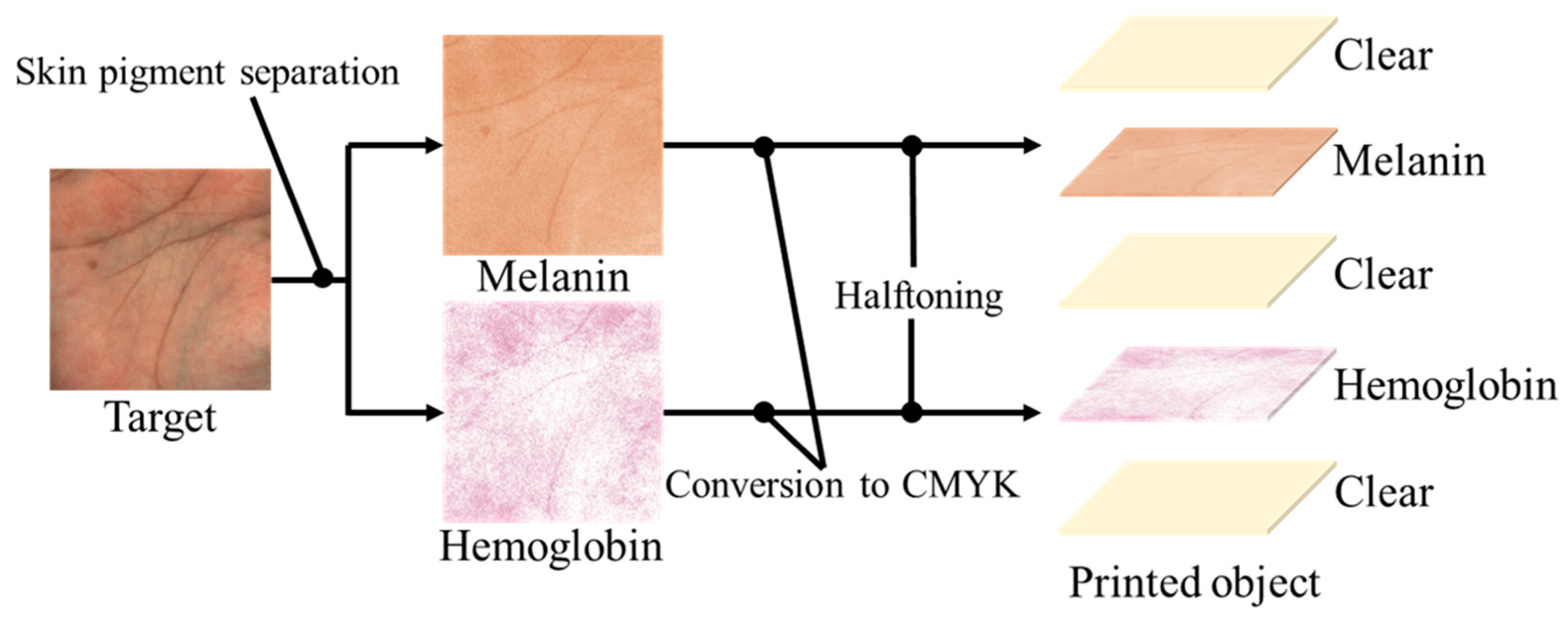




| Sample No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 2nd clear layer | 2 | 2 | 2 | 4 | 4 | 4 | 6 | 6 | 6 |
| 3rd clear layer | 2 | 4 | 6 | 2 | 4 | 6 | 2 | 4 | 6 |
| Negative | Positive |
|---|---|
| Rough | Smooth |
| Rough | Slippery |
| Not-slippery | Slippery |
| Dark | Bright |
| Sober | Brilliant |
| Mat | Glossy |
| Heavy | Light |
| Nonelastic | Elastic |
| Dry | Wet |
| Hard | Soft |
| Cold | Hot |
| Not transparent | Transparent |
| Artificial | Natural |
| Sample No. | Number of 2nd Clear Layers | Number of 3rd Clear Layers | Evaluation Value |
|---|---|---|---|
| 1 | 2 | 2 | 0.9428 |
| 2 | 2 | 4 | 1.5186 |
| 3 | 2 | 6 | 0.6254 |
| 4 | 4 | 2 | −0.5796 |
| 5 | 4 | 4 | 0.9439 |
| 6 | 4 | 6 | 1.3705 |
| 7 | 6 | 2 | −0.0477 |
| 8 | 6 | 4 | 1.3850 |
| 9 | 6 | 6 | 1.4106 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagasawa, K.; Yamamoto, S.; Arai, W.; Hakkaku, K.; Koopipat, C.; Hirai, K.; Tsumura, N. Fabrication of a Human Skin Mockup with a Multilayered Concentration Map of Pigment Components Using a UV Printer. J. Imaging 2022, 8, 73. https://doi.org/10.3390/jimaging8030073
Nagasawa K, Yamamoto S, Arai W, Hakkaku K, Koopipat C, Hirai K, Tsumura N. Fabrication of a Human Skin Mockup with a Multilayered Concentration Map of Pigment Components Using a UV Printer. Journal of Imaging. 2022; 8(3):73. https://doi.org/10.3390/jimaging8030073
Chicago/Turabian StyleNagasawa, Kazuki, Shoji Yamamoto, Wataru Arai, Kunio Hakkaku, Chawan Koopipat, Keita Hirai, and Norimichi Tsumura. 2022. "Fabrication of a Human Skin Mockup with a Multilayered Concentration Map of Pigment Components Using a UV Printer" Journal of Imaging 8, no. 3: 73. https://doi.org/10.3390/jimaging8030073
APA StyleNagasawa, K., Yamamoto, S., Arai, W., Hakkaku, K., Koopipat, C., Hirai, K., & Tsumura, N. (2022). Fabrication of a Human Skin Mockup with a Multilayered Concentration Map of Pigment Components Using a UV Printer. Journal of Imaging, 8(3), 73. https://doi.org/10.3390/jimaging8030073








