Harmonization Strategies in Multicenter MRI-Based Radiomics
Abstract
1. Introduction
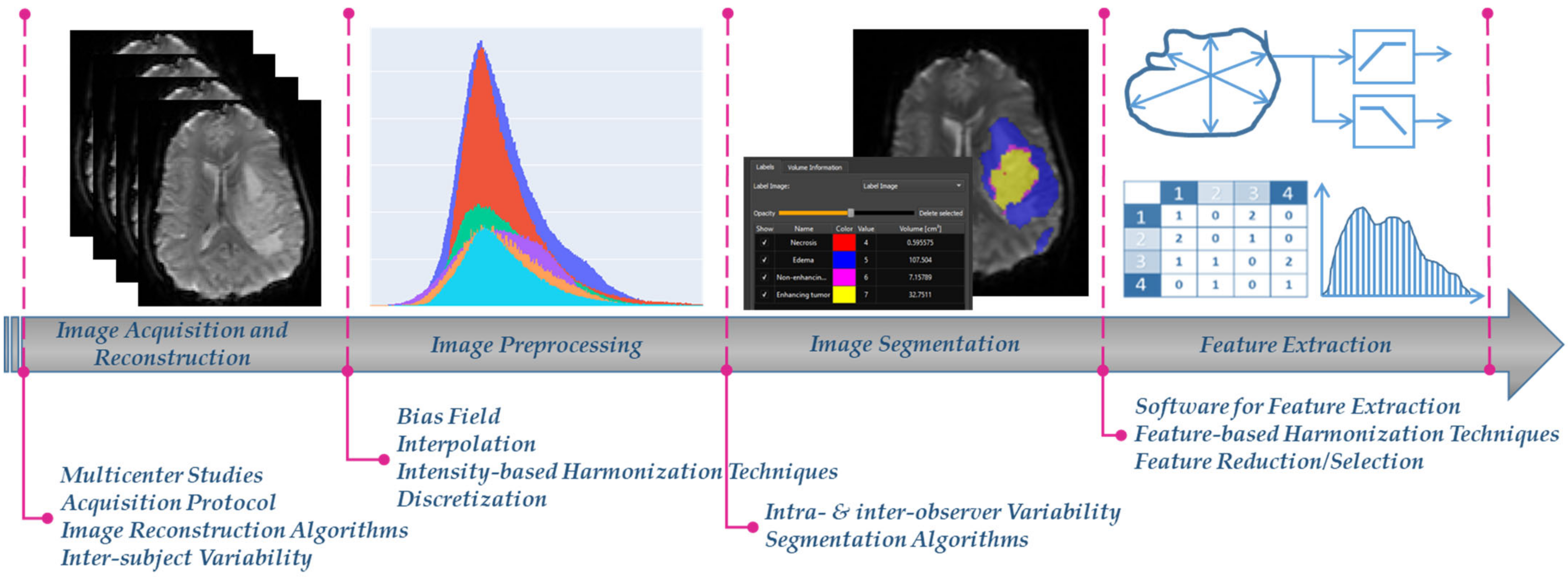
2. Image-Based Harmonization Techniques
2.1. Image Acquisition and Reconstruction
2.2. Image Preprocessing
2.2.1. Interpolation
2.2.2. Bias Field Correction
2.2.3. Intensity Normalization
2.2.4. Discretization
2.3. Image Segmentation
3. Feature-Based Harmonization Techniques
3.1. Batch Effect Reduction
3.1.1. Combining Batches (ComBat)
3.1.2. M-ComBat
3.1.3. B-ComBat, BM-ComBat
3.1.4. Transfer Learning ComBat
3.1.5. Nested ComBat, NestedD ComBat
3.1.6. GMM ComBat
3.1.7. Longitudinal ComBat
3.2. Deep Learning
3.3. Feature Extraction and Reduction/Selection
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gillies, R.J.; Kinahan, P.E.; Hricak, H. Radiomics: Images Are More than Pictures, They Are Data. Radiology 2016, 278, 563–577. [Google Scholar] [CrossRef] [PubMed]
- van Timmeren, J.E.; Cester, D.; Tanadini-Lang, S.; Alkadhi, H.; Baessler, B. Radiomics in Medical Imaging—“How-to” Guide and Critical Reflection. Insights Imaging 2020, 11, 91. [Google Scholar] [CrossRef] [PubMed]
- Mayerhoefer, M.E.; Materka, A.; Langs, G.; Häggström, I.; Szczypiński, P.; Gibbs, P.; Cook, G. Introduction to Radiomics. J. Nucl. Med. 2020, 61, 488–495. [Google Scholar] [CrossRef] [PubMed]
- Da-Ano, R.; Visvikis, D.; Hatt, M. Harmonization Strategies for Multicenter Radiomics Investigations. Phys. Med. Biol. 2020, 65, 24TR02. [Google Scholar] [CrossRef]
- Manikis, G.C.; Ioannidis, G.S.; Siakallis, L.; Nikiforaki, K.; Iv, M.; Vozlic, D.; Surlan-Popovic, K.; Wintermark, M.; Bisdas, S.; Marias, K. Multicenter DSC–MRI-Based Radiomics Predict IDH Mutation in Gliomas. Cancers 2021, 13, 3965. [Google Scholar] [CrossRef]
- Schick, U.; Lucia, F.; Dissaux, G.; Visvikis, D.; Badic, B.; Masson, I.; Pradier, O.; Bourbonne, V.; Hatt, M. MRI-Derived Radiomics: Methodology and Clinical Applications in the Field of Pelvic Oncology. Br. J. Radiol. 2019, 92, 20190105. [Google Scholar] [CrossRef]
- Cuocolo, R.; Cipullo, M.B.; Stanzione, A.; Ugga, L.; Romeo, V.; Radice, L.; Brunetti, A.; Imbriaco, M. Machine Learning Applications in Prostate Cancer Magnetic Resonance Imaging. Eur. Radiol. Exp. 2019, 3, 35. [Google Scholar] [CrossRef]
- Kocher, M.; Ruge, M.I.; Galldiks, N.; Lohmann, P. Applications of Radiomics and Machine Learning for Radiotherapy of Malignant Brain Tumors. Strahlenther. Onkol. 2020, 196, 856–867. [Google Scholar] [CrossRef]
- Ortiz-Ramón, R.; Larroza, A.; Ruiz-España, S.; Arana, E.; Moratal, D. Classifying Brain Metastases by Their Primary Site of Origin Using a Radiomics Approach Based on Texture Analysis: A Feasibility Study. Eur. Radiol. 2018, 28, 4514–4523. [Google Scholar] [CrossRef]
- Stanzione, A.; Verde, F.; Romeo, V.; Boccadifuoco, F.; Mainenti, P.P.; Maurea, S. Radiomics and Machine Learning Applications in Rectal Cancer: Current Update and Future Perspectives. World J. Gastroenterol. 2021, 27, 5306–5321. [Google Scholar] [CrossRef]
- Kniep, H.C.; Madesta, F.; Schneider, T.; Hanning, U.; Schönfeld, M.H.; Schön, G.; Fiehler, J.; Gauer, T.; Werner, R.; Gellissen, S. Radiomics of Brain MRI: Utility in Prediction of Metastatic Tumor Type. Radiology 2019, 290, 479–487. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Chang, K.; Bai, H.X.; Xiao, B.; Su, C.; Bi, W.L.; Zhang, P.J.; Senders, J.T.; Vallières, M.; Kavouridis, V.K.; et al. Machine Learning Reveals Multimodal MRI Patterns Predictive of Isocitrate Dehydrogenase and 1p/19q Status in Diffuse Low- and High-Grade Gliomas. J. Neurooncol. 2019, 142, 299–307. [Google Scholar] [CrossRef] [PubMed]
- Rogers, W.; Thulasi Seetha, S.; Refaee, T.A.G.; Lieverse, R.I.Y.; Granzier, R.W.Y.; Ibrahim, A.; Keek, S.A.; Sanduleanu, S.; Primakov, S.P.; Beuque, M.P.L.; et al. Radiomics: From Qualitative to Quantitative Imaging. Br. J. Radiol. 2020, 93, 20190948. [Google Scholar] [CrossRef]
- Hagiwara, A.; Fujita, S.; Ohno, Y.; Aoki, S. Variability and Standardization of Quantitative Imaging: Monoparametric to Multiparametric Quantification, Radiomics, and Artificial Intelligence. Investig. Radiol. 2020, 55, 601–616. [Google Scholar] [CrossRef]
- Galavis, P.E. Reproducibility and Standardization in Radiomics: Are We There Yet? AIP Publishing LLC.: Merida, Mexico, 2021; p. 020003. [Google Scholar]
- Carré, A.; Klausner, G.; Edjlali, M.; Lerousseau, M.; Briend-Diop, J.; Sun, R.; Ammari, S.; Reuzé, S.; Alvarez Andres, E.; Estienne, T.; et al. Standardization of Brain MR Images across Machines and Protocols: Bridging the Gap for MRI-Based Radiomics. Sci. Rep. 2020, 10, 12340. [Google Scholar] [CrossRef]
- Mi, H.; Yuan, M.; Suo, S.; Cheng, J.; Li, S.; Duan, S.; Lu, Q. Impact of Different Scanners and Acquisition Parameters on Robustness of MR Radiomics Features Based on Women’s Cervix. Sci. Rep. 2020, 10, 20407. [Google Scholar] [CrossRef] [PubMed]
- Ford, J.; Dogan, N.; Young, L.; Yang, F. Quantitative Radiomics: Impact of Pulse Sequence Parameter Selection on MRI-Based Textural Features of the Brain. Contrast Media Mol. Imaging 2018, 2018, 1729071. [Google Scholar] [CrossRef] [PubMed]
- Mali, S.A.; Ibrahim, A.; Woodruff, H.C.; Andrearczyk, V.; Müller, H.; Primakov, S.; Salahuddin, Z.; Chatterjee, A.; Lambin, P. Making Radiomics More Reproducible across Scanner and Imaging Protocol Variations: A Review of Harmonization Methods. J. Pers. Med. 2021, 11, 842. [Google Scholar] [CrossRef]
- Bologna, M.; Corino, V.; Mainardi, L. Technical Note: Virtual Phantom Analyses for Preprocessing Evaluation and Detection of a Robust Feature Set for MRI-radiomics of the Brain. Med. Phys. 2019, 46, 5116–5123. [Google Scholar] [CrossRef]
- Moradmand, H.; Aghamiri, S.M.R.; Ghaderi, R. Impact of Image Preprocessing Methods on Reproducibility of Radiomic Features in Multimodal Magnetic Resonance Imaging in Glioblastoma. J. Appl. Clin. Med. Phys. 2020, 21, 179–190. [Google Scholar] [CrossRef]
- Li, Y.; Ammari, S.; Balleyguier, C.; Lassau, N.; Chouzenoux, E. Impact of Preprocessing and Harmonization Methods on the Removal of Scanner Effects in Brain MRI Radiomic Features. Cancers 2021, 13, 3000. [Google Scholar] [CrossRef] [PubMed]
- Isaksson, L.J.; Raimondi, S.; Botta, F.; Pepa, M.; Gugliandolo, S.G.; De Angelis, S.P.; Marvaso, G.; Petralia, G.; De Cobelli, O.; Gandini, S.; et al. Effects of MRI Image Normalization Techniques in Prostate Cancer Radiomics. Phys. Med. 2020, 71, 7–13. [Google Scholar] [CrossRef] [PubMed]
- Crombé, A.; Kind, M.; Fadli, D.; Le Loarer, F.; Italiano, A.; Buy, X.; Saut, O. Intensity Harmonization Techniques Influence Radiomics Features and Radiomics-Based Predictions in Sarcoma Patients. Sci. Rep. 2020, 10, 15496. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, A.; Vallieres, M.; Dohan, A.; Levesque, I.R.; Ueno, Y.; Saif, S.; Reinhold, C.; Seuntjens, J. Creating Robust Predictive Radiomic Models for Data From Independent Institutions Using Normalization. IEEE Trans. Radiat. Plasma Med. Sci. 2019, 3, 210–215. [Google Scholar] [CrossRef]
- Wahid, K.A.; He, R.; McDonald, B.A.; Anderson, B.M.; Salzillo, T.; Mulder, S.; Wang, J.; Sharafi, C.S.; McCoy, L.A.; Naser, M.A.; et al. Intensity Standardization Methods in Magnetic Resonance Imaging of Head and Neck Cancer. Phys. Imaging Radiat. Oncol. 2021, 20, 88–93. [Google Scholar] [CrossRef]
- Reinhold, J.C.; Dewey, B.E.; Carass, A.; Prince, J.L. Evaluating the Impact of Intensity Normalization on MR Image Synthesis. Proc. SPIE Int. Soc. Opt. Eng. 2019, 10949, 109493H. [Google Scholar]
- Fortin, J.-P.; Cullen, N.; Sheline, Y.I.; Taylor, W.D.; Aselcioglu, I.; Cook, P.A.; Adams, P.; Cooper, C.; Fava, M.; McGrath, P.J.; et al. Harmonization of Cortical Thickness Measurements across Scanners and Sites. NeuroImage 2018, 167, 104–120. [Google Scholar] [CrossRef]
- Beer, J.C.; Tustison, N.J.; Cook, P.A.; Davatzikos, C.; Sheline, Y.I.; Shinohara, R.T.; Linn, K.A. Longitudinal ComBat: A Method for Harmonizing Longitudinal Multi-Scanner Imaging Data. NeuroImage 2020, 220, 117129. [Google Scholar] [CrossRef]
- Ma, C.; Ji, Z.; Gao, M. Neural Style Transfer Improves 3D Cardiovascular MR Image Segmentation on Inconsistent Data 2019. In Medical Image Computing and Computer Assisted Intervention, MICCAI 2019; Springer: Cham, Switzerland, 2019; p. 11765. [Google Scholar] [CrossRef]
- Tian, D.; Zeng, Z.; Sun, X.; Tong, Q.; Li, H.; He, H.; Gao, J.-H.; He, Y.; Xia, M. A Deep Learning-Based Multisite Neuroimage Harmonization Framework Established with a Traveling-Subject Dataset. NeuroImage 2022, 257, 119297. [Google Scholar] [CrossRef]
- Shah, M.; Xiao, Y.; Subbanna, N.; Francis, S.; Arnold, D.L.; Collins, D.L.; Arbel, T. Evaluating Intensity Normalization on MRIs of Human Brain with Multiple Sclerosis. Med. Image Anal. 2011, 15, 267–282. [Google Scholar] [CrossRef]
- Liu, X.; Li, Y.; Qian, Z.; Sun, Z.; Xu, K.; Wang, K.; Liu, S.; Fan, X.; Li, S.; Zhang, Z.; et al. A Radiomic Signature as a Non-Invasive Predictor of Progression-Free Survival in Patients with Lower-Grade Gliomas. NeuroImage Clin. 2018, 20, 1070–1077. [Google Scholar] [CrossRef] [PubMed]
- Lucia, F.; Visvikis, D.; Vallières, M.; Desseroit, M.-C.; Miranda, O.; Robin, P.; Bonaffini, P.A.; Alfieri, J.; Masson, I.; Mervoyer, A.; et al. External Validation of a Combined PET and MRI Radiomics Model for Prediction of Recurrence in Cervical Cancer Patients Treated with Chemoradiotherapy. Eur. J. Nucl. Med. Mol. Imaging 2019, 46, 864–877. [Google Scholar] [CrossRef] [PubMed]
- Peeken, J.C.; Spraker, M.B.; Knebel, C.; Dapper, H.; Pfeiffer, D.; Devecka, M.; Thamer, A.; Shouman, M.A.; Ott, A.; von Eisenhart-Rothe, R.; et al. Tumor Grading of Soft Tissue Sarcomas Using MRI-Based Radiomics. EBioMedicine 2019, 48, 332–340. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Jiang, H.; Wang, X.; Zheng, J.; Zhao, H.; Cheng, Y.; Tao, X.; Wang, M.; Liu, C.; Huang, T.; et al. Treatment Response Prediction of Rehabilitation Program in Children with Cerebral Palsy Using Radiomics Strategy: Protocol for a Multicenter Prospective Cohort Study in West China. Quant. Imaging Med. Surg. 2019, 9, 1402–1412. [Google Scholar] [CrossRef]
- Hognon, C.; Tixier, F.; Gallinato, O.; Colin, T.; Visvikis, D.; Jaouen, V. Standardization of Multicentric Image Datasets with Generative Adversarial Networks. In Proceedings of the IEEE Nuclear Science Symposium and Medical Imaging Conference, Manchester, UK, 26 October–2 November 2019. [Google Scholar]
- Da-ano, R.; Masson, I.; Lucia, F.; Doré, M.; Robin, P.; Alfieri, J.; Rousseau, C.; Mervoyer, A.; Reinhold, C.; Castelli, J.; et al. Performance Comparison of Modified ComBat for Harmonization of Radiomic Features for Multicenter Studies. Sci. Rep. 2020, 10, 10248. [Google Scholar] [CrossRef]
- Moyer, D.; Ver Steeg, G.; Tax, C.M.W.; Thompson, P.M. Scanner Invariant Representations for Diffusion MRI Harmonization. Magn. Reson. Med. 2020, 84, 2174–2189. [Google Scholar] [CrossRef]
- Modanwal, G.; Vellal, A.; Buda, M.; Mazurowski, M.A. MRI Image Harmonization Using Cycle-Consistent Generative Adversarial Network. In Proceedings of the Medical Imaging 2020: Computer-Aided Diagnosis, SPIE, Houston, TX, USA, 16 March 2020; p. 36. [Google Scholar]
- Zhong, J.; Wang, Y.; Li, J.; Xue, X.; Liu, S.; Wang, M.; Gao, X.; Wang, Q.; Yang, J.; Li, X. Inter-Site Harmonization Based on Dual Generative Adversarial Networks for Diffusion Tensor Imaging: Application to Neonatal White Matter Development. Biomed. Eng. OnLine 2020, 19, 4. [Google Scholar] [CrossRef]
- Armanious, K.; Jiang, C.; Fischer, M.; Küstner, T.; Nikolaou, K.; Gatidis, S.; Yang, B. MedGAN: Medical Image Translation Using GANs. Comput. Med. Imaging Graph. 2020, 79, 101684. [Google Scholar] [CrossRef]
- Scalco, E.; Belfatto, A.; Mastropietro, A.; Rancati, T.; Avuzzi, B.; Messina, A.; Valdagni, R.; Rizzo, G. T2w-MRI Signal Normalization Affects Radiomics Features Reproducibility. Med. Phys. 2020, 47, 1680–1691. [Google Scholar] [CrossRef]
- Da-ano, R.; Lucia, F.; Masson, I.; Abgral, R.; Alfieri, J.; Rousseau, C.; Mervoyer, A.; Reinhold, C.; Pradier, O.; Schick, U.; et al. A Transfer Learning Approach to Facilitate ComBat-Based Harmonization of Multicentre Radiomic Features in New Datasets. PLoS ONE 2021, 16, e0253653. [Google Scholar] [CrossRef]
- Saint Martin, M.-J.; Orlhac, F.; Akl, P.; Khalid, F.; Nioche, C.; Buvat, I.; Malhaire, C.; Frouin, F. A Radiomics Pipeline Dedicated to Breast MRI: Validation on a Multi-Scanner Phantom Study. Magn. Reson. Mater. Phys. Biol. Med. 2021, 34, 355–366. [Google Scholar] [CrossRef] [PubMed]
- Dinsdale, N.K.; Jenkinson, M.; Namburete, A.I.L. Deep Learning-Based Unlearning of Dataset Bias for MRI Harmonisation and Confound Removal. NeuroImage 2021, 228, 117689. [Google Scholar] [CrossRef] [PubMed]
- Orlhac, F.; Lecler, A.; Savatovski, J.; Goya-Outi, J.; Nioche, C.; Charbonneau, F.; Ayache, N.; Frouin, F.; Duron, L.; Buvat, I. How Can We Combat Multicenter Variability in MR Radiomics? Validation of a Correction Procedure. Eur. Radiol. 2021, 31, 2272–2280. [Google Scholar] [CrossRef] [PubMed]
- Lafata, K.J.; Wang, Y.; Konkel, B.; Yin, F.-F.; Bashir, M.R. Radiomics: A Primer on High-Throughput Image Phenotyping. Abdom. Radiol. 2021, 47, 2986–3002. [Google Scholar] [CrossRef] [PubMed]
- Pfaehler, E.; van Sluis, J.; Merema, B.B.J.; van Ooijen, P.; Berendsen, R.C.M.; van Velden, F.H.P.; Boellaard, R. Experimental Multicenter and Multivendor Evaluation of the Performance of PET Radiomic Features Using 3-Dimensionally Printed Phantom Inserts. J. Nucl. Med. 2020, 61, 469–476. [Google Scholar] [CrossRef]
- Kaalep, A.; Sera, T.; Rijnsdorp, S.; Yaqub, M.; Talsma, A.; Lodge, M.A.; Boellaard, R. Feasibility of State of the Art PET/CT Systems Performance Harmonisation. Eur. J. Nucl. Med. Mol. Imaging 2018, 45, 1344–1361. [Google Scholar] [CrossRef]
- Boellaard, R.; Delgado-Bolton, R.; Oyen, W.J.G.; Giammarile, F.; Tatsch, K.; Eschner, W.; Verzijlbergen, F.J.; Barrington, S.F.; Pike, L.C.; Weber, W.A.; et al. FDG PET/CT: EANM Procedure Guidelines for Tumour Imaging: Version 2.0. Eur. J. Nucl. Med. Mol. Imaging 2015, 42, 328–354. [Google Scholar] [CrossRef]
- Ly, J.; Minarik, D.; Edenbrandt, L.; Wollmer, P.; Trägårdh, E. The Use of a Proposed Updated EARL Harmonization of 18F-FDG PET-CT in Patients with Lymphoma Yields Significant Differences in Deauville Score Compared with Current EARL Recommendations. EJNMMI Res. 2019, 9, 65. [Google Scholar] [CrossRef]
- Um, H.; Tixier, F.; Bermudez, D.; Deasy, J.O.; Young, R.J.; Veeraraghavan, H. Impact of Image Preprocessing on the Scanner Dependence of Multi-Parametric MRI Radiomic Features and Covariate Shift in Multi-Institutional Glioblastoma Datasets. Phys. Med. Biol. 2019, 64, 165011. [Google Scholar] [CrossRef]
- Zwanenburg, A.; Leger, S.; Vallières, M.; Löck, S. Image Biomarker Standardisation Initiative. Radiology 2020, 295, 328–338. [Google Scholar] [CrossRef]
- Loi, S.; Mori, M.; Benedetti, G.; Partelli, S.; Broggi, S.; Cattaneo, G.M.; Palumbo, D.; Muffatti, F.; Falconi, M.; De Cobelli, F.; et al. Robustness of CT Radiomic Features against Image Discretization and Interpolation in Characterizing Pancreatic Neuroendocrine Neoplasms. Phys. Med. 2020, 76, 125–133. [Google Scholar] [CrossRef] [PubMed]
- Larue, R.T.H.M.; van Timmeren, J.E.; de Jong, E.E.C.; Feliciani, G.; Leijenaar, R.T.H.; Schreurs, W.M.J.; Sosef, M.N.; Raat, F.H.P.J.; van der Zande, F.H.R.; Das, M.; et al. Influence of Gray Level Discretization on Radiomic Feature Stability for Different CT Scanners, Tube Currents and Slice Thicknesses: A Comprehensive Phantom Study. Acta Oncol. 2017, 56, 1544–1553. [Google Scholar] [CrossRef] [PubMed]
- Park, J.E.; Park, S.Y.; Kim, H.J.; Kim, H.S. Reproducibility and Generalizability in Radiomics Modeling: Possible Strategies in Radiologic and Statistical Perspectives. Korean J. Radiol. 2019, 20, 1124. [Google Scholar] [CrossRef] [PubMed]
- Whybra, P.; Parkinson, C.; Foley, K.; Staffurth, J.; Spezi, E. Assessing Radiomic Feature Robustness to Interpolation in 18F-FDG PET Imaging. Sci. Rep. 2019, 9, 9649. [Google Scholar] [CrossRef]
- Song, S.; Zheng, Y.; He, Y. A Review of Methods for Bias Correction in Medical Images. Biomed. Eng. Rev. 2017, 3. [Google Scholar] [CrossRef]
- Zheng, Y.; Grossman, M.; Awate, S.P.; Gee, J.C. Automatic Correction of Intensity Nonuniformity from Sparseness of Gradient Distribution in Medical Images. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2009; Yang, G.-Z., Hawkes, D., Rueckert, D., Noble, A., Taylor, C., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5762, pp. 852–859. ISBN 978-3-642-04270-6. [Google Scholar]
- Li, X.; Li, L.; Lu, H.; Liang, Z. Partial Volume Segmentation of Brain Magnetic Resonance Images Based on Maximum a Posteriori Probability: A PV Segmentation for Brain MR Images. Med. Phys. 2005, 32, 2337–2345. [Google Scholar] [CrossRef]
- Aparajeeta, J.; Nanda, P.K.; Das, N. Modified Possibilistic Fuzzy C-Means Algorithms for Segmentation of Magnetic Resonance Image. Appl. Soft Comput. 2016, 41, 104–119. [Google Scholar] [CrossRef]
- Tustison, N.J.; Avants, B.B.; Cook, P.A.; Zheng, Y.; Egan, A.; Yushkevich, P.A.; Gee, J.C. N4ITK: Improved N3 Bias Correction. IEEE Trans. Med. Imaging 2010, 29, 1310–1320. [Google Scholar] [CrossRef] [PubMed]
- Vovk, U.; Pernus, F.; Likar, B. A Review of Methods for Correction of Intensity Inhomogeneity in MRI. IEEE Trans. Med. Imaging 2007, 26, 405–421. [Google Scholar] [CrossRef] [PubMed]
- Fang, L.; Wang, X. Brain Tumor Segmentation Based on the Dual-Path Network of Multi-Modal MRI Images. Pattern Recognit. 2022, 124, 108434. [Google Scholar] [CrossRef]
- Nguyen, A.A.-T.; Onishi, N.; Carmona-Bozo, J.; Li, W.; Kornak, J.; Newitt, D.C.; Hylton, N.M. Post-Processing Bias Field Inhomogeneity Correction for Assessing Background Parenchymal Enhancement on Breast MRI as a Quantitative Marker of Treatment Response. Tomography 2022, 8, 891–904. [Google Scholar] [CrossRef] [PubMed]
- Collewet, G.; Strzelecki, M.; Mariette, F. Influence of MRI Acquisition Protocols and Image Intensity Normalization Methods on Texture Classification. Magn. Reson. Imaging 2004, 22, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, R.T.; Sweeney, E.M.; Goldsmith, J.; Shiee, N.; Mateen, F.J.; Calabresi, P.A.; Jarso, S.; Pham, D.L.; Reich, D.S.; Crainiceanu, C.M. Statistical Normalization Techniques for Magnetic Resonance Imaging. NeuroImage Clin. 2014, 6, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Fortin, J.-P.; Sweeney, E.M.; Muschelli, J.; Crainiceanu, C.M.; Shinohara, R.T. Removing Inter-Subject Technical Variability in Magnetic Resonance Imaging Studies. NeuroImage 2016, 132, 198–212. [Google Scholar] [CrossRef] [PubMed]
- Nyul, L.G.; Udupa, J.K.; Zhang, X. New Variants of a Method of MRI Scale Standardization. IEEE Trans. Med. Imaging 2000, 19, 143–150. [Google Scholar] [CrossRef] [PubMed]
- Johnson, W.E.; Li, C.; Rabinovic, A. Adjusting Batch Effects in Microarray Expression Data Using Empirical Bayes Methods. Biostatistics 2007, 8, 118–127. [Google Scholar] [CrossRef] [PubMed]
- Horng, H.; Singh, A.; Yousefi, B.; Cohen, E.A.; Haghighi, B.; Katz, S.; Noël, P.B.; Shinohara, R.T.; Kontos, D. Generalized ComBat Harmonization Methods for Radiomic Features with Multi-Modal Distributions and Multiple Batch Effects. Sci. Rep. 2022, 12, 4493. [Google Scholar] [CrossRef]
- Garcia-Dias, R.; Scarpazza, C.; Baecker, L.; Vieira, S.; Pinaya, W.H.L.; Corvin, A.; Redolfi, A.; Nelson, B.; Crespo-Facorro, B.; McDonald, C.; et al. Neuroharmony: A New Tool for Harmonizing Volumetric MRI Data from Unseen Scanners. NeuroImage 2020, 220, 117127. [Google Scholar] [CrossRef]
- Nishar, H.; Chavanke, N.; Singhal, N. Histopathological Stain Transfer Using Style Transfer Network with Adversarial Loss 2020. In Medical Image Computing and Computer Assisted Intervention, MICCAI 2020; Springer: Cham, Switzerland, 2020; p. 12265. [Google Scholar] [CrossRef]
- Xu, Y. Medical Image Processing with Contextual Style Transfer. Hum. Cent. Comput. Inf. Sci 2020, 10, 46. [Google Scholar] [CrossRef]
- Gatys, L.A.; Ecker, A.S.; Bethge, M. Image Style Transfer Using Convolutional Neural Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2414–2423. [Google Scholar]
- Yip, S.S.F.; Aerts, H.J.W.L. Applications and Limitations of Radiomics. Phys. Med. Biol. 2016, 61, R150–R166. [Google Scholar] [CrossRef]
- Duron, L.; Balvay, D.; Vande Perre, S.; Bouchouicha, A.; Savatovsky, J.; Sadik, J.-C.; Thomassin-Naggara, I.; Fournier, L.; Lecler, A. Gray-Level Discretization Impacts Reproducible MRI Radiomics Texture Features. PLoS ONE 2019, 14, e0213459. [Google Scholar] [CrossRef] [PubMed]
- Molina, D.; Pérez-Beteta, J.; Martínez-González, A.; Martino, J.; Velásquez, C.; Arana, E.; Pérez-García, V.M. Influence of Gray Level and Space Discretization on Brain Tumor Heterogeneity Measures Obtained from Magnetic Resonance Images. Comput. Biol. Med. 2016, 78, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Goya-Outi, J.; Orlhac, F.; Calmon, R.; Alentorn, A.; Nioche, C.; Philippe, C.; Puget, S.; Boddaert, N.; Buvat, I.; Grill, J.; et al. Computation of Reliable Textural Indices from Multimodal Brain MRI: Suggestions Based on a Study of Patients with Diffuse Intrinsic Pontine Glioma. Phys. Med. Biol. 2018, 63, 105003. [Google Scholar] [CrossRef] [PubMed]
- Schwier, M.; van Griethuysen, J.; Vangel, M.G.; Pieper, S.; Peled, S.; Tempany, C.; Aerts, H.J.W.L.; Kikinis, R.; Fennessy, F.M.; Fedorov, A. Repeatability of Multiparametric Prostate MRI Radiomics Features. Sci. Rep. 2019, 9, 9441. [Google Scholar] [CrossRef] [PubMed]
- Veres, G.; Vas, N.F.; Lyngby Lassen, M.; Béresová, M.; Krizsan, A.K.; Forgács, A.; Berényi, E.; Balkay, L. Effect of Grey-Level Discretization on Texture Feature on Different Weighted MRI Images of Diverse Disease Groups. PLoS ONE 2021, 16, e0253419. [Google Scholar] [CrossRef]
- Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.-C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.; Sonka, M.; et al. 3D Slicer as an Image Computing Platform for the Quantitative Imaging Network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef]
- Abràmoff, M.D.; Magalhaes, P.J.; Ram, S.G. Image Processing with Image. J. Biophotonics Int. 2004, 11, 36–42. [Google Scholar]
- Traverso, A.; Kazmierski, M.; Welch, M.L.; Weiss, J.; Fiset, S.; Foltz, W.D.; Gladwish, A.; Dekker, A.; Jaffray, D.; Wee, L.; et al. Sensitivity of Radiomic Features to Inter-Observer Variability and Image Pre-Processing in Apparent Diffusion Coefficient (ADC) Maps of Cervix Cancer Patients. Radiother. Oncol. 2020, 143, 88–94. [Google Scholar] [CrossRef]
- Granzier, R.W.Y.; Verbakel, N.M.H.; Ibrahim, A.; van Timmeren, J.E.; van Nijnatten, T.J.A.; Leijenaar, R.T.H.; Lobbes, M.B.I.; Smidt, M.L.; Woodruff, H.C. MRI-Based Radiomics in Breast Cancer: Feature Robustness with Respect to Inter-Observer Segmentation Variability. Sci. Rep. 2020, 10, 14163. [Google Scholar] [CrossRef]
- Saha, A.; Harowicz, M.R.; Mazurowski, M.A. Breast Cancer MRI Radiomics: An Overview of Algorithmic Features and Impact of Inter-reader Variability in Annotating Tumors. Med. Phys. 2018, 45, 3076–3085. [Google Scholar] [CrossRef]
- Chen, H.; He, Y.; Zhao, C.; Zheng, L.; Pan, N.; Qiu, J.; Zhang, Z.; Niu, X.; Yuan, Z. Reproducibility of Radiomics Features Derived from Intravoxel Incoherent Motion Diffusion-Weighted MRI of Cervical Cancer. Acta Radiol. 2021, 62, 679–686. [Google Scholar] [CrossRef] [PubMed]
- Rafiei, S.; Karimi, N.; Mirmahboub, B.; Najarian, K.; Felfeliyan, B.; Samavi, S.; Reza Soroushmehr, S.M. Liver Segmentation in Abdominal CT Images Using Probabilistic Atlas and Adaptive 3D Region Growing. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 6310–6313. [Google Scholar]
- Orkisz, M.; Hernández Hoyos, M.; Pérez Romanello, V.; Pérez Romanello, C.; Prieto, J.C.; Revol-Muller, C. Segmentation of the Pulmonary Vascular Trees in 3D CT Images Using Variational Region-Growing. IRBM 2014, 35, 11–19. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, L.; Liu, G.; Peng, X.; Shi, W.; Xu, H.; Shan, F.; Liu, L. An Unsupervised Semi-Automated Pulmonary Nodule Segmentation Method Based on Enhanced Region Growing. Quant. Imaging Med. Surg. 2020, 10, 233–242. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Darbehani, F.; Zaidi, M.; Wang, B. SAUNet: Shape Attentive U-Net for Interpretable Medical Image Segmentation. In Medical Image Computing and Computer Assisted Intervention, MICCAI 2020; Springer: Cham, Switzerland, 2020; p. 12264. [Google Scholar] [CrossRef]
- Saleem, H.; Shahid, A.R.; Raza, B. Visual Interpretability in 3D Brain Tumor Segmentation Network. Comput. Biol. Med. 2021, 133, 104410. [Google Scholar] [CrossRef]
- Wei, X.; Chen, X.; Lai, C.; Zhu, Y.; Yang, H.; Du, Y. Automatic Liver Segmentation in CT Images with Enhanced GAN and Mask Region-Based CNN Architectures. BioMed Res. Int. 2021, 2021, 9956983. [Google Scholar] [CrossRef] [PubMed]
- da Silva, G.L.F.; Diniz, P.S.; Ferreira, J.L.; França, J.V.F.; Silva, A.C.; de Paiva, A.C.; de Cavalcanti, E.A.A. Superpixel-Based Deep Convolutional Neural Networks and Active Contour Model for Automatic Prostate Segmentation on 3D MRI Scans. Med. Biol. Eng. Comput. 2020, 58, 1947–1964. [Google Scholar] [CrossRef]
- Sandmair, M.; Hammon, M.; Seuss, H.; Theis, R.; Uder, M.; Janka, R. Semiautomatic Segmentation of the Kidney in Magnetic Resonance Images Using Unimodal Thresholding. BMC Res. Notes 2016, 9, 489. [Google Scholar] [CrossRef] [PubMed]
- Khaled, R.; Vidal, J.; Vilanova, J.C.; Martí, R. A U-Net Ensemble for Breast Lesion Segmentation in DCE MRI. Comput. Biol. Med. 2022, 140, 105093. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Medical Image Computing and Computer-Assisted Intervention, MICCAI 2015; Springer: Cham, Switzerland, 2020; p. 9351. [Google Scholar] [CrossRef]
- Yi, D.; Zhou, M.; Chen, Z.; Gevaert, O. 3-D Convolutional Neural Networks for Glioblastoma Segmentation. arXiv 2016, arXiv:1611.04534. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.-A. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Traverso, A.; Wee, L.; Dekker, A.; Gillies, R. Repeatability and Reproducibility of Radiomic Features: A Systematic Review. Int. J. Radiat. Oncol. 2018, 102, 1143–1158. [Google Scholar] [CrossRef]
- Guan, Y.; Li, W.; Jiang, Z.; Chen, Y.; Liu, S.; He, J.; Zhou, Z.; Ge, Y. Whole-Lesion Apparent Diffusion Coefficient-Based Entropy-Related Parameters for Characterizing Cervical Cancers. Acad. Radiol. 2016, 23, 1559–1567. [Google Scholar] [CrossRef] [PubMed]
- Fiset, S.; Welch, M.L.; Weiss, J.; Pintilie, M.; Conway, J.L.; Milosevic, M.; Fyles, A.; Traverso, A.; Jaffray, D.; Metser, U.; et al. Repeatability and Reproducibility of MRI-Based Radiomic Features in Cervical Cancer. Radiother. Oncol. 2019, 135, 107–114. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, A.; Refaee, T.; Leijenaar, R.T.H.; Primakov, S.; Hustinx, R.; Mottaghy, F.M.; Woodruff, H.C.; Maidment, A.D.A.; Lambin, P. The Application of a Workflow Integrating the Variable Reproducibility and Harmonizability of Radiomic Features on a Phantom Dataset. PLoS ONE 2021, 16, e0251147. [Google Scholar] [CrossRef] [PubMed]
- Orlhac, F.; Eertink, J.J.; Cottereau, A.-S.; Zijlstra, J.M.; Thieblemont, C.; Meignan, M.; Boellaard, R.; Buvat, I. A Guide to ComBat Harmonization of Imaging Biomarkers in Multicenter Studies. J. Nucl. Med. 2022, 63, 172–179. [Google Scholar] [CrossRef]
- Andrearczyk, V.; Depeursinge, A.; Müller, H. Neural Network Training for Cross-Protocol Radiomic Feature Standardization in Computed Tomography. J. Med. Imaging 2019, 6, 1. [Google Scholar] [CrossRef] [PubMed]
- Rozantsev, A.; Salzmann, M.; Fua, P. Beyond Sharing Weights for Deep Domain Adaptation. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 801–814. [Google Scholar] [CrossRef]
- Sun, B.; Saenko, K. Deep CORAL: Correlation Alignment for Deep Domain Adaptation. In Computer Vision—ECCV 2016 Workshops; Hua, G., Jégou, H., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2016; Volume 9915, pp. 443–450. ISBN 978-3-319-49408-1. [Google Scholar]
- Foy, J.J.; Armato, S.G.; Al-Hallaq, H.A. Effects of Variability in Radiomics Software Packages on Classifying Patients with Radiation Pneumonitis. J. Med. Imaging 2020, 7, 1. [Google Scholar] [CrossRef]
- Korte, J.C.; Cardenas, C.; Hardcastle, N.; Kron, T.; Wang, J.; Bahig, H.; Elgohari, B.; Ger, R.; Court, L.; Fuller, C.D.; et al. Radiomics Feature Stability of Open-Source Software Evaluated on Apparent Diffusion Coefficient Maps in Head and Neck Cancer. Sci. Rep. 2021, 11, 17633. [Google Scholar] [CrossRef]
- Fornacon-Wood, I.; Mistry, H.; Ackermann, C.J.; Blackhall, F.; McPartlin, A.; Faivre-Finn, C.; Price, G.J.; O’Connor, J.P.B. Reliability and Prognostic Value of Radiomic Features Are Highly Dependent on Choice of Feature Extraction Platform. Eur. Radiol. 2020, 30, 6241–6250. [Google Scholar] [CrossRef]
- Bernatz, S.; Zhdanovich, Y.; Ackermann, J.; Koch, I.; Wild, P.J.; dos Santos, D.P.; Vogl, T.J.; Kaltenbach, B.; Rosbach, N. Impact of Rescanning and Repositioning on Radiomic Features Employing a Multi-Object Phantom in Magnetic Resonance Imaging. Sci. Rep. 2021, 11, 14248. [Google Scholar] [CrossRef]
- Baeßler, B.; Weiss, K.; Pinto dos Santos, D. Robustness and Reproducibility of Radiomics in Magnetic Resonance Imaging: A Phantom Study. Investig. Radiol. 2019, 54, 221–228. [Google Scholar] [CrossRef] [PubMed]
- Xue, C.; Yuan, J.; Lo, G.G.; Chang, A.T.Y.; Poon, D.M.C.; Wong, O.L.; Zhou, Y.; Chu, W.C.W. Radiomics Feature Reliability Assessed by Intraclass Correlation Coefficient: A Systematic Review. Quant. Imaging Med. Surg. 2021, 11, 4431–4460. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, R.T.; Oh, J.; Nair, G.; Calabresi, P.A.; Davatzikos, C.; Doshi, J.; Henry, R.G.; Kim, G.; Linn, K.A.; Papinutto, N.; et al. Volumetric Analysis from a Harmonized Multisite Brain MRI Study of a Single Subject with Multiple Sclerosis. Am. J. Neuroradiol. 2017, 38, 1501–1509. [Google Scholar] [CrossRef] [PubMed]
- Coşkun, M.; YILDIRIM, Ö.; Ayşegül, U.Ç.A.R.; Demir, Y. An Overview of Popular Deep Learning Methods. Eur. J. Tech. 2017, 7, 165–176. [Google Scholar] [CrossRef]
- Dewey, B.E.; Zhao, C.; Reinhold, J.C.; Carass, A.; Fitzgerald, K.C.; Sotirchos, E.S.; Saidha, S.; Oh, J.; Pham, D.L.; Calabresi, P.A.; et al. DeepHarmony: A Deep Learning Approach to Contrast Harmonization across Scanner Changes. Magn. Reson. Imaging 2019, 64, 160–170. [Google Scholar] [CrossRef]
- Scherer, J.; Nolden, M.; Kleesiek, J.; Metzger, J.; Kades, K.; Schneider, V.; Bach, M.; Sedlaczek, O.; Bucher, A.M.; Vogl, T.J.; et al. Joint Imaging Platform for Federated Clinical Data Analytics. JCO Clin. Cancer Inform. 2020, 4, 1027–1038. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, J.P. Radiomics: Rethinking the Role of Clinical Imaging. eLife 2017, 6, e30563. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; El Naqa, I.; Rong, Y. Current Status of Radiomics for Cancer Management: Challenges versus Opportunities for Clinical Practice. J. Appl. Clin. Med. Phys. 2020, 21, 7–10. [Google Scholar] [CrossRef]
- Shur, J.D.; Doran, S.J.; Kumar, S.; ap Dafydd, D.; Downey, K.; O’Connor, J.P.B.; Papanikolaou, N.; Messiou, C.; Koh, D.-M.; Orton, M.R. Radiomics in Oncology: A Practical Guide. RadioGraphics 2021, 41, 1717–1732. [Google Scholar] [CrossRef]
| Reference | MRI Sequences/ Cancer Type | Variation Across | Harmonization Techniques | Clinical Question |
|---|---|---|---|---|
| A. Carre et al. (2020) [16] | T1w, T2w-fl1air (brain-glioma) | 3 centers | Intensity-based | Tumor grade classification |
| M. Bologna et al. (2019) [20] | T1w, T2w (brain) | 27 centers | Intensity-based | Feature stability |
| H. Moradmand et al. (2019) [21] | FLAIR, T1, T1C, and T2 (brain-glioblastoma) | 8 centers | Intensity-based | Edema, necrosis, enhancement, and tumor |
| Y. Li et al. (2021) [22] | T1 (brain) | 2 scanners | Both | Scanner effect removal |
| L. J Isaksson et al. (2020) [23] | T2w (prostate cancer) | 1 scanner | Intensity-based | Cancer identification |
| A. Crombe et al. (2020) [24] | T2w (sarcoma) | 3 centers | Intensity-based | Prediction of metastatic-relapse-free survival |
| Chatterjee et al. (2019) [25] | T2-weighted fast spin echo (denoted as T2); T1-weighted fast gradient echo with DCE-MRI and a postcontrast image (post-Gado); and diffusion-weighted MRI (primary uterine adenocarcinoma) | 2 centers | Intensity-based | Lymphovascular space invasion and cancer staging |
| K.A. Wahid et al. (2021) [26] | T2w (head and neck) | 15 HET cohorts-15 HOM- cohorts | Intensity-based | Radiotherapy treatment |
| J. C. Reinhold et al. (2018) [27] | T1-w, T2-w, and FLAIR (brain) | 1 dataset with 18 patients | Intensity-based | Medical image synthesis |
| J. P. Fortin et al. (2018) [28] | MRI (brain) | 11 scanners | Feature-based | Cortical thickness harmonization |
| J. C. Beer et al. (2019) [29] | Structural MRI (brain) | 58 sites | Feature-based | Alzheimer prediction |
| C. Ma et al. (2019) [30] | 3D Cardiac MRI | 20 scans (10 training and 10 test) | Intensity-based | Image segmentation |
| D. Tian et al. (2022) [31] | T1 MRI (brain) | 12 centers | Intensity-based | Gray matter analysis |
| M. Shah et al. (2011) [32] | T1w, T2w, and PDw (brain) | 10 scanners | Intensity-based | Multiple sclerosis lesion identification |
| Liu et al. (2018) [33] | T2w (brain-glioma) | 2 cohorts | Intensity-based | Prediction of progression-free survival in lower-grade gliomas |
| F. Lucia et al. (2019 [34]) | T1, T2 DWI (cervical cancer) | 3 centers | Feature-based | Cervical cancer prognosis |
| Peeken et al. (2019) [35] | Contrast-enhanced T1-weighted fat saturated (T1FSGd), fat-saturated T2-weighted (T2FS) (sarcoma) | 2 cohorts | Intensity/ feature-based | Classification of low and high grade soft tissue sarcoma |
| Liu et al. (2019) [36] | T1w,T2w-fl1air (brain) | 4 centers | Feature-based | Prediction of the individualized treatment response in children with cerebral palsy |
| C. Hognon et al. (2019) [37] | T1, T1c, T2, FLAIR (glioblastoma) | 3 centers | Intensity-based | Image segmentation |
| R. Da-Ano et al. (2020) [38] | Post-injection gadolinium contrast-enhanced MRI (GADO), T2-weighted MRI (T2) and apparent diffusion coefficients (ADC) maps from diffusion-weighted MRI (cervical cancer) | 3 centers | Feature-based | Prediction and treatment adaptation |
| D. Moyer et al. (2020) [39] | Diffusion MRI (brain) | 15 patients from 2 scanners | Intensity-based | White Matter analysis |
| G. Modanwal et al. (2020) [40] | DCE-MRI (breast cancer) | 124 patients from 2 scanners | Intensity-based | Evaluation |
| J. Zhong et al. (2020) [41] | Neonatal DTI-MRI (brain) | 84 neonates data from 2 sites | Deep Learning | Harmonize neonatal data |
| K. Armanious et al. (2020) [42] | T1 (brain) | 11 patients | Intensity-based | Motion correction |
| Scalco et al. (2020) [43] | T1w, T2w (prostate) | 3 different organs of interest | Intensity-based | Reproducibility estimation |
| R. Da-Ano et al. (2021) [44] | Post-injection gadolinium contrast-enhanced MRI (GADO), T2-weighted MRI (T2) and apparent diffusion coefficients (ADC) maps from diffusion-weighted MRI (cervical cancer) | 3 centers | Feature-based | Prediction |
| Saint Martin et al. (2021) [45] | T1, T2, T1-DCE (breast) | 2 phantoms (2 scanners and 3 dual breast coils) | Both | Lesion classification |
| N.K. Dinsdale et al. (2021) [46] | T1w (neuroimages) | 3 dataset centers | Feature-based | Age prediction and segmentation |
| F. Orlhac et al. (2021) [47] | T1, FLAIR and contrast-enhanced T1-weighted (CE-T1w) images and T2w (brain/prostate) | 2 centers | Feature-based | Impact of harmonization to distinguish between Gleason grades |
| Reference. | Harmonization Method | GitHub |
|---|---|---|
| Reinhold et al. [27] | Fuzzy C-means | https://github.com/jcreinhold/intensity-normalization, accessed on 9 September 2022 |
| Reinhold et al. [27] | Gaussian mixture model (GMM) | https://github.com/jcreinhold/intensity-normalization, accessed on 11 October 2022 |
| Reinhold et al. [27] | Kernel Density Estimate (KDE) | https://github.com/jcreinhold/intensity-normalization, accessed on 30 August 2022 |
| Shinohara et al. [68] | Z-Score | https://github.com/jcreinhold/intensity-normalization, accessed on 8 October 2022; https://github.com/Jfortin1/RAVEL, accessed on 8 October 2022 |
| Shinohara et al. [68] | White Stripe | https://github.com/jcreinhold/intensity-normalization, accessed on 11 September 2022; https://github.com/Jfortin1/RAVEL, accessed on 11 September 2022 |
| Fortin et al. [69] | Ravel | https://github.com/jcreinhold/intensity-normalization, accessed on 12 August 2022; https://github.com/Jfortin1/RAVEL, accessed on 12 August 2022 |
| Nyul et al. [70] | Histogram Matching | https://github.com/jcreinhold/intensity-normalization, accessed on 24 October 2022; https://github.com/Jfortin1/RAVEL, accessed on 24 October 2022; https://github.com/sergivalverde/MRI_intensity_normalization, accessed on 24 October 2022 |
| Johnson et al. [71] Fortin et al. [28] | ComBat, M-Combat | https://github.com/Jfortin1/ComBatHarmonization, accessed on 18 September 2022; https://github.com/ncullen93/neuroCombat/tree/master/neuroCombat, accessed on 18 September 2022 |
| Horng et al. [72] | Nested & GMM ComBat | https://github.com/hannah-horng/generalized-combat, accessed on 3 October 2022 |
| Beer et al. [29] | Longitudinal ComBat | https://github.com/jcbeer/longCombat, accessed on 31 October 2022 |
| Johnson et al. [71] Fortin et al. [28] | ComBaTool Standalone web application | https://forlhac.shinyapps.io/Shiny_ComBat/, accessed on 27 September 2022 |
| Garcia-Dias et al. [73] | NeuroHarmony | https://github.com/garciadias/Neuroharmony, accessed on 23 August 2022 |
| C. Ma et al. [30] | Deep Learning | https://github.com/horsepurve/StyleSegor, accessed on 21 September 2022 |
| D. Tian et al. [31] | Deep Learning | https://github.com/DezhengTian/DeRed-Harmonization, accessed on 22 September 2022 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stamoulou, E.; Spanakis, C.; Manikis, G.C.; Karanasiou, G.; Grigoriadis, G.; Foukakis, T.; Tsiknakis, M.; Fotiadis, D.I.; Marias, K. Harmonization Strategies in Multicenter MRI-Based Radiomics. J. Imaging 2022, 8, 303. https://doi.org/10.3390/jimaging8110303
Stamoulou E, Spanakis C, Manikis GC, Karanasiou G, Grigoriadis G, Foukakis T, Tsiknakis M, Fotiadis DI, Marias K. Harmonization Strategies in Multicenter MRI-Based Radiomics. Journal of Imaging. 2022; 8(11):303. https://doi.org/10.3390/jimaging8110303
Chicago/Turabian StyleStamoulou, Elisavet, Constantinos Spanakis, Georgios C. Manikis, Georgia Karanasiou, Grigoris Grigoriadis, Theodoros Foukakis, Manolis Tsiknakis, Dimitrios I. Fotiadis, and Kostas Marias. 2022. "Harmonization Strategies in Multicenter MRI-Based Radiomics" Journal of Imaging 8, no. 11: 303. https://doi.org/10.3390/jimaging8110303
APA StyleStamoulou, E., Spanakis, C., Manikis, G. C., Karanasiou, G., Grigoriadis, G., Foukakis, T., Tsiknakis, M., Fotiadis, D. I., & Marias, K. (2022). Harmonization Strategies in Multicenter MRI-Based Radiomics. Journal of Imaging, 8(11), 303. https://doi.org/10.3390/jimaging8110303










