DS6, Deformation-Aware Semi-Supervised Learning: Application to Small Vessel Segmentation with Noisy Training Data
Abstract
1. Introduction
Contribution
2. Related Work
2.1. Vessel Segmentation Using Non-DL Techniques
2.2. Deep Learning Techniques
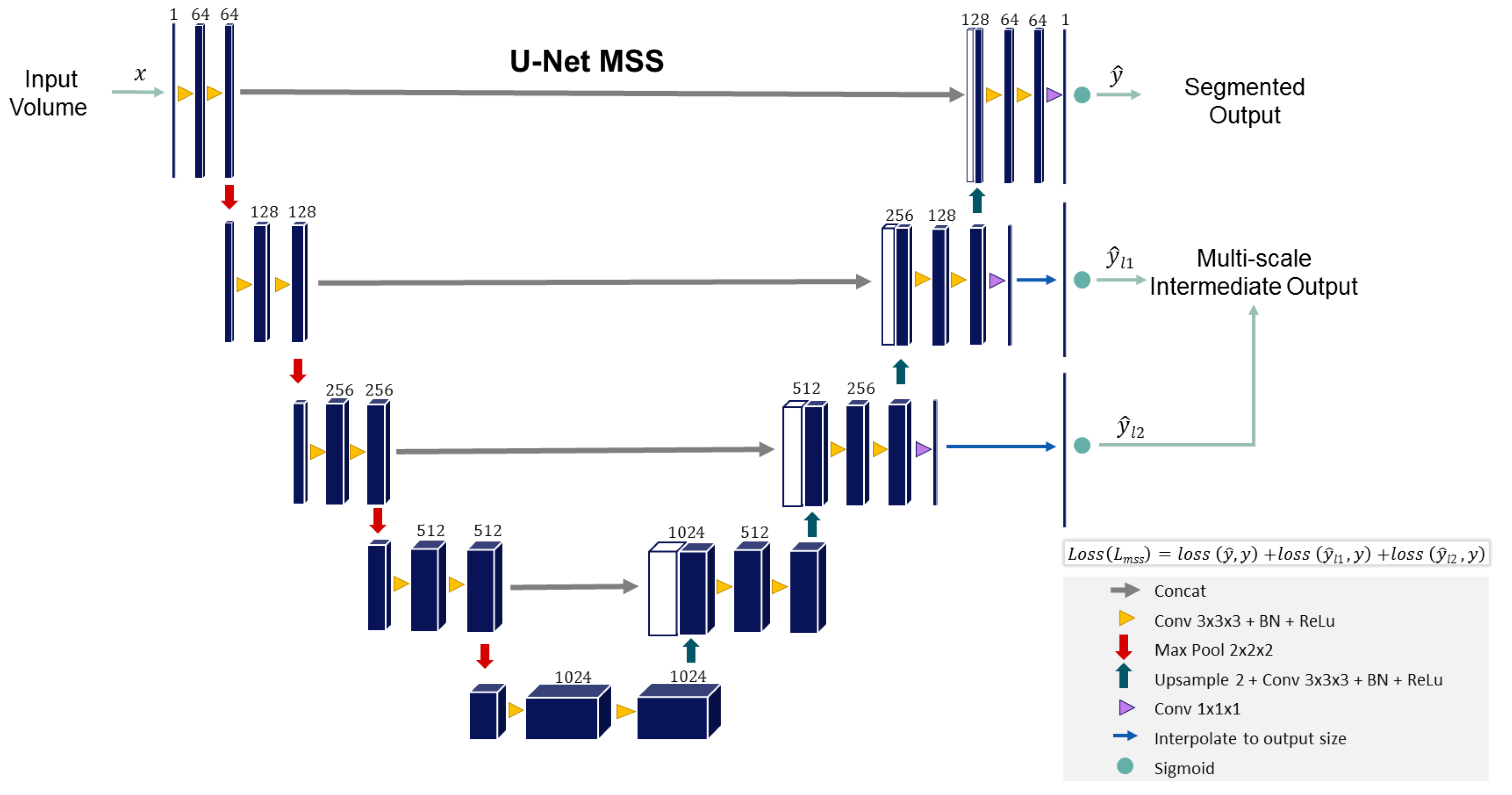
3. Proposed Methodology
4. Datasets and Labels
5. Experimental Setup
6. Evaluation
6.1. On 7T MRA Test Set
Statistical Hypothesis Testing
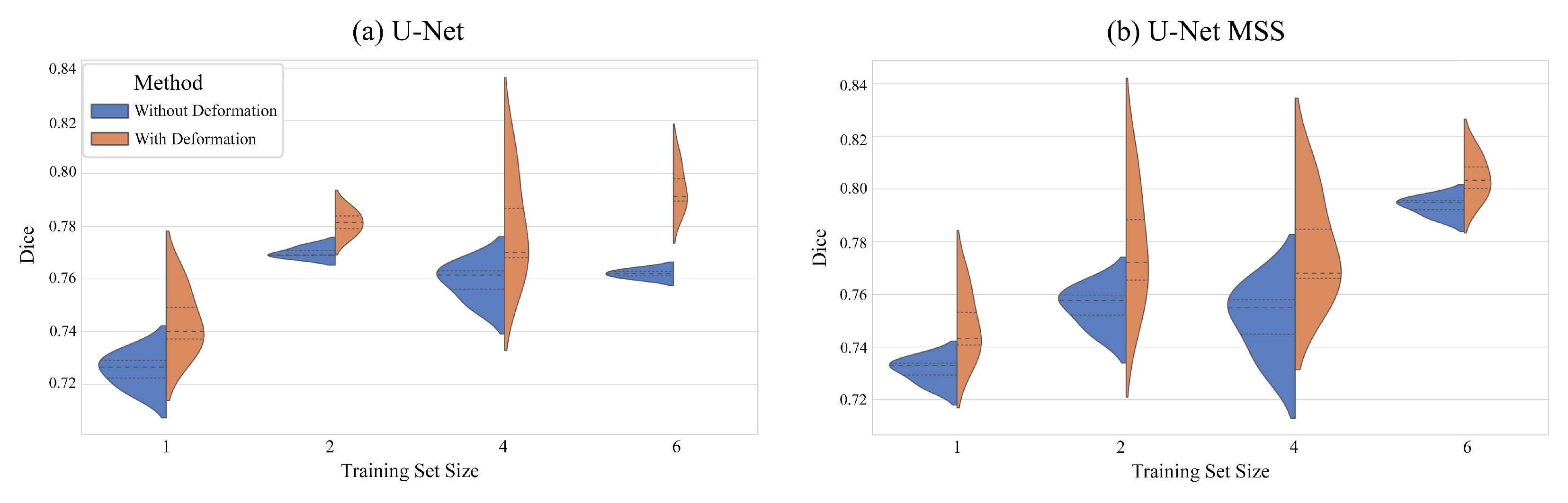
6.2. On the Effect of the Training Set Size
6.3. On a Manually Segmented ROI of 7T MRA
6.4. On Publicly Available Dataset with Lower Resolution than the Training Set: IXI MRA
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Testing with Artefacts
| Artefact Type | Description |
|---|---|
| Random Spike | Adds random stripes in different directions |
| Elastic Deform | Applies dense random elastic deformation |
| Random Noise | Adds random Gaussian noise |
| Random Blur | Blurs the image with Gaussian filter |
| Random Motion | Simulates motion artefacts |
| Random Bias Field | The bias field is modelled as a linear combination of polynomial basis functions. |
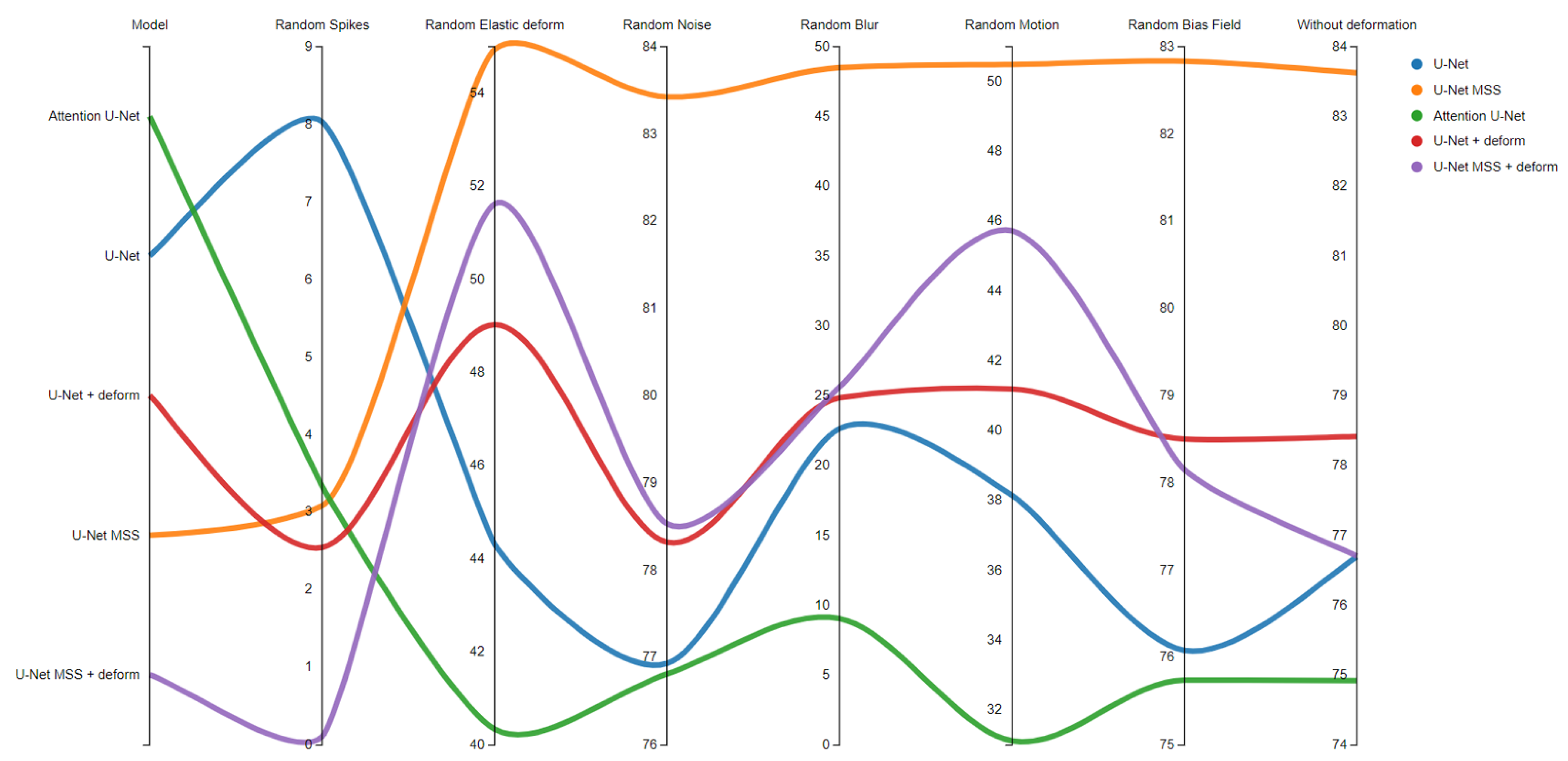

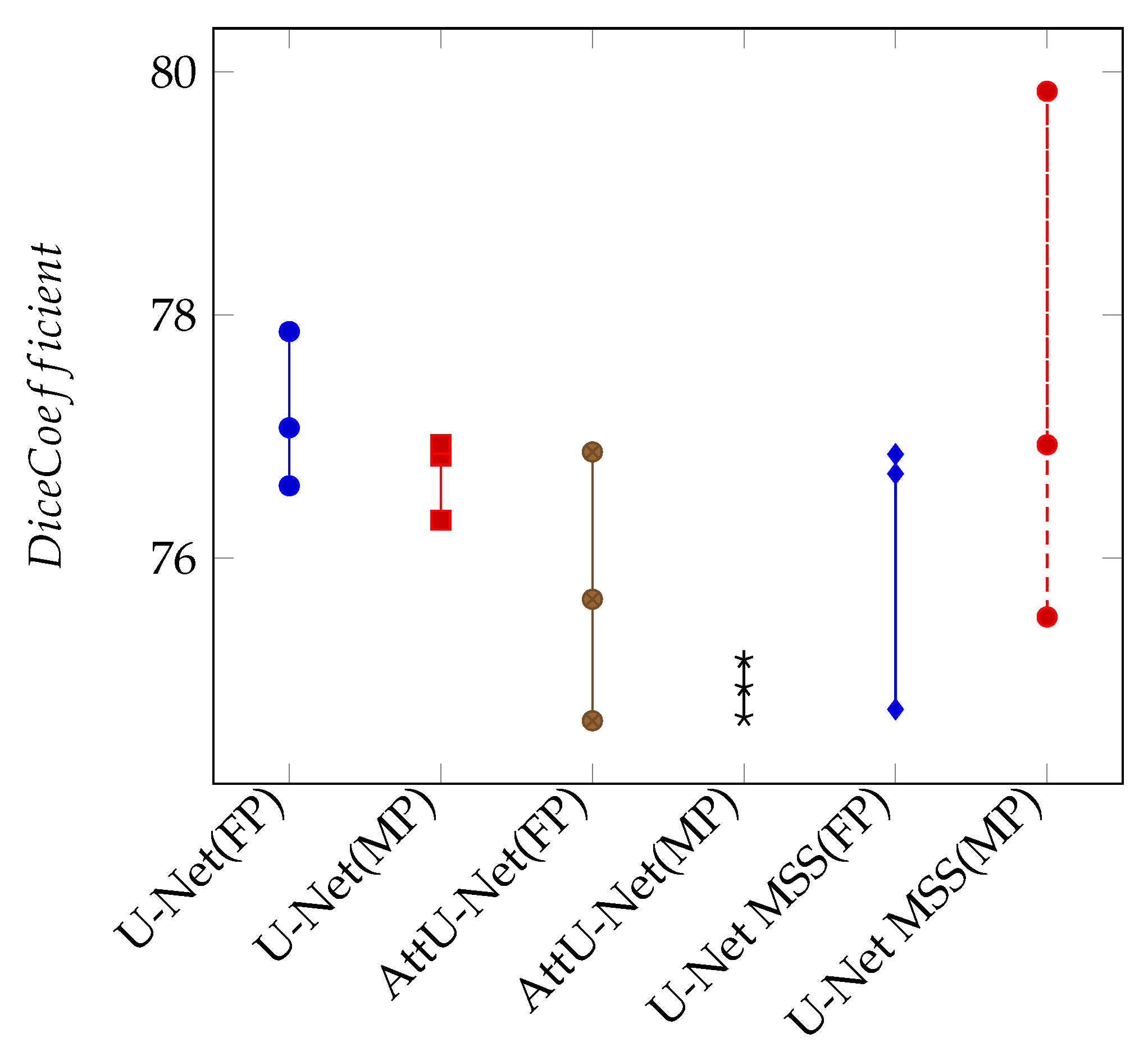
Appendix B. Mixed Precision Training
| Full Precision | Mixed Precision | |||
|---|---|---|---|---|
| Model | Dice Coefficient | IoU | Dice Coefficient | IoU |
| U-Net | 77.22 | 62.89 | 76.93 | 62.51 |
| Attention U-Net | 75.84 | 61.08 | 76.53 | 61.98 |
| U-Net MSS | 76.08 | 61.40 | 77.42 | 63.00 |
References
- Feekes, J.; Hsu, S.; Chaloupka, J.; Cassell, M. Tertiary microvascular territories define lacunar infarcts in the basal ganglia. Ann. Neurol. 2005, 58, 18–30. [Google Scholar] [CrossRef]
- Feekes, J.; Cassell, M. The vascular supply of the functional compartments of the human striatum. Brain J. Neurol. 2006, 129, 2189–2201. [Google Scholar] [CrossRef]
- Wardlaw, J.M.; Smith, C.; Dichgans, M. Mechanisms of sporadic cerebral small vessel disease: Insights from neuroimaging. Lancet Neurol. 2013, 12, 483–497. [Google Scholar] [CrossRef]
- Zwanenburg, J.J.; Van Osch, M.J. Targeting cerebral small vessel disease with MRI. Stroke 2017, 48, 3175–3182. [Google Scholar] [CrossRef]
- Chalkias, E.; Chalkias, I.N.; Bakirtzis, C.; Messinis, L.; Nasios, G.; Ioannidis, P.; Pirounides, D. Differentiating Degenerative from Vascular Dementia with the Help of Optical Coherence Tomography Angiography Biomarkers. Healthcare 2022, 10, 539. [Google Scholar] [CrossRef]
- Duan, Y.; Shan, W.; Liu, L.; Wang, Q.; Wu, Z.; Liu, P.; Ji, J.; Liu, Y.; He, K.; Wang, Y. Primary Categorizing and Masking Cerebral Small Vessel Disease Based on “Deep Learning System”. Front. Neuroinform. 2020, 14, 17. [Google Scholar] [CrossRef]
- Litak, J.; Mazurek, M.; Kulesza, B.; Szmygin, P.; Litak, J.; Kamieniak, P.; Grochowski, C. Cerebral small vessel disease. Int. J. Mol. Sci. 2020, 21, 9729. [Google Scholar] [CrossRef]
- Hendrikse, J.; Zwanenburg, J.J.; Visser, F.; Takahara, T.; Luijten, P. Noninvasive depiction of the lenticulostriate arteries with time-of-flight MR angiography at 7.0 T. Cerebrovasc. Dis. 2008, 26, 624–629. [Google Scholar] [CrossRef] [PubMed]
- Kang, C.K.; Park, C.W.; Han, J.Y.; Kim, S.H.; Park, C.A.; Kim, K.N.; Hong, S.M.; Kim, Y.B.; Lee, K.H.; Cho, Z.H. Imaging and analysis of lenticulostriate arteries using 7.0-Tesla magnetic resonance angiography. Magn. Reson. Med. 2009, 61, 136–144. [Google Scholar] [CrossRef] [PubMed]
- Frangi, A.F.; Niessen, W.J.; Vincken, K.L.; Viergever, M.A. Multiscale vessel enhancement filtering. In Proceedings of the First International Conference Medical Image Computing and Computer-Assisted Intervention—MICCAI’98, Cambridge, MA, USA, 11–13 October 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 130–137. [Google Scholar]
- Bernier, M.; Cunnane, S.C.; Whittingstall, K. The morphology of the human cerebrovascular system. Hum. Brain Mapp. 2018, 39, 4962–4975. [Google Scholar] [CrossRef]
- Jerman, T.; Pernuš, F.; Likar, B.; Špiclin, Ž. Beyond Frangi: An improved multiscale vesselness filter. In Medical Imaging 2015: Image Processing; SPIE: Bellingham, WA, USA, 2015; Volume 9413, p. 94132A. [Google Scholar]
- Sommer, C.; Straehle, C.; Kothe, U.; Hamprecht, F.A. Ilastik: Interactive learning and segmentation toolkit. In Proceedings of the 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Chicago, IL, USA, 30 March–2 April 2011; pp. 230–233. [Google Scholar] [CrossRef]
- Chen, L.; Mossa-Basha, M.; Balu, N.; Canton, G.; Sun, J.; Pimentel, K.; Hatsukami, T.S.; Hwang, J.N.; Yuan, C. Development of a quantitative intracranial vascular features extraction tool on 3D MRA using semiautomated open-curve active contour vessel tracing. Magn. Reson. Med. 2018, 79, 3229–3238. [Google Scholar] [CrossRef] [PubMed]
- Minaee, S.; Boykov, Y.Y.; Porikli, F.; Plaza, A.J.; Kehtarnavaz, N.; Terzopoulos, D. Image segmentation using deep learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3523–3542. [Google Scholar] [CrossRef] [PubMed]
- Ulku, I.; Akagündüz, E. A survey on deep learning-based architectures for semantic segmentation on 2d images. Appl. Artif. Intell. 2022, 36, 2032924. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the 18th International Conference Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning dense volumetric segmentation from sparse annotation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2016; Springer: Cham, Switzerland, 2016; pp. 424–432. [Google Scholar]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. In Proceedings of the Medical Imaging with Deep Learning, Amsterdam, The Netherlands, 4–6 July 2018; Available online: https://openreview.net/forum?id=Skft7cijM (accessed on 16 September 2022).
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.; van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef]
- Liu, X.; Song, L.; Liu, S.; Zhang, Y. A review of deep-learning-based medical image segmentation methods. Sustainability 2021, 13, 1224. [Google Scholar] [CrossRef]
- Zeng, G.; Yang, X.; Li, J.; Yu, L.; Heng, P.-A.; Zheng, G. 3D U-net with multi-level deep supervision: Fully automatic segmentation of proximal femur in 3D MR images. In Lecture Notes in Computer Science, Proceedings of the 8th International Workshop Machine Learning in Medical Imaging (MLMI 2017); Quebec City, QC, Canada, 10 September 2017, Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Bortsova, G.; Dubost, F.; Hogeweg, L.; Katramados, I.; de Bruijne, M. Semi-supervised Medical Image Segmentation via Learning Consistency Under Transformations. In Lecture Notes in Computer Science, Proceedings of the 22nd International Conference Medical Image Computing and Computer Assisted Intervention—MICCAI 2019, Shenzhen, China, 13–17 October 2019; Springer: Cham, Switzerland, 2019; Volume 11769, pp. 810–818. [Google Scholar] [CrossRef]
- Canero, C.; Radeva, P. Vesselness enhancement diffusion. Pattern Recognit. Lett. 2003, 24, 3141–3151. [Google Scholar] [CrossRef]
- Manniesing, R.; Niessen, W. Multiscale vessel enhancing diffusion in CT angiography noise filtering. In Proceedings of the 19th International Conference Information Processing in Medical Imaging (IPMI 2005), Glenwood Springs, CO, USA, 10–15 July 2002; Springer: Berlin/Heidelberg, Germany, 2005; pp. 138–149. [Google Scholar]
- Liao, W.; Rohr, K.; Kang, C.K.; Cho, Z.H.; Fellow, L.; Wörz, S. Automatic 3D segmentation and quantification of lenticulostriate arteries from high-resolution 7 tesla MRA images. IEEE Trans. Image Process. 2016, 25, 400–413. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.Y.; Ghaffari, M.; Alaraj, A.; Flannery, M.; Zhou, X.J.; Linninger, A. Gap-free segmentation of vascular networks with automatic image processing pipeline. Comput. Biol. Med. 2017, 82, 29–39. [Google Scholar] [CrossRef]
- Ahmed Raza, S.E.; Cheung, L.; Epstein, D.; Pelengaris, S.; Khan, M.; Rajpoot, N.M. MIMONet: Gland Segmentation Using Neural Network. In Proceedings of the 21st Annual Conference Medical Image Understanding and Analysis (MIUA 2017), Edinburgh, UK, 11–13 July 2017; Communications in Computer and Information Science Series. Springer: Cham, Switzerland, 2017; Volume 1, pp. 698–706. [Google Scholar] [CrossRef]
- Blanc-Durand, P.; Van Der Gucht, A.; Schaefer, N.; Itti, E.; Prior, J.O. Automatic lesion detection and segmentation of18F-FET PET in gliomas: A full 3D U-Net convolutional neural network study. PLoS ONE 2018, 13, e0195798. [Google Scholar] [CrossRef]
- Fabijańska, A. Segmentation of corneal endothelium images using a U-Net-based convolutional neural network. Artif. Intell. Med. 2018, 88, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Heller, N.; Dean, J.; Papanikolopoulos, N. Imperfect Segmentation Labels: How Much Do They Matter? In Proceedings of the Intravascular Imaging and Computer Assisted Stenting and Large-Scale Annotation of Biomedical Data and Expert Label Synthesis; Stoyanov, D., Taylor, Z., Balocco, S., Sznitman, R., Martel, A., Maier-Hein, L., Duong, L., Zahnd, G., Demirci, S., Albarqouni, S., et al., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 112–120. [Google Scholar]
- Girard, F.; Kavalec, C.; Cheriet, F. Joint segmentation and classification of retinal arteries/veins from fundus images. Artif. Intell. Med. 2019, 94, 96–109. [Google Scholar] [CrossRef] [PubMed]
- Yuan, A.Y.; Gao, Y.; Peng, L.; Zhou, L.; Liu, J.; Zhu, S.; Song, W. Hybrid deep learning network for vascular segmentation in photoacoustic imaging. Biomed. Opt. Express 2020, 11, 6445–6457. [Google Scholar] [CrossRef]
- Yang, S.; Kweon, J.; Roh, J.H.; Lee, J.H.; Kang, H.; Park, L.J.; Kim, D.J.; Yang, H.; Hur, J.; Kang, D.Y.; et al. Deep learning segmentation of major vessels in X-ray coronary angiography. Sci. Rep. 2019, 9, 16897. [Google Scholar] [CrossRef]
- Livne, M.; Rieger, J.; Aydin, O.U.; Taha, A.A.; Akay, E.M.; Kossen, T.; Sobesky, J.; Kelleher, J.D.; Hildebrand, K.; Frey, D.; et al. A U-Net deep learning framework for high performance vessel segmentation in patients with cerebrovascular disease. Front. Neurosci. 2019, 13, 97. [Google Scholar] [CrossRef]
- Bortsova, G.; van Tulder, G.; Dubost, F.; Peng, T.; Navab, N.; van der Lugt, A.; Bos, D.; De Bruijne, M. Segmentation of intracranial arterial calcification with deeply supervised residual dropout networks. In Lecture Notes in Computer Science, Proceedings of the 20th International Conference Medical Image Computing and Computer Assisted Intervention—MICCAI 2017, Quebec City, QC, Canada, 10–13 September 2017; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Zhao, W.; Zeng, Z. Multi Scale Supervised 3D U-Net for Kidney and Tumor Segmentation. arXiv 2020, arXiv:2004.08108. [Google Scholar]
- Bromley, J.; Bentz, J.W.; Bottou, L.; Guyon, I.; LeCun, Y.; Moore, C.; Säckinger, E.; Shah, R. Signature verification using a “siamese” time delay neural network. Int. J. Pattern Recognit. Artif. Intell. 1993, 7, 669–688. [Google Scholar] [CrossRef]
- Simard, P.Y.; Steinkraus, D.; Platt, J.C. Best practices for convolutional neural networks applied to visual document analysis. In Proceedings of the Seventh International Conference on Document Analysis and Recognition, Edinburgh, UK, 6 August 2003; Volume 3. [Google Scholar]
- Castro, E.; Cardoso, J.S.; Pereira, J.C. Elastic deformations for data augmentation in breast cancer mass detection. In Proceedings of the 2018 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Las Vegas, NV, USA, 4–7 March 2018; pp. 230–234. [Google Scholar]
- Chen, D.; Ao, Y.; Liu, S. Semi-supervised learning method of u-net deep learning network for blood vessel segmentation in retinal images. Symmetry 2020, 12, 1067. [Google Scholar] [CrossRef]
- Song, X.; Gao, X.; Ding, Y.; Wang, Z. A handwritten Chinese characters recognition method based on sample set expansion and CNN. In Proceedings of the 2016 3rd International Conference on Systems and Informatics (ICSAI), Shanghai, China, 19–21 November 2016; pp. 843–849. [Google Scholar]
- Knott, G.D. Interpolating Cubic Splines; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000; Volume 18. [Google Scholar]
- Mattern, H.; Sciarra, A.; Godenschweger, F.; Stucht, D.; Lüsebrink, F.; Rose, G.; Speck, O. Prospective motion correction enables highest resolution time-of-flight angiography at 7T. Magn. Reson. Med. 2018, 80, 248–258. [Google Scholar] [CrossRef]
- Sciarra, A.; Mattern, H.; Yakupov, R.; Chatterjee, S.; Stucht, D.; Oeltze-Jafra, S.; Godenschweger, F.; Speck, O. Quantitative evaluation of prospective motion correction in healthy subjects at 7T MRI. Magn. Reson. Med. 2022, 87, 646–657. [Google Scholar] [CrossRef]
- Berg, S.; Kutra, D.; Kroeger, T.; Straehle, C.N.; Kausler, B.X.; Haubold, C.; Schiegg, M.; Ales, J.; Beier, T.; Rudy, M.; et al. ilastik: Interactive machine learning for (bio)image analysis. Nat. Methods 2019, 16, 1226–1232. [Google Scholar] [CrossRef]
- Abraham, N.; Khan, N.M. A Novel Focal Tversky Loss Function With Improved Attention U-Net for Lesion Segmentation. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; pp. 683–687. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019 2019; pp. 8026–8037. [Google Scholar]
- Pérez-García, F.; Sparks, R.; Ourselin, S. TorchIO: A Python library for efficient loading, preprocessing, augmentation and patch-based sampling of medical images in deep learning. Comput. Methods Programs Biomed. 2021, 208, 106236. [Google Scholar] [CrossRef] [PubMed]
- Lowekamp, B.C.; Chen, D.T.; Ibáñez, L.; Blezek, D. The design of SimpleITK. Front. Neuroinform. 2013, 7, 45. [Google Scholar] [CrossRef]
- Sandkühler, R.; Jud, C.; Andermatt, S.; Cattin, P.C. AirLab: Autograd Image Registration Laboratory. arXiv 2018, arXiv:1806.09907. [Google Scholar]
- Micikevicius, P.; Narang, S.; Alben, J.; Diamos, G.; Elsen, E.; Garcia, D.; Ginsburg, B.; Houston, M.; Kuchaiev, O.; Venkatesh, G.; et al. Mixed Precision Training. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Tustison, N.J.; Avants, B.B.; Cook, P.A.; Zheng, Y.; Egan, A.; Yushkevich, P.A.; Gee, J.C. N4ITK: Improved N3 bias correction. IEEE Trans. Med. Imaging 2010, 29, 1310–1320. [Google Scholar] [CrossRef]
- Truong, T.K.; Chakeres, D.W.; Beversdorf, D.Q.; Scharre, D.W.; Schmalbrock, P. Effects of static and radiofrequency magnetic field inhomogeneity in ultra-high field magnetic resonance imaging. Magn. Reson. Imaging 2006, 24, 103–112. [Google Scholar] [CrossRef]
- Smith, S.M. Fast robust automated brain extraction. Hum. Brain Mapp. 2002, 17, 143–155. [Google Scholar] [CrossRef]
- Jenkinson, M.; Pechaud, M.; Smith, S. BET2: MR-based estimation of brain, skull and scalp surfaces. In Proceedings of the Eleventh Annual Meeting of the Organization for Human Brain Mapping, Toronto, ON, Canada, 12–16 June 2005; Volume 17, p. 167. [Google Scholar]
- Jenkinson, M.; Beckmann, C.F.; Behrens, T.E.; Woolrich, M.W.; Smith, S.M. Fsl. Neuroimage 2012, 62, 782–790. [Google Scholar] [CrossRef]
- Li, X.; Yu, L.; Chen, H.; Fu, C.W.; Heng, P.A. Semi-supervised skin lesion segmentation via transformation consistent self-ensembling model. In Proceedings of the British Machine Vision Conference, Newcastle upon Tyne, UK, 3–6 September 2018. [Google Scholar]

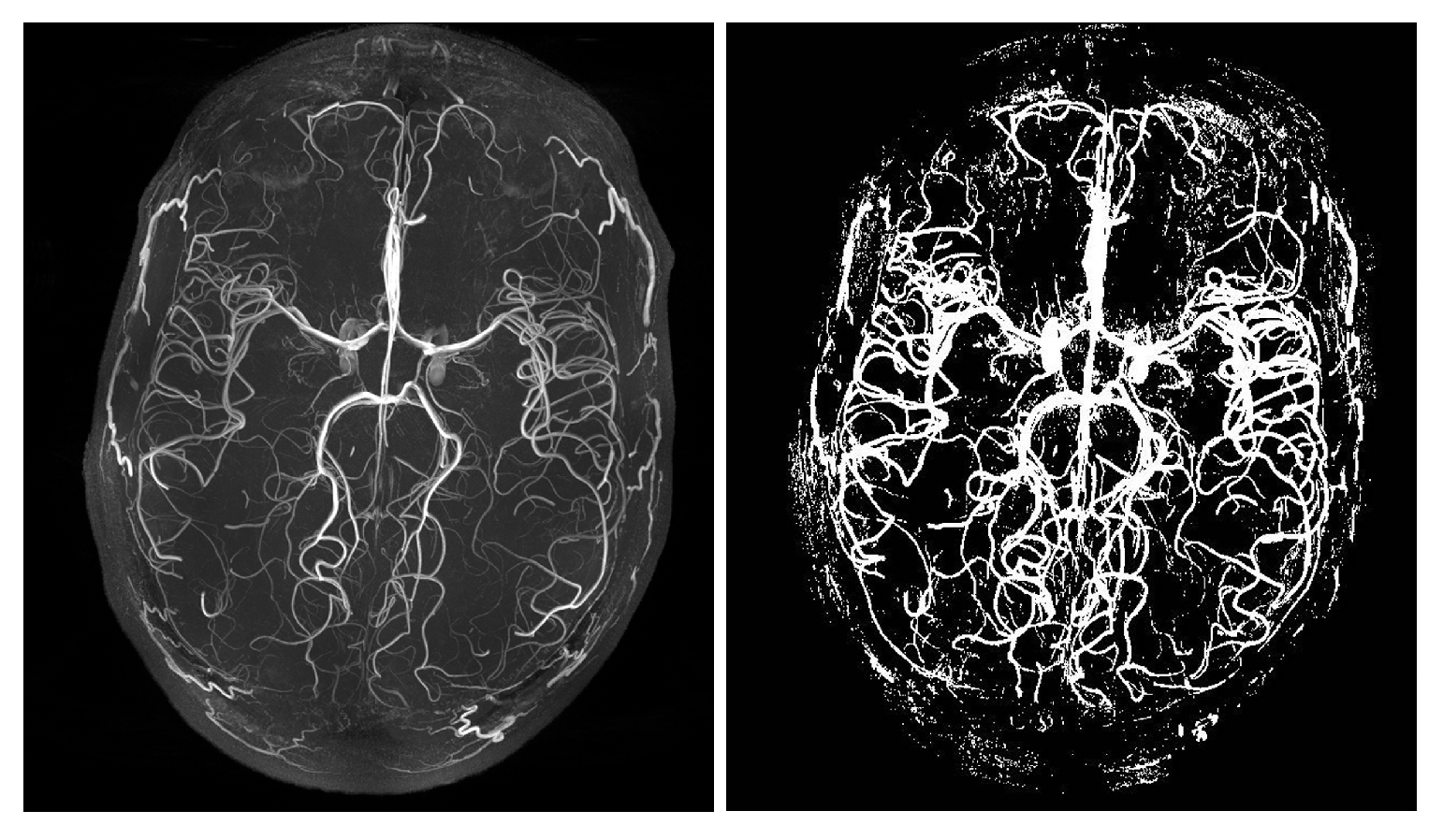
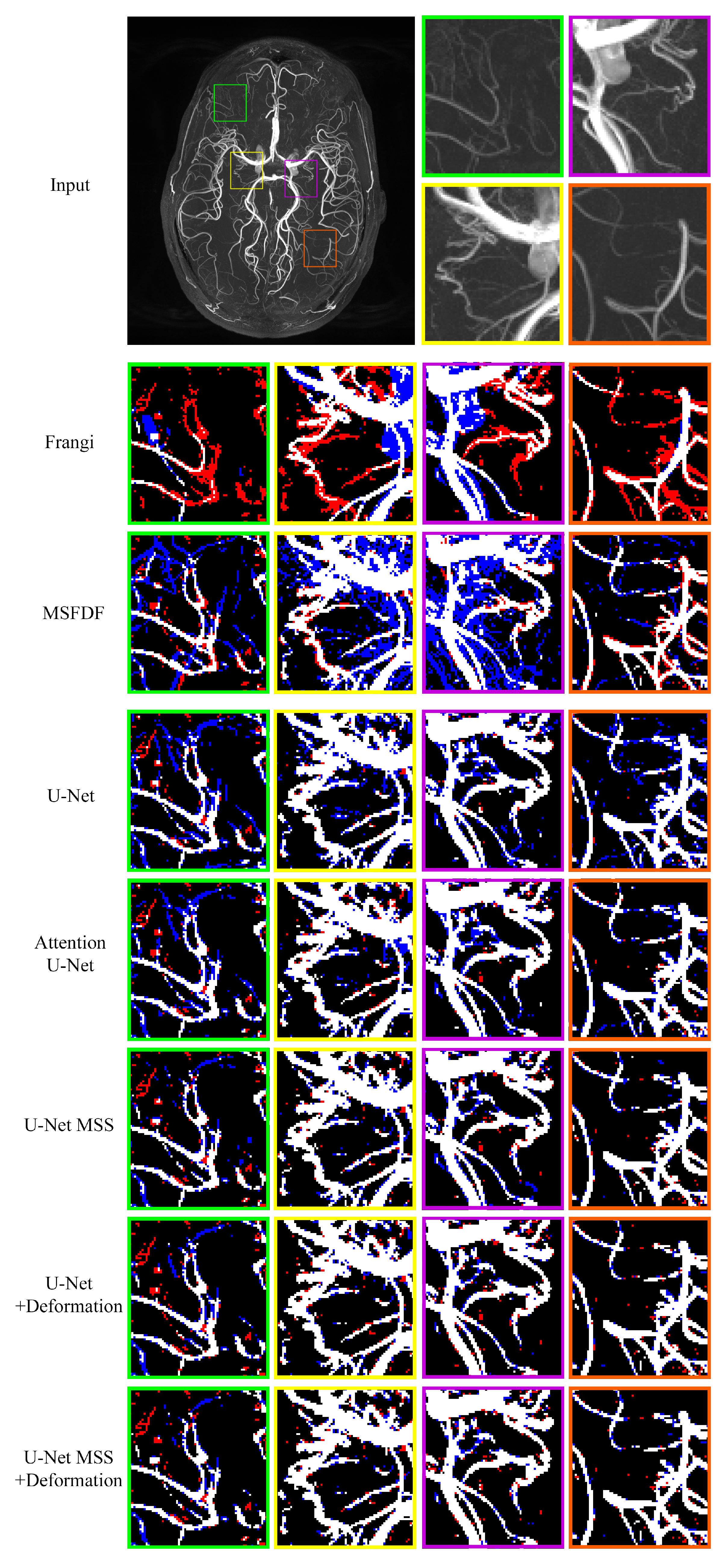



| Type | Method | Dice Coeff. | IoU |
|---|---|---|---|
| Non-DL | Frangi Filter | 51.81 ± 3.09 | 35.00 ± 2.85 |
| Non-DL | MSFDF Pipeline | 48.35 ± 6.34 | 32.04 ± 5.55 |
| DL | Attention U-Net | 76.73 ± 0.22 | 62.25 ± 0.29 |
| DL | U-Net | 76.19 ± 0.17 | 61.54 ± 0.22 |
| DL | U-Net MSS | 79.35 ± 0.35 | 65.81 ± 0.47 |
| DL | U-Net + Deformation | 79.44 ± 0.89 | 65.97 ± 1.23 |
| DL | U-Net MSS + Deformation | 80.44 ± 0.83 | 67.37 ± 1.16 |
| Without Deformation | With Deformation-Aware Learning | ||||
|---|---|---|---|---|---|
| Model | Training Set Size | Dice Coeff. | IoU | Dice Coeff. | IoU |
| U-Net | 1 | 72.52 ± 0.67 | 56.91 ± 0.81 | 74.40 ± 1.25 | 59.25 ± 1.60 |
| 2 | 76.99 ± 0.21 | 62.73 ± 0.36 | 78.13 ± 0.47 | 64.28 ± 0.61 | |
| 4 | 75.88 ± 0.72 | 61.19 ± 0.89 | 77.97 ± 2.06 | 63.96 ± 2.82 | |
| 6 | 76.19 ± 0.17 | 61.54 ± 0.22 | 79.44 ± 0.89 | 65.97 ± 1.23 | |
| U-Net MSS | 1 | 73.11 ± 0.48 | 57.63 ± 0.57 | 74.81 ± 1.32 | 59.78 ± 1.70 |
| 2 | 75.52 ± 0.78 | 60.76 ± 1.07 | 77.84 ± 2.35 | 63.95 ± 3.19 | |
| 4 | 75.02 ± 1.36 | 60.10 ± 1.65 | 77.79 ± 2.05 | 63.76 ± 2.88 | |
| 6 | 79.35 ± 0.35 | 65.81 ± 0.47 | 80.44 ± 0.83 | 67.37 ± 1.16 | |
| Type | Method | Dice Coeff. |
|---|---|---|
| non-DL | MSFDF | 52.39 |
| non-DL | Frangi | 57.59 |
| Training Labels | Ilastik | 50.21 |
| DL | U-Net | 47.45 |
| DL | U-Net MSS | 52.17 |
| DL | U-Net + Deformation | 59.81 |
| DL | U-Net MSS + Deformation | 62.07 |
| 1.5T | 3T | ||||
|---|---|---|---|---|---|
| Model | Patch | Dice Coeff. | IoU | Dice Coeff. | IoU |
| U-Net MSS | 32 | 36.97 ± 0.48 | 22.75 ± 3.69 | 37.74 ± 0.42 | 23.31 ± 3.17 |
| 64 | 39.29 ± 0.36 | 24.49 ± 2.82 | 40.34 ± 0.33 | 25.31 ± 2.58 | |
| 96 | 52.51 ± 0.82 | 35.88 ± 7.44 | 48.25 ± 0.16 | 31.81 ± 1.47 | |
| U-Net MSS + def | 32 | 47.41 ± 0.68 | 31.25 ± 5.91 | 43.95 ± 0.42 | 28.23 ± 3.46 |
| 64 | 43.94 ± 0.39 | 28.22 ± 3.31 | 45.96 ± 0.23 | 29.86 ± 1.97 | |
| 96 | 58.20 ± 0.85 | 41.38 ± 8.28 | 49.90 ± 0.66 | 33.42 ± 5.99 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatterjee, S.; Prabhu, K.; Pattadkal, M.; Bortsova, G.; Sarasaen, C.; Dubost, F.; Mattern, H.; de Bruijne, M.; Speck, O.; Nürnberger, A. DS6, Deformation-Aware Semi-Supervised Learning: Application to Small Vessel Segmentation with Noisy Training Data. J. Imaging 2022, 8, 259. https://doi.org/10.3390/jimaging8100259
Chatterjee S, Prabhu K, Pattadkal M, Bortsova G, Sarasaen C, Dubost F, Mattern H, de Bruijne M, Speck O, Nürnberger A. DS6, Deformation-Aware Semi-Supervised Learning: Application to Small Vessel Segmentation with Noisy Training Data. Journal of Imaging. 2022; 8(10):259. https://doi.org/10.3390/jimaging8100259
Chicago/Turabian StyleChatterjee, Soumick, Kartik Prabhu, Mahantesh Pattadkal, Gerda Bortsova, Chompunuch Sarasaen, Florian Dubost, Hendrik Mattern, Marleen de Bruijne, Oliver Speck, and Andreas Nürnberger. 2022. "DS6, Deformation-Aware Semi-Supervised Learning: Application to Small Vessel Segmentation with Noisy Training Data" Journal of Imaging 8, no. 10: 259. https://doi.org/10.3390/jimaging8100259
APA StyleChatterjee, S., Prabhu, K., Pattadkal, M., Bortsova, G., Sarasaen, C., Dubost, F., Mattern, H., de Bruijne, M., Speck, O., & Nürnberger, A. (2022). DS6, Deformation-Aware Semi-Supervised Learning: Application to Small Vessel Segmentation with Noisy Training Data. Journal of Imaging, 8(10), 259. https://doi.org/10.3390/jimaging8100259








