A Low Redundancy Wavelet Entropy Edge Detection Algorithm
Abstract
1. Introduction
2. Related Work
2.1. First Order
2.2. Second Order
2.3. Entropy Based
2.4. Wavelet Based
2.5. Deep Learning/Machine Learning Based
3. Methodology
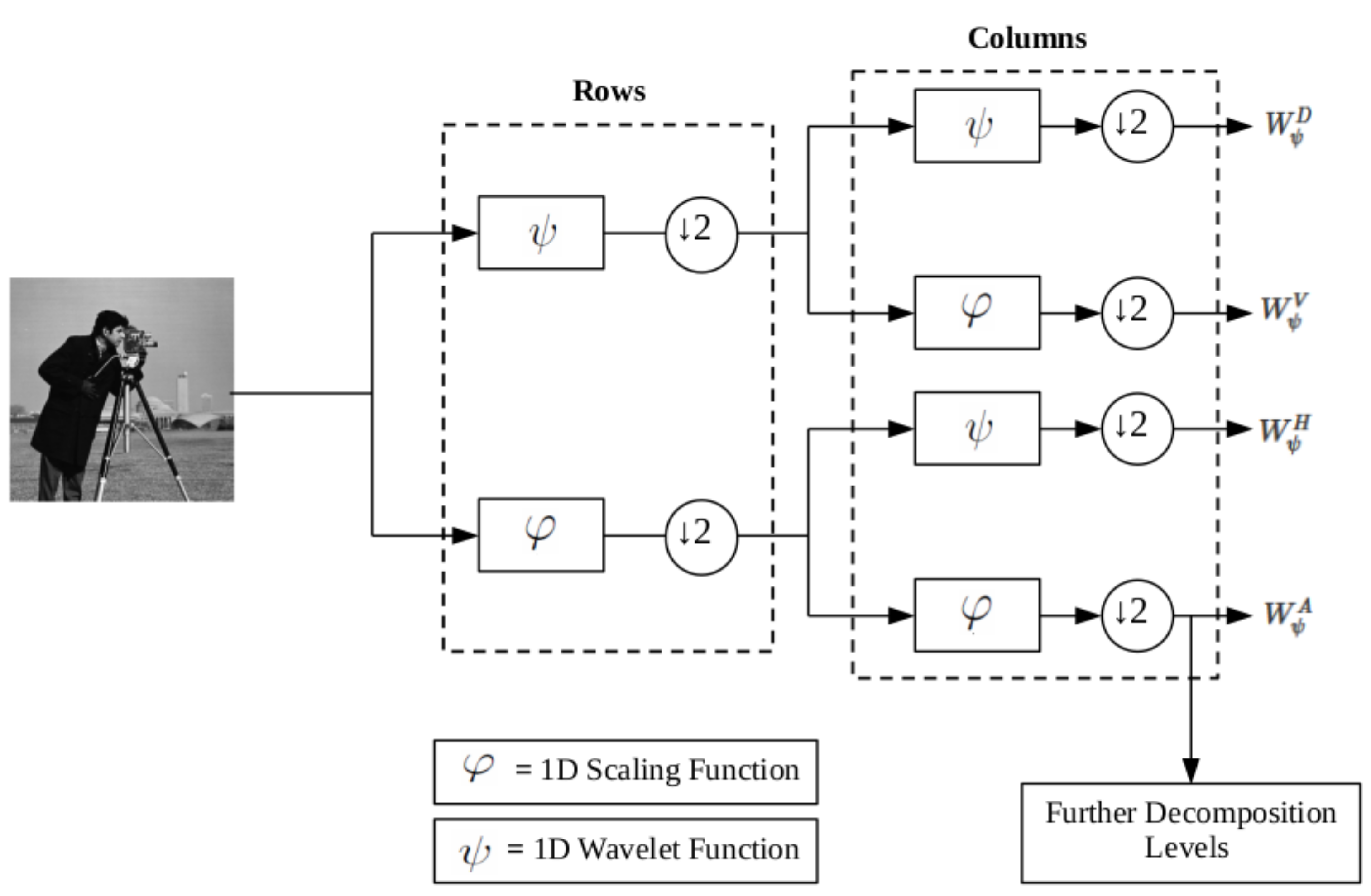
3.1. Wavelet Decomposition
3.2. Wavelet Decomposition Level Selection
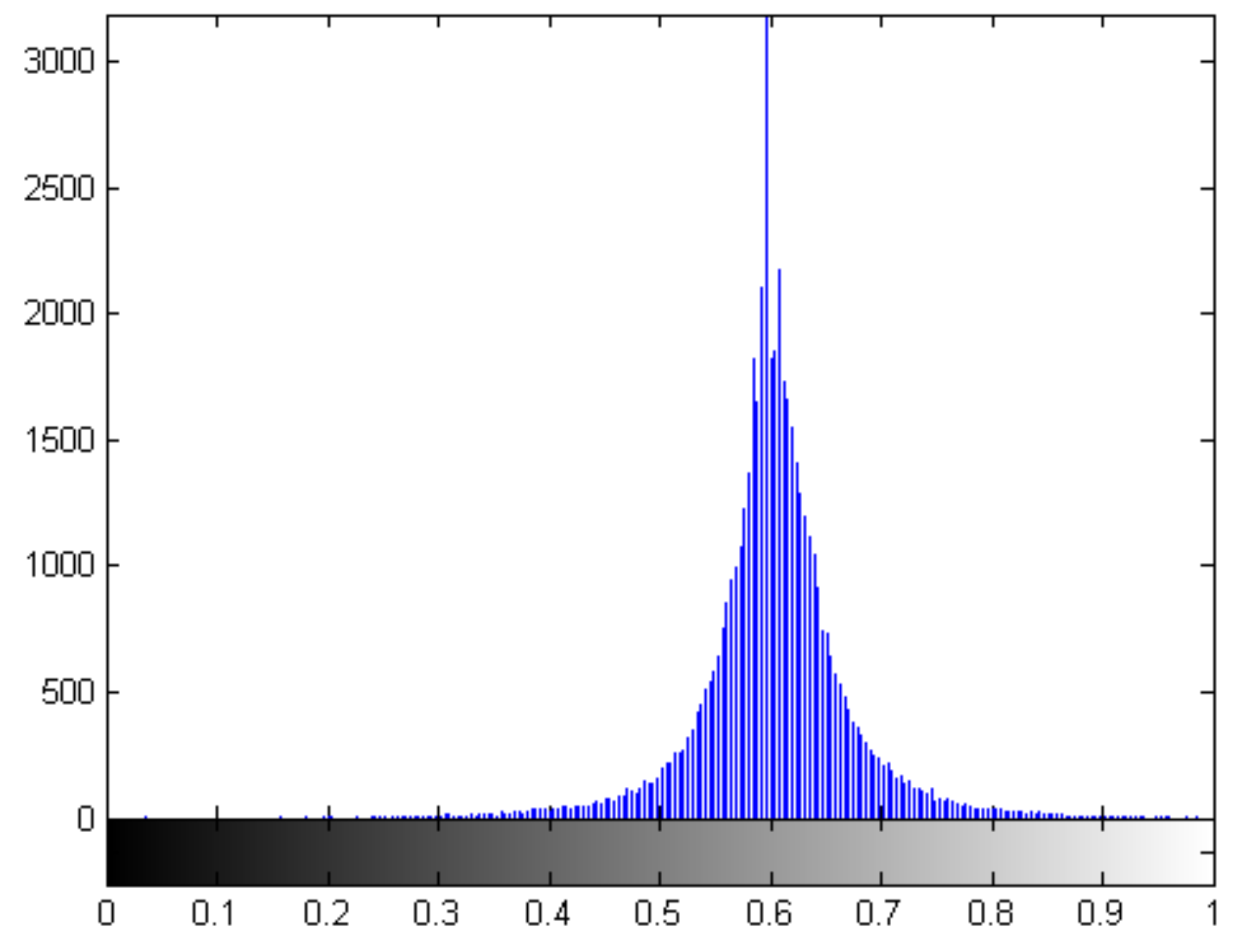
3.3. Entropy Thresholding
4. Results
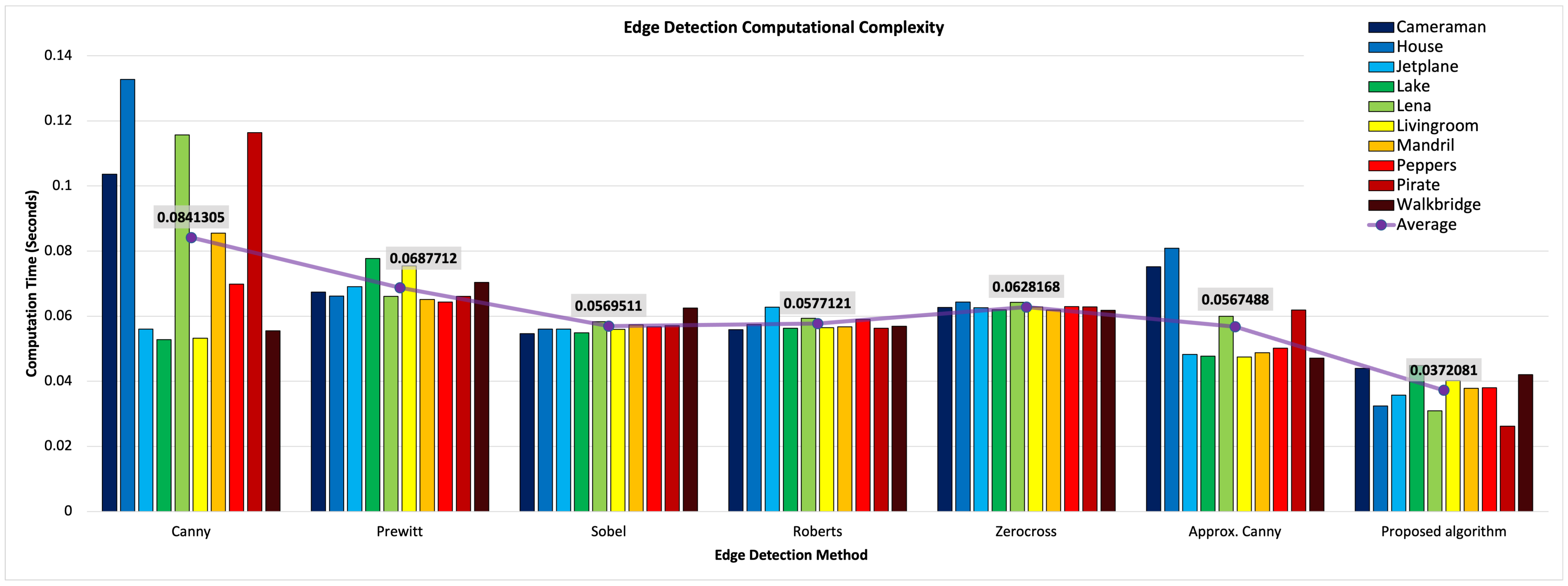
4.1. Computational Efficiency
| Algorithm 1: LRWEEDA edge detection |
 |
4.2. Noise Resilience
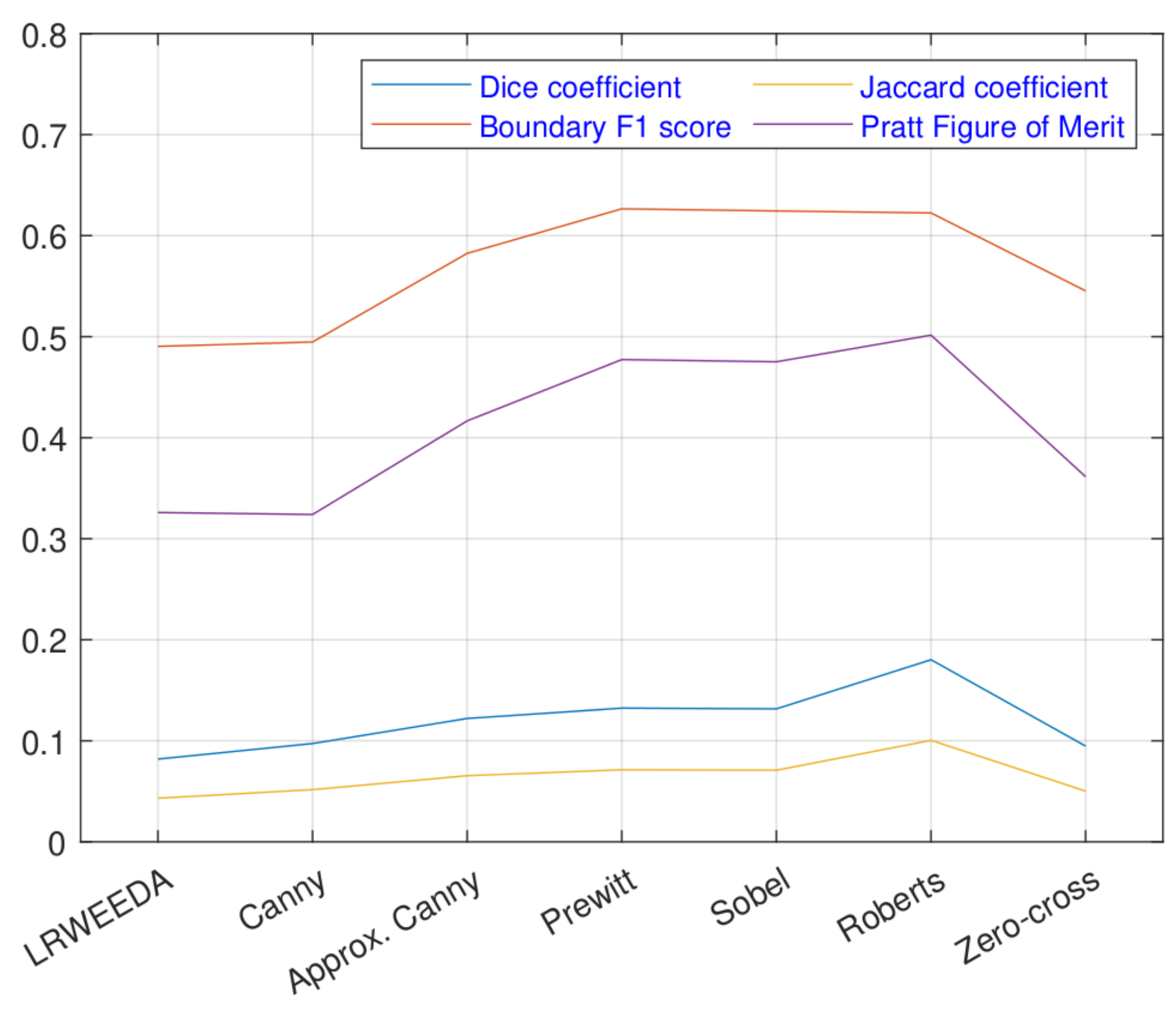
4.3. Performance against Standard Edge Detection Metrics
- The Boundary F1 score is defined as the harmonic mean (F1-measure) of the precision and recall values which measure the matching weight for the predicted boundary and the ground truth boundary, as
- The Jaccard coefficient for two sets is defined as the size of the intersection of the two sets divided by the size of their union as
- Pratt’s FOM uses Euclidean distance to compare two edge images [60]. It multiplies a scale factor ∝ to the Euclidean distance calculated between the two images to penalize displaced edges, aswhere , , and d are, respectively, the detected edges, the ideal edges, the distance between the actual and the ideal edges.
- Qualitative results of the proposed algorithm were obtained and compared with similar edge detection algorithms (Figure 9)
- Ten images were used to calculate the average processing times of the algorithms (Figure 10).
- Noise resilience of the proposed algorithm was analyzed by using four images and compared with Canny (Figure 9).
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, C.M.; Hong, E.J.; Park, R.C. Chest X-ray Outlier Detection Model using Dimension Reduction and Edge Detection. IEEE Access 2021, 9, 86096–86106. [Google Scholar] [CrossRef]
- Dai, W.; Na, J.; Huang, N.; Hu, G.; Yang, X.; Tang, G.; Xiong, L.; Li, F. Integrated edge detection and terrain analysis for agricultural terrace delineation from remote sensing images. Int. J. Geogr. Inf. Sci. 2020, 34, 484–503. [Google Scholar] [CrossRef]
- Gafton, P.; Maraz, E. 2D image relighting with image-to-image translation. arXiv 2020, arXiv:2006.07816. [Google Scholar]
- Li, M.; Lin, Z.; Mech, R.; Yumer, E.; Ramanan, D. Photo-sketching: Inferring contour drawings from images. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 7–11 January 2019; pp. 1403–1412. [Google Scholar]
- Khan, N.H.; Adnan, A. Urdu optical character recognition systems: Present contributions and future directions. IEEE Access 2018, 6, 46019–46046. [Google Scholar] [CrossRef]
- Hirz, M.; Walzel, B. Sensor and object recognition technologies for self-driving cars. Comput.-Aided Des. Appl. 2018, 15, 501–508. [Google Scholar] [CrossRef]
- Ziou, D.; Tabbone, S. Edge detection techniques-an overview. Pattern Recognit. Image Anal. C/C Raspoznavaniye Obraz. Anal. Izobr. 1998, 8, 537–559. [Google Scholar]
- Nadernejad, E.; Sharifzadeh, S.; Hassanpour, H. Edge detection techniques: Evaluations and comparison. Appl. Math. Sci. 2008, 2, 1507–1520. [Google Scholar]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour Detection and Hierarchical Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef]
- Xie, S.; Tu, Z. Holistically-nested edge detection. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 1395–1403. [Google Scholar]
- Orujov, F.; Maskeliūnas, R.; Damaševičius, R.; Wei, W. Fuzzy based image edge detection algorithm for blood vessel detection in retinal images. Appl. Soft Comput. 2020, 94, 106452. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Prewitt, J.M. Object enhancement and extraction. Pict. Process. Psychopictorics 1970, 10, 15–19. [Google Scholar]
- Roberts, L.G. Machine Perception of Three-Dimensional Soups. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, Massachusetts, USA, 1963. [Google Scholar]
- Kanopoulos, N.; Vasanthavada, N.; Baker, R.L. Design of an image edge detection filter using the Sobel operator. IEEE J. Solid-State Circuits 1988, 23, 358–367. [Google Scholar] [CrossRef]
- Basu, M. Gaussian-based edge-detection methods-a survey. IEEE Trans. Syst. Man Cybern. Part C 2002, 32, 252–260. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, M.M.; Hu, X.; Wang, K.; Bai, X. Richer convolutional features for edge detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 22–25 July 2017; pp. 3000–3009. [Google Scholar]
- Poma, X.S.; Riba, E.; Sappa, A. Dense extreme inception network: Towards a robust cnn model for edge detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; pp. 1923–1932. [Google Scholar]
- Gong, X.Y.; Su, H.; Xu, D.; Zhang, Z.T.; Shen, F.; Yang, H.B. An overview of contour detection approaches. Int. J. Autom. Comput. 2018, 15, 656–672. [Google Scholar] [CrossRef]
- Siuzdak, J. A single filter for edge detection. Pattern Recognit. 1998, 31, 1681–1686. [Google Scholar] [CrossRef]
- Peli, T.; Malah, D. A study of edge detection algorithms. Comput. Graph. Image Process. 1982, 20, 1–21. [Google Scholar] [CrossRef]
- Maini, R.; Aggarwal, H. Study and comparison of various image edge detection techniques. Int. J. Image Process. (IJIP) 2009, 3, 1–11. [Google Scholar]
- Waghule, D.R.; Ochawar, R.S. Overview on edge detection methods. In Proceedings of the 2014 International Conference on Electronic Systems, Signal Processing and Computing Technologies (ICESC), Nagpur, India, 9–11 January 2014; pp. 151–155. [Google Scholar]
- Joshi, S.R.; Koju, R. Study and comparison of edge detection algorithms. In Proceedings of the 2012 Third Asian Himalayas International Conference on Internet (AH-ICI), Kathmundu, Nepal, 23–25 November 2012; pp. 1–5. [Google Scholar]
- Torre, V.; Poggio, T.A. On Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 147–163. [Google Scholar] [CrossRef]
- Deriche, R. Using Canny’s criteria to derive a recursively implemented optimal edge detector. Int. J. Comput. Vis. 1987, 1, 167–187. [Google Scholar] [CrossRef]
- Van Vliet, L.J.; Young, I.T.; Verbeek, P.W. Recursive Gaussian derivative filters. In Proceedings of the Fourteenth International Conference on Pattern Recognition (Cat. No. 98EX170), Brisbane, QLD, Australia, 20 August 1998; Volume 1, pp. 509–514. [Google Scholar]
- Pal, N.R.; Pal, S.K. Entropic thresholding. Signal Process. 1989, 16, 97–108. [Google Scholar] [CrossRef]
- Pun, T. Entropic thresholding, a new approach. Comput. Graph. Image Process. 1981, 16, 210–239. [Google Scholar] [CrossRef]
- Shiozaki, A. Edge extraction using entropy operator. Comput. Vision, Graph. Image Process. 1986, 36, 1–9. [Google Scholar] [CrossRef]
- Gull, S.; Skilling, J. Maximum entropy method in image processing. IEE Proc. Commun. Radar Signal Process. 1984, 131, 646–659. [Google Scholar] [CrossRef]
- El-Sayed, M.A. A new algorithm based entropic threshold for edge detection in images. arXiv 2012, arXiv:1211.2500. [Google Scholar]
- Kapur, J.N.; Sahoo, P.K.; Wong, A.K. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vision Graph. Image Process. 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Yang, C. A new operator for detecting edges in images based on modified Tsallis entropy. In Proceedings of the 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet), Xianning, China, 16–18 April 2011; pp. 4671–4674. [Google Scholar] [CrossRef]
- Chang, C.I.; Chen, K.; Wang, J.; Althouse, M.L. A relative entropy-based approach to image thresholding. Pattern Recognit. 1994, 27, 1275–1289. [Google Scholar] [CrossRef]
- Medina-Carnicer, R.; Madrid-Cuevas, F.J.; Fernández-García, N.; Carmona-Poyato, A. Evaluation of global thresholding techniques in non-contextual edge detection. Pattern Recognit. Lett. 2005, 26, 1423–1434. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Singh, B.; Singh, A.P. Edge Detection in Gray Level Images based on the Shannon Entropy. J. Comput. Sci. 2008, 3, 186–191. [Google Scholar] [CrossRef]
- Li, J. A Wavelet Approach to Edge Detection. Master’s Thesis, Sam Houston State University, Huntsville, TX, USA, 2003. [Google Scholar]
- Liu, W.; Ma, Z. Wavelet image threshold denoising based on edge detection. In Proceedings of the IMACS Multiconference on Computational Engineering in Systems Applications, Beijing, China, 4–6 October 2006; Volume 1, pp. 72–78. [Google Scholar]
- Schmeelk, J. Wavelet transforms and edge detectors on digital images. Math. Comput. Model. 2005, 41, 1469–1478. [Google Scholar] [CrossRef]
- Shih, M.Y.; Tseng, D.C. A wavelet-based multiresolution edge detection and tracking. Image Vis. Comput. 2005, 23, 441–451. [Google Scholar] [CrossRef]
- Siddique, J.; Barner, K.E. Wavelet-based multiresolution edge detection utilizing gray level edge maps. In Proceedings of the ICIP 98, 1998 International Conference on Image Processing, Chicago, IL, USA, 7 October 1998; Volume 2, pp. 550–554. [Google Scholar]
- Zhang, L.; Bao, P. Edge detection by scale multiplication in wavelet domain. Pattern Recognit. Lett. 2002, 23, 1771–1784. [Google Scholar] [CrossRef]
- Jiang, W.; Lam, K.M.; Shen, T.Z. Efficient edge detection using simplified Gabor wavelets. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2009, 39, 1036–1047. [Google Scholar] [CrossRef]
- Hao, Y.; Changshun, L.; Lei, P. An improved method of image edge detection based on wavelet transform. In Proceedings of the 2011 IEEE International Conference on Computer Science and Automation Engineering (CSAE), Shanghai, China, 10–12 June 2011; Volume 3, pp. 678–681. [Google Scholar]
- Elaraby, A.E.A.; Owny, E.; Ahmed, H.B.; Heshmat, M.; Hassaballah, M.; Rardy, A.S.A. A Novel Algorithm for Edge Detection of Noisy Medical Images. Int. J. Signal Process. Image Process. Pattern Recognit. 2013, 6, 365–374. [Google Scholar] [CrossRef][Green Version]
- Xishan, T. A Novel Image Edge Detection Algorithm based on Prewitt Operator and Wavelet Transform. Int. J. Adv. Comput. Technol. 2012, 4, 73–82. [Google Scholar]
- Srivastava, G.; Verma, R.; Mahrishi, R.; Rajesh, S. A novel wavelet edge detection algorithm for noisy images. In Proceedings of the ICUMT ’09, International Conference on Ultra Modern Telecommunications Workshops, St. Petersburg, Russia, 12–14 October 2009; pp. 1–8. [Google Scholar] [CrossRef]
- Wu, Y.; He, Y.; Cai, H. Optimal threshold selection algorithm in edge detection based on wavelet transform. Image Vis. Comput. 2005, 23, 1159–1169. [Google Scholar] [CrossRef]
- Vetterli, M.; Kovacevic, J. Wavelets and Subband Coding; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Bertasius, G.; Shi, J.; Torresani, L. Deepedge: A multi-scale bifurcated deep network for top-down contour detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8–10 June 2015; pp. 4380–4389. [Google Scholar]
- Shen, W.; Wang, X.; Wang, Y.; Bai, X.; Zhang, Z. Deepcontour: A deep convolutional feature learned by positive-sharing loss for contour detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8–10 June 2015; pp. 3982–3991. [Google Scholar]
- He, J.; Zhang, S.; Yang, M.; Shan, Y.; Huang, T. Bi-directional cascade network for perceptual edge detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 3828–3837. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Graps, A. An introduction to wavelets. IEEE Comput. Sci. Eng. 1995, 2, 50–61. [Google Scholar] [CrossRef]
- Chakrabarti, C.; Vishwanath, M. Efficient realizations of the discrete and continuous wavelet transforms: From single chip implementations to mappings on SIMD array computers. IEEE Trans. Signal Process. 1995, 43, 759–771. [Google Scholar] [CrossRef]
- Nelson, M.; Gailly, J.L. The Data Compression Book; M&T Books: New York, NY, USA, 1996; Volume 2. [Google Scholar]
- Wei, D.; Rajashekar, U.; Bovik, A.C. 3.4—Wavelet Denoising for Image Enhancement. In Handbook of Image and Video Processing, 2nd ed.; Bovik, A., Ed.; Communications, Networking and Multimedia; Academic Press: Burlington, MA, USA, 2005; pp. 157–165. [Google Scholar] [CrossRef]
- Csurka, G.; Larlus, D.; Perronnin, F.; Meylan, F. What is a good evaluation measure for semantic segmentation? Bmvc 2013, 27, 10–5244. [Google Scholar]
- Abdou, I.E.; Pratt, W.K. Quantitative design and evaluation of enhancement/thresholding edge detectors. Proc. IEEE 1979, 67, 753–763. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Y.; Scully, T.; Perera, A.G.; Lambert, A.; Chahl, J. A Low Redundancy Wavelet Entropy Edge Detection Algorithm. J. Imaging 2021, 7, 188. https://doi.org/10.3390/jimaging7090188
Tao Y, Scully T, Perera AG, Lambert A, Chahl J. A Low Redundancy Wavelet Entropy Edge Detection Algorithm. Journal of Imaging. 2021; 7(9):188. https://doi.org/10.3390/jimaging7090188
Chicago/Turabian StyleTao, Yiting, Thomas Scully, Asanka G. Perera, Andrew Lambert, and Javaan Chahl. 2021. "A Low Redundancy Wavelet Entropy Edge Detection Algorithm" Journal of Imaging 7, no. 9: 188. https://doi.org/10.3390/jimaging7090188
APA StyleTao, Y., Scully, T., Perera, A. G., Lambert, A., & Chahl, J. (2021). A Low Redundancy Wavelet Entropy Edge Detection Algorithm. Journal of Imaging, 7(9), 188. https://doi.org/10.3390/jimaging7090188







