Roadmap on Digital Holography-Based Quantitative Phase Imaging
Abstract
:1. Introduction
2. Application of Holography to Microscopy in Biology: Label-Free Live Cell Imaging with Digital Holographic Microscopy
2.1. Status
2.2. Current and Future Challenges
2.3. Advances in Science and Technology to Meet Challenges
2.4. Concluding Remarks
3. Principle and Application of Tomographic Phase Microscopy in Biology
3.1. Tomographic Phase Microscopy
3.2. Future Challenges
3.3. Holography Applied to Microscopy in Biology and Medicine
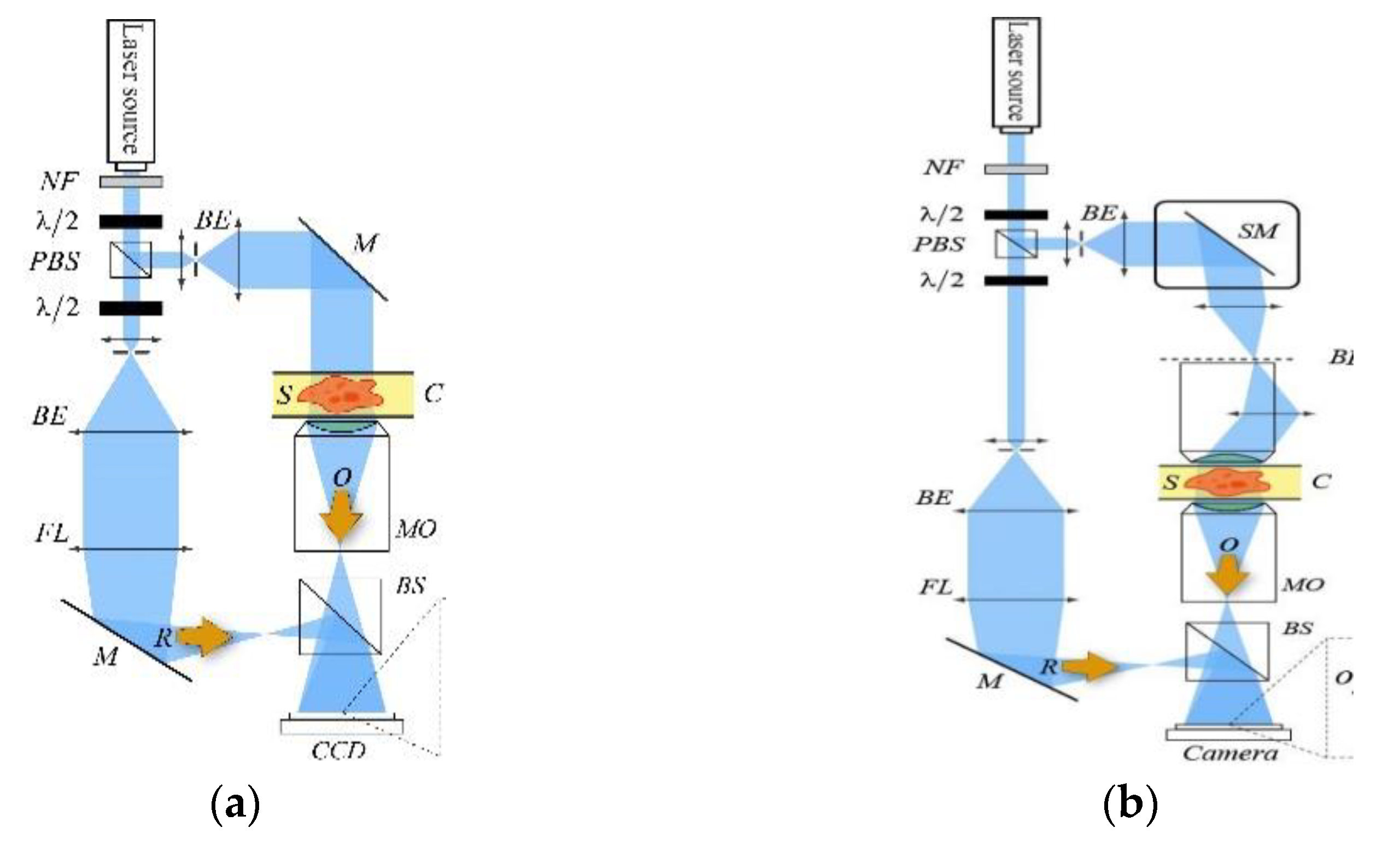
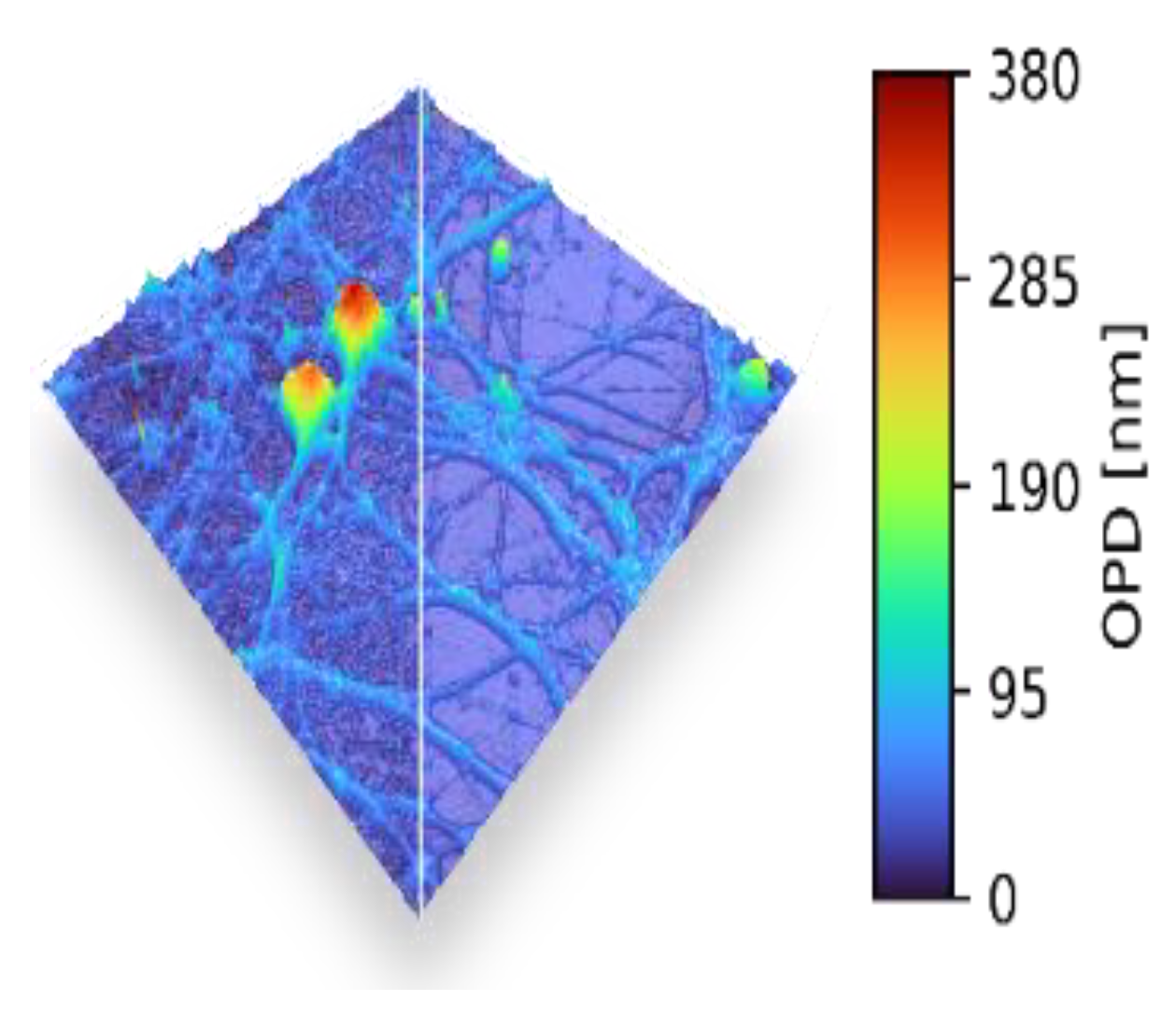
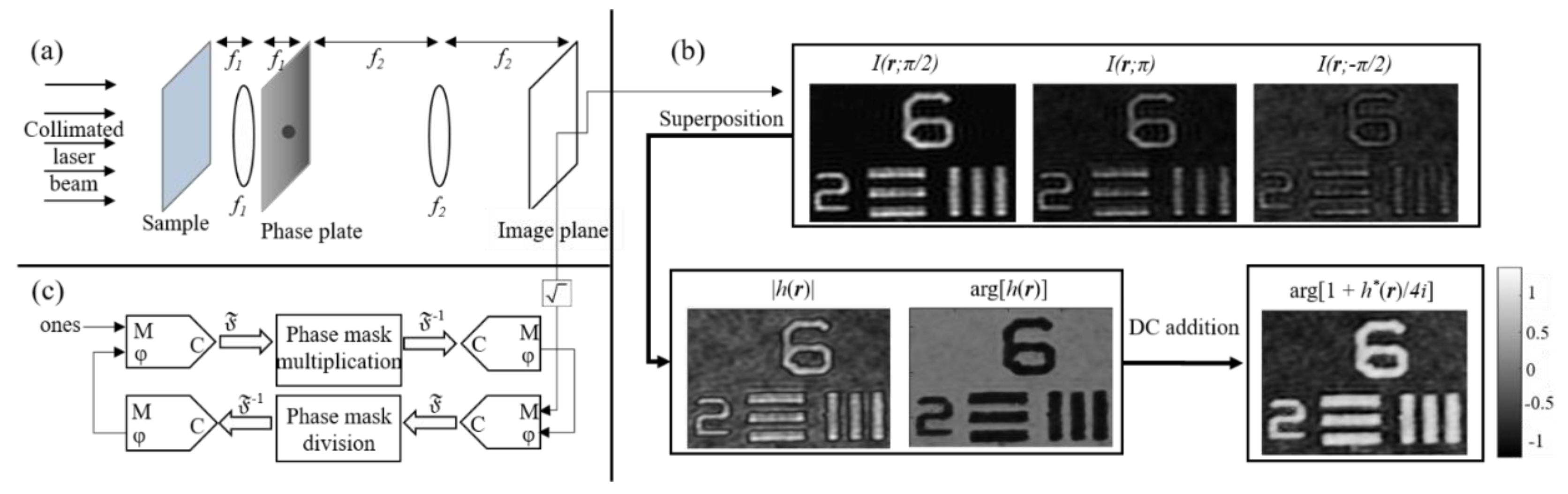
4. Quantitative Phase Imaging by Self-Reference on-Axis Holography
4.1. Status
4.2. Current and Future Challenges
≅∣exp(iξ)+Σn anφn(r/MT)∣2,
4.3. Advances in Science and Technology to Meet Challenges
4.4. Concluding Remarks
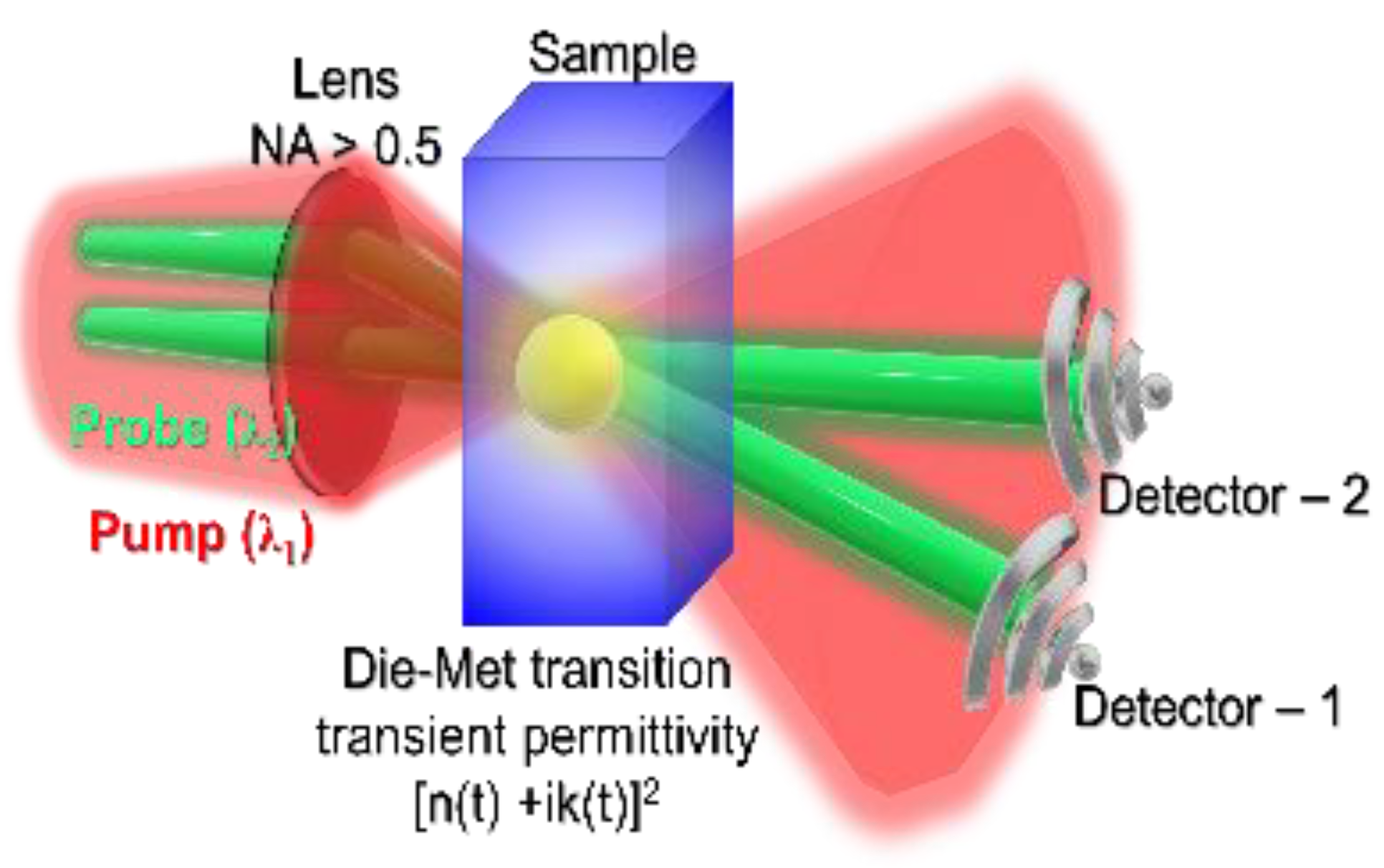
5. Tracking Ultra-Fast Material Transformation with Permittivity Transient
5.1. Status
5.2. Current and Future Challenges
5.3. Advances in Science and Technology to Meet Challenges
5.4. Concluding Remarks
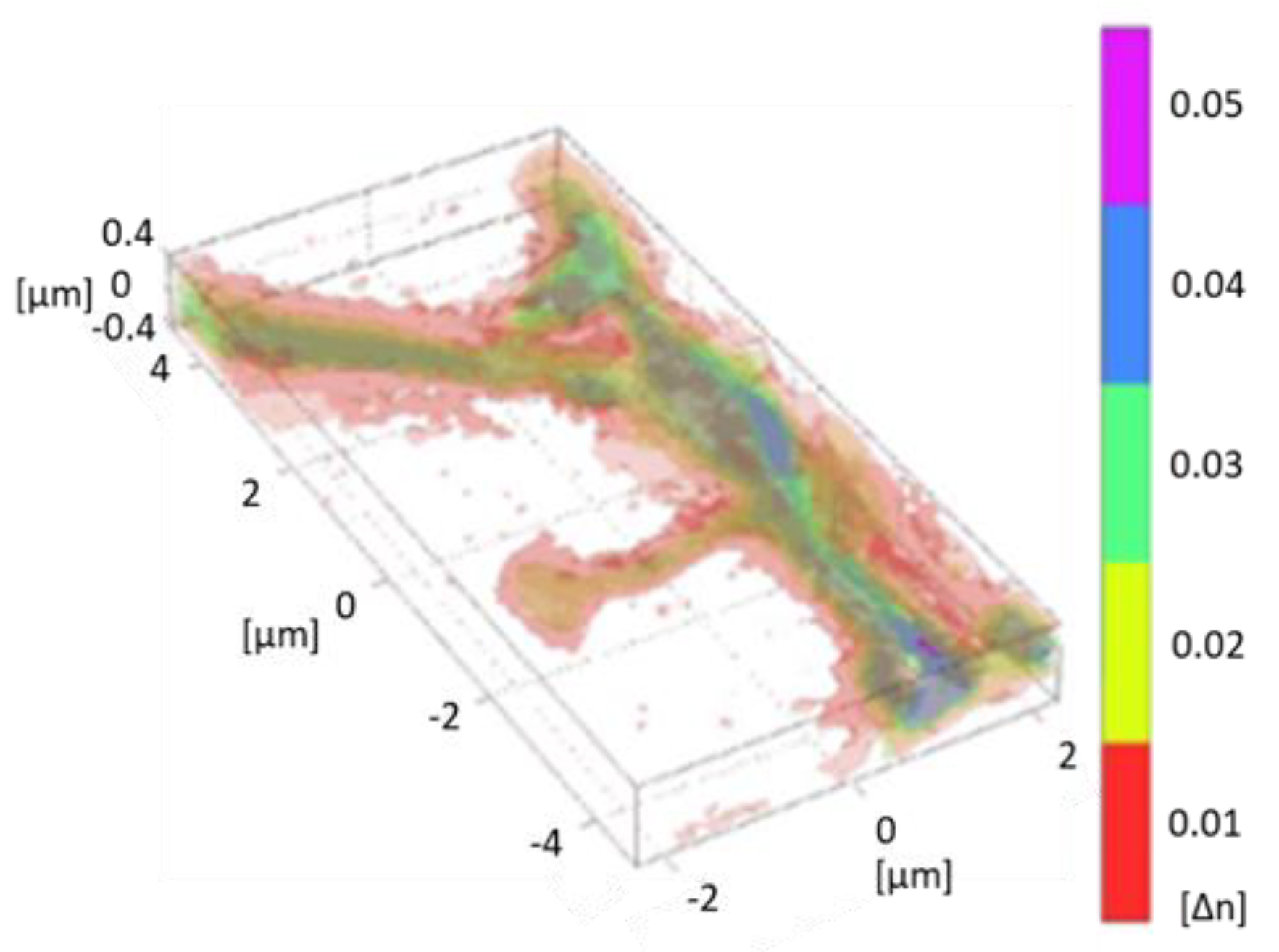
6. Three-Dimensional Quantitative Phase Imaging
6.1. Status
6.2. Current and Future Challenges
6.2.1. Image Quality
6.2.2. Imaging Throughput and Data Size
6.2.3. Interpreting 3D Data
6.3. Advances in Science and Technology to Meet Challenges
6.4. Concluding Remarks
7. 3D QPI: Integrated Dual-Mode Tomography
7.1. Status
7.2. Current and Future Challenges
7.3. Advances in Science and Technology to Meet Challenges
7.4. Concluding Remarks
8. Ultra-Scale High-Contrast Holographic Tomography
8.1. Status
8.2. Current and Future Challenges
8.2.1. Ultra-Scale HT
8.2.2. High contrast HT
8.3. Advances in Science and Technology to Meet Challenges
8.4. Concluding Remarks
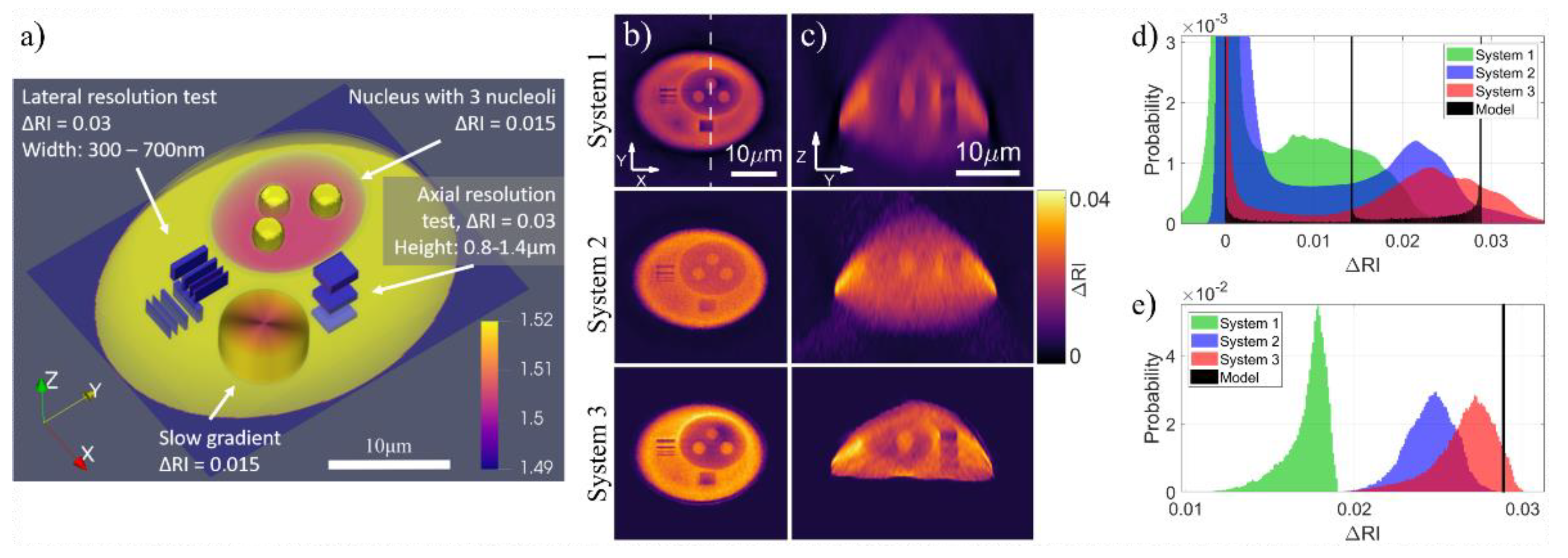
9. Metrology Aspects in 3D QPI
9.1. Status
9.2. Current and Future Challenges
9.3. Advances in Science and Technology to meet Challenges
9.4. Concluding Remarks
10. From Computational to Neural Microscopy
10.1. Status
10.2. Current and Future Challenges
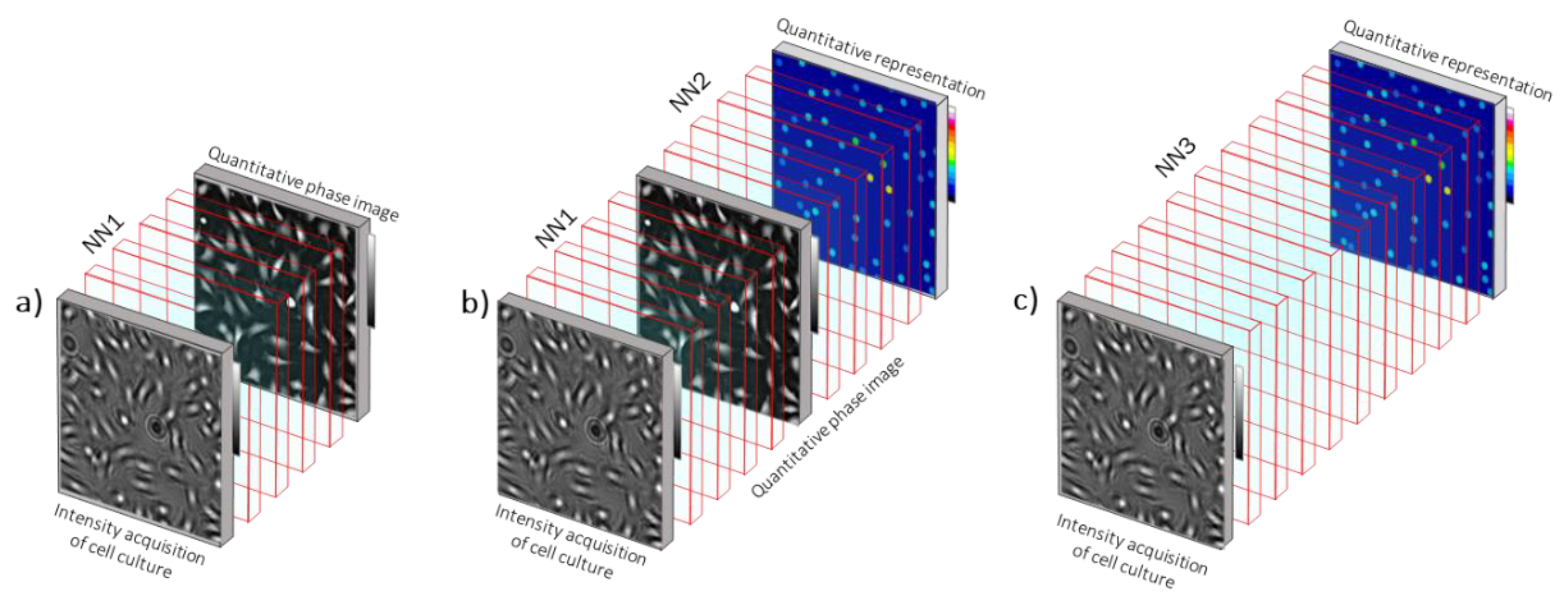
10.3. Advances in Science and Technology to Meet Challenges
10.4. Concluding Remarks
11. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Popescu, G. Quantitative Phase Imaging of Cells and Tissues; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Shaked, N.T.; Zalevsky, Z.; Satterwhite, L.L. Biomedical Optical Phase Microscopy and Nanoscopy; Academic Press: London, UK, 2012. [Google Scholar]
- Kemper, B.; Von Bally, G. Digital holographic microscopy for live cell applications and technical inspection. Appl. Opt. 2008, 47, A52–A61. [Google Scholar] [CrossRef]
- Cotte, Y.; Toy, F.; Jourdain, P.; Pavillon, N.; Boss, D.; Magistretti, P.; Marquet, P.; Depeursinge, C. Marker-free phase nanoscopy. Nat. Photonics 2013, 7, 113–117. [Google Scholar] [CrossRef]
- Park, Y.; Depeursinge, C.; Popescu, G. Quantitative phase imaging in biomedicine. Nat. Photonics 2018, 12, 578–589. [Google Scholar] [CrossRef]
- Sung, Y.; Choi, W.; Fang, Y.C.; Badizadegan, K.; Dasari, R.; Feld, M. Optical diffraction tomography for high resolution live cell imaging. Opt. Express 2009, 17, 266–277. [Google Scholar] [CrossRef]
- Balasubramani, V.; Kuś, A.; Tu, H.Y.; Cheng, C.J.; Baczewska, M.; Krauze, W.; Kujawińska, M. Holographic tomography: Techniques and biomedical applications [Invited]. Appl. Opt. 2021, 60, B65–B80. [Google Scholar] [CrossRef]
- Wang, Z.; Millet, L.; Mir, M.; Ding, H.; Unarunotai, S.; Rogers, J.; Gillette, M.U.; Popescu, G. Spatial light interference microscopy (SLIM). Opt. Express 2011, 19, 1016–1026. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Kandel, M.E.; Rubessa, M.; Wheeler, M.B.; Popescu, G. Gradient light interference microscopy for 3D imaging of unlabeled specimens. Nat. Commun. 2017, 8, 210. [Google Scholar] [CrossRef]
- Bon, P.; Maucort, G.; Wattellier, B.; Monneret, S. Quadriwave lateral shearing interferometry for quantitative phase microscopy of living cells. Opt. Express 2009, 17, 13080–13094. [Google Scholar] [CrossRef]
- Lue, N.; Bewersdorf, J.; Lessard, M.D.; Badizadegan, K.; Dasari, R.R.; Feld, M.S.; Popescu, G. Tissue refractometry using Hilbert phase microscopy. Opt. Lett. 2007, 32, 3522–3524. [Google Scholar] [CrossRef]
- Trusiak, M.; Mico, V.; Garcia, J.; Patorski, K. Quantitative phase imaging by single-shot Hilbert–Huang phase microscopy. Opt. Lett. 2016, 41, 4344–4347. [Google Scholar] [CrossRef]
- Zheng, G.; Horstmeyer, R.; Yang, C. Wide-field, high-resolution Fourier ptychographic microscopy. Nat. Photonics 2013, 7, 739–745. [Google Scholar] [CrossRef]
- Sun, J.; Chen, Q.; Zhang, J.; Fan, Y.; Zuo, C. Single-shot quantitative phase microscopy based on color-multiplexed Fourier ptychography. Opt. Lett. 2018, 43, 3365–3368. [Google Scholar] [CrossRef]
- Paganin, D.; Nugent, K.A. Noninterferometric phase imaging with partially coherent light. Phys. Rev. Lett. 1998, 80, 2586–2589. [Google Scholar] [CrossRef]
- Gabor, D. Microscopy by Reconstructed Wave-Fronts. Proceedings of the Royal Society of London. Ser. A Math. Phys. Sci. 1949, 197, 454–487. [Google Scholar]
- Wolf, E. Three-dimensional structure determination of semi-transparent object from holographic data. Opt. Commun. 1969, 1, 153–156. [Google Scholar] [CrossRef]
- Cuche, E.; Marquet, P.; Depeursinge, C. Simultaneous amplitude-contrast and quantitative phase-contrast microscopy by numerical reconstruction of Fresnel off-axis holograms. Appl. Opt. 1999, 38, 6994–7001. [Google Scholar] [CrossRef]
- Marquet, P.; Rappaz, B.; Magistretti, P.J.; Cuche, E.; Emery, Y.; Colomb, T.; Depeursinge, C. Digital holographic microscopy: A noninvasive contrast imaging technique allowing quantitative visualization of living cells with subwavelength axial accuracy. Opt. Lett. 2005, 30, 468–470. [Google Scholar] [CrossRef] [Green Version]
- Rappaz, B.; Charrière, F.; Depeursinge, C.; Magistretti, P.J.; Marquet, P. Simultaneous cell morphometry and refractive index measurement with dual-wavelength digital holographic microscopy and dye-enhanced dispersion of perfusion medium. Opt. Lett. 2008, 33, 744–746. [Google Scholar] [CrossRef]
- Boss, D.; Kühn, J.; Jourdain, P.; Depeursinge, C.; Magistretti, P.J.; Marquet, P. Measurement of absolute cell volume, osmotic membrane water permeability, and refractive index of transmembrane water and solute flux by digital holographic microscopy. J. Biomed. Opt. 2013, 18, 36007. [Google Scholar] [CrossRef]
- Colomb, T.; Cuche, E.; Depeursinge, C. Birefringence measurement by use of digital holographic microscopy: Examples with fiber optics and concrete samples. In Optical Measurement Systems for Industrial Inspection Iv, Pts 1 and 2; Spie-Int Society Optical Engineering: Bellingham, WA, USA, 2005. [Google Scholar]
- Depeursinge, C.; Marquet, P.; Pavillon, N. Application of Digital Holographic Micros-copy in Biomedicine. In Handbook of Biomedical Optics; Boas, D.A., Pitris, C., Ramanujam, N., Eds.; CRC Press: Boca Raton, FL, USA, 2011; pp. 617–647. [Google Scholar]
- Kastl, L.; Isbach, M.; Dirksen, D.; Schnekenburger, J.; Kemper, B. Quantitative phase imaging for cell culture quality control. Cytometry A. 2017, 91, 470–481. [Google Scholar] [CrossRef] [Green Version]
- Connor, T.O.; Rawat, S.; Markman, A.; Javidi, B. Automatic cell identification and visualization using digital holographic microscopy with head mounted augmented reality devices. Appl. Opt. 2018, 57, B197–B204. [Google Scholar]
- Rubin, M.; Stein, O.; Turko, N.A.; Nygate, N.; Roitshtain, D.; Karako, L.; Barnea, I.; Giryes, R.; Shaked, N.T. TOP-GAN: Stain-free cancer cell classification using deep learning with a small training set. Med. Image Anal. 2019, 57, 176–185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benzerdjeb, N.; Garbar, C.; Camparo, P.; Sevestre, H. Digital Holographic Microscopy as Screening Tool for Cervical Cancer Preliminary Study. Cancer Cytopathol. 2016, 124, 573–580. [Google Scholar] [CrossRef]
- Croft, L.V.; Mulders, J.A.; Richard, D.J.; Byrne, K.O. Digital Holographic Imaging as a Method for Quantitative, Live Cell Imaging of Drug Response to Novel Targeted Cancer Therapies. Methods Mol. Biol. 2019, 2054, 171–183. [Google Scholar]
- Kühn, J.; Shaffer, E.; Mena, J.; Breton, B.; Parent, J.; Rappaz, B.; Chambon, M.; Emery, Y.; Magistretti, P.; Depeursinge, C.; et al. Label-free cytotoxicity screening assay by digital holographic microscopy. Assay Drug Dev. Technol. 2013, 11, 101–107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barer, R. Determination of dry mass, thickness, solid and water concentration in living cells. Nature 1953, 172, 1097–1098. [Google Scholar] [CrossRef]
- Krizova, A.; Collakova, J.; Dostal, Z.; Kvasnica, L.; Uhlirova, H.; Zikmund, T.; Vesely, P.; Chmelik, R. Dynamic phase differences based on quantitative phase imaging for the objective evaluation of cell behavior. J. Biomed. Opt. 2015, 20, 111214. [Google Scholar] [CrossRef]
- Rappaz, B.; Cano, E.; Colomb, T.; Kühn, J.; Depeursinge, C.; Simanis, V.; Magistretti, P.J.; Marquet, P. Noninvasive characterization of the fission yeast cell cycle by monitoring dry mass with digital holographic microscopy. J. Biomed. Opt. 2009, 14, 034049. [Google Scholar] [CrossRef]
- Cintora, P.; Arikkath, J.; Kandel, M.; Popescu, G.; Best-Popescu, C. Cell Density Modulates Intracellular MassTransport in Neural Networks. Cytom. Part A 2017, 91, 503–509. [Google Scholar] [CrossRef] [Green Version]
- Di Caprio, G.; Ferrara, M.A.; Miccio, L.; Merola, F.; Memmolo, P.; Ferraro, P.; Coppola, G. Holographic imaging of unlabelled sperm cells for semen analysis: A review. J. Biophotonics 2015, 10, 779–789. [Google Scholar] [CrossRef] [Green Version]
- Bianco, V.; Memmolo, P.; Leo, M.; Montresor, S.; Distante, C.; Paturzo, M.; Picart, P.; Javidi, B.; Ferraro, P. Strategies for reducing speckle noise in digital holography. Light Sci. Appl. 2018, 7, 48. [Google Scholar] [CrossRef]
- Pan, F.; Yang, L.; Xiao, W. Coherent noise reduction in digital holographic microscopy by averaging multiple holograms recorded with a multimode laser. Opt. Express 2017, 25, 21815–21825. [Google Scholar] [CrossRef] [PubMed]
- Loiselle, C.L.; Bélanger, E.; Marquet, P. Polychromatic digital holographic microscopy: A quasicoherent-noise-free imaging technique to explore the connectivity of living neuronal networks. Neurophotonics 2020, 7, 040501. [Google Scholar]
- Girshovitz, P.; Shaked, N.T. Generalized cell morphological parameters based on interferometric phase microscopy and their application to cell life cycle characterization. Biomed. Opt. Express 2012, 3, 1757–1773. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boss, D.; Hoffmann, A.; Rappaz, B.; Depeursinge, C.; Magistretti, P.J.; Van de Ville, D.; Marquet, P. Spatially-resolved eigenmode decomposition of red blood cells membrane fluctuations questions the role of ATP in flickering. PLoS ONE 2012, 7, e40667. [Google Scholar] [CrossRef] [PubMed]
- Eldridge, W.J.; Sheinfeld, A.; Rinehart, M.T.; Wax, A. Imaging deformation of adherent cells due to shear stress using quantitative phase imaging. Opt. Lett. 2016, 15, 352–355. [Google Scholar] [CrossRef]
- Lue, N.; Popescu, G.; Ikeda, T.; Dasari, R.R.; Badizadegan, K.; Feld, M.S. Live cell refractometry using microfluidic devices. Opt. Lett. 2006, 31, 2759–2761. [Google Scholar] [CrossRef]
- Kemper, B.; Kosmeier, S.; Langehanenberg, P.; Von Bally, G.; Bredebusch, I.; Domschke, W.; Schnekenburger, J. Integral refractive index determination of living suspension cells by multifocus digital holographic phase contrast microscopy. J. Biomed. Opt. 2007, 12, 054009. [Google Scholar] [CrossRef]
- Curl, C.L.; Bellair, C.J.; Harris, P.J.; Allman, B.E.; Roberts, A.; Nugent, K.A.; Delbridge, L.M. Single cell volume measurement by quantitative phase microscopy (QPM): A case study of erythrocyte morphology. Cell Physiol. Biochem. 2006, 17, 193–200. [Google Scholar] [CrossRef]
- Bélanger, E.; Lévesque, S.A.; Rioux-Pellerin, E.; Lavergne, P.; Marquet, P. Measuring Absolute Cell Volume Using Quantitative-Phase Digital Holographic Microscopy and a Low-Cost, Open-Source, and 3D-Printed Flow Chamber. Front. Phys. 2019, 7, 172. [Google Scholar] [CrossRef] [Green Version]
- Rappaz, B.; Barbul, A.; Emery, Y.; Korenstein, R.; Depeursinge, C.; Magistretti, P.J.; Marquet, P. Comparative study of human erythrocytes by digital holographic microscopy, confocal microscopy, and impedance volume analyzer. Cytometry. A 2008, 73, 895–903. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.A.; Soubies, E.; Ayoub, A.; Lim, J.; Psaltis, D.; Unser, M. Three-dimensional optical diffraction tomography with Lippmann Schwinger model. IEEE Trans. Comput. Imaging 2020, 6, 727–738. [Google Scholar] [CrossRef] [Green Version]
- Marian, A.; Charrière, F.; Colomb, T.; Montfort, F.; Kühn, J.; Marquet, P.; Depeursinge, C. On the complex three-dimensional amplitude point spread function of lenses and microscope objectives: Theoretical aspects, simulations and measurements by digital holography. J. Microsc. 2007, 225, 156–169. [Google Scholar] [CrossRef] [PubMed]
- Hillman, T.R.; Gutzler, T.; Alexandrov, S.A.; Sampson, D.D. High-resolution, wide-field object reconstruction with synthetic aperture Fourier holographic optical microscopy. Opt. Express 2009, 17, 7873–7892. [Google Scholar] [CrossRef]
- Picazo, J.A.; Zalevsky, Z.; Garcia, J.; Mico, V. Superresolved spatially multiplexed interferometric microscopy. Opt. Lett. 2017, 42, 927–930. [Google Scholar] [CrossRef]
- Zheng, C.; Jin, D.; He, Y.; Lin, H.; Hu, J.; Yaqoob, Z.; So, P.T.C.; Zhou, R. High spatial and temporal resolution synthetic aperture phase microscopy. Adv. Photonics 2020, 2, 065002. [Google Scholar] [CrossRef]
- Kim, M.K. Wavelength-scanning digital interference holography for optical section imaging. Opt. Lett. 1999, 24, 1693–1695. [Google Scholar] [CrossRef]
- Montfort, F.; Colomb, T.; Charriere, F.; Kuhn, J.; Marquet, P.; Cuche, E.; Herminjard, S.; Depeursinge, C. Submicrometer optical tomography by multiple-wavelength digital holographic microscopy. Appl. Opt. 2006, 45, 8209–8217. [Google Scholar] [CrossRef]
- Kühn, J.; Montfort, F.; Colomb, T.; Rappaz, B.; Moratal, C.; Pavillon, N.; Marquet, P.; Depeursinge, C. Submicrometer tomography of cells by multiple-wavelength digital holographic microscopy in reflection. Opt. Lett. 2009, 34, 653–655. [Google Scholar] [CrossRef]
- Cuche, E.; Poscio, P.; Depeursinge, C. Optical tomography by means of a numerical low-coherence holographic technique. J. Opt. 1997, 28, 260–264. [Google Scholar] [CrossRef]
- Massatsch, P.; Charrière, F.; Cuche, E.; Marquet, P.; Depeursinge, C. Time-domain optical coherence tomography with digital holographic microscopy. Appl. Opt. 2005, 44, 1806–1812. [Google Scholar] [CrossRef] [Green Version]
- Delacrétaz, Y.; Pavillon, N.; Lang, F.; Depeursinge, C. Off-axis low coherence interferometry contouring. Opt. Commun. 2009, 282, 4595–4601. [Google Scholar] [CrossRef]
- Haeberle, O.; Belkebir, K.; Giovaninni, H.; Sentenac, A. Tomographic diffractive microscopy: Basics, techniques and perspectives. J. Mod. Opt. 2010, 57, 686–699. [Google Scholar] [CrossRef] [Green Version]
- Jin, D.; Zhou, R.J.; Yaqoob, Z.; So, P.T.C. Tomographic phase microscopy: Principles and applications in bioimaging. J. Opt. Soc. Am. B 2017, 34, B64–B77. [Google Scholar] [CrossRef] [Green Version]
- Lauer, V. New approach to optical diffraction tomography yielding a vector equation of diffraction tomography and a novel tomographic microscope. J. Microsc. 2002, 205, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Charriere, F.; Marian, A.; Montfort, F.; Kuehn, J.; Colomb, T.; Cuche, E.; Marquet, P.; Depeursinge, C. Cell refractive index tomography by digital holographic microscopy. Opt. Lett. 2006, 31, 178–180. [Google Scholar] [CrossRef]
- Choi, W.; Fang-Yen, C.; Badizadegan, K.; Oh, S.; Lue, N.; Dasari, R.R.; Feld, M.F. Tomographic phase microscopy. Nat. Methods 2007, 4, 717–719. [Google Scholar] [CrossRef] [PubMed]
- Debailleul, M.; Georges, V.; Simon, B.; Morin, R.; Haeberle, O. High-resolution three-dimensional tomographic diffractive microscopy of transparent inorganic and biological samples. Opt. Lett. 2009, 34, 79–81. [Google Scholar] [CrossRef] [Green Version]
- Soto, J.M.; Rodrigo, J.A.; Alieva, T. Partially coherent illumination engineering for enhanced refractive index tomography. Opt. Lett. 2018, 43, 4699–4702. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Kandel, M.E.; Hu, C.; Lee, Y.J.; Popesu, G. Wolf phase tomography (WPT) of transparent structures using partially coherent illumination. Light Sci. Appl. 2020, 9, 142. [Google Scholar] [CrossRef]
- Cotte, Y.; Toy, M.F.; Pavillon, N.; Depeursinge, C. Microscopy image resolution improvement by deconvolution of complex fields. Opt. Express 2010, 18, 19462–19478. [Google Scholar] [CrossRef] [PubMed]
- Sandoz, P.A.; Tremblay, C.; Van der Goot, F.G.; Frechin, M. Image-based analysis of living mammalian cells using label-free 3D refractive index maps reveals new organelle dynamics and dry mass flux. PLoS Biol. 2019, 17, e3000553. [Google Scholar] [CrossRef] [Green Version]
- Kandel, M.E.; He, Y.R.; Lee, Y.J.; Chen, T.H.Y.; Sullivan, K.M.; Aydin, O.; Saif, M.T.A.; Kong, H.; Sobh, N.; Popescu, G. Phase imaging with computational specificity (PICS) for measuring dry mass changes in sub-cellular compartments. Nat. Commun. 2020, 11, 6256. [Google Scholar] [CrossRef] [PubMed]
- Guo, R.; Mirsky, S.K.; Barnea, I.; Dudaie, M.; Shaked, N.T. Quantitative phase imaging by wide-field interferometry with variable shearing distance uncoupled from the off-axis angle. Opt. Express 2020, 28, 5617–5628. [Google Scholar] [CrossRef] [PubMed]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; Chapter 4. [Google Scholar]
- Hai, N.; Rosen, J. Coded aperture correlation holographic microscope for single-shot quantitative phase and amplitude imaging with extended field of view. Opt. Express 2019, 28, 27372–27386. [Google Scholar] [CrossRef] [PubMed]
- Hai, N.; Rosen, J. Single-plane and multiplane quantitative phase imaging by self-reference on-axis holography with phase-shifting method. Opt. Express 2021, 29, 24210–24225. [Google Scholar] [CrossRef]
- Hai, N.; Rosen, J. Phase-contrast-based holographic quantitative phase imaging by only two exposures. In Proceedings of the CLEO 2021, Online, 9–14 May 2021. [Google Scholar]
- Hai, N.; Rosen, J. Phase contrast-based phase retrieval: A bridge between qualitative phase contrast and quantitative phase imaging by phase retrieval algorithms. Opt. Lett. 2020, 45, 5812–5815. [Google Scholar] [CrossRef]
- Juodkazis, S.; Nishimura, K.; Tanaka, S.; Misawa, H.; Gamaly, E.G.; Luther-Davies, B.; Hallo, L.; Nicolai, P.; Tikhonchuk, V.T. Laser-induced microexplosion confined in the bulk of a sapphire crystal: Evidence of multimegabar pressures. Phys. Rev. Lett. 2006, 96, 166101. [Google Scholar] [CrossRef] [Green Version]
- Vailionis, A.; Gamaly, E.G.; Mizeikis, V.; Yang, W.; Rode, A.V.; Juodkazis, S. Evidence of superdense aluminium synthesized by ultrafast microexplosion. Nat. Commun. 2011, 2, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Zhong, L.; Wang, J.; Sheng, H.; Zhang, Z.; Mao, S.X. Formation of monatomic metallic glasses through ultrafast liquid quenching. Nature 2014, 512, 177–180. [Google Scholar] [CrossRef]
- Stoian, R.; Colombier, J.P. Advances in ultrafast laser structuring of materials at the nanoscale. Nanophotonics 2020, 9, 4665–4688. [Google Scholar] [CrossRef]
- Hunter, W.R. Measurement of Optical Constants in the Vacuum Ultraviolet Spectral Region; Academic Press: San Diego, CA, USA, 1998; pp. 69–88. [Google Scholar]
- Hayasaki, Y.; Iwata, K.; Hasegawa, S.; Takita, A.; Juodkazis, S. Time resolved axial-view of the dielectric breakdown under tight focusing in glass. Opt. Mater. Express 2011, 1, 1399–1408. [Google Scholar] [CrossRef]
- Hayasaki, Y.; Isaka, M.; Takita, A.; Hasegawa, S.; Juodkazis, S. Photoacoustic sub-micrometer modifications of glass by pair of femtosecond laser pulses. Opt. Mater. Express 2012, 2, 691–699. [Google Scholar] [CrossRef]
- Hayasaki, Y.; Isaka, M.; Takita, A.; Juodkazis, S. Time-resolved interferometry of femtosecond-laser induced processes under tight focusing and close-to optical breakdown inside borosilicate glass. Opt. Express 2011, 19, 5725–5734. [Google Scholar] [CrossRef] [PubMed]
- Hayasaki, Y.; Fukuda, S.I.; Hasegawa, S.; Juodkazis, S. Two-color pump-probe interferometry of ultra-fast light-matter interaction. Sci. Rep. 2017, 7, 10405. [Google Scholar] [CrossRef] [Green Version]
- Gamaly, E.G.; Rode, A.V. Ultrafast re-structuring of the electronic landscape of transparent dielectrics: New material states (Die-Met). Appl. Phys. A 2018, 124, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Shao, Z.; Cao, X.; Luo, H.; Jin, P. Recent progress in the phase-transition mechanism and modulation of vanadium dioxide materials. NPG Asia Mater. 2018, 10, 581–605. [Google Scholar] [CrossRef] [Green Version]
- Makarov, S.V.; Zalogina, A.S.; Tajik, M.; Zuev, D.A.; Rybin, M.V.; Kuchmizhak, A.A.; Juodkazis, S.; Kivshar, Y. Light-Induced Tuning and Reconfiguration of Nanophotonic Structures. Laser Photonics Rev. 2017, 11, 1700108. [Google Scholar] [CrossRef]
- Sun, Q.; Jiang, H.B.; Liu, Y.; Wu, Z.X.; Yang, H.; Gong, Q.H. Diagnose parameters of plasma induced by femtosecond laser pulse in quartz and glasses. Front. Phys. China 2016, 1, 67–71. [Google Scholar] [CrossRef]
- Ryu, M.; Honda, R.; Balčytis, A.; Vongsvivut, J.; Tobin, M.J.; Juodkazis, S.; Morikawa, J. Hyperspectral mapping of anisotropy. Nanoscale Horiz. 2019, 4, 1443–1449. [Google Scholar] [CrossRef]
- Anand, V.; Ng, S.H.; Katkus, T.; Juodkazis, S. Spatio-Spectral-Temporal Imaging of Fast Transient Phenomena Using a Random Array of Pinholes. Adv. Photonics Res. 2021, 2, 2000032. [Google Scholar] [CrossRef]
- Anand, V.; Katkus, T.; Linklater, D.P.; Ivanova, E.P.; Juodkazis, S. Lensless Three-Dimensional Quantitative Phase Imaging Using Phase Retrieval Algorithm. J. Imaging 2020, 6, 99. [Google Scholar] [CrossRef] [PubMed]
- Gabor, D.A. New microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef]
- Carter, W.H. Computational reconstruction of scattering objects from holograms. J. Opt. Soc. Am. A 1970, 60, 306–314. [Google Scholar] [CrossRef]
- Fercher, A.; Bartelt, H.; Becker, H.; Wiltschko, E. Image formation by inversion of scattered field data: Experiments and computational simulation. Appl. Opt. 1979, 18, 2427–2439. [Google Scholar] [CrossRef] [PubMed]
- Park, C.; Lee, K.; Baek, Y.; Park, Y. Low-coherence optical diffraction tomography using a ferroelectric liquid crystal spatial light modulator. Opt. Express 2020, 28, 39649–39659. [Google Scholar] [CrossRef]
- Kuś, A.; Krauze, W.; Kujawińska, M. Active limited-angle tomographic phase microscope. J. Biomed. Opt. 2015, 20, 111216. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Diez-Silva, M.; Popescu, G.; Lykotrafitis, G.; Choi, W.; Feld, M.S.; Suresh, S. Refractive index maps and membrane dynamics of human red blood cells parasitized by Plasmodium falciparum. Proc. Natl. Acad. Sci. USA 2008, 105, 13730–13735. [Google Scholar] [CrossRef] [Green Version]
- Oh, J.; Ryu, J.S.; Lee, M.; Jung, J.; Han, S.; Chung, H.J.; Park, Y. Three-dimensional label-free observation of individual bacteria upon antibiotic treatment using optical diffraction tomography. Biomed. Opt. Express 2020, 11, 1257–1267. [Google Scholar] [CrossRef]
- Devaney, A. Inverse-scattering theory within the Rytov approximation. Opt. Lett. 1981, 6, 374–376. [Google Scholar] [CrossRef]
- Hugonnet, H.; Kim, Y.W.; Lee, M.; Shin, S.; Hruban, R.H.; Hong, S.-M.; Park, Y. Multiscale label-free volumetric holographic histopathology of thick-tissue slides with subcellular resolution. Adv. Photonics 2021, 3, 026004. [Google Scholar] [CrossRef]
- Gustafsson, M.G.; Shao, L.; Carlton, P.M.; Wang, C.R.; Golubovskaya, I.N.; Cande, W.Z.; Agard, D.A.; Sedat, J.W. Three-dimensional resolution doubling in wide-field fluorescence microscopy by structured illumination. Biophys. J. 2008, 94, 4957–4970. [Google Scholar] [CrossRef] [Green Version]
- Shin, S.; Kim, D.; Kim, K.; Park, Y. Super-resolution three-dimensional fluorescence and optical diffraction tomography of live cells using structured illumination generated by a digital micromirror device. Sci. Rep. 2018, 8, 9183. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barer, R.; Tkaczyk, S. Refractive index of concentrated protein solutions. Nature 1954, 173, 821–822. [Google Scholar] [CrossRef] [PubMed]
- Kamilov, U.S.; Papadopoulos, I.N.; Shoreh, M.H.; Goy, A.; Vonesch, C.; Unser, M.; Psaltis, D. Learning approach to optical tomography. Optica 2015, 2, 517–522. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Ren, D.; Liu, H.Y.; Chowdhury, S.; Waller, L. Multi-layer Born multiple-scattering model for 3D phase microscopy. Optica 2020, 7, 394–403. [Google Scholar] [CrossRef]
- Liu, H.Y.; Liu, D.; Mansour, H.; Boufounos, P.T.; Waller, L.; Kamilov, U.S. SEAGLE: Sparsity-driven image reconstruction under multiple scattering. IEEE Trans. Comput. Imaging 2017, 4, 73–86. [Google Scholar] [CrossRef] [Green Version]
- Baek, Y.; Lee, K.; Shin, S.; Park, Y. Kramers–Kronig holographic imaging for high-space-bandwidth product. Optica 2019, 6, 45–51. [Google Scholar] [CrossRef]
- Baek, Y.; Park, Y. Intensity-based holographic imaging via space-domain Kramers–Kronig relations. Nat. Photonics 2021, 15, 354–360. [Google Scholar] [CrossRef]
- Horstmeyer, R.; Chung, J.; Ou, X.; Zheng, G.; Yang, C. Diffraction tomography with Fourier ptychography. Optica 2016, 3, 827–835. [Google Scholar] [CrossRef]
- Li, J.; Matlock, A.C.; Li, Y.; Chen, Q.; Zuo, C.; Tian, L. High-speed in vitro intensity diffraction tomography. Adv. Photonics 2019, 1, 066004. [Google Scholar] [CrossRef]
- Shin, S.; Kim, K.; Yoon, J.; Park, Y. Active illumination using a digital micromirror device for quantitative phase imaging. Opt. Lett. 2015, 40, 5407–5410. [Google Scholar] [CrossRef]
- Lee, K.; Kim, K.; Kim, G.; Shin, S.; Park, Y. Time-multiplexed structured illumination using a DMD for optical diffraction tomography. Opt. Lett. 2017, 42, 999–1002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soto, J.M.; Rodrigo, J.A.; Alieva, T. Label-free quantitative 3D tomographic imaging for partially coherent light microscopy. Opt. Express 2017, 25, 15699–15712. [Google Scholar] [CrossRef] [PubMed]
- Ryu, D.; Ryu, D.; Baek, Y.; Cho, H.; Kim, G.; Kim, Y.S.; Lee, Y.; Kim, Y.; Ye, J.C.; Min, H.S. DeepRegularizer: Rapid Resolution Enhancement of Tomographic Imaging using Deep Learning. IEEE Trans. Biomed. Eng. 2020, 40, 1508–1518. [Google Scholar] [CrossRef] [PubMed]
- Kim, G.; Ahn, D.; Kang, M.; Jo, Y.; Ryu, D.; Kim, H.; Song, J.; Ryu, J.S.; Choi, G.; Chung, H.J.; et al. Rapid and label-free identification of individual bacterial pathogens exploiting three-dimensional quantitative phase imaging and deep learning. bioRxiv 2019. [Google Scholar] [CrossRef] [Green Version]
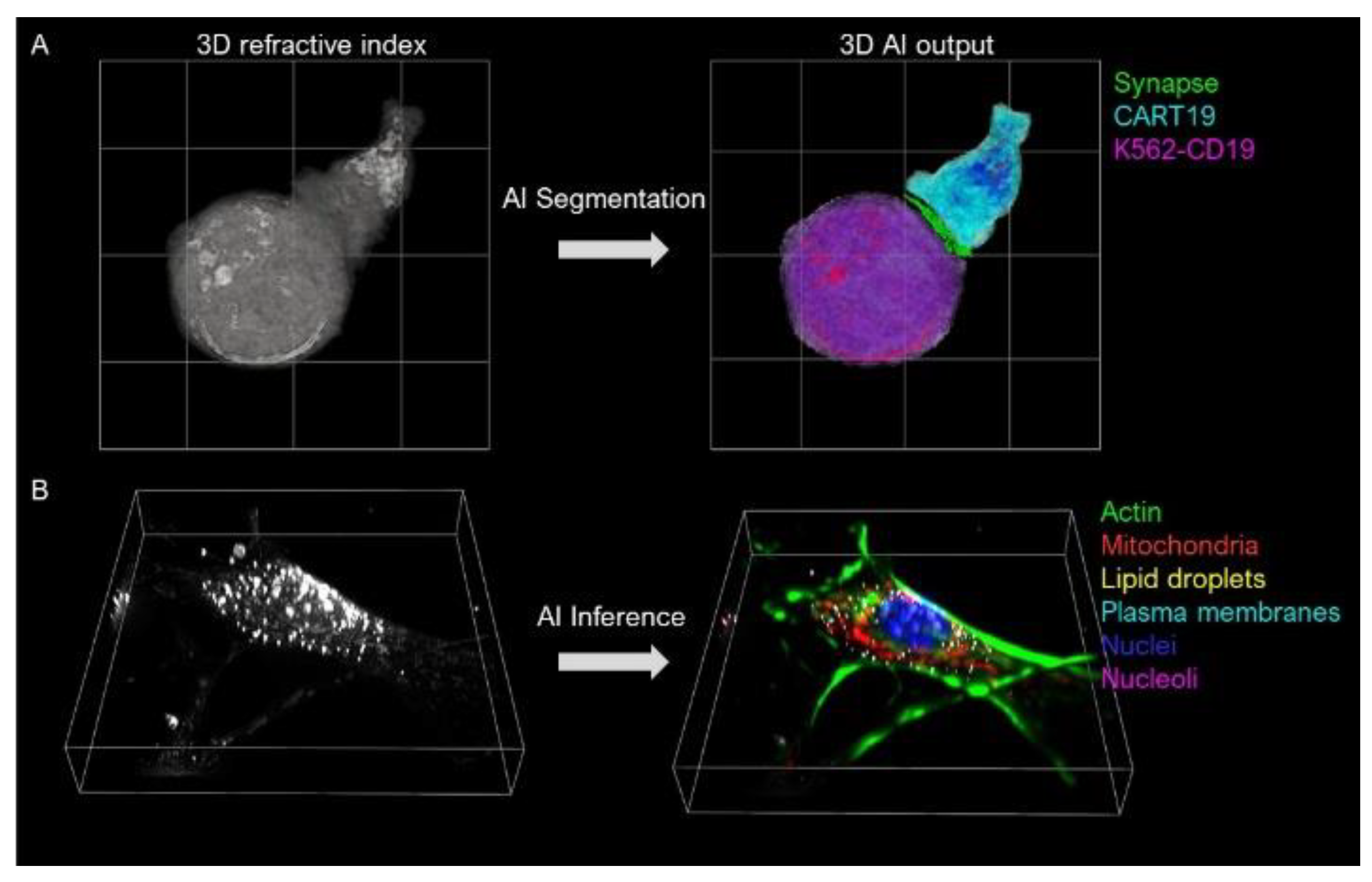
- Lee, M.; Lee, Y.H.; Song, J.; Kim, G.; Jo, Y.; Min, H.; Kim, C.H.; Park, Y.J.E. Deep-learning-based three-dimensional label-free tracking and analysis of immunological synapses of CAR-T cells. eLife 2020, 9, e49023. [Google Scholar] [CrossRef]
- Jo, Y.; Cho, H.; Park, W.S.; Kim, G.; Ryu, D.; Kim, Y.S.; Lee, M.; Joo, H.; Jo, H.; Lee, S. Data-driven multiplexed microtomography of endogenous subcellular dynamics. bioRxiv 2020. [Google Scholar] [CrossRef]
- Kim, E.H.; Park, S.; Kim, Y.K.; Moon, M.; Park, J.; Lee, K.J.; Lee, S.; Kim, Y.P. Self-luminescent photodynamic therapy using breast cancer targeted proteins. Sci. Adv. 2020, 6, eaba3009. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Ahn, J.W.; Jo, Y.; Kang, H.Y.; Kim, H.J.; Cheon, Y.; Kim, J.W.; Park, Y.; Lee, S.; Park, K. Label-free tomographic imaging of lipid droplets in foam cells for machine-learning-assisted therapeutic evaluation of targeted nanodrugs. ACS Nano 2020, 14, 1856–1865. [Google Scholar] [CrossRef]
- Esposito, M.; Fang, C.; Cook, K.C.; Park, N.; Wei, Y.; Spadazzi, C.; Bracha, D.; Gunaratna, R.T.; Laevsky, G.; DeCoste, C.J. TGF-β-induced DACT1 biomolecular condensates repress Wnt signalling to promote bone metastasis. Nat. Cell Biol. 2021, 23, 257–267. [Google Scholar] [CrossRef]
- Kim, K.; Yoon, J.; Park, Y. Simultaneous 3D visualization and position tracking of optically trapped particles using optical diffraction tomography. Optica 2015, 2, 343–346. [Google Scholar] [CrossRef]
- Kim, K.; Park, Y. Tomographic active optical trapping of arbitrarily shaped objects by exploiting 3D refractive index maps. Nat. Commun. 2017, 8, 1–8. [Google Scholar] [CrossRef]
- Chatterjee, A.; Sanchez, J.A.C.; Yamauchi, T.; Taupin, V.; Couvrette, J.; Gorodetsky, A.A. Cephalopod-inspired optical engineering of human cells. Nat. Commun. 2020, 11, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Kak, A.C.; Slaney, M. Principles of Computerized Tomographic Imaging; IEEE Press: New York, NY, USA, 1988. [Google Scholar]
- Kou, S.S.; Sheppard, C.J.R. Image formation in holographic tomography. Opt. Lett. 2008, 33, 2362–2364. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.Y.; Chin, L.K.; Ser, W.; Chen, H.F.; Hsieh, C.M.; Lee, C.H.; Sung, K.B.; Ayi, T.C.; Yap, P.H.; Liedberg, B.; et al. Cell refractive index for cell biology and disease diagnosis: Past, present and future. Lab Chip 2016, 16, 634–644. [Google Scholar] [CrossRef]
- Balasubramani, V.; Tu, H.Y.; Lai, X.J.; Cheng, C.J. Adaptive wavefront correction structured illumination holographic tomography. Sci. Rep. 2019, 9, 10489. [Google Scholar] [CrossRef]
- Vertu, S.; Yamada, I.; Delaunay, J.J.; Haeberlé, O.; Flüge, J. Diffraction microtomography with sample rotation: Primary result on the influence of a missing apple core in the recorded frequency space. Proc. SPIE 2009, 7390, 7390–7391. [Google Scholar]
- Kostencka, J.; Kozacki, T.; Kuś, A.; Kujawińska, M. Accurate approach to capillary-supported optical diffraction tomography. Opt. Express 2015, 23, 7908–7923. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, H.C.; Tu, H.Y.; Liu, C.Y.; Cheng, C.J. Optically driven full-angle sample rotation for tomographic imaging in digital holographic microscopy. Opt. Lett. 2017, 42, 1321–1324. [Google Scholar] [CrossRef]
- Balasubramani, V.; Anand, V.; Rai, M.R.; Rosen, J.; Cheng, C.J.; Minin, O.V.; Minin, I.V. Binary square axicon with chiral focusing properties for optical trapping. Opt. Eng. 2020, 59, 041204. [Google Scholar]
- Balasubramani, V.; Lai, X.J.; Lin, Y.C.; Cheng, C.J. Integrated dual-tomography for refractive index analysis of free-floating single living cell with isotropic superresolution. Sci. Rep. 2018, 8, 5943. [Google Scholar]
- Cheng, C.J.; Chien, K.C.C.; Lin, Y.C. Digital hologram for data augmentation in learning-based pattern classification. Opt. Lett. 2018, 43, 5419–5422. [Google Scholar] [CrossRef]
- Balasubramani, V.; Tu, H.Y.; Haung, H.C.; Cheng, C.J. All-optical dual-tomography for free-floating live cell imaging and analysis. In Imaging and Applied Optics Congress; Optical Society of America: Washington, DC, USA, 2020; paper HF1G.3C. [Google Scholar]
- Balasubramani, V.; Montresor, S.; Tu, H.Y.; Huang, C.H.; Picart, P.; Cheng, C.J. Influence of noise-reduction techniques in sparse-data sample rotation tomographic imaging. App. Opt. 2021, 60, B81–B87. [Google Scholar] [CrossRef]
- Schürmann, M.; Cojoc, G.; Girardo, S.; Ulbricht, E.; Guck, J.; Muller, P. Three-dimensional correlative single-cell imaging utilizing fluorescence and refractive index tomography. J. Biophotonics 2017, 11, e201700145. [Google Scholar] [CrossRef] [Green Version]
- Tahara, T.; Quan, X.; Otani, R.; Takaki, Y.; Matoba, O. Digital holography and its multidimensional imaging applications: A review. Microscopy 2018, 67, 55–67. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Malek, M.; Poon, I.; Jiang, L.; Siddiquee, A.M.; Sheppard, C.J.R.; Roberts, A.; Quiney, H.; Zhang, D.; Yuan, X.; et al. Simultaneous dual-contrast three-dimensional imaging in live cells via optical diffraction tomography and fluorescence. Photonics Res. 2019, 7, 1042–1050. [Google Scholar] [CrossRef]
- Quan, X.; Nitta, K.; Matoba, O.; Xia, P.; and Awatsuji, Y. Phase and fluorescence imaging by combination of digital holographic microscopy and fluorescence microscopy. Opt. Rev. 2015, 22, 349–353. [Google Scholar] [CrossRef]
- Dudenkova, V.V.; Zakharov, Y.N. Multimodal combinational holographic and fluorescence fluctuation microscopy to obtain spatial super-resolution. J. Phys. Conf. Ser. 2016, 737, 012069. [Google Scholar] [CrossRef] [Green Version]
- Smolyanskaya, O.A.; Lazareva, E.N.; Nalegaev, S.S.; Petrov, N.V.; Zaytsev, K.I.; Timoshina, P.A.; Tuchina, D.K.; Toropova, Y.G.; Kornyushin, O.V.; Babenko, A.Y.; et al. Multimodal Optical Diagnostics of Glycated Biological Tissues. Biochemistry 2019, 84, S124–S143. [Google Scholar] [CrossRef]
- Matoba, O.; Quan, X.; Xia, P.; Awatsuji, Y.; Nomura, T. Multimodal Imaging Based on Digital Holography. Proc. IEEE 2017, 105, 906–923. [Google Scholar] [CrossRef]
- Zernike, F. How I discovered phase contrast. Science 1955, 121, 345–349. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W.; Lawrence, R.W. Digital image formation from electronically detected holograms. Appl. Phys. Lett. 1967, 11, 77–79. [Google Scholar] [CrossRef]
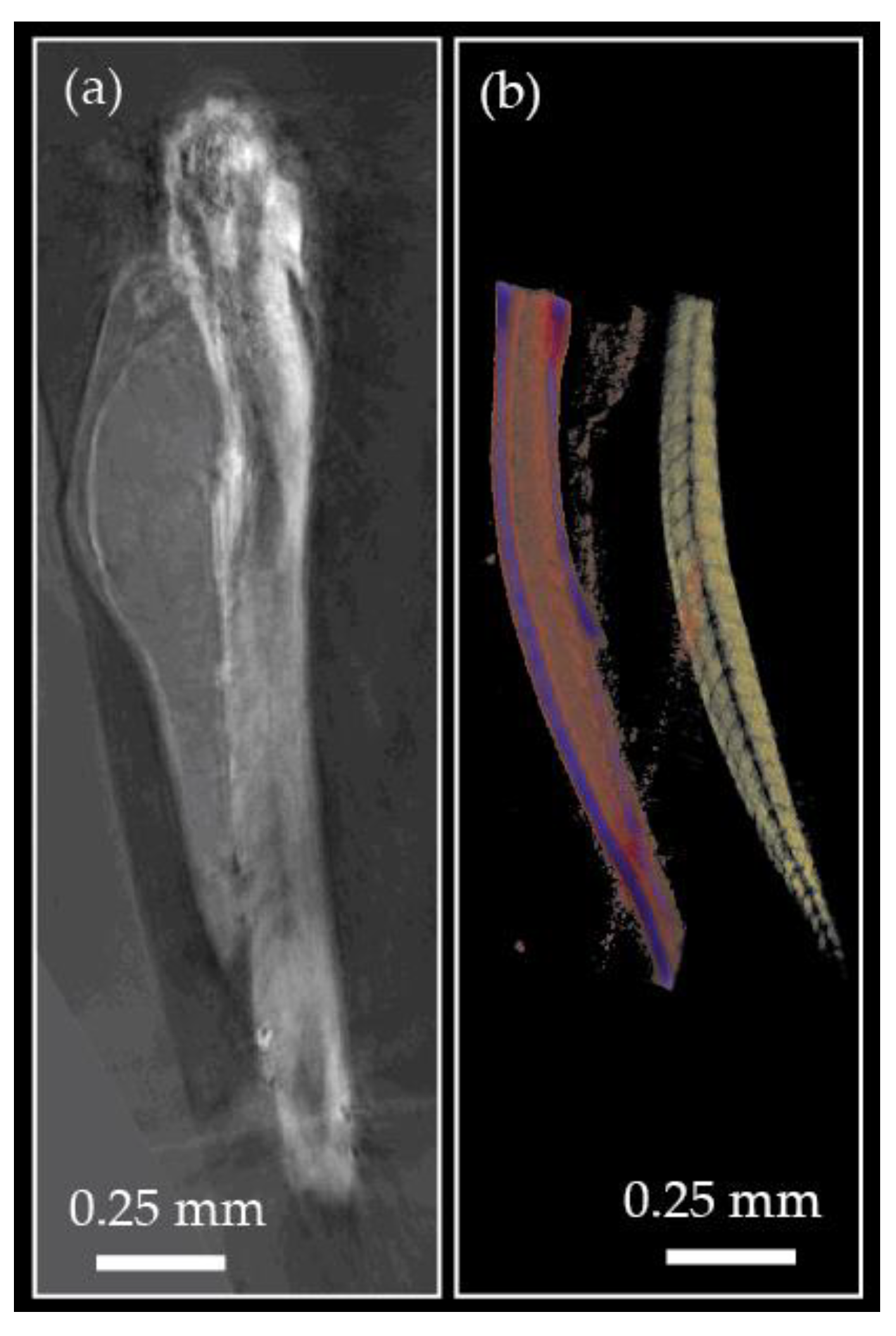
- Van Rooij, J.; Kalkman, J. Large scale high sensitivity optical diffraction tomography of zebrafish. Biomed. Opt. Express 2019, 10, 357859. [Google Scholar] [CrossRef]
- Kim, K.; Yoon, J.; Park, Y.K. Large-scale optical diffraction tomography for inspection of optical plastic lenses. Opt. Lett. 2016, 41, 934. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Wang, H.; Li, Y.; Zhang, H. Elimination of zero-order diffraction and conjugate image in off-axis digital holography. J. Mod. Opt. 2009, 56, 2377. [Google Scholar] [CrossRef]
- Kostencka, J.; Kozacki, T.; Józwik, M. Holographic tomography with object rotation and two-directional off-axis illumination. Opt. Express 2017, 25, 23920. [Google Scholar] [CrossRef]
- Simon, B.; Debailleul, M.; Houkal, M.; Ecoffet, C.; Bailleul, J.; Lambert, J.; Spangenberg, A.; Liu, H.; Soppera, O.; Haeberlé, O. Tomographic diffractive microscopy with isotropic resolution. Optica 2017, 4, 460. [Google Scholar] [CrossRef]
- Lim, J.; Lee, K.; Jin, K.H.; Shin, S.; Lee, S.; Park, Y.; Ye, J.C. Comparative study of iterative reconstruction algorithms for missing cone problems in optical diffraction tomography. Opt. Express 2015, 23, 16933. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, P.; Zhou, R.; Kim, Y.-H.; Peres, C.; Diaspro, A.; Kuang, C.; Yaqoob, Z.; So, P.T.C. Pushing phase and amplitude sensitivity limits in interferometric microscopy. Opt. Lett. 2016, 41, 1656–1659. [Google Scholar] [CrossRef] [Green Version]
- Kostencka, J.; Kozacki, T.; Dudek, M.; Kujawińska, M. Noise suppressed optical diffraction tomography with autofocus correction. Opt. Express 2014, 22, 5731. [Google Scholar] [CrossRef] [PubMed]
- Van Rooij, J.; Kalkman, J. Polarization contrast optical diffraction tomography. Biomed. Opt. Express 2020, 11, 2109. [Google Scholar] [CrossRef] [Green Version]
- Saba, A.; Lim, J.; Ayoub, A.B.; Antoine, E.E.; Psaltis, D. Polarization-sensitive optical diffraction tomography. Optica 2021, 8, 402–408. [Google Scholar] [CrossRef]
- Menzel, M.; Axer, M.; Amunts, K.; De Raedt, H.; Michielsen, K. Diattenuation Imaging reveals different brain tissue properties. Sci. Rep. 2019, 9, 1939. [Google Scholar] [CrossRef]
- Choi, H.; Li, Z.; Jeong, K.; Zuponcic, J.; Ximenes, E.; Turek, J.; Ladisch, M.; Nolte, D.D. Phase-sensitive intracellular Doppler fluctuation spectroscopy. Phys. Rev. Appl. 2021, 15, 024043. [Google Scholar] [CrossRef]
- Jo, Y.; Cho, H.; Lee, S.Y.; Choi, G.; Kim, G.; Min, H.-S.; Park, Y.K. Quantitative Phase Imaging and Artificial Intelligence: A Review. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Shu, X.; Sansare, S.; Jin, D.; Zeng, X.; Tong, K.-Y.; Pandey, R.; Zhou, R. Artificial-Intelligence-Enabled Reagent-Free Imaging Hematology Analyzer. Adv. Intell. Syst. 2021, 3, 2000277. [Google Scholar] [CrossRef]
- Gómez, V.H.; Herazo, E.L.; Smith, S.T. X-ray computed tomography: From medical imaging to dimensional metrology. Precis. Eng. 2019, 60, 544–569. [Google Scholar] [CrossRef]
- Ferrucci, M.; Leach, R.K.; Giusca, C.; Carmignato, S.; Dewulf, W. Towards geometrical calibration of x-ray computed tomography systems—A review. Meas. Sci. Technol. 2015, 26, 092003. [Google Scholar] [CrossRef]
- Filippou, V.; Tsoumpas, C. Recent advances on the development of phantoms using 3D printing for imaging with CT, MRI, PET, SPECT, and ultrasound. Med. Phys. 2018, 45, e740–e760. [Google Scholar] [CrossRef]
- Kujawińska, M.; Krauze, W.; Baczewska, M.; Kuś, A.; Ziemczonok, M. Comparative study of laboratory and commercial limited-angle holographic tomography setups. In Proceedings of the SPIE 10887, Quantitative Phase Imaging V, San Francisco, CA, USA, 4 March 2019; pp. 1–7. [Google Scholar]
- Ziemczonok, M.; Kuś, A.; Wasylczyk, P.; Kujawińska, M. 3D-printed biological cell phantom for testing 3D quantitative phase imaging systems. Sci. Rep. 2019, 9, 18872. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ziemczonok, M.; Kuś, A.T.; Kujawinska, M. Quantifying the performance of holographic tomography systems using the 3D-printed biological cell phantom. In Proceedings of the SPIE 11249, Quantitative Phase Imaging VI, San Francisco, CA, USA, 14 February 2020; pp. 1–7. [Google Scholar] [CrossRef]
- LaFratta, C.; Baldacchini, T. Two-Photon Polymerization Metrology: Characterization Methods of Mechanisms and Microstructures. Micromachines 2017, 8, 101. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Chi-Pong Tsui, G.; Deng, Y.; Tang, C.-Y. Two-photon polymerization nanolithography technology for fabrication of stimulus-responsive micro/nano-structures for biomedical applications. Nanotechnol. Rev. 2020, 9, 1118–1136. [Google Scholar] [CrossRef]
- Park, C.; Shin, S.; Park, Y. Generalized quantification of three-dimensional resolution in optical diffraction tomography using the projection of maximal spatial bandwidths. J. Opt. Soc. Am. A 2018, 35, 1891. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Horstmeyer, R.; Heintzmann, R.; Popescu, G.; Waller, L.; Yang, C. Standardizing the resolution claims for coherent microscopy. Nat. Photonics 2016, 10, 68–71. [Google Scholar] [CrossRef]
- Huang, J.; Bao, Y.; Gaylord, T.K. Three-dimensional phase optical transfer function in axially symmetric microscopic quantitative phase imaging. J. Opt. Soc. Am. A 2020, 37, 1857. [Google Scholar] [CrossRef]
- De Groot, P.J. The instrument transfer function for optical measurements of surface topography. J. Phys. Photonics 2021, 3, 024004. [Google Scholar] [CrossRef]
- Waller, L. Physics-constrained computational imaging. In Emerging Topics in Artificial Intelligence 2020; International Society for Optics and Photonics: Bellingham, DC, USA, 2020; p. 11469. [Google Scholar]
- Belthangady, C.; Royer, L.A. Applications, promises, and pitfalls of deep learning for fluorescence image reconstruction. Nat. Methods 2019, 16, 1215–1225. [Google Scholar] [CrossRef]
- McCann, M.T.; Jin, K.H.; Unser, M. Convolutional neural networks for inverse problems in imaging: A review. IEEE Signal Process. Mag. 2017, 34, 85–95. [Google Scholar] [CrossRef] [Green Version]
- Rivenson, Y.; Wu, Y.; Ozcan, A. Deep learning in holography and coherent imaging. Light Sci. Appl. 2019, 8, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Bostan, E.; Heckel, R.; Chen, M.; Kellman, M.; Waller, L. Deep phase decoder: Self-calibrating phase microscopy with an untrained deep neural network. Optica 2020, 7, 559–562. [Google Scholar] [CrossRef] [Green Version]
- Tian, L.; Waller, L. 3D intensity and phase imaging from light field measurements in an LED array microscope. Optica 2015, 2, 104–111. [Google Scholar] [CrossRef]
- Pierré, W.; Hervé, L.; Allier, C.; Morales, S.; Grudinin, S.; Chowdhury, S.; Dhellemmes, M. Deep learning framework applied to optical diffraction tomography (ODT). In Three-Dimensional and Multidimensional Microscopy: Image Acquisition and Processing; International Society for Optics and Photonics: Bellingham, DC, USA, 2021; Volume 11649, p. 116490F. [Google Scholar]
- Li, J.; Mengu, D.; Yardimci, N.T.; Luo, Y.; Li, X.; Veli, M.; Ozcan, A. Spectrally encoded single-pixel machine vision using diffractive networks. Sci. Adv. 2021, 7, eabd7690. [Google Scholar] [CrossRef] [PubMed]
- Pinkard, H.; Stuurman, N.; Ivanov, I.E.; Anthony, N.M.; Ouyang, W.; Li, B.; Waller, L. Pycro-Manager: Open-source software for customized and reproducible microscope control. Nat. Methods 2021, 18, 226–228. [Google Scholar] [CrossRef] [PubMed]
- Tomocube. 2021. Available online: http://www.tomocube.com (accessed on 1 January 2021).
- Lyncee Tec. 2021. Available online: https://www.lynceetec.com (accessed on 13 July 2021).
- Nanolive. 2021. Available online: https://www.nanolive.com (accessed on 1 July 2021).


| Iterative | Phase-Shifting | Expected Thickness | |
|---|---|---|---|
| 2 Exposures | 3 Exposures | ||
| 45.3 ± 5.6 nm | 45.4 ± 3.7 nm | 48 ± 6.1 nm | 50 nm |
| 119 ± 8.1 nm | 99.8 ± 10.5 nm | 94.7 ± 11.3 nm | 100 nm |
| 211 ± 7.6 nm | 200 ± 7.7 nm | 199 ± 6.4 nm | 200 nm |
| 310 ± 9.5 nm | 298 ± 6.3 nm | 300 ± 3.3 nm | 300 nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balasubramani, V.; Kujawińska, M.; Allier, C.; Anand, V.; Cheng, C.-J.; Depeursinge, C.; Hai, N.; Juodkazis, S.; Kalkman, J.; Kuś, A.; et al. Roadmap on Digital Holography-Based Quantitative Phase Imaging. J. Imaging 2021, 7, 252. https://doi.org/10.3390/jimaging7120252
Balasubramani V, Kujawińska M, Allier C, Anand V, Cheng C-J, Depeursinge C, Hai N, Juodkazis S, Kalkman J, Kuś A, et al. Roadmap on Digital Holography-Based Quantitative Phase Imaging. Journal of Imaging. 2021; 7(12):252. https://doi.org/10.3390/jimaging7120252
Chicago/Turabian StyleBalasubramani, Vinoth, Małgorzata Kujawińska, Cédric Allier, Vijayakumar Anand, Chau-Jern Cheng, Christian Depeursinge, Nathaniel Hai, Saulius Juodkazis, Jeroen Kalkman, Arkadiusz Kuś, and et al. 2021. "Roadmap on Digital Holography-Based Quantitative Phase Imaging" Journal of Imaging 7, no. 12: 252. https://doi.org/10.3390/jimaging7120252
APA StyleBalasubramani, V., Kujawińska, M., Allier, C., Anand, V., Cheng, C.-J., Depeursinge, C., Hai, N., Juodkazis, S., Kalkman, J., Kuś, A., Lee, M., Magistretti, P. J., Marquet, P., Ng, S. H., Rosen, J., Park, Y. K., & Ziemczonok, M. (2021). Roadmap on Digital Holography-Based Quantitative Phase Imaging. Journal of Imaging, 7(12), 252. https://doi.org/10.3390/jimaging7120252