A Data-Centric Augmentation Approach for Disturbed Sensor Image Segmentation
Abstract
1. Introduction
2. State of the Art
3. PAMONO Sensor Image Streams
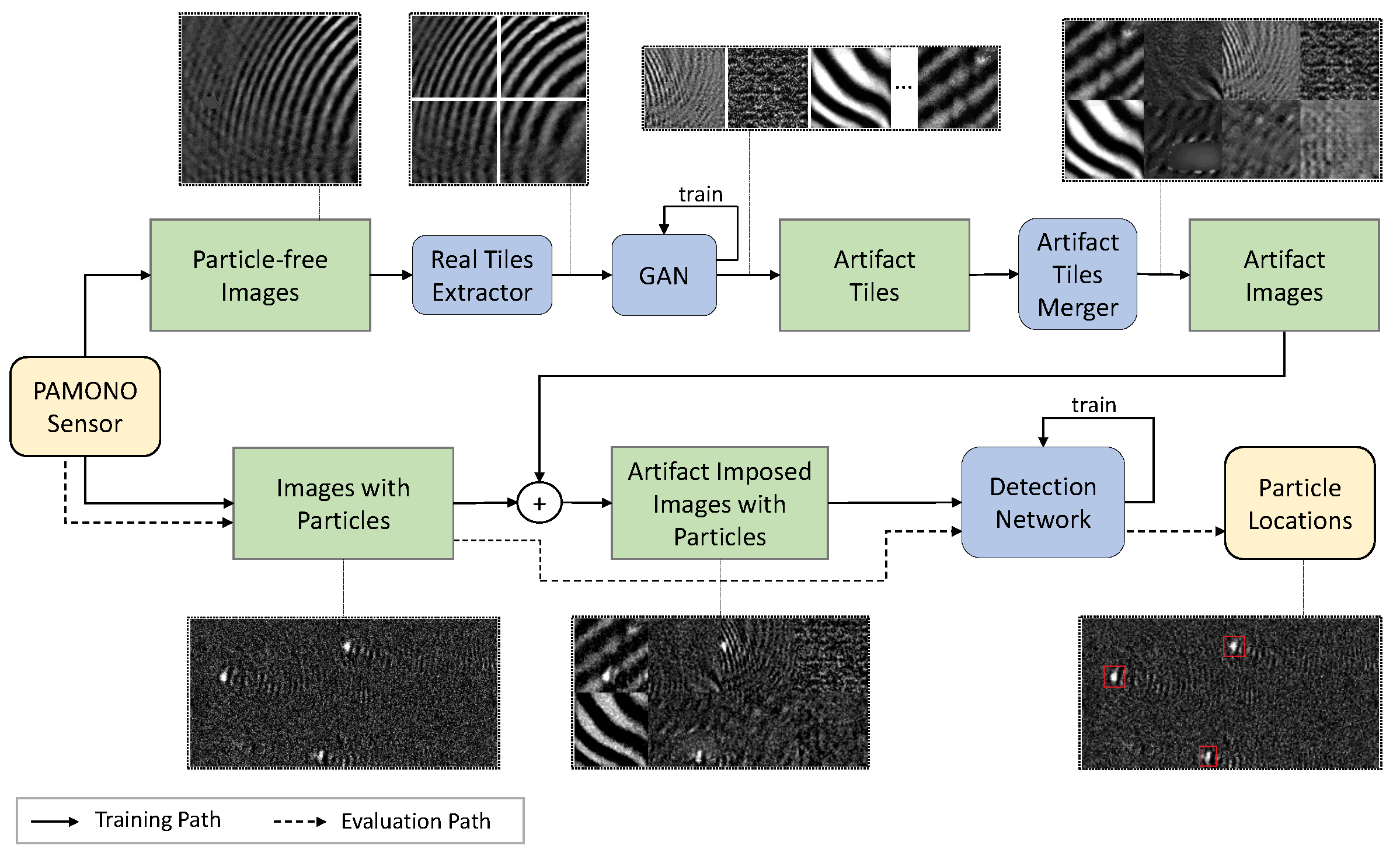
4. Methods
4.1. Artifact Overlays Based on Synthetic Artifacts
4.2. Real Artifacts as Overlays
4.3. Procedurally Generated Artifact Signals
5. Experiments
6. Discussion
7. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chan, T.F.; Shen, J. Image Processing and Analysis: Variational, PDE, Wavelet, and Stochastic Methods; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Lesser, M. Charge-Coupled Device (CCD) Image Sensors. In High Performance Silicon Imaging, 2nd ed.; Woodhead Publishing Series in Electronic and Optical Materials; Durini, D., Ed.; Woodhead Publishing: Sawston, UK, 2020; Chapter 3; pp. 75–93. [Google Scholar] [CrossRef]
- Choubey, B.; Mughal, W.; Gouveia, L. CMOS Circuits for High-Performance Imaging. In High Performance Silicon Imaging, 2nd ed.; Woodhead Publishing Series in Electronic and Optical Materials; Durini, D., Ed.; Woodhead Publishing: Sawston, UK, 2020; Chapter 5; pp. 119–160. [Google Scholar] [CrossRef]
- Konnik, M.; Welsh, J. High-Level Numerical Simulations of Noise in CCD and CMOS Photosensors: Review and Tutorial. arXiv 2014, arXiv:1412.4031. [Google Scholar]
- Burger, H.C.; Schuler, C.J.; Harmeling, S. Image Denoising: Can Plain Neural Networks Compete with BM3D? In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2392–2399. [Google Scholar] [CrossRef]
- Tian, H. Noise Analysis in CMOS Image Sensors. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2000. [Google Scholar]
- Arce, G.R.; Bacca, J.; Paredes, J.L. Nonlinear Filtering for Image Analysis and Enhancement. In Handbook of Image and Video Processing, 2nd ed.; Bovik, A., Ed.; Communications, Networking and Multimedia; Academic Press: Cambridge, MA, USA, 2005; Chapter 3.2; pp. 109–132. [Google Scholar] [CrossRef]
- Zhang, M.; Gunturk, B. Compression Artifact Reduction with Adaptive Bilateral Filtering. Proc. SPIE 2009, 7257. [Google Scholar] [CrossRef]
- Tian, C.; Fei, L.; Zheng, W.; Xu, Y.; Zuo, W.; Lin, C.W. Deep Learning on Image Denoising: An Overview. arXiv 2020, arXiv:1912.13171. [Google Scholar] [CrossRef]
- Münch, B.; Trtik, P.; Marone, F.; Stampanoni, M. Stripe and Ring Artifact Removal With Combined Wavelet—Fourier Filtering. Opt. Express 2009, 17, 8567–8591. [Google Scholar] [CrossRef]
- Charles, B. Image Noise Models. In Handbook of Image and Video Processing, 2nd ed.; Bovik, A., Ed.; Communications, Networking and Multimedia; Academic Press: Cambridge, MA, USA, 2005; Chapter 4.5; pp. 397–409. [Google Scholar] [CrossRef]
- Boitard, R.; Cozot, R.; Thoreau, D.; Bouatouch, K. Survey of Temporal Brightness Artifacts in Video Tone Mapping. HDRi 2014: Second International Conference and SME Workshop on HDR Imaging. 2014, Volume 9. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.646.1334&rep=rep1&type=pdf (accessed on 5 October 2021).
- Mustafa, W.A.; Khairunizam, W.; Yazid, H.; Ibrahim, Z.; Shahriman, A.; Razlan, Z.M. Image Correction Based on Homomorphic Filtering Approaches: A Study. In Proceedings of the International Conference on Computational Approach in Smart Systems Design and Applications (ICASSDA), Kuching, Malaysia, 15–17 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Delon, J.; Desolneux, A. Stabilization of Flicker-Like Effects in Image Sequences through Local Contrast Correction. SIAM J. Imaging Sci. 2010, 3, 703–734. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, X.; Wang, S.; Cheng, C.; Huang, Y.; Yang, K.; Li, Y. BLNet: A Fast Deep Learning Framework for Low-Light Image Enhancement with Noise Removal and Color Restoration. arXiv 2021, arXiv:2106.15953. [Google Scholar]
- Rashid, S.; Lee, S.Y.; Hasan, M.K. An Improved Method for the Removal of Ring Artifacts in High Resolution CT Imaging. EURASIP J. Adv. Signal Process. 2012, 2012, 93. [Google Scholar] [CrossRef]
- Hoff, M.; Andre, J.; Stewart, B. Artifacts in Magnetic Resonance Imaging. In Image Principles, Neck, and the Brain; Saba, L., Ed.; Taylor & Francis Ltd.: Abingdon, UK, 2016; pp. 165–190. [Google Scholar] [CrossRef]
- Lv, X.; Ren, X.; He, P.; Zhou, M.; Long, Z.; Guo, X.; Fan, C.; Wei, B.; Feng, P. Image Denoising and Ring Artifacts Removal for Spectral CT via Deep Neural Network. IEEE Access 2020, 8, 225594–225601. [Google Scholar] [CrossRef]
- Liu, J.; Liu, D.; Yang, W.; Xia, S.; Zhang, X.; Dai, Y. A Comprehensive Benchmark for Single Image Compression Artifact Reduction. IEEE Trans. Image Process. 2020, 29, 7845–7860. [Google Scholar] [CrossRef]
- Vo, D.T.; Nguyen, T.Q.; Yea, S.; Vetro, A. Adaptive Fuzzy Filtering for Artifact Reduction in Compressed Images and Videos. IEEE Trans. Image Process. 2009, 18, 1166–1178. [Google Scholar] [CrossRef][Green Version]
- Kırmemiş, O.; Bakar, G.; Tekalp, A.M. Learned Compression Artifact Removal by Deep Residual Networks. arXiv 2018, arXiv:1806.00333. [Google Scholar]
- Xu, Y.; Gao, L.; Tian, K.; Zhou, S.; Sun, H. Non-Local ConvLSTM for Video Compression Artifact Reduction. arXiv 2019, arXiv:1910.12286. [Google Scholar]
- Xu, Y.; Zhao, M.; Liu, J.; Zhang, X.; Gao, L.; Zhou, S.; Sun, H. Boosting the Performance of Video Compression Artifact Reduction with Reference Frame Proposals and Frequency Domain Information. arXiv 2021, arXiv:2105.14962. [Google Scholar]
- Stankiewicz, O.; Lafruit, G.; Domański, M. Multiview Video: Acquisition, Processing, Compression, and Virtual View Rendering. In Academic Press Library in Signal Processing; Chellappa, R., Theodoridis, S., Eds.; Academic Press: Cambridge, MA, USA, 2018; Volume 6, Chapter 1; pp. 3–74. [Google Scholar] [CrossRef]
- Drap, P.; Lefèvre, J. An Exact Formula for Calculating Inverse Radial Lens Distortions. Sensors 2016, 16, 807. [Google Scholar] [CrossRef] [PubMed]
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcuoglu, K. Spatial Transformer Networks. arXiv 2015, arXiv:1506.02025. [Google Scholar]
- Del Gallego, N.P.; Ilao, J.; Cordel, M. Blind First-Order Perspective Distortion Correction Using Parallel Convolutional Neural Networks. Sensors 2020, 20, 4898. [Google Scholar] [CrossRef]
- Lagendijk, R.L.; Biemond, J. Basic Methods for Image Restoration and Identification. In Handbook of Image and Video Processing, 2nd ed.; Bovik, A., Ed.; Communications, Networking and Multimedia; Academic Press: Cambridge, MA, USA, 2005; Chapter 3.5; pp. 167–181. [Google Scholar] [CrossRef]
- Merchant, F.A.; Bartels, K.A.; Bovik, A.C.; Diller, K.R. Confocal Microscopy. In Handbook of Image and Video Processing, 2nd ed.; Bovik, A., Ed.; Communications, Networking and Multimedia; Academic Press: Cambridge, MA, USA, 2005; Chapter 10.9; pp. 1291–1309. [Google Scholar] [CrossRef]
- Maragos, P. 3.3—Morphological Filtering for Image Enhancement and Feature Detection. In Handbook of Image and Video Processing, 2nd ed.; Bovik, A., Ed.; Communications, Networking and Multimedia; Academic Press: Cambridge, MA, USA, 2005; pp. 135–156. [Google Scholar] [CrossRef]
- He, D.; Cai, D.; Zhou, J.; Luo, J.; Chen, S.L. Restoration of Out-of-Focus Fluorescence Microscopy Images Using Learning-Based Depth-Variant Deconvolution. IEEE Photonics J. 2020, 12, 1–13. [Google Scholar] [CrossRef]
- Xu, G.; Liu, C.; Ji, H. Removing Out-of-Focus Blur From a Single Image. arXiv 2018, arXiv:1808.09166. [Google Scholar]
- Lesser, M. Charge Coupled Device (CCD) Image Sensors. In High Performance Silicon Imaging; Durini, D., Ed.; Woodhead Publishing: Sawston, UK, 2014; Chapter 3; pp. 78–97. [Google Scholar] [CrossRef]
- Bigas, M.; Cabruja, E.; Forest, J.; Salvi, J. Review of CMOS Image Sensors. Microelectron. J. 2006, 37, 433–451. [Google Scholar] [CrossRef]
- Guan, J.; Lai, R.; Xiong, A.; Liu, Z.; Gu, L. Fixed Pattern Noise Reduction for Infrared Images Based on Cascade Residual Attention CNN. Neurocomputing 2020, 377, 301–313. [Google Scholar] [CrossRef]
- Yang, L.; Liu, S.; Salvi, M. A Survey of Temporal Antialiasing Techniques. Comput. Graph. Forum 2020, 39, 607–621. [Google Scholar] [CrossRef]
- Vasconcelos, C.; Larochelle, H.; Dumoulin, V.; Roux, N.L.; Goroshin, R. An Effective Anti-Aliasing Approach for Residual Networks. arXiv 2020, arXiv:2011.10675. [Google Scholar]
- Zhong, Z.; Zheng, Y.; Sato, I. Towards Rolling Shutter Correction and Deblurring in Dynamic Scenes. arXiv 2021, arXiv:2104.01601. [Google Scholar]
- Zhuang, B.; Tran, Q.H.; Ji, P.; Cheong, L.F.; Chandraker, M. Learning Structure-And-Motion-Aware Rolling Shutter Correction. In Proceedings of the 32nd IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–21 June 2019; pp. 4546–4555. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a Fast and Flexible Solution for CNN-Based Image Denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef]
- Broaddus, C.; Krull, A.; Weigert, M.; Schmidt, U.; Myers, G. Removing Structured Noise with Self-Supervised Blind-Spot Networks. In Proceedings of the IEEE 17th International Symposium on Biomedical Imaging (ISBI), Iowa City, IA, USA, 3–7 April 2020; pp. 159–163. [Google Scholar] [CrossRef]
- He, Z. Deep Learning in Image Classification: A Survey Report. In Proceedings of the 2nd International Conference on Information Technology and Computer Application (ITCA), Guangzhou, China, 18–20 December 2020; pp. 174–177. [Google Scholar] [CrossRef]
- Minaee, S.; Boykov, Y.; Porikli, F.; Plaza, A.; Kehtarnavaz, N.; Terzopoulos, D. Image Segmentation Using Deep Learning: A Survey. arXiv 2020, arXiv:2001.05566. [Google Scholar]
- Liu, L.; Ouyang, W.; Wang, X.; Fieguth, P.; Chen, J.; Liu, X.; Pietikäinen, M. Deep Learning for Generic Object Detection: A Survey. Int. J. Comput. Vis. 2020, 128, 261–318. [Google Scholar] [CrossRef]
- Teimoorinia, H.; Kavelaars, J.J.; Gwyn, S.D.J.; Durand, D.; Rolston, K.; Ouellette, A. Assessment of Astronomical Images Using Combined Machine-Learning Models. Astron. J. 2020, 159, 170. [Google Scholar] [CrossRef]
- Li, P.; Chen, X.; Shen, S. Stereo R-CNN based 3D Object Detection for Autonomous Driving. arXiv 2019, arXiv:1902.09738. [Google Scholar]
- Caicedo, J.C.; Roth, J.; Goodman, A.; Becker, T.; Karhohs, K.W.; Broisin, M.; Molnar, C.; McQuin, C.; Singh, S.; Theis, F.J.; et al. Evaluation of Deep Learning Strategies for Nucleus Segmentation in Fluorescence Images. Cytom. Part A 2019, 95, 952–965. [Google Scholar] [CrossRef] [PubMed]
- Çallı, E.; Sogancioglu, E.; van Ginneken, B.; van Leeuwen, K.G.; Murphy, K. Deep Learning for Chest X-Ray Analysis: A Survey. Med. Image Anal. 2021, 72, 102125. [Google Scholar] [CrossRef] [PubMed]
- Lundervold, A.S.; Lundervold, A. An Overview of Deep Learning in Medical Imaging Focusing on MRI. Z. Med. Phys. 2019, 29, 102–127. [Google Scholar] [CrossRef]
- Kulathilake, K.A.S.H.; Abdullah, N.A.; Sabri, A.Q.M.; Lai, K.W. A Review on Deep Learning Approaches for Low-Dose Computed Tomography Restoration. Complex Intell. Syst. 2021. [Google Scholar] [CrossRef]
- Srinidhi, C.L.; Ciga, O.; Martel, A.L. Deep Neural Network Models for Computational Histopathology: A Survey. Med. Image Anal. 2021, 67, 101813. [Google Scholar] [CrossRef] [PubMed]
- Puttagunta, M.; Ravi, S. Medical Image Analysis Based on Deep Learning Approach. Multimed. Tools Appl. 2021. [Google Scholar] [CrossRef] [PubMed]
- Lenssen, J.E.; Shpacovitch, V.; Siedhoff, D.; Libuschewski, P.; Hergenröder, R.; Weichert, F. A Review of Nano-Particle Analysis with the PAMONO-Sensor. Biosens. Adv. Rev. 2017, 1, 81–100. [Google Scholar]
- Lenssen, J.E.; Toma, A.; Seebold, A.; Shpacovitch, V.; Libuschewski, P.; Weichert, F.; Chen, J.J.; Hergenröder, R. Real-Time Low SNR Signal Processing for Nanoparticle Analysis with Deep Neural Networks. In International Conference on Bio-Inspired Systems and Signal Processing (BIOSIGNALS); SciTePress: Funchal, Portugal, 2018. [Google Scholar]
- Yayla, M.; Toma, A.; Chen, K.H.; Lenssen, J.E.; Shpacovitch, V.; Hergenröder, R.; Weichert, F.; Chen, J.J. Nanoparticle Classification Using Frequency Domain Analysis on Resource-Limited Platforms. Sensors 2019, 19, 4138. [Google Scholar] [CrossRef] [PubMed]
- Wüstefeld, K.; Weichert, F. An Automated Rapid Test for Viral Nanoparticles Based on Spatiotemporal Deep Learning. In Proceedings of the IEEE Sensors, Rotterdam, The Netherlands, 25–28 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Jabbar, A.; Li, X.; Omar, B. A Survey on Generative Adversarial Networks: Variants, Applications, and Training. arXiv 2020, arXiv:2006.05132. [Google Scholar]
- Karras, T.; Aittala, M.; Hellsten, J.; Laine, S.; Lehtinen, J.; Aila, T. Training Generative Adversarial Networks With Limited Data. arXiv 2020, arXiv:2006.06676. [Google Scholar]
- Jain, V.; Seung, S. Natural Image Denoising With Convolutional Networks. Adv. Neural Inf. Process. Syst. 2008, 21, 769–776. [Google Scholar]
- Andina, D.; Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E. Deep Learning for Computer Vision: A Brief Review. Comput. Intell. Neurosci. 2018, 2018, 7068349. [Google Scholar]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep Image Prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9446–9454. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Learning Enriched Features for Real Image Restoration and Enhancement. In Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 492–511. [Google Scholar]
- Gu, S.; Rigazio, L. Towards Deep Neural Network Architectures Robust to Adversarial Examples. arXiv 2014, arXiv:1412.5068. [Google Scholar]
- Zhao, Y.; Ossowski, J.; Wang, X.; Li, S.; Devinsky, O.; Martin, S.P.; Pardoe, H.R. Localized Motion Artifact Reduction on Brain MRI Using Deep Learning With Effective Data Augmentation Techniques. arXiv 2020, arXiv:2007.05149. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Mane, D.; Vasudevan, V.; Le, Q.V. AutoAugment: Learning Augmentation Strategies from Data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 113–123. [Google Scholar]
- Frid-Adar, M.; Diamant, I.; Klang, E.; Amitai, M.; Goldberger, J.; Greenspan, H. GAN-Based Synthetic Medical Image Augmentation for Increased CNN Performance in Liver Lesion Classification. Neurocomputing 2018, 321, 321–331. [Google Scholar] [CrossRef]
- Han, C.; Rundo, L.; Araki, R.; Nagano, Y.; Furukawa, Y.; Mauri, G.; Nakayama, H.; Hayashi, H. Combining Noise-to-Image and Image-to-Image GANs: Brain MR Image Augmentation for Tumor Detection. IEEE Access 2019, 7, 156966–156977. [Google Scholar] [CrossRef]
- Sandfort, V.; Yan, K.; Pickhardt, P.J.; Summers, R.M. Data Augmentation Using Generative Adversarial Networks (CycleGAN) To Improve Generalizability in CT Segmentation Tasks. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Han, C.; Murao, K.; Noguchi, T.; Kawata, Y.; Uchiyama, F.; Rundo, L.; Nakayama, H.; Satoh, S. Learning More With Less: Conditional PGGAN-Based Data Augmentation for Brain Metastases Detection Using Highly-Rough Annotation on MR Images. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 119–127. [Google Scholar]
- Han, C.; Kitamura, Y.; Kudo, A.; Ichinose, A.; Rundo, L.; Furukawa, Y.; Umemoto, K.; Li, Y.; Nakayama, H. Synthesizing Diverse Lung Nodules Wherever Massively: 3D Multi-Conditional GAN-Based CT Image Augmentation for Object Detection. In Proceedings of the 2019 International Conference on 3D Vision (3DV), Québec City, QC, Canada, 16–19 September 2019; pp. 729–737. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Liang, A.; Liu, Q.; Wen, G.; Jiang, Z. The Surface-Plasmon-Resonance Effect of Nanogold/Silver and Its Analytical Applications. TrAC Trends Anal. Chem. 2012, 37, 32–47. [Google Scholar] [CrossRef]
- Shpacovitch, V.; Sidorenko, I.; Lenssen, J.E.; Temchura, V.; Weichert, F.; Müller, H.; Überla, K.; Zybin, A.; Schramm, A.; Hergenröder, R. Application of the PAMONO-sensor for Quantification of Microvesicles and Determination of Nano-particle Size Distribution. Sensors 2017, 17, 244. [Google Scholar] [CrossRef]
- Siedhoff, D. A Parameter-Optimizing Model-Based Approach to the Analysis of Low-SNR Image Sequences for Biological Virus Detection. Ph.D. Thesis, TU Dortmund, Dortmund, Germany, 2016. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Marr, D.; Hildreth, E. Theory of Edge Detection. Proc. R. Soc. Lond. Ser. B 1980, 207, 187–217. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. arXiv 2016, arXiv:1606.04797. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sokolova, M.; Japkowicz, N.; Szpakowicz, S. Beyond Accuracy, F-Score and ROC: A Family of Discriminant Measures for Performance Evaluation. In AI 2006: Advances in Artificial Intelligence; Sattar, A., Kang, B.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1015–1021. [Google Scholar]



| Artifact Type | Correlated | Temporally Changing | Artifact Sources | Algorithmic Methods for Reduction | ||
|---|---|---|---|---|---|---|
| Yes | No | Yes | No | |||
| Shot noise [4,6] | • | • | environment | classic filters (e.g., median filter) [7], bilateral filtering [8], neural networks [9], wavelet/Fourier filtering [10] | ||
| Readout noise [6] | • | • | electronics | |||
| Thermal noise [11] | • | • | environment, electronics | |||
| Salt and pepper noise [7] | • | • | electronics | |||
| Random telegraph noise [4] | • | • | electronics | |||
| Temporal contrast/ brightness inconsistencies [12] | • | • | electronics, environment, software | homomorphic filtering [13], stabilization algorithms [14], temporal filtering [12], neural networks [15] | ||
| Line, stripe, wave and ring artifacts [16,17] | • | • | electronics, environment, optics | wavelet/Fourier filtering [10], spatial filtering [16], neural networks [18] | ||
| Compression artifacts [19] | • | • | software | bilateral filtering [8], fuzzy filtering [20] neural networks [19,21,22,23] | ||
| Projective distortions [24] | • | • | optics | model-based calculations [25], neural networks [26,27] | ||
| Out-of-focus effects [28,29] | • | • | optics | morphological filtering [30], neural networks [31,32] | ||
| Fixed pattern noise [33,34] | • | • | electronics, environment, optics | reference imaging [33], neural networks [35] | ||
| Aliasing [36] | • | • | software | anti-aliasing algorithms [36], neural networks [37] | ||
| Rolling shutter effects [38] | • | • | electronics | neural networks [39] | ||
| Metric | Average F1-Score | Minimum F1-Score | Average Count Exactness | Minimum Count Exactness | |
| Augmentation | |||||
| No augmentation | |||||
| Only direct augmentation | |||||
| Procedurally generated waves | |||||
| Real artifacts | |||||
| GAN-generated artifacts | 0.84 | 0.55 | 0.79 | 0.48 | |
| Data Group | Highly Visible Particles | Stronger Noises or Temporal Inconsistencies | Wave-like Artifacts | ||||
|---|---|---|---|---|---|---|---|
| Metric | F1 | CE | F1 | CE | F1 | CE | |
| Augmentation | |||||||
| No augmentation | |||||||
| Only direct augmentation | |||||||
| Procedurally generated waves | |||||||
| Real artifacts | |||||||
| GAN-generated artifacts | 0.92 | 0.88 | 0.78 | 0.71 | 0.73 | 0.66 | |
| Metric | Average FP per Image | Maximum FP per Image | |
| Augmentation | |||
| No augmentation | |||
| Only direct augmentation | |||
| Procedurally generated waves | |||
| Real tiles artifacts | |||
| GAN-generated artifacts | 0.02 | 0.05 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roth, A.; Wüstefeld, K.; Weichert, F. A Data-Centric Augmentation Approach for Disturbed Sensor Image Segmentation. J. Imaging 2021, 7, 206. https://doi.org/10.3390/jimaging7100206
Roth A, Wüstefeld K, Weichert F. A Data-Centric Augmentation Approach for Disturbed Sensor Image Segmentation. Journal of Imaging. 2021; 7(10):206. https://doi.org/10.3390/jimaging7100206
Chicago/Turabian StyleRoth, Andreas, Konstantin Wüstefeld, and Frank Weichert. 2021. "A Data-Centric Augmentation Approach for Disturbed Sensor Image Segmentation" Journal of Imaging 7, no. 10: 206. https://doi.org/10.3390/jimaging7100206
APA StyleRoth, A., Wüstefeld, K., & Weichert, F. (2021). A Data-Centric Augmentation Approach for Disturbed Sensor Image Segmentation. Journal of Imaging, 7(10), 206. https://doi.org/10.3390/jimaging7100206






