Structural Similarity Measurement Based Cost Function for Stereo Matching of Automotive Applications
Abstract
1. Introduction
2. Related Work
3. The Proposed Cost Function
3.1. SSIM Based Cost Function ()
3.2. SSIM Gradient Variant ()
4. Experimental Results
- The KITTI 2012 is divided into two sets, training one which contains 194 stereo pairs and 195 stereo pairs in the testing one.
- The KITTI 2015 dataset contains 200 training stereo pairs and 200 testing pairs.
4.1. Evaluation of the Discriminative Ability of the Proposed Costs
4.2. Evaluation of the Proposed Costs Using the Adaptive Aggregation Technique
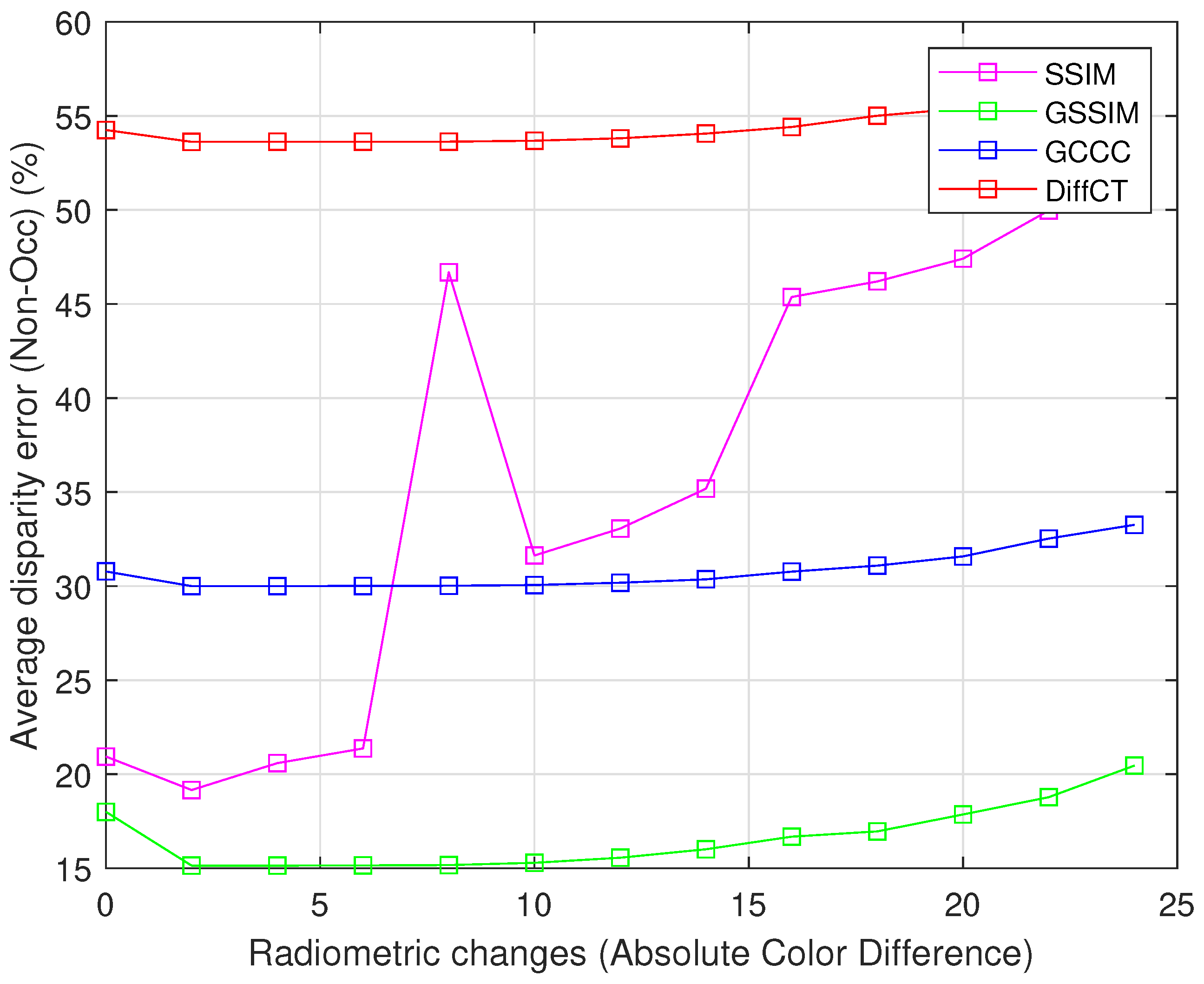
4.3. Sensitivity of the Cost Functions in the Presence of Radiometric Distortions
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Foix, S.; Alenya, G.; Torras, C. Lock-in time-of-flight (tof) cameras: A survey. IEEE Sens. J. 2011, 11, 1917–1926. [Google Scholar] [CrossRef]
- Schwarz, B. Mapping the world in 3D. Nat. Photonics 2010, 4, 429–430. [Google Scholar] [CrossRef]
- Hsieh, Y.; McKeown, D.; Perlant, F. Performance evaluation of scen registration and stereo matching for artographic feature extraction. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 214–238. [Google Scholar] [CrossRef]
- Vincent, E.; Laganiére, R. Detecting and matching feature points. J. Vis. Commun. Image Represent. 2005, 16, 38–54. [Google Scholar] [CrossRef]
- Veksler, O. Stereo correspondence by dynamic programming on a tree. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; Volume 2, pp. 384–390. [Google Scholar]
- Sun, J.; Zheng, N.N.; Shum, H.Y. Stereo matching using belief propagation. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 787–800. [Google Scholar]
- Kolmogorov, V.; Zabih, R. Computing visual correspondence with occlusions using graph cuts. In Proceedings of the Eighth IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; Volume 2, pp. 508–515. [Google Scholar]
- Rhemann, C.; Hosni, A.; Bleyer, M.; Rother, C.; Gelautz, M. Fast cost-volume filtering for visual correspondence and beyond. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 504–511. [Google Scholar]
- Yoon, K.J.; Kweon, I.S. Adaptive support-weight approach for correspondenc search. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 650–656. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Lu, J.; Lafruit, G. Cross-based local stereo matching using orthogonal integral images. IEEE Trans. Circuits Syst. Video Technol. 2009, 19, 1073–1079. [Google Scholar] [CrossRef]
- Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? the kitti vision benchmark suite. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2020; pp. 3354–3361. [Google Scholar]
- Menze, M.; Geiger, A. Object scene flow for autonomous vehicles. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3061–3070. [Google Scholar]
- Zabih, R.; Woodfill, J. Non-parametric local transforms for computing visual correspondence. In Proceedings of the Third European Conference on Computer Vision, Stockholm, Sweden, 2–6 May 1994; Volume 2, pp. 151–158. [Google Scholar]
- Hirschmuller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 328–341. [Google Scholar] [CrossRef] [PubMed]
- Klaus, A.; Sormann, M.; Karner, K. Segment-based stereo matching using belief propagation and a self-adapting dissimilarity measure. In Proceedings of the 18th International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006; Volume 3, pp. 15–18. [Google Scholar]
- Mei, X.; Sun, X.; Zhou, M.; Jiao, S.; Wang, H.; Zhang, X. On building an accurate stereo matching system on graphics hardware. In Proceedings of the IEEE International Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011; pp. 467–474. [Google Scholar]
- Stentoumis, C.; Grammatikopoulos, L.; Kalisperakis, I.; Karras, G. On accurate dense stereo-matching using a local adaptive multi-cost approach. ISPRS J. Photogramm. Remote Sens. 2014, 91, 29–49. [Google Scholar] [CrossRef]
- Saygili, G.; van der Maaten, L.; Hendriks, E.A. Adaptive stereo similarity fusion using confidence measures. Comput. Vis. Image Underst. 2015, 135, 95–108. [Google Scholar] [CrossRef]
- Hirschmuller, H.; Scharstein, D. Evaluation of cost functions for stereo matching. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Hirschmuller, H.; Scharstein, D. Evaluation of stereo matching costs on images with radiometric differences. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 1582–1599. [Google Scholar] [CrossRef] [PubMed]
- Miron, A.; Ainouz, S.; Rogozan, A.; Bensrhair, A. A robust cost function for stereo matching of road scenes. Pattern Recognit. Lett. 2014, 38, 70–77. [Google Scholar] [CrossRef]
- Zeglazi, O.; Rziza, M.; Amine, A.; Demonceaux, C. Accurate dense stereo matching for road scenes. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 720–724. [Google Scholar]
- Xu, Y.; Long, Q.; Mita, S.; Tehrani, H.; Ishimaru, K.; Shirai, N. Real-time stereo vision system at nighttime with noise reduction using simplified non-local matching cost. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; pp. 998–1003. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.-M. A non-local algorithm for image denoising. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 60–65. [Google Scholar]
- Fei, L.; Yan, L.; Chen, C.; Ye, Z.; Zhou, J. OSSIM: An Object-Based Multiview Stereo Algorithm Using SSIM Index Matching Cost. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6737–6949. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]


| Cost Functions | 3-px Threshold | |
|---|---|---|
| Non-Occluded | All | |
| [22] | 54.25 | 55.30 |
| [23] | 30.78 | 32.34 |
| 20.94 | 22.73 | |
| 18.00 | 19.86 | |
| Cost Functions | No Aggregation Method | Aggregation Method | ||
|---|---|---|---|---|
| D1—All (Non-Occluded) | D1—All (All) | D1—All (Non-Occluded) | D1—All (All) | |
| [22] | 50.74 | 49.87 | 18.63 | 20.05 |
| [23] | 27.52 | 28.76 | 14.63 | 16.05 |
| 15.23 | 16.69 | 11.08 | 13.06 | |
| 15.38 | 16.83 | 10.06 | 12.07 | |
| Cost functions | 2 px Threshold | 3 px Threshold | 5 px Threshold | |||
|---|---|---|---|---|---|---|
| Non-Occluded | All | Non-Occluded | All | Non-Occluded | All | |
| [22] | 20.08 | 21.88 | 12.97 | 14.91 | 9.70 | 11.63 |
| [23] | 20.47 | 22.27 | 11.93 | 13.89 | 10.19 | 12.18 |
| 16.39 | 18.29 | 11.08 | 13.06 | 8.18 | 10.17 | |
| 14.06 | 16.00 | 10.06 | 12.07 | 7.83 | 9.83 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeglazi, O.; Rziza, M.; Amine, A.; Demonceaux, C. Structural Similarity Measurement Based Cost Function for Stereo Matching of Automotive Applications. J. Imaging 2020, 6, 77. https://doi.org/10.3390/jimaging6080077
Zeglazi O, Rziza M, Amine A, Demonceaux C. Structural Similarity Measurement Based Cost Function for Stereo Matching of Automotive Applications. Journal of Imaging. 2020; 6(8):77. https://doi.org/10.3390/jimaging6080077
Chicago/Turabian StyleZeglazi, Oussama, Mohammed Rziza, Aouatif Amine, and Cédric Demonceaux. 2020. "Structural Similarity Measurement Based Cost Function for Stereo Matching of Automotive Applications" Journal of Imaging 6, no. 8: 77. https://doi.org/10.3390/jimaging6080077
APA StyleZeglazi, O., Rziza, M., Amine, A., & Demonceaux, C. (2020). Structural Similarity Measurement Based Cost Function for Stereo Matching of Automotive Applications. Journal of Imaging, 6(8), 77. https://doi.org/10.3390/jimaging6080077





