Figure 1.
(First line) Segmentation of bunny model using MeTis algorithm in (a) 70, (b) 100 and (c) 200 parts. (Second line) The corresponding reconstructed models without applying overlapping process (edge effect is apparent).
Figure 1.
(First line) Segmentation of bunny model using MeTis algorithm in (a) 70, (b) 100 and (c) 200 parts. (Second line) The corresponding reconstructed models without applying overlapping process (edge effect is apparent).
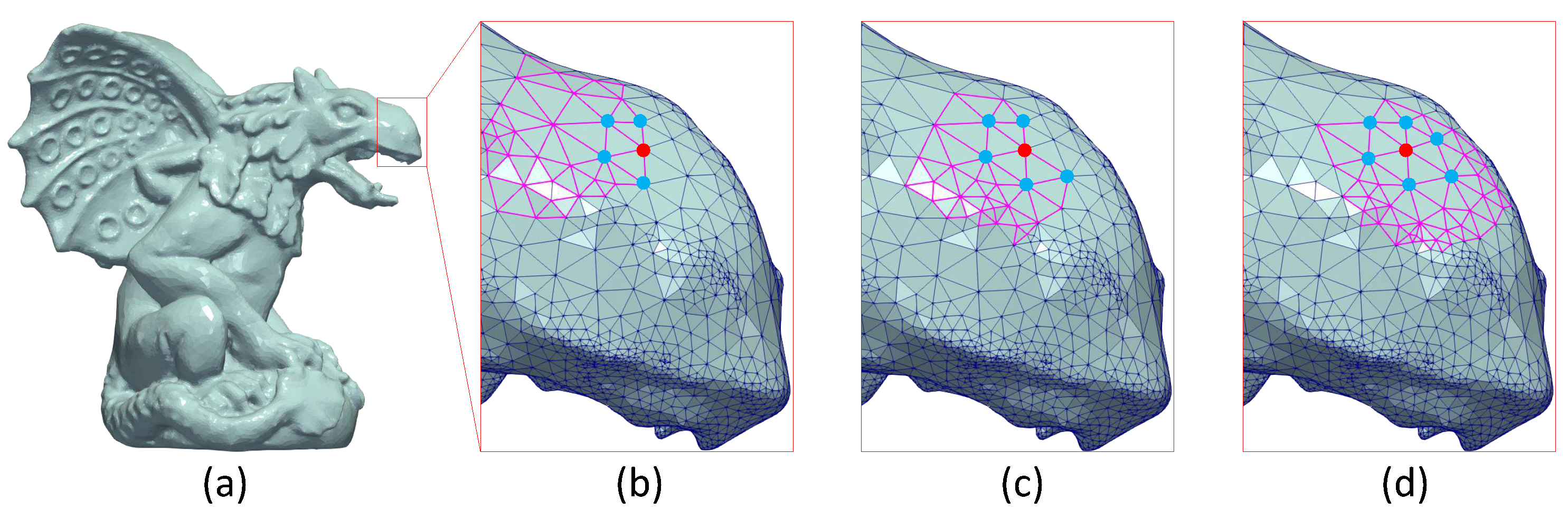
Figure 2.
The red point has different degree in each submesh of the (a) original model (Gargoyle model), the corresponding weights are: (b) w = 4, (c) w = 5, (d) w = 6.
Figure 2.
The red point has different degree in each submesh of the (a) original model (Gargoyle model), the corresponding weights are: (b) w = 4, (c) w = 5, (d) w = 6.
Figure 3.
Overlapped parts means that each boundary point belongs to more than one part and its degree may vary significantly between different parts.
Figure 3.
Overlapped parts means that each boundary point belongs to more than one part and its degree may vary significantly between different parts.
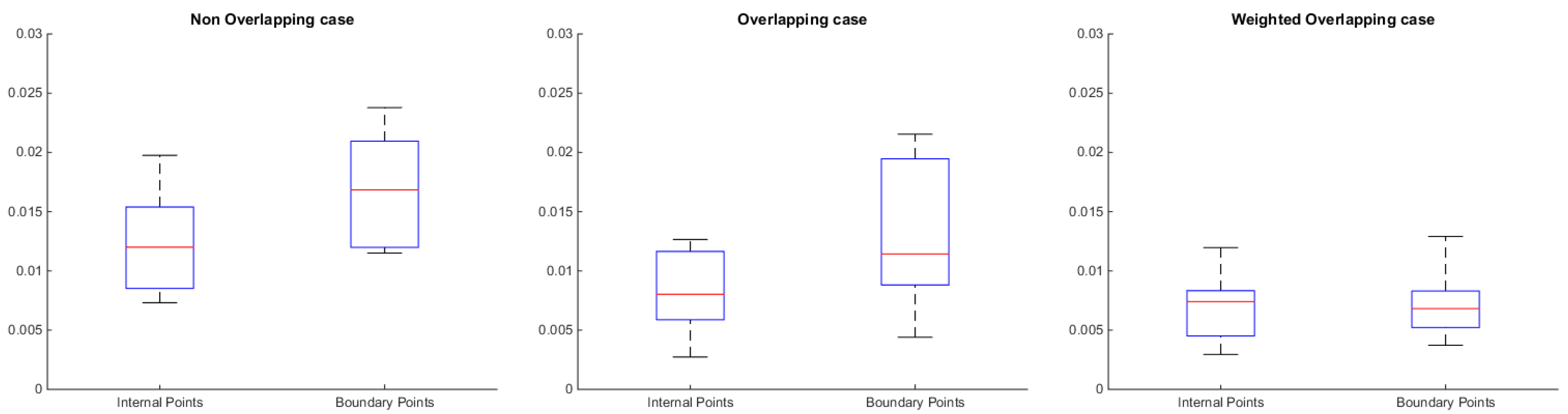
Figure 4.
Standard deviation of the reconstructed error in the internal and the boundary points of each submesh for each one of the aforementioned cases.
Figure 4.
Standard deviation of the reconstructed error in the internal and the boundary points of each submesh for each one of the aforementioned cases.
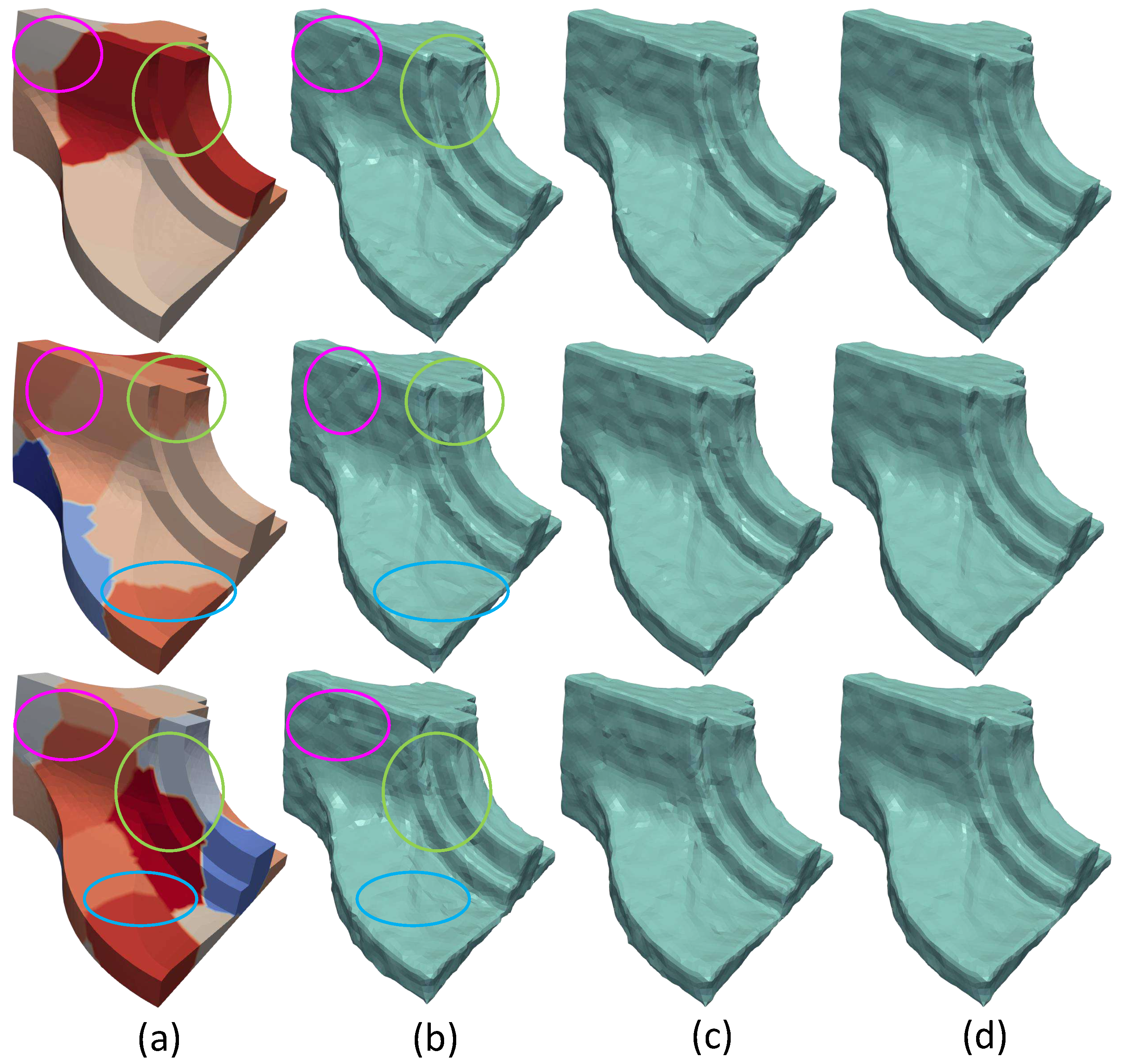
Figure 5.
(a) The model separated in different number of parts (10, 15 and 20, respectively). Additionally, indicative areas have been selected where two or more submeshes are connected; (b) Non Overlapping case, the edge effect is apparent in areas where submeshes are connected; (c) Overlapping case, the edge effect have been mitigated but have not been eliminated yet. The bigger the number of the partitioning the more intense the problem of the effect; (d) Weighted Overlapping case, the results seem to be independent and unaffected of the partitioning (Fandisk ).
Figure 5.
(a) The model separated in different number of parts (10, 15 and 20, respectively). Additionally, indicative areas have been selected where two or more submeshes are connected; (b) Non Overlapping case, the edge effect is apparent in areas where submeshes are connected; (c) Overlapping case, the edge effect have been mitigated but have not been eliminated yet. The bigger the number of the partitioning the more intense the problem of the effect; (d) Weighted Overlapping case, the results seem to be independent and unaffected of the partitioning (Fandisk ).
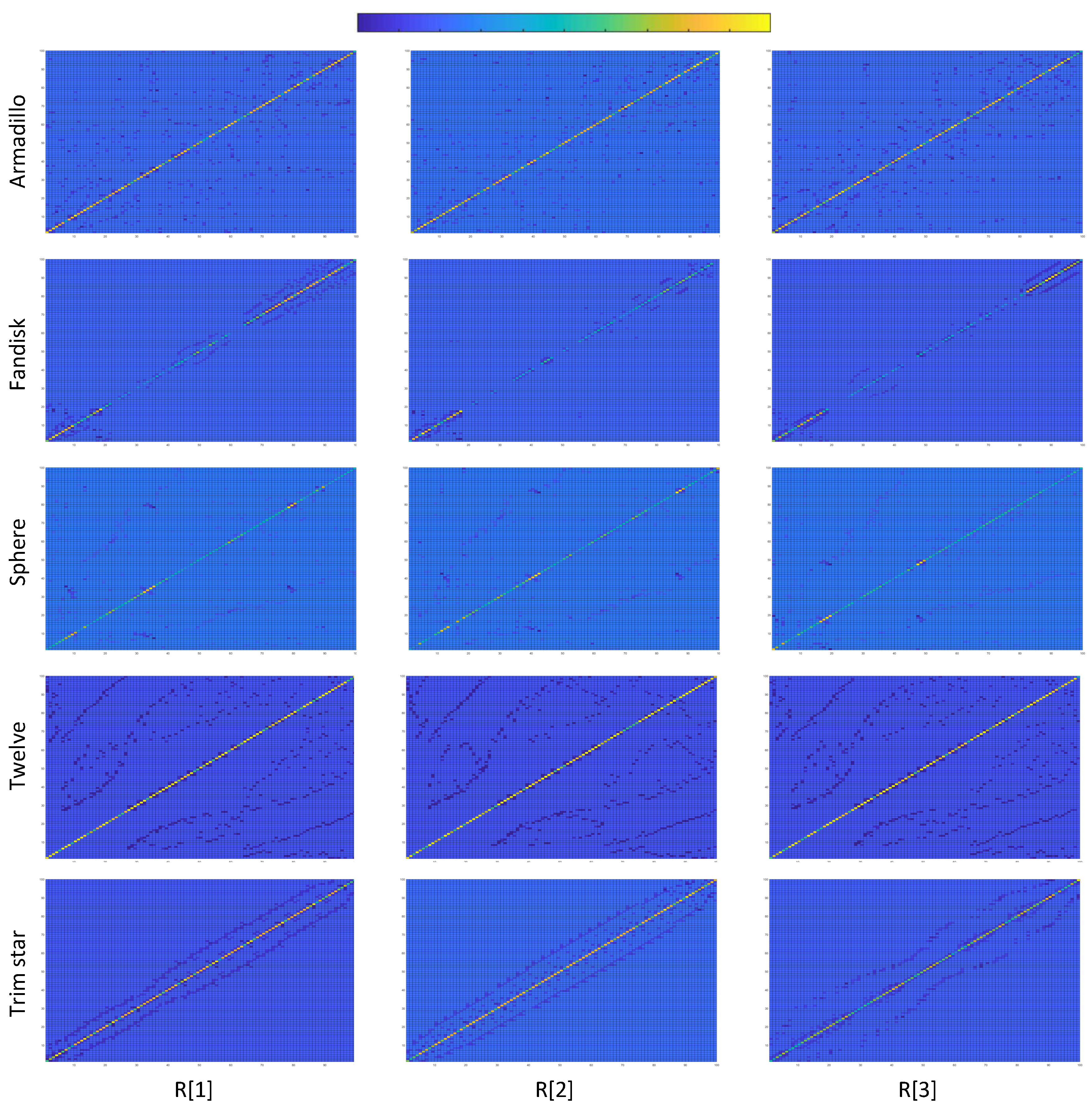
Figure 6.
Laplacian matrices of different submeshes for different models in color based on the values of their cells. It can be easily observed that different submeshes of the same model follow a similar form while they are totally different in comparison with submeshes of different meshes.
Figure 6.
Laplacian matrices of different submeshes for different models in color based on the values of their cells. It can be easily observed that different submeshes of the same model follow a similar form while they are totally different in comparison with submeshes of different meshes.
Figure 7.
(First line) Original and Noisy mesh. (Second line) Coarse denoising meshes separated by Metis in (a) 25 submeshes, (b) 50 submeshes, (c) 70 submeshes, (d) 100 submeshes.
Figure 7.
(First line) Original and Noisy mesh. (Second line) Coarse denoising meshes separated by Metis in (a) 25 submeshes, (b) 50 submeshes, (c) 70 submeshes, (d) 100 submeshes.
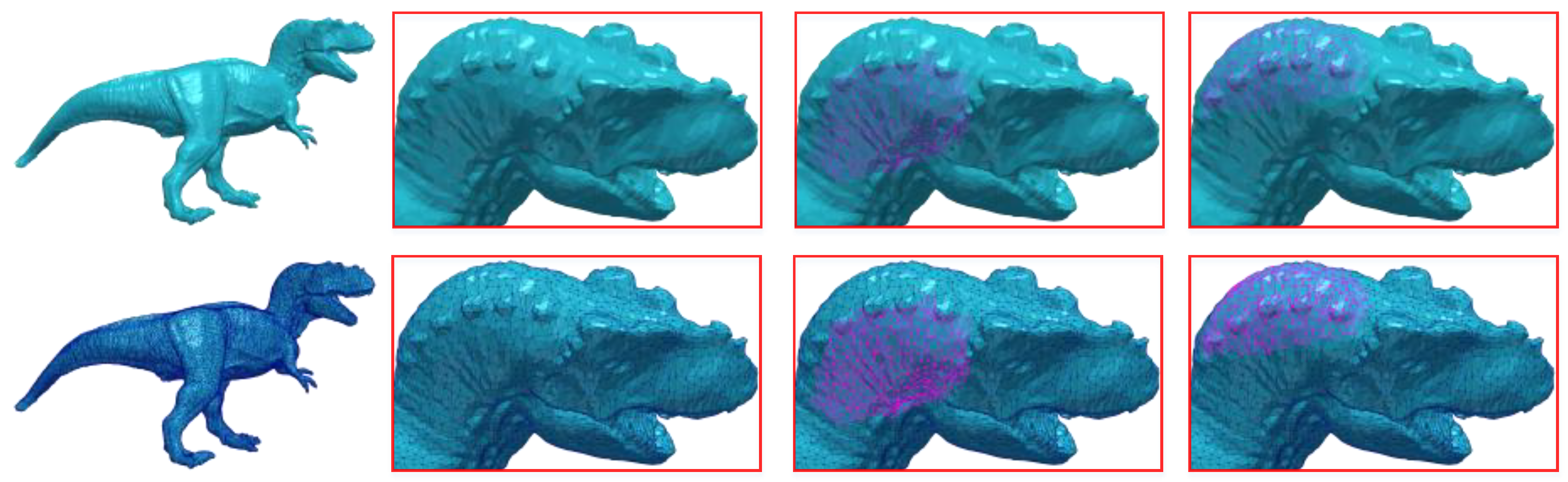
Figure 8.
Coarse denoising meshes with 70 equal-sized overlapped submeshes consisting of (a) 532 vertices (max), (b) 558 vertices (1.05 · max), (c) 585 vertices (1.10 · max), (d) 611 vertices (1.15 · max), (e) 638 vertices (1.20 · max), (f) 665 vertices (1.25 · max).
Figure 8.
Coarse denoising meshes with 70 equal-sized overlapped submeshes consisting of (a) 532 vertices (max), (b) 558 vertices (1.05 · max), (c) 585 vertices (1.10 · max), (d) 611 vertices (1.15 · max), (e) 638 vertices (1.20 · max), (f) 665 vertices (1.25 · max).
Figure 9.
Face normals of: (a) The original noise-free mesh; (b) the noisy mesh; (c) Smoothed reconstructed model.
Figure 9.
Face normals of: (a) The original noise-free mesh; (b) the noisy mesh; (c) Smoothed reconstructed model.
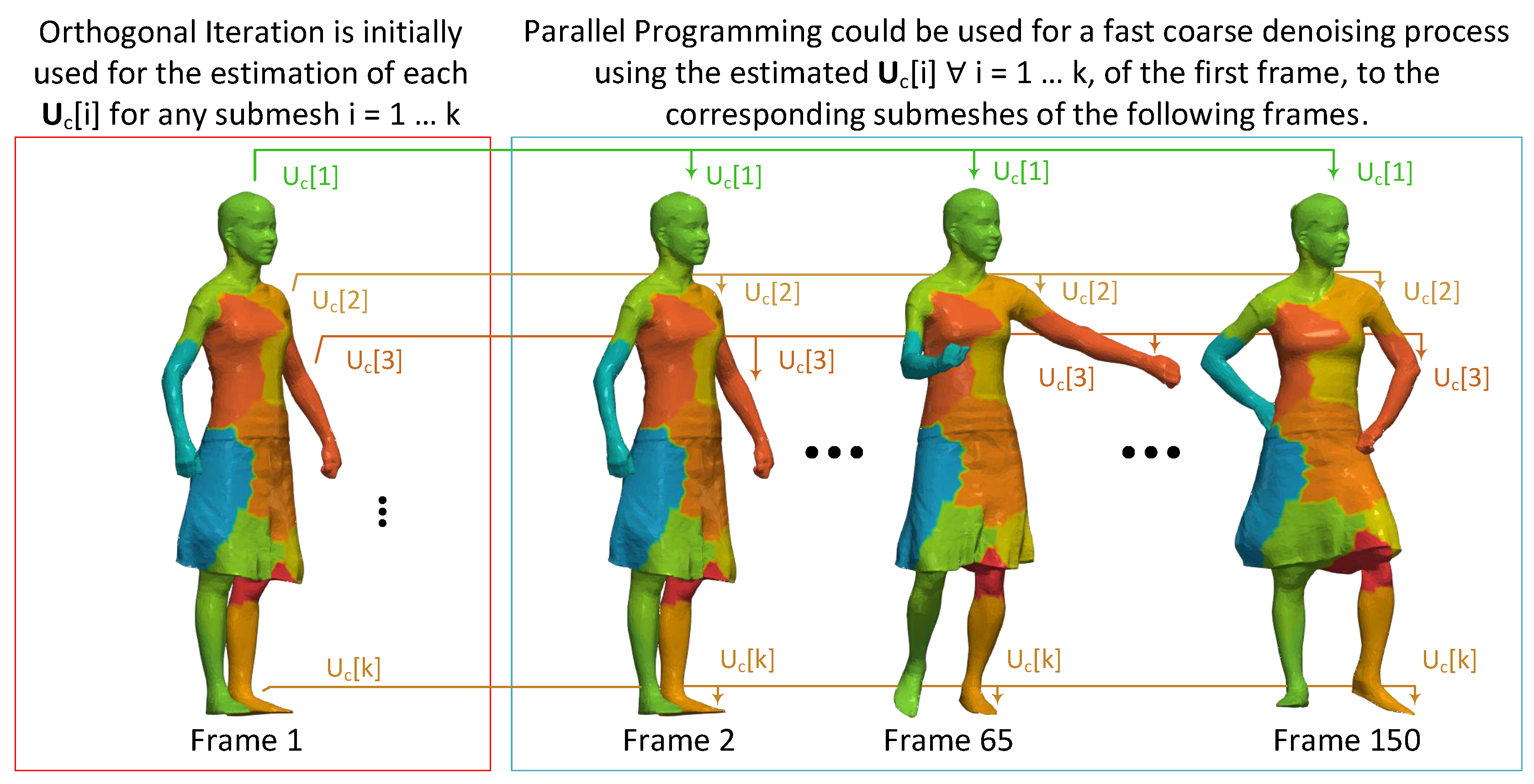
Figure 10.
Parallel programming schema for high-performance coarse denoising of a 3D dynamic mesh.
Figure 10.
Parallel programming schema for high-performance coarse denoising of a 3D dynamic mesh.
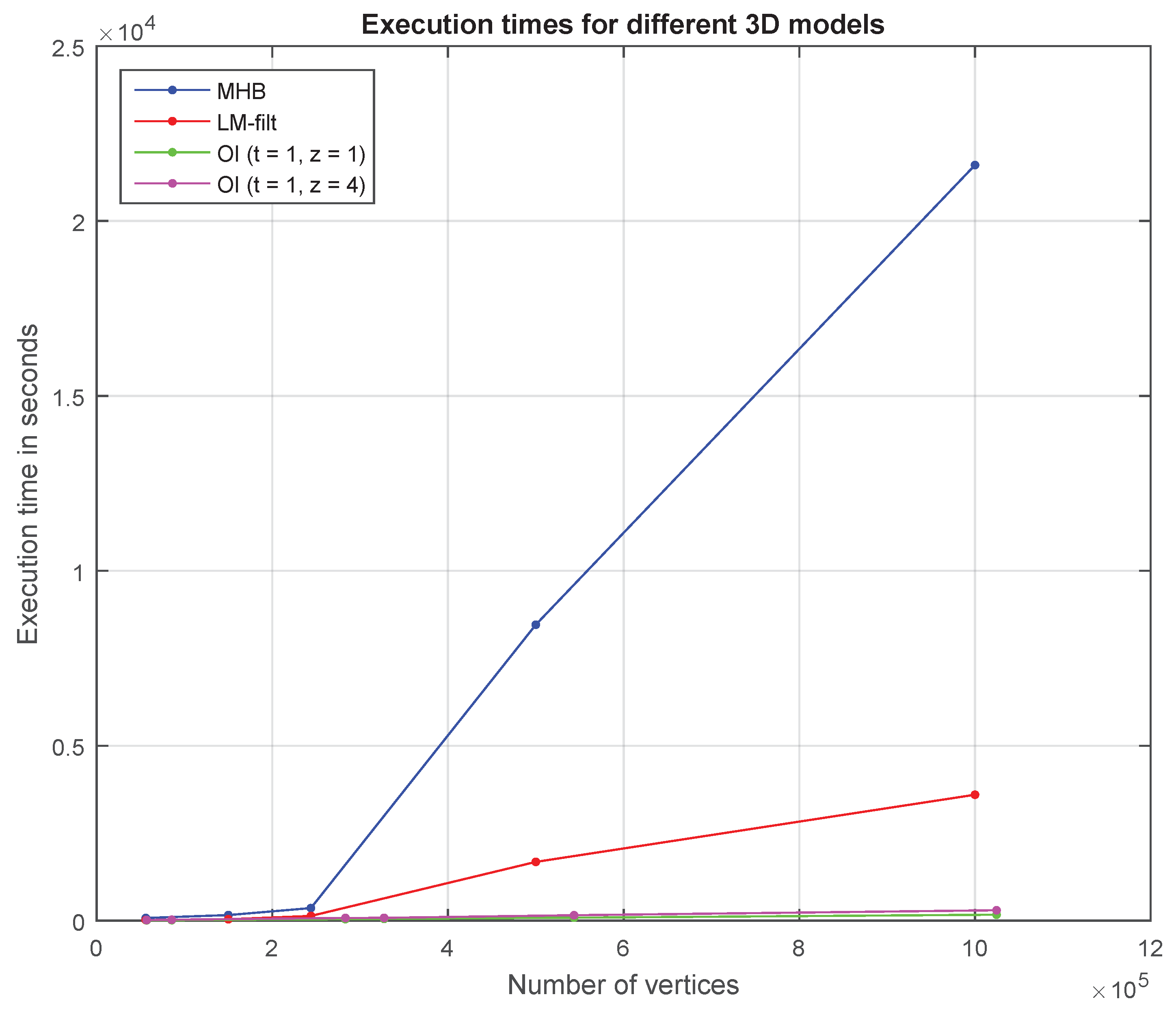
Figure 11.
Execution times for different 3D models.
Figure 11.
Execution times for different 3D models.
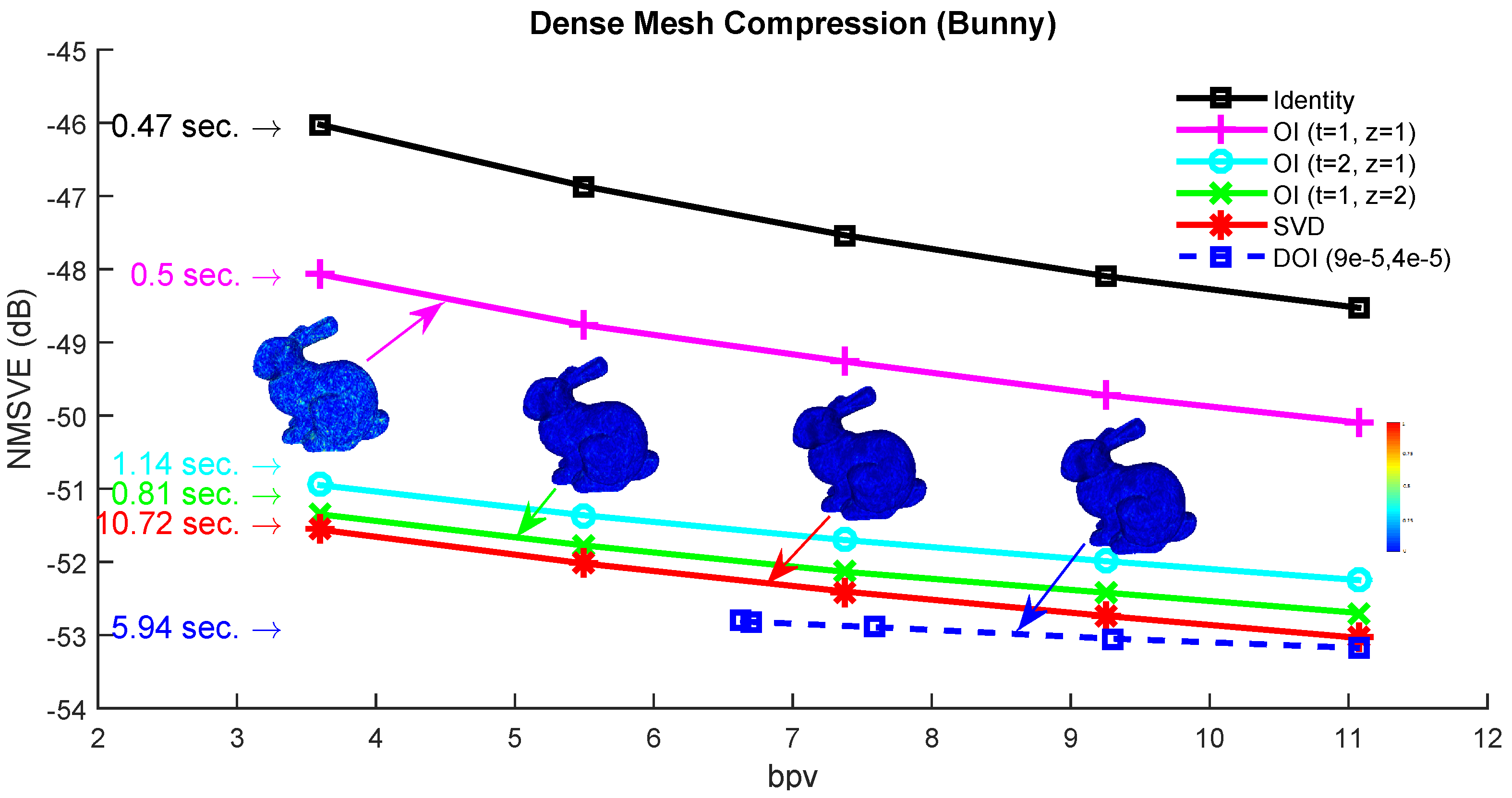
Figure 12.
Normalized mean square visual error (NMSVE) of the reconstructed models per different bpv for different compared approaches.
Figure 12.
Normalized mean square visual error (NMSVE) of the reconstructed models per different bpv for different compared approaches.
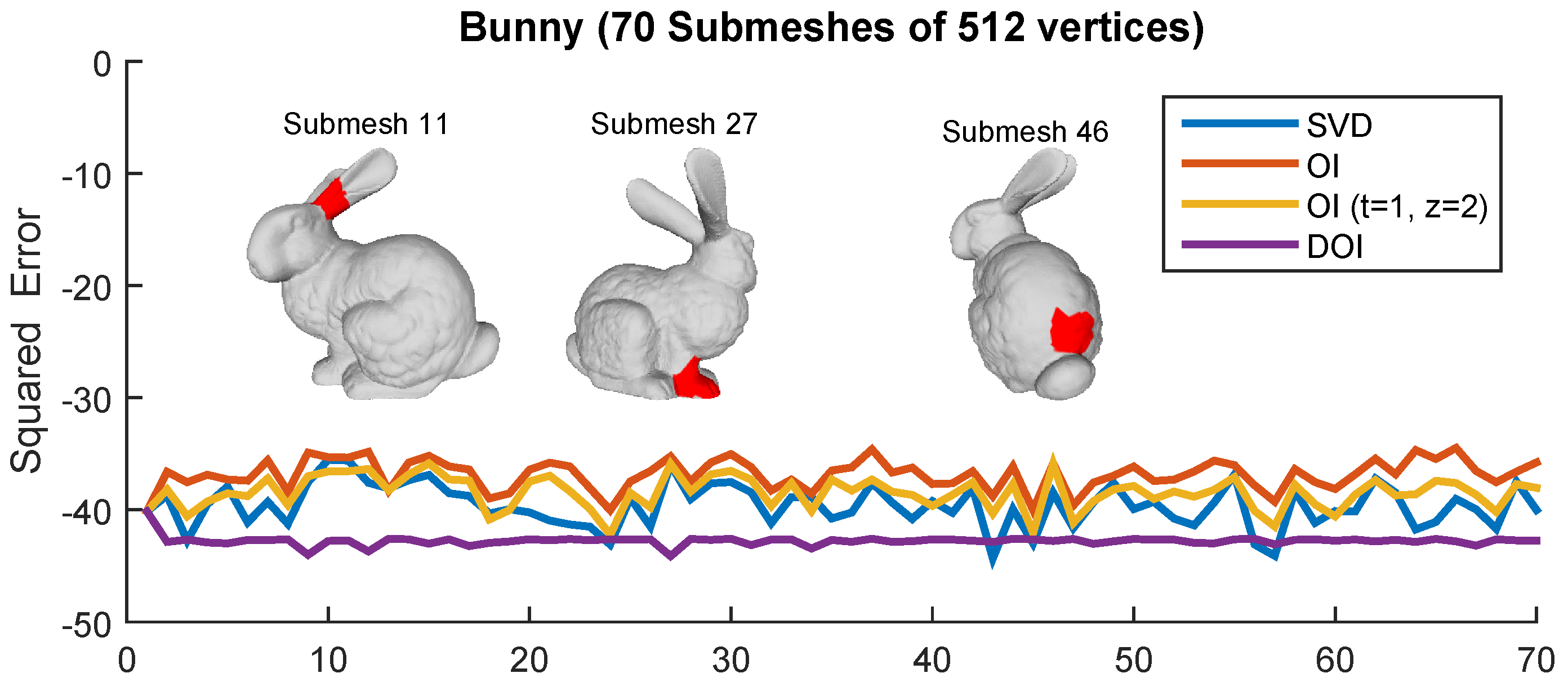
Figure 13.
Squared error per each submesh for different approaches.
Figure 13.
Squared error per each submesh for different approaches.
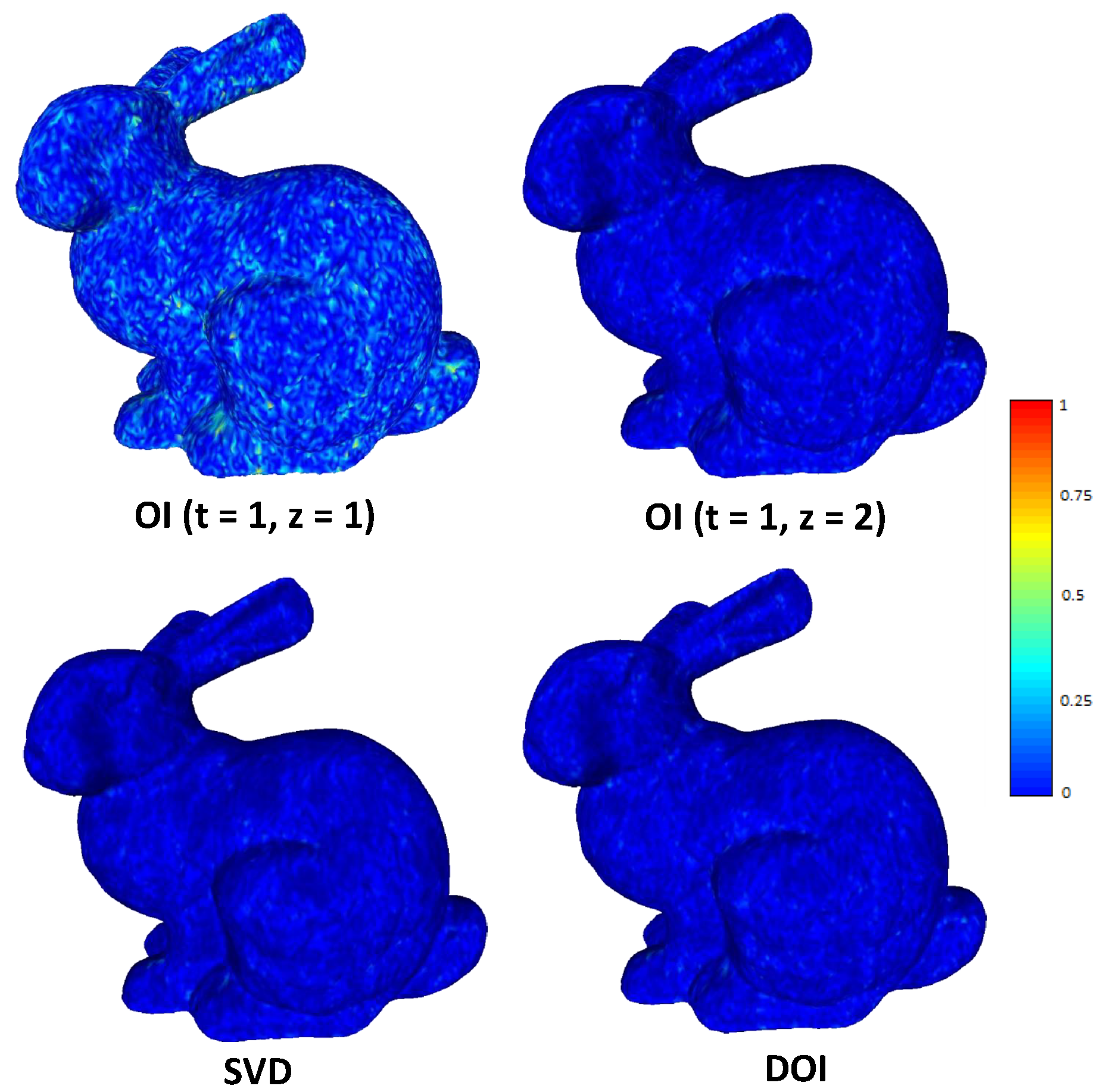
Figure 14.
Heatmap visualazation of normal difference with bpv 5.64 for different reconstructed approaches.
Figure 14.
Heatmap visualazation of normal difference with bpv 5.64 for different reconstructed approaches.
Figure 15.
(a) NMSVE vs bpv plot of the Dragon model (437,645 vertices); (b) normal difference with bpv 7.06. The arrow represents the speed-up in execution time compared to SVD.
Figure 15.
(a) NMSVE vs bpv plot of the Dragon model (437,645 vertices); (b) normal difference with bpv 7.06. The arrow represents the speed-up in execution time compared to SVD.
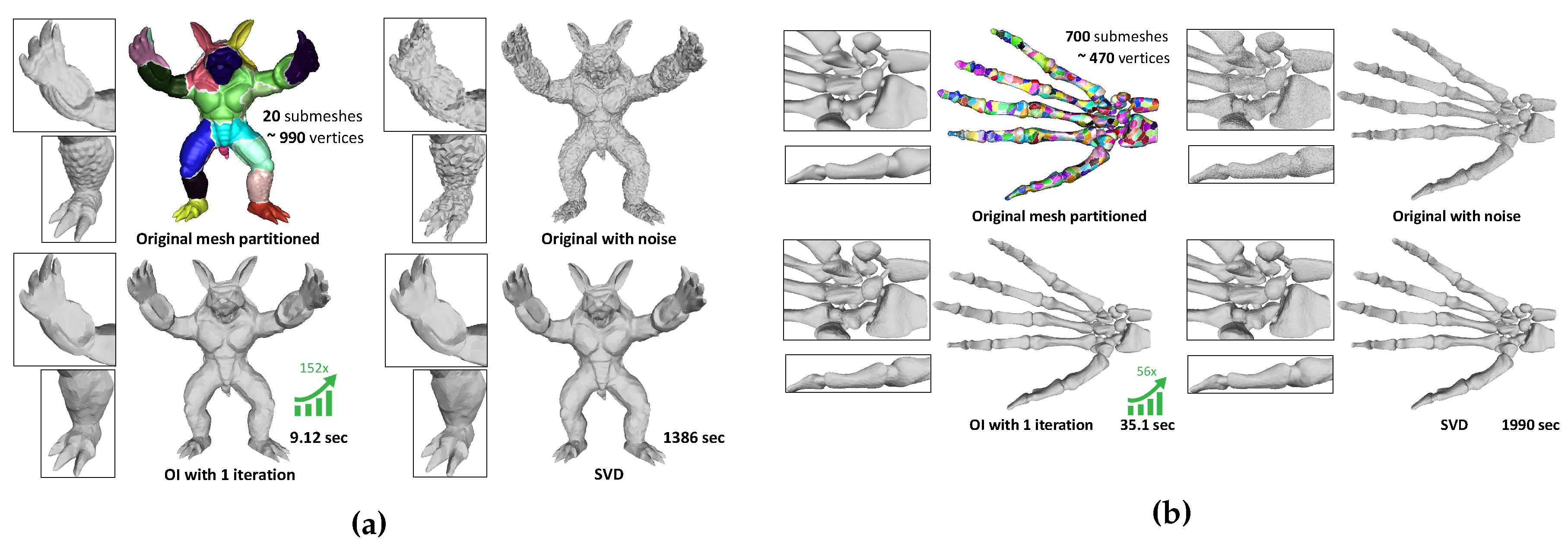
Figure 16.
Filtering of 3D models (a) Armadillo (20,002 vertices) using and (b) Hand (327,323 vertices) using with noise: . Each color represents a submesh, and the arrow depicts the speed-up in execution time compared to SVD.
Figure 16.
Filtering of 3D models (a) Armadillo (20,002 vertices) using and (b) Hand (327,323 vertices) using with noise: . Each color represents a submesh, and the arrow depicts the speed-up in execution time compared to SVD.
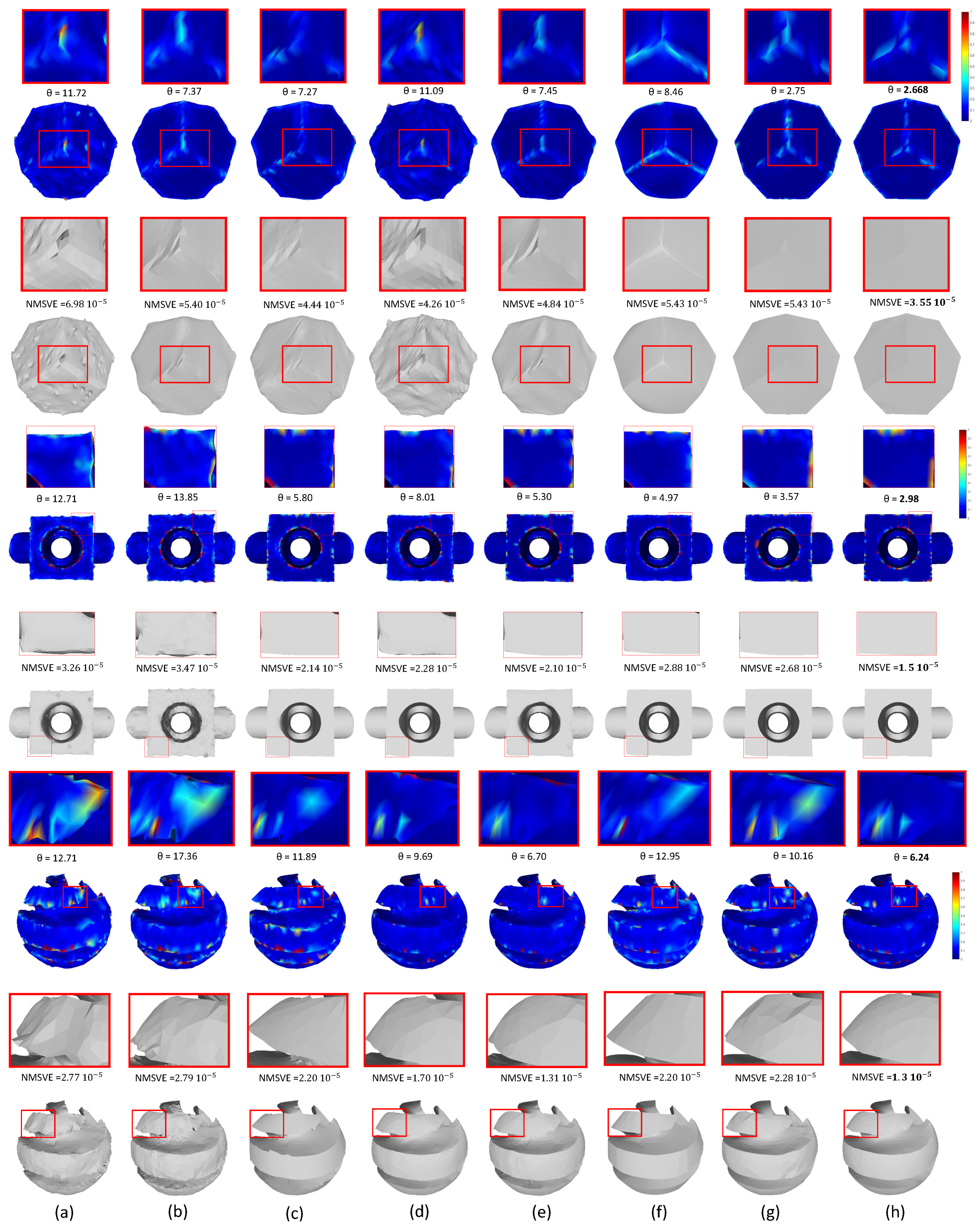
Figure 17.
Denoising results for different methods and heatmap visualization; (
a) bilateral [
41]; (
b) non-iterative [
45]; (
c) Fast and Effective [
46]; (
d) Bilateral (l) [
42]; (
e) Bilateral (
g) [
42]; (
f)
minimization [
47]; (
g) Guided normal filtering [
43]; (
h) Our Approach.
Figure 17.
Denoising results for different methods and heatmap visualization; (
a) bilateral [
41]; (
b) non-iterative [
45]; (
c) Fast and Effective [
46]; (
d) Bilateral (l) [
42]; (
e) Bilateral (
g) [
42]; (
f)
minimization [
47]; (
g) Guided normal filtering [
43]; (
h) Our Approach.
Figure 18.
(Left) Three-dimensional scanned cup and wallet with abnormalities. (Right) Denoising results in respect of features.
Figure 18.
(Left) Three-dimensional scanned cup and wallet with abnormalities. (Right) Denoising results in respect of features.
Table 1.
Mean squared error between the of different models and the mean of each model. The lowest value per row is highlighted in bold.
Table 1.
Mean squared error between the of different models and the mean of each model. The lowest value per row is highlighted in bold.
| | Armadillo | Fandisk | Sphere | Trim Star | Twelve |
|---|
| Armadillo | 0.0606 | 13.9720 | 10.0905 | 1.2347 | 37.4199 |
| Fandisk | 15.6144 | 1.4120 | 11.1582 | 8.4506 | 29.8815 |
| Sphere | 10.4615 | 11.4700 | 0.8857 | 3.9065 | 26.4125 |
| Trim star | 1.3122 | 8.5019 | 3.919 | 0.6095 | 29.6996 |
| Twelve | 37.8481 | 30.2103 | 26.6648 | 30.0618 | 4.5641 |
Table 2.
Mean Normal Difference using different number of segments (Bunny Model with 34,817 vertices). We also compare the mean normal difference by using normal average and weighted average based on the number of the connected vertices.
Table 2.
Mean Normal Difference using different number of segments (Bunny Model with 34,817 vertices). We also compare the mean normal difference by using normal average and weighted average based on the number of the connected vertices.
| Number of Submeshes | Number of Vertices per Segment | MND Using Simple Average | MND Using Weighted Average |
|---|
| 25 | 1392 | 0.0921 | 0.0915 |
| 40 | ~870 | 0.0931 | 0.0925 |
| 50 | ~696 | 0.0941 | 0.0934 |
| 70 | ~497 | 0.0960 | 0.0952 |
| 100 | ~348 | 0.0988 | 0.0980 |
| 200 | ~174 | 0.1039 | 0.1028 |
| 500 | ~69 | 0.1163 | 0.1150 |
Table 3.
Mean normal difference using different size of equal-sized overlapped submeshes (Julio Model with 36,201 vertices 70 segments).
Table 3.
Mean normal difference using different size of equal-sized overlapped submeshes (Julio Model with 36,201 vertices 70 segments).
| Type of Overlapping | Number of Vertices per Segment | Coarse Denoising MND | Fine Denoising MND |
|---|
| max | 532 | 0.1248 | 0.1176 |
| 1.05 · max | 558 | 0.1228 | 0.1173 |
| 1.10 · max | 585 | 0.1203 | 0.1172 |
| 1.15 · max | 611 | 0.1188 | 0.1169 |
| 1.20 · max | 638 | 0.1174 | 0.1169 |
| 1.25 · max | 665 | 0.1164 | 0.1164 |
Table 4.
Mean normal difference using different size of equal-sized overlapped submeshes (Julio Model with 36,201 vertices 100 segments).
Table 4.
Mean normal difference using different size of equal-sized overlapped submeshes (Julio Model with 36,201 vertices 100 segments).
| Type of Overlapping | Number of Vertices per Segment | Coarse Denoising MND | Fine Denoising MND |
|---|
| max | 372 | 0.1276 | 0.1189 |
| 1.05 · max | 390 | 0.1248 | 0.1187 |
| 1.10 · max | 409 | 0.1228 | 0.1185 |
| 1.15 · max | 427 | 0.1208 | 0.1183 |
| 1.20 · max | 446 | 0.1184 | 0.1174 |
| 1.25 · max | 465 | 0.1175 | 0.1168 |
Table 5.
Mean normal difference using different size of equal-sized overlapped submeshes (Julio Model with 36,201 vertices 50 segments).
Table 5.
Mean normal difference using different size of equal-sized overlapped submeshes (Julio Model with 36,201 vertices 50 segments).
| Type of Overlapping | Number of Vertices per Segment | Coarse Denoising MND | Fine Denoising MND |
|---|
| max | 741 | 0.1229 | 0.1167 |
| 1.05 · max | 778 | 0.1207 | 0.1166 |
| 1.10 · max | 815 | 0.1188 | 0.1163 |
| 1.15 · max | 852 | 0.1172 | 0.1160 |
| 1.20 · max | 889 | 0.1160 | 0.1159 |
| 1.25 · max | 926 | 0.1159 | 0.1158 |
Table 6.
Evaluation of the experimental results using different metrics. The lowest value per each row is highlighted in bold.
Table 6.
Evaluation of the experimental results using different metrics. The lowest value per each row is highlighted in bold.
| | Metrics | Bilateral [41] | Non-[45] Iterative | Fast & [46] Effective | Bilateral (l) [42] | Bilateral (g) [42] | l0 min [47] | Guided Normal [43]
Filtering | Our Approach |
|---|
| Twelve (0.5) | | 11.7204 | 11.093 | 7.4519 | 7.3683 | 7.271 | 8.4626 | 2.7542 | 2.668 |
| Dmean d | 0.017 | 0.0155 | 0.0115 | 0.0129 | 0.0123 | 0.0317 | 0.0128 | 0.006 |
| Dmax d | 0.1357 | 0.1074 | 0.0728 | 0.0947 | 0.0741 | 0.1357 | 0.1594 | 0.0995 |
| dist n | 0.1434 | 0.1301 | 0.1051 | 0.1055 | 0.1073 | 0.1518 | 0.0809 | 0.0645 |
| NMSVE | | | | | | | | |
| Dmean n | 0.2113 | 0.2002 | 0.1349 | 0.1322 | 0.1331 | 0.1627 | 0.0519 | 0.0465 |
| Block (0.4) | | 12.7155 | 13.8501 | 5.8023 | 8.0165 | 5.3062 | 4.9734 | 3.572 | 2.9826 |
| Dmean d | 0.1873 | 0.1425 | 0.0857 | 0.096 | 0.0744 | 0.1922 | 0.1066 | 0.0544 |
| Dmax d | 0.8781 | 0.8684 | 0.8206 | 0.7009 | 0.8759 | 0.6836 | 0.9967 | 0.6479 |
| dist n | 0.236 | 0.2179 | 0.1536 | 0.17 | 0.1462 | 0.1911 | 0.1443 | 0.1064 |
| NMSVE | | | | | | | | |
| Dmean n | 0.3134 | 0.3106 | 0.1422 | 0.1866 | 0.128 | 0.1808 | 0.1131 | 0.0788 |
| Fandisk (0.7) | | 22.4862 | 27.9264 | 13.1918 | 15.0545 | 14.2553 | 6.2186 | 6.3721 | 6.0669 |
| Dmean d | 0.0376 | 0.0366 | 0.0276 | 0.0321 | 0.0294 | 0.0293 | 0.0291 | 0.0155 |
| Dmax d | 0.2412 | 0.2093 | 0.2048 | 0.188 | 0.1987 | 0.1373 | 0.1865 | 0.1207 |
| dist n | 0.5803 | 0.6209 | 0.5447 | 0.5739 | 0.5739 | 0.4529 | 0.4495 | 0.4065 |
| NMSVE | | | | | | | | |
| Dmean n | 0.403 | 0.4937 | 0.2353 | 0.2713 | 0.2535 | 0.1221 | 0.119 | 0.1104 |