Combination of LBP Bin and Histogram Selections for Color Texture Classification
Abstract
1. Introduction
- (1)
- To obtain more discriminative, robust and compact LBP-based features, the first strategy consists of identifying the most informative pattern groups based on some rules or on the predefinition of patterns of interest. The uniform LBP operator, where a reduced number of discriminant bins are a priori chosen among all the available ones, is an example of predefinied compact LBP [5].
- (2)
- The second strategy is based on feature extraction approaches, which project features into a new feature space, with a lower dimensionality, where the new constructed features are usually combinations of the original features. Chan et al. use a linear discriminant analysis to project high-dimensional color LBP bins into a discriminant space [6]. Banerji et al. apply Principal Component Analysis (PCA) to reduce the feature dimensionality of the concatenating LBP features extracted from different color spaces. Zhao et al. compare different dimensionality reduction methods on LBP features, e.g., PCA, kernel PCA and Laplacian PCA [7]. Hussain et al. exploit the complementarity of three sets of features, including LBP, and applies partial least squares for improving their object class recognition approach [8].
- (3)
- The third strategy consists of applying feature selection methods in order to find the most discriminative patterns [9]. Smith and Windeatt apply the fast correlation-based filtering algorithm [10] to select the LBP patterns that are the most correlated with the target class [11]. This algorithm starts with the full set of features, calculates dependences of features thanks to symmetrical uncertainty, and finds the best subset using backward selection technique with sequential search strategy. Lahdenoja et al. define a discrimination concept of symmetry for uniform patterns to reduce the feature dimensionality [12]. In this approach, the patterns with a higher level of symmetry are shown to have more discriminative power. Maturana et al. use an algorithm based on Fisher-like class separability criterion to select the neighbors used in the computation of LBP [13]. Liao et al. introduce Dominant Local Binary patterns (DLBP) which consider the most frequently occurred patterns in a texture image [14]. To compute the DLBP feature vectors from an input image, a pattern histogram which considers all the patterns in the input image is constructed and the histogram bins are sorted in descending order. The occurrence frequencies corresponding to the most frequently occurred patterns in the input image are served as the feature vectors. Guo et al. propose a Fisher separation criterion to learn the most reliable and robust patterns by using intra-class and inter-class distances [15]. This approach, which proposes to learn the most reliable and robust dominant bins by considering intra-class similarity and inter-class dissimilarity, is very interesting since it outperforms Ojala’s uniform LBP operator and Liao’s DLBP in the experiments on three texture databases. It has also been recently extended to the multi color space domain [16].
- (4)
- A fourth strategy to reduce the dimension of the feature space based on LBP histograms was proposed by Porebski et al. in 2013 [17]. In this approach, the most discriminant LBP histograms are selected in their entirety out of the different LBP histograms extracted from a color texture. It fundamentally differs from all the previous approaches which select the bins of the LBP histograms or project them into a discriminant space. Several scores were proposed in the literature to evaluate the relevance of histograms: the Intra-Class Similarity score (ICS-score), proposed by Porebski et al. [17], which is based on an intra-class similarity measure; the Adapted Supervised Laplacian score (ASL-score) and Adapted Laplacian score (AL-score), proposed by Kalakech et al. [18,19], which evaluates the relevance of the histograms using the local properties of the image data; the Simba-2 score, proposed by Mouhajid et al. [20], which is based on the hypothesis margin and the distance; and the Sparse Adapted Supervised Laplacian score (SpASL-score) [21], which is based on the ASL-score and a sparse representation. The LBP histogram selection approach using ICS or ASL scores was recently extended to the multi color space domain and showed its relevance compared to the bin selection approach proposed by Guo [16].
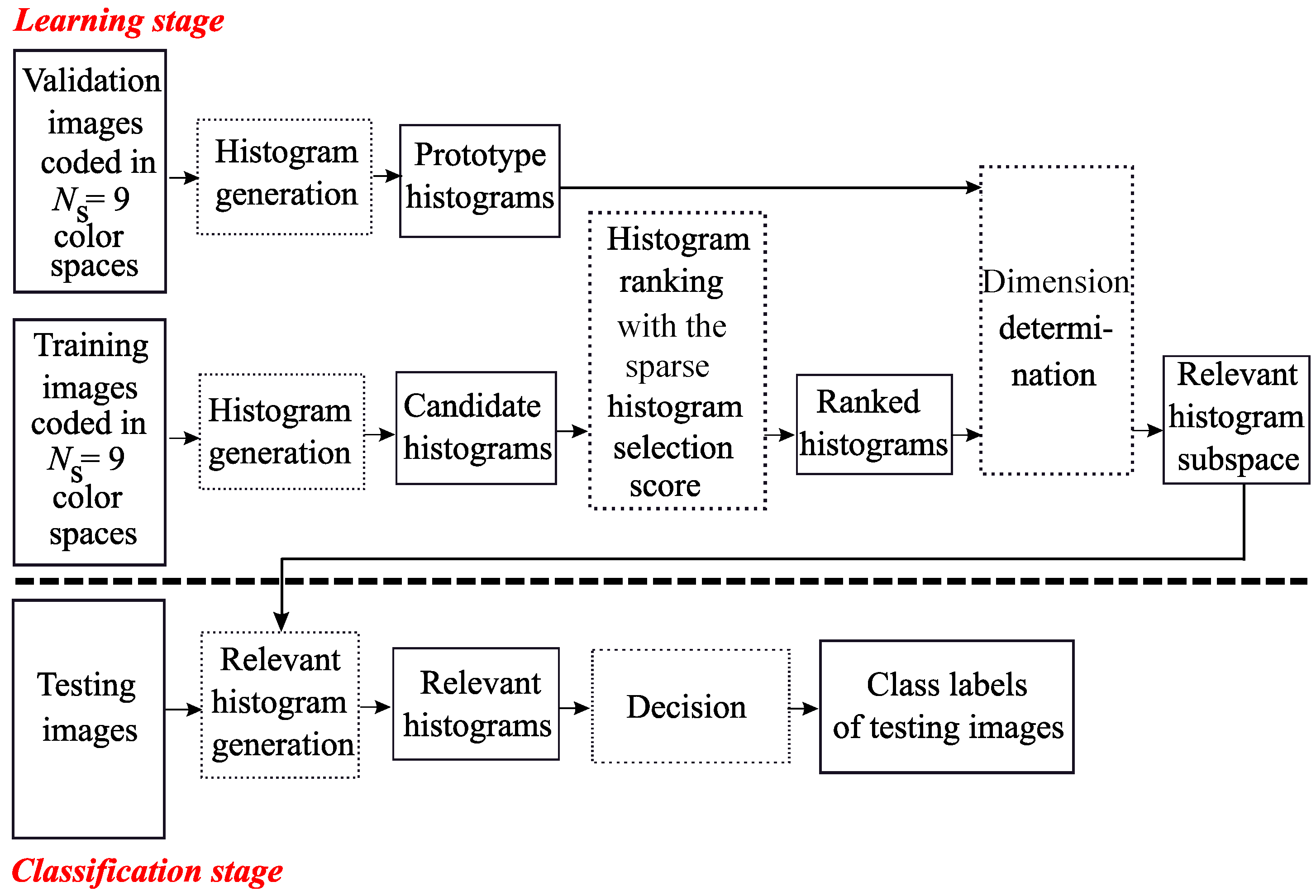
- For the first minor contribution, the LBP histogram selection approach proposed in [21], using the SpASL-score, is extended to the multi color space domain to define the Sparse Multi Color Space Histogram Selection (Sparse-MCSHS).
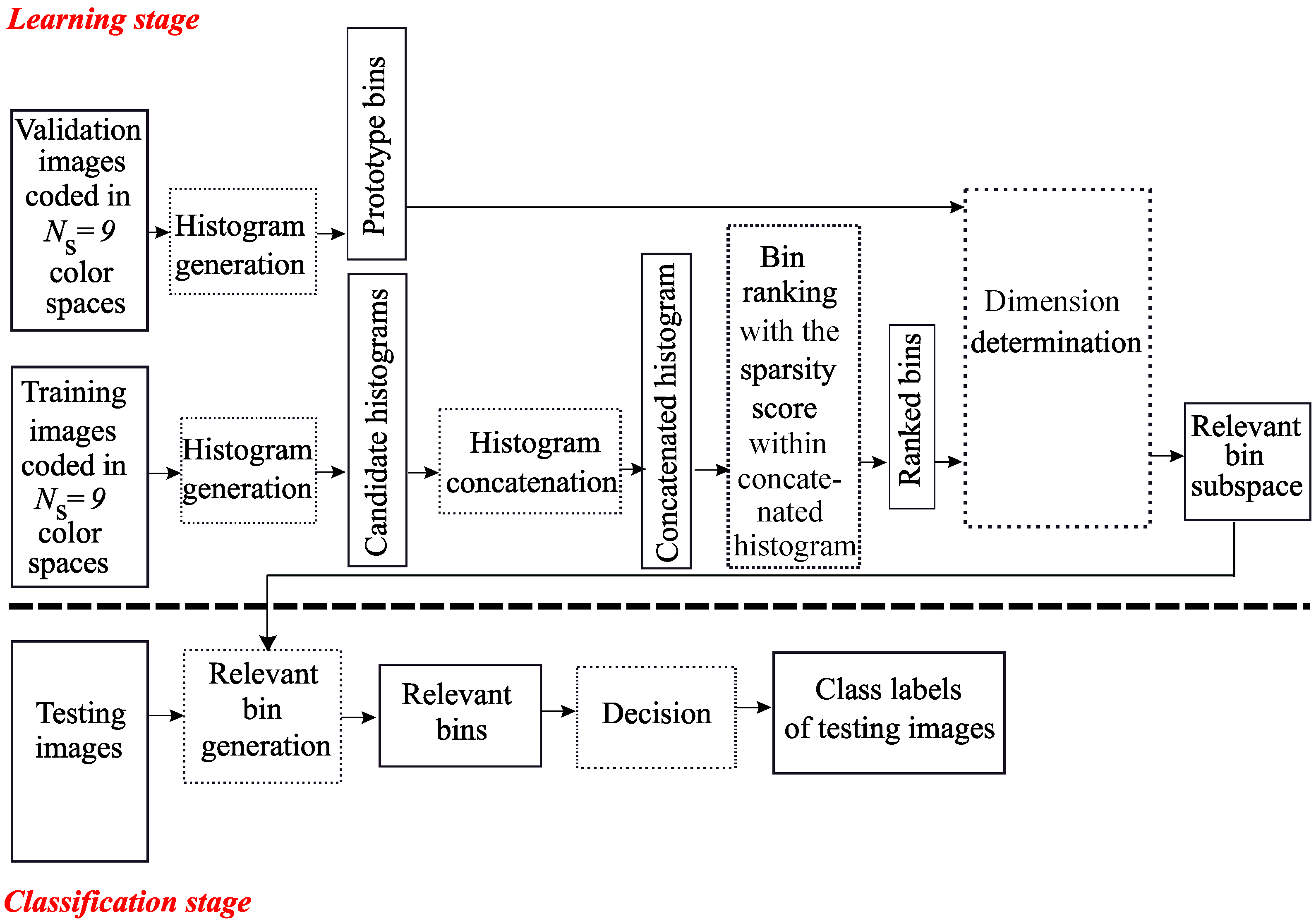
- We then propose comparing this Sparse-MCSHS approach with a multi color space bin selection approach, also based on a sparse representation. For this purpose, the sparsity score proposed by Liu [22] is used for selecting the most discriminant bins of LBP histograms extracted from images coded in several color spaces, leading to the Sparse Multi Color Space Bin Selection (Sparse-MCSBS) approach. This second minor contribution corresponds to the MCSBS approach proposed in [16] that was extended to a sparse representation.
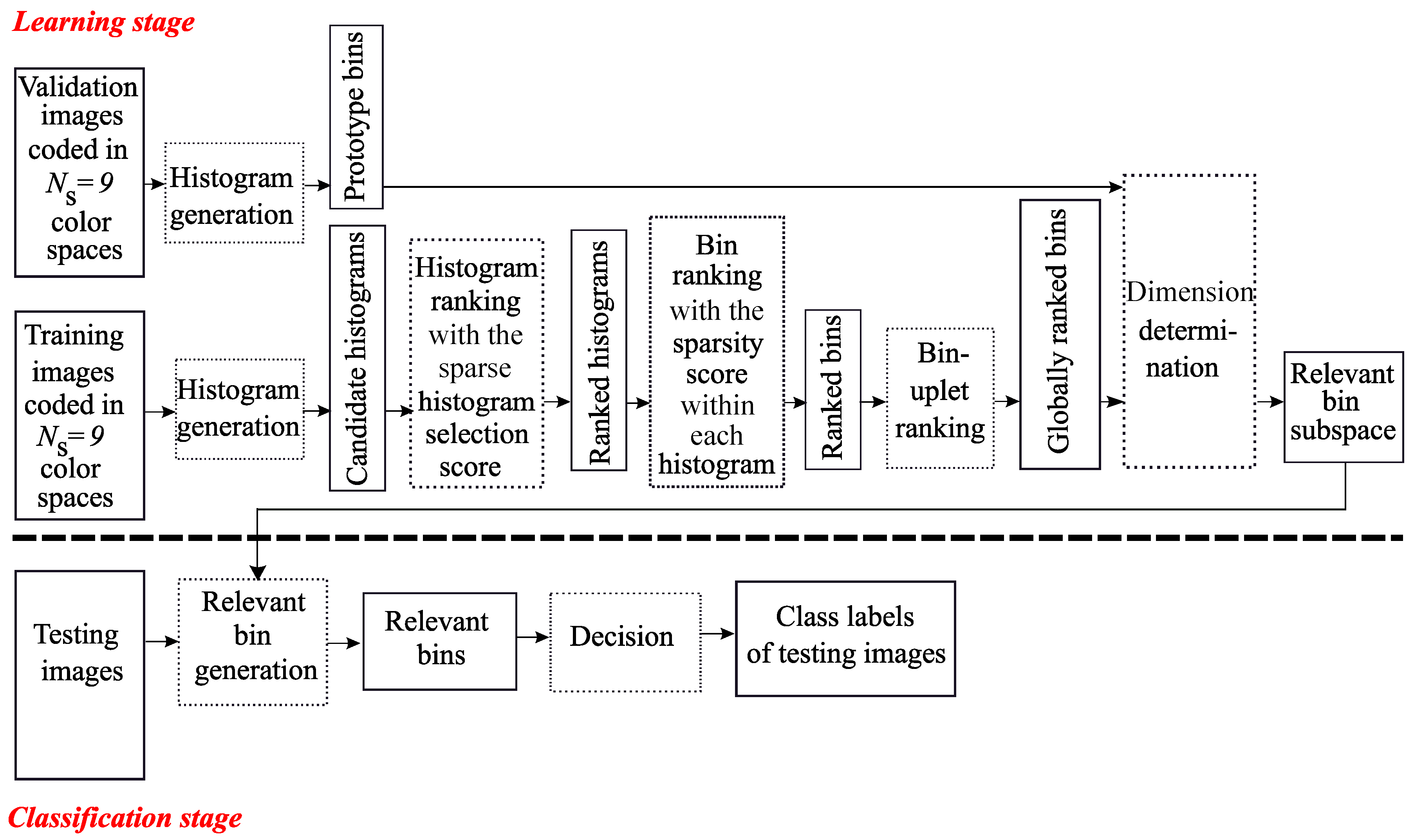
- These two approaches, Sparse-MCSHS and Sparse-MCSBS, are then combined to form the Sparse-MCSHBS approach (Sparse Multi Color Space Histogram and Bin Selection). This combination of bin and histogram selections represents the main contribution of the paper since such a combination for selecting relevant LBP bins was never previously proposed.
2. Color LBP Histograms
- (1)
- In the first strategy, the original LBP operator is computed from the luminance image and combined with color features. For example, Mäenpää or Ning proposed to represent the color texture by concatenating the 3D color histogram of the color image and the LBP histogram of the corresponding luminance image [31,32]. Cusano et al. propose a texture descriptor which combines a luminance LBP histogram with color features based on the local color contrast [33].
- (2)
- The second strategy is a marginal approach that consists of applying the original LBP operator independently on each of the three components of the color image, without considering the spatial interactions between the levels of two different color components. The texture descriptor is obtained by concatenating the three resulting LBP histograms. This within component strategy was applied by several authors [34,35,36,37,38].
- (3)
- The third strategy consists of taking into account the spatial interactions within and between color components. To describe color texture, Opponent Color LBP (OCLBP) was defined [31]. For this purpose, the LBP operator is applied on each pixel and for each pair of components denoted , . In this definition, opposing pairs such as and are considering to be highly redundant, and so, one of each pair is taken into consideration in the analysis. This leads to characterize a texture with only six histograms pairs , , , , , out of the nine available ones. However, these a priori chosen six histograms are not always the most relevant according to the different considered data sets [17] and it is preferable to consider the Extended Opponent Color LBP (EOCLBP). This way to describe the color textures with LBP was proposed by Pietikäinen in 2002 [37]. It consists of taking into account each color component independently and each possible pair of color components, leading to nine different histograms: three within-component and six between-component , , , , , LBP histograms. These nine histograms are finally concatenated so that a color texture image is represented in a -dimensional feature space. The OCLBP and EOCLBP have often been considered to classify color texture images [6,17,18,31,39,40]. Recently, Lee et al. propose another color LBP variant for face recognition tasks, the local color vector binary pattern [41]. In the proposed approach, each color texture image is characterized by the color norm pattern and the color angular patterns via LBP texture operation.
- (4)
- The fourth strategy consists of analyzing the spatial interactions between the colors of the neighboring pixels based on the consideration of an order relation between colors following a vectorial approach. Instead of comparing the color components of pixels, Porebski et al. represent the color of pixels by a vector and compare the color vectors of the neighboring pixels with the color vector of the central one [42]. They use a partial color order relation based on the Euclidean distance for comparing the rank of color. As a result, a single color LBP histogram is obtained instead of the 6 or 9 provided by OCLBP or EOCLBP, respectively [17,18]. Another possible way consists of defining a suitable total ordering in the color space. This strategy was investigated by Ledoux et al. who propose the Mixed Color Order LBP (MCOLBP) [43]. Finally, in order to give a single code by color LBP, the quaternion representation can be considered. Quaternion is shown to be an efficient mathematical tool for representing color images based on a hypercomplex representation [44]. Lan et al. have thus proposed the Quaternionic Local Binary Pattern (QLBP) that makes use of quaternion to represent each pixel color by a complex number including all color components at one time. Under this representation, the dimension of QLBP is equal to the dimension of a grayscale LBP. QLBP was applied for person re-identification problems by Lan and Chahla in [45,46] and was then extended in [47] for color image classification.
3. Sparse-MCSHS and Sparse-MCSBS Approaches
3.1. Considered Color Spaces
- and , which belong to the primary space family,
- and , which are luminance-chrominance spaces,
- , which is an independent color component space,
- HSV, HSI, HLS and I-HLS, which belong to the perceptual space family.
3.2. Candidate Color Texture Descriptors
3.3. Sparse-MCSHS Approach
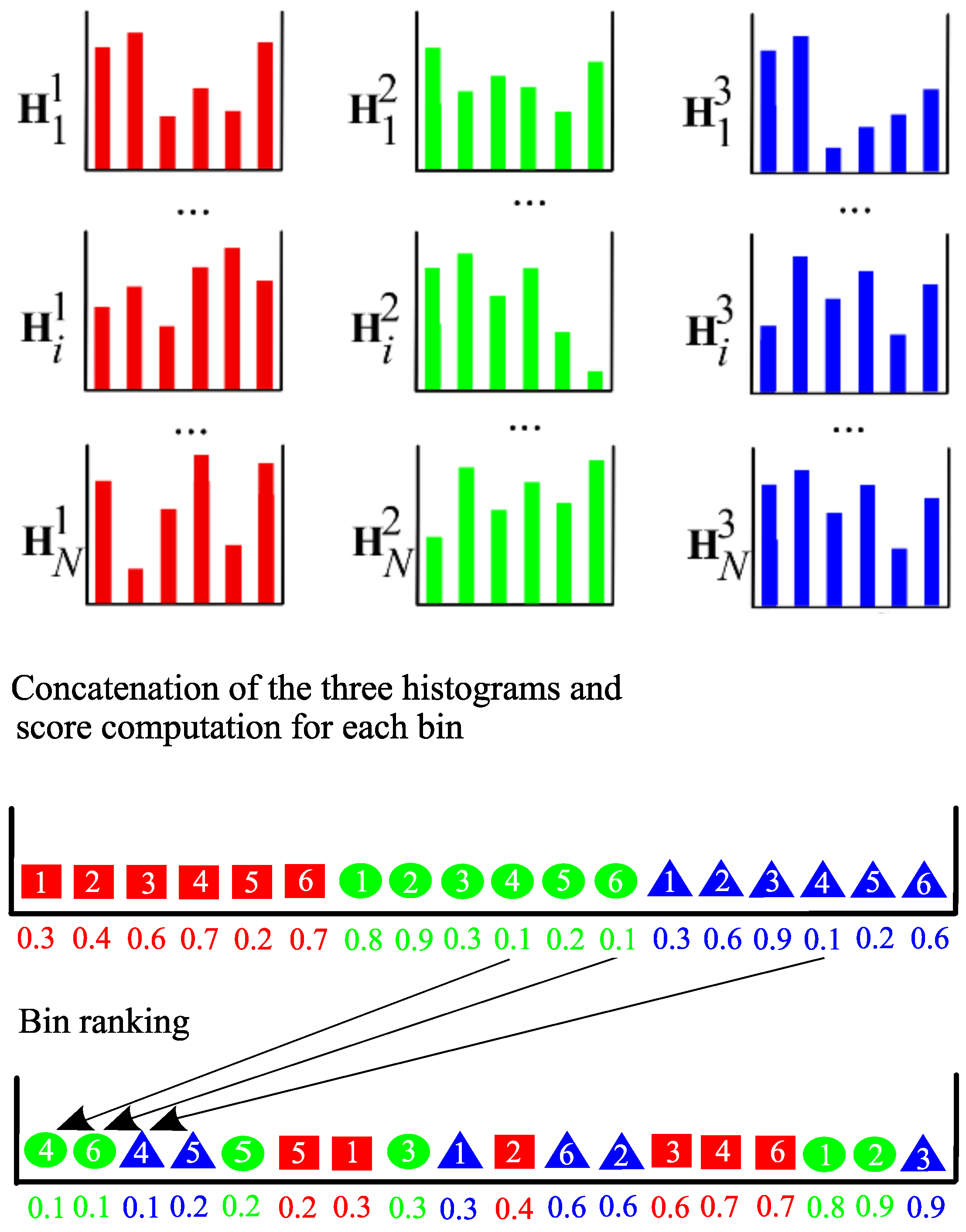
3.4. Sparse-MCSBS Approach
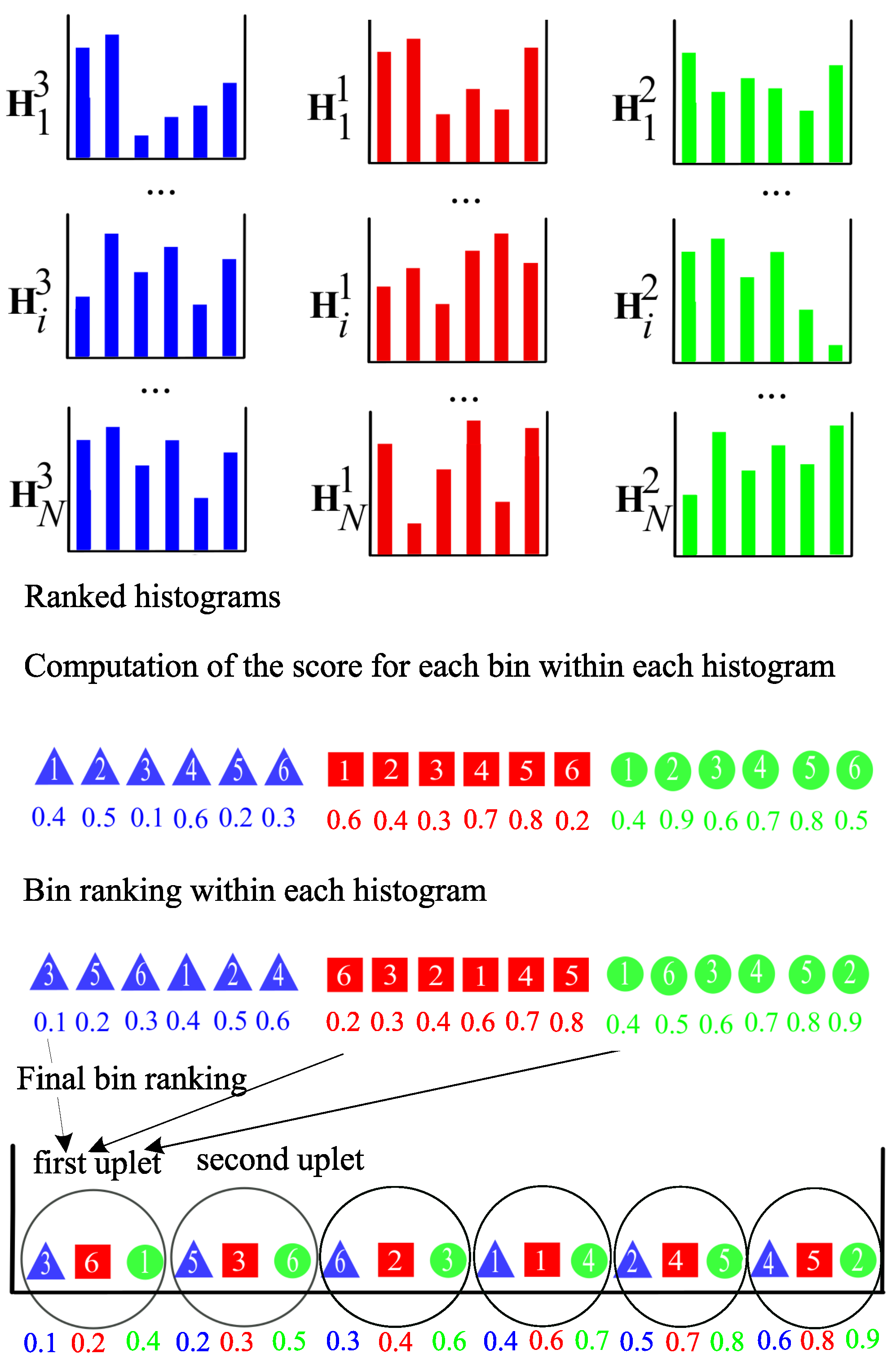
4. Combination of Bin and Histogram Selections
5. Experiments
5.1. Considered Color Texture Datasets
5.2. Performance Evaluation and Comparisons
5.3. Validation of the Proposed LBP-Based Feature Selection Strategies
5.4. Processing Times
6. Conclusions
- First we extended the multi color space domain with the LBP histogram selection approach using the SpASL-score to define the Sparse Multi Color Space Histogram Selection (Sparse-MCSHS).
- We then compared this approach with a new multi color space bin selection approach, also based on a sparse representation: the Sparse Multi Color Space Bin Selection (Sparse-MCSBS) approach.
- A combination of bin and histogram selections (the Sparse-MCSHBS approach) was finally developed and evaluated on several benchmark texture databases.
Author Contributions
Funding
Conflicts of Interest
References
- Mirmehdi, M.; Xie, X.; Suri, J. Handbook of Texture Analysis; Imperial College Press: London, UK, 2009. [Google Scholar]
- Liu, L.; Chen, J.; Fieguth, P.; Zhao, G.; Chellappa, R.; Pietikäinen, M. From BOW to CNN: Two decades of texture representation for texture classification. Int. J. Comput. Vis. 2019, 127, 74–109. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Harwood, D. A comparative study of texture measures with classification based on featured distributions. Pattern Recognit. 1996, 29, 51–59. [Google Scholar] [CrossRef]
- Pietikainen, M.; Hadid, A.; Zhao, G.; Ahonen, T. Computer Vision Using Local Binary Patterns; Springer: London, UK, 2011; Volume 40. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Chan, C.H.; Kittler, J.; Messer, K. Multispectral local binary pattern histogram for component-based color face verification. In Proceedings of the First IEEE International Conference on Biometrics: Theory, Applications, and Systems 2007, Crystal City, VA, USA, 27–29 September 2007; pp. 1–7. [Google Scholar]
- Zhao, D.; Lin, Z.; Tang, Z. Laplacian PCA and its applications. In Proceedings of the 11th IEEE International Conference on Computer Vision IEEE 2007, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Hussain, S.U.; Triggs, W. Feature sets and dimensionality reduction for visual object detection. In Proceedings of the British Machine Vision Conference, Wales, UK, 30 August–2 September 2010; BMVA Press: Guildford, UK, 2010; p. 112. [Google Scholar]
- Huang, D.; Shan, C.; Ardabilian, M.; Wang, Y.; Chen, L. Local binary patterns and its application to facial image analysis: a survey. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2011, 41, 765–781. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H. Feature selection for high-dimensional data: A fast correlation-based filter solution. In Proceedings of the 20th International Conference on International Conference on Machine Learning 2003, Washington, DC, USA, 21–24 August 2003; AAAI Press: Menlo Park, CA, USA, 2003; Volume 3, pp. 856–863. [Google Scholar]
- Smith, R.S.; Windeatt, T. Facial expression detection using filtered local binary pattern features with ECOC classifiers and platt scaling. In Proceedings of the First Workshop on Applications of Pattern Analysis 2010, Windsor, UK, 1–3 September 2010; pp. 111–118. [Google Scholar]
- Lahdenoja, O.; Laiho, M.; Paasio, A. Reducing the feature vector length in local binary pattern based face recognition. In Proceedings of the IEEE International Conference on Image Processing 2005, Genova, Italy, 14 September 2005; Volume 2, p. II-914. [Google Scholar]
- Maturana, D.; Mery, D.; Soto, A. Learning discriminative local binary patterns for face recognition. In Proceedings of the 2011 IEEE International Conference on Automatic Face & Gesture Recognition and Workshops (FG 2011), Santa Barbara, CA, USA, 21–25 March 2011; pp. 470–475. [Google Scholar]
- Liao, S.; Law, M.W.K.; Chung, A.C.S. Dominant Local Binary Patterns for texture classification. IEEE Trans. Image Process. 2009, 18, 1107–1118. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Zhao, G.; Pietikainen, M.; Xu, Z. Descriptor learning based on fisher separation criterion for texture classification. In Proceedings of the 10th Asian Conference on Computer Vision, Queenstown, New Zealand, 8–12 November 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 185–198. [Google Scholar]
- Porebski, A.; TruongHoang, V.; Vandenbroucke, N.; Hamad, D. Multi-color space local binary pattern-based feature selection for texture classification. J. Electron. Imaging 2018, 27, 1–15. [Google Scholar]
- Porebski, A.; Vandenbroucke, N.; Hamad, D. LBP histogram selection for supervised color texture classification. In Proceedings of the 20th IEEE International Conference on Image Processing 2013, Melbourne, Australia, 15–18 September 2013; pp. 3239–3243. [Google Scholar]
- Kalakech, M.; Porebski, A.; Vandenbroucke, N.; Hamad, D. A new LBP histogram selection score for color texture classification. In Proceedings of the 5th IEEE International Conference on Image Processing Theory, Tools and Applications, Orleans, France, 10–13 November 2015; pp. 242–247. [Google Scholar]
- Kalakech, M.; Porebski, A.; Vandenbroucke, N.; Hamad, D. Unsupervised Local Binary Pattern histogram selection scores for color texture classification. J. Imaging 2018, 4, 112. [Google Scholar] [CrossRef]
- Moujahid, A.; Abanda, A.; Dornaika, F. Feature extraction using block-based Local Binary Pattern for face recognition. Proc. Intell. Robot. Comput. Vis. XXXIII Alg. Tech. 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- Hoang, V.T.; Porebski, A.; Vandenbroucke, N.; Hamad, D. LBP histogram selection based on sparse representation for color texture classification. In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications 2017, Porto, Portugal, 27 February–1 March 2017; Volume 4, pp. 476–483. [Google Scholar]
- Liu, M.; Zhang, D. Sparsity score: a novel graph-preserving feature selection method. Int. J. Pattern Recognit. Artif. Intell. 2014, 28, 1450009. [Google Scholar] [CrossRef]
- Liu, L.; Fieguth, P.; Guo, Y.; Wang, X.; Pietikäinen, M. Local binary features for texture classification: Taxonomy and experimental study. Pattern Recognit. 2017, 62, 136–160. [Google Scholar] [CrossRef]
- Asada, N.; Matsuyama, T. Color image analysis by varying camera aperture. In Proceedings of the 11th International Conference on Pattern Recognitio, Computer Vision and Applications 1992, The Hague, The Netherlands, 30 August–3 September 1992; pp. 466–469. [Google Scholar]
- Drimbarean, A.; Whelan, P.F. Experiments in colour texture analysis. Pattern Recognit. Lett. 2001, 22, 1161–1167. [Google Scholar] [CrossRef]
- Gonzalez-Rufino, E.; Carrion, P.; Cernadas, E.; Fernandez-Delgado, M.; Dominguez-Petit, R. Exhaustive comparison of colour texture features and classification methods to discriminate cells categories in histological images of fish ovary. Pattern Recognit. 2013, 46, 2391–2407. [Google Scholar] [CrossRef]
- Kandaswamy, U.; Schuckers, S.A.; Adjeroh, D. Comparison of texture analysis schemes under nonideal conditions. IEEE Trans. Image Process. 2011, 20, 2260–2275. [Google Scholar] [CrossRef]
- Palm, C.; Lehmann, T.M. Classification of color textures by Gabor filtering. Mach. Graph. Vis. Int. J. 2002, 11, 195–219. [Google Scholar]
- Cernadas, E.; Fernandez-Delgado, M.; Gonzalez-Rufino, E.; Carrion, P. Influence of normalization and color space to color texture classification. Pattern Recognit. 2017, 61, 120–138. [Google Scholar] [CrossRef]
- Khan, F.S.; Anwer, R.M.; Van de Weijer, J.; Felsberg, M.; Laaksonen, J. Compact color-texture description for texture classification. Pattern Recognit. Lett. 2015, 51, 16–22. [Google Scholar] [CrossRef]
- Maenpaa, T.; Pietikainen, M. Classification with color and texture: jointly or separately? Pattern Recognit. 2004, 37, 1629–1640. [Google Scholar] [CrossRef]
- Ning, J.; Zhang, L.; Zhang, D.; Wu, C. Robust object tracking using joint color-texture histogram. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 1245–1263. [Google Scholar] [CrossRef]
- Cusano, C.; Napoletano, P.; Schettini, R. Combining local binary patterns and local color contrast for texture classification under varying illumination. J. Opt. Soc. Am. A 2014, 31, 1453. [Google Scholar] [CrossRef]
- Banerji, S.; Verma, A.; Liu, C. LBP and color descriptors for image classification. In Cross Disciplinary Biometric Systems; Springer: Berlin/Heidelberg, Germany, 2012; pp. 205–225. [Google Scholar]
- Choi, J.; Plataniotis, K.N.; Ro, Y.M. Using colour local binary pattern features for face recognition. In Proceedings of the 17th IEEE International Conference on Image Processing 2010, Hong Kong, China, 26–29 September 2010; pp. 4541–4544. [Google Scholar]
- Han, G.; Zhao, C. A scene images classification method based on local binary patterns and nearest-neighbor classifier. In Proceedings of the Eighth IEEE International Conference on Intelligent Systems Design and Applications, Kaohsiung, Taiwan, 26–28 November 2008; pp. 100–104. [Google Scholar]
- Pietikainen, M.; Maenpaa, T.; Viertola, J. Color texture classification with color histograms and local binary patterns. In Workshop on Texture Analysis in Machine Vision 2002; Computer Science: Oulu, Finland, 2002; pp. 109–112. [Google Scholar]
- Zhu, C.; Bichot, C.E.; Chen, L. Image region description using orthogonal combination of local binary patterns enhanced with color information. Pattern Recognit. 2013, 46, 1949–1963. [Google Scholar] [CrossRef]
- Chelali, F.Z.; Djeradi, A. CSLBP and OCLBP local descriptors for speaker identification from video sequences. In Proceedings of the IEEE International Conference on Complex Systems 2015, Marrakech, Morocco, 23–25 November 2015; pp. 1–7. [Google Scholar]
- Porebski, A.; Vandenbroucke, N.; Hamad, D. A fast embedded selection approach for color texture classification using degraded LBP. In Proceedings of the IEEE International Conference on Image Processing Theory, Tools and Applications 2015, Orleans, France, 10–13 November 2015; pp. 254–259. [Google Scholar]
- Lee, S.H.; Choi, J.Y.; Ro, Y.M.; Plataniotis, K.N. Local color vector binary patterns from multichannel face images for face recognition. IEEE Trans. Image Process. 2012, 21, 2347–2353. [Google Scholar] [CrossRef] [PubMed]
- Porebski, A.; Vandenbroucke, N.; Macaire, L. Haralick feature extraction from LBP images for color texture classification. In Proceedings of the IEEE International Conference on Image Processing Theory, Tools and Applications 2008, Sousse, Tunisia, 23–26 November 2008; pp. 1–8. [Google Scholar]
- Ledoux, A.; Losson, O.; Macaire, L. Color local binary patterns: compact descriptors for texture classification. J. Electron. Imaging 2016, 25, 061404. [Google Scholar] [CrossRef]
- Bihan, N.L.; Sangwine, S.J. Quaternion principal component analysis of color images. In Proceedings of the IEEE International Conference on Image Processing 2003, Barcelona, Spain, 14–17 September 2003; Volume 1, p. I-809. [Google Scholar]
- Chahla, C.; Snoussi, H.; Abdallah, F.; Dornaika, F. Discriminant quaternion local binary pattern embedding for person re-identification through prototype formation and color categorization. Eng. Appl. Artif. Intell. 2017, 58, 27–33. [Google Scholar] [CrossRef]
- Lan, R.; Zhou, Y.; Tang, Y.Y.; Chen, C.P. Person reidentification using quaternionic local binary pattern. In Proceedings of the IEEE International Conference on Multimedia and Expo 2014, Chengdu, China, 14–18 July 2014; pp. 1–6. [Google Scholar]
- Lan, R.; Lu, H.; Zhou, Y.; Liu, Z.; Luo, X. An LBP encoding scheme jointly using quaternionic representation and angular information. Neural Comput. Appl. 2019, 32, 4317–4323. [Google Scholar] [CrossRef]
- Lan, R.; Zhou, Y. Quaternion-Michelson descriptor for color image classification. IEEE Trans. Image Process. 2016, 25, 5281–5292. [Google Scholar] [CrossRef]
- Alata, O.; Quintard, L. Is there a best color space for color image characterization or representation based on Multivariate Gaussian Mixture Model? Comput. Vis. Image Underst. 2009, 113, 867–877. [Google Scholar] [CrossRef]
- Bello-Cerezo, R.; Bianconi, F.; Fernandez, A.; Gonzalez, E.; DiMaria, F. Experimental comparison of color spaces for material classification. J. Electron. Imaging 2016, 25, 061406. [Google Scholar] [CrossRef]
- Chaves-Gonzalez, J.M.; Vega-Rodriguez, M.A.; Gomez-Pulido, J.A.; Sanchez-Perez, J.M. Detecting skin in face recognition systems: A colour spaces study. Digit. Signal Process. 2010, 20, 806–823. [Google Scholar] [CrossRef]
- Porebski, A.; Vandenbroucke, N.; Macaire, L.; Hamad, D. A new benchmark image test suite for evaluating colour texture classification schemes. Multimed. Tools Appl. 2014, 70, 543–556. [Google Scholar] [CrossRef]
- Charrier, C.; Lebrun, G.; Lezoray, O. Evidential segmentation of microscopic color images with pixel classification posterior probabilities. J. Multimed. 2007, 2, 18607811. [Google Scholar] [CrossRef]
- Chindaro, S.; Sirlantzis, K.; Deravi, F. Texture classification system using colour space fusion. Electron. Lett. 2005, 41, 589–590. [Google Scholar] [CrossRef]
- Chindaro, S.; Sirlantzis, K.; Fairhurst, M.C. ICA-based multi-colour space texture classification system. Electron. Lett. 2006, 42, 1208–1209. [Google Scholar] [CrossRef]
- Mignotte, M. A de-texturing and spatially constrained K-means approach for image segmentation. Pattern Recognit. Lett. 2011, 32, 359–367. [Google Scholar] [CrossRef]
- Busin, L.; Vandenbroucke, N.; Macaire, L. Color spaces and image segmentation. In Advances in Imaging and Electron Physics; Elsevier: Amsterdam, The Netherlands, 2009; Volume 151, pp. 65–168. [Google Scholar]
- Laguzet, F.; Romero, A.; Gouiffès, M.; Lacassagne, L.; Etiemble, D. Color tracking with contextual switching: Real-time implementation on CPU. J. -Real-Time Image Process. 2015, 10, 403–422. [Google Scholar] [CrossRef]
- Stern, H.; Efros, B. Adaptive color space switching for tracking under varying illumination. Image Vis. Comput. 2005, 23, 353–364. [Google Scholar] [CrossRef]
- Vandenbroucke, N.; Busin, L.; Macaire, L. Unsupervised color-image segmentation by multicolor space iterative pixel classification. J. Electron. Imaging 2015, 24, 023032. [Google Scholar] [CrossRef]
- Cointault, F.; Guerin, D.; Guillemin, J.P.; Chopinet, B. In field Triticum aestivum ear counting using color texture image analysis. N. Z. J. Crop. Hortic. Sci. 2008, 36, 117–130. [Google Scholar] [CrossRef]
- Nanni, L.; Lumini, A. Fusion of color spaces for ear authentication. Pattern Recognit. 2009, 42, 1906–1913. [Google Scholar] [CrossRef]
- Porebski, A.; Vandenbroucke, N.; Macaire, L. Supervised texture classification: color space or texture feature selection? Pattern Anal. Appl. 2013, 16, 1–18. [Google Scholar] [CrossRef]
- Vandenbroucke, N.; Macaire, L.; Postaire, J.G. Color image segmentation by pixel classification in an adapted hybrid color space. Application to soccer image analysis. Comput. Vis. Image Underst. 2003, 90, 190–216. [Google Scholar] [CrossRef]
- Qazi, I.U.H.; Alata, O.; Burie, J.C.; Moussa, A.; Fernandez-Maloigne, C. Choice of a pertinent color space for color texture characterization using parametric spectral analysis. Pattern Recognit. 2011, 44, 16–31. [Google Scholar] [CrossRef]
- Dash, M.; Liu, H. Feature selection for classification. Intell. Data Anal. 1997, 1, 131–156. [Google Scholar] [CrossRef]
- Liu, H.; Yu, L. Toward integrating feature selection algorithms for classification and clustering. IEEE Trans. Knowl. Data Eng. 2005, 17, 491–502. [Google Scholar]
- Tang, J.; Alelyani, S.; Liu, H. Feature Selection for Classification: A Review. In Data Classification: Algorithms and Applications; CRC Press: Cleveland, OH, USA, 2014; pp. 37–64. [Google Scholar]
- Ojala, T.; Maenpaa, T.; Pietikainen, M.; Viertola, J.; Kyllonen, J.; Huovinen, S. Outex—New framework for empirical evaluation of texture analysis algorithms. In Proceedings of the 16th International Conference on Pattern Recognition 2002, Quebec City, QC, Canada, 11–15 August 2002; Volume 1, pp. 701–706. [Google Scholar]
- Backes, A.R.; Casanova, D.; Bruno, O.M. Color texture analysis based on fractal descriptors. Pattern Recognit. 2012, 45, 1984–1992. [Google Scholar] [CrossRef]
- Bianconi, F.; Fernandez, A.; Gonzalez, E.; Saetta, S. Performance analysis of colour descriptors for parquet sorting. Expert Syst. Appl. 2013, 40, 1636–1644. [Google Scholar] [CrossRef]
- Bello-Cerezo, R.; Bianconi, F.; Di Maria, F.; Napoletano, P.; Smeraldi, F. Comparative Evaluation of Hand-Crafted Image Descriptors vs. Off-the-Shelf CNN-Based Features for Colour Texture Classification under Ideal and Realistic Conditions. Appl. Sci. 2019, 9, 738. [Google Scholar] [CrossRef]
- Lakmann, R. Barktex Benchmark Database of Color Textured Images. Koblenz-Landau University. 1998. Available online: ftp://ftphost.uni-koblenz.de/outgoing/vision/Lakmann/BarkTex (accessed on 23 June 2020).
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. IGoing deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2015, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Arvis, V.; Debain, C.; Berducat, M.; Benassi, A. Generalization of the cooccurrence matrix for colour images: application to colour texture classification. Image Anal. Stereol. 2004, 23, 63–72. [Google Scholar] [CrossRef]
- Alvarez, S.; Vanrell, M. Texton theory revisited: A bag-of-words approach to combine textons. Pattern Recognit. 2012, 45, 4312–4325. [Google Scholar] [CrossRef]
- Liu, P.; Guo, J.M.; Chamnongthai, K.; Prasetyo, H. Fusion of color histogram and LBP-based features for texture image retrieval and classification. Inf. Sci. 2017, 390, 95–111. [Google Scholar] [CrossRef]
- Cusano, C.; Napoletano, P.; Schettini, R. Illuminant invariant descriptors for color texture classification. In Computational Color Imaging; Springer: Berlin/Heidelberg, Germany, 2013; pp. 239–249. [Google Scholar]
- Mehta, R.; Egiazarian, K. Dominant Rotated Local Binary Patterns (DRLBP) for texture classification. Pattern Recognit. Lett. 2016, 71, 16–22. [Google Scholar] [CrossRef]
- Guo, J.M.; Prasetyo, H.; Lee, H.; Yao, C. Image retrieval using indexed histogram of Void-and-Cluster Block Truncation Coding. Signal Process. 2016, 123, 143–156. [Google Scholar] [CrossRef]
- Aptoula, E.; Lefèvre, S. On morphological color texture characterization. In Proceedings of the International Symposium on Mathematical Morphology 2007, Rio de Janeiro, Brazil, 10–13 October 2007; pp. 153–164. [Google Scholar]
- Kabbai, L.; Abdellaoui, M.; Douik, A. Image classification by combining local and global features. Vis. Comput. 2019, 35, 679–693. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, D.; Zhang, D. A completed modeling of local binary pattern operator for texture classification. IEEE Trans. Image Process. 2010, 19, 1657–1663. [Google Scholar] [PubMed]
- Martà nez, R.A.; Richard, N.; Fernandez, C. Alternative to colour feature classification using colour contrast ocurrence matrix. In The International Conference on Quality Control by Artificial Vision; International Society for Optics and Photonics: Le Creusot, France, 2015; p. 953405. [Google Scholar]
- Fernandez, A.; Alvarez, M.X.; Bianconi, F. Texture description through histograms of equivalent patterns. J. Math. Imaging Vis. 2013, 45, 76–102. [Google Scholar] [CrossRef]
- Hammouche, K.; Losson, O.; Macaire, L. Fuzzy aura matrices for texture classification. Pattern Recognit. 2015, 53, 212–228. [Google Scholar] [CrossRef]
- Naresh, Y.G.; Nagendraswamy, H.S. Classification of medicinal plants: An approach using modified LBP with symbolic representation. Neurocomputing 2016, 173, 1789–1797. [Google Scholar] [CrossRef]
- Gonçalves, W.N.; da Silva, N.R.; da Fontoura Costa, L.; Bruno, O.M. Texture recognition based on diffusion in networks. Inf. Sci. 2016, 364–365, 51–71. [Google Scholar] [CrossRef]
- Wang, J.; Fan, Y.; Li, N. Combining fine texture and coarse color features for color texture classification. J. Electron. Imaging 2017, 26, 1. [Google Scholar]
- Ratajczak, R.; Bertrand, S.; Crispim-Junior, C.; Tougne, L. Efficient bark recognition in the wild. In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP’19) 2019, Prague, Czech Republic, 25–27 February 2019. [Google Scholar]
- Alimoussa, M.; Vandenbroucke, N.; Porebski, A.; Oulad Haj Thami, R.; El Fkihi, S.; Hamad, D. Compact color texture representation by feature selection in multiple color spaces. In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP’19), Prague, Czech Republic, 25–27 February 2019. [Google Scholar]
- Dernoncourt, D.; Hanczar, B.; Zucker, J.-D. Analysis of feature selection stability on high dimension and small sample data. Comput. Stat. Data Anal. 2014, 71, 681–693. [Google Scholar] [CrossRef]
| Dataset Name | Image Size | Nb of Classes | Nb of Training Images | Nb of Testing Images |
|---|---|---|---|---|
| Outex | 128 × 128 | 68 | 680 | 680 |
| USPTex | 128 × 128 | 191 | 1146 | 1146 |
| STex | 128 × 128 | 476 | 3808 | 3808 |
| Parquet | to | 38 | 114 | 114 |
| NewBarktex | 64 × 64 | 6 | 816 | 816 |
| Color Spaces | Without Selection | Bin Selection | Histogram Selection | Combination of Both | ||||
|---|---|---|---|---|---|---|---|---|
| RGB | 73.2 | 2304 | 79.0 | 1109 | 81.3 | 1024 | 83.7 | 1016 |
| rgb | 74.4 | 2304 | 74.4 | 2242 | 77.1 | 768 | 77.9 | 1530 |
| 71.7 | 2304 | 74.4 | 1198 | 79.5 | 1792 | 80.5 | 1764 | |
| HSV | 70.5 | 2304 | 79.5 | 500 | 81.0 | 768 | 81.0 | 768 |
| 72.1 | 2304 | 77.5 | 836 | 80.6 | 1536 | 82.1 | 1524 | |
| HLS | 70.1 | 2304 | 78.0 | 319 | 81.0 | 768 | 81.0 | 768 |
| I-HLS | 72.1 | 2304 | 72.7 | 1813 | 78.8 | 512 | 79.1 | 762 |
| HSI | 71.7 | 2304 | 79.2 | 533 | 79.8 | 768 | 79.8 | 768 |
| 71.6 | 2304 | 77.0 | 370 | 79.3 | 1792 | 82.5 | 1778 | |
| Average in single space | 71.9 | 2304 | 76.9 | 991 | 79.8 | 1081 | 80.8 | 1186 |
| Multiple color spaces | 20,736 | 754 | 9472 | 11,985 | ||||
| Features | Color Space | Accuracy |
|---|---|---|
| RSCCM + MCSFS [52] | 28 color spaces | 96.6 |
| EOCLBP + Sparse-MCSHBS | 9 color spaces | 95.7 |
| EOCLBP + Sparse-MCSHS | 9 color spaces | 95.6 |
| EOCLBP + MCSHS-ICS [16] | 9 color spaces | 95.6 |
| 3D Color histogram [31] | HSV | 95.4 |
| EOCLBP + Sparse-MCSBS | 9 color spaces | 95.2 |
| 3D Color histogram [65] | I-HLS | 94.5 |
| Haralick features [77] | RGB | 94.1 |
| EOCLBP (with selection method) [18] | RGB | 93.4 |
| EOCLBP (with selection method) [17] | RGB | 92.9 |
| EOCLBP + MCSBS-Guo [16] | 9 color spaces | 92.9 |
| RSCCM (with selection method) [63] | HLS | 92.5 |
| Between color component LBP histogram [31] | RGB | 92.5 |
| Quaternion-Michelson Descriptor [48] | RGB | 91.3 |
| Texton [78] | RGB | 90.3 |
| Combine color and LBP-based features [79] | RGB | 90.2 |
| Intensity-Color Contrast Descriptor [80] | RGB | 89.3 |
| DRLBP [81] | RGB | 89.0 |
| Autoregressive models and 3D color histogram [65] | I-HLS | 88.9 |
| Halftoning Local Derivative Pattern and Color Histogram [82] | RGB | 88.2 |
| Autoregressive models [83] | 88.0 | |
| Within color component LBP histogram [31] | RGB | 87.8 |
| CWEUL LTP [84] | RGB | 87.4 |
| Mix color order LBP histogram [43] | RGB | 87.1 |
| Color angles LBP [41] | RGB | 86.2 |
| LBP and local color contrast [33] | RGB | 85.3 |
| CLBP (Completed LBP) [85] | RGB | 84.4 |
| Color contrast occurrence matrix [86] | RGB | 82.6 |
| Soft color descriptors [50] | HSV | 81.4 |
| Histograms of equivalent patterns [87] | RGB | 80.9 |
| Fuzzy aura matrices [88] | RGB | 80.2 |
| Pretrained AlexNet convolutional neural network | RGB | 78.5 |
| Pretrained GoogleNet convolutional neural network | RGB | 77.9 |
| Modified LBP [89] | RGB | 67.3 |
| Features | Color Space | Accuracy |
|---|---|---|
| EOCLBP + Sparse-MCSHBS | 9 color spaces | 98.1 |
| EOCLBP + MCSHS-ASL [16] | 9 color spaces | 97.6 |
| EOCLBP + Sparse-MCSHS | 9 color spaces | 97.4 |
| EOCLBP + MCSBS-Guo [16] | 9 color spaces | 97.3 |
| EOCLBP + Sparse-MCSBS | 9 color spaces | 94.8 |
| Quaternion-Michelson Descriptor [48] | RGB | 94.2 |
| Halftoning Local Derivative Pattern and Color Histogram [82] | RGB | 93.9 |
| Quaternionic local angular binary pattern [47] | RGB | 93.8 |
| Pretrained GoogleNet convolutional neural network | RGB | 92.2 |
| DRLBP [81] | RGB | 89.4 |
| Color angles [41] | RGB | 88.8 |
| Local multi-resolution patterns [90] | Luminance | 86.7 |
| Mix color order LBP histogram [43] | RGB | 84.2 |
| LBP and local color contrast [33] | RGB | 82.9 |
| Pretrained AlexNet convolutional neural network | RGB | 78.3 |
| CLBP [85] | RGB | 72.3 |
| Soft color descriptors [50] | 58.0 |
| Features | Color Space | Accuracy |
|---|---|---|
| EOCLBP + Sparse-MCSHBS | 9 color spaces | 98.1 |
| EOCLBP + Sparse-MCSHS | 9 color spaces | 96.7 |
| EOCLBP + MCSBS-Guo [16] | 9 color spaces | 96.7 |
| EOCLBP + MCSHS-ASL [16] | 9 color spaces | 96.1 |
| EOCLBP + Sparse-MCSBS | 9 color spaces | 94.7 |
| Pretrained GoogleNet convolutional neural network | RGB | 92.9 |
| Pretrained AlexNet convolutional neural network | RGB | 90.8 |
| DRLBP [81] | RGB | 89.4 |
| Color contrast occurrence matrix [86] | RGB | 76.7 |
| Soft color descriptors [50] | 55.3 |
| Features | Color Space | Accuracy |
|---|---|---|
| Pretrained GoogleNet convolutional neural network | RGB | 92.9 |
| EOCLBP + Sparse-MCSHBS | 9 color spaces | 83.3 |
| EOCLBP + Sparse-MCSHS | 9 color spaces | 82.5 |
| EOCLBP + Sparse-MCSBS | 9 color spaces | 79.8 |
| EOCLBP + MCSBS-Guo [16] | 9 color spaces | 79.0 |
| EOCLBP + MCSHS-ICS [16] | 9 color spaces | 75.4 |
| EOCLBP (with selection method) [17] | RGB | 71.9 |
| Fisher separation criteria-based learning LBP [15] | RGB | 68.4 |
| Pretrained AlexNet convolutional neural network | RGB | 68.4 |
| Features | Color Space | Accuracy |
|---|---|---|
| Pretrained AlexNet convolutional neural network | RGB | 90.6 |
| EOCLBP + Sparse-MCSHBS | 9 color spaces | 88.4 |
| EOCLBP + MCSHS-ICS [16] | 9 color spaces | 88.0 |
| EOCLBP + MCSBS-Guo [16] | 9 color spaces | 87.8 |
| EOCLBP + Sparse-MCSHS | 9 color spaces | 87.3 |
| Completed local binary count [91] | RGB | 84.3 |
| EOCLBP + Sparse-MCSBS | 9 color spaces | 83.6 |
| Pretrained GoogleNet convolutional neural network | RGB | 82.8 |
| EOCLBP (with selection method) [17] | RGB | 81.4 |
| EOCLBP (with selection method) [18] | RGB | 81.4 |
| LBP and local color contrast [41] | RGB | 80.2 |
| Between color component LBP [37] | RGB | 79.9 |
| Light combination of LBP [92] | HSV | 78.8 |
| Mix color order LBP histogram [43] | RGB | 77.7 |
| CWEUL LTP [84] | RGB | 76.6 |
| RSCCM + MCSFS [52] | 20 color spaces | 75.9 |
| CLBP [85] | RGB | 72.8 |
| Color angles [33] | RGB | 71.0 |
| DRLBP [81] | RGB | 61.4 |
| Color histograms [31] | RGB | 58.6 |
| Approach | Relative Ranking | Average Accuracy | ||||
|---|---|---|---|---|---|---|
| Outex | USPTex | STex | Parquet | NewBarkTex | ||
| EOCLBP + Sparse-MCSHBS | 1 | 1 | 1 | 2 | 2 | 92.7 |
| EOCLBP + Sparse-MCSHS | 2 | 2 | 2 | 3 | 3 | 91.9 |
| EOCLBP + Sparse-MCSBS | 3 | 3 | 3 | 4 | 4 | 89.6 |
| Pretrained GoogleNet CNN | 5 | 4 | 4 | 1 | 5 | 87.7 |
| Pretrained AlexNet CNN | 4 | 5 | 5 | 5 | 1 | 81.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porebski, A.; Truong Hoang, V.; Vandenbroucke, N.; Hamad, D. Combination of LBP Bin and Histogram Selections for Color Texture Classification. J. Imaging 2020, 6, 53. https://doi.org/10.3390/jimaging6060053
Porebski A, Truong Hoang V, Vandenbroucke N, Hamad D. Combination of LBP Bin and Histogram Selections for Color Texture Classification. Journal of Imaging. 2020; 6(6):53. https://doi.org/10.3390/jimaging6060053
Chicago/Turabian StylePorebski, Alice, Vinh Truong Hoang, Nicolas Vandenbroucke, and Denis Hamad. 2020. "Combination of LBP Bin and Histogram Selections for Color Texture Classification" Journal of Imaging 6, no. 6: 53. https://doi.org/10.3390/jimaging6060053
APA StylePorebski, A., Truong Hoang, V., Vandenbroucke, N., & Hamad, D. (2020). Combination of LBP Bin and Histogram Selections for Color Texture Classification. Journal of Imaging, 6(6), 53. https://doi.org/10.3390/jimaging6060053






