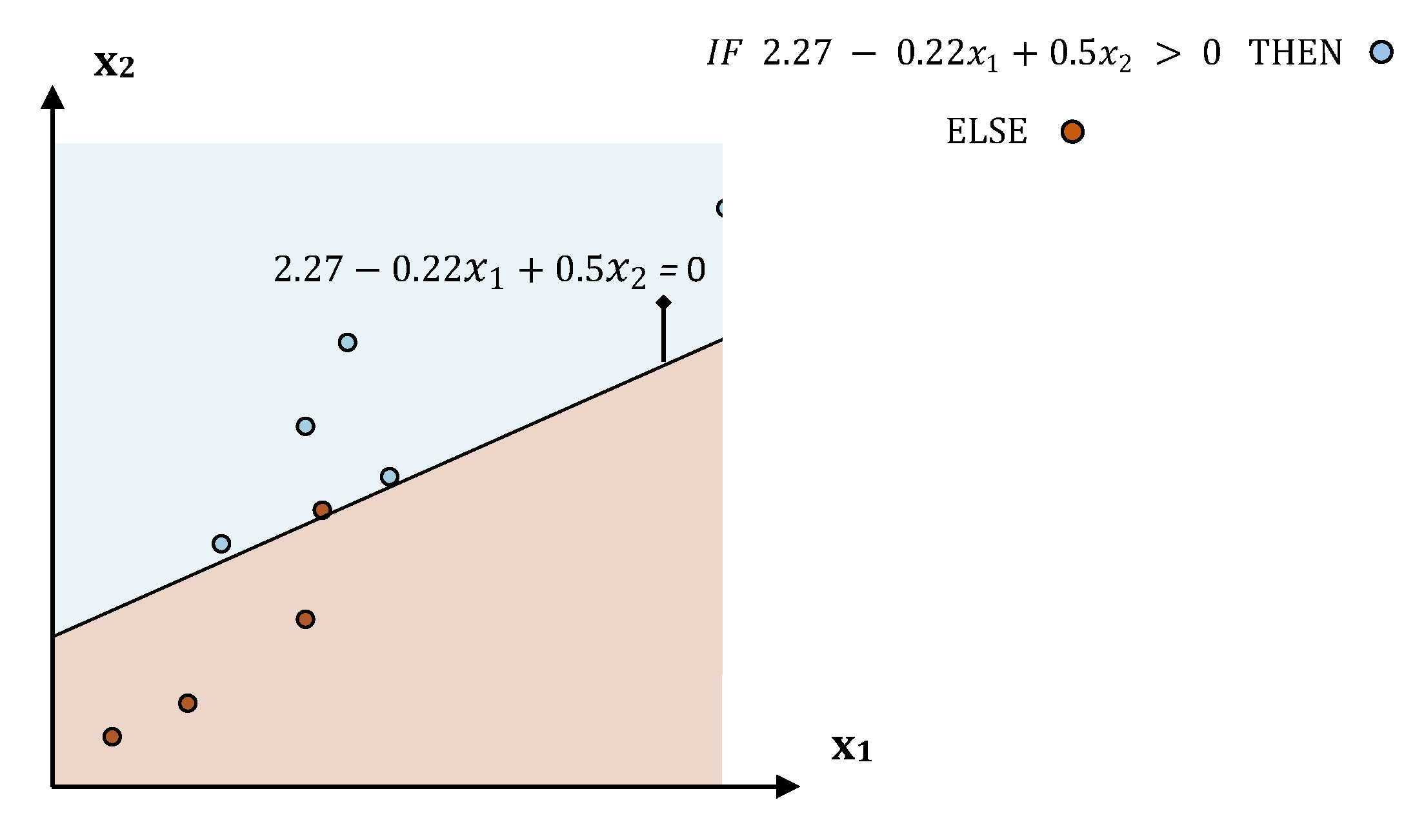1. Introduction
Image classification is a very popular machine learning domain in which Convolutional Neural Networks (CNNs) [
1] have been successfully applied on wide range of image classification problems. These networks are able to filter out noise and extract useful information from the initial images’ pixel representation and use it as input for the final prediction model. CNN-based models are able to achieve remarkable prediction performance although in general they need very large number of input instances. Nevertheless, this model’s great limitation and drawback is that it is almost totally unable to interpret and explain its predictions, since its inner workings and its prediction function is not transparent due to its high complexity mechanism [
2].
In recent days, interpretability/explainability in machine learning domain has become a significant issue, since much of real-world problems require reasoning and explanation on predictions, while it is also essential to understand the model’s prediction mechanism in order to trust it and make decisions on critical issues [
3,
4]. The European Union General Data Protection Regulation (GDPR) which was enacted in 2016 and took effect in 2018, demanded a “right to explanation” for decisions performed by automated and artificial intelligent algorithmic systems. This new regulation promotes to develop algorithmic frameworks which will ensure an explanation for every Machine Learning decision while this demand will be legally mandated by the GDPR. The term right to explanation [
5] refers to the explanation that an algorithm must give, especially on decisions which affect human individual rights and critical issues. For example, a person who applies for a bank loan and was not approved may ask for an explanation which could be “The bank loan was rejected because you are underage. You need to be over 18 years old in order to apply.” It is obvious that there could be plenty of other reasons for his rejection, however the explanation has to be short and comprehensive [
6], presenting the most significant reason for his rejection, while it would be very helpful if the explanation provides also a fast solution for this individual in order to counter the rejection decision.
Explainability can also assist in building efficient machine learning models and secures that they are reliable in practice [
6]. For example, let assume that a model classified an image as a “cat” followed by explanations like “because there is a tree in image”. In this scenario, the model associated the whole image as a cat based on a tree which is indeed pictured in the image, but the explanation is obviously based on an incorrect feature (the tree). Thus, explainability revealed some hidden weaknesses that this model may have even if its testing prediction accuracy is accidentally very high. An explainable model can reveal the significant features which affect a prediction. Subsequently, humans can then determine if these features are actually correct, based on their domain knowledge, in order to make the model reliable and generalize well in every new instance in real world applications. For example, a possible “correct” feature which would prove that the model makes reliable predictions could be “this image is classified as a cat because the model identified sharp contours” this explanation would reflect that the model associated the cat with its nails which is probably a unique and correct feature that represents a cat.
Medical applications such as cancer prediction, is another example where explainability is essential since it is considered a critical and a “life or death” prediction problem, in which high forecasting accuracy and interpretation are two equally essential and significant tasks to achieve. However, this is generally a very difficult task, since there is a “trade-off” between interpretation and accuracy [
4]. Imaging (Radiology) tests for cancer is a medical area in which radiologists try to identify signs of cancer utilizing imaging tests, sending forms of energy such as magnetic fields, in order to take pictures of the inner human body. A radiologist is a doctor who specializes in imaging analysis techniques and is authorized to interpret images of these tests and write a report of his/her findings. This report finally is sent to the patient’s doctor while a copy of this report is sent to the patient records. CNNs have proved that they are almost as accurate as these specialists on predicting cancer from images. However, reasoning and explanation of their predictions is one of their greatest limitations in contrast to the radiologists which are able (and obligated) to analyze, interpret and explain their decision based on the features they managed to identify in an image. For example, an explanation/reasoning of a diagnosis/prediction of a case image could probably be: “This image probably is classified as cancer because the tumor area is large, its texture color is white followed by high density and irregular shape.”
Developing an accurate and interpretable model at the same time is a very challenging task as typically there is a trade-off between interpretation and accuracy [
7]. High accuracy often requires developing complicated black box models while interpretation requires developing simple and less complicated models, which are often less accurate. Deep neural networks are some examples of powerful, in terms of accuracy, prediction models but they are totally non-interpretable (black box models), while decision trees and logistic regression are some classic examples of interpretable models (white box models) which are usually not as accurate. In general, interpretability methods can be divided into two main categories, intrinsic and post-hoc [
6]. Intrinsic methods are considered the prediction models which are by nature interpretable, such as all the white box models like decision trees and linear models, while post-hoc methods utilize secondary models in order to explain the predictions of a black box model.
Local Interpretable Model-agnostic Explanations (LIME) [
8], One-variable-at-a-Time approach [
9], counterfactual explanations [
10] and SHapley Additive exPlanations (SHAP) [
6] are some state of the art examples of post-hoc interpretable models. Grad-CAM [
11] is a very popular post-hoc explanation technique applied on CNNs models making them more transparent. This algorithm aims to interpret any CNN model by “returning” the most significant pixels which contributed to the final prediction via a visual heatmap of each image. Nevertheless, explainability properties such as fidelity, stability, trust and representativeness of explanations (some essential properties which define an explanation as “good explanation”) constitute some of the main issues and problems of post hoc methods in contrast to intrinsic models. Our proposed prediction framework is intrinsic model able to provide high quality explanations (good explanations).
In a recent work, Pintelas et al. [
7], proposed an intrinsic interpretable Grey-Box ensemble model exploiting black-box model’s accuracy and white-box model’s explainability. The main objective was the enlargement of a small initial labeled dataset via a large pool of unlabeled data adding black-box’s most confident predictions. Then, a decision tree model (intrinsic interpretable model) was trained with the final augmented dataset while the prediction and explanation were performed by the white box model. However, one basic limitation is that the application of a decision tree classifier or any white box classifier on raw image data without a robust feature extraction framework would be totally inefficient since it would require an enormous amount of images in order to build an accurate and robust image classification model. In addition, the interpretation of this tree would be too complicated since the explanations would rely on individual pixels. Our proposed prediction framework would be able to provide stable/robust and accurate predictions followed by explanations based on meaningful high-level features extracted from every image.
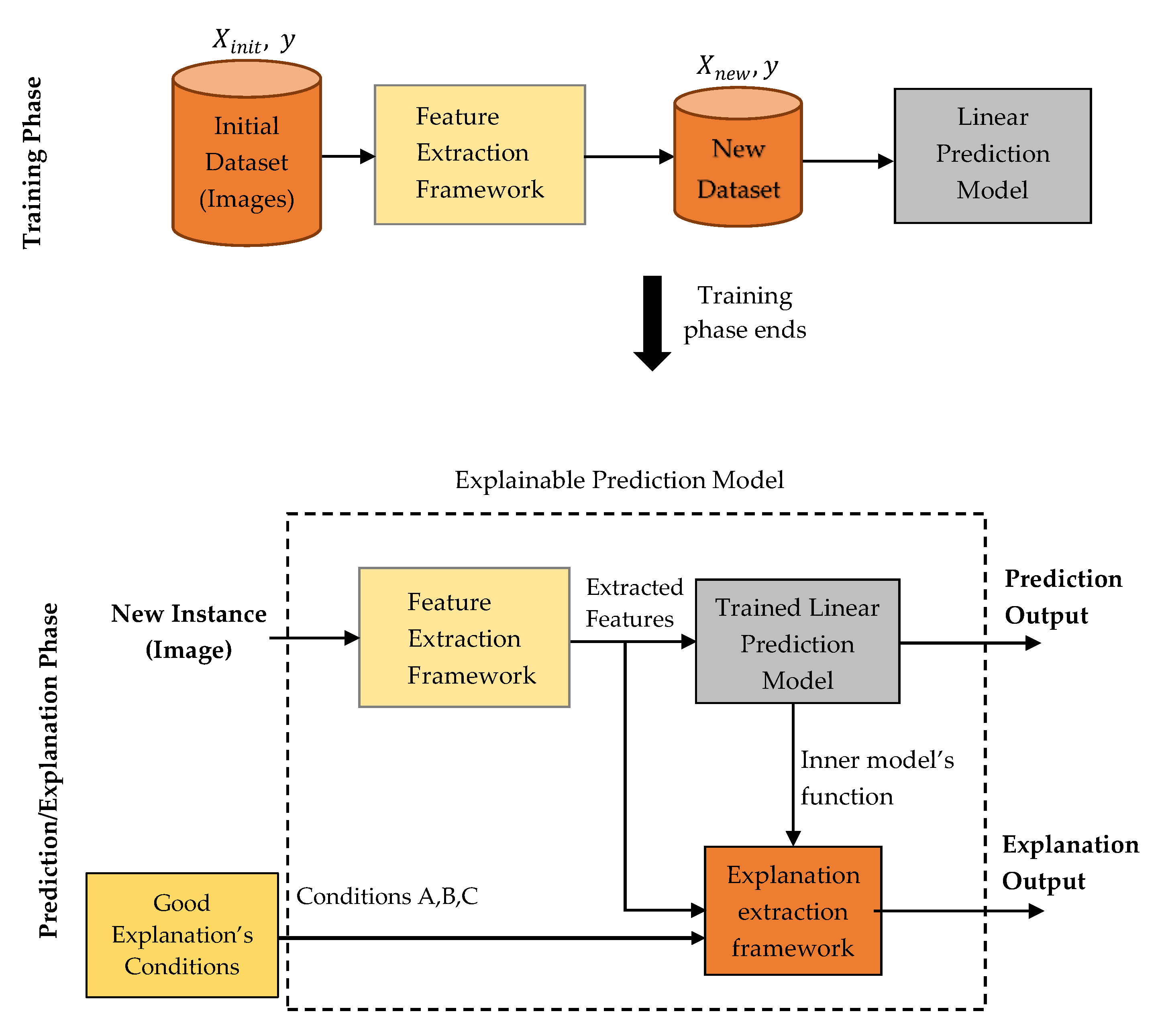
This paper proposes an explainable machine learning prediction framework for image classification problems. In short, it is composed by a feature extraction and an explanation extraction framework followed by some proposed “conditions” which aim to validate the quality of any model’s predictions explanations for every application domain. The feature extraction framework is based on traditional image processing tools and provides a transparent and well-defined high level feature representation input, meaningful in human terms, while these features will be used for training a simple white box model. These extracted features aim to describe specific properties found in an image based on texture and contour analysis. The feature explanation framework aims to provide good explanations for every individual prediction by exploiting the white box model’s inner function with respect to the extracted features and our defined conditions. It is worth mentioning that the proposed framework is general and can potentially be applied to any image classification task. However, this work aims to apply this framework on tasks where interpretation and explainability are vitally and significantly prominent. To this end, it was chosen to perform a case study application on Magnetic Resonance Imaging (MRI) for brain cancer prediction. In particular, we aim to diagnose and interpret glioma, which is a very dangerous type of tumor, being in most cases a malignant cancer [
12], versus other tumor types, which are most of the times benign. Some examples of extracted meta-features for this case study are tumor’s size, tumor’s shape, texture irregularity level and tumor’s color.
The contribution of this work lies on the development of an accurate and robust prediction framework, being also intrinsic interpretable, able to make high quality explanations and make reasoning and justification on its predictions for image classification tasks. For this task, it is proposed a feature extraction framework which creates transparent and meaningful high level features from images and an explanation extraction framework which exploits a linear model’s inner function in order to make good explanations. Furthermore, we propose and define some conditions which aim to validate the quality of any model’s explanations on every application domain. In particular, if one model verifies all these conditions, then its predictions’ explanations can be considered as good. Finally, 3 types of presentation forms are also proposed for the prediction’s explanations with respect to the target audience and the application domain.
The remainder of this paper is organized as follows.
Section 2 presents in a very detailed way our proposed research framework while
Section 3 presents our experimental results, regarding the prediction accuracy and model interpretation/explanation. In
Section 4, a brief discussion regarding our proposed framework is conducted. Finally,
Section 5 sketches our conclusive remarks and possible future research.
3. Results
In this section, we present our experimental results regarding to the proposed explainable prediction framework for image classification tasks, applying it on glioma prediction from MRI as a case study application scenario. In our experiments, all utilized machine learning models (
Table 5) were trained using the new data representation which was created via our feature extraction framework and validated using a 10-fold cross-validation using the performance metrics: Accuracy
(),
-score (
, Sensitivity
(), Specificity
(), Positive Predictive Value
(), Negative Predictive Value
() and the Area Under the Curve (
) [
21]. It was considered not essential to conduct experiments based on the initial dataset (raw images) since such experiments were already performed by various CNN models based on transfer learning approach on previous works [
22,
23] managing to achieve around to 99% accuracy score. It is worth mentioning that since this work proposes an explainable intrinsic prediction model, obviously our goal is not to surpass the performance of these powerful black box models but manage to achieve a decent performance score with powerful explainability.
Our experiments were performed via two phases. In the first phase, various white box (WB) models were compared while in the second phase, the best identified WB model was compared with various black box (BB) models.
Table 5 depicts all the utilized machine learning models and their basic tuning parameters. All Decision Trees (DT) models were evaluated based on their
parameter. A high depth leads to a complex decision function while a low depth leads to a simple function but probably to biased predictions. The basic version of decision tree algorithm used in our experiments was CART algorithm since it was identified to exhibit superior performance comparing to other decision tree algorithms [
24]. On Naive Bayes (NB) [
20] classifier, no parameters were specified.
All Neural Networks (NNs) are fully connected networks composed by two hidden layers each and
refers to the number of Neurons in Layer
. The basic tuning parameter of a Logistic Regression (LR) constitutes the regularization parameter
, just like in Support Vector Machine (SVM) [
25], where small values specify stronger regularization. All SVM models were composed by a radial basis function kernel. We have to mention that all these models’ parameters were identified via exhaustive and thorough experiments in order to incur the best performance results. Finally, the k-NN [
26] was implemented based on the Euclidean distance metric, while the basic tuning parameter is the number of neighbors
.
3.1. Experimental Results
Table 6 presents the performance comparison of WB models regarding the predefined performance metrics. LR
1 exhibited the best classification score (94%) while NB exhibited the worst (77%).
Table 7 presents the performance comparison of the best identified WB model (LR
1) comparing to the BB models. LR
1 managed to be as accurate as the best identified BB models (NN
3 and SVM
2). This probably means that our feature extraction framework managed to filter out the noise and the complexity of the initial image representation. As a result, this framework creates a robust and simpler data representation that simple linear models can efficiently be applied on, while powerful BB models like NN are becoming unnecessary.
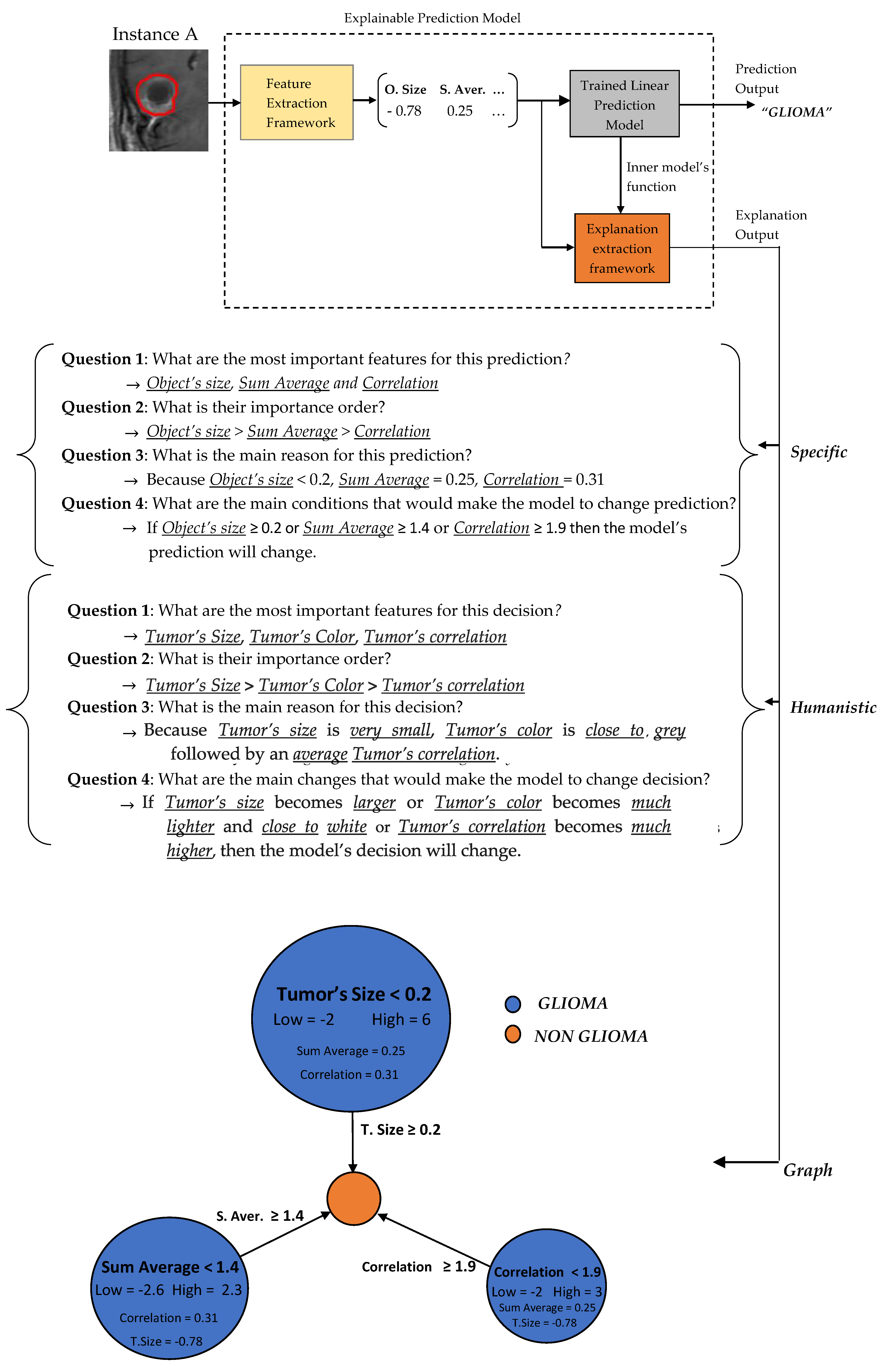
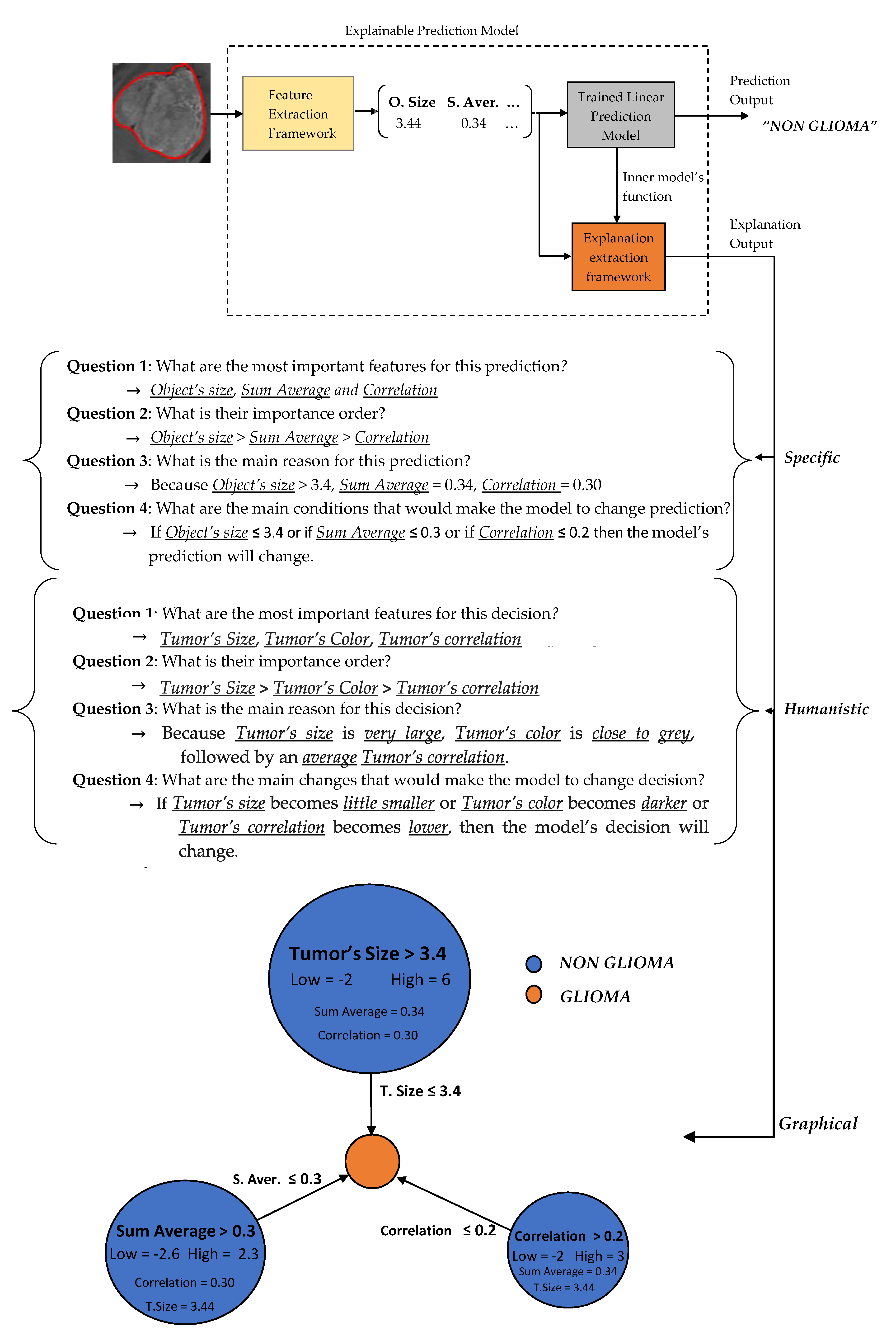
3.2. Predictions Explanations
In the sequel, our framework’s explanation output is presented for some case study predictions. The final prediction model is the LR
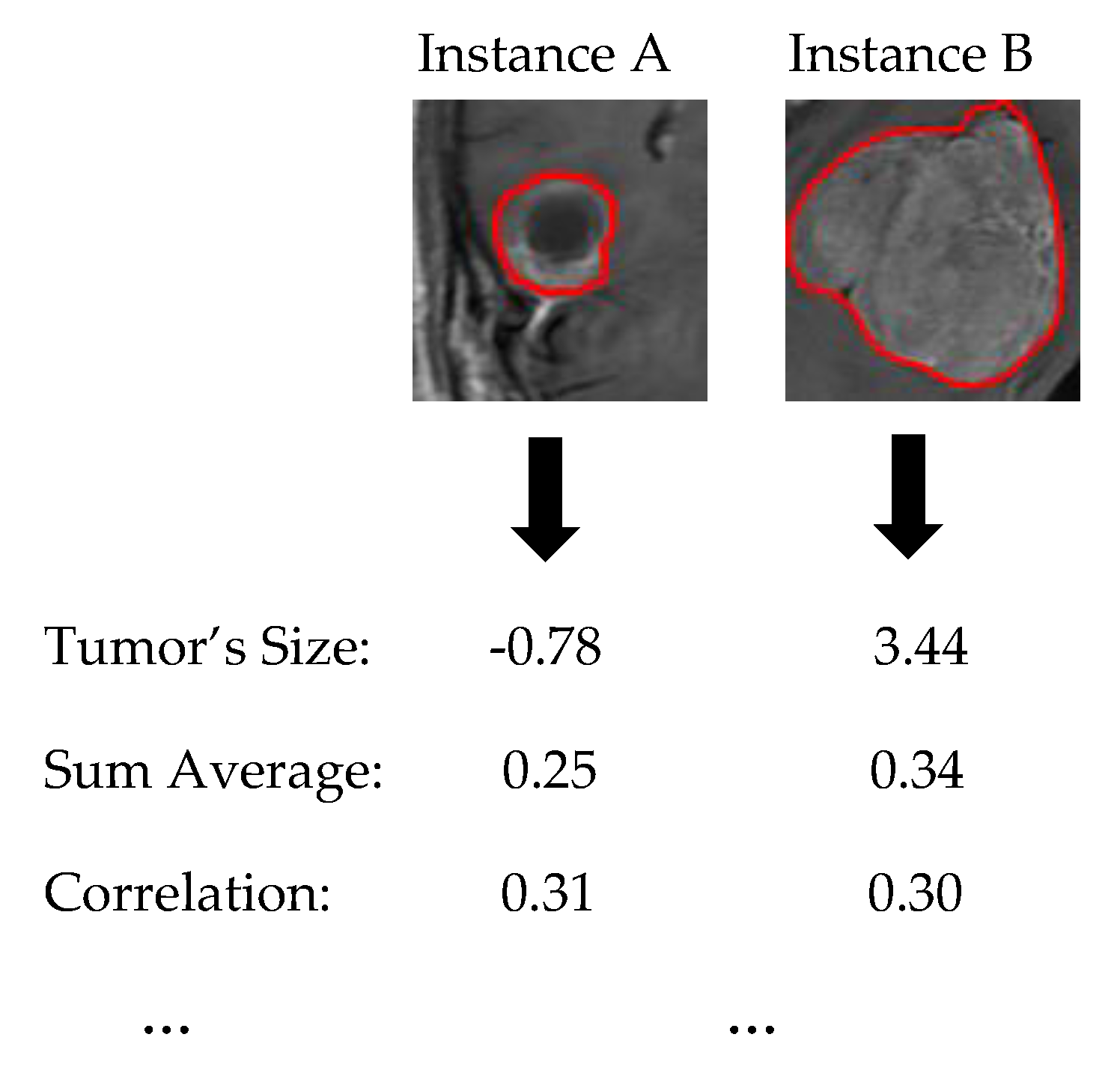
1. Let assume two new instances as presented in
Figure 6.
Two basic language forms are proposed for our model’s explanation output, graph diagrams and questions–answers forms as presented in
Figure 7 and
Figure 8, which were extracted via the formulas described in
Section 2.3.4 regarding the predefined conditions A, B and C. The graph diagram provides in a compact, comprehensive and visual form, information which can easily fast extracted by just investigating every node. Each node represents one feature followed by an explanation rule in which a specific prediction output is qualified. The three displayed nodes represent the three most important identified features while the size of each node represents the importance factor of the corresponding feature.
A questions–answers form is probably one of the best ways to provide explanations since this is the main fundamental way that humans make explanations (more details in
Section 2.3.2). As already mentioned before, the proper choice of the language is highly depended by the audience. Therefore, we also propose two types of questions–answers forms, Specific and Humanistic form. In specific form, the answers are extracted directly by the graph diagram without any information loss providing all details of graph’s information. In humanistic form the answers are extracted via a preprocessing step aiming to simplify the explanation and convert it to a more human like explanation, by approximating the initial model’s features to easier understandable abstract features (meta-features) specified by the application domain. For example, in our case the Object size can be converted to Tumor Size, the Sum Average to Tumor’s Color (more details for Sum Average feature are presented in
Section 2.4). Additionally, every quantitative value has to be converted to qualitative such as Small, Average, Large. For this step is essential the knowledge of a High and Low value of each feature in order to create such qualitative terms.
4. Discussion
In this study, a new prediction framework was proposed, which is able to provide accurate and explainable predictions on image classification tasks. Our experimental results indicate that our model is able to achieve a sufficient classification score comparing to state of the art CNN approaches being also intrinsic interpretable able to provide good explanations for every prediction/decision result.
One major difference comparing to other state of the art explanation frameworks for image classification tasks, is that our approach is not performing pixels based explanations. By the term pixels based (or pixel returns) we mean that the explanations are based on the visual interpretation of the most important identified pixels that determined a specific prediction. For example, if a model classified as a cat, an image which presents a cat and a dog, then meaningful pixel base explanation would probably return the cat’s pixels revealing that the model classified the image utilizing the proper area of pixels. However, if the task was to recognize an owner’s missing cat, then the identification of high level features which uniquely describe this cat would be essential. Such features could be cat’s size, cat’s color, cat’s color irregularity level and cat’s number of legs. In such cases, the model’s prediction explanation would be useful to rely on such high level features instead of just specific pixels. If the main reason for this prediction was just that this cat has 3 legs and blue color then pixel returns probably could not reveal any useful explanation and reasoning.
As already mentioned our explanation approach is not pixel based but higher level feature based. By this term it is meant that the explanations are performed via a higher level feature representation input, in contrast to raw pixels which are the lowest level input (initial representation). Such high level features can describe the unique properties that groups of pixels possess in every image such as color of an image, color irregularity level, shape irregularity of objects lied in an image, number of objects lied in an image and so on. Obviously, these high-level feature inputs have to be understandable to humans since the model’s predictions’ explanations would be useless. For example, if a model classified an image as a dog because without any knowledge about what the feature x means and how was calculated, then such explanation can be considered meaningless. Where instead if it was known that the feature is the size of an object in an image or the color value of an image and so on, then we would be able to make reasoning about the model’s decision and easily understand it.
Nevertheless, creating high level image features being also understandable to humans is a complex task. There is no guarantee that utilizing these features as an input for the machine model would lead to high prediction performance, as probably there are a lot of other hidden unutilized features lied in an image that are probably useful for the specific classification problem. It is hard to identify a priori such features since they are actually found out and crafted by a human sense based approach, while it could make more sense to seek the assistance of an expert with respect to the application domain. In contrast, automatic methods such as CNN models manage to automatically identify useful features in images avoiding this painful human based feature extraction process. However, these features that automatic methods manage to identify are not interpretable and explainable to humans, whereas features crafted by humans can be transparent, meaningful and understandable. This is the trade-off that we need to endure if the objective is the development of interpretable prediction models. Traditional feature extraction approaches, specialized expertise, specific knowledge domain regarding the application and the art of creating useful features for machine learning problems followed by new innovative strategies and techniques can constitute essential key elements in explainable artificial intelligent era.
5. Conclusions and Future Work
In this work, an accurate, robust and explainable prediction framework was proposed for image classification tasks proposing three types of explanations outputs with respect to the audience domain. Comparing to most approaches, our method is intrinsic interpretable providing good explanations relying on high-level feature representation inputs, extracted by images. These features aim to describe the properties that the pixels of an image possess such as its texture irregularity level, object’s shape, size, etc. One basic limitation of our approach is that some of these features are probably only understandable by image analysts and specific human experts. However, we made an attempt to qualitatively explain what such features describe in simple human terms in order to make our model’s explanation output more attractive and viable to a much wider audience.
Last but not least, in our experiments we utilized all features, even the least significant. We attempted to reduce the number of features in this dataset by analyzing the correlation between the features as well as their significance and by applying some feature selection techniques [
27,
28,
29]. However, any attempt of removing any features was leading to decrease the overall performance of the prediction model; hence, no feature was removed. We point out the feature selection processing was not in the scope of our work since our main objective was the development and the presentation of an explainable machine learning framework for image classification tasks. Clearly, an interpretable prediction model, exhibiting even better forecasting ability, could be developed through the imposition of sophisticated feature selection techniques as a pre-processing step.
In future work, we aim to incorporate and identify features more understandable to human, being also very informative for the machine learning prediction models. In addition, it is worth investigating whether an interpretable prediction model exhibiting even better forecasting ability could be developed through the imposition of penalty functions together with the application of feature selection techniques or through additional optimized configuration of the proposed model. Finally, we also aim to develop more sophisticated algorithmic methods in order to improve the prediction performance accuracy of intrinsic white box models. Such algorithms could simplify the initial structure complexity and nonlinearity level of the initial dataset, in order to efficiently train simple white box models.