Unsupervised Clustering of Hyperspectral Paper Data Using t-SNE
Abstract
1. Introduction
2. Materials and Methods
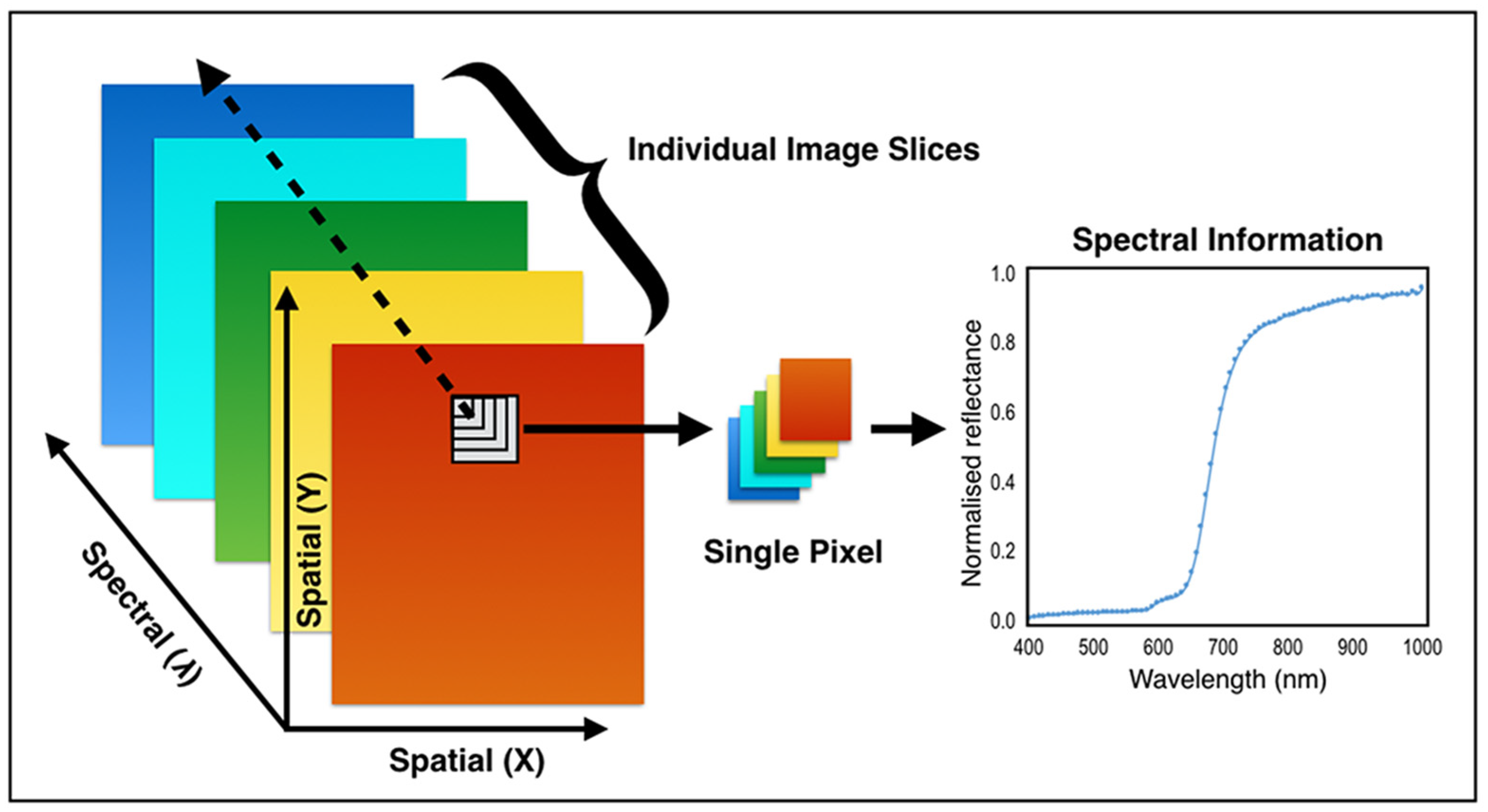
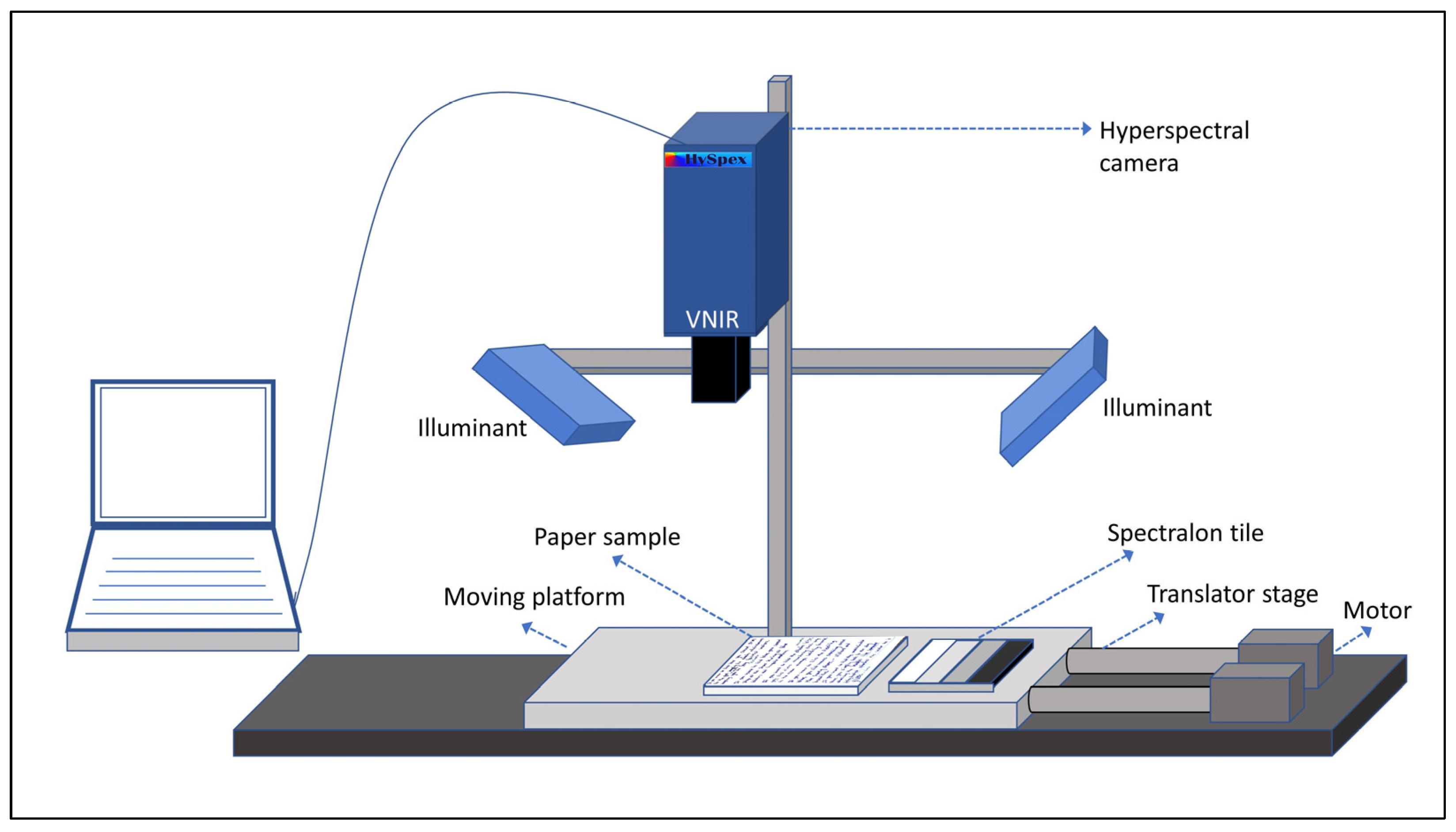
2.1. Hyperspectral Acquisition
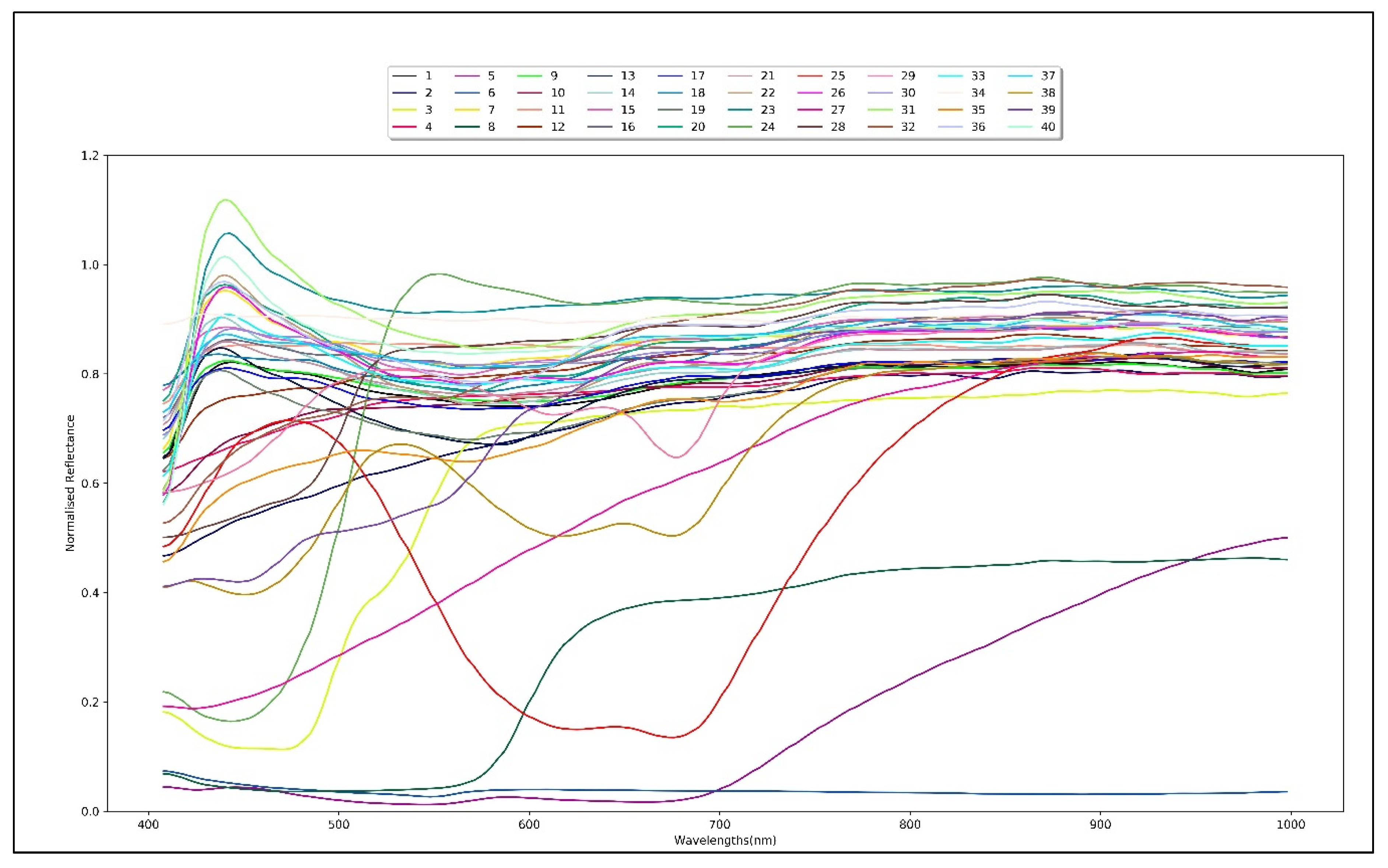
2.2. Samples and Data
2.3. t-Distributed Stochastic Neighbor Embedding (t-SNE)
2.4. Principal Component Analysis (PCA)
2.5. Clustering Performance Evaluation
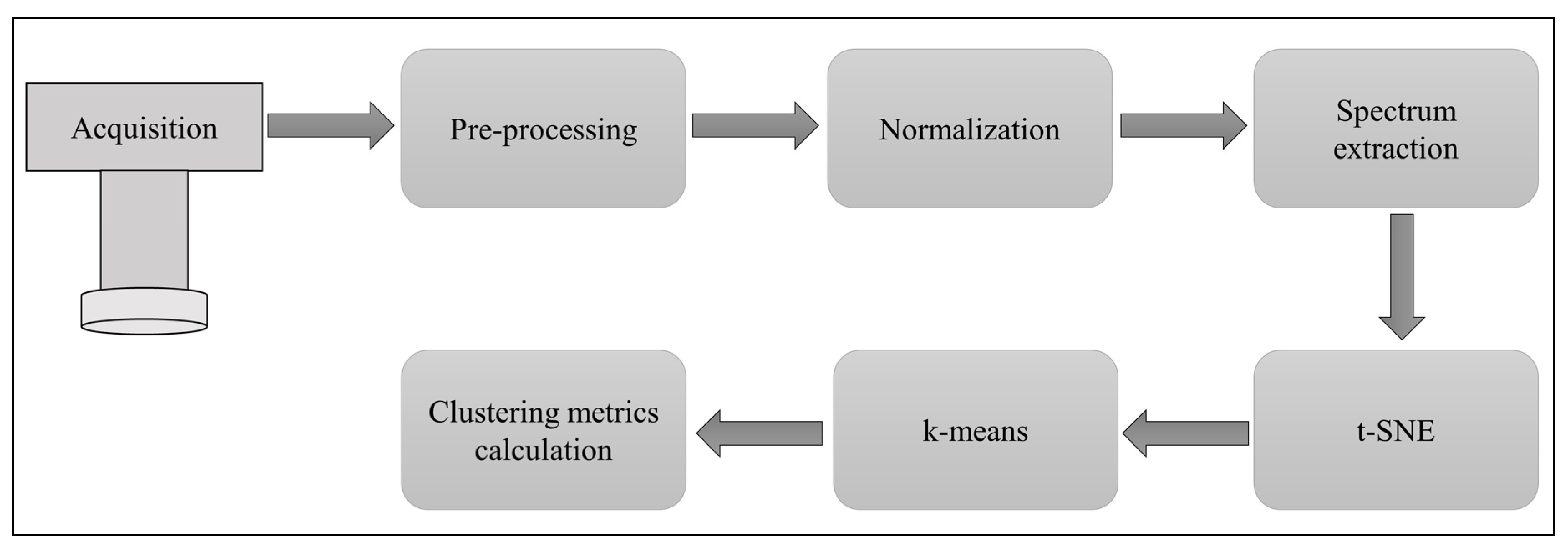
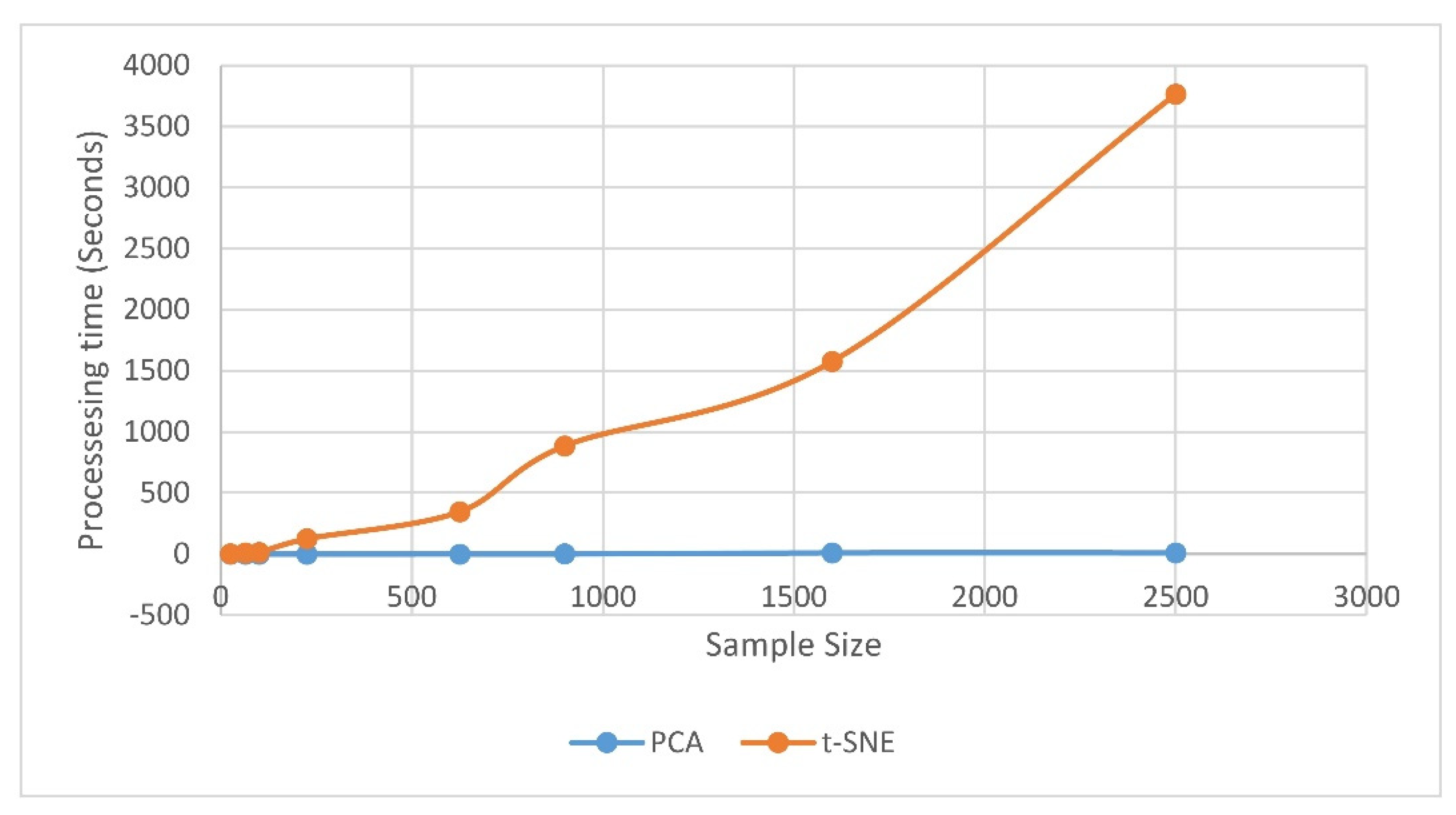
2.6. Data Processing
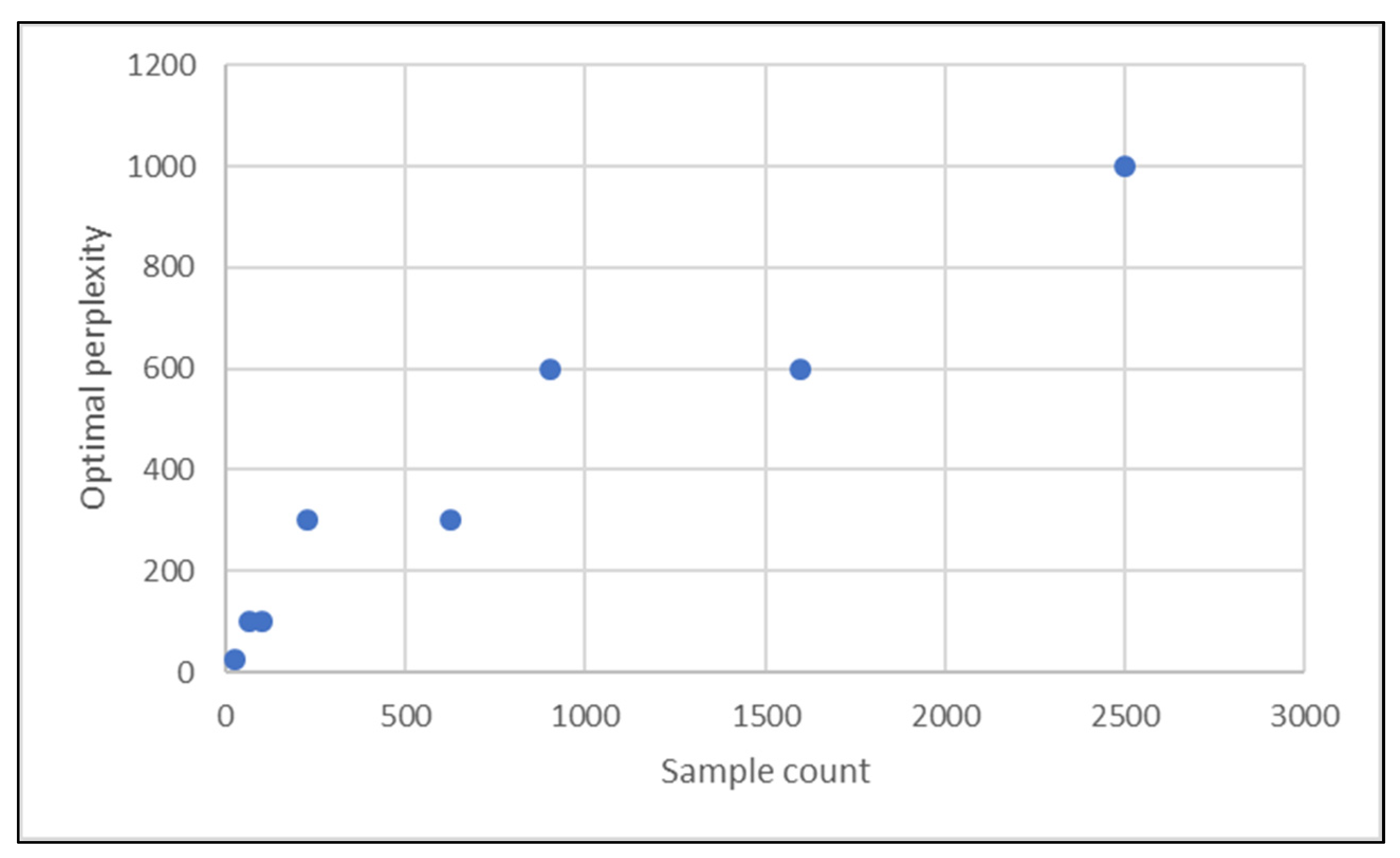
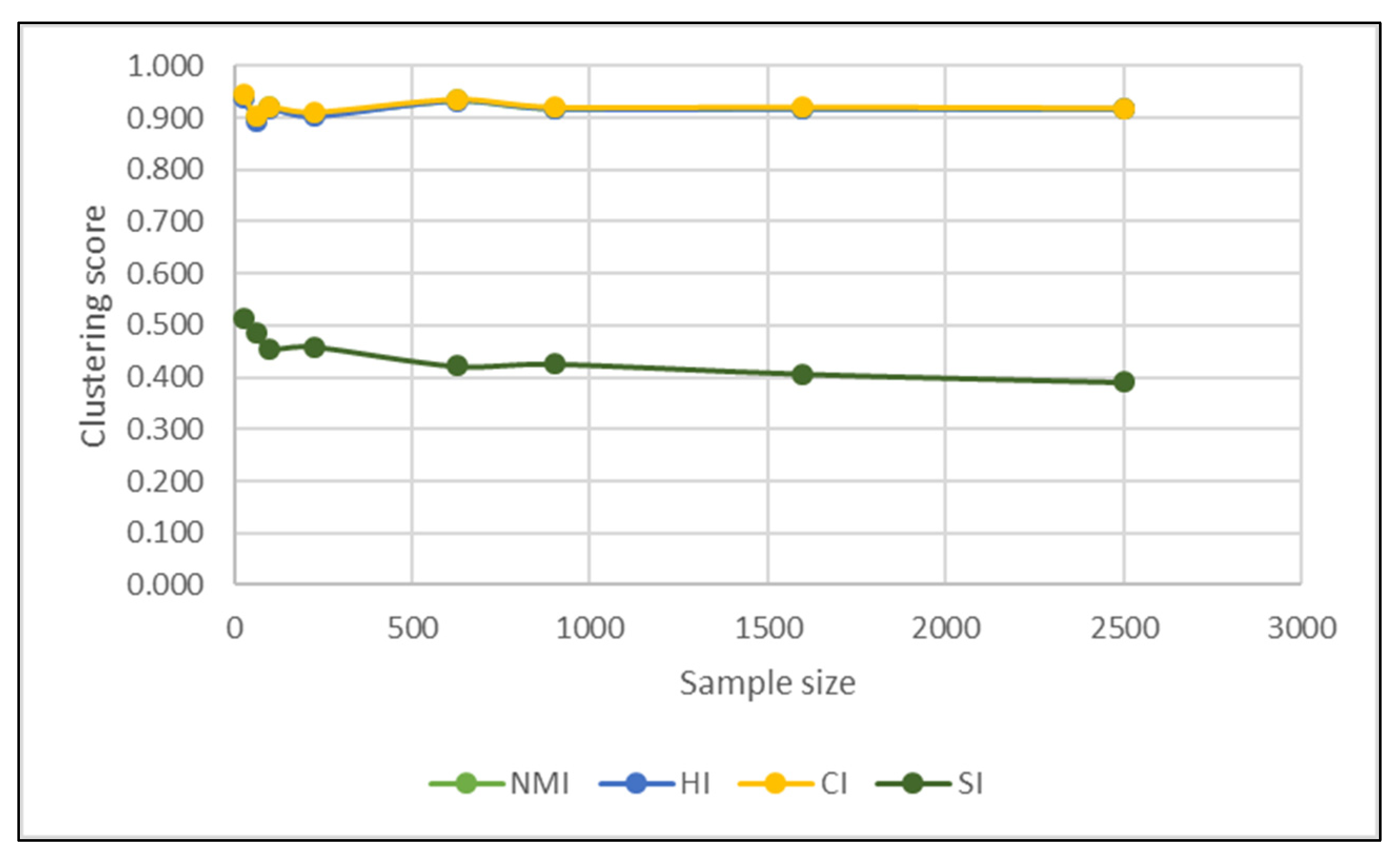
3. Results and Discussions
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kumar, R.; Kumar, V.; Sharma, V. Discrimination of various paper types using diffuse reflectance ultraviolet-visible near-infrared (UV-Vis-NIR) spectroscopy: forensic application to questioned documents. Appl. Spectrosc. 2015, 69, 714–720, 2015. [Google Scholar] [CrossRef] [PubMed]
- Brunelle, R.L.; Reed, R.W. Forensic examination of ink and Paper, Forensic Examination of Ink and Paper; Charles C Thomas Springfield: Springfield, IL, USA, 1984. [Google Scholar]
- Lee, L.C.; Liong, C.Y.; Osman, K.; Jemain, A.A. Comparison of several variants of principal component analysis (PCA) on forensic analysis of paper based on IR spectrum. AIP Conf. Proc. 2016, 1750. [Google Scholar] [CrossRef]
- Braz, A.; López-López, M.; García-Ruiz, C. Raman spectroscopy for forensic analysis of inks in questioned documents. Forensic Sci. Int. 2013, 232, 206–212. [Google Scholar] [CrossRef] [PubMed]
- Mokrzycki, G.M. Advances in Document Examination: The video spectral comparator 2000. Forensic Sci. Commun. 1999, 1, 1–6. [Google Scholar]
- Havermans, J.; Aziz, H.A.; Scholten, H. Non destructive detection of iron gall inks by means of multispectral imaging. Part 1: Development of the detection system. Restaurator 2003, 24, 55–60. [Google Scholar] [CrossRef]
- Edelman, G.J.; Gaston, E.; van Leeuwen, T.G.; Cullen, P.J.; Aalders, M.C.G. Hyperspectral imaging for non-contact analysis of forensic traces. Forensic Sci. Int. 2012, 223, 28–39. [Google Scholar] [CrossRef]
- ElMasry, G.; Kamruzzaman, M.; Sun, D.W.; Allen, P. Principles and applications of hyperspectral imaging in quality evaluation of agro-food products: A review. Crit. Rev. Food Sci. Nutr. 2012, 52, 999–1023. [Google Scholar] [CrossRef]
- Lu, G.; Fei, B. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 010901. [Google Scholar] [CrossRef]
- Tatzer, P.; Wolf, M.; Panner, T. Industrial application for inline material sorting using hyperspectral imaging in the NIR range. Real Time Imaging 2005, 11, 99–107. [Google Scholar] [CrossRef]
- Fischer, C.; Kakoulli, I. Multispectral and hyperspectral imaging technologies in conservation: Current research and potential applications. Stud. Conserv. 2014, 51, 3–16. [Google Scholar] [CrossRef]
- Devassy, B.M.; George, S. Ink Classification Using Convolutional Neural Network. In Proceedings of the 12th Norwegian Information Security Conference 2019 (NISK), Narvik, Norway, 25–27 November 2019. [Google Scholar]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
- Timmerman, M.E. Principal Component Analysis. J. Am. Stat. Assoc. 2003, 98, 464. [Google Scholar] [CrossRef]
- Martel, E.; Lazcano, R.; López, J.; Madroñal, D.; Salvador, R.; López, S.; Juarez, E.; Guerra, R.; Sanz, C.; Sarmiento, R. Implementation of the Principal Component Analysis onto high-performance computer facilities for hyperspectral dimensionality reduction: Results and comparisons. Remote Sens. 2018, 10, 864. [Google Scholar] [CrossRef]
- Farrell, M.D.; Mersereau, R.M. On the impact of PCA dimension reduction for hyperspectral detection of difficult targets. IEEE Geosci. Remote Sens. Lett. 2005, 2, 192–195. [Google Scholar] [CrossRef]
- Wang, J.; Chang, C.I. Independent component analysis-based dimensionality reduction with applications in hyperspectral image analysis. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1586–1600. [Google Scholar] [CrossRef]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of hyperspectral images with regularized linear discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Renard, N.; Bourennane, S.; Blanc-Talon, J. Denoising and dimensionality reduction using multilinear tools for hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2008, 5, 138–142. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, J.E.; Bruce, L.M. Locality-preserving dimensionality reduction and classification for hyperspectral image analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1185–1198. [Google Scholar] [CrossRef]
- Plaza, A.; Martínez, P.; Plaza, J.; Pérez, R. Dimensionality reduction and classification of hyperspectral image data using sequences of extended morphological transformations. IEEE Trans. Geosci. Remote Sens. 2005, 43, 466–479. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2625. [Google Scholar]
- Abdelmoula, W.M.; Balluff, B.; Englert, S.; Dijkstra, J.; Reinders, M.J.T.; Walch, A.; McDonnell, L.A.; Lelieveldt, B.P.F. Data-driven identification of prognostic tumor subpopulations using spatially mapped t-SNE of Mass spectrometry imaging data. Proc. Natl. Acad. Sci. USA. 2016, 113, 12244–12249. [Google Scholar] [CrossRef] [PubMed]
- Taskesen, E.; Reinders, M.J.T. 2D representation of transcriptomes by t-SNE exposes relatedness between human tissues. PLoS ONE 2016, 11. [Google Scholar] [CrossRef] [PubMed]
- Rauber, P.E.; Falcão, A.X.; Telea, A.C. Visualizing time-dependent data using dynamic t-SNE. Eurographics Conf. Vis. 2016. [Google Scholar] [CrossRef]
- Takamatsu, K.; Murakami, K.; Kozaki, Y.; Bannaka, K.; Noda, I.; Lim, R.J.W.; Kenichiro, M.; Nakamura, T.; Nakata, Y. A New Way of Visualizing Curricula Using Competencies: Cosine Similarity and t-SNE. In Proceedings of the 2018 7th International Congress on Advanced Applied Informatics, IIAI-AAI 2018, Yonago, Japan, 8–13 July 2018; pp. 390–395. [Google Scholar] [CrossRef]
- Chen, Y.; Du, S.; Quan, H. Feature Analysis and Optimization of Underwater Target Radiated Noise Based on t-SNE. In Proceedings of the 2018 10th International Conference on Wireless Communications and Signal Processing, WCSP 2018, Hangzhou, China, 18–20 October 2018. [Google Scholar] [CrossRef]
- Pouyet, E.; Rohani, N.; Katsaggelos, A.K.; Cossairt, O.; Walton, M. Innovative data reduction and visualization strategy for hyperspectral imaging datasets using t-SNE approach. Pure Appl. Chem. 2018, 90, 493–506. [Google Scholar] [CrossRef]
- Song, W.; Wang, L.; Liu, P.; Choo, K.K.R. Improved t-SNE based manifold dimensional reduction for remote sensing data processing. Multimed. Tools Appl. 2019, 78, 4311–4326. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, L.; Zhuo, L.; Liang, X.; Li, J. An efficient hyperspectral image retrieval method: Deep spectral-spatial feature extraction with DCGAN and dimensionality reduction using t-SNE-based NM hashing. Remote Sens. 2018, 10, 271. [Google Scholar] [CrossRef]
- Ravi, D.; Fabelo, H.; Callic, G.M.; Yang, G.Z. Manifold embedding and semantic segmentation for intraoperative guidance with hyperspectral brain imaging. IEEE Trans. Med. Imaging 2017, 36, 1845–1857. [Google Scholar] [CrossRef]
- Binu, M.D.; Sony, G. Dimensionality reduction and visualisation of hyperspectral ink data Using t-SNE. Forensic Sci. Int. 2020. [Google Scholar] [CrossRef]
- HySpex VNIR 1800. Available online: https://www.hyspex.no (accessed on 3 February 2020).
- Contrast Multi-Step Target. Available online: https://www.labspherestore.com/ (accessed on 3 February 2020).
- Kingman, J.F.C.; Kullback, S. Information Theory and Statistics; Dover Publications Inc.: Mineola, NY, USA, 2007; Volume 54. [Google Scholar]
- Smith, L. A tutorial on Principal Components Analysis. Commun. Stat. Theory Methods 1988, 17, 3157–3175. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-means clustering algorithm. Appl. Stat. 2006, 28, 100. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- McDaid, A.F.; Greene, D.; Hurley, N. Normalized Mutual Information to evaluate overlapping community finding algorithms. arXiv 2011, arXiv:1110.2515. [Google Scholar]
- Rosenberg, A.; Hirschberg, J. V-measure: A conditional entropy-based external cluster evaluation measure. Comput. Linguist. 2007, 1, 410–420. [Google Scholar]
- Kambhatla, N.; Leen, T.K. Fast non-linear dimension reduction. In Proceedings of the IEEE International Conference on Neural Networks-Conference Proceedings, San Francisco, CA, USA, 28 March–1 April 1993; Volume 1993, pp. 1213–1218. [Google Scholar] [CrossRef]

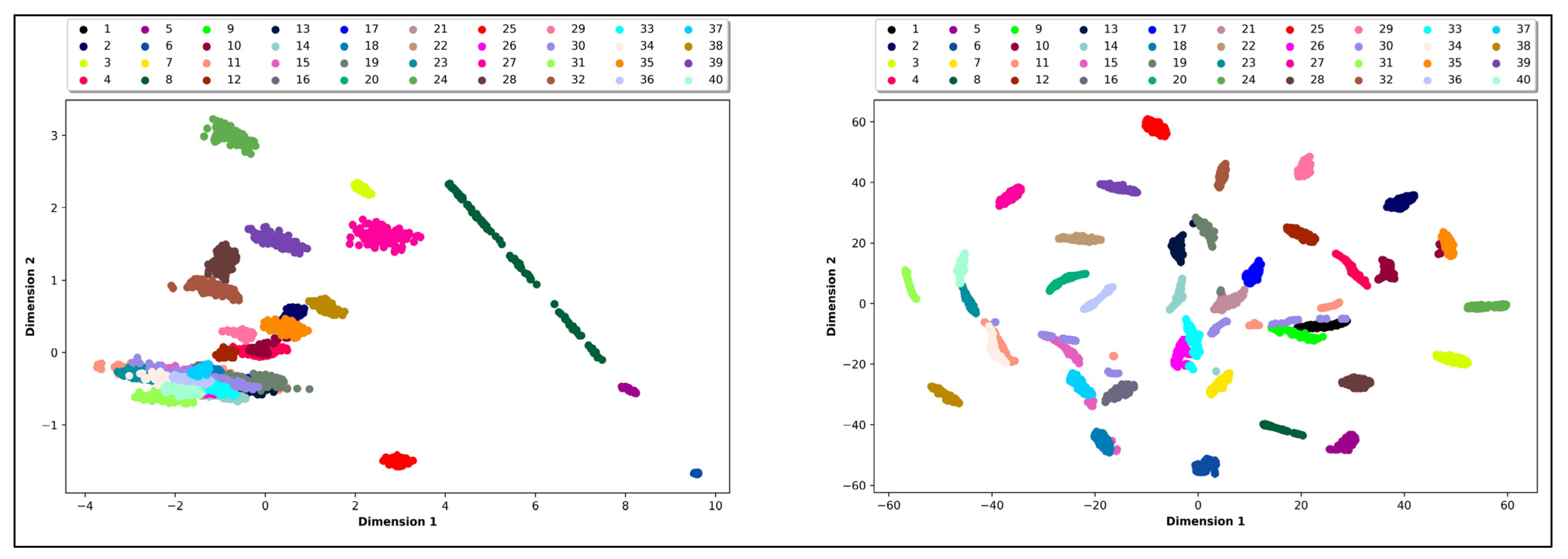
| Validation Indices | PCA | t-SNE |
|---|---|---|
| NMI | 0.72 | 0.92 |
| HI | 0.70 | 0.92 |
| CI | 0.75 | 0.92 |
| SI | 0.34 | 0.44 |
| Sample Count | 25 | 64 | 100 | 225 | 625 | 900 | 1600 | 2500 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimal Perplexity | 25 | 100 | 100 | 300 | 300 | 600 | 600 | 1000 | ||||||||
| PCA | t-SNE | PCA | t-SNE | PCA | t-SNE | PCA | t-SNE | PCA | t-SNE | PCA | t-SNE | PCA | t-SNE | PCA | t-SNE | |
| NMI | 0.78 | 0.94 | 0.76 | 0.90 | 0.74 | 0.92 | 0.73 | 0.91 | 0.70 | 0.93 | 0.70 | 0.92 | 0.69 | 0.92 | 0.69 | 0.92 |
| HI | 0.75 | 0.94 | 0.73 | 0.90 | 0.71 | 0.92 | 0.71 | 0.90 | 0.67 | 0.93 | 0.68 | 0.92 | 0.67 | 0.92 | 0.67 | 0.92 |
| CI | 0.81 | 0.94 | 0.79 | 0.91 | 0.76 | 0.92 | 0.75 | 0.91 | 0.72 | 0.94 | 0.73 | 0.92 | 0.71 | 0.92 | 0.72 | 0.92 |
| SI | 0.39 | 0.51 | 0.38 | 0.48 | 0.37 | 0.46 | 0.34 | 0.46 | 0.31 | 0.42 | 0.33 | 0.43 | 0.29 | 0.41 | 0.31 | 0.39 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melit Devassy, B.; George, S.; Nussbaum, P. Unsupervised Clustering of Hyperspectral Paper Data Using t-SNE. J. Imaging 2020, 6, 29. https://doi.org/10.3390/jimaging6050029
Melit Devassy B, George S, Nussbaum P. Unsupervised Clustering of Hyperspectral Paper Data Using t-SNE. Journal of Imaging. 2020; 6(5):29. https://doi.org/10.3390/jimaging6050029
Chicago/Turabian StyleMelit Devassy, Binu, Sony George, and Peter Nussbaum. 2020. "Unsupervised Clustering of Hyperspectral Paper Data Using t-SNE" Journal of Imaging 6, no. 5: 29. https://doi.org/10.3390/jimaging6050029
APA StyleMelit Devassy, B., George, S., & Nussbaum, P. (2020). Unsupervised Clustering of Hyperspectral Paper Data Using t-SNE. Journal of Imaging, 6(5), 29. https://doi.org/10.3390/jimaging6050029






