Redesigned Skip-Network for Crowd Counting with Dilated Convolution and Backward Connection
Abstract
1. Introduction
- The proposed network utilized the backward connection for passing high-level features from deeper layers to shallower layers and reducing false positives in crowd counting.
- Dilated convolution is introduced in skip-network to increase the receptive field sizes while keeping the information of high-level features for a feature map integration in the skip connection.
2. Related Work
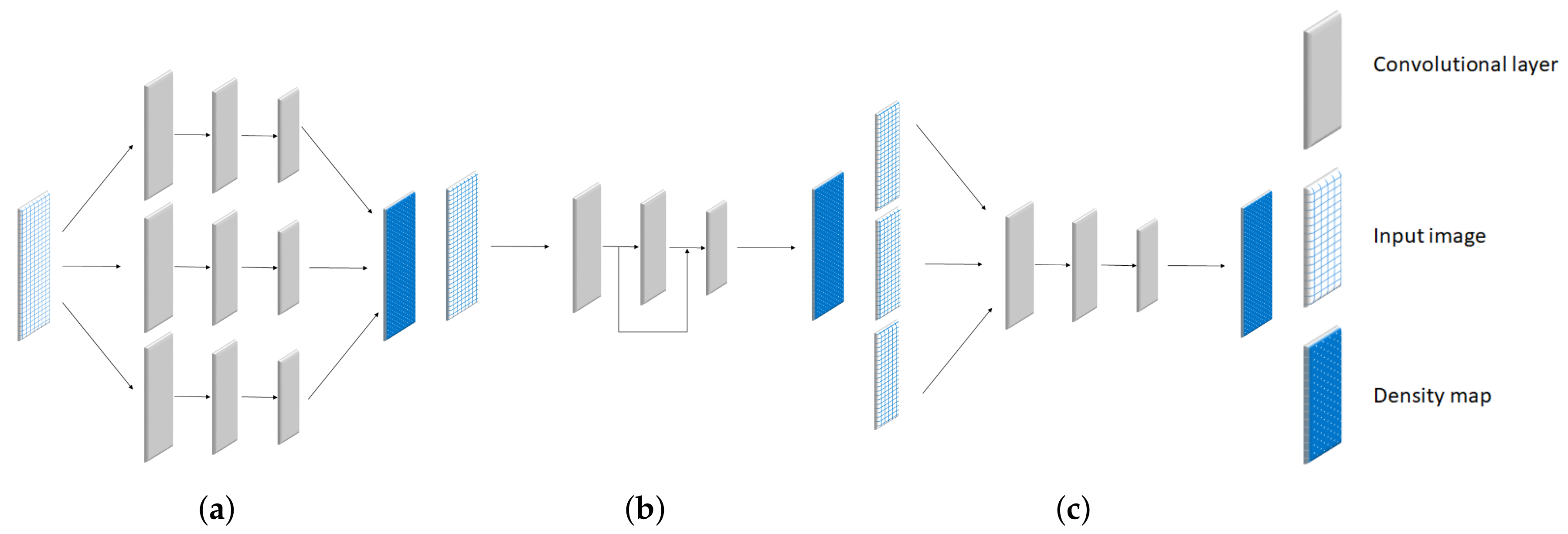
2.1. Multi-Column Network
2.2. Skip-Network
2.3. Multi-Scale Network
3. Density Map for Object Counting
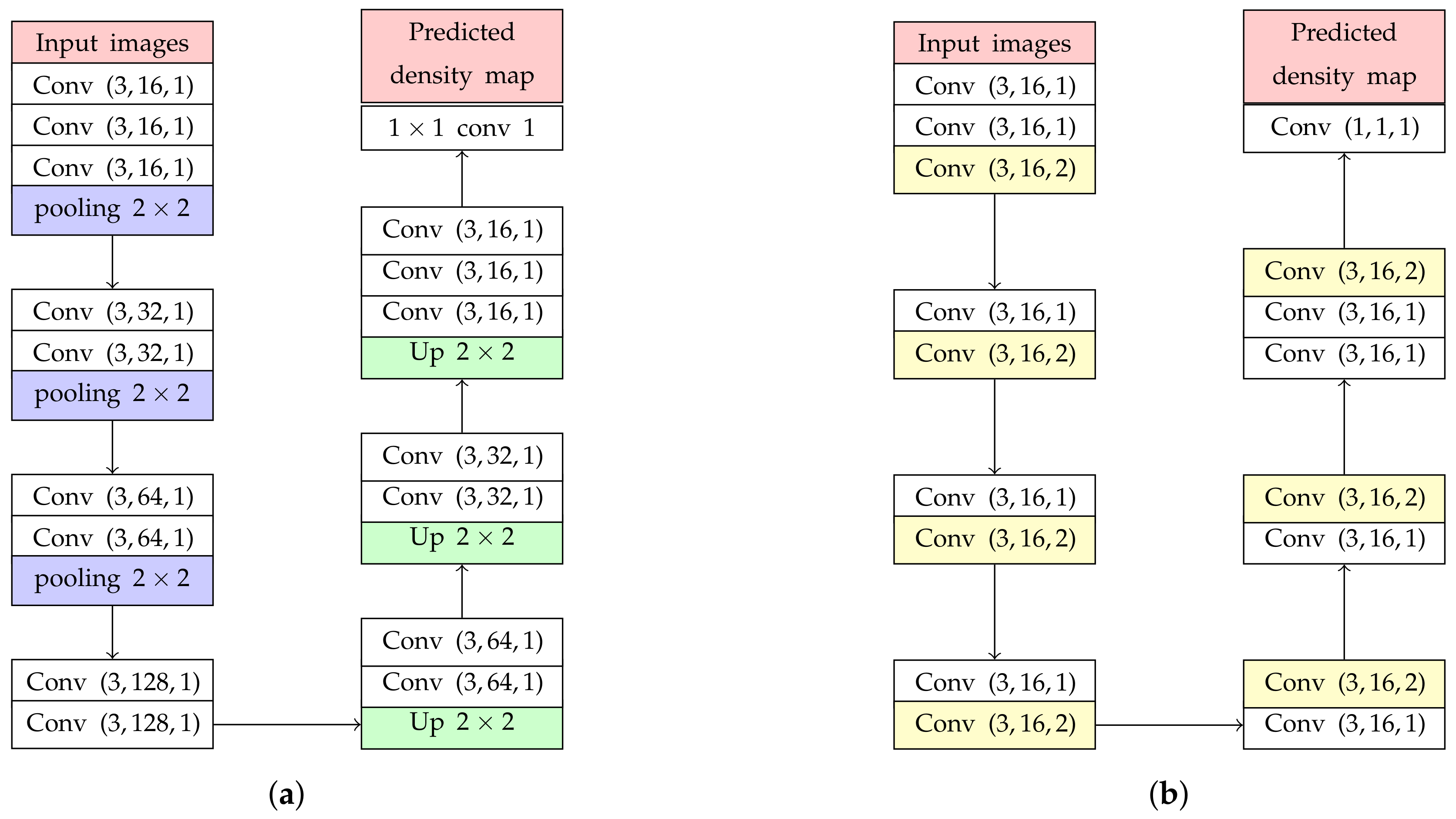
4. Estimation Network Architecture
4.1. Backbone Network
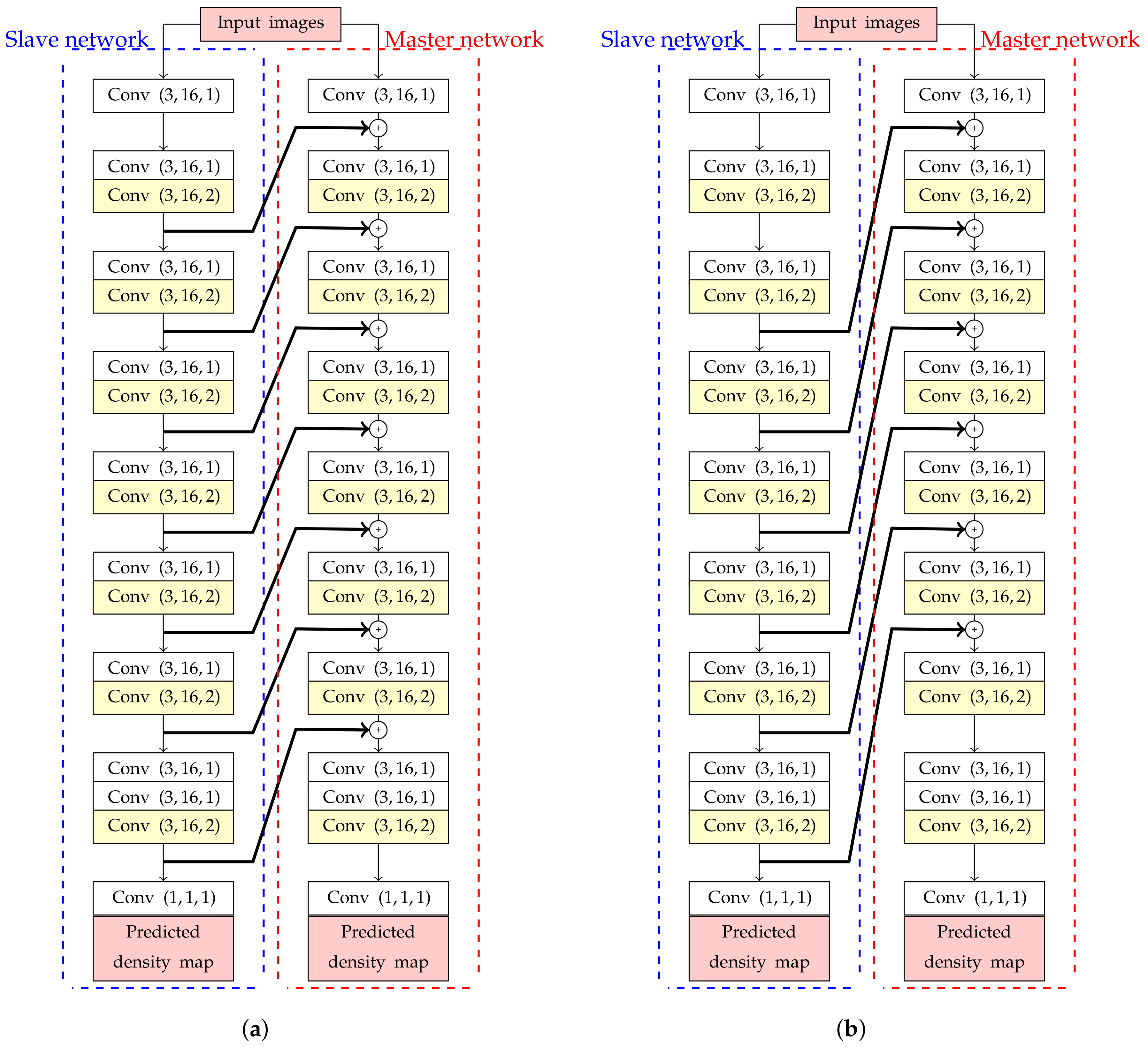
4.2. Backward Connection
- Shallower layers can recognize the characteristic of a feature map from the deeper layer to emphasize low-level features, which can be considered as the main features of crowd images.
- Since CNNs have a hierarchical network architecture, the performance for crowd counting with large object can be improved.
5. Training Method
5.1. Optimization of an Estimation Network
- More spatial information is preserved in a density map. Even though a crowd image contains the same number of objects, the pattern or spatial distribution can be different. Therefore, an estimation network can be optimized or handled for various conditions of crowd images.
- In the optimization process, the size of an object or Gaussian kernel is suitable for learning on CNN. The spatial kernel in Conv layers can be adapted to different sizes whose perspective effect varies significantly. Thus, spatial kernels are more semantic meaningful, and consequently, they improve the accuracy of crowd counting.
5.2. Data Augmentation
6. Experimental Results
6.1. Evaluation Metric
6.2. Crowd Counting Dataset
6.2.1. Shanghaitech Dataset
- Part A: There are 300 training and 182 testing images collected randomly crawled from the internet.
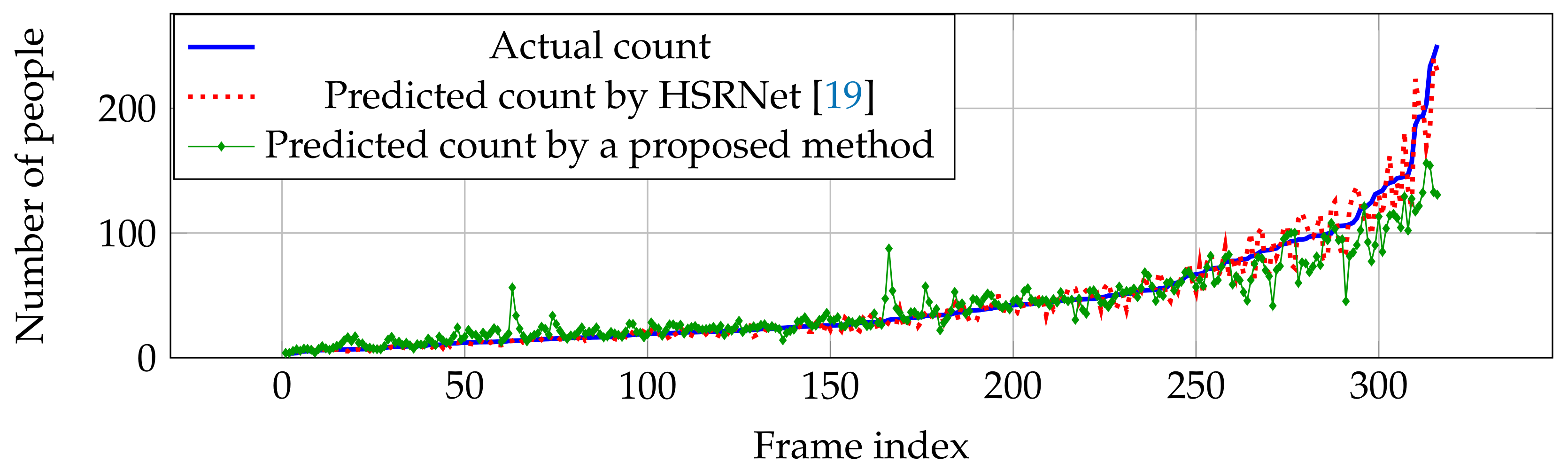
- Part B: There are 400 training and 316 testing images taken from crowded scenes on Shanghai streets.
6.2.2. UCF _CC _50 Dataset
6.2.3. TRANCOS Dataset
6.3. Ablations on Shanghaitech Part A
6.4. Counting Evaluation and Comparison
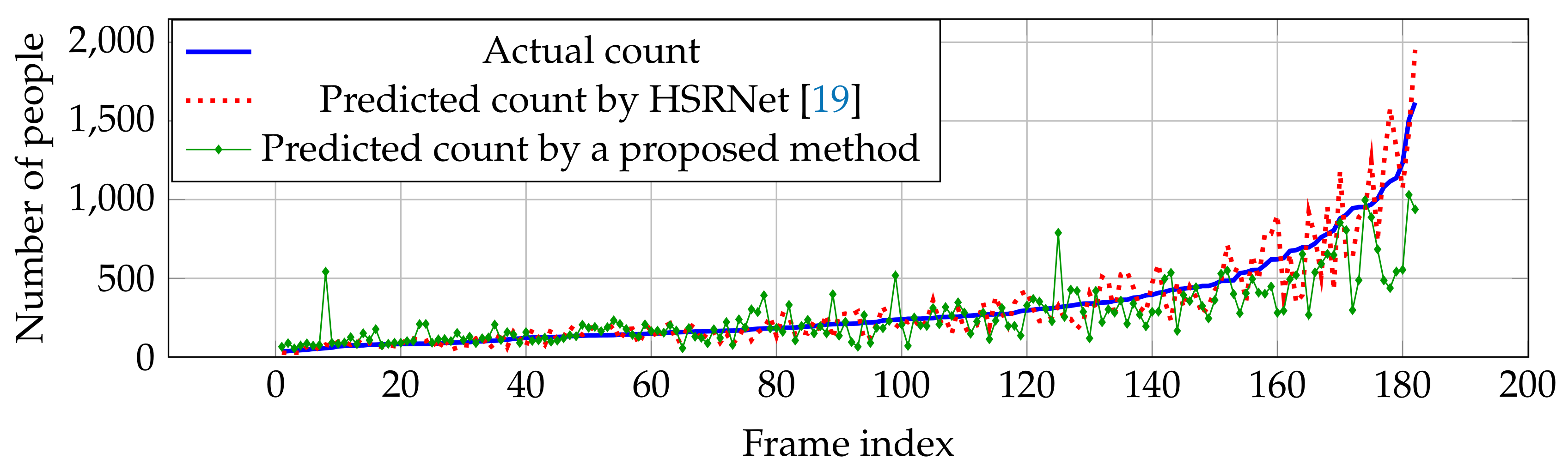
6.4.1. Shanghaitech Dataset
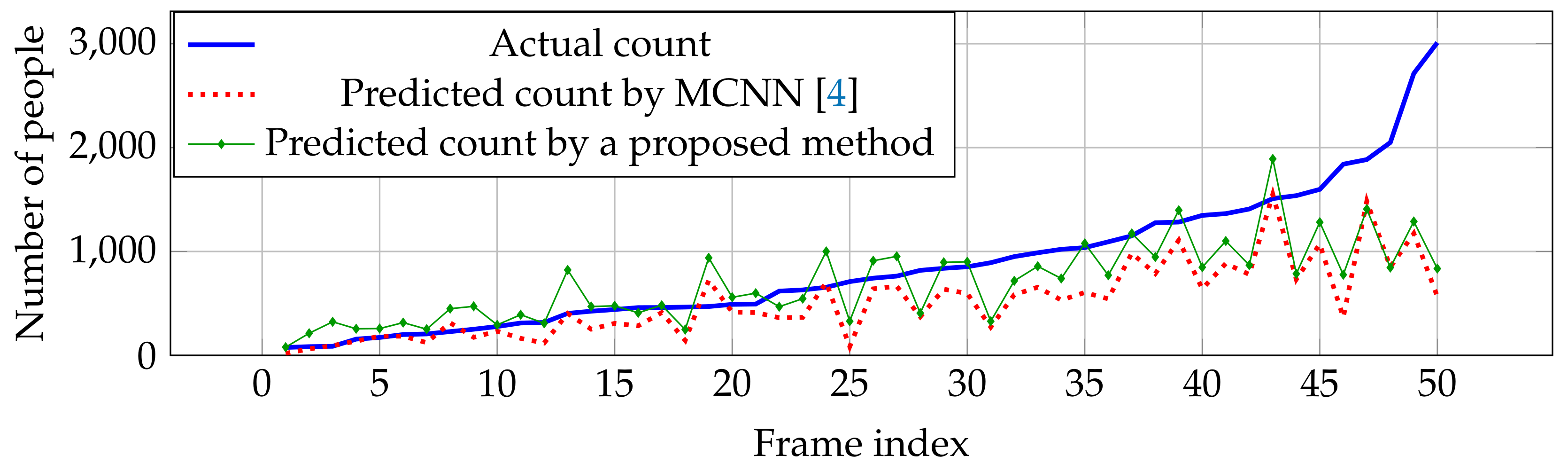
6.4.2. UCF_CC_50
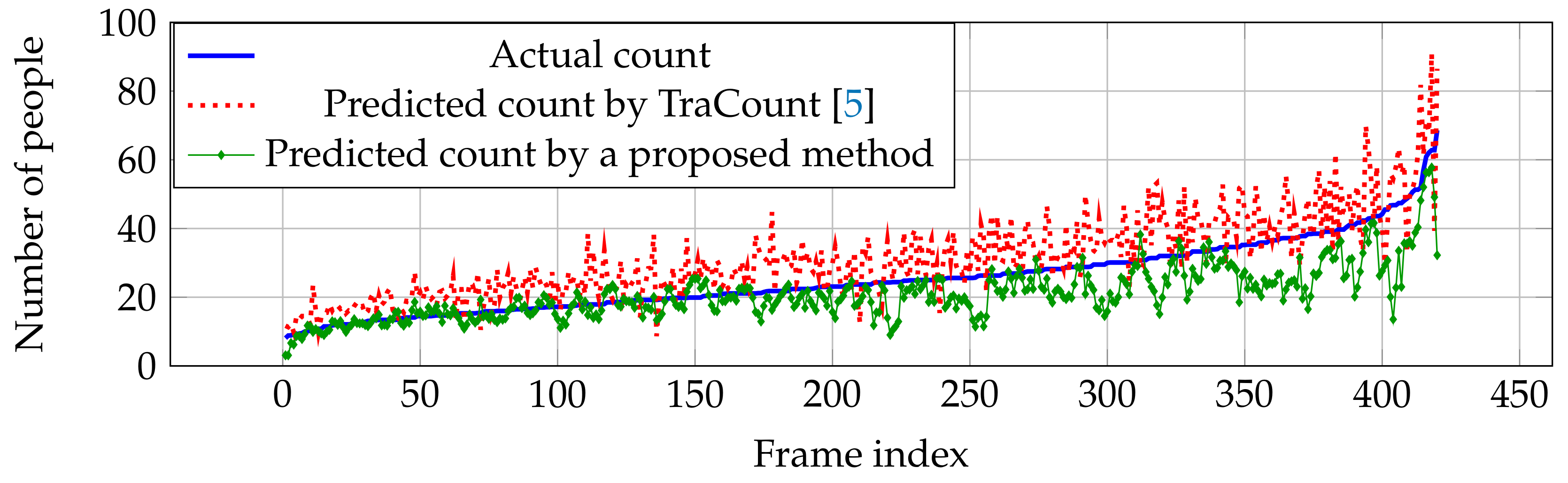
6.4.3. TRANCOS Dataset
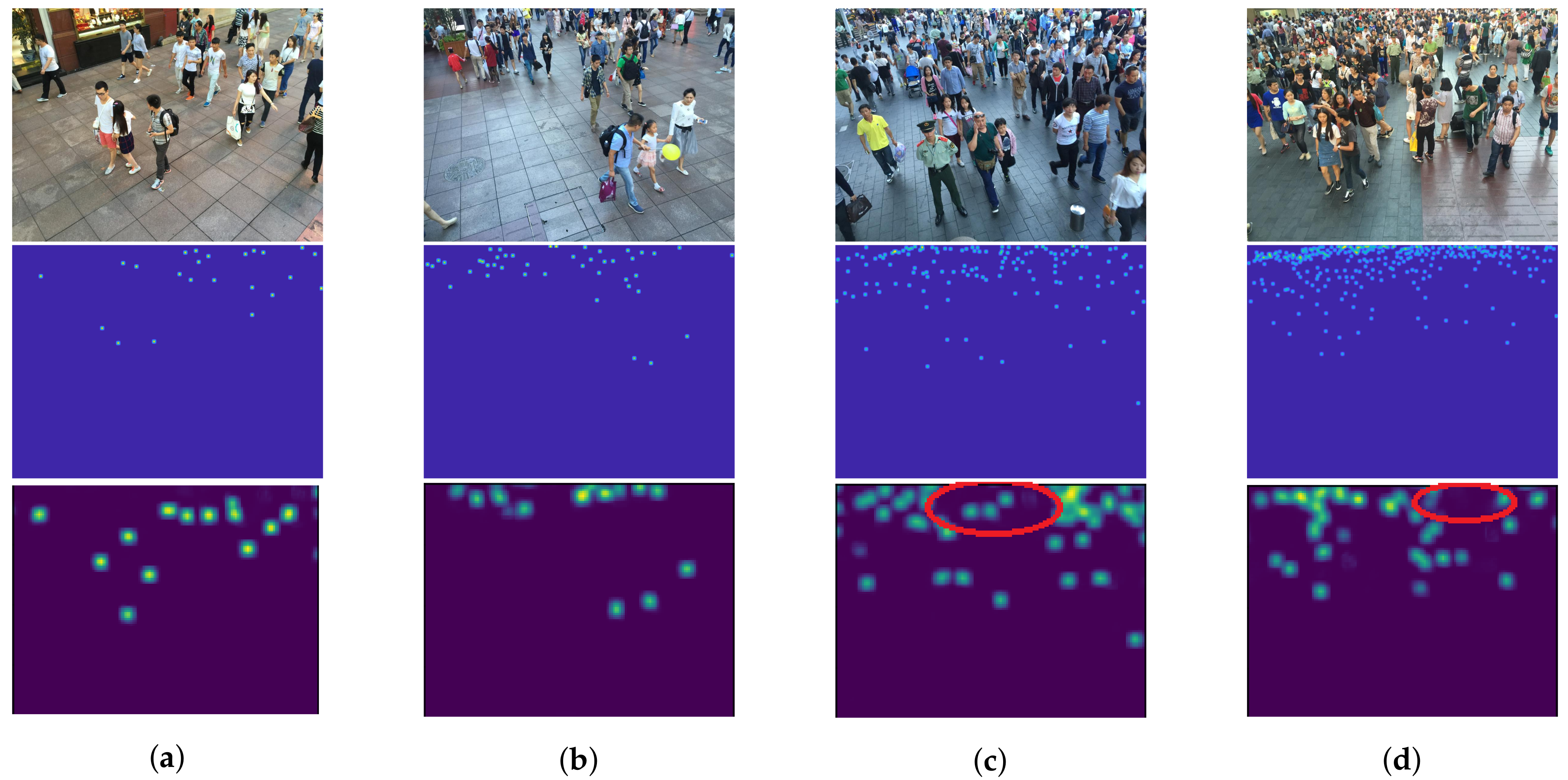
6.5. Density Map Assessment
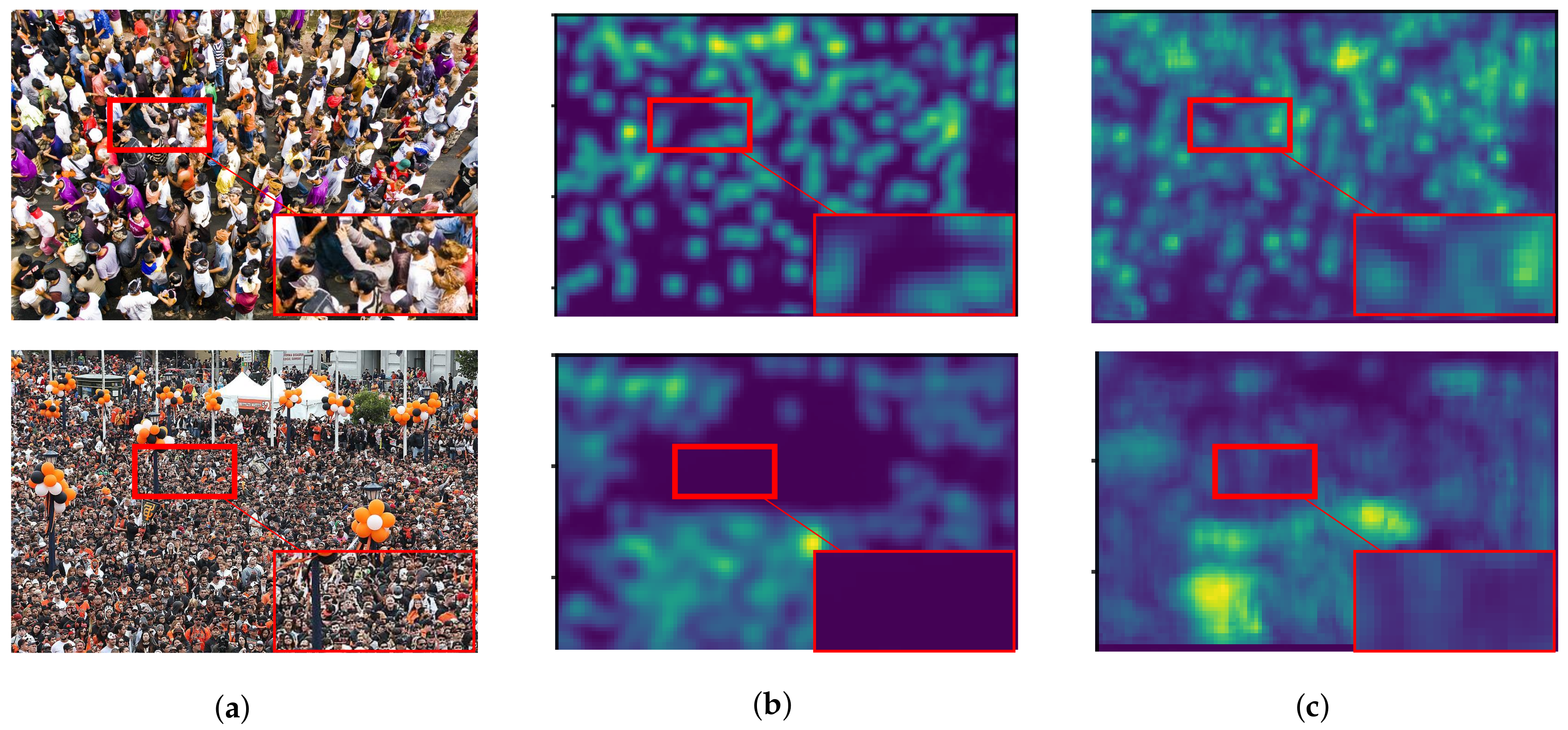
6.5.1. Object Scale and Crowd Density
6.5.2. Crowd Image Quality
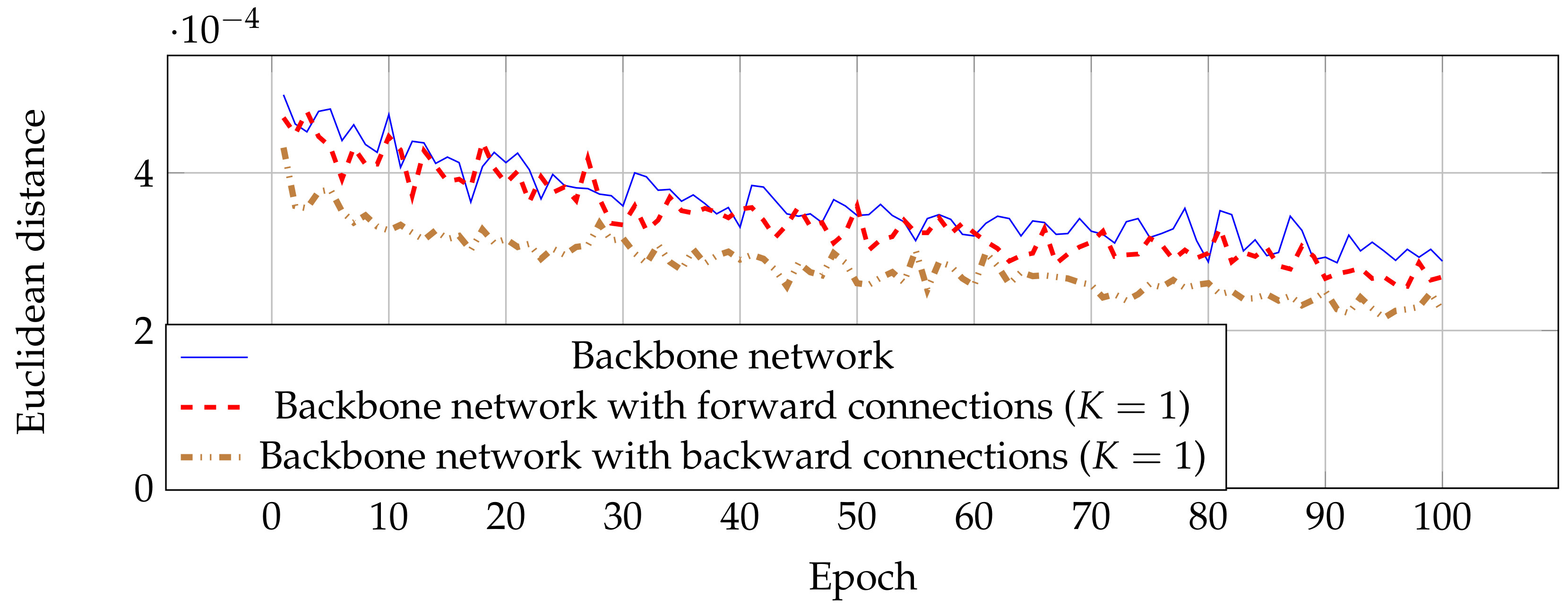
6.5.3. Effect on Dilated Convolution
7. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Onoro-Rubio, D.; López-Sastre, R.J. Towards perspective-free object counting with deep learning. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 615–629. [Google Scholar]
- Sam, D.B.; Surya, S.; Babu, R.V. Switching convolutional neural network for crowd counting. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4031–4039. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Zhang, Y.; Zhou, D.; Chen, S.; Gao, S.; Ma, Y. Single-image crowd counting via multi-column convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 589–597. [Google Scholar]
- Surya, S.; Babu, R.V. TraCount: A deep convolutional neural network for highly overlapping vehicle counting. In Proceedings of the Tenth Indian Conference on Computer Vision, Graphics and Image Processing, Guwahati, India, 18–22 December 2016; p. 46. [Google Scholar]
- Boominathan, L.; Kruthiventi, S.S.; Babu, R.V. Crowdnet: A deep convolutional network for dense crowd counting. In Proceedings of the 24th ACM International Conference on Multimedia, Amsterdam, The Netherlands, 15–19 October 2016; pp. 640–644. [Google Scholar]
- Kumagai, S.; Hotta, K.; Kurita, T. Mixture of counting cnns: Adaptive integration of cnns specialized to specific appearance for crowd counting. arXiv 2017, arXiv:1703.09393. [Google Scholar]
- Eigen, D.; Fergus, R. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2650–2658. [Google Scholar]
- Sindagi, V.A.; Patel, V.M. A survey of recent advances in cnn-based single image crowd counting and density estimation. Pattern Recognit. Lett. 2018, 107, 3–16. [Google Scholar] [CrossRef]
- Wang, L.; Yin, B.; Guo, A.; Ma, H.; Cao, J. Skip-connection convolutional neural network for still image crowd counting. Appl. Intell. 2018, 48, 3360–3371. [Google Scholar] [CrossRef]
- Marsden, M.; McGuinness, K.; Little, S.; O’Connor, N.E. Fully convolutional crowd counting on highly congested scenes. arXiv 2016, arXiv:1612.00220. [Google Scholar]
- Sooksatra, S.; Yoshitaka, A.; Kondo, T.; Bunnun, P. The Density-Aware Estimation Network for Vehicle Counting in Traffic Surveillance System. In Proceedings of the 15th International Conference on Signal-Image Technology & Internet-Based Systems, SITIS 2019, Sorrento-Naples, Italy, 26–29 November 2019; pp. 231–238. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Li, Y.; Zhang, X.; Chen, D. Csrnet: Dilated convolutional neural networks for understanding the highly congested scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1091–1100. [Google Scholar]
- Gao, G.; Gao, J.; Liu, Q.; Wang, Q.; Wang, Y. CNN-based Density Estimation and Crowd Counting: A Survey. arXiv 2020, arXiv:2003.12783. [Google Scholar]
- Idrees, H.; Saleemi, I.; Seibert, C.; Shah, M. Multi-source multi-scale counting in extremely dense crowd images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2547–2554. [Google Scholar]
- Guerrero-Gómez-Olmedo, R.; Torre-Jiménez, B.; López-Sastre, R.; Maldonado-Bascón, S.; Onoro-Rubio, D. Extremely overlapping vehicle counting. In Proceedings of the Iberian Conference on Pattern Recognition and Image Analysis (IbPRIA), Santiago de Compostela, Spain, 17–19 June 2015. [Google Scholar]
- Sindagi, V.A.; Patel, V.M. Generating high-quality crowd density maps using contextual pyramid cnns. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1861–1870. [Google Scholar]
- Zou, Z.; Liu, Y.; Xu, S.; Wei, W.; Wen, S.; Zhou, P. Crowd Counting via Hierarchical Scale Recalibration Network. arXiv 2020, arXiv:2003.03545. [Google Scholar]
- Huang, S.; Li, X.; Cheng, Z.Q.; Zhang, Z.; Hauptmann, A. Stacked Pooling for Boosting Scale Invariance of Crowd Counting. arXiv 2018, arXiv:1808.07456. [Google Scholar]
- Shi, X.; Li, X.; Wu, C.; Kong, S.; Yang, J.; He, L. A Real-Time Deep Network for Crowd Counting. arXiv 2020, arXiv:2002.06515. [Google Scholar]
- Rodriguez, M.; Laptev, I.; Sivic, J.; Audibert, J.Y. Density-aware person detection and tracking in crowds. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2423–2430. [Google Scholar]
- Lempitsky, V.; Zisserman, A. Learning to count objects in images. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010; pp. 1324–1332. [Google Scholar]




| Estimation Network | RMSE | MAE |
|---|---|---|
| Estimation network with pooling layers (Figure 3a) | 175.75 | 144.6 |
| Backbone network (Figure 3b) | 170.71 | 128.31 |
| Backbone network with forward connections () | 166.53 | 116.66 |
| Backbone network with forward connections () | 171.19 | 122.11 |
| Backbone network with forward connections () | 176.04 | 130.21 |
| Backbone network with backward connections () | 165.56 | 87.31 |
| Backbone network with backward connections () | 172.22 | 123.96 |
| Backbone network with backward connections () | 280.13 | 256.41 |
| Estimation Networks | ShanghaiTech A | ShanghaiTech B | UCF_CC_50 | TRANCOS | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| MCNN [4] | 173.2 | 110.2 | 41.1 | 26.2 | 509.1 | 377.6 | 18.28 | 11.05 |
| CP-CNN [18] | 106.2 | 73.6 | 30.1 | 20.1 | - | - | - | - |
| Switching-CNN [2] | 135 | 90.4 | 33.4 | 21.6 | - | - | - | - |
| HSRNet [19] | 100.3 | 62.3 | 11.8 | 7.2 | - | - | - | - |
| Deep-stacked [20] | 150.6 | 93.9 | 33.9 | 18.7 | - | - | - | - |
| C-CNN [21] | 141.7 | 88.7 | 22.1 | 14.9 | - | - | - | - |
| Rodriguez et al. [22] | - | - | - | - | 487.1 | 493.4 | - | - |
| Lempitsky et al. [23] | - | - | - | - | 541.6 | 419.5 | - | - |
| Hydra net [1] | - | - | - | - | - | - | 16.74 | 10.99 |
| TraCount [5] | - | - | - | - | - | - | 11.85 | 8.12 |
| Proposed method | 165.56 | 87.31 | 19.41 | 15.76 | 507.96 | 358.83 | 10.65 | 7.38 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sooksatra, S.; Kondo, T.; Bunnun, P.; Yoshitaka, A. Redesigned Skip-Network for Crowd Counting with Dilated Convolution and Backward Connection. J. Imaging 2020, 6, 28. https://doi.org/10.3390/jimaging6050028
Sooksatra S, Kondo T, Bunnun P, Yoshitaka A. Redesigned Skip-Network for Crowd Counting with Dilated Convolution and Backward Connection. Journal of Imaging. 2020; 6(5):28. https://doi.org/10.3390/jimaging6050028
Chicago/Turabian StyleSooksatra, Sorn, Toshiaki Kondo, Pished Bunnun, and Atsuo Yoshitaka. 2020. "Redesigned Skip-Network for Crowd Counting with Dilated Convolution and Backward Connection" Journal of Imaging 6, no. 5: 28. https://doi.org/10.3390/jimaging6050028
APA StyleSooksatra, S., Kondo, T., Bunnun, P., & Yoshitaka, A. (2020). Redesigned Skip-Network for Crowd Counting with Dilated Convolution and Backward Connection. Journal of Imaging, 6(5), 28. https://doi.org/10.3390/jimaging6050028





