Automatic Recognition of Dendritic Solidification Structures: DenMap
Abstract
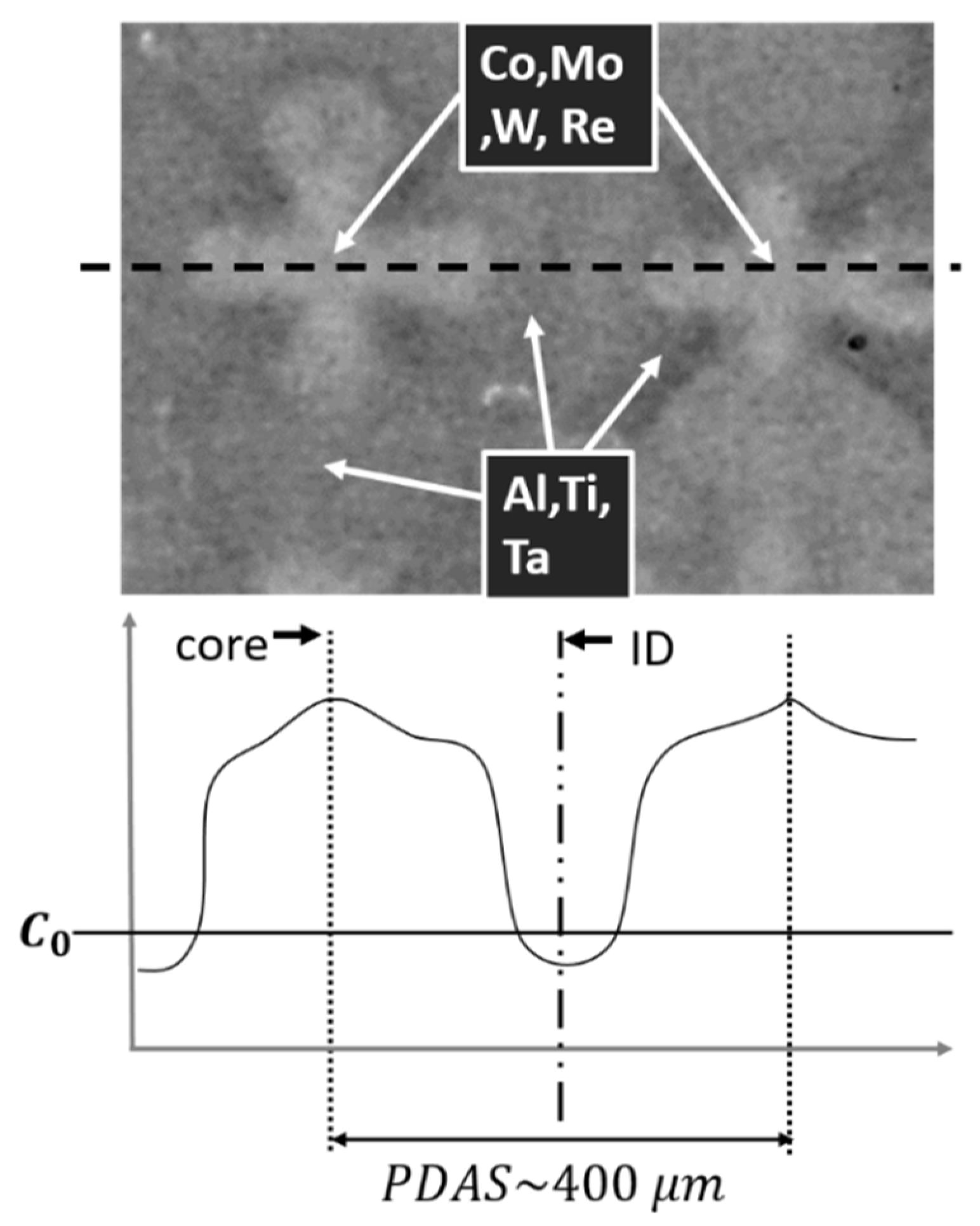
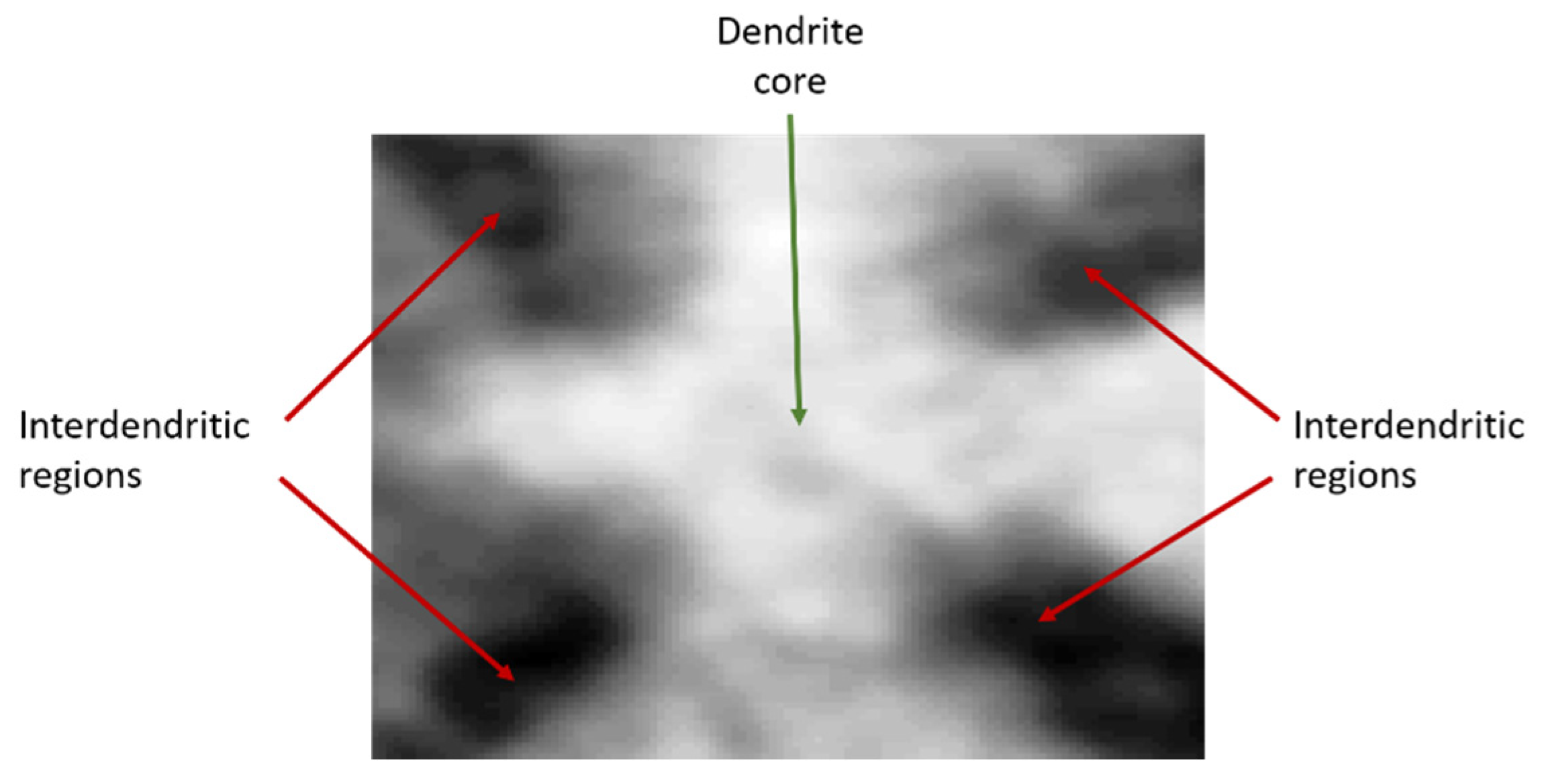
1. Introduction
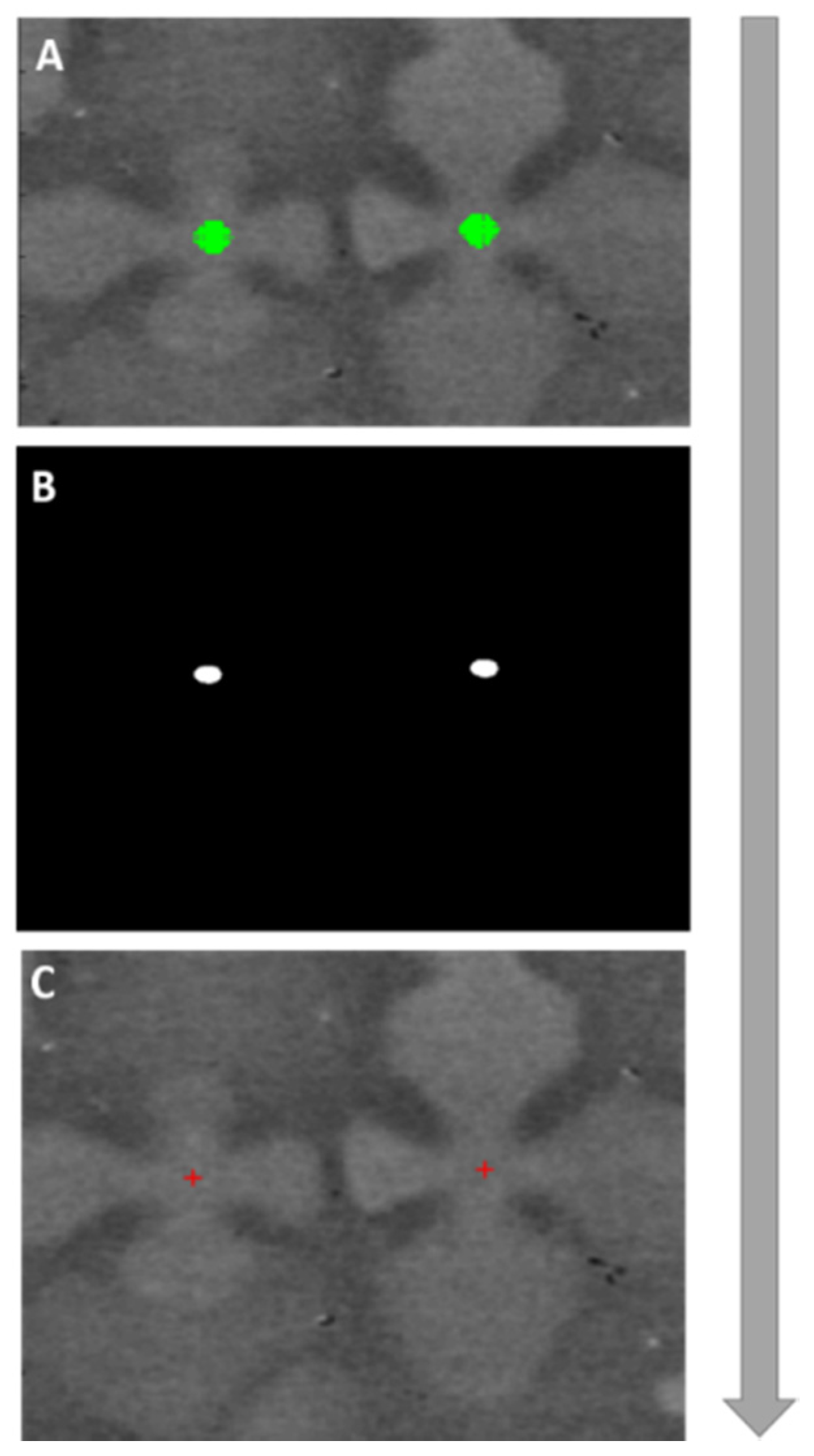
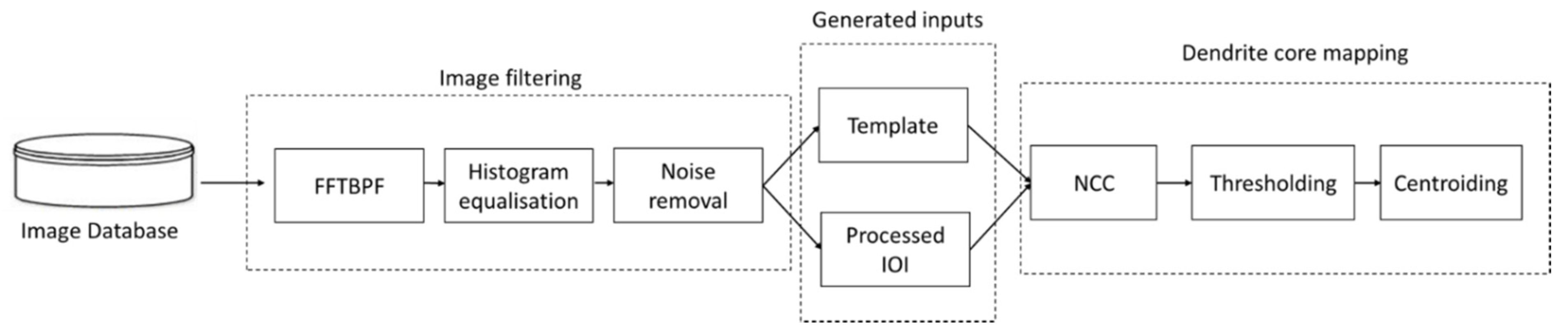
2. DenMap—Algorithm for Auto-Detection of Dendrite Cores
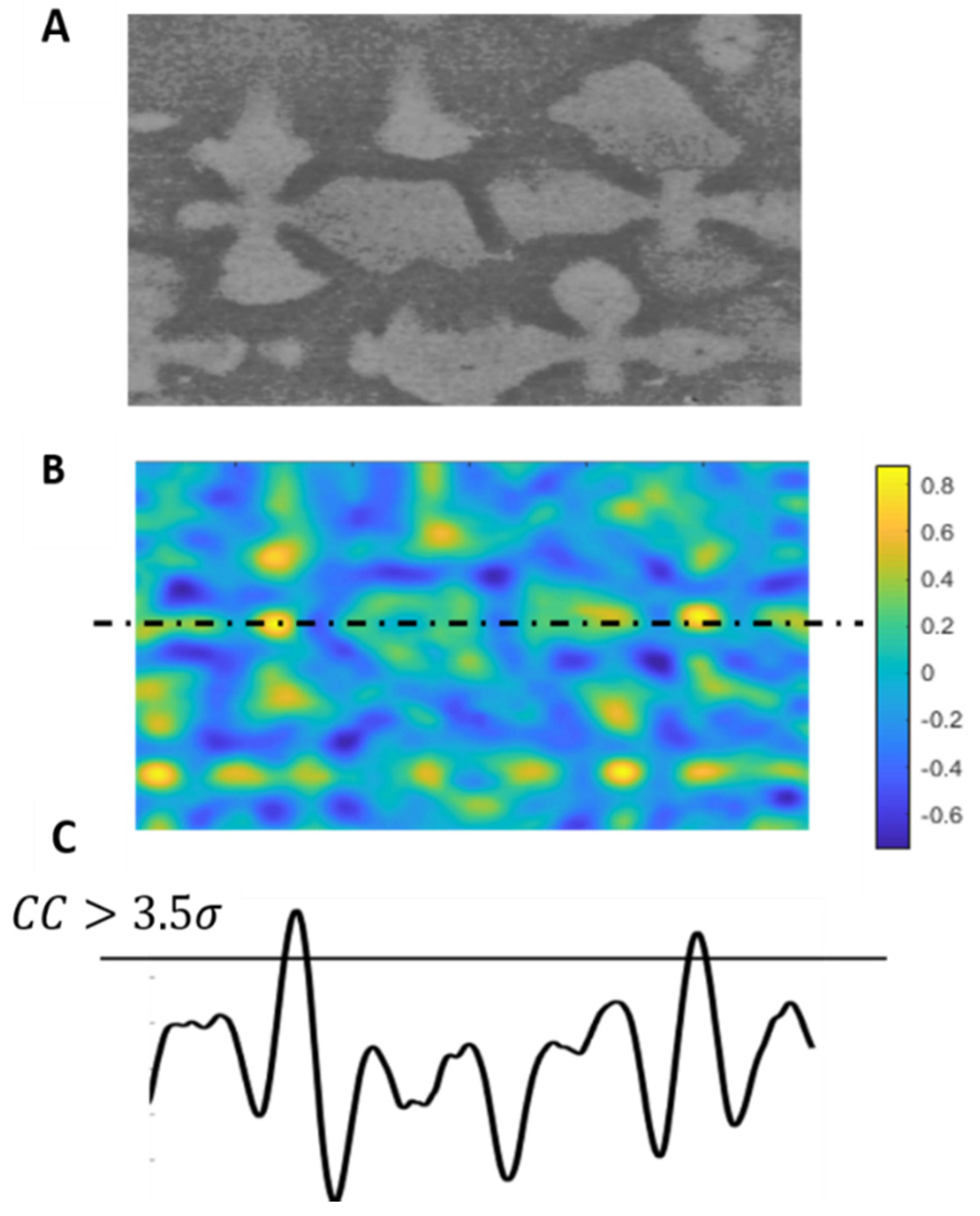
2.1. Normalised Cross-Correlation (NCC) Algorithm
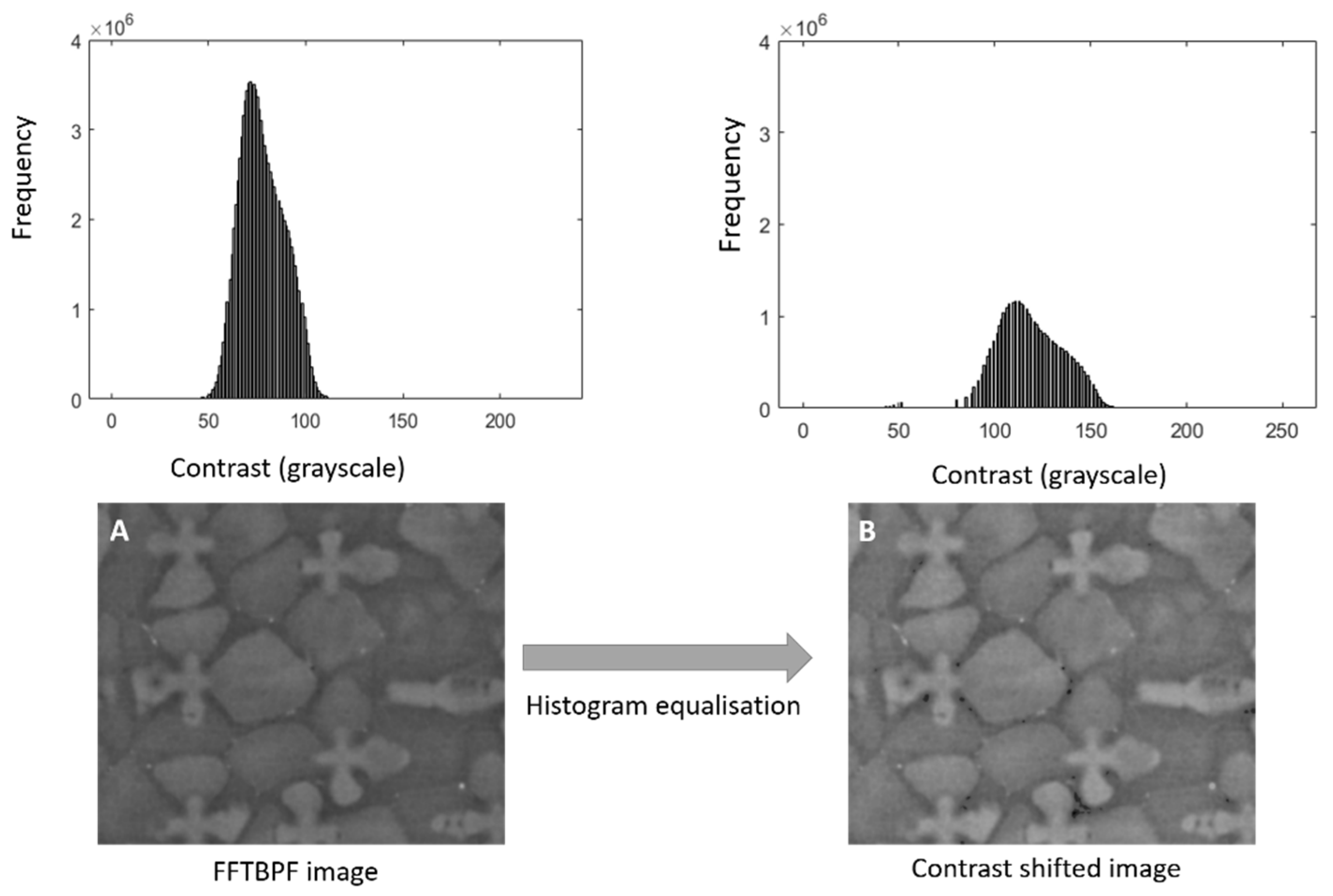
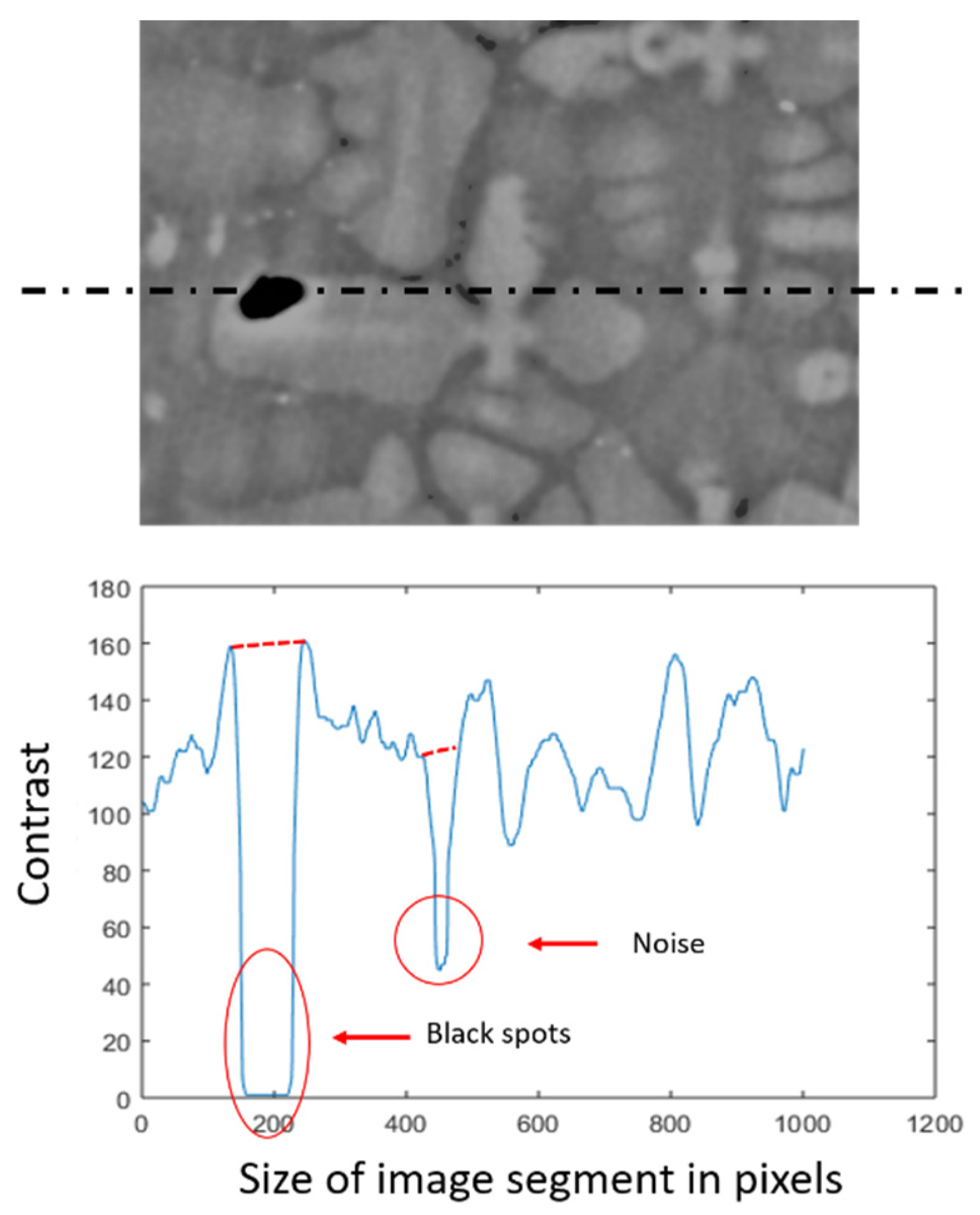
2.2. Filtering—Improving Accuracy
2.3. Thresholding for Sequential Similarity Detection (SSDA)
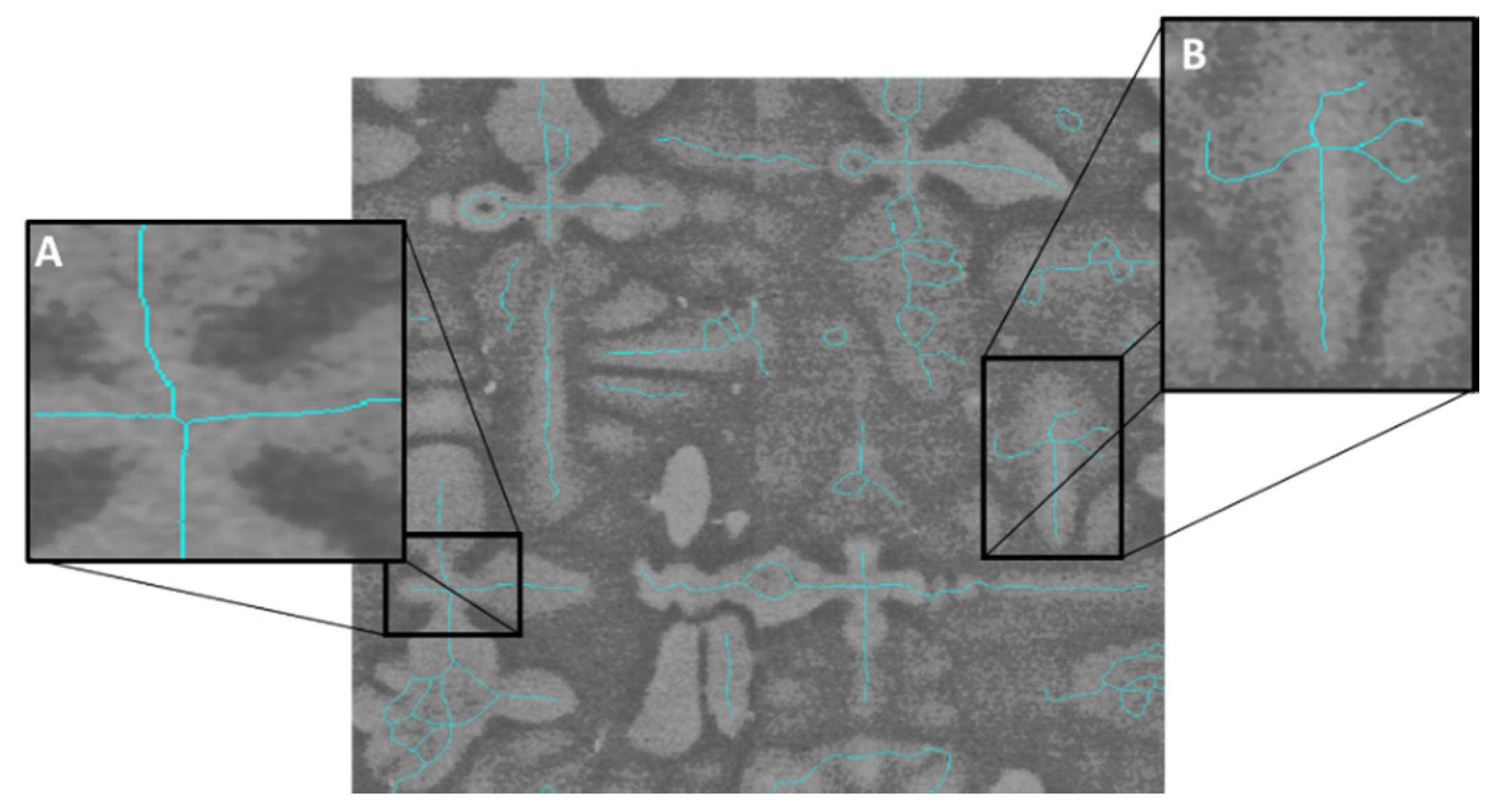
3. Testing and DenMap Performance
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Matache, G.; Stefanescu, D.; Puscasu, C.; Alexandrescu, E. Dendritic segregation and arm spacing in directionally solidified CMSX-4 superalloy. Int. J. Cast Met. Res. 2016, 29, 303–316. [Google Scholar] [CrossRef]
- Epishin, A.; Link, T.; Bruckner, U.; Fedelich, B.; Portella, P.D. Effects of segregation in nickel-base superalloys: Dendritic stresses. Superalloys 2004, 2004, 537–543. [Google Scholar]
- Giamei, A.F.; Kear, B.H. On the nature of freckles in nickel base superalloys. Metall. Trans. 1970, 1, 2185–2192. [Google Scholar] [CrossRef]
- Ridolfi, M.R.; Tassa, O.; de Rosa, G. Study on the formation of stray grains during directional solidification of nickel-based superalloys. Mater. Sci. Forum 2017, 879, 1582–1587. [Google Scholar] [CrossRef]
- Dai, H.J.; Dong, H.B.; Atkinson, H.; Lee, P. Simulation of the Columnar-to-Equiaxed Transition in Alloy Solidification—The Effect of Nucleation Undercooling, Density of Nuclei in Bulk Liquid and Alloy Solidification Range on the Transition. Solid State Phenom. 2008, 139, 129–134. [Google Scholar] [CrossRef]
- Santos, G.A.; Goulart, P.R.; Couto, A.A.; Garcia, A. Primary Dendrite ARM Spacing Effects upon Mechanical Properties of an AL–3Wt%CU–1Wt%LI Alloy. In Properties and Characterization of Modern Materials; Öchsner, A., Altenbach, H., Eds.; Springer Singapore: Singapore, 2017; pp. 215–229. [Google Scholar]
- Somboonsuk, K.; Mason, J.T.; Trivedi, R. Interdendritic spacing: Part I. experimental studies. Metall. Mater. Trans. A 1984, 15, 967–975. [Google Scholar] [CrossRef]
- Somboonsuk, K.; Trivedi, R. Dynamical studies of dendritic growth. Acta Metall. 1985, 33, 1051–1060. [Google Scholar] [CrossRef]
- Trivedi, R.; Somboonsuk, K. Pattern formation during the directional solidification of binary systems. Acta Metall. 1985, 33, 1061–1068. [Google Scholar] [CrossRef]
- Kearsey, R.M.; Beddoes, J.C.; Jones, P.; Au, P. Compositional design considerations for microsegregation in single crystal superalloy systems. Intermetallics 2004, 12, 903–910. [Google Scholar] [CrossRef]
- McCartney, D.G.; Hunt, J.D. Measurements of cell and primary dendrite arm spacings in directionally solidified aluminium alloys. Acta Metall. 1981, 29, 1851–1863. [Google Scholar] [CrossRef]
- Flemings, M.C. Solidification processing. Metall. Trans. 1974, 5, 2121–2134. [Google Scholar] [CrossRef]
- Jacobi, H.; Schwerdtfeger, K. Dendrite morphology of steady state unidirectionally solidified steel. Metall. Trans. A 1976, 7, 811–820. [Google Scholar] [CrossRef]
- Tschopp, M.; Oppedal, A.L.; Miller, J.D.; Groeber, M.A.; Rosenberger, A.H.; Solanki, K. Characterizing primary dendritic microstructures to quantify the processing-structure-property relationship in single crystal nickel-based superalloys. TMS Annu. Meet. 2013, 2013, 301–310. [Google Scholar]
- Tschopp, M.A.; Miller, J.D.; Oppedal, A.L.; Solanki, K.N. Characterizing the local primary dendrite arm spacing in directionally solidified dendritic microstructures. Metall. Mater. Trans. A 2014, 45, 426–437. [Google Scholar] [CrossRef]
- Tschopp, M.A.; Miller, J.D.; Oppedal, A.L.; Solanki, K.N. Evaluating local primary dendrite arm spacing characterization techniques using synthetic directionally solidified dendritic microstructures. Metall. Mater. Trans. A 2015, 46, 4610–4628. [Google Scholar] [CrossRef]
- Tiryakioğlu, M. On the statistical distribution of primary and secondary dendrite arm spacing in cast metals. Mater. Sci. Technol. 2019, 35, 509–511. [Google Scholar] [CrossRef]
- Takaki, T.; Sakane, S.; Ohno, M.; Shibuta, Y.; Shimokawabe, T.; Aoki, T. Primary arm array during directional solidification of a single-crystal binary alloy: Large-scale phase-field study. Acta Mater. 2016, 118, 230–243. [Google Scholar] [CrossRef]
- Warnken, N.; Reed, R.C. On the characterization of directionally solidified dendritic microstructures. Metall. Mater. Trans. A 2011, 42, 1675–1683. [Google Scholar] [CrossRef]
- Miller, J.; Strangwood, M.; Steinbach, S.; Warnken, N. Skeletonisation to Find the Centre of Dendrites Traced from a 2D Microstructural Image. Solidif. Process. 2017, 2017, 1–4. [Google Scholar]
- Sa, I.; Ge, Z.; Dayoub, F.; Upcroft, B.; Perez, T.; McCool, C. DeepFruits: A fruit detection system using deep neural networks. Sensors 2016, 16, 1222. [Google Scholar] [CrossRef]
- Lewis, J.P. Fast normalized cross-correlation. Ind. Light Magic 2001, 10. [Google Scholar]
- Hemalatha, R.; Thamizhvani, T.; Dhivya, A.J.A.; Joseph, J.E.; Babu, B.; Chandrasekaran, R. Active contour based segmentation techniques for medical image analysis. Med Biol. Image Anal. 2018, 17. [Google Scholar] [CrossRef]
- Xu, C.; Prince, J.L. Snakes, shapes, and gradient vector flow. IEEE Trans. Image Process. 1998, 7, 359–369. [Google Scholar] [PubMed]
- Tsai, D.M.; Lin, C.T. Fast normalized cross correlation for defect detection. Pattern Recognit. Lett. 2003, 24, 2625–2631. [Google Scholar] [CrossRef]
- Fitch, A.J.; Kadyrov, A.; Christmas, W.J.; Kittler, J. Fast robust correlation. IEEE Trans. Image Process. 2005, 14, 1063–1073. [Google Scholar] [CrossRef] [PubMed]
- Tsai, D.M.; Lai, S.C. Defect detection in periodically patterned surfaces using independent component analysis. Pattern Recognit. 2008, 41, 2812–2832. [Google Scholar] [CrossRef]
- Feng, Z.; Qingming, H.; Wen, G. Image matching by normalized cross-correlation. In Proceedings of the 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 14–19 May 2006; Volume 2. [Google Scholar]
- Zhao, F.; Huang, Q.; Wang, H.; Gao, W. MOCC: A fast and robust correlation-based method for interest point matching under large scale changes. EURASIP J. Adv. Signal Process. 2010, 2010, 410628. [Google Scholar] [CrossRef][Green Version]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]
- Gayer, A.; Saya, A.; Shiloh, A. Automatic recognition of welding defects in real-time radiography. NDT Int. 1990, 23, 131–136. [Google Scholar] [CrossRef]
- Barnea, D.I.; Silverman, H.F. A Class of Algorithms for Fast Digital Image Registration. IEEE Trans. Comput. 1972, 21, 179–186. [Google Scholar] [CrossRef]



| Sample Code | Image Resolution | Total Number of Cores | Numbers of Detected Cores | False Positives | Missed out Cores | Accuracy (%) |
|---|---|---|---|---|---|---|
| P73L | 4772 × 7005 | 224 | 221 | 0 | 3 | 98.7 |
| P73R | 6550 × 7002 | 266 | 268 | 3 | 1 | 98.5 |
| P82L | 5592 × 8369 | 250 | 250 | 2 | 2 | 98.4 |
| P82ZL | 5556 × 8423 | 247 | 248 | 2 | 1 | 98.8 |
| P82ZR | 6553 × 7033 | 243 | 236 | 0 | 7 | 97.1 |
| R13AL | 5595 × 5641 | 252 | 253 | 3 | 2 | 98.0 |
| R13AR | 5620 × 5633 | 255 | 257 | 3 | 1 | 98.4 |
| R13ZL | 4690 × 7044 | 209 | 210 | 2 | 1 | 98.6 |
| R13ZR | 5633 × 7031 | 256 | 257 | 2 | 1 | 98.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nenchev, B.; Strickland, J.; Tassenberg, K.; Perry, S.; Gill, S.; Dong, H. Automatic Recognition of Dendritic Solidification Structures: DenMap. J. Imaging 2020, 6, 19. https://doi.org/10.3390/jimaging6040019
Nenchev B, Strickland J, Tassenberg K, Perry S, Gill S, Dong H. Automatic Recognition of Dendritic Solidification Structures: DenMap. Journal of Imaging. 2020; 6(4):19. https://doi.org/10.3390/jimaging6040019
Chicago/Turabian StyleNenchev, Bogdan, Joel Strickland, Karl Tassenberg, Samuel Perry, Simon Gill, and Hongbiao Dong. 2020. "Automatic Recognition of Dendritic Solidification Structures: DenMap" Journal of Imaging 6, no. 4: 19. https://doi.org/10.3390/jimaging6040019
APA StyleNenchev, B., Strickland, J., Tassenberg, K., Perry, S., Gill, S., & Dong, H. (2020). Automatic Recognition of Dendritic Solidification Structures: DenMap. Journal of Imaging, 6(4), 19. https://doi.org/10.3390/jimaging6040019






