Multiple-Exposure Image Fusion for HDR Image Synthesis Using Learned Analysis Transformations †
Abstract
1. Introduction
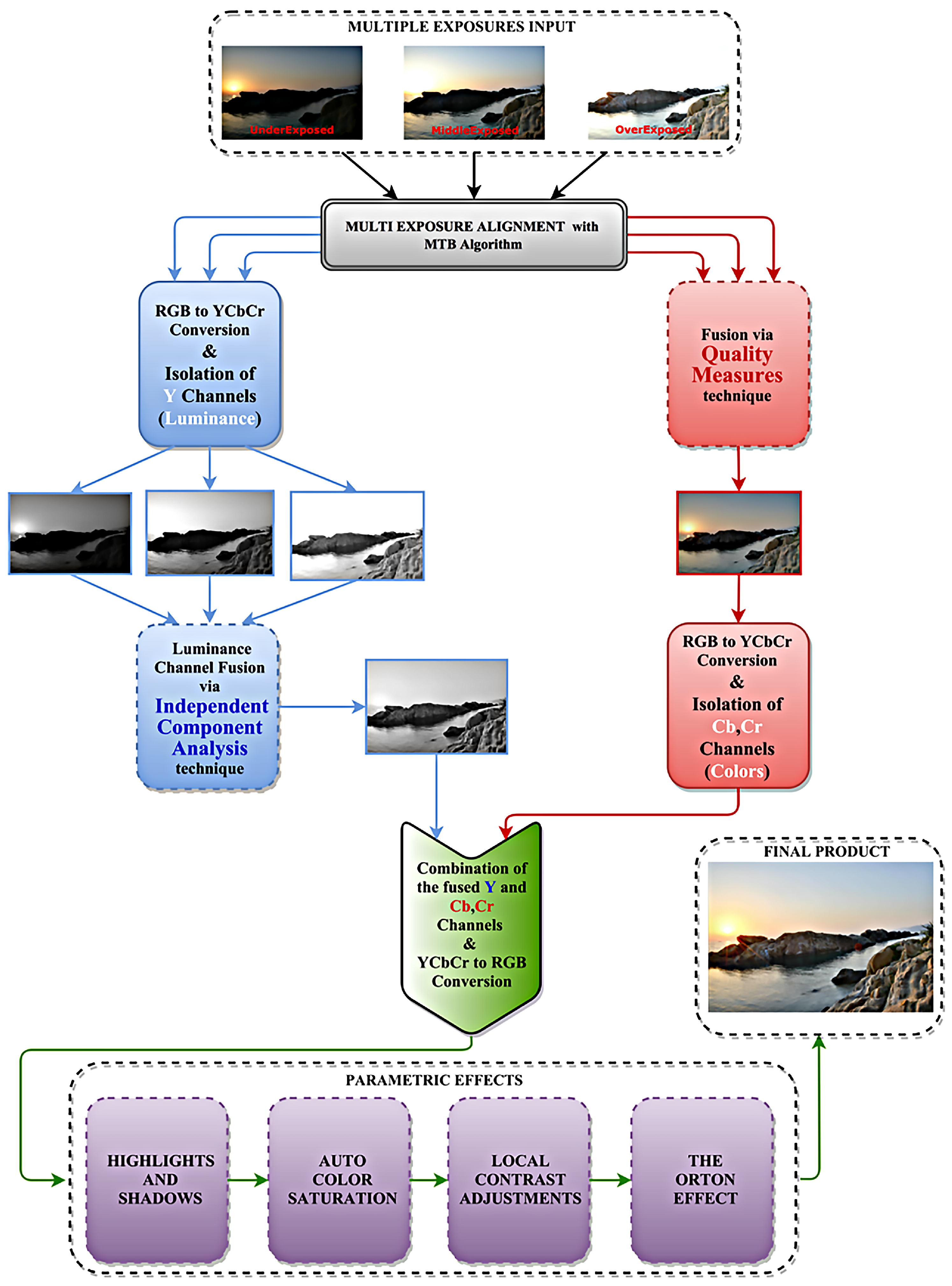
2. The Proposed Multiple-Exposure Image-Fusion System
2.1. Image Alignment—Color System Conversion
2.2. Luminance Channels Fusion
Fusion in the ICA Domain
2.3. Color Channels Fusion
- Contrast: a Laplacian edge-detection filter is applied to the grayscale version of each exposure. The grayscale version is estimated by forming a weighted sum of the and B components in the form: . The absolute value of this filter response results in the index C that is used to define the image’s contrast. This simple procedure produces large weights on edges and texture, i.e., emphasizing the existence of these image elements.
- Color saturation: When a picture gets more exposed, colors tend to lose their sharpness and get more saturated. In this case, the image becomes more vivid, thus saturated colors must be preserved in general. Therefore, we estimate a measurement of color saturation S, which is based on the standard deviation of the R, G, and B channels of a neighborhood around each pixel.
- Well-exposedness: The intensity channel can highlight whether a pixel is well exposed or not. The main aim of this metric is to retain intensities that are not close to zero (under-exposed intensities) or close to one (over-exposed). Each pixel intensity x is weighted by a factor that depends on its distance to 0.5. This is performed by using the Gaussian function curve: , where is usually equal to 0.2. The Gaussian curve is applied independently to both Cb and Cr channels. The two curves are then multiplied to create the well-exposedness measure E.
2.4. Fused Image Reconstruction and Post-Processing
3. Experiments
3.1. Methods Compared
3.2. Comparison Metric
3.3. Dataset and Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Debevec, P.E.; Malik, J. Recovering High Dynamic Range Radiance Maps from Photographs. In Proceedings of the ACM SIGGRAPH, Los Angeles, CA, USA, 11–15 August 2008. [Google Scholar]
- Reinhard, E.; Stark, M.; Shirley, P.; Ferwerda, J. Photographic tone reproduction for digital images. In Proceedings of the ACM SIGGRAPH, San Antonio, TX, USA, 23–26 July 2002. [Google Scholar]
- Mertens, T.; Kautz, J.; Reeth, F.V. Exposure Fusion. In Proceedings of the 15th Pacific Conference on Computer Graphics and Applications, Maui, HI, USA, 29 October–2 November 2007. [Google Scholar]
- Mitianoudis, N.; Stathaki, T. Optimal Contrast Correction for ICA-based Fusion of Multimodal Images. IEEE Sens. J. 2008, 8, 2016–2026. [Google Scholar] [CrossRef]
- Bogoni, L.; Hansen, M. Pattern-selective color image fusion. Pattern Recognit. 2001, 34, 1515–1526. [Google Scholar] [CrossRef]
- Vonikakis, V.; Bouzos, O.; Andreadis, I. Multi Exposure Image Fusion Based on Illumination Estimation. In Proceedings of the SIPA, Chania, Greece, 22–24 June 2011; pp. 135–142. [Google Scholar]
- Tico, M.; Gelfand, N.; Pulli, K. Motion-Blur-Free Exposure Fusion. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 3321–3324. [Google Scholar]
- Jinno, T.; Okuda, M. Multiple Exposure Fusion for High Dynamic Range Image Acquisition. IEEE Trans. Image Process. 2012, 21, 358–365. [Google Scholar] [CrossRef] [PubMed]
- Shen, R.; Cheng, I.; Shi, J.; Basu, A. Generalized Random Walks for Fusion of Multi-Exposure Images. IEEE Trans. Image Process. 2011, 20, 3634–3646. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Kang, X. Fast multi-exposure image fusion with median filter and recursive filter. IEEE Trans. Consum. Electron. 2012, 58, 626–632. [Google Scholar] [CrossRef]
- Mitianoudis, N.; Stathaki, T. Pixel-based and Region-based Image Fusion schemes using ICA bases. Inf. Fusion 2007, 8, 131–142. [Google Scholar] [CrossRef]
- Mitianoudis, N.; Antonopoulos, S.; Stathaki, T. Region-based ICA Image Fusion using Textural Information. In Proceedings of the Region-based ICA Image Fusion using Textural Information (DSP2013), Fira, Greece, 1–3 July 2013. [Google Scholar]
- Piella, G. A general framework for multiresolution image fusion: From pixels to regions. Inf. Fusion 2003, 4, 259–280. [Google Scholar] [CrossRef]
- Farid, M.S.; Mahmood, A.; Al-Maadeed, S.A. Multi-focus image fusion using Content Adaptive Blurring. Inf. Fusion 2019, 45, 96–112. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Y.; Blum, R.S.; Han, J.; Tao, D. Sparse representation based multi-sensor image fusion for multi-focus and multi-modality images: A review. Inf. Fusion 2018, 40, 57–75. [Google Scholar] [CrossRef]
- Merianos, I.; Mitianoudis, N. A Hybrid Multiple Exposure Image Fusion Approach for HDR Image Synthesis. In Proceedings of the 2016 IEEE International Conference on Imaging Systems and Techniques (IST), Chania, Greece, 4–6 October 2016. [Google Scholar]
- Ward, G. Fast, Robust Image Registration for Compositing High Dynamic Range Photographs from Handheld Exposures. J. Graph. Tools 2003, 8, 17–30. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Hoyer, P.O.; Oja, E. Image Denoising by Sparse Code Shrinkage. In Intelligent Signal Processing; Haykin, S., Kosko, B., Eds.; IEEE Press: Piscataway, NJ, USA, 2001. [Google Scholar]
- Hyvärinen, A.; Karhunen, J.; Oja, E. Independent Component Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the Sixth International IEEE Conference on Computer Vision, Bombay, India, 4–7 January 1998; pp. 839–846. [Google Scholar]
- Sarkar, A.; Caviedes, J.; Subedar, M. Joint Enhancement of Lightness, Color and Contrast of Images and Video. U.S. Patent US8,477,247 B2, 22 May 2013. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Pearson: London, UK, 2017. [Google Scholar]
- Orton, M. The Orton Effect. 2012. Available online: http://www.michaelortonphotography.com/ ortoneffect.html (accessed on 22 February 2019).
- Raman, S.; Chaudhuri, S. Bilateral Filter Based Compositing for Variable Exposure Photography. In Proceedings of the Eurographics, Munich, Germany, 30 March–3 April 2009; pp. 1–4. [Google Scholar]
- Ma, K.; Zeng, K.; Wang, Z. Perceptual Quality Assessment for Multi-Exposure Image Fusion. IEEE Trans. Image Process. 2015, 24, 3345–3356. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, R.; Peleg, T.; Elad, M. Analysis K-SVD: A Dictionary-Learning Algorithm for the Analysis Sparse Model. IEEE Trans. Signal Process. 2013, 61, 661–677. [Google Scholar] [CrossRef]
- Dai, W.; Xu, T.; Wang, W. Simultaneous Codeword Optimisation (SimCO) for Dictionary Update and Learning. IEEE Trans. Signal Process. 2012, 60, 6340–6353. [Google Scholar] [CrossRef]
- Dong, J.; Wang, W.; Dai, W.; Plumbley, M.; Han, Z. Analysis SimCO algorithms for sparse analysis model based dictionary learning. IEEE Trans. Signal Process. 2016, 64, 417–431. [Google Scholar] [CrossRef]






| Method | Illumination Estimation [6] | HybridHDR | DynamicPhoto | Mertens [3] | Raman [25] | FMMR [10] |
|---|---|---|---|---|---|---|
| Flowers | 0.9675 | 0.9720 | 0.9705 | 0.9642 | 0.9064 | 0.9215 |
| Mask | 0.9531 | 0.9748 | 0.9777 | 0.9323 | 0.9163 | 0.9335 |
| SeaRock | 0.9562 | 0.9444 | 0.8822 | 0.9316 | 0.8964 | 0.9133 |
| Paris | 0.9643 | 0.9662 | 0.9698 | 0.9522 | 0.853 | 0.8935 |
| Sec.Beach | 0.9624 | 0.9381 | 0.9360 | 0.9508 | 0.9270 | 0.8884 |
| Garden | 0.9536 | 0.9588 | 0.9724 | 0.9369 | 0.9010 | 0.946 |
| Kluki | 0.9605 | 0.9552 | 0.9652 | 0.9601 | 0.8988 | 0.9352 |
| Hills | 0.9665 | 0.9671 | 0.9686 | 0.9386 | 0.9166 | 0.8661 |
| OldHouse | 0.9669 | 0.9770 | 0.9753 | 0.9743 | 0.9591 | 0.907 |
| SeaCave | 0.9706 | 0.9641 | 0.9491 | 0.9336 | 0.8813 | 0.9133 |
| Average | 0.9621 | 0.9617 | 0.9566 | 0.9474 | 0.9088 | 0.9188 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merianos, I.; Mitianoudis, N. Multiple-Exposure Image Fusion for HDR Image Synthesis Using Learned Analysis Transformations. J. Imaging 2019, 5, 32. https://doi.org/10.3390/jimaging5030032
Merianos I, Mitianoudis N. Multiple-Exposure Image Fusion for HDR Image Synthesis Using Learned Analysis Transformations. Journal of Imaging. 2019; 5(3):32. https://doi.org/10.3390/jimaging5030032
Chicago/Turabian StyleMerianos, Ioannis, and Nikolaos Mitianoudis. 2019. "Multiple-Exposure Image Fusion for HDR Image Synthesis Using Learned Analysis Transformations" Journal of Imaging 5, no. 3: 32. https://doi.org/10.3390/jimaging5030032
APA StyleMerianos, I., & Mitianoudis, N. (2019). Multiple-Exposure Image Fusion for HDR Image Synthesis Using Learned Analysis Transformations. Journal of Imaging, 5(3), 32. https://doi.org/10.3390/jimaging5030032






