Evaluating the Performance of Structure from Motion Pipelines
Abstract
1. Introduction
2. Review of Structure from Motion
2.1. SfM Building Blocks
2.2. Incremental SfM Pipelines
3. Evaluation Method for SfM 3D Reconstruction
- Alignment and registration
- Evaluation of sparse point cloud
- Evaluation of camera pose
- Evaluation of dense point cloud
3.1. Alignment and Registration
- For each point of the cloud to be aligned, look for the nearest point in the reference cloud.
- Search for a transformation (rotation and translation) that globally minimizes the distance (measured by RMSE) between the pairs of points identified in the previous step; it can include the removal of statistical outliers and pairs of points whose distance exceeds a given maximum allowed limit.
- Align the point clouds using the results from previous step.
- If the stop criterion has been verified, terminate and return the identified optimal transformation; otherwise re-iterate all phases.
3.2. Evaluation of Sparse Point Cloud
3.3. Evaluation of Camera Pose
3.4. Evaluation of Dense Point Cloud
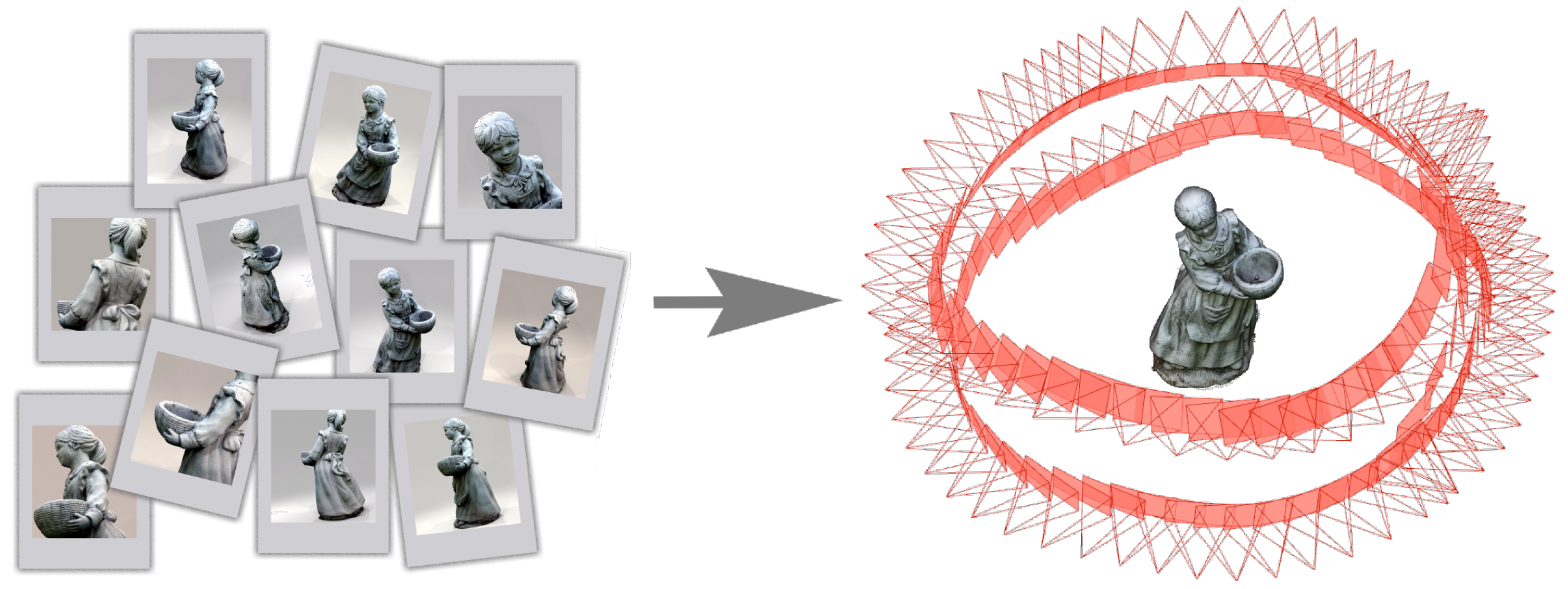
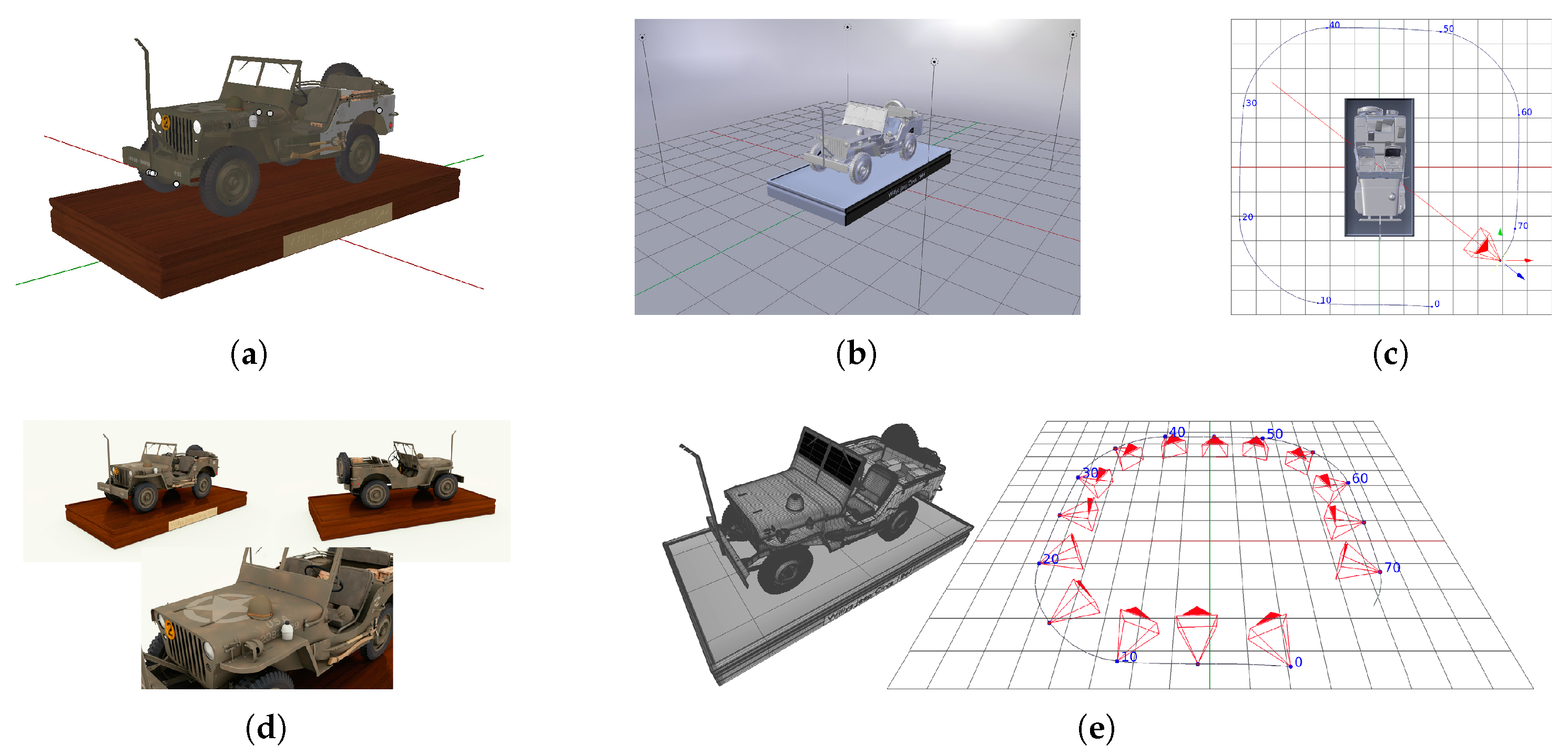
4. Synthetic Datasets Creation and Pipeline Evaluation: Blender Plug-In
- import the main object of the reconstruction and setup a scene with lights for illumination and uniform background walls. Also, the parameters for the path tracing rendering engine are set.
- add a camera and setup its intrinsic calibration parameters. Animate the camera using circular rotations around the object to observe the scene from different view points.
- render the set of images and add EXIF metadata of intrinsic camera parameters used by SfM pipelines.
- eventually, geometry ground truth can be exported. This is not necessary if next steps are processed using this plug-in as the current scene will be used as ground truth.
- run the SfM pipelines listed in Section 2.2.
- import the reconstructed point cloud form SfM output and allow the user to manually eliminate parts that do not belong to the main object of the reconstruction.
- align the reconstructed point cloud to the ground truth using the Iterative Closest Point algorithm (ICP).
- evaluate the reconstructed cloud by computing the distance between the cloud and the ground truth and generating statistical information like min, max and average distance values and also reconstructed point count.
5. Experimental Results
- Statue [67]—set of images about a statue of height 10.01 m, composed of 121 images
- Empire Vase [68]—set of images about an ancient vase of height 0.92 m, composed of 86 images
- Bicycle [69]—set of images about a bicycle of height 2.66 m, composed of 86 images
- Hydrant [70]—set of images about an hydrant of height 1.00 m, composed of 66 images
- Jeep [71]—set of images about a miniature jeep of height 2.48 m, composed of 141 images
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Real Datasets Creation: Guidelines
- The object to be reconstructed must not have a too uniform geometry and must have a varied texture. If the object has a uniform geometry and a repeated or monochromatic texture it becomes difficult for the SfM pipeline to correctly estimate the pose of the cameras that have acquired the images.
- The set must be composed of a number of images sufficient to cover the entire surface of the object to be rebuilt. Parts of the object not included in the dataset cannot be reconstructed; thus resulting in a geometry with missing parts or not accurately reconstructed.
- The images must portray, at least in pairs, common parts of the object to be rebuilt. If an area of the object is included only in a single image, it is not possible to correctly estimate 3D points for the reconstruction. Depending on the implementation of the pipeline, the reconstruction could improve with the increase of images that portray the same portion of the object from different view points; this because the 3D points can be estimated and confirmed through multiple images.
- The quality of the reconstruction also depends on the quality of the images. Sets of images with a good resolution and level of detail should lead to a good reconstruction. The use of poor quality or wide-angle optics requires that the reconstruction pipelines take into account the presence of radial distortions.
- The intrinsic parameters of the camera must be known for each image. In particular, the pipelines makes use of focal length, sensor size and image size to estimate the distance of the observed points and to generate the sparse point cloud. If the sensor size is unknown, the focal length in 35 mm format can be used.The accuracy of the intrinsic calibration parameters is of particular importance when the images composing the dataset have been acquired with different cameras; the imprecision of these parameters introduces imprecisions in camera pose estimation and points triangulation. It should also be taken into consideration that if the images have been cropped, the original intrinsic calibration parameters are no longer valid and must be recalculated.
- Along with the images, ground truth must also be available. This is not necessary for the reconstruction but is used to evaluate the quality of the obtained results.In order to be able to globally evaluate the SfM+MVS pipeline, it is sufficient to have the ground truth of the model to be reconstructed in the form of a mesh or a dense points cloud; this allows to compare the geometries.To make a better evaluation of the SfM pipeline, it is also necessary to know the actual camera pose of each image of the dataset. In this way, by comparing the ground truth with the reconstruction, it is possible to provide a measure of the accuracy of the estimated camera poses.
References
- Poznanski, A. Visual Revolution of the Vanishing of Ethan Carter. 2014. Available online: http://www.theastronauts.com/2014/03/visual-revolution-vanishing-ethan-carter/ (accessed on 18 June 2018).
- Hamilton, A.; Brown, K. Photogrammetry and Star Wars Battlefront. 2016. Available online: https://www.ea.com/frostbite/news/photogrammetry-and-star-wars-battlefront (accessed on 18 June 2018).
- Saurer, O.; Fraundorfer, F.; Pollefeys, M. OmniTour: Semi-automatic generation of interactive virtual tours from omnidirectional video. In Proceedings of the 3DPVT2010 (International Symposium on 3D Data Processing, Visualization and Transmission), Paris, France, 17–20 May 2010. [Google Scholar]
- Nocerino, E.; Lago, F.; Morabito, D.; Remondino, F.; Porzi, L.; Poiesi, F.; Rota Bulo, S.; Chippendale, P.; Locher, A.; Havlena, M.; et al. A smartphone-based 3D pipeline for the creative industry-The replicate eu project. 3D Virtual Reconstr. Vis. Complex Arch. 2017, 42, 535–541. [Google Scholar] [CrossRef]
- Muratov, O.; Slynko, Y.; Chernov, V.; Lyubimtseva, M.; Shamsuarov, A.; Bucha, V. 3DCapture: 3D Reconstruction for a Smartphone. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 75–82. [Google Scholar]
- SmartMobileVision. SCANN3D. Available online: http://www.smartmobilevision.com (accessed on 18 June 2018).
- Bernardini, F.; Bajaj, C.L.; Chen, J.; Schikore, D.R. Automatic reconstruction of 3D CAD models from digital scans. Int. J. Comput. Geom. Appl. 1999, 9, 327–369. [Google Scholar] [CrossRef]
- Izadi, S.; Kim, D.; Hilliges, O.; Molyneaux, D.; Newcombe, R.; Kohli, P.; Shotton, J.; Hodges, S.; Freeman, D.; Davison, A.; et al. KinectFusion: Real-time 3D reconstruction and interaction using a moving depth camera. In Proceedings of the 24th Annual ACM Symposium on User Interface Software and Technology, Santa Barbara, CA, USA, 16–19 October 2011; ACM: New York, NY, USA, 2011; pp. 559–568. [Google Scholar]
- Starck, J.; Hilton, A. Surface capture for performance-based animation. IEEE Comput. Graph. Appl. 2007, 27, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Carlbom, I.; Terzopoulos, D.; Harris, K.M. Computer-assisted registration, segmentation, and 3D reconstruction from images of neuronal tissue sections. IEEE Trans. Med. Imaging 1994, 13, 351–362. [Google Scholar] [CrossRef] [PubMed]
- Noh, Z.; Sunar, M.S.; Pan, Z. A Review on Augmented Reality for Virtual Heritage System; Springer: Berlin/Heidelberg, Germany, 2009; pp. 50–61. [Google Scholar]
- Remondino, F. Heritage recording and 3D modeling with photogrammetry and 3D scanning. Remote Sens. 2011, 3, 1104–1138. [Google Scholar] [CrossRef]
- Özyeşil, O.; Voroninski, V.; Basri, R.; Singer, A. A survey of structure from motion. Acta Numer. 2017, 26, 305–364. [Google Scholar] [CrossRef]
- Schönberger, J.L.; Frahm, J.M. Structure-from-Motion Revisited. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Ko, J.; Ho, Y.S. 3D Point Cloud Generation Using Structure from Motion with Multiple View Images. In Proceedings of the The Korean Institute of Smart Media Fall Conference, Kwangju, South Korea, 28–29 October 2016; pp. 91–92. [Google Scholar]
- Wu, C. Towards linear-time incremental structure from motion. In Proceedings of the 2013 International conference on IEEE 3D Vision-3DV 2013, Seattle, WA, USA, 29 June–1 July 2013; pp. 127–134. [Google Scholar]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Photo tourism: Exploring photo collections in 3D. ACM Trans. Graph. (TOG) 2006, 25, 835–846. [Google Scholar] [CrossRef]
- Furukawa, Y.; Hernández, C. Multi-view stereo: A tutorial. Found. Trends Comput. Graph. Vis. 2015, 9, 1–148. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Moons, T.; Van Gool, L.; Vergauwen, M. 3D reconstruction from multiple images part 1: Principles. Found. Trends Comput. Graph. Vis. 2010, 4, 287–404. [Google Scholar] [CrossRef]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle adjustment—A modern synthesis. In International Workshop on Vision Algorithms; Springer: Berlin/Heidelberg, Germany, 1999; pp. 298–372. [Google Scholar]
- Schönberger, J.L.; Zheng, E.; Pollefeys, M.; Frahm, J.M. Pixelwise View Selection for Unstructured Multi-View Stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016. [Google Scholar]
- Sweeney, C. Theia Multiview Geometry Library: Tutorial & Reference. Available online: http://theia-sfm.org (accessed on 30 July 2018).
- Moulon, P.; Monasse, P.; Marlet, R.; OpenMVG. An Open Multiple View Geometry Library. Available online: https://github.com/openMVG/openMVG (accessed on 30 July 2018).
- Wu, C. VisualSFM: A Visual Structure from Motion System. 2011. Available online: http://ccwu.me/vsfm/ (accessed on 30 July 2018).
- Wu, C.; Agarwal, S.; Curless, B.; Seitz, S.M. Multicore bundle adjustment. In Proceedings of the 2011 IEEE Conference on IEEE Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 20–25 June 2011; pp. 3057–3064. [Google Scholar]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the world from internet photo collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef]
- Fuhrmann, S.; Langguth, F.; Goesele, M. MVE-A Multi-View Reconstruction Environment. In Proceedings of the Eurographics Workshop on Graphics and Cultural Heritage (GCH), Darmstadt, Germany, 6–8 October 2014; pp. 11–18. [Google Scholar]
- Zhao, L.; Huang, S.; Dissanayake, G. Linear SFM: A hierarchical approach to solving structure-from-motion problems by decoupling the linear and nonlinear components. ISPRS J. Photogramm. Remote Sens. 2018, 141, 275–289. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Gao, X.S.; Hou, X.R.; Tang, J.; Cheng, H.F. Complete solution classification for the perspective-three-point problem. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 930–943. [Google Scholar]
- Stewenius, H.; Engels, C.; Nistér, D. Recent developments on direct relative orientation. ISPRS J. Photogramm. Remote Sens. 2006, 60, 284–294. [Google Scholar] [CrossRef]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. Epnp: An accurate o (n) solution to the pnp problem. Int. J. Comput. Vis. 2009, 81, 155. [Google Scholar] [CrossRef]
- Agarwal, S.; Mierle, K. Ceres Solver. Available online: http://ceres-solver.org (accessed on 30 July 2018).
- Chum, O.; Matas, J. Matching with PROSAC-progressive sample consensus. In Proceedings of the Computer Society Conference on IEEE Computer Vision and Pattern Recognition (CVPR 2005), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 220–226. [Google Scholar]
- Schönberger, J.L.; Price, T.; Sattler, T.; Frahm, J.M.; Pollefeys, M. A vote-and-verify strategy for fast spatial verification in image retrieval. In Asian Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 321–337. [Google Scholar]
- Chum, O.; Matas, J.; Kittler, J. Locally optimized RANSAC. In Joint Pattern Recognition Symposium; Springer: Berlin/Heidelberg, Germany, 2003; pp. 236–243. [Google Scholar]
- Alcantarilla, P.F.; Solutions, T. Fast explicit diffusion for accelerated features in nonlinear scale spaces. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 1281–1298. [Google Scholar]
- Muja, M.; Lowe, D. Fast Approximate Nearest Neighbors with Automatic Algorithm Configuration. In Proceedings of the VISAPP 2009—4th International Conference on Computer Vision Theory and Applications, Lisboa, Portugal, 5–8 February 2009; Volume 1, pp. 331–340. [Google Scholar]
- Cheng, J.; Leng, C.; Wu, J.; Cui, H.; Lu, H. Fast and accurate image matching with cascade hashing for 3D reconstruction. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 1–8. [Google Scholar]
- Rousseeuw, P.J. Least Median of Squares Regression. J. Am. Stat. Assoc. 1984, 79, 871–880. [Google Scholar] [CrossRef]
- Moisan, L.; Moulon, P.; Monasse, P. Automatic homographic registration of a pair of images, with a contrario elimination of outliers. Image Proc. On Line 2012, 2, 56–73. [Google Scholar] [CrossRef]
- Hesch, J.A.; Roumeliotis, S.I. A direct least-squares (DLS) method for PnP. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 383–390. [Google Scholar]
- Lindstrom, P. Triangulation made easy. In Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010; pp. 1554–1561. [Google Scholar]
- Bujnak, M.; Kukelova, Z.; Pajdla, T. A general solution to the P4P problem for camera with unknown focal length. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2008), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Hartley, R.I.; Sturm, P. Triangulation. Comput. Vis. Image Underst. 1997, 68, 146–157. [Google Scholar] [CrossRef]
- Raguram, R.; Frahm, J.M.; Pollefeys, M. A comparative analysis of RANSAC techniques leading to adaptive real-time random sample consensus. In Proceedings of the European Conference on Computer Vision, Marseille, France, 12–18 October 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 500–513. [Google Scholar]
- Kukelova, Z.; Bujnak, M.; Pajdla, T. Real-time solution to the absolute pose problem with unknown radial distortion and focal length. In Proceedings of the 2013 IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013; pp. 2816–2823. [Google Scholar]
- Fragoso, V.; Sen, P.; Rodriguez, S.; Turk, M. EVSAC: accelerating hypotheses generation by modeling matching scores with extreme value theory. In Proceedings of the 2013 IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013; pp. 2472–2479. [Google Scholar]
- Arya, S.; Mount, D.M.; Netanyahu, N.S.; Silverman, R.; Wu, A.Y. An optimal algorithm for approximate nearest neighbor searching fixed dimensions. J. ACM 1998, 45, 891–923. [Google Scholar] [CrossRef]
- Lourakis, M.; Argyros, A. The Design and Implementation of a Generic Sparse Bundle Adjustment Software Package Based on the Levenberg-Marquardt Algorithm; Technical Report, Technical Report 340; Institute of Computer Science-FORTH: Heraklion, Greece, 2004. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Tefera, Y.; Poiesi, F.; Morabito, D.; Remondino, F.; Nocerino, E.; Chippendale, P. 3DNOW: IMAGE-BASED 3D RECONSTRUCTION AND MODELING VIA WEB. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 1097–1103. [Google Scholar] [CrossRef]
- Horn, B.K. Closed-form solution of absolute orientation using unit quaternions. JOSA A 1987, 4, 629–642. [Google Scholar] [CrossRef]
- Girardeau-Montaut, D. CloudCompare (Version 2.8.1) [GPL Software]. 2017. Available online: http://www.cloudcompare.org/ (accessed on 18 June 2018).
- Besl, P.J.; McKay, N.D. Method for Registration of 3-D Shapes; Sensor Fusion IV: Control Paradigms and Data Structures; International Society for Optics and Photonics; Institute of Electrical and Electronics: New York, NY, USA, 1992; Volume 1611, pp. 586–607. [Google Scholar]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the 2001 Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar]
- Meagher, D.J. Octree enCoding: A New Technique for the Representation, Manipulation and Display of Arbitrary 3-d Objects by Computer; Electrical and Systems Engineering Department Rensseiaer Polytechnic Institute Image Processing Laboratory: New York, NY, USA, 1980. [Google Scholar]
- Eberly, D. Distance between Point and Triangle in 3D. Geometric Tools. 1999. Available online: https://www.geometrictools.com/Documentation/DistancePoint3Triangle3.pdf (accessed on 30 July 2018).
- Knapitsch, A.; Park, J.; Zhou, Q.Y.; Koltun, V. Tanks and Temples: Benchmarking Large-Scale Scene Reconstruction. ACM Trans. Graph. (TOG) 2017, 36, 78. [Google Scholar] [CrossRef]
- Zollhöfer, M.; Dai, A.; Innmann, M.; Wu, C.; Stamminger, M.; Theobalt, C.; Nießner, M. Shading-based refinement on volumetric signed distance functions. ACM ACM Trans. Graph. (TOG) 2015, 34, 96. [Google Scholar] [CrossRef]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A comparison and evaluation of multi-view stereo reconstruction algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; Volume 1, pp. 519–528. [Google Scholar]
- Foundation, B. Blender. 1995. Available online: https://www.blender.org/ (accessed on 18 June 2018).
- Marelli, D.; Bianco, S.; Celona, L.; Ciocca, G. A Blender plug-in for comparing Structure from Motion pipelines. In Proceedings of the 2018 IEEE 8th International Conference on Consumer Electronics (ICCE), Berlin, Germany, 2–5 September 2018. [Google Scholar]
- Free 3D User Dgemmell1960. Statue. 2017. Available online: https://free3d.com/3d-model/statue-92429.html (accessed on 18 June 2018).
- Blend Swap User Geoffreymarchal. Empire Vase. 2017. Available online: https://www.blendswap.com/blends/view/90518 (accessed on 18 June 2018).
- Blend Swap User Milkyduhan. BiCycle Textured. 2013. Available online: https://www.blendswap.com/blends/view/67563 (accessed on 18 June 2018).
- Blend Swap User b82160. High Poly Hydrant. 2017. Available online: https://www.blendswap.com/blends/view/87541 (accessed on 18 June 2018).
- Blend Swap User BMF. Willys Jeep Circa 1944. 2016. Available online: https://www.blendswap.com/blends/view/82687 (accessed on 18 June 2018).
- Marelli, D.; Bianco, S.; Ciocca, G. Available online: http://www.ivl.disco.unimib.it/activities/evaluating-the-performance-of-structure-from-motion-pipelines/ (accessed on 18 June 2018).
- Furukawa, Y.; Ponce, J. Accurate, Dense, and Robust Multi-View Stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef] [PubMed]
- Furukawa, Y.; Curless, B.; Seitz, S.M.; Szeliski, R. Towards Internet-scale Multi-view Stereo. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]


| Feature Extraction | Feature Matching | Geometric Verification | Image Registration | Triangulation | Bundle Adjustment | Robust Estimation | |
|---|---|---|---|---|---|---|---|
| COLMAP | SIFT [31] | Exaustive | 4 Point for Homography [20] | P3P [32] | sampling-based DLT [14] | Multicore BA [27] | RANSAC [19] |
| Sequential | 5 Point Relative Pose [33] | EPnP [34] | Ceres Solver [35] | PROSAC [36] | |||
| Vocabulary Tree [37] | 7 Point for F-matrix [20] | LO-RANSAC [38] | |||||
| Spatial [14] | 8 Point for F-matrix [20] | ||||||
| Transitive [14] | |||||||
| OpenMVG | SIFT [31] | Brute force | affine transformation | 6 Point DLT [20] | linear (DLT) [20] | Ceres Solver [35] | Max-Consensus |
| AKAZE [39] | ANN [40] | 4 Point for Homography [20] | P3P [32] | RANSAC [19] | |||
| Cascade Hashing [41] | 8 Point for F-matrix [20] | EPnP [34] | LMed [42] | ||||
| 7 Point for F-matrix [20] | AC-Ransac [43] | ||||||
| 5 Point Relative Pose [33] | |||||||
| Theia | SIFT [31] | Brute force | 4 Point for Homography [20] | P3P [32] | linear (DLT) [20] | Ceres Solver [35] | RANSAC [19] |
| Cascade Hashing [41] | 5 Point Relative Pose [33] | PNP (DLS) [44] | 2-view [45] | PROSAC [36] | |||
| 8 Point for F-matrix [20] | P4P [46] | Midpoint [47] | Arrsac [48] | ||||
| P5P [49] | N-view [20] | Evsac [50] | |||||
| LMed [42] | |||||||
| VisualSFM | SIFT [31] | Exaustive | n/a | n/a | n/a | Multicore BA [27] | RANSAC [19] |
| Sequential | |||||||
| Preemptive [16] | |||||||
| Bundler | SIFT [31] | ANN [51] | 8 Point for F-matrix [20] | DLT based [20] | N-view [20] | SBA [52] | RANSAC [19] |
| Ceres Solver [35] | |||||||
| MVE | SIFT [31] + SURF [53] | Low-res + exaustive [29] | 8 Point for F-matrix [20] | P3P [32] | linear (DLT) [20] | own LM BA | RANSAC [19] |
| Cascade Hashing |
| Model | COLMAP | OpenMVG | Theia | VisualSFM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [m] | s [m] | [m] | s [m] | [m] | s [m] | [m] | s [m] | |||||
| Statue | 0.034 | 0.223 | 9k | 0.057 | 0.267 | 4k | 0.020 | 0.039 | 8k | 0.185 | 0.236 | 6k |
| Empire Vase | 0.005 | 0.152 | 8k | 0.013 | 0.191 | 2k | 0.002 | 0.005 | 8k | 0.007 | 0.013 | 5k |
| Bicycle | 0.042 | 0.365 | 5k | 0.156 | 1.705 | 7k | 0.027 | 0.086 | 2k | 0.056 | 0.796 | 4k |
| Hydrant | 0.206 | 0.300 | 2k | – | – | 28 | 0.045 | 0.123 | 89 | 0.029 | 0.032 | 1k |
| Jeep | 0.053 | 1.058 | 6k | 0.057 | 0.686 | 4k | 0.012 | 0.016 | 8k | 0.055 | 0.124 | 5k |
| Ignatius | 0.009 | 0.021 | 23k | 0.013 | 0.032 | 12k | 0.023 | 0.022 | 10k | 0.054 | 0.124 | 14k |
| Model | COLMAP | OpenMVG | Theia | VisualSFM | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [m] | [m] | [] | [m] | [m] | [m] | [] | [m] | [m] | [m] | [] | [m] | [m] | [m] | [] | [m] | |||||
| Statue | 100 | 0.08 | 0.01 | 0.04 | 0.05 | 100 | 0.27 | 0.03 | 0.47 | 0.22 | 100 | 1.86 | 0.09 | 0.45 | 0.22 | 100 | 1.45 | 0.91 | 3.55 | 2.88 |
| E. Vase | 100 | 0.01 | 0.01 | 0.51 | 0.05 | 83 | 0.78 | 1.62 | 32.19 | 64.89 | 100 | 0.13 | 0.07 | 0.91 | 0.35 | 94 | 0.15 | 0.14 | 4.91 | 5.07 |
| Bicycle | 88 | 0.04 | 0.02 | 0.25 | 0.19 | 94 | 0.60 | 1.09 | 7.00 | 12.53 | 37 | 0.60 | 0.03 | 1.10 | 0.31 | 47 | 0.27 | 0.14 | 1.32 | 1.03 |
| Hydrant | 82 | 2.63 | 2.09 | 72.28 | 64.98 | 3 | – | – | – | – | 6 | 3.49 | 0.29 | 174.27 | 0.51 | 80 | 2.43 | 1.76 | 66.29 | 58.90 |
| Jeep | 63 | 0.04 | 0.02 | 0.26 | 0.11 | 92 | 0.24 | 1.32 | 4.80 | 26.33 | 95 | 0.43 | 0.42 | 1.33 | 5.67 | 83 | 1.02 | 2.79 | 9.68 | 22.84 |
| Ignatius | 100 | n.a. | n.a. | n.a. | n.a. | 100 | n.a. | n.a. | n.a. | n.a. | 100 | n.a. | n.a. | n.a. | n.a. | 100 | n.a. | n.a. | n.a. | n.a. |
| Model | COLMAP | OpenMVG | Theia | VisualSFM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [m] | s [m] | [m] | s [m] | [m] | s [m] | [m] | s [m] | |||||
| Statue | 0.009 | 0.023 | 75k | 0.008 | 0.027 | 86k | 0.010 | 0.011 | 84k | 0.065 | 0.049 | 76k |
| Empire Vase | 0.001 | 0.001 | 390k | 0.001 | 0.004 | 246k | 0.002 | 0.002 | 356k | 0.005 | 0.007 | 240k |
| Bicycle | 0.013 | 0.012 | 74k | 0.062 | 0.146 | 69k | 0.018 | 0.020 | 46k | 0.021 | 0.025 | 44k |
| Hydrant | 0.008 | 0.017 | 42k | – | – | – | 0.080 | 0.147 | 11k | 0.008 | 0.014 | 40k |
| Jeep | 0.010 | 0.016 | 236k | 0.008 | 0.016 | 471k | 0.014 | 0.019 | 448k | 0.048 | 0.056 | 281k |
| Ignatius | 0.004 | 0.004 | 155k | 0.003 | 0.004 | 161k | 0.018 | 0.019 | 109k | 0.017 | 0.031 | 76k |
| Model | COLMAP | OpenMVG | Theia | VisualSFM | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SfM | MVS | SfM | MVS | SfM | MVS | SfM | MVS | |||||||||
| t [s] | t [s] | t [s] | t [s] | t [s] | t [s] | t [s] | t [s] | |||||||||
| Statue | 59 | 897 | 86 | 1062 | 43 | 1359 | 115 | 1300 | 196 | 1984 | 98 | 1249 | 86 | 1406 | 144 | 1452 |
| Empire Vase | 53 | 897 | 154 | 2101 | 28 | 628 | 130 | 1734 | 129 | 1988 | 134 | 1926 | 62 | 1226 | 159 | 2095 |
| Bicycle | 98 | 896 | 117 | 1356 | 57 | 1467 | 146 | 1720 | 63 | 1722 | 58 | 548 | 64 | 1226 | 68 | 641 |
| Hydrant | 19 | 894 | 55 | 793 | 16 | 1547 | – | – | 17 | 2048 | 3 | 1249 | 36 | 997 | 56 | 1452 |
| Jeep | 38 | 897 | 121 | 1812 | 69 | 1550 | 275 | 3209 | 213 | 2083 | 280 | 3293 | 109 | 1406 | 254 | 3078 |
| Ignatius | 1225 | 1825 | 430 | 5082 | 401 | 1555 | 494 | 5926 | 992 | 2588 | 484 | 5626 | 1639 | 2381 | 345 | 4742 |
| COLMAP | OpenMVG | Theia | VisualSFM | |
|---|---|---|---|---|
| Statue |  |  |  |  |
| Empire Vase |  |  |  |  |
| Bicycle |  |  |  |  |
| Hydrant |  | n.a. |  |  |
| Jeep |  |  |  |  |
| Ignatius |  |  |  |  |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianco, S.; Ciocca, G.; Marelli, D. Evaluating the Performance of Structure from Motion Pipelines. J. Imaging 2018, 4, 98. https://doi.org/10.3390/jimaging4080098
Bianco S, Ciocca G, Marelli D. Evaluating the Performance of Structure from Motion Pipelines. Journal of Imaging. 2018; 4(8):98. https://doi.org/10.3390/jimaging4080098
Chicago/Turabian StyleBianco, Simone, Gianluigi Ciocca, and Davide Marelli. 2018. "Evaluating the Performance of Structure from Motion Pipelines" Journal of Imaging 4, no. 8: 98. https://doi.org/10.3390/jimaging4080098
APA StyleBianco, S., Ciocca, G., & Marelli, D. (2018). Evaluating the Performance of Structure from Motion Pipelines. Journal of Imaging, 4(8), 98. https://doi.org/10.3390/jimaging4080098






