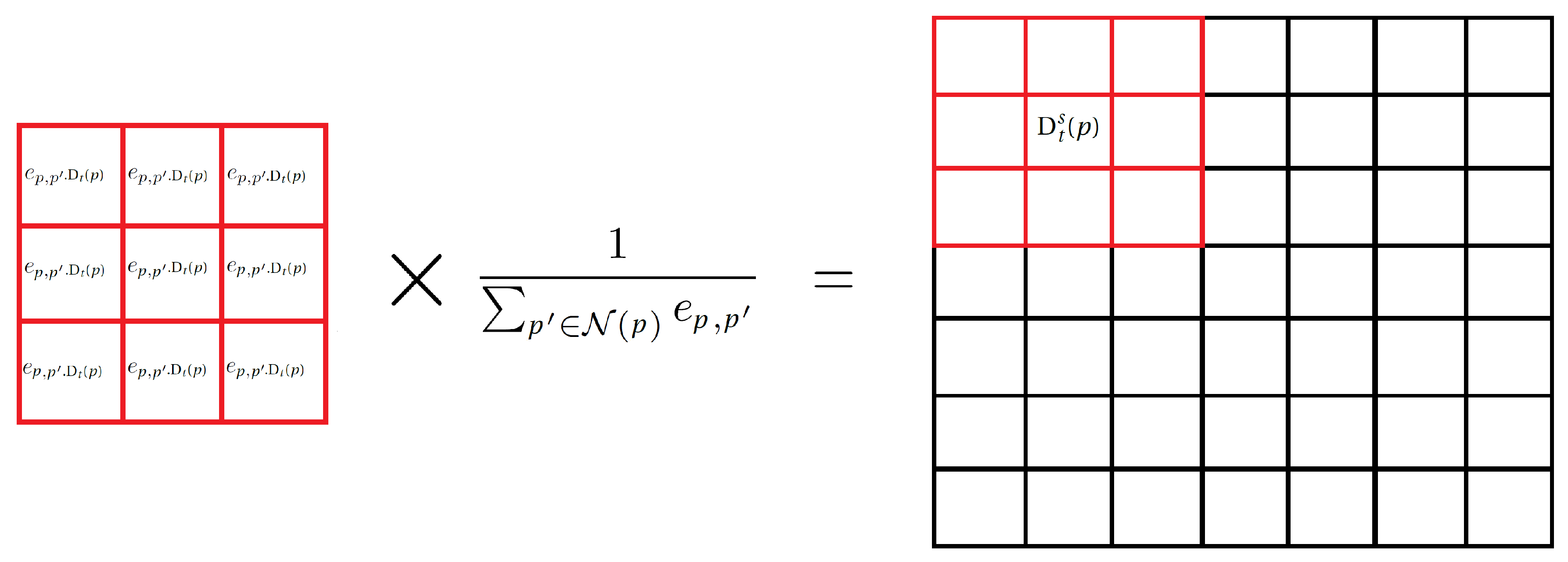1. Introduction
Background extraction, also known as foreground detection, or background subtraction, is a conventional technique in the field of frame processing and computer vision, in which the foreground of a frame (often a set of moving objects) is extracted for on-line or off-line processings (object recognition, etc.). Generally the regions of a frame of interest are objects (humans, cars, texts, etc.).
Many issues prevent such a basic technique from giving good background subtraction results. Indeed, it often fails in real videos: for instance when the frame is spoiled by noise, or when a little change in the environment disturbs the motion detection—typically illumination, shadow, slight movement and so on.
This problem can be roughly solved with very basic algorithms, based on the difference between a background-frame model and the current frame [
1,
2], but the videos often contain disruptive elements that may defeat such methods. In particular, dynamic backgrounds, or lightning variations in videos, can greatly complicate the classification of a pixel as foreground or background.
To deal with such complex videos (most often natural scenes), background subtraction methods based on more advanced modeling tools have therefore been developed.
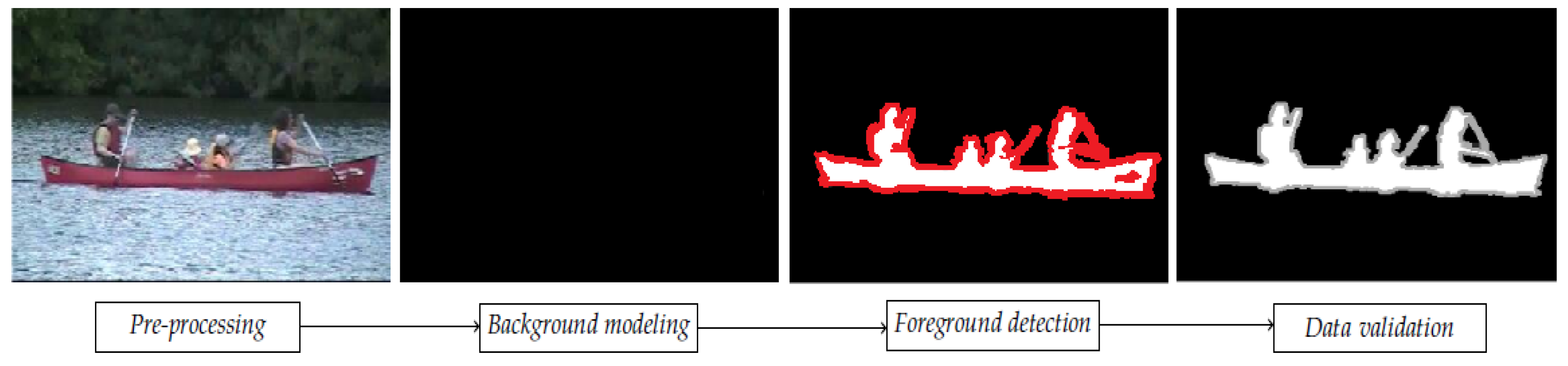
Most of them follow a simple flow diagram (cf.
Figure 1), structured in four major steps: pre-processing, background modeling, foreground detection and data validation. The produced result consists in a sequence of foreground masks, which tend to estimate the “ground truth” foreground mask of the corresponding video frame (cf.
Figure 1, fourth and first image). Detection and tracking of moving foregrounds can be considered as lower-level vision tasks, intended to prepare the understanding of the high-level event (decision-making).
There are many challenges in developing a good background subtraction algorithm. First of all, it must be robust with regard to lighting changes. Then, it must avoid detecting non-stationary background elements such as oscillating leaves, rain, snow and shadows. Moreover, the internal background model must react quickly to changes in background such as starting and stopping vehicles for example. A good background subtraction algorithm must handle moving foregrounds that first blend in the background and then appear in the foreground later.
The problem of identifying moving foregrounds in a complex environment is still far from being completely solved, and new algorithms are regularly added to the literature. Today, the challenge in background subtraction mining is to develop robust, accurate and efficient approaches on complex videos.
According to Bouwmans et al. [
4], three main conditions are necessary for the proper operation of background subtraction in video surveillance: the camera must be fixed, the lighting should be constant and the background should be static.
In practice, various disturbances can come to undermine these conditions, and constitute many challenges for the subtraction of patterns:
Noise in the frame: it is often due to a source of poor quality frames (for example, webcam frames, or heavily compressed).
Camera Jitter: video can be captured by unstable cameras, for example, because of vibrations or wind. The amplitude of the jitter can vary from one video sequence to another.
Automatic camera settings: most modern cameras have auto-focus, automatic gain control, auto white balance, and automatic brightness control. These adjustments change the dynamics in the color levels between the different frames in the sequence.
Lighting changes: they can be relatively progressive, as in an outdoor scene (movement of the sun), or sudden as the lighting of a lamp in an indoor scene. Illumination strongly affects the appearance of the background and causes false detection.
Bootstrap: when the first frames of a video contain still foregrounds, the initialization of the background model may pose a problem. Bootstrap techniques can then be used.
Dynamic background: some parts of the scenery may contain motions (fountain, cloud movement, swaying tree branches, water wave, etc.), but should be considered background. Such movements may be periodic or irregular (eg, traffic lights, undulating trees). Managing such a dynamic background is a very difficult task.
Camouflage: intentionally or not, some foregrounds may be confused with the surrounding background. This is a critical problem in monitoring applications. And it particularly affects temporal differentiation methods.
Opening foreground: when a displaced foreground object contains uniformly colored regions, some of its pixels may be detected as motionless, and consequently as background.
Sleeping foreground: a foreground element that becomes immobile, may be incorporated into the background. Depending on the context, this is not necessarily desirable.
Shadows: shadows can be detected as foreground, and can come either from background elements or moving foregrounds [
5].
Moving background “objects”: some parts of the background may move. In this case these objects should not be classified as foreground.
Inserted background elements: a new background “object” can be inserted. Depending on the context, these objects should not be considered as part of the foreground.
Start of moving foreground: when a “foreground” initially confused with the background starts moving, the background parts then revealed are called “ghosts”; they should be quickly assimilated to the background.
Weather variations: the detection of moving foreground becomes a very difficult task when videos are captured in shower weather conditions, such as in winter, with for example snowstorms, snow on the ground, fog, strong winds (turbulence).
To overcome these obstacles, a lot of research has been devoted to develop new and performing algorithms. The common approach is to perform a background subtraction, which consists in modeling the background scene, so as to detect foreground objects as pixel regions not compatible with the model. This is the approach we focus on.
This paper is organized as follows: in the following section we review the most popular methods to extract backgrounds (often based on Gaussian Mixture Models, GMMs, classic GMMs and fuzzy GMMs).
Section 3 introduces Gaussian Mixture Models in background modeling, and its type-2 fuzzy set extension FGMMs.
Section 4 proposes a new decision under uncertainty technique using an interval comparison method, we name IV-FGMM (Interval-Valued Fuzzy Gaussian Mixture Model).
Section 5 presents a comparison with methods based on GMMs and fuzzy sets FGMMs. Finally
Section 6 presents the conclusion and the perspectives of this work.
2. Background
In this section we present some common approaches to background detection, considering the uncertainty added to the process. Indeed the previous listed challenges represent a high level of uncertainty for algorithms, and this is the point of view we consider.
2.1. Common Approaches
The most common techniques use a density function of the pixel values over the video frames, as a by-pixel probabilistic background modeling. Decision is then frequently obtained from a maximum likelihood-like decision method. Many algorithms using Gaussian models have been proposed [
6,
7,
8,
9,
10,
11,
12,
13,
14]. Most of them use a single Gaussian density function per pixel. However, pixel values that may have more complex distributions and Gaussian mixtures are generally preferred.
Stauffer and Grimson early developed one of the most important Gaussian Mixture Models (GMMs)-based algorithms for real-time background subtraction [
12], also called MoG (Mixture of Gaussians). He first proposed a multi-modal distribution allowing a complex background modeling, then an algorithm to update this model in real-time. Each Gaussian mode is then assumed to model either background pixel values (the most frequent values) or foreground pixel values (the less frequent ones). This model is able to fit background changes, more or less quickly according to an adjustable learning rate. Bouwmans et al. provided a review and an original classification of the numerous improvements of this initial GMM subtraction algorithm [
15].
Reduction dimension and learning techniques were also investigated to extract background. Classic ACP methods were first investigated. For example, Oliver et al. [
16] used subspace learning to compress the background (the so-called eigenbackground). In an other way, Lin et al. proposed to learn background model via classification [
17]. Wang et al. proposed to improve target detection by coupling it with tracking [
18], when Tavakkoli et al. proposed an SVM approach for foreground region detection in videos with quasi-stationary backgrounds [
19]. In the same way they proposed a support vector data description approach for background modeling in videos with quasi-stationary backgrounds [
20].
2.2. Recent Approaches
A great number of improvements of the GMM techniques have been proposed. Varadarajan et al. [
21] proposed a generalization of the GMM algorithm where the spatial relationship between the pixels is taken into account. Basically, the classification of the pixel does not depend only on its GMM, but also on its neighbors. Gaussian mixtures are associated with regions rather than pixels. Initialization, as the update of the parameters GMM, is significantly different from the classic method.
Another important method based on GMM and proposed by Martins [
22] is the method of robust and computationally efficient method, BMOG, which greatly increases the performance of the GMM method [
12]. The computational complexity in BMOG is kept low, making it applicable in real time. The solution proposed in this method combines two main contributions: the use of a more appropriate color space than the classic
RGB,
CIE L*a*b, as well as a procedure to dynamically adapt the GMM learning rate.
Chen et al. proposed a “sharable” GMM based background subtraction approach [
23], in which GMMs are shared by neighbor pixels. Each pixel dynamically searches the best matched model in the neighborhod. This kind of space-sharing way is particularly robust to camera jitter and dynamic background. El-Gammal et al. [
24] proposed a novel non-parametric background model that estimates the probability of observed pixel intensity values based on a sample of intensity values for each pixel. This model can adapt to the scene changes quickly and enables it to be very sensitive to the detection of moving targets. In the same way, another approach based on GMM was proposed by Haines and Xiang [
25], built on a non-parametric density estimate (DE), which avoids over-/under-fitting. In the literature, outside of GMMs based methods, we also considered optical flow methods to take advantage of temporal continuity in our work. Many methods for background subtraction are indeed based on optical flow (whose concept was first studied in the 1940).We call “optical flow” the estimated velocity field from the variations of the brightness, its calculation is a standard low level processing in frame processing.
The two basic methods of optical flow are Horn and Schunck’s [
26], and that of Lucas and Kanade [
27]. They have many applications, such as fluid motion analysis in experimental physics, or in higher level processing, such as three-dimensional scene reconstruction.
Many other algorithms have been proposed since the two founding articles. In particular Farneback [
28] proposed an extension of the Lucas algorithm, which allows to estimate the movement of all pixels from two consecutive frames.
This optical flow technique has been applied to our problem, in order to exploit the temporal continuity between the consecutive frames of a video. Thus Chauhan and Krishan [
29] combine GMMs with the optical flow for bottom extraction.
Then Chen et al. [
30] proposed a similar, more sophisticated technique, based on the following steps:
use of the minimal weight spanning tree, to define a dissimilarity between each pair of pixels in the frame, based on the calculation of the path of maximal color continuity between two pixels. This dissimilarity is used to define a concept of neighborhood more relevant than a simple geometric distance.
estimation of the optical flow using the fast algorithm of [
31], using robust estimators M-smooth.
computation and fusion of spatial decisions (obtained thanks to the previously calculated dissimilarity) and temporal (obtained thanks to the optical flow).
Recently Javed et al. [
32] proposed a background-foreground modeling based on spatio–temporal sparse subspace clustering with success. St-Charles and Biloteau [
33] proposed an efficient method (named SuBSENSE) using a spatio–temporal Local Binary Similarity Patterns (LBSP) descriptor instead of simply relying on pixel intensities as its core component, it keeps memory usage, complexity and speed at acceptable levels for online applications. St-Charles et al. also proposed another method [
34] based on local binary patterns as well as color information, also called multi-Q method (multi-objectives method). Moreover, parameters are automatically adjusted by pixel-level feedback loops. Varghese in [
35] proposed an efficient method for integrated shadow detection and background subtraction, to identify background, foreground regions, and shadow in a video sequence.
More recently some improvements in dimension reduction techniques have been proposed, as the robust PCA technique (via Principal Component Pursuit) [
4], the decomposition into low-rank plus additive matrices for Background/Foreground separation [
36]. This make it possible to use of large-scale dataset. Robust low rank matrix decomposition with IRLS scheme (Iteratively Reweighted Least Squares) have also been cited in that case [
37]. By computing tensors instead of matrices, dimension reduction techniques make it possible to detect other abnormalities (blob motion, ...). Javed et al. proposed a stochastic decomposition into low rank and sparse tensor for robust background subtraction [
38], while Sobral et al. proposed an incremental and multi-feature tensor subspace learning applied for background modeling and subtraction [
39].
These last years, many researchers applied deep learning to background subtraction for more robust algorithms [
40,
41,
42,
43,
44,
45]. Xu et al. proposed an efficient method for dynamic background based on deep auto-encoder networks [
43], where the auto-encoder is an artificial neural network used for unsupervised learning of efficient codings. Zhang [
42] proposed a deep learning based block-wise scene analysis method equipped with a binary spatio–temporal scene model. Based on the stacked denoising auto-encoder, the deep learning module of the proposed method aims at learning an effective deep image representation encoding the intrinsic scene information. This method can be easily applied to real-time automated video analysis in different scenes due to extremely fast running speed and low memory usage. Brunetti et al. [
44] published an interesting survey of techniques for pedestrian detection and tracking using deep learning.
2.3. Fuzzy Approaches
There are many methods and theories to model uncertainties and among them fuzzy modeling (fuzzy sets, or FSs in the sequel). In general, uncertainty as a subjective phenomenon can be modeled by very different theories depending on the causes of uncertainty, the type and amount of available information, the requirements of the observer, and so on. Many models are associated with these uncertainties: probabilistic models, theory of evidence, Dempster-Shafer, fuzzy sets ... Random phenomenons are very well taken into account by the probability theory (the applications of “Gaussian mixtures” in processing frames and videos are very numerous to date). Dubois and Prade [
46] presented an interesting comparison of these techniques. More recently Sugeno presented a classification of the different uncertainties that can be modeled using FSs: fuzziness, incompleteness, randomness, non-specificity of information, etc. [
47].
Fuzzy sets are often associated with vague knowledge modeling (“a high tree”, “a high heat”), but they are not limited to this type of uncertainty. They are quite capable of modeling other forms of inaccuracy, in well-defined situations, by choosing the most suitable model (fuzzy classic models, type-2 models, etc.), as we will present in this paper.
An important drawback of GMM methods relies in the ambiguity of the “most likely mode” (either foreground or background) associated to a given pixel value. This happens when two Gaussian modes are very close and overlap. Some fuzzy methods were introduced to take into account this ambiguity and the imprecision of mode distributions. Particularly, Bouwmans et al. proposed a background modeling method [
13] based on type-2 fuzzy GMMs [
48]. But as further explained, the introduced fuzziness is not fully exploited, because of a crisp mode selection.
Recently Chiranjeevi et al. proposed several methods for background subtraction using classifiers based on different pixel features (fuzzy correlograms, fuzzy statistical texture features), whose decisions are then aggregated by fuzzy integrals [
49,
50,
51,
52,
53,
54]. Fuzzy concepts have been introduced at different levels of the general background subtraction process, as we recall now [
55]:
Fuzzy Background Modeling: many recent approaches are based on a multimodal background model. The model usually used is the Gaussian mixture [
11]. The parameters are often initialized using a training sequence, which contains insufficient or noisy data. So the parameters are not well determined.
In this context, models of type-1 or type-2 Fuzzy Gaussian mixture [
13,
56,
57] allow to take into account this inaccuracy.
Fuzzy Foreground Detection: this category of methods does not explicitly introduce imprecision in their data or models - that is, in the form of fuzzy sets—but they measure the membership of pixels to the foreground class, through fuzzy degrees, obtained by normalizing the similarity measures (or dissimilarity) in
. [
58,
59,
60,
61,
62]
Fuzzy Background Maintenance: the idea is to update the background model according to the fuzzy membership degrees of the pixel to the background and foreground classes, these fuzzy degrees coming from a fuzzy detection. This fuzzy adaptive background maintenance provides robust handling of lighting changes and shadows.
Kim et al. [
63] and then Gutti et al. [
64] presented background subtraction algorithms exploiting this technique. They both use a fuzzy color histogram (FCH), in order to attenuate the color variations generated by the background movements while highlighting moving objects.
These methods efficiently handle the background noise of scenes with dynamic (temporal) textures.
Fuzzy Post-Processing: a fuzzy inference engine can be applied to the current and previous foreground masks to detach the moving foreground from the dynamic background. In [
65] such a method is proposed, which uses a color feature and a median filtering [
55].
2.4. Problem and Contribution
In order to take into account the global uncertainty considering background subtraction, and to propose a more robust method to dynamic changes, Darwich in [
66] first proposed a method based on type-2 fuzzy GMMs. Its main idea was to consider fuzzy likehood functions to build fuzzy decisions to achieve more robustness, and to use this fuzziness in a spatial fusion of the fuzzy detection responses in the pixel neighborhood. Indeed, the main problem considering background subtraction is to be robust to dynamic changes (when videos have hard conditions as light change, weather change, ...) and our approach is particularly devoted to that drawback using type-2 fuzzy sets to model the uncertainty. In this paper, we propose to take into account the ambiguity of the mode selection, using a type-2 fuzzy approach. Unlike most methods in literature, the mode selection and the classification are completely fuzzy modeled.
The fuzziness is preserved from its introduction in the GMM model until the final binary decision.
Moreover, uncertainty is exploited to weight the participation of new information “sources” in the decision-making process. This additional information comes from the hypothesis of spatial and temporal homogeneity of the class of a pixel in a video sequence. Thus the method we propose is a decision under uncertainty method using intervals based on type-2 FSs. We now recall the basics of a fuzzy GMM, namely FGMMs, and the method we propose (namely IV-FGMM) in the following section.
3. Toward Fuzziness in Gaussian Mixture Models for Background Subtraction
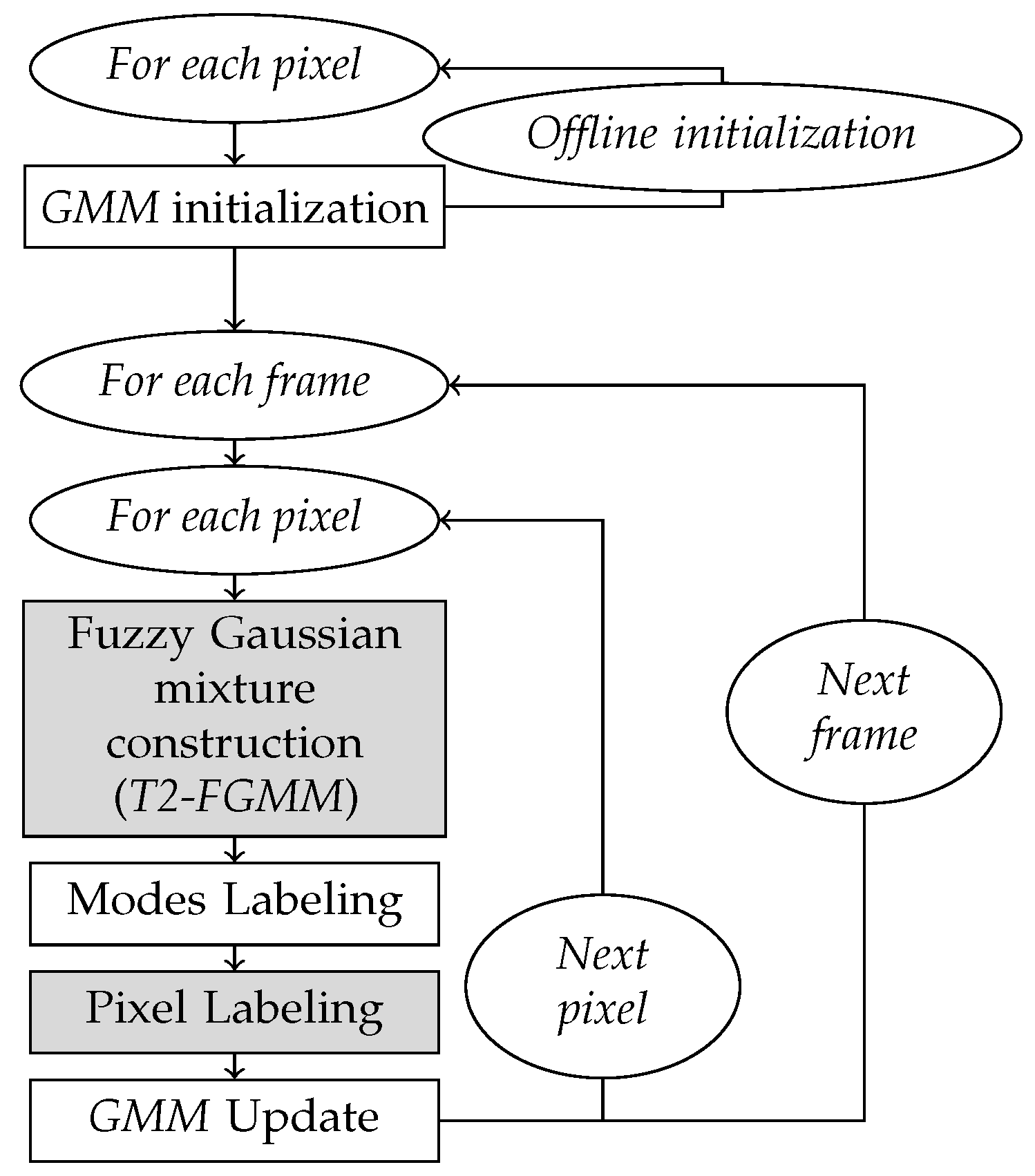
3.1. GMM for Background Subtraction
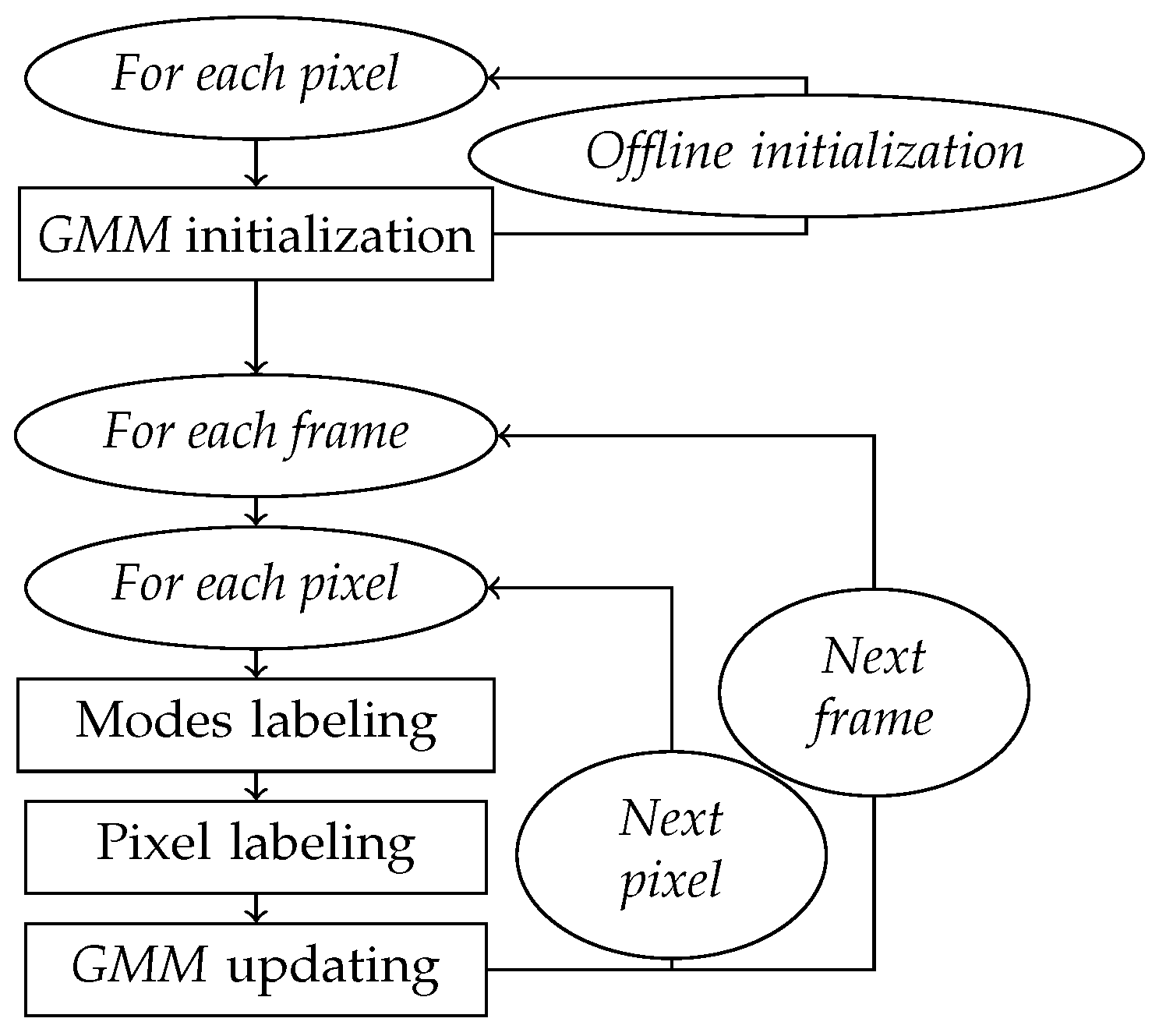
The flowchart in
Figure 2 shows the different steps of the basic subtraction method based on a mixture of Gaussians. The details of each of these steps are presented below.
Distribution of data coming from several groups may be well modeled by a probabilistic mixture model, with one distribution component (or mode) per group. In the current application, values of a pixel over time may be characterized by such a mixture model: each mode being either associated to the background or to the foreground.
Gaussian Mixing Model (GMM) is the most popular technique to model the background and foreground state of a pixel [
13]. GMM have the ability of universal approximation, because they can fit any density function, if they contain enough mixture [
67].
Let
be the frame of the video
t and
p the studied pixel—of coordinates
—and
its (RGB) value in the frame
. The sample of values of this particular pixel in time is then designated as follows:
with
T the number of frames.
The GMM associated to pixel
p in
RGB color space at frame
t is composed of
K weighted Gaussian functions:
with:
K: the number of modes of the mixture,
: Gaussian density function of the kth Gaussian mode of p, in the frame t,
: the weight of mode k,
: its center vector,
: its covariance matrix.
And with
the multivariate Gaussian function:
To simplify the calculation, the co-variance matrix is often assumed to be diagonal:
with
I the identity matrix of size 3 × 3.
This means that the R, G, B pixel levels are assumed independent with equal variances. This is probably not true, but this assumption avoids expensive matrix inversion with respect to model accuracy.
3.1.1. Step 1: GMM Initialization
This is an optional steps when the ideal is to apply the EM (expectation-maximization) algorithm on a part of the video, but we can also initialize a single mode per pixel (of weight 1), starting from the levels of the first frame.
3.1.2. Step 2: Mode Labeling
Each Gaussian mode is classified as either Background or Foreground. This critical association is obtained from an empirical rule: the more frequent and precise the mode, the more likely it models Background colors.
Specifically, the
K modes are sorted according to their priority level
. The first
modes are then labeled Background. The value of
is determined by a threshold
:
3.1.3. Step 3: Pixel Labeling
The third step is to classify the pixel. In most methods, the pixel is assigned the class of the closest mode center, under the constraint:
where
is a constant coefficient, to be adapted for each video.
If none of the modes satisfy this constraint, then the lowest priority mode is replaced by a new Gaussian centered on the current intensity
, with a priori variance weight [
12].
3.1.4. Step 4: Updating GMM
Stauffer [
12] proposes to operate as follows:
Then a new frame can be processed.
3.2. Type-2 Fuzzy Sets
Ordinary fuzzy sets (or FS) are currently used in image processing [
68]. These techniques consider that the spatial ambiguity among pixels has inherent vagueness rather than randomness. However, there remain some sources of uncertainty in ordinary (or precise) fuzzy sets (see [
69]): in the fuzzy set design (e.g. in symbolic description), in the fact that measurements may be noisy or that the data used to calibrate the parameters of ordinary fuzzy sets may also be noisy. These uncertainties can be linked to video disturbances described in the introduction. So, since fuzzy sets were introduced by Zadeh [
70], many new approaches treating imprecision and uncertainty were proposed (see [
46] for a rapid discussion about some of these theories). Among these, is a well-known generalization of an ordinary fuzzy set, the interval-valued fuzzy set, first introduced by Zadeh [
71].
3.2.1. Introduction to Type-2 Fuzzy Sets
Type-2 Fuzzy sets have been proposed for the purpose of modeling and minimizing the effects of uncertainties in fuzzy logic systems. Their representation of uncertainty is even more developed than that of previous models. For example, they were used in a type-2 fuzzy controller [
72], and the development of efficient classifiers based on “fuzzy c-means” [
73]. But their characterization and manipulation are more complex than conventional fuzzy sets, which greatly penalizes their use, especially in video.
Let
X be the domain of discourse. Whereas each element of
X is mapped to a single value by type-1 fuzzy set membership function, they are mapped to a (type-1) fuzzy set by type-2 fuzzy set ones [
74]. The T2FS was introduced by Zadeh in 1975 and was extended (among others) by Karnik and Mendel in 1998 [
75].
Karnik et al. defined a fuzzy set
, using a characteristic function
with two parameters:
Each value is associated to a fuzzy number in the domain , rather than to a singleton—too precise—(like type-1 fuzzy sets). So, for the considered x, associates to any element u of this domain, a membership degree—now a singleton—of .
Karnik et al. further defined two simpler membership functions for breaking out type-2 fuzzy sets:
the primary membership function: for each , it associates the minimal interval containing the set of membership degrees u such that ; this interval is the support of the type-1 fuzzy number associated to x by .
the secondary membership function: for each
, it is the membership function of the type-1 fuzzy set associated to
x by
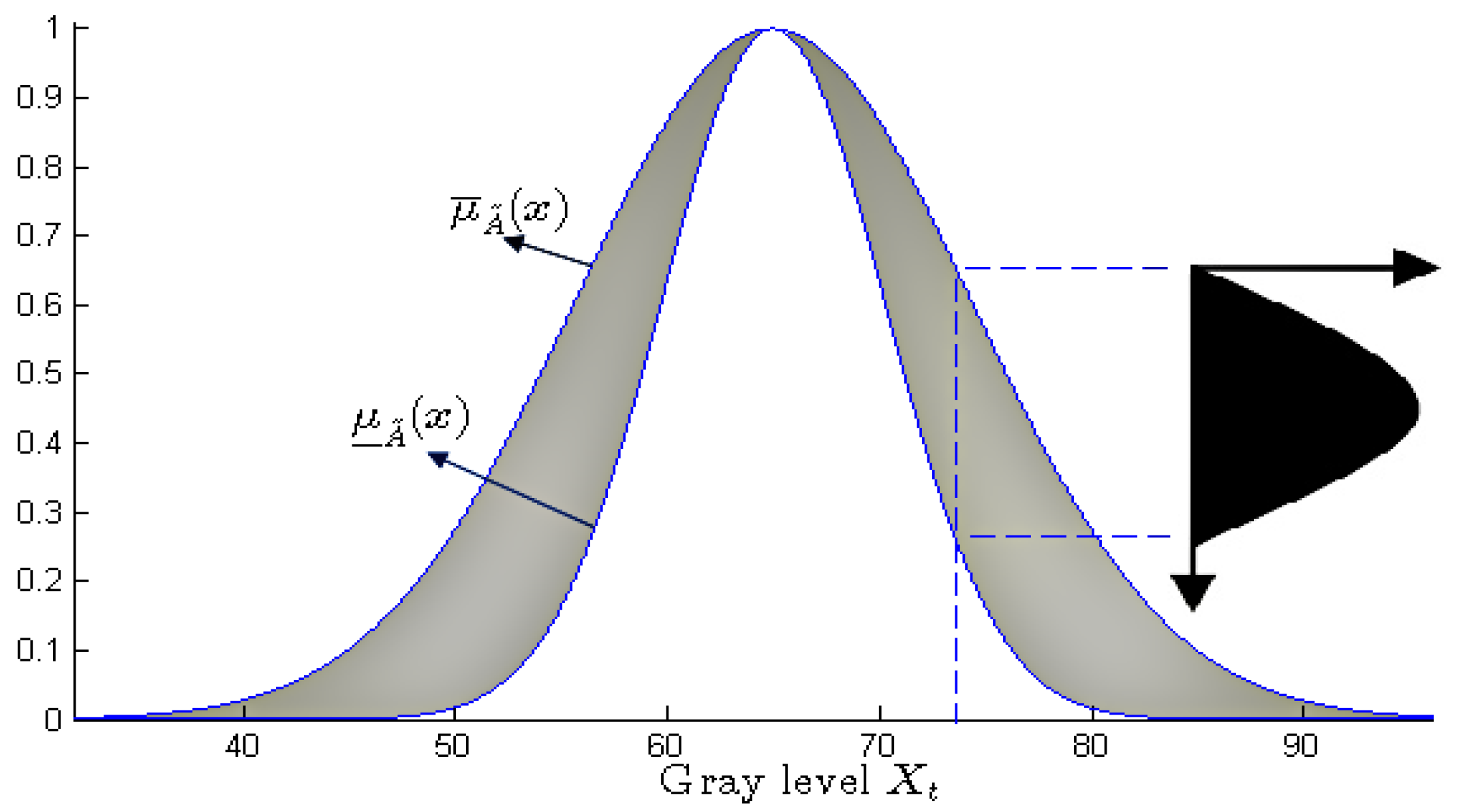
. Such a secondary membership function is drawn in
Figure 3, in black color.
Finally, Karnik et al. denote the region covering the set of
intervals defined on
X (the primary functions of
) using the term footprint of uncertainty (or
FOU, cf.
Figure 3, in gray):
The surface of this footprint measures the “fuzzy amount” of the primary membership functions. It is bounded by an upper and a lower function, which are type-1 fuzzy membership functions. They account for the global imprecision of the primary membership functions.
3.2.2. Interval-Valued Fuzzy Sets
General T2FS framework may be simplified, by defining secondary membership functions as crisp intervals: such T2FSs are called Interval-Valued Fuzzy Sets (IVFSs) [
46].
The Interval-Valued Fuzzy Sets have been proposed to overcome the excessive precision of the membership degrees of type-1 fuzzy subsets [
76] but with less computational complexity than T2FSs.
Their principle consists in framing the membership functions of the type-1 fuzzy sets, by two membership functions: one which limits the possible membership degrees lower, the other higher.
Two membership functions are enough to model an IVFS:
This simplification of T2FSs represents a crucial advantage for a software implementation. This is why IVFSs are the most used T2FSs in frame processing [
77].
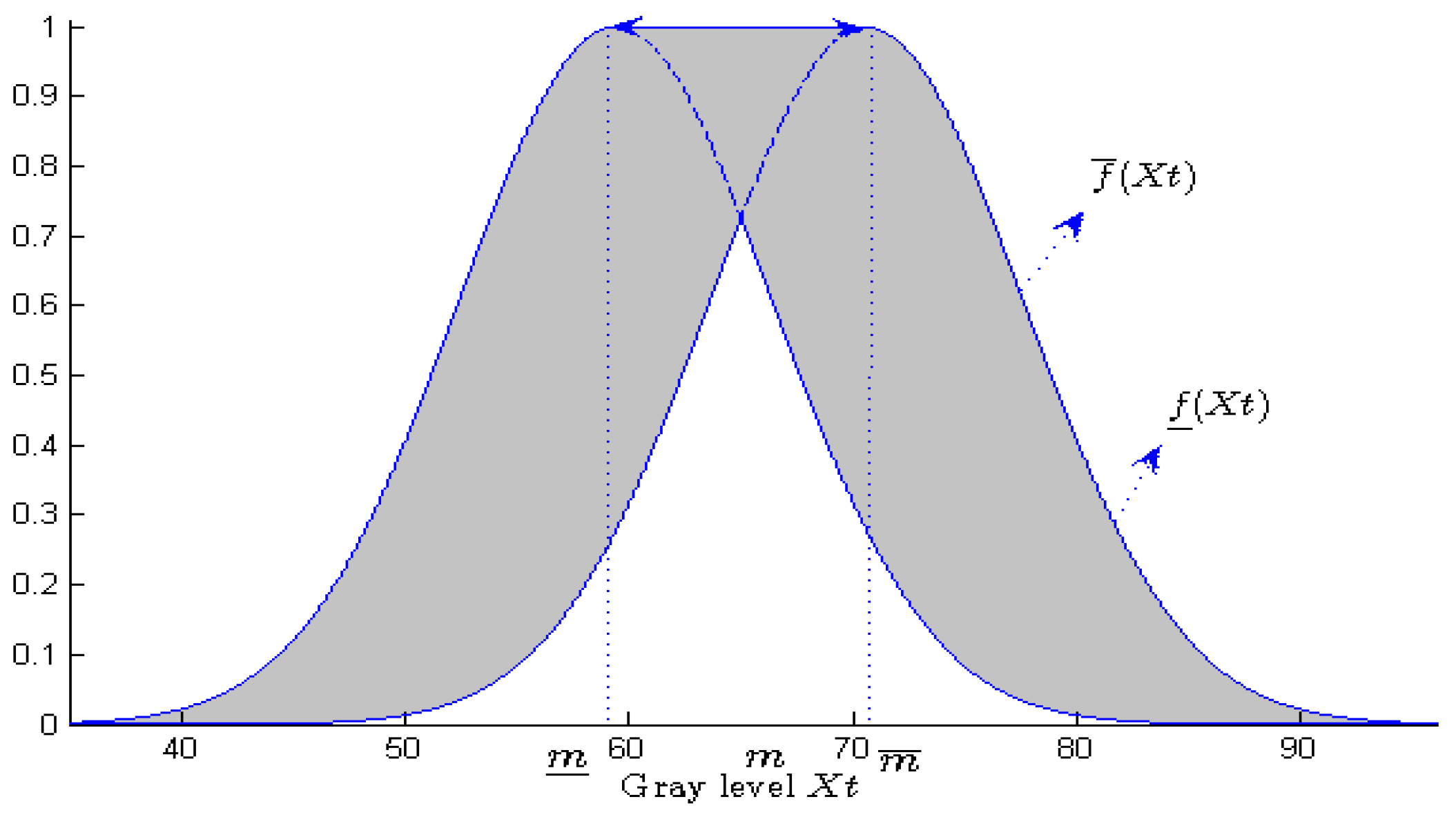
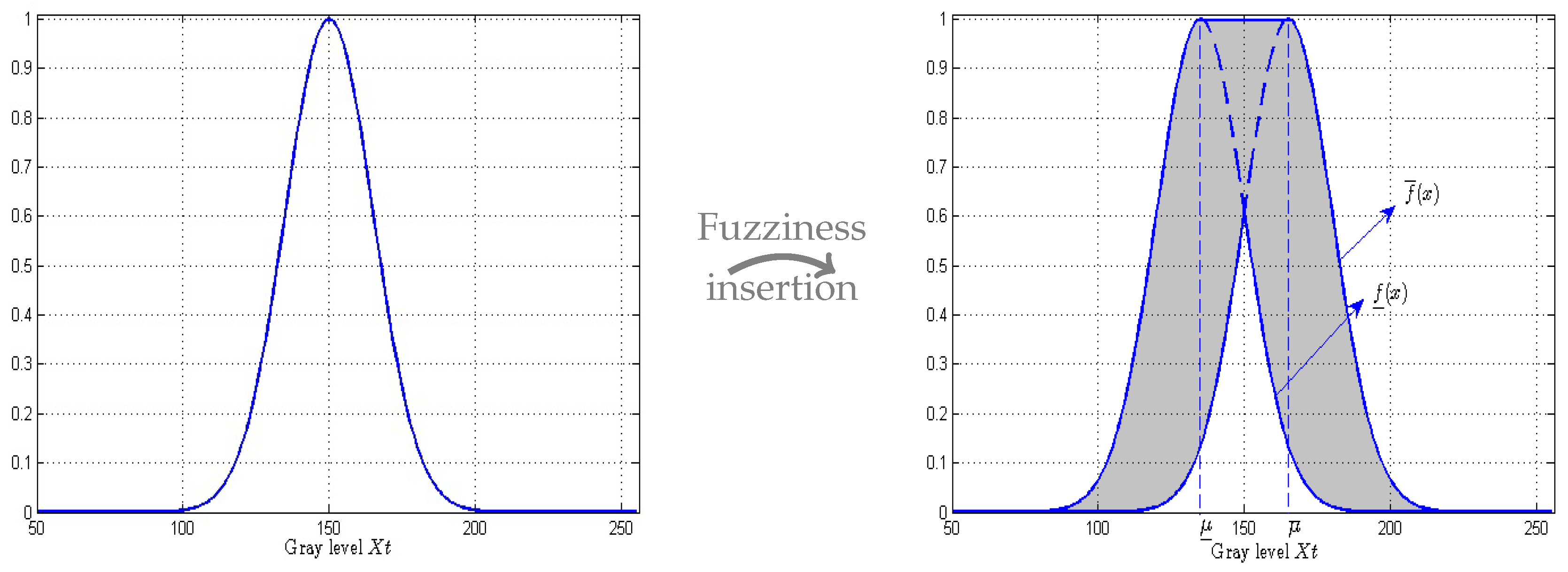
Those two membership functions are frequently built from a single ordinary Gaussian function. A common procedure consists in introducing imprecision in its mean parameter [
78]. We then consider that the true value
is not precisely known, but that it belongs to a half-
-length interval centered on
where
is a value
depending on the video :
Lower and upper membership functions are then obtained by shifting the mean value inside its domain, and retaining maximal and minimal values of the Gaussian function
:
Figure 4 illustrates this building. Let us note that the larger the mean interval, the larger the
FOU (and hence the uncertainty) of the resulting T2FS.
Upper and lower membership functions could be defined—in a way quite similar—by considering an imprecise variance [
48]. In this paper, we consider only the previous procedure.
3.3. Background Modeling Using T2-FGMM with Uncertain Mean
Bouwmans et al. introduced Type-2 Fuzzy sets to handle uncertainty in GMM mixtures used for background subtraction [
13]. They applied the GMM uncertain model proposed by Zeng et al. in paper Type-2 Fuzzy Gaussian Mixture Model [
48].
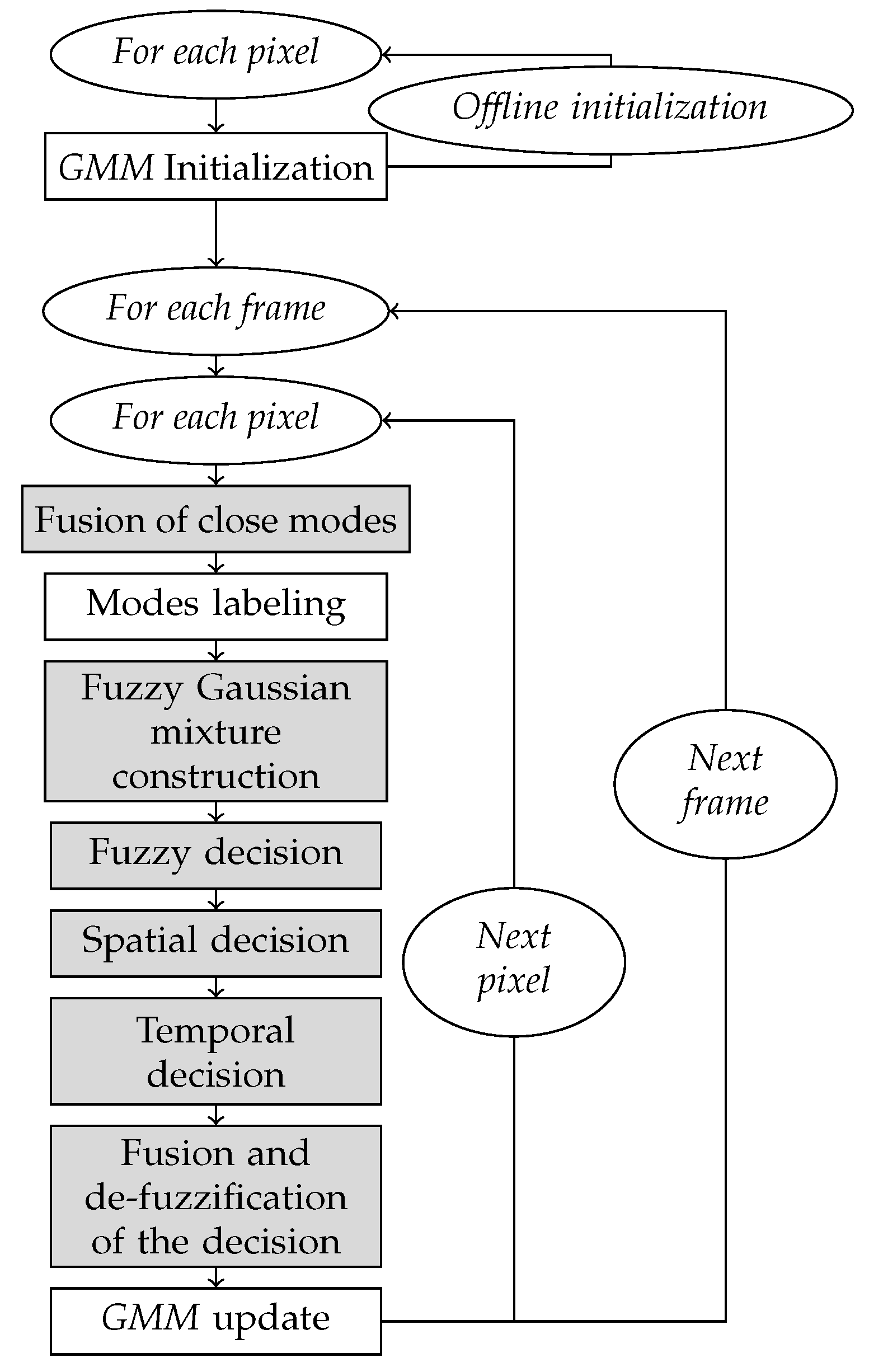
In fact, Fuzzy type-2 model only appears in the final decision step of the method. Previous steps consist in a classic GMM approach.
The algorithm is shown in
Figure 5. In the next part, we only focus to the two modified steps (with respect to the classic GMM method), grayed out, with the steps 1 is the same initialization steps in GMM classic method.
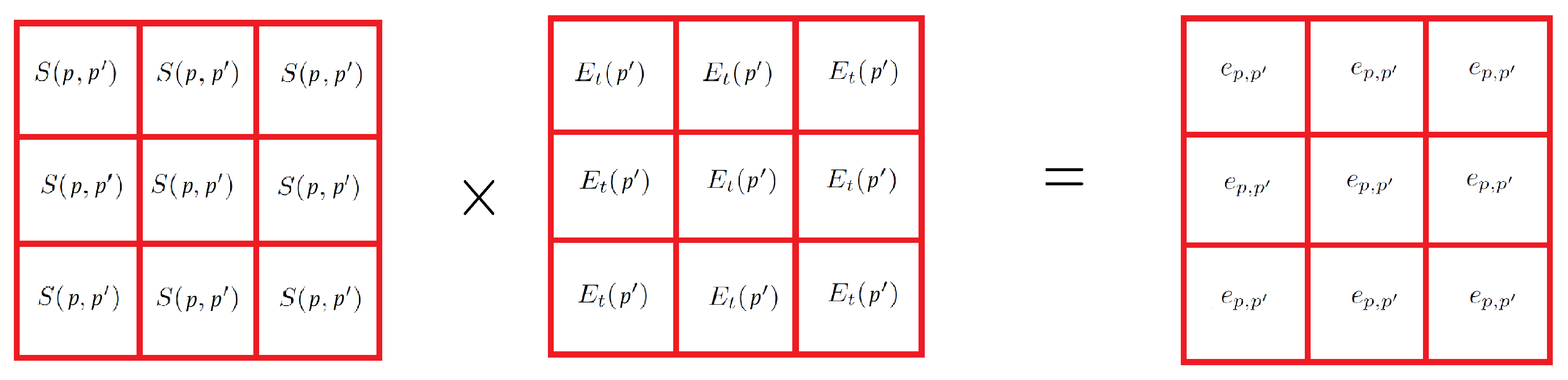
3.3.1. Step 2 : Fuzzy GMM Construction
Figure 6 illustrates how the Fuzzy Gaussian mode is built from Equation (
14).
3.3.2. Step 3: Pixel Labeling
Most methods estimate the pixel class from the distance between its gray level and the center of the closest mode. This means that the pixel is labeled according to the first mode compatible with its value (gray-level in our case).
Type-2 fuzzy sets are introduced in this step, with two membership functions and . By construction, they remain centered on the center of the crisp-valued Gaussian function f.
Bouwmans et al. [
13,
56,
57] based the class labeling on the length of the “log-likelihood” interval at the
x level of the current pixel. The pixel is labeled with the label of the “best matching” Gaussian mode,
ie. the first ranked mode (according to
) whose membership bounds in
x make this inequality true:
with
a constant factor.
If this inequality cannot be asserted for any mode in x, then the last sorted mode is replaced by a new one, centered in x.
This choice is clearly justified by Bouwmans et al. They show that indicator
is a decreasing monotonous function of distance
:
So, the larger the normalized (log-likelihood) interval, the closer the pixel-value to the center of the mode. Consequently, the larger the interval, the more likely the mode.
Let us note that, because of their prior sorting, modes with highest weights and lowest variance—likely Background modes—are tested first: if a pixel is compatible with such a mode, it is then labeled Background.
4. The Proposed IV-FGMM-ST (Interval-Valued Fuzzy GMM spatio–Temporal) Method
4.1. Originality of the Proposed Method
The algorithm proposed in this paper mainly differs from previous work through the following points:
T2FS uncertainty is used to handle the possible ambiguity of the mode estimation.
Fuzzy modeling is preserved until the final binary decision.
Uncertainty is used to weight the participation of several “information sources” in a fusion classification process.
The proposed algorithm is illustrated in
Figure 7. Original steps are grayed out.
4.2. Fuzzy Decision
The main goal considering the fuzzy decision is to deal with a fuzzy decision for each pixel instead of the binary decision used in most methods, in order to avoid wrong classifications that come from the ambiguity in the decision process.
Aggregation of Imprecise Intervals
Unlike the T2-FGMM method—also based on a fuzzy GMM—model, we propose to construct a “preference” fuzzy measure between the 2 possible decisions (background, Foreground), associated with a “rejection” score, designed to ensure the lack of knowledge.
The first modification lies in the Pixel labeling Step.
For each mode k, the IVFS associates to pixel p in frame t—of value —a normalized density interval: .
All mode intervals are aggregated using a weighted average, according to their label. Weights are defined by Zeng’s priority levels (used in the mode ranking):
with
.
More precisely, two label intervals are built by aggregation:
to assess the hypothesis “pixel value matches a Foreground region”, and
to assess the opposite hypothesis. A supplementary interval—called
for reject—is built to represent non-significant likelihood levels, from an a priori threshold
:
Then the fuzzy decision between Foreground and Background alternatives is built by comparing both intervals and .
For this purpose, we use a variant of the Sengupta’s acceptability index [
79]. This index assesses the “grade of acceptability of the first interval to be inferior to the second interval”:
with:
Note that this index only applies if the center of is lower than that of .
We propose the following (slight) variant, to eliminate this condition, and normalize the measure in
[
66]:
Finally, the fuzzy decision between the Foreground and Background assumptions of the
p pixel is constructed by comparing the intervals
and
according to the acceptability index variant:
Let us note that values higher (respectively lower) than induce a foreground (r. Background) class, while values close to just indicate a lack of preference.
To complete this fuzzy decision measure, a confidence level
is built, by comparing both intervals to a rejection interval
. The idea behind this is to make sure that at least one of the two intervals is significant enough.
4.3. Complementary Decisions
The previous fuzzy decision give us a first estimate of the object pixels. But in a noisy video, or with a complex (dynamic) background, some decisions will remain ambiguous, due to a lack of information. We therefore decide to reinforce the decision by considering spatial or temporal coherence.
4.3.1. Fuzzy Spatial Decision
Here, we consider the spatial continuity hypothesis: pixels neighbors are likely to belong the same class. A neighborhood is defined using a window (for example).
Each pixel p in the frame t is now characterized by a fuzzy decision and a confidence level . The decision value indicates which class Foreground and Background is preferred. And the confidence value associated with this decision establishes its future contribution to spatial decision making.
The proposed procedure consists in a spatial fusion: fuzzy decisions of neighbor pixels are merged to avoid false detection on isolated pixels.
Firstly, the window
is centered on the current pixel
p and filled with its similarities with the 8 closest neighbors. The similarity between the
p pixel and its neighbor
is defined using a Gaussian kernel:
with
a tuning parameter.
The similarities are then weighted by the confidence degrees of all neighbors of p.
The aggregated fuzzy decision of
p is defined as a weighted average
Figure 8:
with:
4.3.2. Fuzzy Temporal Decision
We propose to integrate an optical flow calculation in the method, to exploit the temporal continuity of the decisions. To summarize, the pixel velocity field is estimated, based on the hypothesis of brightness conservation (that is to say that the brightness of a physical point of the frame—likely to move—does not change over time).
In our method, we use an efficient and robust optical flow estimation algorithm, designed by Gunnar Farneback [
28].
We propose the following algorithm, to enrich the class information of pixel p of the frame t:
4.4. Merging Decisions
First spatial and temporal fuzzy decisions are merged to a fuzzy final decision, which is then “defuzzyfied”.
4.4.1. Final Fuzzy Decision
The final—spatio–temporal—decision is defined as a weighted average:
where
and
respectively denote the decision and the final fuzzy confidence of pixel
p.
4.5. Defuzzification of the Fuzzy Final Decision
The binary decision is obtained by rounding
towards its nearest integer if the final confidence level is high enough, else set to 1 (Foreground) otherwise:
After this final decision step, a binary mask frame can be fulfilled, to mark the locations of the Foreground pixels.
4.6. Other Step Changes (with Respect to T2-FGMM Method)
4.6.1. GMM Update
In T2-FGMM-like methods, updating the GMM model consists in reinforcing the unique mode associated to the pixel (the most “likely” one).
In our case, the final decision comes from the aggregation of several complementary decisions, conceived from different GMM models (according to the pixels or to the frame), and also from several modes (according to several Background and Foreground intervals).
However, we propose to apply such a single mode reinforcement. It first involves identifying the mode to reinforce. In practice, we look for the most likely mode
of the same class (Foreground or Background):
The selection fails when the likelihood of the optimal mode is below the R rejection threshold. In this case, a new Gaussian mode replaces the lowest priority one (lowest ), centered on the pixel level , with a weight initialized to .
Once the update is carried out, the algorithm resumes at the beginning of the loop, to the step of merging the close modes (cf.
Figure 7).
4.6.2. Fusion of Close Modes
This step was proposed to remedy to overlapping Gaussian modes. The stage is divided into two parts:
Computation of similarity
between each pair of modes
. Two modes are similar, if the center of one mode has a high (crisp) likelihood degree to the other mode:
Merging modes: each pair of Gaussian modes whose similarity is strong enough (
) is merged into a single new mode, following the common formula [
80]:
5. Validation Steps and Comparison to Methods Based on GMM and Fuzzy GMM
5.1. Base of Reference Videos
In this work we use the complete database from the site [
81], which provides realistic and hard-to-process videos, captured by camera. They are representative of indoor and outdoor scenes captured in surveillance, smart environment and video database scenarios. It is arranged in several video categories: thermal camera, shadows, intermittent foreground motion, camera jitter, dynamic background, bad weather, low frame rate, PTZ camera, night, baseline, turbulence. All quantitative evaluations of the proposed method were computed on [
82], University of Littoral’s computing server (Université du Littoral Côte d’Opale: Dunkerque, France).
5.2. Performance Indicators
Each pixel is subject to a decision, either right or wrong, which can be classified in one of these 4 categories (see
Table 1):
Once cumulated over all the video frames, each class number assesses a performance of the Foreground/Background recognition procedure:
: True Positives number (i.e., right Foreground decisions).
: False Positive number (i.e., wrong Foreground decisions).
: True Negative number (i.e.. right Background decisions).
: False Negatives number (i.e., wrong Background decisions).
More synthetic performance indicators are defined as combinations of these numbers (see
Table 2).
These usual parameters have the following meanings:
: proportion of pixels in the background correctly identified.
: proportion of foreground pixels correctly identified.
F-measure: geometric mean of Recall and Precision; it takes its values between 0 and 1, 1 being associated with maximal performance.
: proportion of decision errors.
: proportion of pixels in the background false identified.
5.3. Validation of the Method Steps
To validate the different steps of the method, we worked on a single reference video: the video Canoe. From the video category Dynamic background (from the site [
3]), it shows the passage of a boat on a river, with changing reflections. This is a small video (dimensions 320 × 240), with 30 frames per second, and 1189 frames in total.
We have selected it because it is a typical video of its category, which does not normally offer any particular difficulty to the subtraction algorithms. The parameters of our method have been optimized to best adapt to this video. The list of parameters is recalled in the
Table 3.
We optimized these parameters in order to ensure the best object detection, which is evaluated by the-synthetic-indicator of F-measure.
Below is the procedure followed:
Generation of a set of parameters sets (2443 sets, obtained by combining heuristically chosen parameter values). Each set of parameters assigns a unique combination of values to all parameters.
Selection of the best parameters set, according to the complete variant (spatio–temporal) method: this set is obtained by maximizing the
F-measure (cf.
Table 4).
Launching calculations with the optimized parameter set, with several variants of our IV-FGMM method (obtained by activating/deactivating certain steps).
5.3.1. Results Analysis
Table 5 shows the performances of the different variants of our method on the video Canoe, obtained with the optimized parameter set.
5.3.2. Interest of Spatial and Fuzzy Parts of the Method
We can easily note that the decision process is mainly improved (F-measure of 0.911 for the binary/spatial variant against 0.564 for the binary variant) when using the integration of spatial information.
To realize—more qualitatively—the importance of the different steps of the method, we show now some classification results on an image of the sequence: the image 965, where we can observe the passage of the canoe (cf. the 2 upper images of the
Figure 10, showing the
Figure 10a and its expected ground Truth
Figure 10)
The images in the
Figure 10 make it possible to visualize the results of the detection of the objects, according to the various method variants studied. The advantage of the (spatial/fuzzy ) merge step can be observed: it eliminates many classification errors.
The temporal contribution is less obvious (0.943 for the fuzzy/spatio–temporal variant). It would probably be a little more complex to exploit the optical flow, to obtain a significant gain.
5.4. Optimizing the Parameters in the Video Category “Dynamic Background”
To evaluate our method, we have optimized again the parameter set for the the most complete version of our method (i.e. the fuzzy spatio–temporal), over the whole dynamic background video set, by maximizing the F-measure ( in the tables).
In that, we did not exactly apply the official protocol of the site ChangeDetection: it would have been necessary to optimize the average F-measure on the videos of all the categories. But given the large number of parameter combinations to test, we had to restrict ourselves to the category we were most interested in (dynamic background).
The optimized parameter set is presented in
Table 6.
The set of the selected methods used for comparison is presented in
Table 7 below.
5.5. Results Comparison
The results of methods GMM-GS, GMM-Z, KDE-G, RMoG, and BMOG directly come from [
81] from the site [
81].
For the deep learning method CNN, the average F-measure score for the “dynamic background” category is taken from the article [
41].
For the other methods, we used the BGSLibrary [
85] library, with the default settings for each method.
An exception is made considering the T2-FGMM method (cf.
Section 3.3): the scores being surprisingly low, we tried to optimize them. We were expecting performances closer to ours, because of the similarities between the two methods. The parameters were obtained after maximizing the
F-measure on all videos of the “dynamic background” category (on a set of heuristically defined parameter sets). The combinations obtained for all T2-FGMM variants are given in
Table 8.
The
Table 9 gathers all the results useful for comparing the methods.
5.6. Analysis of Results
Table 9 first shows that our method gives comparable, if not better, results to the other methods, including those based on a GMM model (fuzzy or not fuzzy one), except for the methods BMOG and RMoG.
Compared to our method, RMoG makes a more extensive use of the pixel neighborhood: first in the initialization step, then in the update phase. As BMOG, it then uses a more appropriate color space than the classic RGB—CIE L*a*b—as well as a dynamic learning rate mechanism. In the SharedModel method, Chen et al. use all matched models in a region to find an optimal model. In our case, an exhaustive search for all the matched models in a region around the center pixel using the model of maximum probability for the foreground and background model is performed. The DP-GMM method has a good F-measure score compared to our method, but it’s a non-parametric DE method that considers an enrichment step. In this method, a Markov random field is built considering a node for each pixel, connected using a four-way neighbourhood. It is a binary labeling problem, where each pixel in each frame either belongs to the foreground or to the background. The uncertainty is taken into account in a different way in our method (fuzzy methodology), and we use different steps to make the method robust using adjustable parameters. SBBS method has a good result when we modeled the background at pixel level with a collection of previously observed background pixel values, and we use a ghost suppression mechanism with median filtering. SuBSENSE method also has a good result when St-Charles et al. use spatio–temporal binary features as well as color information to detect changes.
In this evaluation CNN achieves the maximal averaged F-measure (0.876). It is a very efficient method, but it is a supervised method which needs a huge learning database, whereas all other methods are unsupervised. The comparison is consequently not “fair”.
Apart from these four methods, which exploit information of a different nature, our method obtains very good results.
In particular, it achieves one of the best scores with video Fountaine2 (), higher than the other methods. It is a relatively complex video, because of the movement of water particles coming from the large fountain.
We note here that video Fountaine1 is a difficult challenge for all methods. Its unusual complexity is due to the changing pace of its four fountains, the very small size of the foreground, and its color, very close to that of the background.
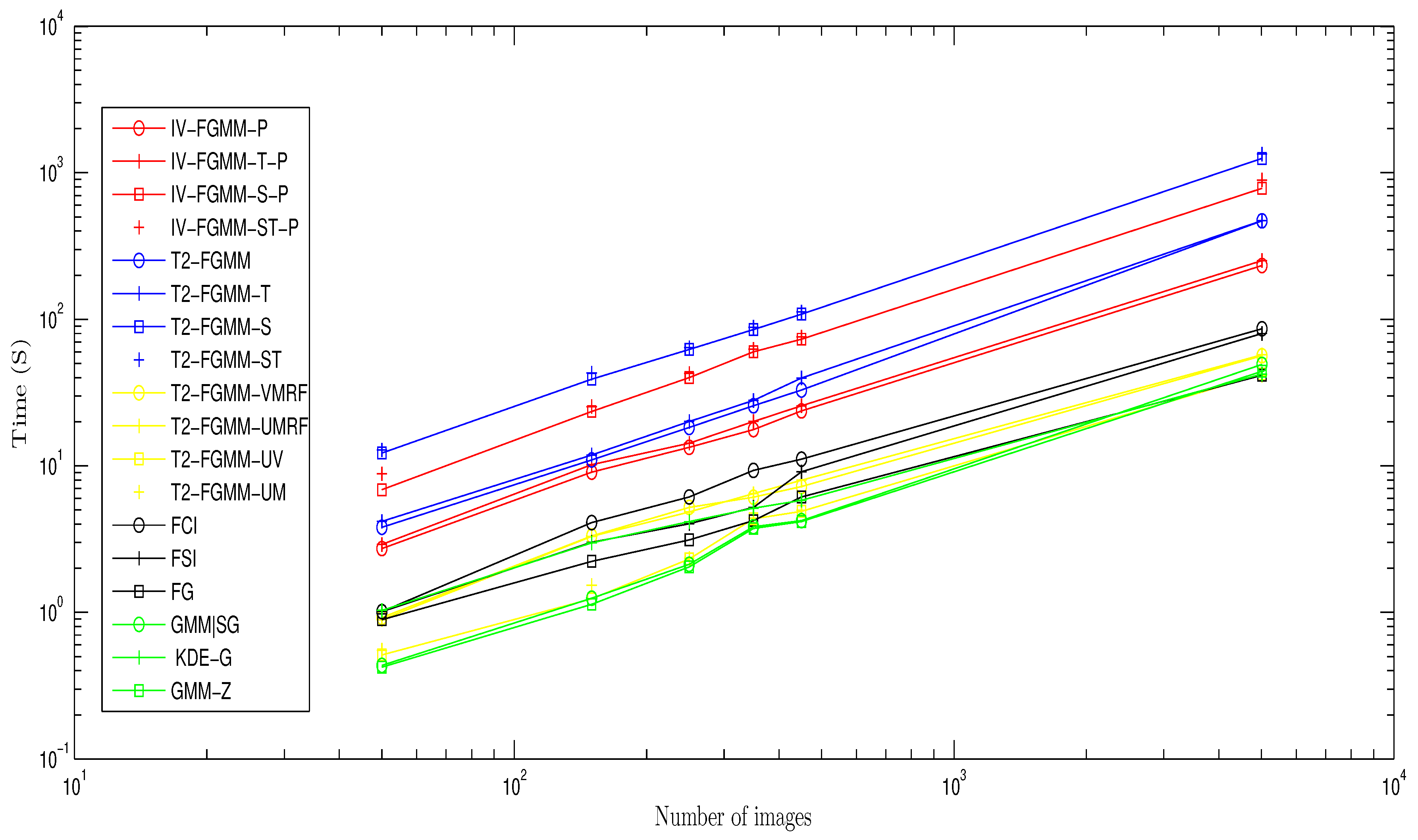
6. Comparison of Calculation Time for the Different Methods
Given the algorithmic complexity of some methods, we performed our comparison on a “lightened” video. We built it by extracting a sequence of consecutive images from the video fountaine1 (between 50 and 5016, with 30 frames per second), and then reducing them to .
We then tested all GMM based methods (except RMoG, BMOG, SuBSENSE, DP-GMM, see the following comment) on this video sequence, with a computer equipped with a Intel CPU (R) Core (TM) , with of RAM.
Considering our method, we compared several versions:
With parallelization on 4 cores (their name is suffixed by -P), and without parallelization (without suffix).
The fuzzy decision method (IV-FGMM, IV-FGMM-P), with temporal decision only (IV-FGMM-T, IV-FGMM-TP), with spatial decision alone ( IV-FGMM-S, IV-FGMM-SP), and the full space-time version (IV-FGMM-ST, IV-FGMM-ST-P).
We note that our method ranks 7th, which is very satisfying for a prototyping algorithm
Figure 11.
According to their authors, BMOG and SuBSENSE methods allow a calculation close to real time thus they do not appear on the comparison chart. We do not consider the DP-GMM method that has been implemented on a GPU.
The methods T2-FGMM are fast, more than our different variants, which have similar complexities (approximately equal slopes). Our method is indeed not economic for calculations, especially for intervals. And it becomes particularly expensive when integrating spatio–temporal fusion, so we need to optimize them in the future.
7. Conclusions
In this work, we proposed an original unsupervised method of background subtraction, based on a type-2 fuzzy Gaussian mixture, particularly robust to the dynamic changes of the background. The method proceeds per pixel, first computing and then aggregating the responses of different complementary fuzzy classifiers, each of them using a piece of information from the pixel: its color, the classes of its neighborhood, and its pixel class in previous frames.
The use of interval-valued fuzzy sets, and the way the fuzziness is preserved all along the classification process, tend to limit the errors coming from the model and from the estimation of its parameters. The method is so particularly devoted to videos with dynamic background, lighting changes or noisy.
We compared the proposed method to powerful recent algorithms of the literature. We focused on the “dynamic background” catalog of the benchmark database [
81] from the site [
81]. The method proved to be very efficient compared to most of the tested methods. This attests its relevance to process dynamic background change in videos.
Future work will consist in enriching the proposed fusion process with new relevant features, especially with textures and colors (and with another color space than RGB). Temporal fusion also needs to be improved because its current contribution to the method performance is minor.
Another important future work would be to deal with a more extensive use of fuzzy set: from the initialization to the end of the process, instead of dealing only with the main (decision-making) step.
Regarding the uncertainty handled in the background model, we turned to IV fuzzy sets, for their computation simplicity. We could prefer the richer formalism of Pythagorean numbers, and see if the method can then gain in performance.
Finally, recent deep learning techniques are another promising research way. Recently, several authors [
40,
86] successfully started to use them for background modeling, and for all categories of videos. For example, one could consider integrating uncertainty management into these techniques, using fuzzy sets. This may be a promising association to deal with most of the challenges of real videos in the future.