Event Centroiding Applied to Energy-Resolved Neutron Imaging at LANSCE
Abstract
:1. Introduction
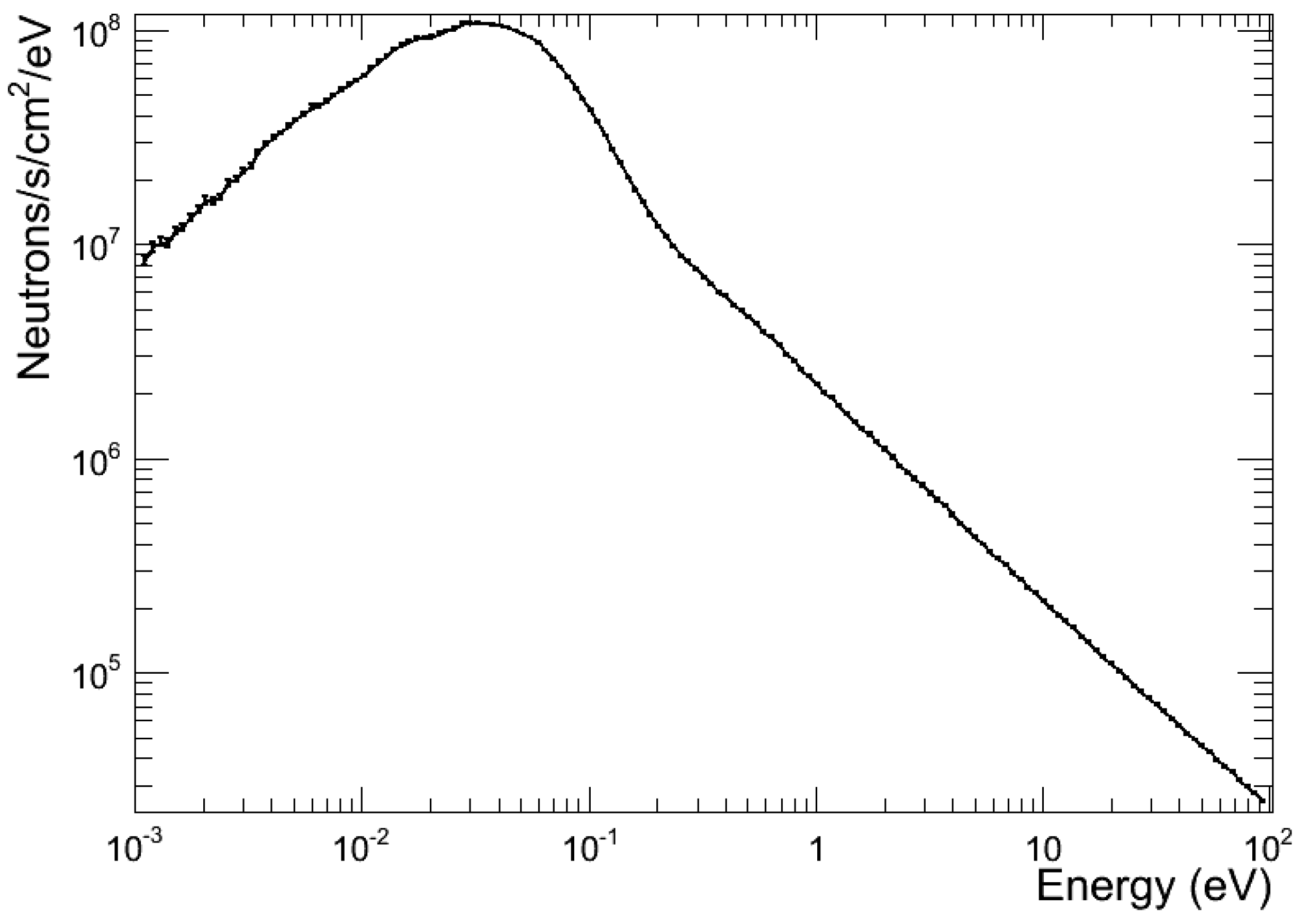
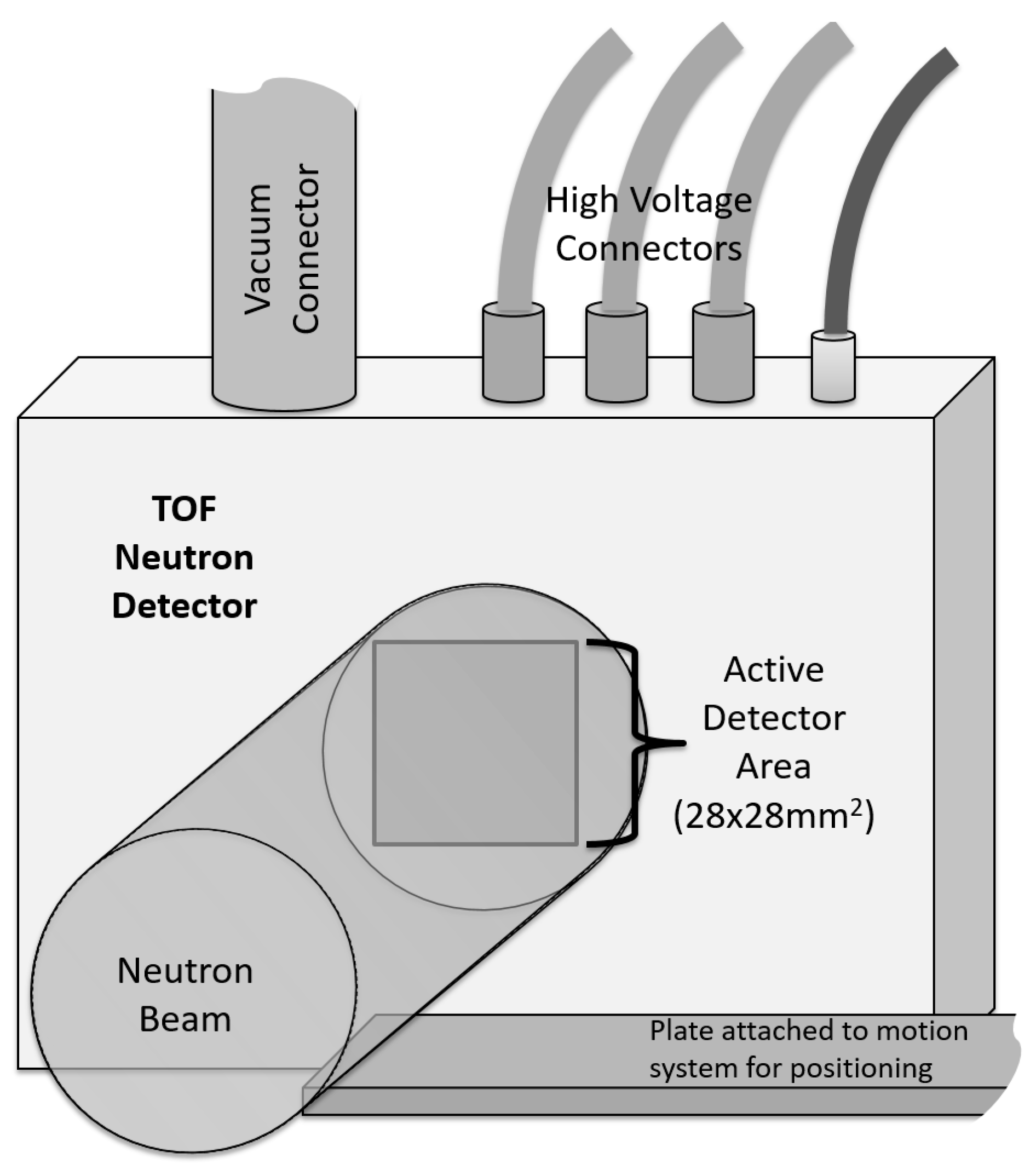
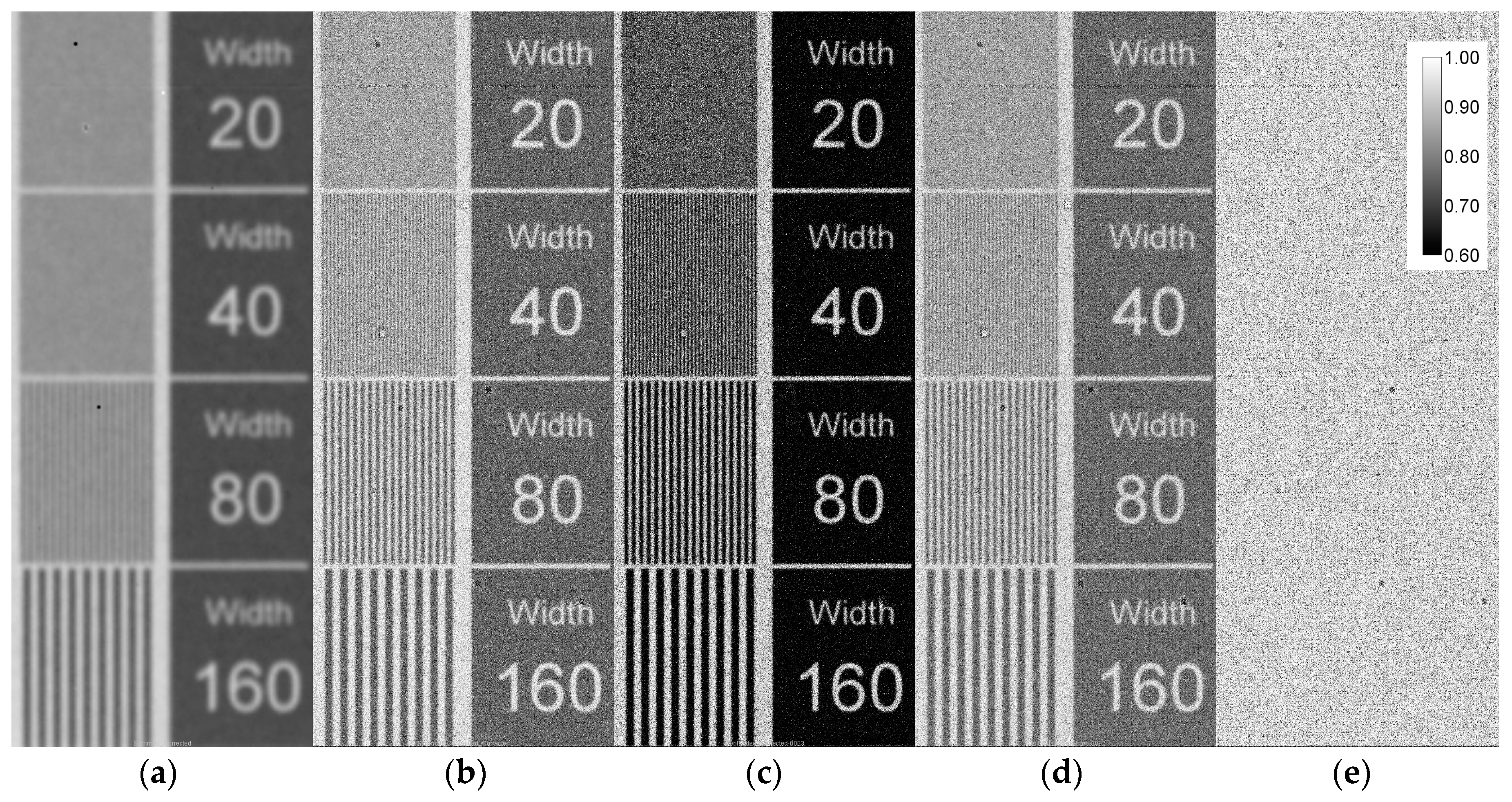
2. Materials and Methods
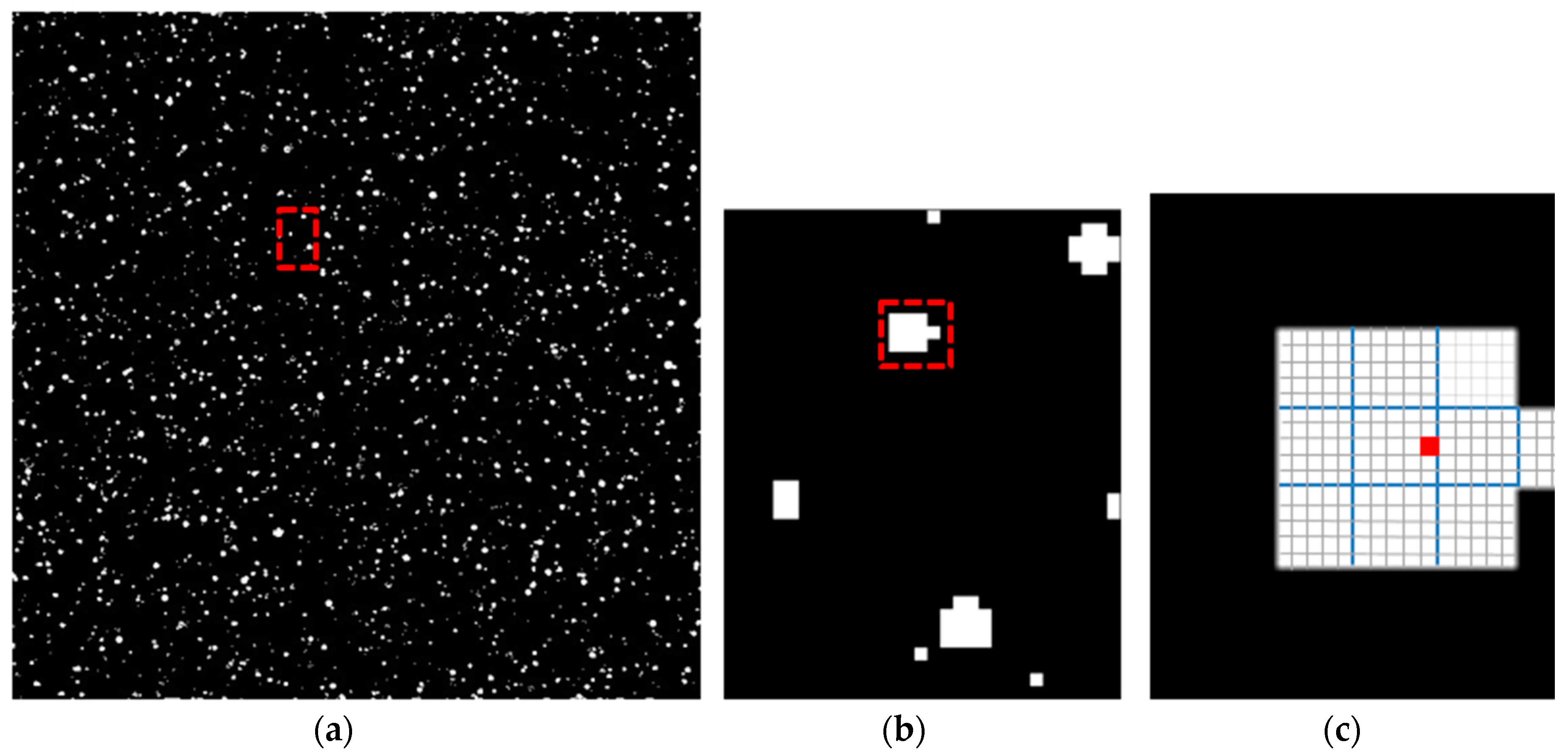
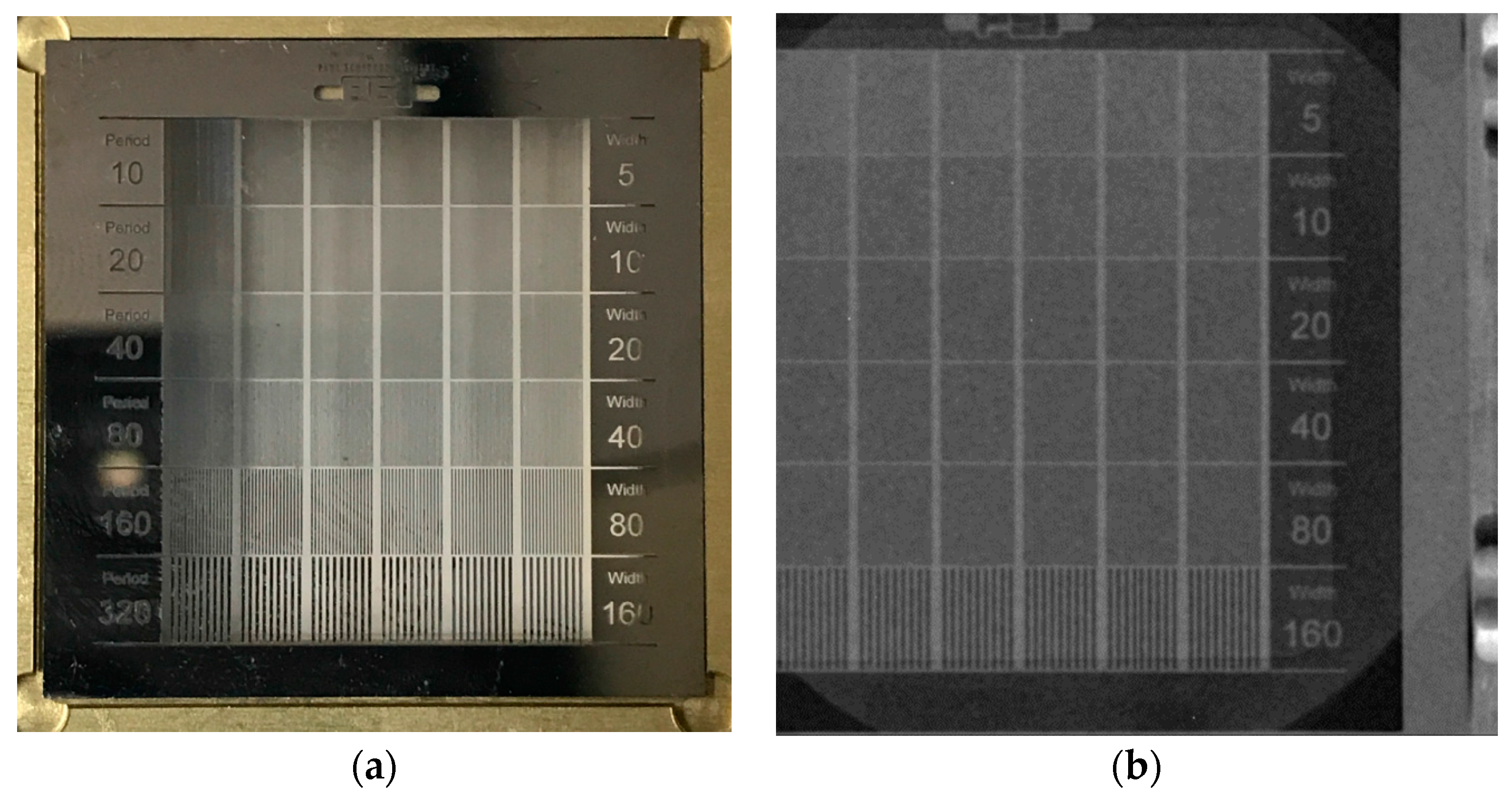
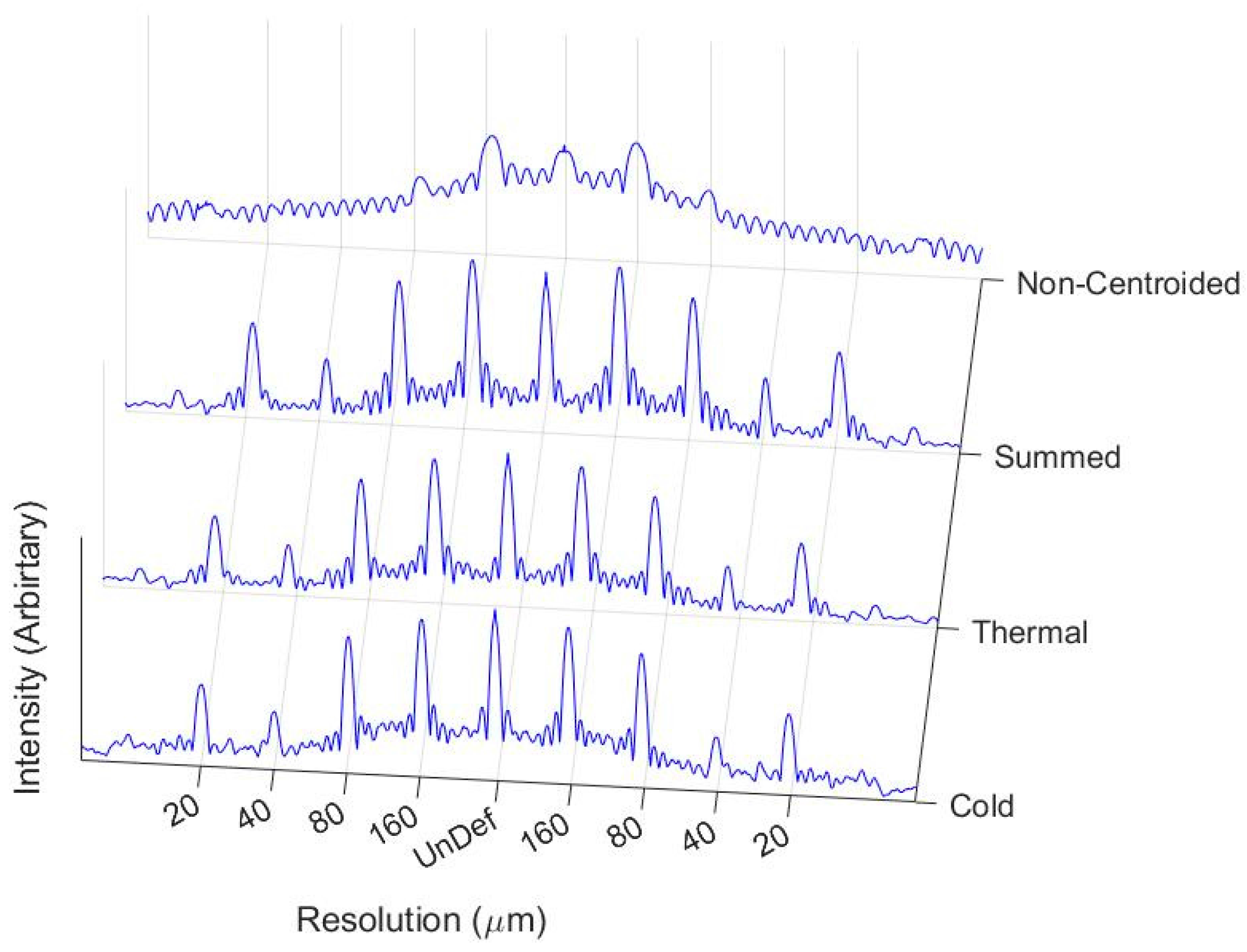
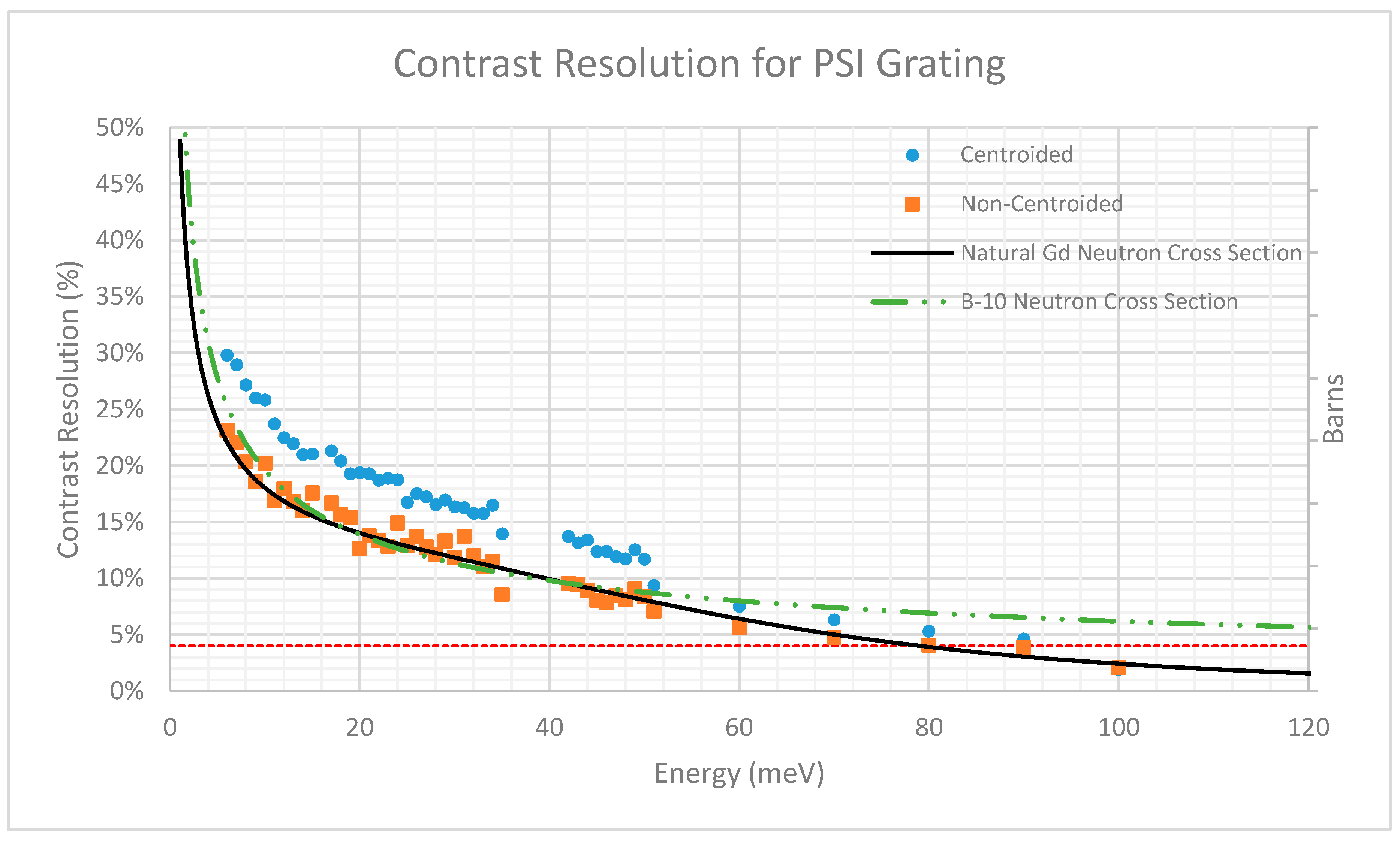
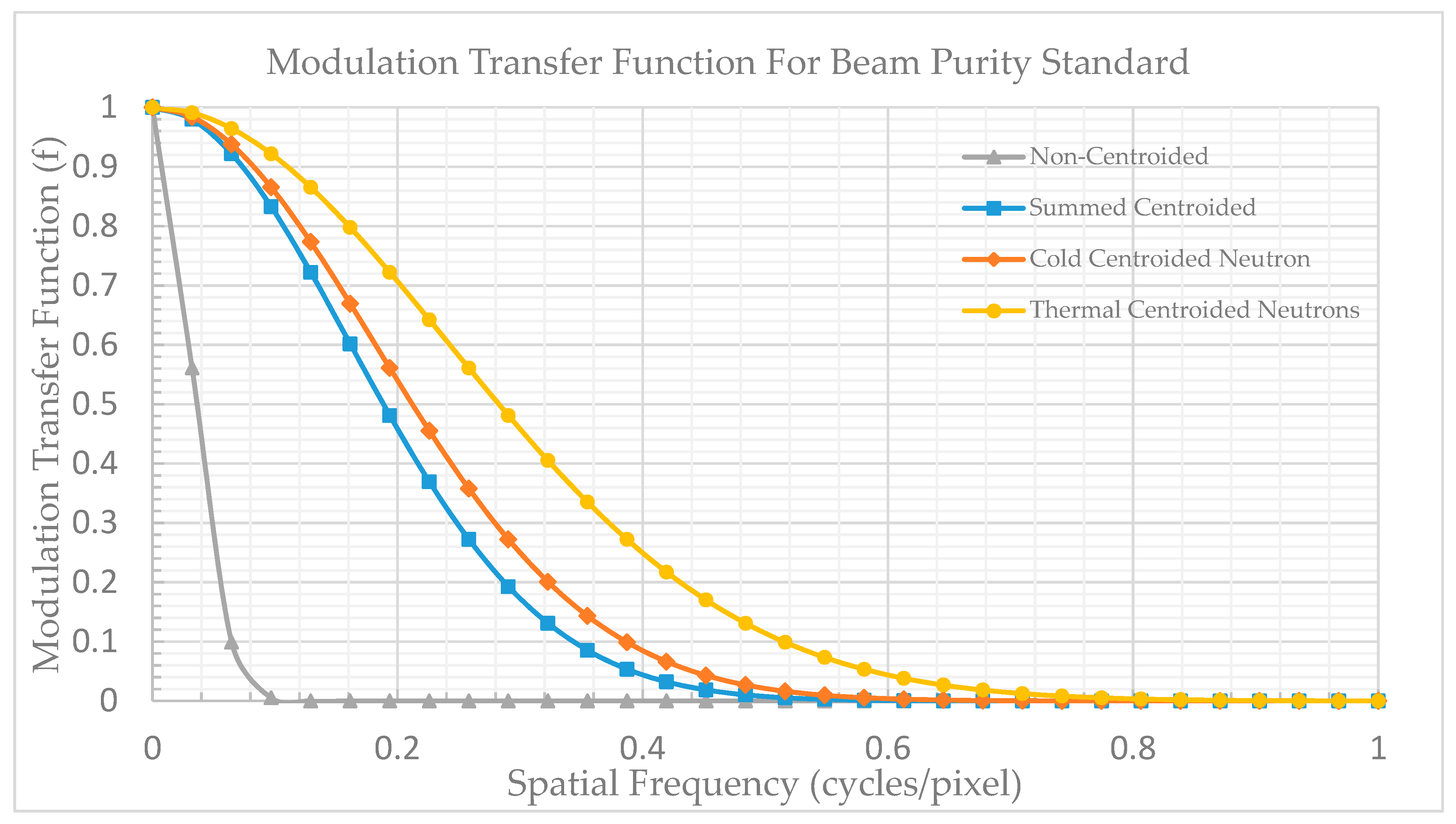
3. Results
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lehmann, E.H. Neutron Imaging Methods and Applications in Neutron Applications in Earth, Energy and Environmental Sciences; Springer: Berlin, Germany, 2009; pp. 319–348. [Google Scholar]
- Strobl, M.; Manke, I.; Kardjilov, N.; Hilger, A.; Dawson, M.; Banhart, J. Advances in neutron radiography and tomography. J. Phys. D 2009, 42, 243001. [Google Scholar] [CrossRef]
- Kardjilov, N.; Manke, I.; Hilger, A.; Strobl, M.; Banhart, J. Neutron imaging in materials science. Mater. Today 2011, 14, 248–256. [Google Scholar] [CrossRef]
- Lehmann, E.H.; Grunzweig, C.; Peetermans, S.; Kaestner, A.; Mannes, D. Advances in Neutron Radiology for Nondestructive Testing. Mater. Eval. 2014, 72, 437–442. [Google Scholar]
- Schillebeeckx, P.; Borella, A.; Emiliani, F.; Gorini, G.; Kockelmann, W.; Kopecky, S.; Lampoudis, C.; Moxon, M.; Cippo, E.P.; Postma, H.; et al. Neutron resonance spectroscopy for the characterization of materials and objects. J. Instrum. 2012, 7, C03009. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Vogel, S.C.; Mocko, M.; Bourke, M.A.; Yuan, V.; Nelson, R.O.; Brown, D.W.; Feller, W.B. Non-destructive studies of fuel pellets by neutron resonance absorption radiography and thermal neutron radiography. J. Nucl. Mater. 2013, 440, 633–646. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Losko, A.S.; Vogel, S.C.; Byler, D.D.; McClellan, K.J.; Bourke, M.A.; Vallerga, J.V. Non-contact measurement of partial gas pressure and distribution of elemental composition using energy-resolved neutron imaging. AIP Adv. 2017, 7, 015315. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Feller, W.B.; Downing, R.G. Efficiency optimization of microchannel plate (MCP) neutron imaging detectors. I. Square channels with 10 B doping. Nucl. Instrum. Methods Phys. Res. 2005, 539, 278–311. [Google Scholar] [CrossRef]
- Siegmund, O.H.; Vallerga, J.V.; Tremsin, A.S.; Mcphate, J.; Feller, B. High spatial resolution neutron sensing microchannel plate detectors. Nucl. Instrum. Methods Phys. Res. 2007, 576, 178–182. [Google Scholar] [CrossRef]
- Tremsin, A.S.; McPhate, J.B.; Vallerga, J.V.; Siegmund, O.H.; Feller, W.B.; Lehmann, E.; Dawson, M. Improved efficiency of high resolution thermal and cold neutron imaging. Nucl. Instrum. Methods Phys. Res. 2011, 628, 415–418. [Google Scholar] [CrossRef]
- Tremsin, A.S.; McPhate, J.B.; Kockelmann, W.A.; Vallerga, J.V.; Siegmund, O.H.; Feller, W.B. Energy-resolving neutron transmission radiography at the ISIS pulsed spallation source with a high-resolution neutron counting detector. IEEE Trans. Nucl. Sci. 2009, 56, 2931–2937. [Google Scholar] [CrossRef]
- Kockelmann, W.; Zhang, S.Y.; Kelleher, J.F.; Nightingale, J.B.; Burca, G.; James, J.A. IMAT—A new imaging and diffraction instrument at ISIS. Phys. Procedia 2013, 43, 100–110. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Vogel, S.C.; Mocko, M.; Bourke, M.A.; Yuan, V.; Nelson, R.O.; Brown, D.W.; Feller, W.B. Energy resolved neutron radiography at LANSCE pulsed neutron facility. Neutron News 2013, 24, 28–32. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Shinohara, T.; Kai, T.; Ooi, M.; Kamiyama, T.; Kiyanagi, Y.; Shiota, Y.; McPhate, J.B.; Vallerga, J.V.; Siegmund, O.H.; et al. Neutron resonance transmission spectroscopy with high spatial and energy resolution at the J-PARC pulsed neutron source. Nucl. Instrum. Methods Phys. Res. 2014, 746, 47–58. [Google Scholar] [CrossRef]
- Bilheux, H.Z.; Bilheux, J.C.; Bailey, W.B.; Keener, W.S.; Davis, L.E.; Herwig, K.W.; Cekanova, M. Neutron imaging at the Oak Ridge National Laboratory: Application to biological research. In Proceedings of the 2014 Annual Oak Ridge National Laboratory Biomedical Science and Engineering Center Conference (BSEC), Oak Ridge, TN, USA, 6–8 May 2014. [Google Scholar]
- Larson, N.M. Updated User’s Guide for Sammy: Multilevel R-Matrix Fits to Neutron Data Using Bayes’ Equations; Oak Ridge National Laboratory (ORNL): Oak Ridge, TN, USA, 2008.
- Lynn, J.E.; Trela, W.J. Resonance neutron methods for determining statistical properties of phonon spectra. Nucl. Instrum. Methods Phys. Res. 1996, 108, 147–158. [Google Scholar] [CrossRef]
- Lynn, J.E.; Kwei, G.H.; Trela, W.J.; Yuan, V.W.; Cort, B.; Martinez, R.J.; Vigil, F.A. Vibrational properties of Pu and Ga in a Pu-Ga alloy from neutron-resonance Doppler spectroscopy. Phys. Rev. B. 1998, 58, 11408. [Google Scholar] [CrossRef]
- Lynn, J.E.; Trela, W.J.; Meggers, K. Neutron Doppler broadening studies of tantalum and tungsten metal. Nucl. Instrum. Methods Phys. Res. 2002, 192, 318–330. [Google Scholar] [CrossRef]
- Yuan, V.W.; Bowman, J.D.; Funk, D.J.; Morgan, G.L.; Rabie, R.L.; Ragan, C.E.; Quintana, J.P.; Stacy, H.L. Shock temperature measurement using neutron resonance spectroscopy. Phys. Rev. Lett. 2005, 94, 125504. [Google Scholar] [CrossRef] [PubMed]
- Vogel, S.C.; Losko, A.S.; Pokharel, R.; Ickes, T.L.; Hunter, J.F.; Brown, D.W.; Voit, S.L.; Tremsin, A.S.; Bourke, M.A.; McClellan, K.J. Non-Destructive Preirradiation Assessment of UN/U-Si “LANL1” ATF Formulation; Los Alamos National Lab: Los Alamos, NM, USA, 2016.
- Tremsin, A.S.; Makowska, M.G.; Perrodin, D.; Shalapska, T.; Khodyuk, I.V.; Trtik, P.; Boillat, P.; Vogel, S.C.; Losko, A.S.; Strobl, M.; et al. In situ diagnostics of the crystal-growth process through neutron imaging: Application to scintillators. J. Appl. Crystallogr. 2016, 49, 743–755. [Google Scholar] [CrossRef] [PubMed]
- Tremsin, A.S.; Perrodin, D.; Losko, A.S.; Vogel, S.C.; Shinohara, T.; Oikawa, K.; Peterson, J.H.; Zhang, C.; Derby, J.J.; Zlokapa, A.M.; et al. In-situ Observation of Phase Separation During Growth of Cs2LiLaBr6: Ce Crystals Using Energy-Resolved Neutron Imaging. Cryst. Growth Des. 2017, 17, 6372–6381. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Perrodin, D.; Losko, A.S.; Vogel, S.C.; Bourke, M.A.; Bizarri, G.A.; Bourret, E.D. Real-time Crystal Growth Visualization and Quantification by Energy-Resolved Neutron Imaging. Sci. Rep. 2017, 7, 46275. [Google Scholar] [CrossRef] [PubMed]
- Wenk, H.R.; Lutterotti, L.; Vogel, S. Texture analysis with the new HIPPO TOF diffractometer. Nucl. Instrum. Methods Phys. Res. 2003, 515, 575–588. [Google Scholar] [CrossRef]
- Bourke, M.A.; Dunand, D.C.; Ustundag, E. SMARTS—A spectrometer for strain measurement in engineering materials. Appl. Phys. A 2002, 74, S1707–S1709. [Google Scholar] [CrossRef]
- Bergmann, B.; Nelson, R.O.; O’Donnell, J.M.; Pospisil, S.; Solc, J.; Takai, H.; Vykydal, Z. Time-of-flight measurement of fast neutrons with Timepix detectors. J. Instrum. 2014, 9, C05048. [Google Scholar] [CrossRef]
- King, N.S.; Ables, E.; Adams, K.; Alrick, K.R.; Amann, J.F.; Balzar, S.; Barnes, P.D., Jr.; Crow, M.L.; Cushing, S.B.; Eddleman, J.C.; et al. An 800-MeV proton radiography facility for dynamic experiments. Nucl. Instrum. Methods Phys. Res. 1999, 424, 84–91. [Google Scholar] [CrossRef]
- Tremsin, A.S.; McPhate, J.B.; Vallerga, J.V.; Siegmund, O.H.; Feller, W.B.; Lehmann, E.; Kaestner, A.; Boillat, P.; Panzner, T.; Filges, U. Neutron radiography with sub-15 μm resolution through event centroiding. Nucl. Instrum. Methods Phys. Res. 2012, 688, 32–40. [Google Scholar] [CrossRef]
- Hussey, D.S.; LaManna, J.M.; Baltic, E.; Jacobson, D.L. Neutron imaging detector with 2 μm spatial resolution based on event reconstruction of neutron capture in gadolinium oxysulfide scintillators. Nucl. Instrum. Methods Phys. Res. 2017, 866, 9–12. [Google Scholar] [CrossRef]
- Mocko, M.; Muhrer, G.; Tovesson, F. Advantages and limitations of nuclear physics experiments at an ISIS-class spallation neutron source. Nucl. Instrum. Methods Phys. Res. 2008, 589, 455–464. [Google Scholar] [CrossRef]
- Ino, T.; Ooi, M.; Kiyanagi, Y.; Kasugai, Y.; Maekawa, F.; Takada, H.; Muhrer, G.; Pitcher, E.J.; Russell, G.J. Measurement of neutron beam characteristics at the Manuel Lujan Jr. neutron scattering center. Nucl. Instrum. Methods Phys. Res. 2004, 525, 496–510. [Google Scholar] [CrossRef]
- Grünzweig, C.; Frei, G.; Lehmann, E.; Kühne, G.; David, C. Highly absorbing gadolinium test device to characterize the performance of neutron imaging detector systems. Rev. Sci. Instrum. 2007, 78, 053708. [Google Scholar] [CrossRef] [PubMed]
- Siegmund, O.H.; Vallerga, J.V.; Tremsin, A.S.; Feller, W.B. High spatial and temporal resolution neutron imaging with microchannel plate detectors. IEEE Trans. Nucl. Sci. 2009, 56, 1203–1209. [Google Scholar] [CrossRef]
- Tremsin, A.S. High resolution neutron counting detectors with microchannel plates and their applications in neutron radiography, diffraction and resonance absorption imaging. Neutron News 2012, 23, 35–38. [Google Scholar] [CrossRef]
- Dennison, E.W.; Stanton, R.H. Ultra-Precise Star Tracking Using Charge Coupled Devices (CCDs). In Proceedings of the SPIE 0252 Smart Sensors, San Diego, CA, USA, 1 January 1980. [Google Scholar]
- Kaestner, A.P.; Kis, Z.; Radebe, M.J.; Mannes, D.; Hovind, J.; Grünzweig, C.; Kardjilov, N.; Lehmann, E.H. Samples to Determine the Resolution of Neutron Radiography and Tomography. Phys. Procedia 2017, 88, 258–265. [Google Scholar] [CrossRef]
- Hendrick, R.E.; Raff, U.; Stark, D.D.; Bradley, W.G. Magnetic Resonance Imaging, 2nd ed.; Mosby Year Book: St. Louis, MO, USA, 1992; pp. 109–144. [Google Scholar]
- STM E545-14. Standard Test Method for Determining Image Quality in Direct Thermal Neutron Radiographic Examination; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Nray Services Inc. 56A Head Street Dundas Ontario; Nray Services Inc.: Dundas, ON, Canada.
- Neitzel, U.; Egbert, B.; Gerhard, H.; Paul, R. Determination of the modulation transfer function using the edge method: Influence of scattered radiation. Med. Phys. 2004, 31, 3485–3491. [Google Scholar] [CrossRef] [PubMed]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borges, N.P.; Losko, A.S.; Vogel, S.C. Event Centroiding Applied to Energy-Resolved Neutron Imaging at LANSCE. J. Imaging 2018, 4, 40. https://doi.org/10.3390/jimaging4020040
Borges NP, Losko AS, Vogel SC. Event Centroiding Applied to Energy-Resolved Neutron Imaging at LANSCE. Journal of Imaging. 2018; 4(2):40. https://doi.org/10.3390/jimaging4020040
Chicago/Turabian StyleBorges, Nicholas P., Adrian S. Losko, and Sven C. Vogel. 2018. "Event Centroiding Applied to Energy-Resolved Neutron Imaging at LANSCE" Journal of Imaging 4, no. 2: 40. https://doi.org/10.3390/jimaging4020040
APA StyleBorges, N. P., Losko, A. S., & Vogel, S. C. (2018). Event Centroiding Applied to Energy-Resolved Neutron Imaging at LANSCE. Journal of Imaging, 4(2), 40. https://doi.org/10.3390/jimaging4020040





