Partition and Inclusion Hierarchies of Images: A Comprehensive Survey
Abstract
1. Introduction
- Block-based representations (on binary images [3,4,5] and grayscale images [6,7,8]) divide the image into the set of (rectangular) arrays of pixels. It has fewer elements than pixel-based representations, but the image data are still not interpreted. Most common applications include image compression [3,6,7], segmentation [5,6], and feature and attribute extraction [4,5,8].
- Compressed (or frequency) domain representations store the image as a set of coefficients in a transform domain, such as Fourier transform [9,10], wavelets [10,11,12], ridgelets [13], contourlets [14], etc. Typical uses include image compression [10,11], denoising [13,15], reconstruction [12], texture analysis and segmentation [16]. Their advantage is a reduced image size, but they are sensitive to translation, rotation and scaling [17] and make it difficult to manipulate localized image content.
- Region-based representations group similar connected pixels using a segmentation algorithm, typically producing an over-segmentation. The resulting regions are often called superpixels [18], with the region adjacency information kept in a region-adjacency graph (RAG) [19] or combinatorial maps [20]. Different approaches include normalized cuts [21], graph-based segmentation by Felzenszwalb and Huttenlocher [22] and watershed segmentation [23,24], with a comparison in [18]. The reduced number of regions based on interpreting image information keeps the representational accuracy [2], but further unions of regions need to be considered to detect semantic structures [25].
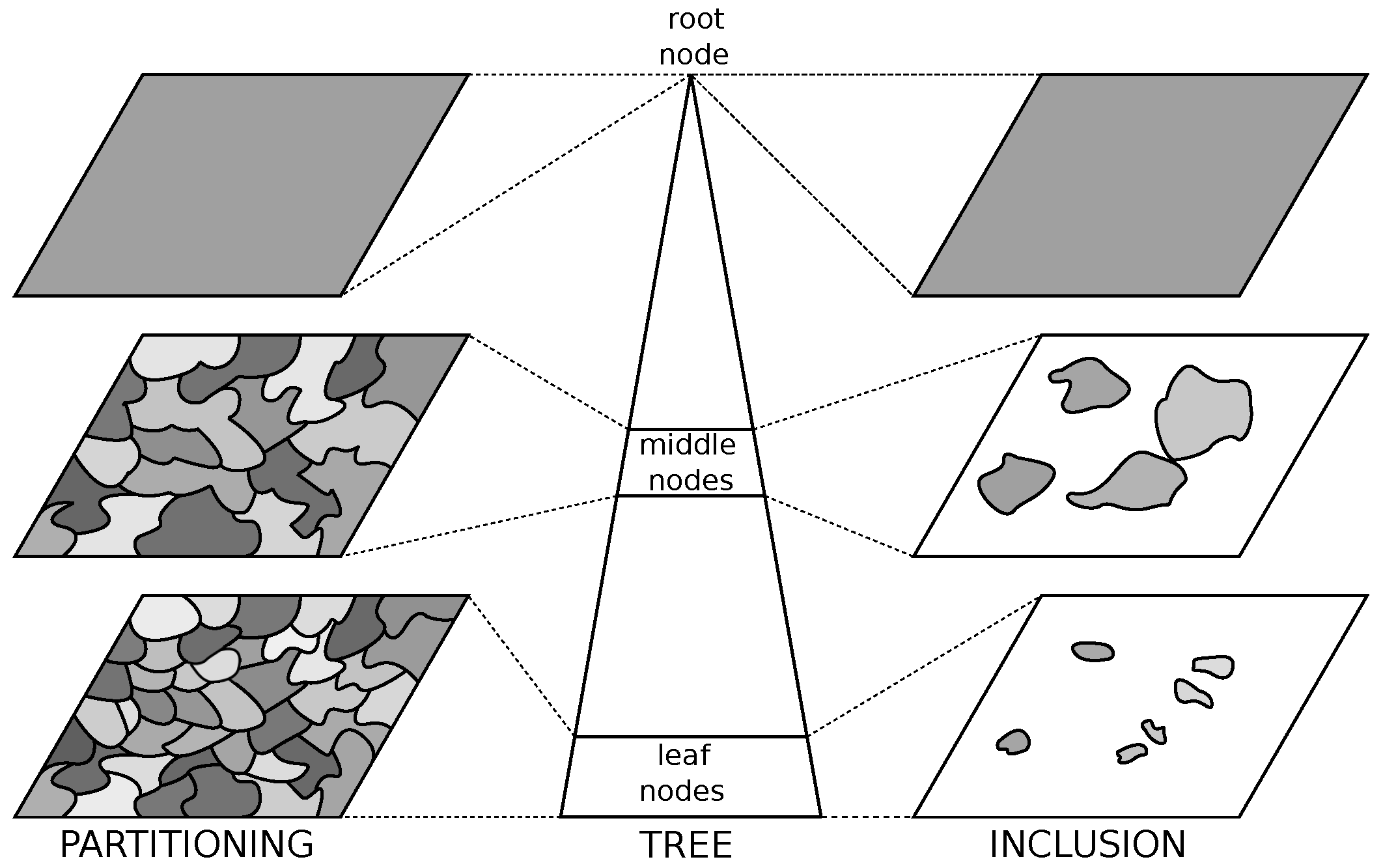
- Hierarchical representations propose those most likely unions of regions on different scales of the image, from fine to coarse [25]. They enrich the horizontal relations between regions present in (partial) segmentations [26,27] with vertical inclusion information between regions at different scales. Initially, they were used for image filtering [2,28,29], segmentation [30,31,32] and boundary detection [33] but have since been applied to a vast amount of domains and applications (cf. Table 3).
2. Related Work
3. Image Representation
3.1. Images as Graphs
3.2. Manipulating Image Components
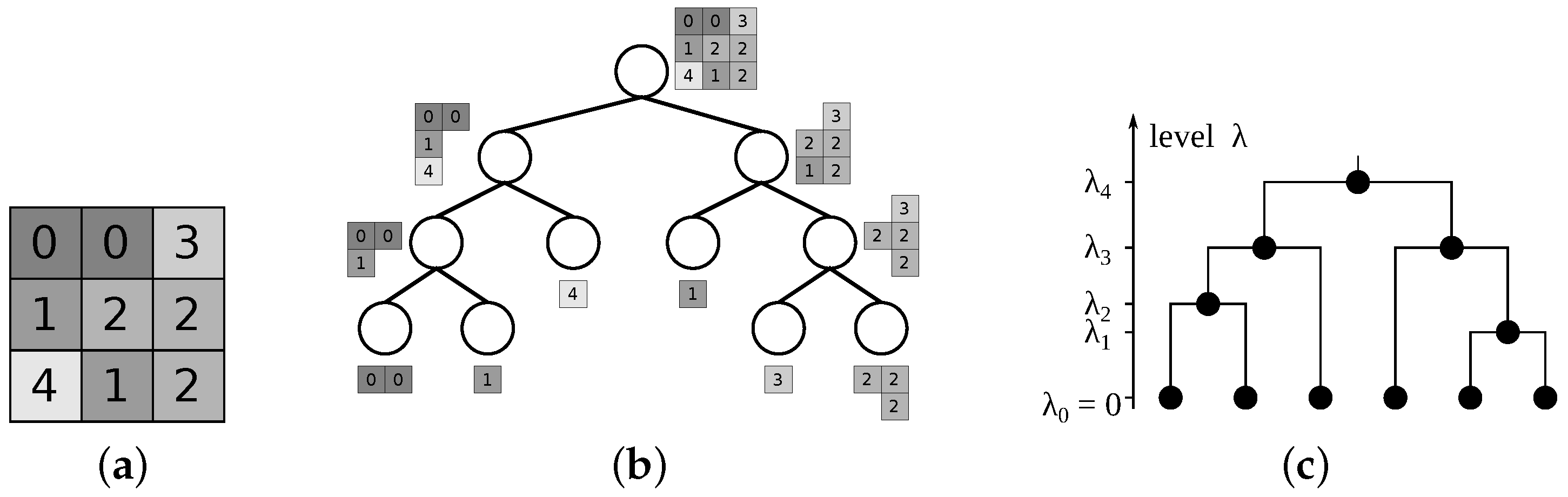
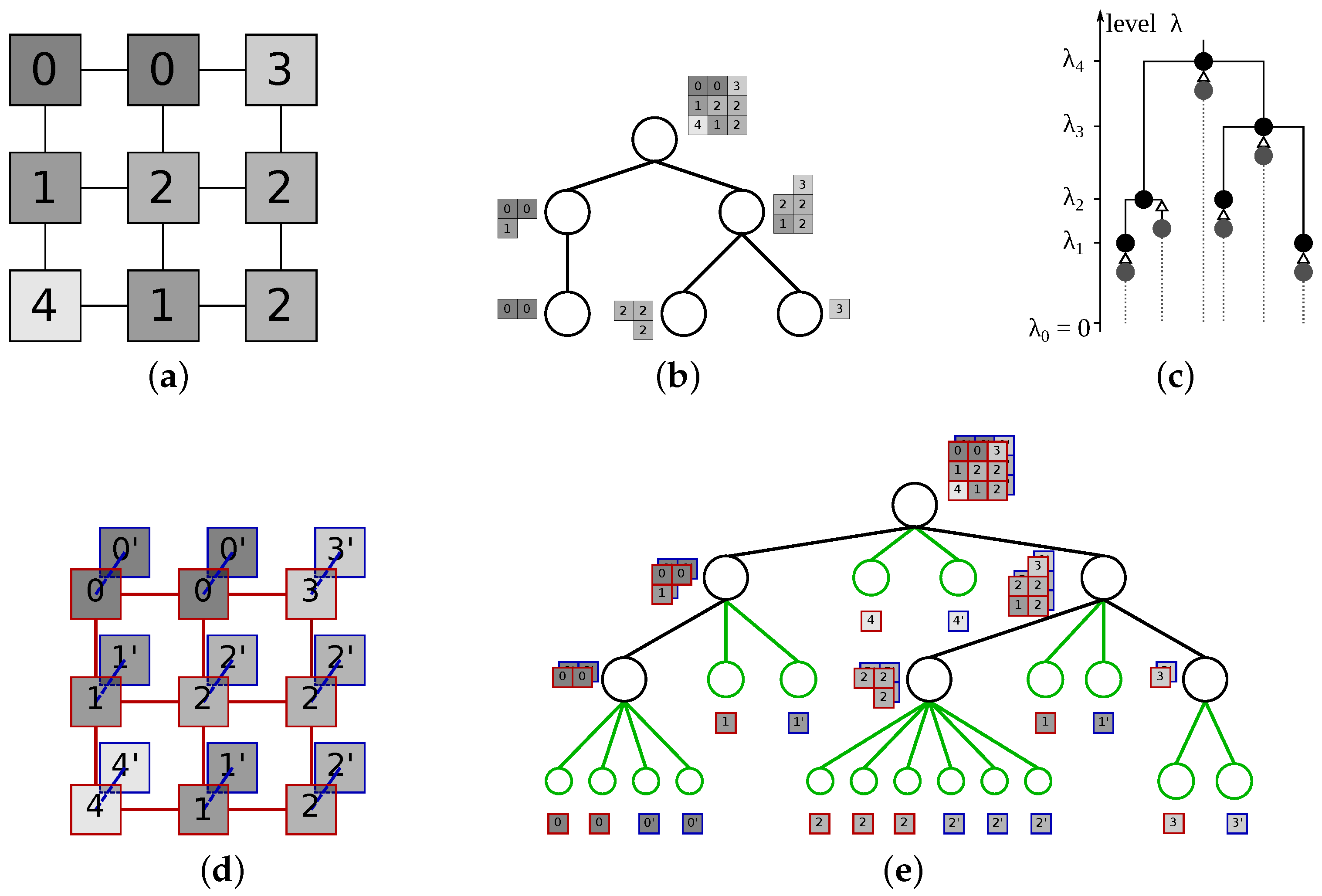
4. Component Trees
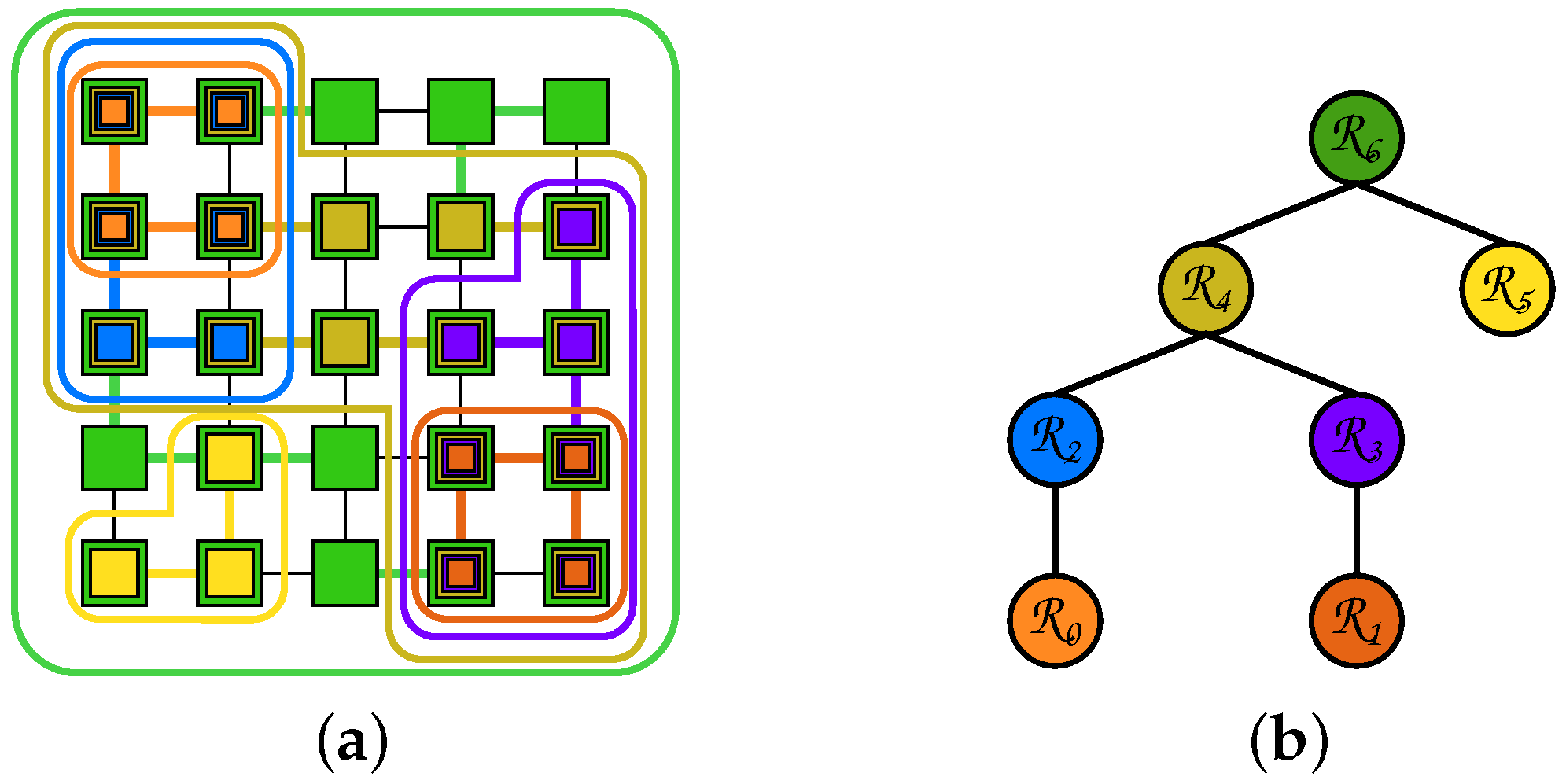
4.1. Hierarchies of Partitions and Partial Partitions
- ,
- for each two elements the following holds: or .
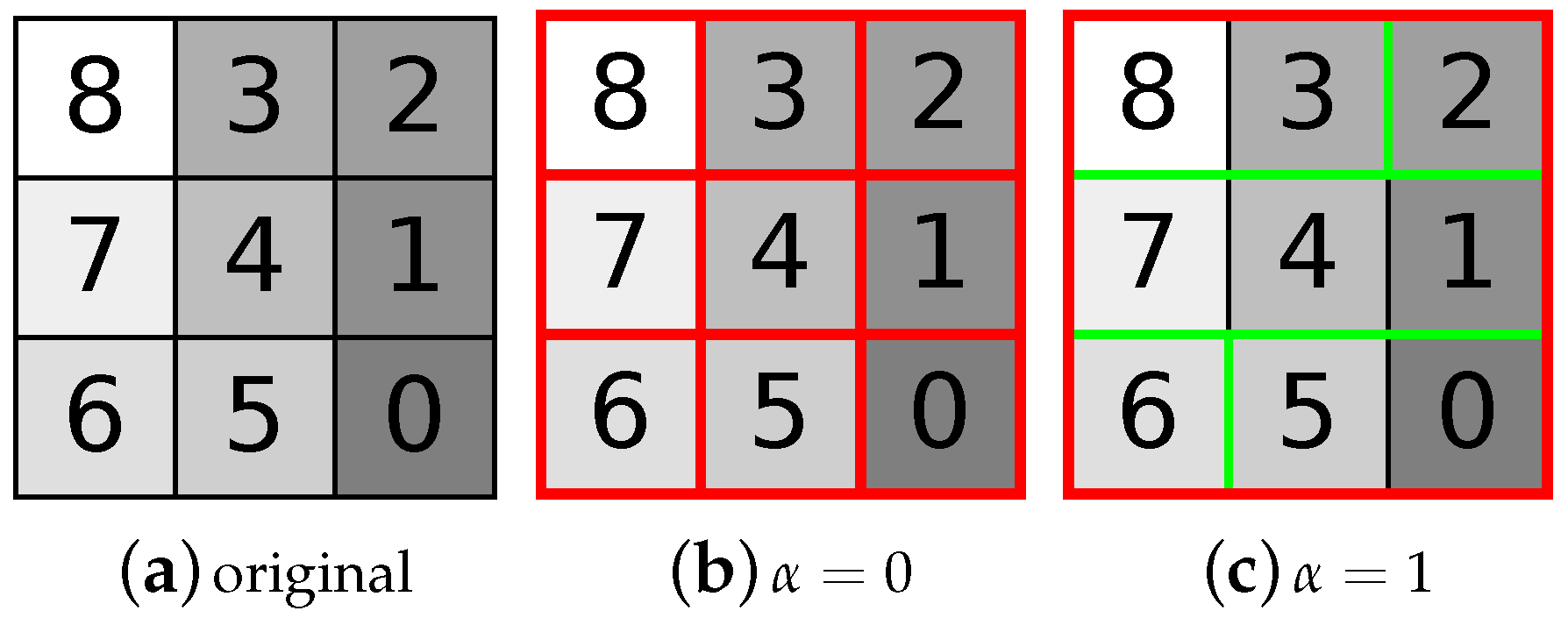
4.2. Construction Differences between Inclusion and Partitioning Hierarchies
- Region model defines how regions and their unions are represented. It reflects the characteristics of the regions used in the construction process.
- Merging criterion or similarity (or dissimilarity) measure describes the interest of possible merges. It is based on the region model.
- Merging order defines the rules used to merge the regions and which merge to perform next based on the merging criterion.
4.3. Indexing the Hierarchy
5. Analysis of Tree Characteristics
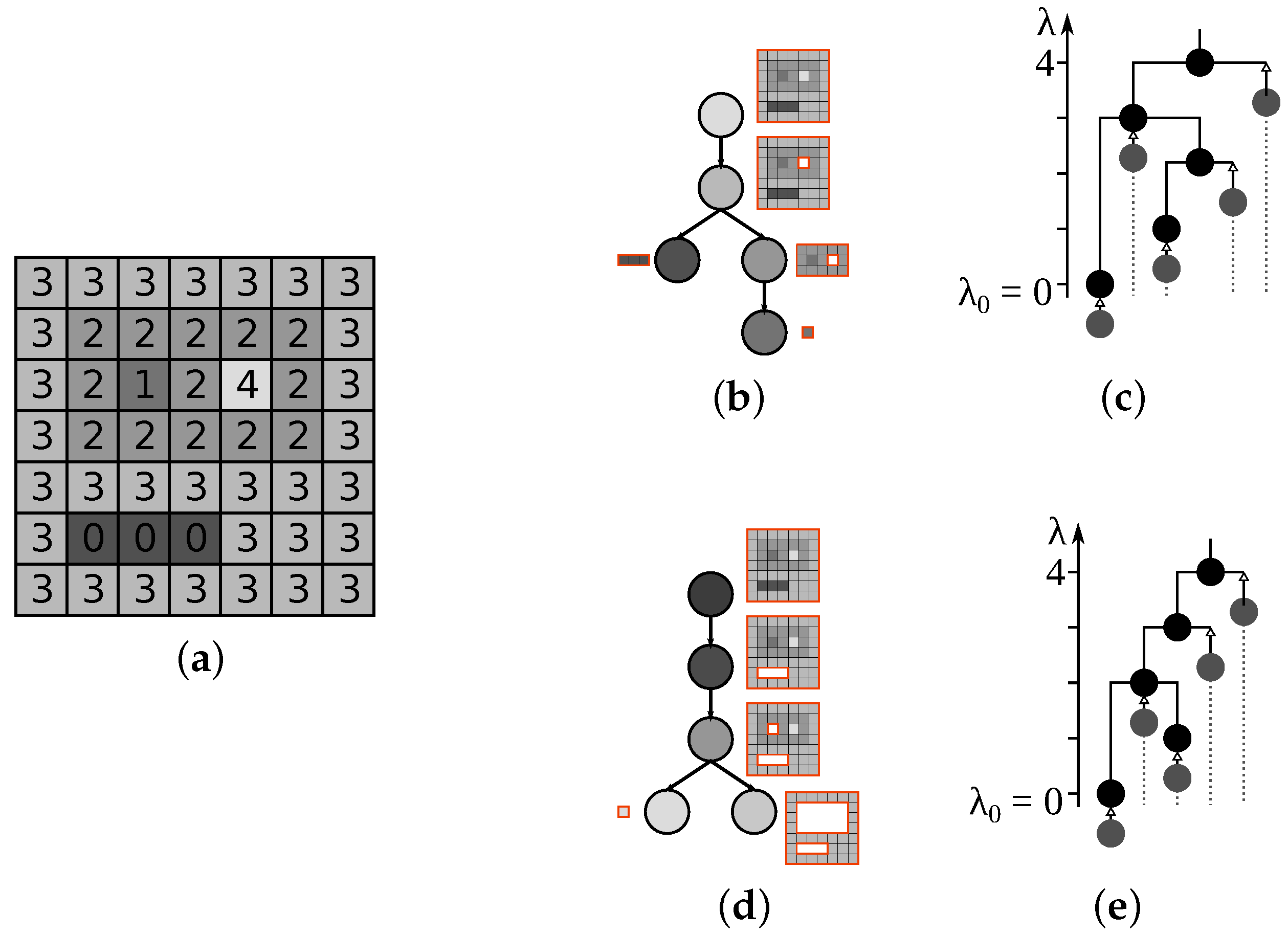
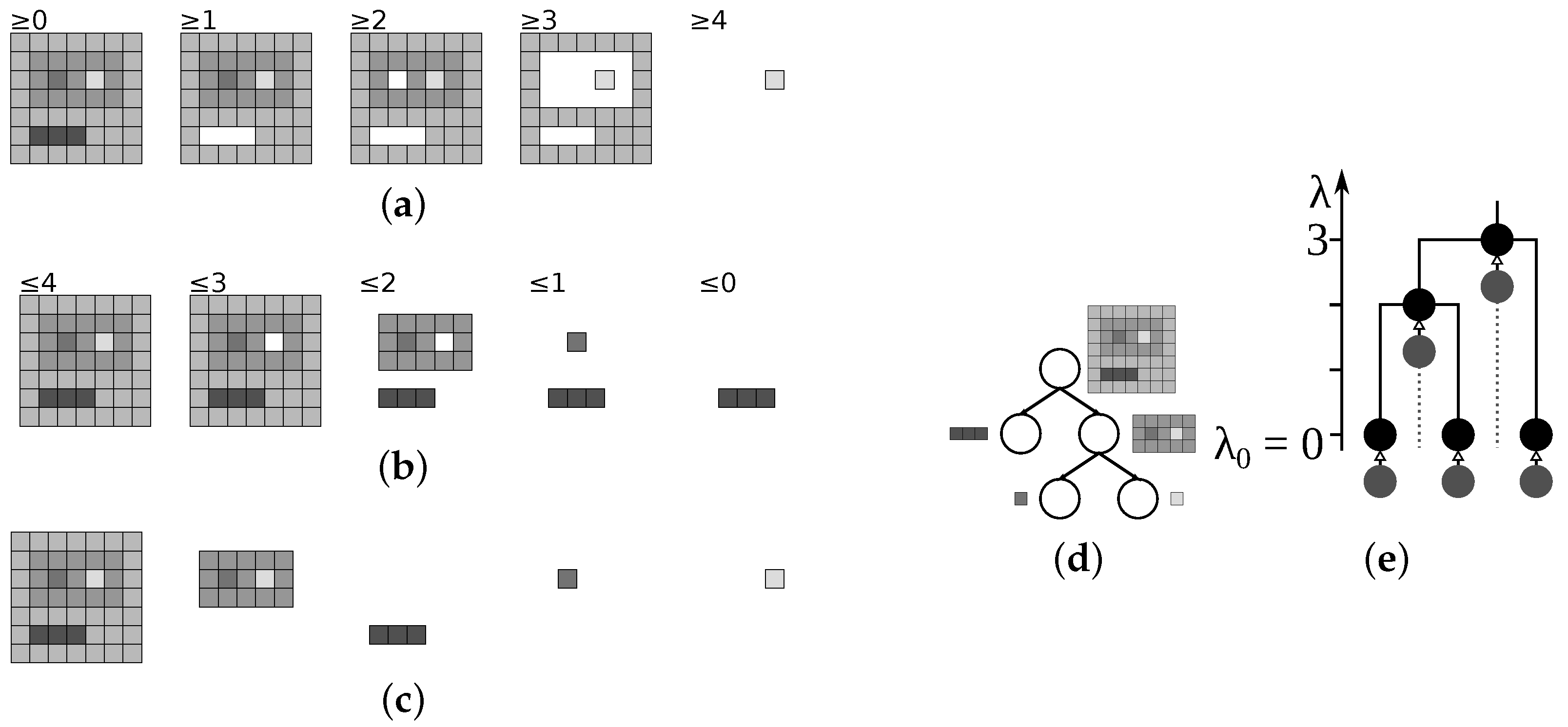
5.1. Min and Max-Trees
- a parent node to all the previously constructed nodes at lower levels which are included in the region of the new node: , ; or
- a leaf node if it does not include the regions of any previous nodes.
5.2. Tree of Shapes
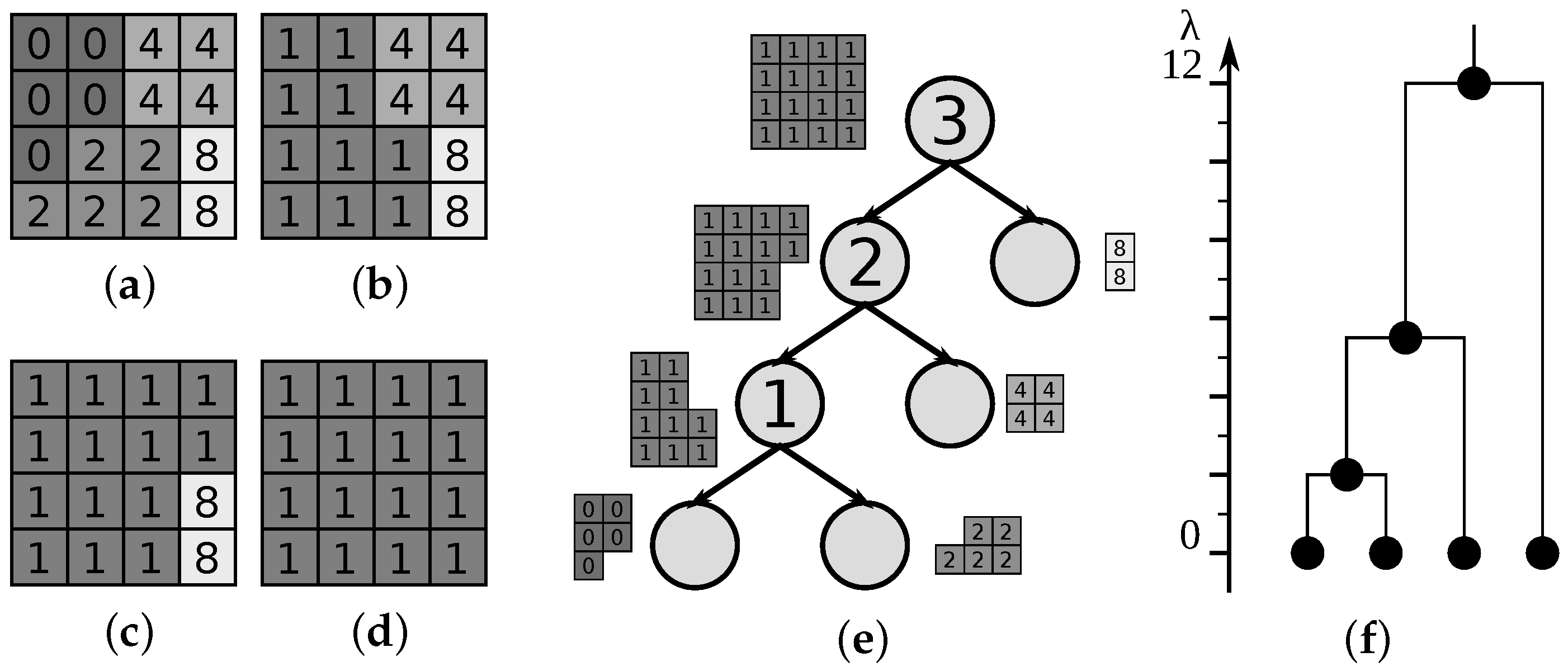
5.3. Binary Partition Tree
- if a node m of is a leaf node, then ,
- if a node m is created as a union of regions corresponding to the nodes and (i.e., ), and the dissimilarity between the regions in the moment of merging was , the level of the new node m is calculated according to:
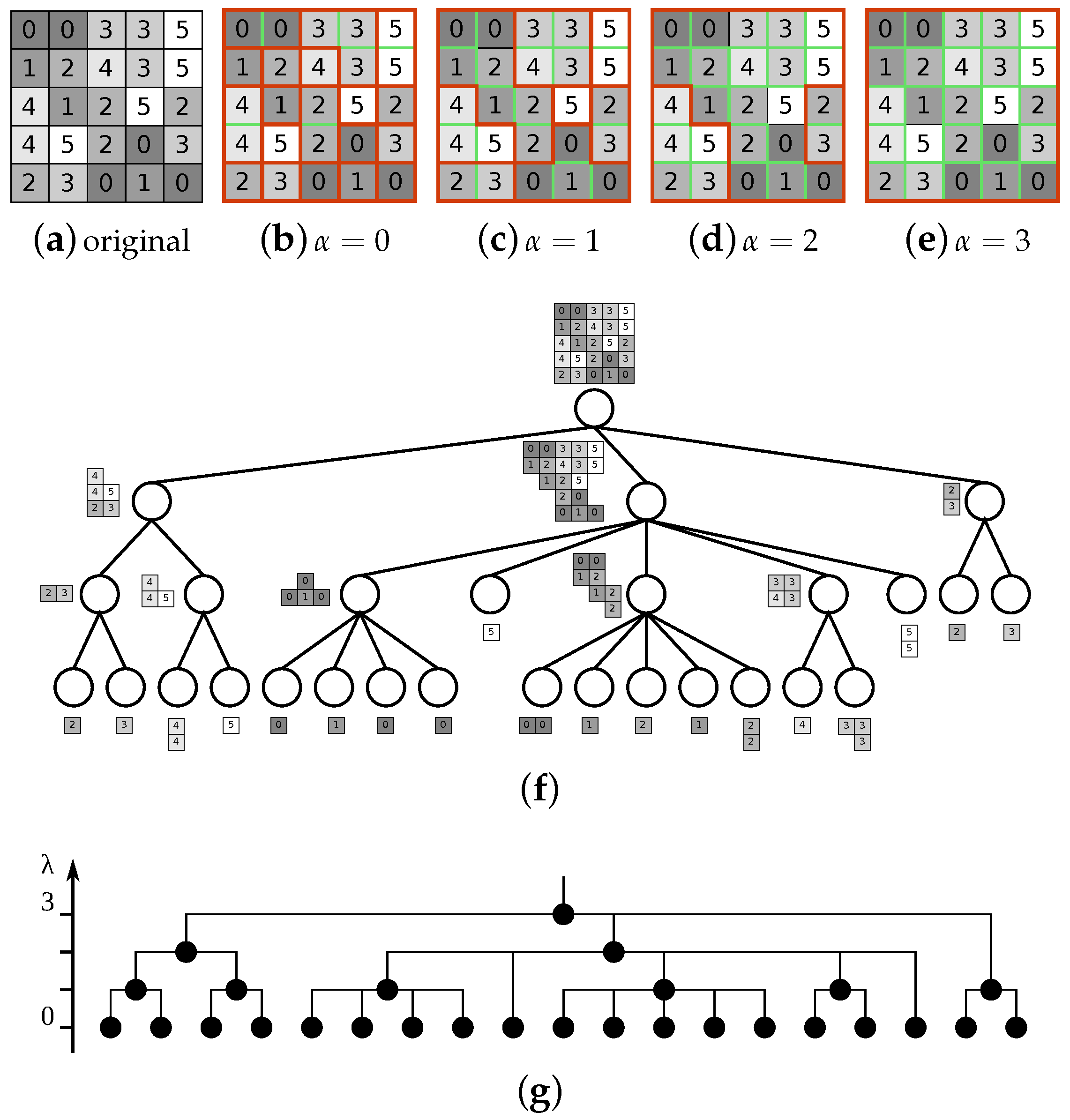
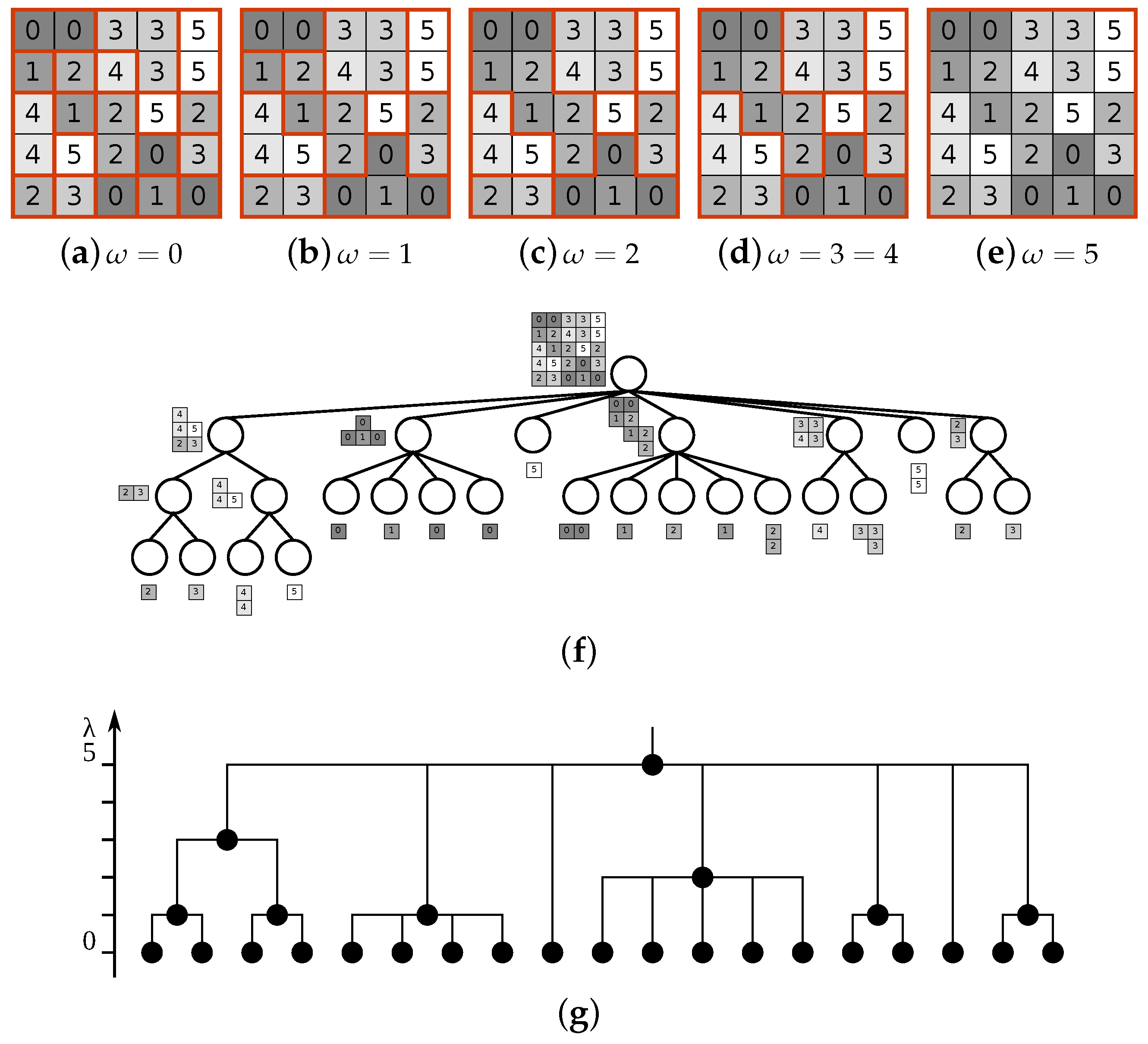
5.4. -Tree
- The region model for each region is the boundary of that region, .
- The merging criterion defines the similarity between two neighboring regions as the lowest edge (valued by gray level difference) common to models of both regions: .
- The merging order dictates that, in the i-th step, all regions with the similarity equal to i should be merged.
5.5. -Tree
- The region model for is the boundary of that region, , and minimal and maximal pixel values: .
- The merging criterion defines the similarity between all allowed sets of regions such that the subgraph of I generated by the union of all the region vertice sets: is connected. The weight of such a merge between a set of regions is:
- The merging order dictates that in the i-th step, all the sets of regions of maximal extent with the similarity equal to i should be merged.
6. Construction Algorithms
7. Applications and Future Directions
7.1. Comparative Summary
7.2. Open Challenges
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Soille, P. Morphological Image Analysis: Principles and Applications; Springer: Berlin, Germany, 2003. [Google Scholar]
- Salembier, P.; Garrido, L. Binary Partition Tree as an Efficient Representation for Image Processing, Segmentation, and Information Retrieval. IEEE Trans. Image Process. 2000, 9, 561–576. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, S.; Fahmy, M. Binary Image Compression Using Efficient Partitioning into Rectangular Regions. IEEE Trans. Commun. 1995, 43, 1888–1893. [Google Scholar] [CrossRef]
- Flusser, J. Refined Moment Calculation Using Image Block Representation. IEEE Trans. Image Process. 2000, 9, 1977–1978. [Google Scholar] [CrossRef] [PubMed]
- Perantonis, S.; Gatos, B.; Papamarkos, N. Block decomposition and segmentation for fast Hough transform evaluation. Pattern Recognit. 1999, 32, 811–824. [Google Scholar] [CrossRef]
- Won, C. A Block-Based MAP Segmentation for Image Compressions. IEEE Trans. Circuits Syst. Video Technol. 1998, 8, 592–601. [Google Scholar]
- Chung, K.; Wu, J. Improved Image Compression using S-Tree and Shading Approach. IEEE Trans. Commun. 2000, 48, 748–751. [Google Scholar] [CrossRef]
- Chung, K.; Chen, P. An efficient algorithm for computing moments on a block representation of a grey-scale image. Pattern Recognit. 2005, 38, 2578–2586. [Google Scholar] [CrossRef]
- De Castro, E.; Morandi, C. Registration of Translated and Rotated Images Using Finite Fourier Transforms. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 700–703. [Google Scholar] [CrossRef] [PubMed]
- Vetterli, M.; Kovačević, J. Wavelets and Subband Coding; Prentice Hall PTR: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Mallat, S. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Lee, T. Image Representation Using 2D Gabor Wavelets. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 959–971. [Google Scholar]
- Do, M.; Vetterli, M. The Finite Ridgelet Transform for Image Representation. IEEE Trans. Image Process. 2003, 12, 16–28. [Google Scholar] [CrossRef] [PubMed]
- Do, M.; Vetterli, M. The Contourlet Transform: An Efficient Directional Multiresolution Image Representation. IEEE Trans. Image Process. 2005, 14, 2091–2106. [Google Scholar] [CrossRef] [PubMed]
- Mallat, S.; Hwang, W. Singularity Detection and Processing with Wavelets. IEEE Trans. Inf. Theory 1992, 38, 617–643. [Google Scholar] [CrossRef]
- Bovik, A.; Clark, M.; Geisler, W. Multichannel Texture Analysis Using Localized Spatial Filters. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 55–73. [Google Scholar] [CrossRef]
- Monasse, P. Morphological Representation of Digital Images and Application to Registration. Ph.D. Thesis, Paris-Dauphine University, Paris, France, 2000. [Google Scholar]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Rosenfeld, A. Adjacency in digital pictures. Inf. Control 1974, 26, 24–33. [Google Scholar] [CrossRef]
- Lienhardt, P. Topological models for boundary representation: A comparison with n-dimensional generalized maps. Comput. Aided Des. 1991, 23, 59–82. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar]
- Felzenszwalb, P.; Huttenlocher, D. Efficient graph-based image segmentation. Int. J. Comput. Vis. 2004, 59, 167–181. [Google Scholar] [CrossRef]
- Vincent, L.; Soille, P. Watersheds in digital spaces: An efficient algorithm based on immersion simulations. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 583–598. [Google Scholar] [CrossRef]
- Cousty, J.; Bertrand, G.; Najman, L.; Couprie, M. Watershed Cuts: Minimum Spanning Forests and the Drop of Water Principle. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 1362–1374. [Google Scholar] [CrossRef] [PubMed]
- Vilaplana, V.; Marques, F.; Salembier, P. Binary Partition Trees for Object Detection. IEEE Trans. Image Process. 2008, 17, 2201–2216. [Google Scholar] [CrossRef] [PubMed]
- Serra, J. A Lattice Approach to Image Segmentation. J. Math. Imaging Vis. 2006, 24, 83–130. [Google Scholar] [CrossRef]
- Ronse, C. Partial Partitions, Partial Connections and Connective Segmentation. J. Math. Imaging Vis. 2008, 32, 97–125. [Google Scholar] [CrossRef]
- Jones, R. Component trees for image filtering and segmentation. Comput. Vis. Image Underst. 1997, 75, 215–228. [Google Scholar] [CrossRef]
- Salembier, P.; Oliveras, A.; Garrido, L. Antiextensive Connected Operators for Image and Sequence Processing. IEEE Trans. Image Process. 1998, 7, 555–570. [Google Scholar] [CrossRef] [PubMed]
- Garrido, L.; Salembier, P.; Garcia, D. Extensive operators in partition lattices for image sequence analysis. Signal Process. 1998, 66, 157–180. [Google Scholar] [CrossRef]
- Meyer, F. an overview of morphological segmentation. Int. J. Pattern Recognit. Artif. Intell. 2001, 15, 1089–1118. [Google Scholar] [CrossRef]
- Horowitz, S.L.; Pavlidis, T. Picture segmentation by a tree traversal algorithm. J. ACM 1976, 23, 368–388. [Google Scholar] [CrossRef]
- Tanimoto, S.; Pavlidis, T. a hierarchical data structure for picture processing. Comput. Graph. Image Process. 1975, 4, 104–119. [Google Scholar] [CrossRef]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Hoiem, D.; Efros, A.A.; Hebert, M. Recovering occlusion boundaries from an image. Int. J. Comput. Vis. 2011, 91, 328–346. [Google Scholar] [CrossRef]
- Uijlings, J.R.; Van De Sande, K.E.A.; Gevers, T.; Smeulders, A.W.M. Selective search for object recognition. Int. J. Comput. Vis. 2013, 104, 154–171. [Google Scholar] [CrossRef]
- Monasse, P.; Guichard, F. Fast Computation of a Contrast-Invariant Image Representation. IEEE Trans. Image Process. 2000, 9, 860–872. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Zhang, A. Monotonic tree. In Proceedings of the 10th International Conference, DGCI 2002, Bordeaux, France, 3–5 April 2002; Volume 2301, pp. 114–123. [Google Scholar]
- Géraud, T.; Carlinet, E.; Crozet, S.; Najman, L. A quasi-linear algorithm to compute the tree of shapes of nD images. In Proceedings of the 11th International Symposium, ISMM 2013, Uppsala, Sweden, 27–29 May 2013; Volume 7883, pp. 97–108. [Google Scholar]
- Cousty, J.; Najman, L.; Perret, B. Constructive Links between Some Morphological Hierarchies on Edge-Weighted Graphs. In Proceedings of the 11th International Symposium, ISMM 2013, Uppsala, Sweden, 27–29 May 2013; Volume 7883, pp. 85–96. [Google Scholar]
- Cousty, J.; Najman, L. Incremental Algorithm for Hierarchical Minimum Spanning Forests and Saliency of Watershed Cuts. In Proceedings of the 10th International Symposium, ISMM 2011, Verbania-Intra, Italy, 6–8 July 2011; Volume 6671, pp. 272–283. [Google Scholar]
- Soille, P. Constrained Connectivity for Hierarchical Image Partitioning and Simplification. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1132–1145. [Google Scholar] [CrossRef] [PubMed]
- Ouzounis, G.; Soille, P. Pattern Spectra from Partition Pyramids and Hierarchies. In Proceedings of the 10th International Symposium, ISMM 2011, Verbania-Intra, Italy, 6–8 July 2011; Volume 6671, pp. 108–119. [Google Scholar]
- Najman, L.; Soille, P. On Morphological Hierarchical Representations for Image Processing and Spatial Data Clustering. In Applications of Discrete Geometry and Mathematical Morphology; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7346, pp. 43–67. [Google Scholar]
- Ronse, C. Adjunctions on the lattices of partitions and of partial partitions. Appl. Algebr. Eng. Commun. Comput. 2010, 21, 343–396. [Google Scholar] [CrossRef]
- Ronse, C. Ordering partial partitions for image segmentation and filtering: Merging, creating and inflating blocks. J. Math. Imaging Vis. 2014, 49, 202–233. [Google Scholar] [CrossRef]
- Ronse, C. Orders for Simplifying Partial Partitions. J. Math. Imaging Vis. 2017, 58, 382–410. [Google Scholar] [CrossRef]
- Najman, L.; Meyer, F. A short tour of mathematical morphology on edge and vertex weighted graphs. In Image Processing and Analysis with Graphs; Lezoray, O., Grady, L., Eds.; CRC Press: Boca Raton, FL, USA, 2012; pp. 141–174. [Google Scholar]
- Bosilj, P.; Lefèvre, S.; Kijak, E. Hierarchical Image Representation Simplification Driven by Region Complexity. In Proceedings of the 17th International Conference, Naples, Italy, 9–13 September 2013; Volume 8156, pp. 562–571. [Google Scholar]
- Sokal, R.; Rohlf, F. The comparison of dendrograms by objective methods. Taxon 1962, 11, 33–40. [Google Scholar] [CrossRef]
- Kiran, B.R.; Serra, J. Global–local optimizations by hierarchical cuts and climbing energies. Pattern Recognit. 2014, 47, 12–24. [Google Scholar] [CrossRef]
- Salembier, P.; Wilkinson, M. Connected Operators. IEEE Signal Process. Mag. 2009, 26, 136–157. [Google Scholar] [CrossRef]
- Najman, L.; Cousty, J.; Perret, B. Playing with Kruskal: Algorithms for Morphological Trees in Edge-Weighted Graphs. In Proceedings of the 11th International Symposium, ISMM 2013, Uppsala, Sweden, 27–29 May 2013; Volume 7883, pp. 135–146. [Google Scholar]
- Cousty, J.; Najman, L.; Kenmochi, Y.; Guimarães, S. Hierarchical segmentations with graphs: quasi-at zones, minimum spanning trees, and saliency maps. J. Math. Imaging Vis. 2016. [Google Scholar] [CrossRef]
- Najman, L.; Cousty, J. a graph-based mathematical morphology reader. Pattern Recognit. Lett. 2014, 47, 3–17. [Google Scholar] [CrossRef]
- Berge, C. Graphs and Hypergraphs; North-Holland Publishing Company: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Ouzounis, G.; Wilkinson, M. Mask-based second-generation connectivity and attribute filters. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 990–1004. [Google Scholar] [CrossRef] [PubMed]
- Ouzounis, G.; Wilkinson, M. Hyperconnected attribute filters based on k-flat zones. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 224–239. [Google Scholar] [CrossRef] [PubMed]
- Perret, B.; Lefèvre, S.; Collet, C.; Slezak, É. Hyperconnections and hierarchical representations for grayscale and multiband image processing. IEEE Trans. Image Process. 2012, 21, 14–27. [Google Scholar] [CrossRef] [PubMed]
- Ronse, C. Set-theoretical algebraic approaches to connectivity in continuous or digital spaces. J. Math. Imaging Vis. 1998, 8, 41–58. [Google Scholar] [CrossRef]
- Serra, J. Mathematical morphology for Boolean lattices. In Image Analysis and Mathematical Morphology, II: Theoretical Advances; Academic Press: Cambridge, MA, USA, 1988; pp. 37–58. [Google Scholar]
- Ghamisi, P.; Dalla Mura, M.; Benediktsson, J.A. a Survey on Spectral-Spatial Classification Techniques Based on Attribute Profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2335–2353. [Google Scholar] [CrossRef]
- Cavallaro, G.; Dalla Mura, M.; Benediktsson, J.A.; Bruzzone, L. Extended self-dual attribute profiles for the classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1690–1694. [Google Scholar] [CrossRef]
- Damodaran, B.B.; Höhle, J.; Lefèvre, S. Attribute profiles on derived features for urban land cover classification. Photogramm. Eng. Remote Sens. 2017, 83, 183–193. [Google Scholar] [CrossRef]
- Wilkinson, M. a fast component-tree algorithm for high dynamic-range images and second generation connectivity. In Proceedings of the 18th IEEE International Conference on Image Processing (ICIP), Brussels, Belgium, 11–14 September 2011; pp. 1021–1024. [Google Scholar]
- Serra, J.; Salembier, P. Connected operators and pyramids. In Proceedings of the SPIE Image Algebra and Morphological Image Processing, San Diego, CA, USA, 11–16 July 1993; pp. 65–76. [Google Scholar]
- Salembier, P.; Serra, J. Flat zones filtering, connected operators, and filters by reconstruction. IEEE Trans. Image Process. 1995, 4, 1153–1160. [Google Scholar] [CrossRef] [PubMed]
- Meyer, F.; Najman, L. Segmentation, minimum spanning tree and hierarchies. In Mathematical Morphology: From Theory to Applications; Najman, L., Talbot, H., Eds.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Najman, L. On the Equivalence Between Hierarchical Segmentations and Ultrametric Watersheds. J. Math. Imaging Vis. 2011, 40, 231–247. [Google Scholar] [CrossRef]
- Guigues, L.; Cocquerez, J.P.; Le Men, H. Scale-sets image analysis. Int. J. Comput. Vis. 2006, 68, 289–317. [Google Scholar] [CrossRef]
- Serra, J. Hierarchies and Optima. Discrete Geometry for Computer Imagery, DGCI 2011; Debled-Rennesson, I., Domenjoud, E., Kerautret, B., Even, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6607. [Google Scholar]
- Kiran, B.R.; Serra, J. Scale space operators on hierarchies of segmentations. In ternational Conference on Scale Space and Variational Methods in Computer Vision; Springer: Berlin/Heidelberg, Germany, 2013; pp. 331–342. [Google Scholar]
- Kiran, B.R.; Serra, J. Ground truth energies for hierarchies of segmentations. In Proceedings of the 11th International Symposium, ISMM 2013, Uppsala, Sweden, 27–29 May 2013; Volume 7883, pp. 123–134. [Google Scholar]
- Kiran, B.R.; Serra, J. Braids of partitions. In Proceedings of the 12th International Symposium, ISMM 2015, Reykjavik, Iceland, 27–29 May 2015; Volume 9082, pp. 217–228. [Google Scholar]
- Serra, J.; Kiran, B.R. Constrained Optimization on Hierarchies and Braids of Partitions. In Proceedings of the 12th International Symposium, ISMM 2015, Reykjavik, Iceland, 27–29 May 2015; Volume 9082, pp. 229–240. [Google Scholar]
- Tochon, G.; Dalla Mura, M.; Chanussot, J. Segmentation of Multimodal Images based on Hierarchies of Partitions. In Proceedings of the 12th International Symposium, ISMM 2015, Reykjavik, Iceland, 27–29 May 2015; Volume 9082, pp. 241–252. [Google Scholar]
- Najman, L.; Schmitt, M. Geodesic saliency of watershed contours and hierarchical segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 1163–1173. [Google Scholar] [CrossRef]
- Lu, H.; Woods, J.; Ghanbari, M. Binary partition tree analysis based on region evolution and its application to tree simplification. IEEE Trans. Image Process. 2007, 16, 1131–1138. [Google Scholar] [CrossRef] [PubMed]
- Johnson, S. Hierarchical clustering schemes. Psychometrika 1967, 32, 241–254. [Google Scholar] [CrossRef] [PubMed]
- Jardine, C.; Jardine, N.; Sibson, R. The structure and construction of taxonomic hierarchies. Math. Biosci. 1967, 1, 173–179. [Google Scholar] [CrossRef]
- Sneath, P. The application of computers to taxonomy. J Gen. Microbiol. 1957, 17, 201–226. [Google Scholar] [CrossRef] [PubMed]
- Maia, D.S.; de Albuquerque Araujo, A.; Cousty, J.; Najman, L.; Perret, B.; Talbot, H. Evaluation of Combinations of Watershed Hierarchies. In Proceedings of the 13th International Symposium, ISMM 2017, Fontainebleau, France, 15–17 May 2017; Volume 10225, pp. 133–145. [Google Scholar]
- Caselles, V.; Monasse, P. Geometric Description of Images as Topographic Maps; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Berger, C.; Géraud, T.; Levillain, R.; Widynski, N.; Baillard, A.; Bertin, E. Effective component tree computation with application to pattern recognition in astronomical imaging. In Proceedings of the IEEE International Conference on Image Processing, San Antonio, TX, USA, 16 September–19 October 2007; Volume 4, pp. IV-41–IV-44. [Google Scholar]
- Xu, Y.; Géraud, T.; Najman, L. Connected Filtering on Tree-Based Shape-Spaces. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1126–1140. [Google Scholar] [CrossRef] [PubMed]
- Monasse, P.; Guichard, F. Scale-space from a level lines tree. J. Vis. Commun. Image Represent. 2000, 11, 224–236. [Google Scholar] [CrossRef]
- Ballester, C.; Caselles, V.; Monasse, P. The tree of shapes of an image. ESAIM Control Optim. Calc. Var. 2003, 9, 1–18. [Google Scholar] [CrossRef]
- Grimaud, M. New measure of contrast: The dynamics. In Proc. SPIE 1769, Proceedings of the International Society for Optics and Photonics: Bellingham, WA, USA, 1992; Gader, P.D., Dougherty, E.R., Serra, J.C., Eds.; SPIE: Bellingham, WA, USA; pp. 292–305.
- Song, Y. a topdown algorithm for computation of level line trees. IEEE Trans. Image Process. 2007, 16, 2107–2116. [Google Scholar] [CrossRef] [PubMed]
- Jalba, A.C.; Westenberg, M.A. a comparison of two tree representations for data-driven volumetric image filtering. In Proceedings of the 10th International Symposium, ISMM 2011, Verbania-Intra, Italy, 6–8 July 2011; Volume 6671, pp. 405–416. [Google Scholar]
- Vichik, A.; Keshet, R.; Malah, D. Self-dual morphology on tree semilattices and applications. In Proceedings of the 8th International Symposium on Mathematical Morphology, Rio de Janeiro, Brazil, 10–13 October 2007; Volume 10225, pp. 49–60. [Google Scholar]
- Kruskal, J. On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Am. Math. Soc. 1956, 7, 48–50. [Google Scholar] [CrossRef]
- Morris, O.; Lee, M.d.J.; Constantinides, A. Graph theory for image analysis: An approach based on the shortest spanning tree. Commun. Radar Signal Process. 1986, 133, 146–152. [Google Scholar] [CrossRef]
- Silva, A.; de Alencar Lotufo, R. New extinction values from efficient construction and analysis of extended attribute component tree. In Proceedings of the SIBGRAPI’08 XXI Brazilian Symposium on Computer Graphics and Image Processing, Campo Grande, Brazil, 12–15 October 2008; pp. 204–211. [Google Scholar]
- Soille, P.; Grazzini, J. Constrained Connectivity and Transition Regions. In Proceedings of the 9th International Symposium, ISMM 2009, Groningen, The Netherlands, 24–27 August 2009; Volume 5720, pp. 59–69. [Google Scholar]
- Soille, P. Constrained connectivity for the processing of very-high-resolution satellite images. Int. J. Remote Sens. 2010, 31, 5879–5893. [Google Scholar] [CrossRef]
- Soille, P. Preventing Chaining through Transitions While Favouring It within Homogeneous Regions. In Proceedings of the 10th International Symposium, ISMM 2011, Verbania-Intra, Italy, 6–8 July 2011; Volume 6671, pp. 96–107. [Google Scholar]
- Nagao, M.; Matsuyama, T.; Ikeda, Y. Region extraction and shape analysis in aerial photographs. Comput. Vis. Graph. 1979, 10, 195–223. [Google Scholar] [CrossRef]
- Meyer, F. The levelings. In Proceedings of the Fourth International Symposium on Mathematical Morphology and Its Applications to Image and Signal Processing, Amsterdam, The Netherlands, 3–5 June 1998; pp. 199–206. [Google Scholar]
- Soille, P. On genuine connectivity relations based on logical predicates. In Proceedings of the 14th International Conference on Image Analysis and Processing, Modena, Italy, 10–14 September 2007; pp. 487–492. [Google Scholar]
- Carlinet, E.; Géraud, T. a comparative review of component tree computation algorithms. IEEE Trans. Image Process. 2014, 23, 3885–3895. [Google Scholar] [CrossRef] [PubMed]
- Moschini, U.; Meijster, A.; Wilkinson, M. a Hybrid Shared-Memory Parallel Max-Tree Algorithm for Extreme Dynamic-Range Images. IEEE Trans. Pattern Anal. Mach. Intell. 2018, in press. [Google Scholar] [CrossRef] [PubMed]
- Nistér, D.; Stewénius, H. Linear time maximally stable extremal regions. In Proceedings of the 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008; Volume 5303, pp. 183–196. [Google Scholar]
- Tarjan, R.E. Efficiency of a good but not linear set union algorithm. J. ACM 1975, 22, 215–225. [Google Scholar] [CrossRef]
- Najman, L.; Couprie, M. Building the Component Tree in Quasi-Linear Time. IEEE Trans. Image Process. 2006, 15, 3531–3539. [Google Scholar] [CrossRef] [PubMed]
- Najman, L.; Géraud, T. Discrete set-valued continuity and interpolation. In Proceedings of the 11th International Symposium, ISMM 2013, Uppsala, Sweden, 27–29 May 2013; Volume 7883, pp. 37–48. [Google Scholar]
- Guigues, L. Modèles Multi-Échelles Pour la Segmentation D’images. Ph.D. Thesis, École Doctorale Sciences et Ingénierie, Cergy-Pontoise, France, 2003. [Google Scholar]
- Duda, R.; Hart, P.; Stork, D. Pattern Classification; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Al-Dujaili, A.; Merciol, F.; Lefèvre, S. GraphBPT: An efficient hierarchical data structure for image representation and probabilistic inference. In Proceedings of the 12th International Symposium, ISMM 2015, Reykjavik, Iceland, 27–29 May 2015; Volume 9082, pp. 301–312. [Google Scholar]
- Havel, J.; Merciol, F.; Lefèvre, S. Efficient Schemes for Computing α-tree Representations. In Proceedings of the Mathematical Morphology and Its Applications to Signal and Image Processing, Uppsala, Sweden, 27–29 May 2013; Volume 7883, pp. 111–122. [Google Scholar]
- Havel, J.; Merciol, F.; Lefèvre, S. Efficient tree construction for multiscale image representation and processing. J. Real Time Image Process. 2016. [Google Scholar] [CrossRef]
- Bender, M.; Farach-Colton, M. The LCA problem revisited. In Proceedings of the 4th Latin American Symposium, Punta del Esk, Uruguay, 10–14 April 2000; Volume 1776, pp. 88–94. [Google Scholar]
- Westenberg, M.; Roerdink, J.; Wilkinson, M. Volumetric attribute filtering and interactive visualization using the max-tree representation. IEEE Trans. Image Process. 2007, 16, 2943–2952. [Google Scholar] [CrossRef] [PubMed]
- Perret, B.; Collet, C. Connected image processing with multivariate attributes: An unsupervised Markovian classification approach. Comput.Vis. Image Underst. 2015, 133, 1–14. [Google Scholar] [CrossRef]
- Kiwanuka, F.N.; Wilkinson, M.H.F. Automatic attribute threshold selection for morphological connected attribute filters. Pattern Recognit. 2016, 53, 59–72. [Google Scholar] [CrossRef]
- Xu, Y.; Géraud, T.; Najman, L. Morphological filtering in shape spaces: Applications using tree-based image representations. In Proceedings of the 2012 21st International Conference on Pattern Recognition (ICPR), Tsukuba, Japan, 11–15 November 2012; pp. 485–488. [Google Scholar]
- Carlinet, E.; Géraud, T. A Color Tree of Shapes with Illustrations on Filtering, Simplification, and Segmentation. In Proceedings of the 12th International Symposium, ISMM 2015, Reykjavik, Iceland, 27–29 May 2015; Volume 363–374, p. 9082. [Google Scholar]
- Xu, Y.; Géraud, T.; Najman, L. Hierarchical image simplification and segmentation based on Mumford–Shah-salient level line selection. Pattern Recognit. Lett. 2016, 83, 278–286. [Google Scholar] [CrossRef]
- Aptoula, E.; Weber, J.; Lefèvre, S. Vectorial quasi-flat zones for color image simplification. In Proceedings of the 11th International Symposium, ISMM 2013, Uppsala, Sweden, 27–29 May 2013; Volume 7883, pp. 231–242. [Google Scholar]
- Marcotegui, B.; Serna, A.; Hernández, J. Ultimate Opening Combined with Area Stability Applied to Urban Scenes. In Proceedings of the 13th International Symposium, ISMM 2017, Fontainebleau, France, 15–17 May 2017; pp. 261–268. [Google Scholar]
- Xu, Y.; Géraud, T.; Najman, L. Context-based energy estimator: Application to object segmentation on the tree of shapes. In Proceedings of the 2012 19th IEEE International Conference on Image Processing (ICIP), Orlando, FL, USA, 30 September–3 October 2012; pp. 1577–1580. [Google Scholar]
- Song, Y.; Zhang, A. Analyzing scenery images by monotonic tree. Multimed. Syst. 2003, 8, 495–511. [Google Scholar] [CrossRef]
- Cardelino, J.; Randall, G.; Bertalmio, M.; Caselles, V. Region based segmentation using the tree of shapes. In Proceedings of the 2006 IEEE International Conference on Image Processing, Atlanta, GA, USA, 8–11 October 2006; pp. 2421–2424. [Google Scholar]
- Igual, L. Image Segmentation and Compression Using the Tree of Shapes of an Image. Motion Estimation. Ph.D. Thesis, Pompeu Fabra University, Barcelona, Spain, 2006. [Google Scholar]
- Meyer, F. Minimum spanning forests for morphological segmentation. Math. Morphol. Appl. Image Process. 1994, 77–84. [Google Scholar] [CrossRef]
- Valero, S.; Salembier, P.; Chanussot, J. Comparison of merging orders and pruning strategies for binary partition tree in hyperspectral data. In Proceedings of the 2010 17th IEEE International Conference on Image Processing (ICIP), Hong Kong, China, 26–29 September 2010; pp. 2565–2568. [Google Scholar]
- Veganzones, M.; Tochon, G.; Dalla Mura, M.; Plaza, A.; Chanussot, J. Hyperspectral Image Segmentation Using a New Spectral Unmixing-Based Binary Partition Tree Representation. IEEE Trans. Image Process. 2014, 23, 3574–3589. [Google Scholar] [CrossRef] [PubMed]
- Tochon, G.; Feret, J.B.; Valero, S.; Martin, R.E.; Knapp, D.E.; Salembier, P.; Chanussot, J.; Asner, G.P. On the use of binary partition trees for the tree crown segmentation of tropical rainforest hyperspectral images. Remote Sens. Environ. 2015, 159, 318–331. [Google Scholar] [CrossRef]
- Merciol, F.; Lefèvre, S. Fast image and video segmentation based on alpha-tree multiscale representation. In Proceedings of the 2012 Eighth International Conference on Signal Image Technology and Internet Based Systems (SITIS), Naples, Italy, 25–29 November 2012. [Google Scholar]
- Merciol, F.; Lefèvre, S. Buffering hierarchical representation of color video streams for interactive object selection. In Proceedings of the 16th International Conference, ACIVS 2015, Catania, Italy, 26–29 October 2015. [Google Scholar]
- Tushabe, F.; Wilkinson, M. Image Preprocessing for Compression: Attribute Filtering. In Proceedings of the World Congress on Engineering & Computer Science, San Francisco, CA, USA, 24–26 October 2007. [Google Scholar]
- Solé, A.; Caselles, V.; Sapiro, G.; Arándiga, F. Morse description and geometric encoding of digital elevation maps. IEEE Trans. Image Process. 2004, 13, 1245–1262. [Google Scholar] [CrossRef] [PubMed]
- Urbach, E. Intelligent Object Detection Using Trees. In Proceedings of the 12th International Symposium, ISMM 2015, Reykjavik, Iceland, 27–29 May 2015; Volume 9082, pp. 289–300. [Google Scholar]
- Teeninga, P.; Moschini, U.; Trager, S.; Wilkinson, M. Improved Detection of Faint Extended Astronomical Objects Through Statistical Attribute Filtering. In Proceedings of the 12th International Symposium, ISMM 2015, Reykjavik, Iceland, 27–29 May 2015; Volume 9082, pp. 157–168. [Google Scholar]
- Benediktsson, J.A.; Bruzzone, L.; Chanussot, J.; Dalla Mura, M.; Salembier, P.; Valero, S. Hierarchical Analysis of Remote Sensing Data: Morphological Attribute Profiles and Binary Partition Trees. In Proceedings of the 10th International Symposium, ISMM 2011, Verbania-Intra, Italy, 6–8 July 2011; Volume 6671, pp. 306–319. [Google Scholar]
- Valero, S.; Salembier, P.; Chanussot, J. Object recognition in hyperspectral images using Binary Partition Tree representation. Pattern Recognit. Lett. 2015, 56, 45–51. [Google Scholar] [CrossRef]
- Tochon, G.; Chanussot, J.; Dalla Mura, M.; Bertozzi, A.L. Object Tracking by Hierarchical Decomposition of Hyperspectral Video Sequences: Application to Chemical Gas Plume Tracking. IEEE Trans. Geosci. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Desolneux, A.; Moisan, L.; Morel, J.M. Edge detection by Helmholtz principle. J. Math. Imaging Vis. 2001, 14, 271–284. [Google Scholar] [CrossRef]
- Xu, Y.; Monasse, P.; Géraud, T.; Najman, L. Tree-based morse regions: A topological approach to local feature detection. IEEE Trans. Image Process. 2014, 23, 5612–5625. [Google Scholar] [CrossRef] [PubMed]
- Bosilj, P.; Kijak, E.; Lefèvre, S. Beyond MSER: Maximally Stable Regions using Tree of Shapes. In Proceedings of the Conference: British Machine Vision Conference 2015, Swansea, UK, 7–10 September 2015. [Google Scholar]
- Dalla Mura, M.; Benediktsson, J.A.; Waske, B.; Bruzzone, L. Extended profiles with morphological attribute filters for the analysis of hyperspectral data. Int. J. Remote Sens. 2010, 31, 5975–5991. [Google Scholar] [CrossRef]
- Bosilj, P.; Wilkinson, M.; Kijak, E.; Lefèvre, S. Local 2D Pattern Spectra as Connected Region Descriptors. Math. Morphol. Theory Appl. 2016. [Google Scholar] [CrossRef]
- Pham, M.; Aptoula, E.; Lefèvre, S. Feature profile from attribute filtering for classification of remote sensing images. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 249–256. [Google Scholar] [CrossRef]
- Pham, M.; Aptoula, E.; Lefèvre, S. Local Feature-Based Attribute Profiles for Optical Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, in press. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Benediktsson, J.A.; Bruzzone, L. Self-dual attribute profiles for the analysis of remote sensing images. In Proceedings of the 10th International Symposium, ISMM 2011, Verbania-Intra, Italy, 6–8 July 2011; Volume 6671, pp. 320–330. [Google Scholar]
- Bosilj, P.; Damodaran, B.; Aptoula, E.; Dalla Mura, M.; Lefèvre, S. Attribute Profiles from Partitioning Trees. In Proceedings of the 13th International Symposium, ISMM 2017, Fontainebleau, France, 15–17 May 2017; pp. 381–392. [Google Scholar]
- Gueguen, L.; Hamid, R. Toward a Generalizable Image Representation for Large-Scale Change Detection: Application to Generic Damage Analysis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3378–3387. [Google Scholar] [CrossRef]
- Tushabe, F.; Wilkinson, M. Content-based image retrieval using combined 2D attribute pattern spectra. In Proceedings of the 8th Workshop of the Cross-Language Evaluation Forum, Budapest, Hungary, 19–21 September 2007. [Google Scholar]
- Bosilj, P.; Aptoula, E.; Lefèvre, S.; Kijak, E. Retrieval of Remote Sensing Images with Pattern Spectra Descriptors. ISPRS In. J. Geo-Inf. 2016, 5, 228. [Google Scholar] [CrossRef]
- Aptoula, E. Remote Sensing Image Retrieval with Global Morphological Texture Descriptors. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3023–3034. [Google Scholar] [CrossRef]
- Urbach, E.; Roerdink, J.; Wilkinson, M. Connected Shape-Size Pattern Spectra for Rotation and Scale-Invariant Classification of Gray-Scale Images. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 272–285. [Google Scholar] [CrossRef] [PubMed]
- Aptoula, E.; Dalla Mura, M.; Lefèvre, S. Vector attribute profiles for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3208–3220. [Google Scholar] [CrossRef]
- Lefèvre, S.; Chapel, L.; Merciol, F. Hyperspectral image classification from multiscale description with constrained connectivity and metric learning. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014. [Google Scholar]
- Merciol, F.; Lefèvre, S. Fast Building Extraction by Multiscale Analysis of Digital Surface Models. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]
- Cavallaro, G.; Dalla Mura, M.; Benediktsson, J.A.; Plaza, A. Remote sensing image classification using attribute filters defined over the tree of shapes. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3899–3911. [Google Scholar] [CrossRef]
- Aptoula, E. The impact of multivariate quasi-flat zones on the morphological description of hyperspectral images. Int. J Remote Sens. 2014, 35, 3482–3498. [Google Scholar] [CrossRef]
- Alonso-González, A.; López-Martínez, C.; Salembier, P. PolSAR time series processing with binary partition trees. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3553–3567. [Google Scholar] [CrossRef]
- Perret, B.; Lefevre, S.; Collet, C.; Slezak, É. Connected Component Trees for Multivariate Image Processing and Applications in Astronomy. In Proceedings of the 2010 20th International Conference on Pattern Recognition (ICPR), Istanbul, Turkey, 23–26 August 2010. [Google Scholar]
- Kurtz, C.; Naegel, B.; Passat, N. Connected filtering based on multivalued component-trees. IEEE Trans. Image Process. 2014, 23, 5152–5164. [Google Scholar] [CrossRef] [PubMed]
- Merciol, F.; Balem, T.; Lefèvre, S. Efficient and Large-Scale Land Cover Classification using Multiscale Image Analysis. In Proceedings of the 2017 Conference on Big Data from Space, Toulouse, France, 28–30 November 2017. [Google Scholar]
- Salembier, P.; Foucher, S. Optimum Graph Cuts for Pruning Binary Partition Trees of Polarimetric SAR Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5493–5502. [Google Scholar] [CrossRef]
- Zanoguera, F.; Meyer, F. On the implementation of non-separable vector levelings. In Proceedings of the Mathematical Morphology : Proceedings of the VIth International Symposium ISMM 2002, Sydney, 3–5 April 2002; pp. 369–377. [Google Scholar]
- Aptoula, E.; Lefevre, S. a comparative study on multivariate mathematical morphology. Pattern Recognit. 2007, 40, 2914–2929. [Google Scholar] [CrossRef]
- Passat, N.; Naegel, B. Component-trees and multivalued images: Structural properties. J. Math. Imaging Vis. 2014, 49, 37–50. [Google Scholar] [CrossRef]
- Forssén, P.E. Maximally stable colour regions for recognition and matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007. [Google Scholar]
- Carlinet, E.; Géraud, T. MToS: A tree of shapes for multivariate images. IEEE Trans. Image Process. 2015, 24, 5330–5442. [Google Scholar] [CrossRef] [PubMed]
- Perret, B.; Cousty, J.; Tankyevych, O.; Talbot, H.; Passat, N. Directed Connected Operators: Asymmetric Hierarchies for Image Filtering and Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1162–1176. [Google Scholar] [CrossRef] [PubMed]

| Tree | Max Tree | Min Tree | Tree of Shapes |
|---|---|---|---|
| Dual tree | Min tree | Max tree | self-dual |
| Type of objects | dark objects | bright objects | shapes |
| Complete representation? | Yes | Yes | Yes |
| Construction complexity | |||
| Additionalparameters | No | No | No |
| Tree | Binary Partition Tree | -Tree | -Tree |
|---|---|---|---|
| Dual tree | self-dual | self-dual | self-dual |
| Type of objects | unions of initial partition | -CC (quasi flat zones) | -CC |
| Complete representation? | Yes | Yes | Yes |
| Construction complexity | |||
| Additional parameters | Initial partition, | No | No |
| region model, | |||
| similarity measure |
| Application Domain | Inclusion | Partitioning | |||
|---|---|---|---|---|---|
| Min/Max | ToS | BPT | -Tree | -Tree | |
| filtering/simplification | [28,52,85,105,113,114,115] | [37,65,116,117,118] | [52] | [42,95] | [42,119] |
| image/video segmentation | [28,29,114,120] | [117,118,121,122,123,124] | [2,109,125,126,127,128] | [42,44,129,130] | [42,44,119] |
| image compression | [131] | [124,132] | |||
| object detection & tracking | [133,134] | [25,135,136,137] | |||
| feature/edge detection | [103] | [83,138,139,140] | |||
| pixel/feature description | [62,141,142,143,144] | [63,144,145] | [146] | [146] | |
| image comparison | [37] | ||||
| change detection | [147] | ||||
| image retrieval | [103,142,148,149] | [140] | [150] | ||
| classification | [64,151,152] | [153,154,155] | [156] | ||
| time series processing | [157] | ||||
| astronomical imaging | [84,114,134,158] | ||||
| remote sensing (inc. hyperspectral imaging) | [62,64,141,143,144,147,149,152,159,160] | [63,144,145,155] | [126,127,128,135,136,161] | [153] | [119,156] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bosilj, P.; Kijak, E.; Lefèvre, S. Partition and Inclusion Hierarchies of Images: A Comprehensive Survey. J. Imaging 2018, 4, 33. https://doi.org/10.3390/jimaging4020033
Bosilj P, Kijak E, Lefèvre S. Partition and Inclusion Hierarchies of Images: A Comprehensive Survey. Journal of Imaging. 2018; 4(2):33. https://doi.org/10.3390/jimaging4020033
Chicago/Turabian StyleBosilj, Petra, Ewa Kijak, and Sébastien Lefèvre. 2018. "Partition and Inclusion Hierarchies of Images: A Comprehensive Survey" Journal of Imaging 4, no. 2: 33. https://doi.org/10.3390/jimaging4020033
APA StyleBosilj, P., Kijak, E., & Lefèvre, S. (2018). Partition and Inclusion Hierarchies of Images: A Comprehensive Survey. Journal of Imaging, 4(2), 33. https://doi.org/10.3390/jimaging4020033






