Exploiting Multiple Detections for Person Re-Identification
Abstract
:1. Introduction
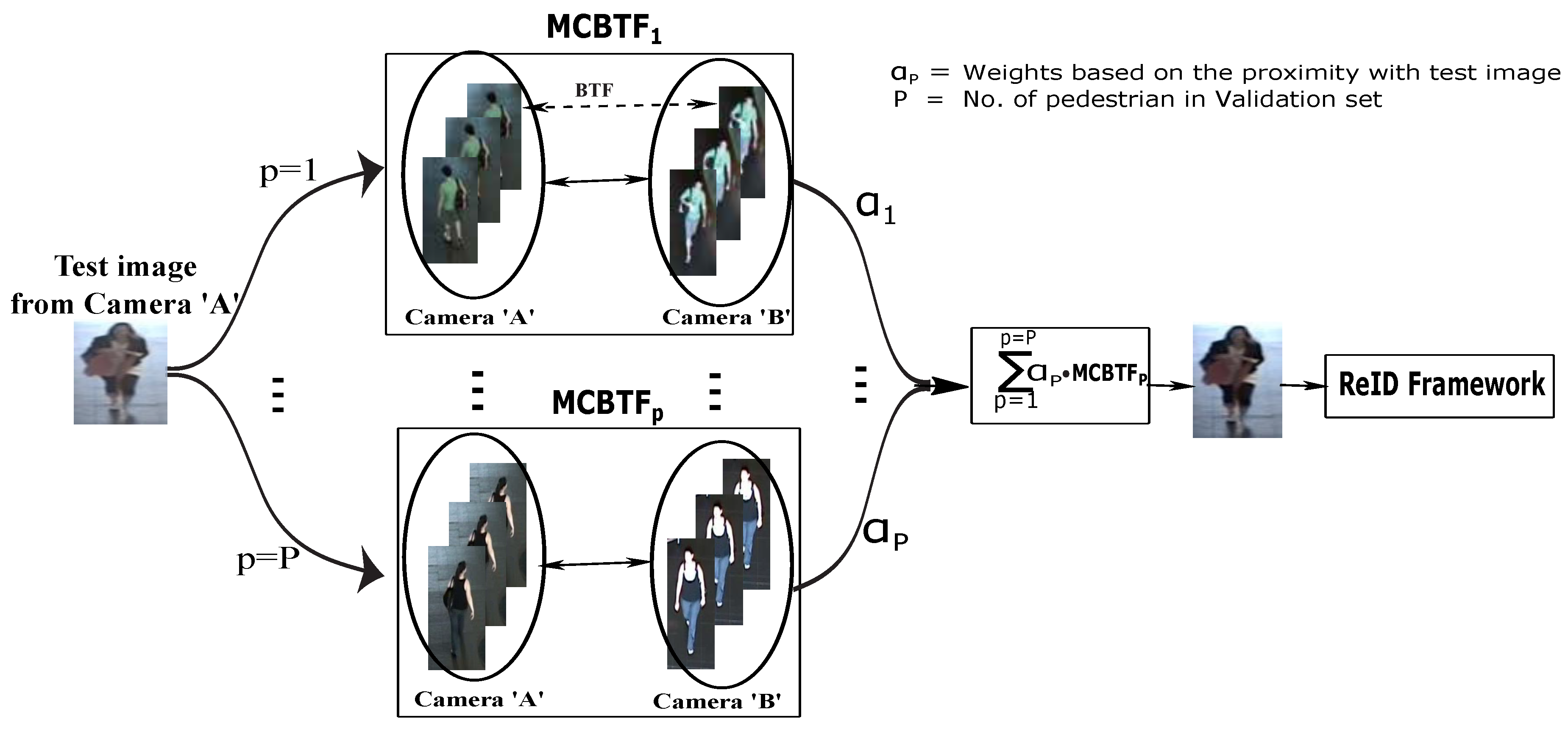
- We propose the use of the cumulative weighted brightness transfer function (CWBTF). Our approach assigns unequal weights to each CBTF which, exploiting multiple detections, is more robust than the previous approaches based on single pairs. Our technique is general and strongly outperforms previous appearance transfer function-based methods.
- We propose an improved stel component analysis (improved SCA) segmentation technique, which is quite effective for pedestrian segmentation.
- A rigorous experimental phase validating the advantages of our approach over existing alternatives on multiple benchmark datasets with variable numbers of cameras.
2. Related Work
3. Cumulative Weighted Brightness Transfer Function (CWBTF)
4. Re-Identification with CWBTF
4.1. Pedestrian Segmentation by Improved SCA
4.2. Feature Extraction and Matching
5. Experiments
5.1. Datasets and Settings
5.2. Re-Identification by Improved SCA Segmentation Technique
5.3. Re-Identification by CWBTF
- (i)
- Among other alternatives, ICT [35] performs worst while the number of the training samples for mapping the transfer function is lower compared to their corresponding test sets, unlike CWBTF, where all the experiments have been carried out for fewer training samples as well as for the same setup for fair comparisons.
- (ii)
- Since the VIPeR dataset is a single-shot dataset, our proposed CWBTF method cannot show its dominance like other multi-shot datasets. From the experimental results of the VIPeR dataset, it can easily be seen that unreliable single-detection-based BTFs did not perform like multiple-detection-based BTFs. Still, rank-1 of CWBTF is marginally outperforming the state of the art.
- (iii)
- For the CAVIAR4REID dataset, transform learning methods have less effect on the performance since there is not much illumination variation between the cameras. Nevertheless, the brightness appearance transfer methods proposed in WBTF [4], CBTF [3] and MBTF [1] work better than ICT [35], while considering a smaller number of training samples, which is actually more realistic for ReID. Moreover, using multiple detection for learning brightness transfer, as in our CWBTF approach, outperforms all the single-detection-based state-of-the-art methods. The experimental results reported in the Table 4 support all our claims discussed above. So far, the performance of WFS [37] beats our methods as well as all the other considered state-of-the-art methods by a good margin. The possible reasons include the fact that WFS uses high-dimensional features, using color as well as texture-based features, while we use low-dimensional features using only color-based features. Again, for the CAVIAR4REID dataset, applying transform learning methods has less effect on the performance, since there is not much illumination variation across the cameras. So, the use of such texture-based features along with color-based features has resulted in relatively high re-identification performance for this dataset.
- (iv)
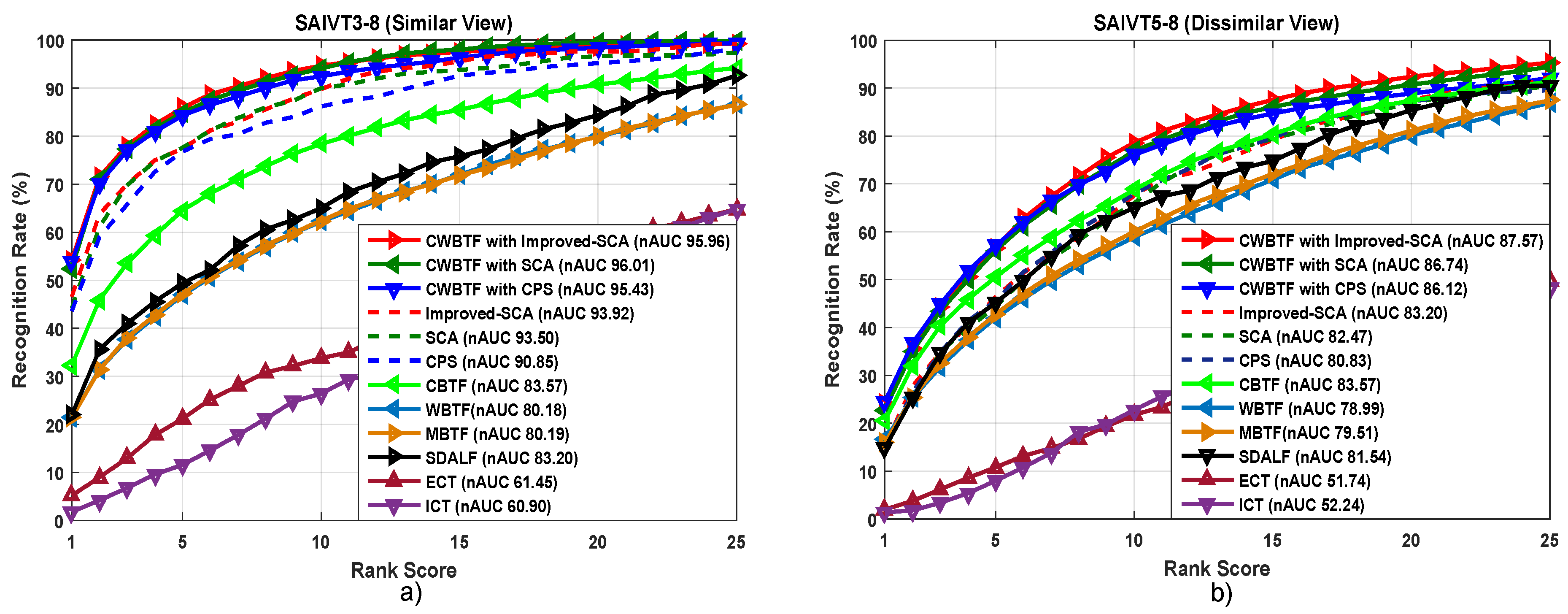
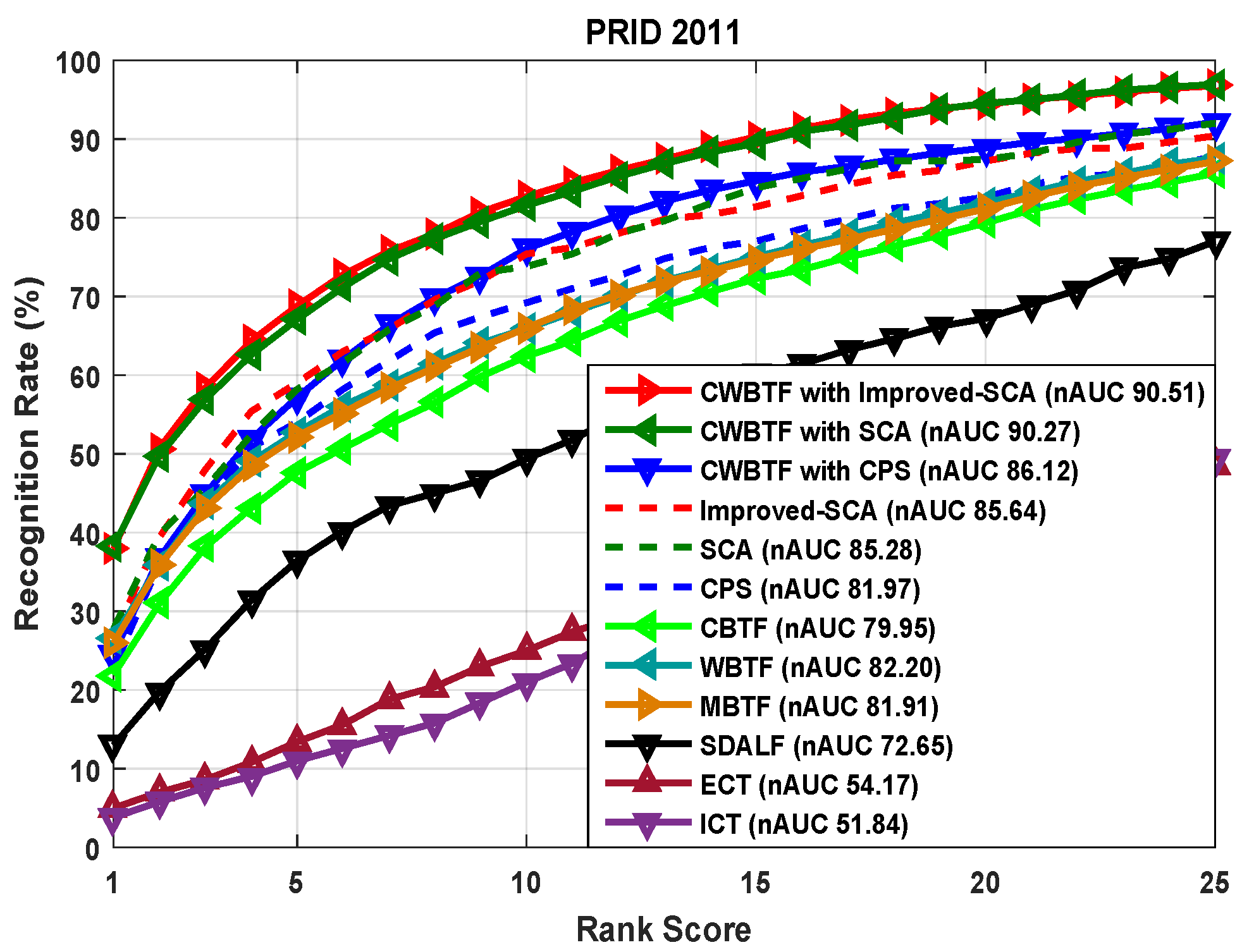
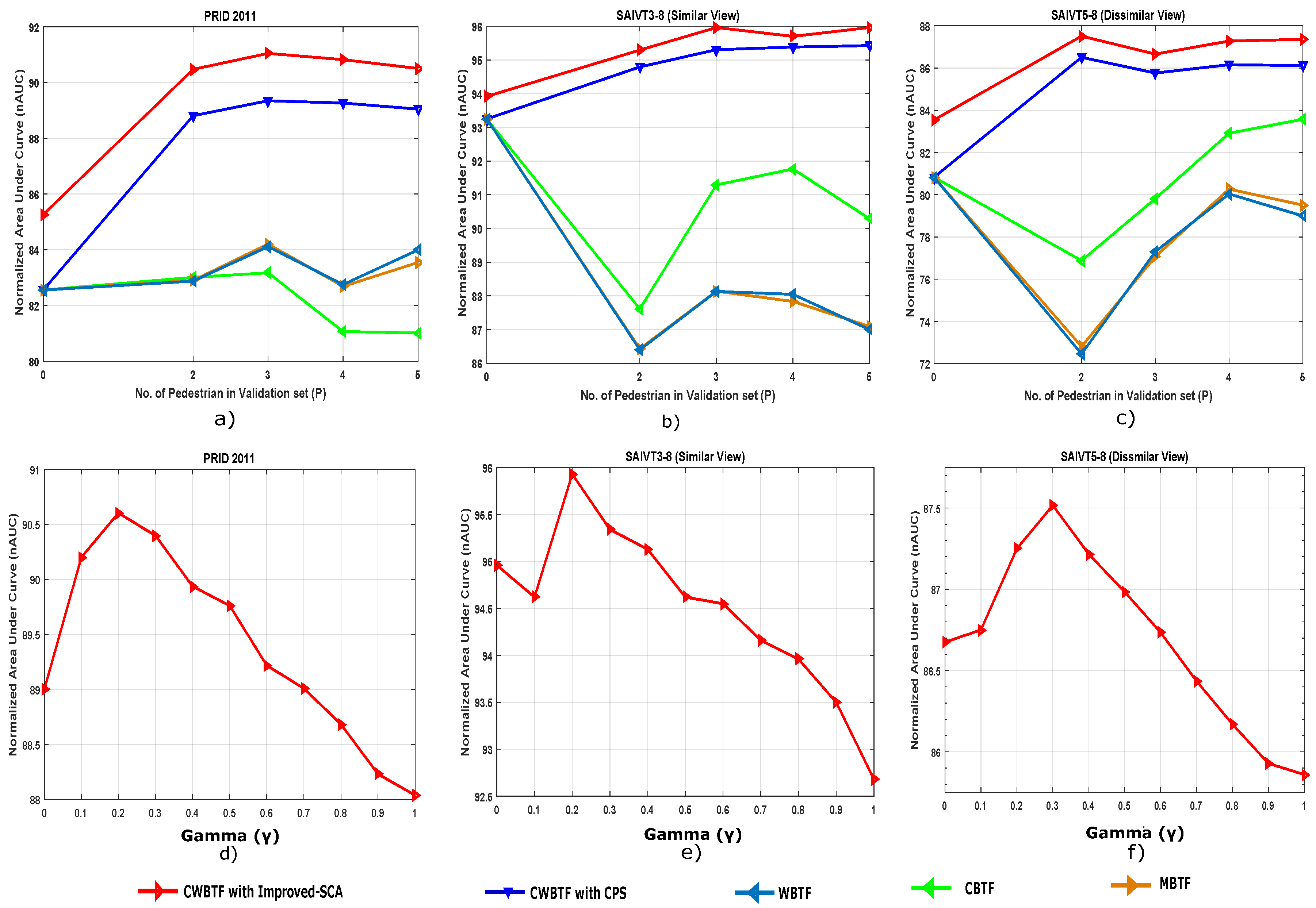
- As mentioned earlier, the images in PRID 2011 are captured from outdoor environments and there exists a significant amount of illumination variation between the cameras. Thus, applying brightness transfer methods has a significant effect on the performance reported in Figure 7. The availability of multiple shots for the proposed CWBTF improves the re-identification accuracy, further outperforming all the state-of-the-art methods.
- (v)
- Images in the SAIVT-SoftBio dataset are taken from an indoor environment and are also characterized by varying illumination across cameras, like PRID 2011. Consequently, adopting brightness transfer to map the illumination from one camera to another directly influences the re-identification accuracy, irrespective of the indoor or outdoor condition. The results reported in Figure 6 prove this assertion.
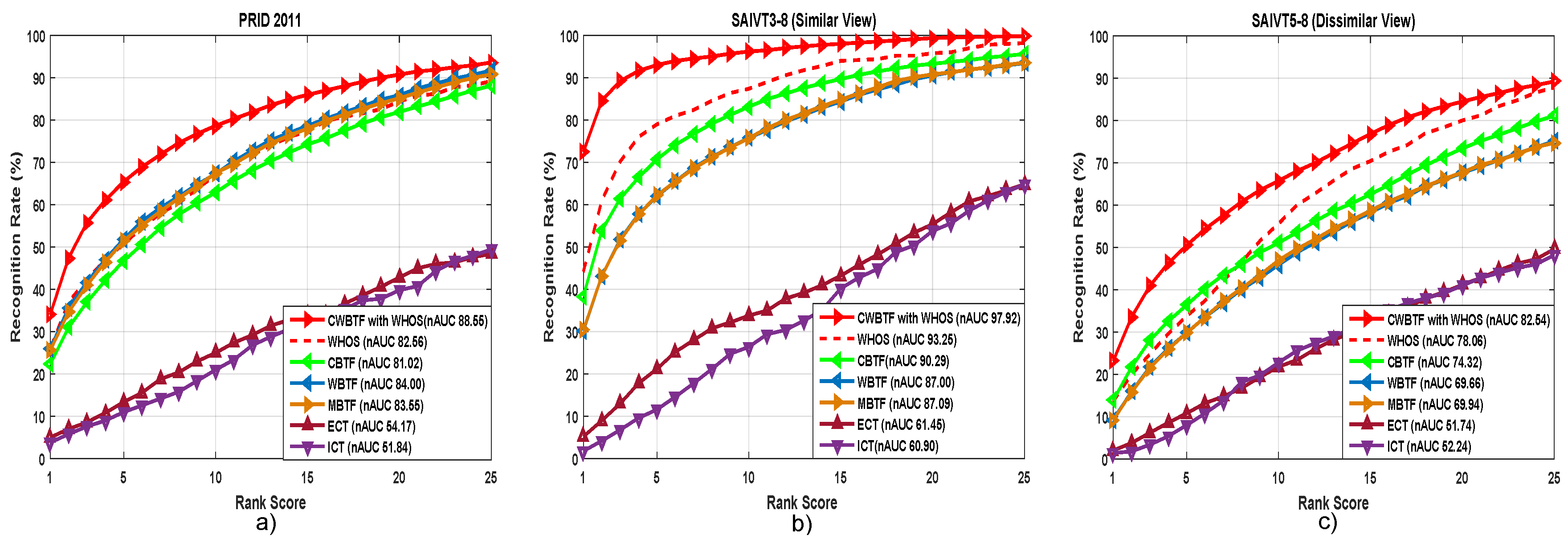
5.4. Effect of Feature Representation: Analysis with WHOS Feature
5.5. Effect of Parameter Variations
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Javed, O.; Shafique, K.; Rasheed, Z.; Shah, M. Modeling inter-camera space–time and appearance relationships for tracking across non-overlapping views. Comput. Vis. Image Underst. 2008, 109, 146–162. [Google Scholar] [CrossRef]
- Porikli, F. Inter-camera color calibration by correlation model function. In Proceedings of the International Conference on Image Processing (Cat. No.03CH37429), Barcelona, Spain, 14–17 September 2003. [Google Scholar]
- Prosser, B.J.; Gong, S.; Xiang, T. Multi-camera Matching using Bi-Directional Cumulative Brightness Transfer Functions. In Proceedings of the British Machine Conference, New York, NY, USA, 1–4 September 2008. [Google Scholar]
- Datta, A.; Brown, L.M.; Feris, R.; Pankanti, S. Appearance modeling for person re-identification using weighted brightness transfer functions. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012), Tsukuba, Japan, 11–15 November 2012. [Google Scholar]
- Chen, X.; Bhanu, B. Soft Biometrics Integrated Multi-target Tracking. In Proceedings of the 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014. [Google Scholar]
- Bird, N.D.; Masoud, O.; Papanikolopoulos, N.P.; Isaacs, A. Detection of loitering individuals in public transportation areas. In IEEE Trans. Intell. Trans. Syst. 2005, 6, 167–177. [Google Scholar] [CrossRef]
- Gheissari, N.; Sebastian, T.B.; Hartley, R. Person reidentification using spatiotemporal appearance. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006. [Google Scholar]
- Wang, X.; Doretto, G.; Sebastian, T.; Rittscher, J.; Tu, P. Shape and appearance context modeling. In Proceedings of the IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007. [Google Scholar]
- Hamdoun, O.; Moutarde, F.; Stanciulescu, B.; Steux, B. Person re-identification in multi-camera system by signature based on interest point descriptors collected on short video sequences. In Proceedings of the Second ACM/IEEE International Conference on Distributed Smart Cameras, Stanford, CA, USA, 7–11 September 2008. [Google Scholar]
- Farenzena, M.; Bazzani, L.; Perina, A.; Murino, V.; Cristani, M. Person re-identification by symmetry-driven accumulation of local features. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Cheng, D.S.; Cristani, M.; Stoppa, M.; Bazzani, L.; Murino, V. Custom pictorial structures for re-identification. In Proceedings of the 22nd British Machine Vision Conference, Dundee, Scotland, 29 August–2 September 2011. [Google Scholar]
- Bhuiyan, A.; Perina, A.; Murino, V. Person re-identification by discriminatively selecting parts and features. In Proceedings of the Computer Vision—ECCV 2014 Workshops, Zurich, Switzerland, 6–7 September 2014. [Google Scholar]
- Corvee, E.; Bremond, F.; Thonnat, M. Pedestrian detection via classification on riemannian manifolds. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1713–1727. [Google Scholar]
- Corvee, E.; Bremond, F.; Thonnat, M. Person re-identification using spatial covariance regions of human body parts. In Proceedings of the 7th IEEE International Conference on Advanced Video and Signal Based Surveillance, Boston, MA, USA, 29 August–1 September 2010. [Google Scholar]
- Bak, S.; Corvee, E.; Bremond, F.; Thonnat, M. Multiple-shot human re-identification by mean riemannian covariance grid. In Proceedings of the 8th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Klagenfurt, Austria, 30 August–2 September 2011. [Google Scholar]
- Wu, Y.; Minoh, M.; Mukunoki, M.; Li, W.; Lao, S. Collaborative sparse approximation for multiple-shot across-camera person re-identification. In Proceedings of the Collaborative Sparse Approximation for Multiple-Shot Across-Camera Person Re-Identification, Beijing, China, 18–21 September 2012. [Google Scholar]
- Kviatkovsky, I.; Adam, A.; Rivlin, E. Color invariants for person reidentification. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1622–1634. [Google Scholar] [CrossRef] [PubMed]
- Gray, D.; Tao, H. Viewpoint invariant pedestrian recognition with an ensemble of localized features. In Proceedings of the 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008. [Google Scholar]
- Schwartz, W.R.; Davis, L.S. Learning discriminative appearance-based models using partial least squares. In Proceedings of the XXII Brazilian Symposium on Computer Graphics and Image, Rio de Janiero, Brazil, 11–15 October 2009. [Google Scholar]
- Mignon, A.; Jurie, F. Pcca: A new approach for distance learning from sparse pairwise constraints. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Hirzer, M.; Roth, P.M.; Köstinger, M.; Bischof, H. Relaxed pairwise learned metric for person re-identification. In Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2014. [Google Scholar]
- Li, Z.; Chang, S.; Liang, F.; Huang, T.S.; Cao, L.; Smith, J.R. Learning locally-adaptive decision functions for person verification. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Zheng, W.-S.; Gong, S.; Xiang, T. Reidentification by relative distance comparison. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 635–668. [Google Scholar]
- Köstinger, M.; Hirzer, M.; Wohlhart, P.; Roth, P.M.; Bischof, H. Large scale metric learning from equivalence constraints. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Pedagadi, S.; Orwell, J.; Velastin, S.; Boghossian, B. Local fisher discriminant analysis for pedestrian re-identification. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Zheng, W.-S.; Gong, S.; Xiang, T. Person re-identification by probabilistic relative distance comparison. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011. [Google Scholar]
- Xiong, F.; Gou, M.; Camps, O.; Sznaier, M. Person re-identification using kernel-based metric learning methods. In Proceedings of the 13th European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Yi, D.; Lei, Z.; Liao, S.; Li, S.Z. Deep Metric Learning for Person Re-identification. In Proceedings of the 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014. [Google Scholar]
- Cheng, D.; Gong, Y.; Zhou, S.; Wang, J.; Zheng, N. Person re-identification by multi-channel parts-based CNN with improved triplet loss function. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Varior, R.R.; Haloi, M.; Wang, G. Gated siamese convolutional neural network architecture for human re-identification. In Proceedings of the 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Ahmed, E.; Jones, M.; Marks, T.K. An improved deep learning architecture for person re-identification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Xiao, T.; Li, H.; Ouyang, W.; Wang, X. Learning deep feature representations with domain guided dropout for person re-identification. arXiv, 2016; arXiv:1604.07528. [Google Scholar]
- Varior, R.R.; Shuai, B.; Lu, J.; Xu, D.; Wang, G. A siamese long short-term memory architecture for human re-identification. In Proceedings of the 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Yan, Y.; Ni, B.; Song, Z.; Ma, C.; Yan, Y.; Yang, X. Person Re-identification via Recurrent Feature Aggregation. In Proceedings of the 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Avraham, T.; Gurvich, I.; Lindenbaum, M.; Markovitch, S. Learning implicit transfer for person re-identification. In Proceedings of the Computer Vision, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Yulia, B.; Tamar, A.; Michael, L. Transitive Re-Identification. In Proceedings of the British Machine Vision Conference, Bristol, UK, 9–13 September 2013. [Google Scholar]
- Martinel, N.; Das, A.; Micheloni, C.; Roy-Chowdhury, A.K. Re-identification in the function space of feature warps. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1656–1669. [Google Scholar] [CrossRef] [PubMed]
- Jojic, N.; Perina, A.; Cristani, M.; Murino, V.; Frey, B. Stel component analysis: Modeling spatial correlations in image class structur. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Bazzani, L.; Cristani, M.; Murino, V. Symmetry-driven accumulation of local features for human characterization and re-identification. Comput. Vis. Image Underst. 2013, 117, 130–144. [Google Scholar] [CrossRef]
- Forssén, P.E. Maximally stable colour regions for recognition and matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007. [Google Scholar]
- Cheng, D.S.; Cristani, M. Person re-identification by articulated appearance matching. In Person Re-Identification; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Hirzer, M.; Beleznai, C.; Roth, P.M.; Bischof, H. Person re-identification by descriptive and discriminative classification. In Proceedings of the 17th Scandinavian Conference, Ystad, Sweden, May 2011. [Google Scholar]
- Bialkowski, A.; Denman, S.; Sridharan, S.; Fookes, C.; Lucey, P. A database for person re-identification in multi-camera surveillance networks. In Proceedings of the 2012 International Conference on Digital Image Computing Techniques and Applications (DICTA), Fremantle, Australia, 3–5 December 2012. [Google Scholar]
- Su, C.; Yang, F.; Zhang, S.; Tian, Q.; Davis, L.S.; Gao, W. Multi-task learning with low rank attribute embedding for person re-identification. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Cancela, B.; Hospedales, T.M.; Gong, S. Open-world person re-identification by multi-label assignment inference. In Proceedings of the British Machine Vision Conference (BMVC), Nottingham, UK, 1–5 September 2014. [Google Scholar]
- Karanam, S.; Li, Y.; Radke, R.J. Person re-identification with discriminatively trained viewpoint invariant dictionaries. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Das, A.; Chakraborty, A.; Roy-Chowdhury, A.K. Consistent re-identification in a camera network. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Kodirov, E.; Xiang, T.; Fu, Z.; Gong, S. Person Re-Identification by Unsupervised ℓ1 Graph Learning. In Proceedings of the 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Bhuiyan, A.; Mirmahboub, B.; Perina, A.; Murino, V. Person Re-identification Using Robust Brightness Transfer Functions Based on Multiple Detections. In Proceedings of the 18th International Conference, Genoa, Italy, 7–11 September 2015. [Google Scholar]
- Bhuiyan, A.; Perina, A.; Murino, V. Exploiting multiple detections to learn robust brightness transfer functions in re-identification systems. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec, QC, Canada, 27–30 September 2015. [Google Scholar]
- Mirmahboub, B.; Kiani, H.; Bhuiyan, A.; Perina, A.; Zhang, B.; Del Bue, A.; Murino, V. Person re-identification using sparse representation with manifold constraints. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2015. [Google Scholar]
- Panda, R.; Bhuiyan, A.; Murino, V.; Roy-Chowdhury, A.K. Unsupervised Adaptive Re-identification in Open World Dynamic Camera Networks. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2015. [Google Scholar]
- Lisanti, G.; Masi, I.; Bagdanov, A.D.; Del Bimbo, A. Person re-identification by iterative re-weighted sparse ranking. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1629–1642. [Google Scholar] [CrossRef] [PubMed]




| Methods | CAVIAR4REID | PRID2011 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| r = 1 | r = 5 | r = 10 | r = 15 | nAUC | r = 1 | r = 5 | r = 10 | r = 15 | nAUC | |
| SDALF [10] | 11.5 | 38.5 | 62 | 74.5 | 73.80 | 13 | 36.4 | 49.4 | 60.2 | 72.65 |
| CPS [11] | 20.25 | 53 | 71 | 83. 25 | 82.01 | 22.8 | 50.6 | 66.4 | 75.6 | 81.97 |
| SCA [12] | 22.75 | 59.25 | 71.5 | 81.75 | 82.63 | 27.2 | 59.8 | 73.6 | 82.2 | 85.28 |
| Improved SCA | 23.95 | 54.75 | 73.75 | 86 | 83.10 | 28.6 | 58.2 | 74 | 84.2 | 85.64 |
| Methods | SAIVT (cameras 3–8) | SAIVT(cameras 5–8) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| r = 1 | r = 5 | r = 10 | r = 15 | nAUC | r = 1 | r = 5 | r = 10 | r = 15 | nAUC | |
| SDALF [10] | 22 | 49.4 | 65 | 84.4 | 83.20 | 14.8 | 45.2 | 65 | 85.4 | 81.54 |
| CPS [11] | 39.4 | 72 | 83.2 | 93 | 90.85 | 13.6 | 46.6 | 66.2 | 82.4 | 80.83 |
| SCA [12] | 43.2 | 77.2 | 89.4 | 96.4 | 93.50 | 16 | 45.40 | 66.8 | 86.2 | 82.47 |
| Improved SCA | 45.4 | 80 | 88.8 | 97.2 | 93.92 | 15.2 | 48.40 | 69 | 87.20 | 83.20 |
| Methods | r = 1 | r = 5 | r = 10 | r = 15 | r = 20 | nAUC |
|---|---|---|---|---|---|---|
| ICT [35] | 14.4 | 42.5 | 60 | 71.3 | 76.5 | 95.3 |
| ECT [35] | 16.3 | 43.2 | 61.2 | 70.5 | 75.7 | 95.2 |
| MBTF [1] | 15.24 | 44.37 | 63.28 | 70.25 | 74.25 | 94.8 |
| WBTF [4] | 16.17 | 44.35 | 61.5 | 70.75 | 74.75 | 94.95 |
| SDALF [10] | 21.34 | 42.73 | 63.23 | 70.8 | 74 | 93.15 |
| CPS [11] | 25.84 | 43.7 | 65.51 | 72 | 76.2 | 94.23 |
| SCA [12] | 23.24 | 42.64 | 63.85 | 71.8 | 76 | 94.4 |
| CBTF [3] | 25.32 | 44.3 | 67.28 | 71.28 | 77.32 | 94.23 |
| CWBTF with CPS [50] | 26.15 | 45.12 | 68.31 | 72.15 | 77.12 | 95.1 |
| CBTF with SCA [3] | 24.12 | 43.12 | 67.2 | 72.3 | 77 | 95.2 |
| CWBTF with SCA [50] | 24.82 | 43.62 | 67.9 | 72.5 | 77 | 95.4 |
| WFS [37] | 25.81 | - | 69.86 | - | 83.67 | - |
| Improved SCA | 31.42 | 45.3 | 68.21 | 71.2 | 75.8 | 95.35 |
| CBTF with improved SCA [3] | 31.8 | 47.2 | 67.21 | 72.5 | 78.3 | 95.7 |
| CWBTF with improved SCA | 32.14 | 46.25 | 69.21 | 73.28 | 79.6 | 96.18 |
| Methods | r = 1 | r = 5 | r = 10 | r = 15 | r = 20 | nAUC |
|---|---|---|---|---|---|---|
| ICT [35] | 8 | 32.75 | 52.25 | 65.25 | 77 | 71.19 |
| ECT [35] | 9.5 | 40 | 60 | 73.25 | 83.25 | 75.19 |
| MBTF [1] | 14.25 | 44 | 63.5 | 76.75 | 83.75 | 77.56 |
| WBTF [4] | 16.25 | 45.5 | 65.5 | 76.75 | 83.75 | 77.79 |
| SDALF [10] | 11.5 | 38.5 | 62 | 74.5 | 83 | 73.80 |
| CPS [11] | 20.25 | 53 | 71 | 83. 25 | 89.25 | 82.01 |
| SCA [12] | 22.75 | 59.25 | 71.5 | 81.75 | 89.25 | 82.63 |
| CBTF [3] | 17.82 | 44 | 62 | 75.33 | 84.88 | 77.79 |
| CWBTF with CPS [50] | 21.75 | 55.10 | 74 | 85.13 | 91.63 | 83.28 |
| CBTF with SCA [3] | 23.10 | 59.5 | 74.33 | 83.5 | 90.25 | 82.90 |
| CWBTF with SCA [50] | 23.15 | 59.05 | 75.13 | 84.27 | 90.52 | 83.82 |
| WFS [37] | 32.4 | 89 | 92 | 96 | 98 | 83.61 |
| Improved SCA | 23.95 | 54.75 | 73.75 | 86 | 91.5 | 83.10 |
| CBTF with improved SCA [3] | 24.75 | 56.2 | 74.75 | 85 | 90.5 | 83.61 |
| CWBTF with improved SCA | 24.25 | 58 | 76.05 | 86 | 91.97 | 84.11 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhuiyan, A.; Perina, A.; Murino, V. Exploiting Multiple Detections for Person Re-Identification. J. Imaging 2018, 4, 28. https://doi.org/10.3390/jimaging4020028
Bhuiyan A, Perina A, Murino V. Exploiting Multiple Detections for Person Re-Identification. Journal of Imaging. 2018; 4(2):28. https://doi.org/10.3390/jimaging4020028
Chicago/Turabian StyleBhuiyan, Amran, Alessandro Perina, and Vittorio Murino. 2018. "Exploiting Multiple Detections for Person Re-Identification" Journal of Imaging 4, no. 2: 28. https://doi.org/10.3390/jimaging4020028
APA StyleBhuiyan, A., Perina, A., & Murino, V. (2018). Exploiting Multiple Detections for Person Re-Identification. Journal of Imaging, 4(2), 28. https://doi.org/10.3390/jimaging4020028




