Small Angle Scattering in Neutron Imaging—A Review
Abstract
1. Introduction
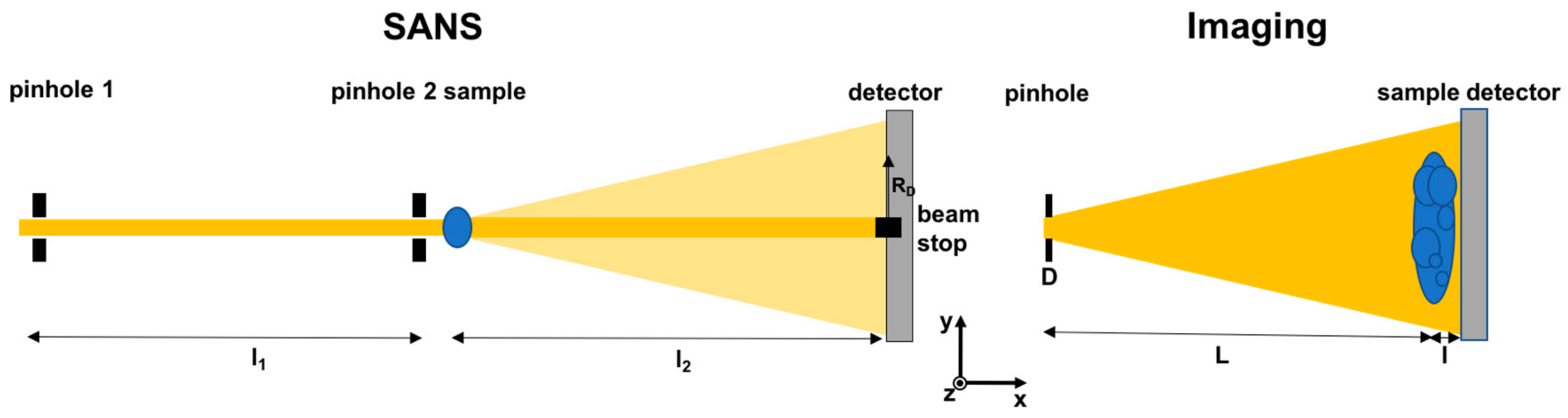
1.1. Basic Concept of Imaging
1.2. Basic Concept of SANS
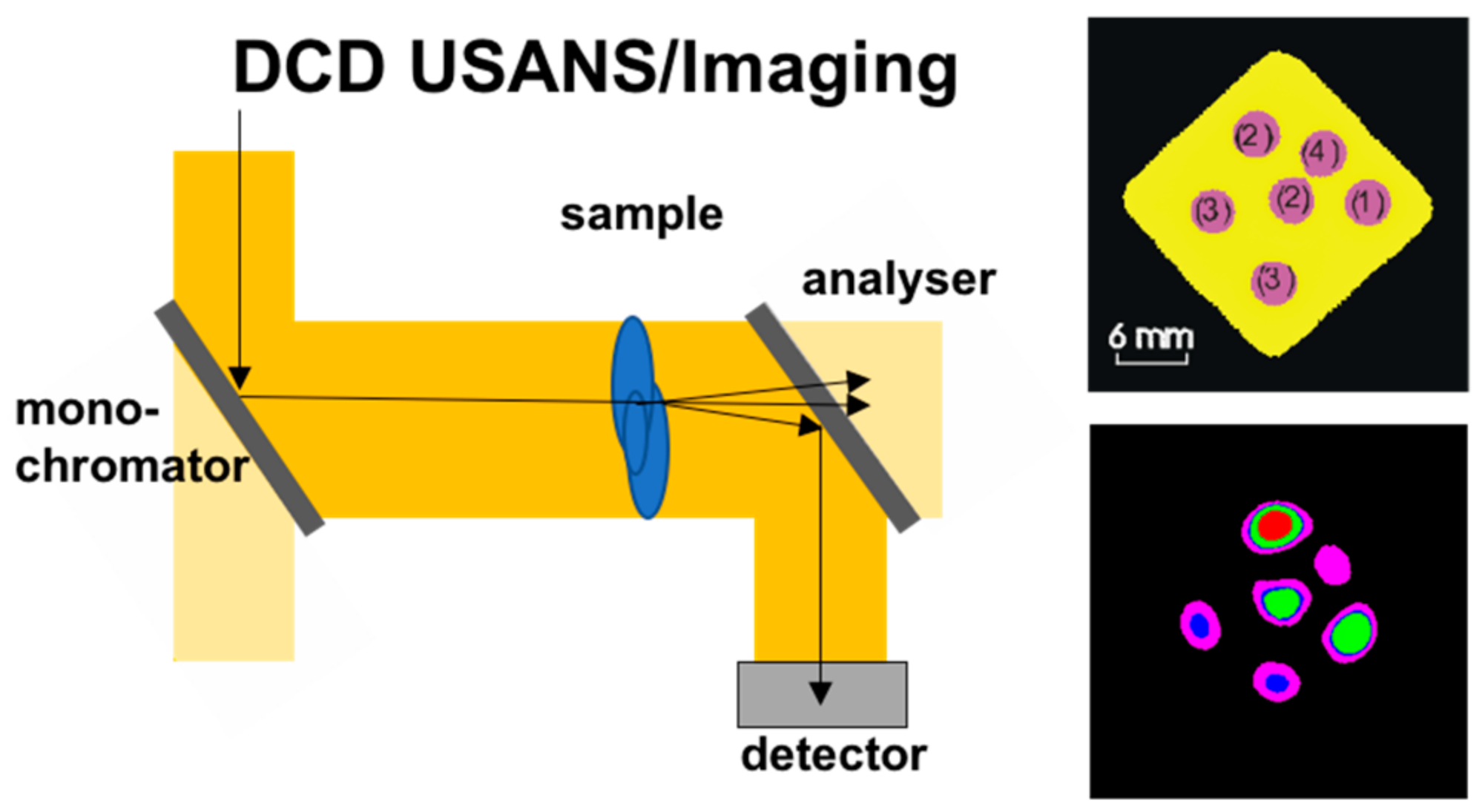
1.3. Initial Approaches of SANS in Imaging
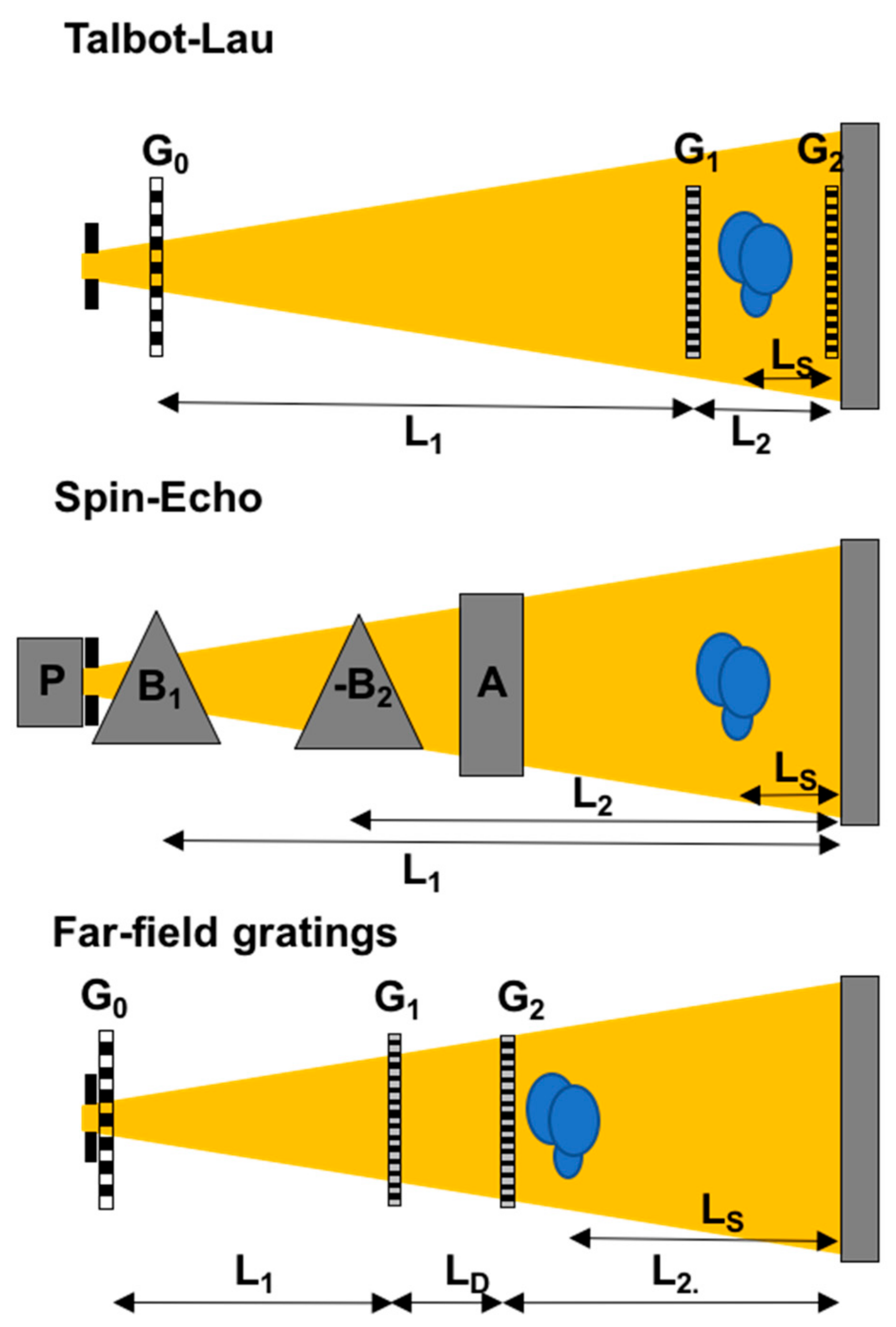
2. Beam Modulation Techniques for SANS and Imaging
2.1. Neutron Grating Interferometry (NGI)
2.2. Spin-Echo Modulation (SEM)
3. Dark-Field Imaging (DFI)
3.1. Modulated Beam Dark-Field Contrast Theory
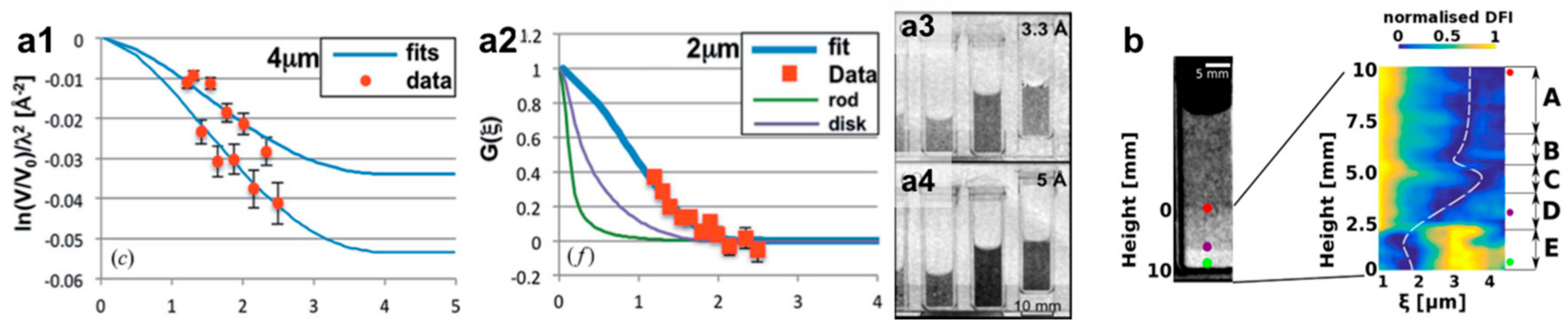
3.2. Quantitative Dark-Field Contrast Imaging
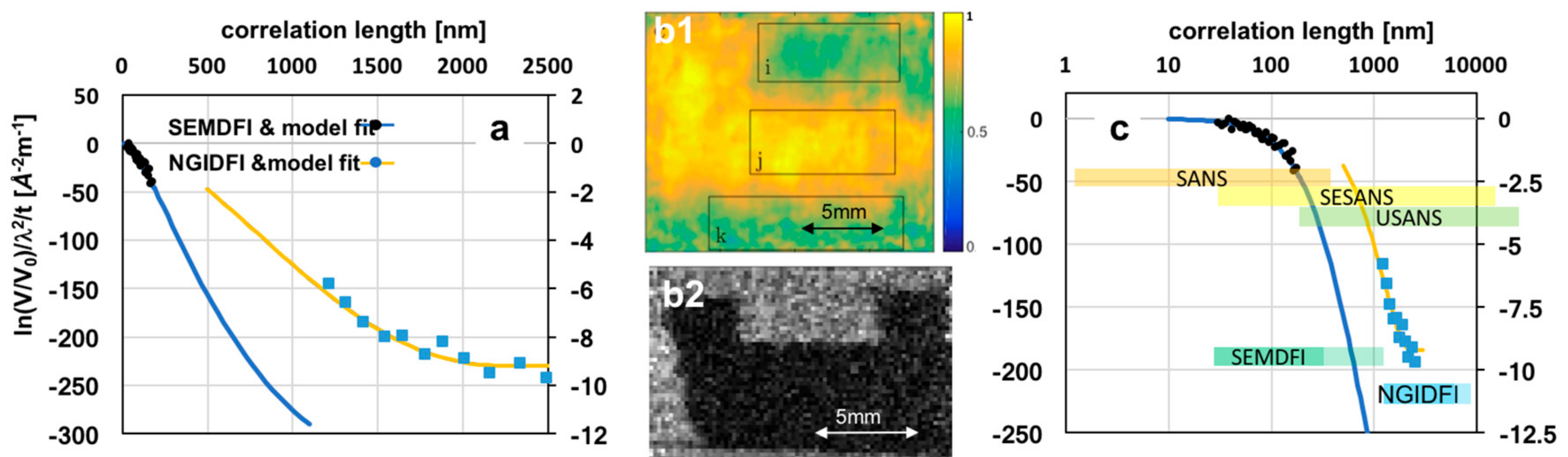
4. Discussion
5. Outlook
5.1. Progress in Grating-Based DFI
5.2. Progress in Spin-Echo Modulated DFI
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Feigin, L.; Svergun, D. Structure Analysis by Small-Angle X-ray and Neutron Scattering; Plenum Press: New York, NY, USA, 1987. [Google Scholar]
- Strobl, M.; Kardjilov, N.; Hilger, A.; Manke, I.; Banhart, J. Topical Review: Advances in neutron radiography and tomography. J. Phys. D 2009, 42, 21. [Google Scholar] [CrossRef]
- Williams, S.H.; Hilger, A.; Kardjilov, N.; Manke, I.; Strobl, M.; Douissard, P.A.; Martin, T.; Riesemeier, H.; Banhart, J. Detection system for microimaging with neutrons. J. Instrum. 2012, 7, P02014. [Google Scholar] [CrossRef]
- Treimer, W.; Strobl, M.; Hilger, A. Development of a tuneable channel cut crystal. Phys. Lett. A 2001, 289, 151–154. [Google Scholar] [CrossRef]
- Rekveldt, M.T. Novel SANS instrument using neutron spin echo. Nucl. Instrum. Methods B 1996, 114, 366–370. [Google Scholar] [CrossRef]
- Trtik, P.; Lehmann, E.H. Progress in high-resolution neutron imaging at the Paul Scherrer Institut—The Neutron Microscope project. J. Phys. Conf. Ser. 2016, 746, 01200. [Google Scholar] [CrossRef]
- Zhou, Z.; Bouwman, W.G.; Schut, H.; Desert, S.; Jestin, J.; Hartmann, S.; Pappas, C. From Nanopores to Macropores: Fractal Morphology of Graphite. Carbon 2016, 96, 541–547. [Google Scholar] [CrossRef]
- Penfold, J.; Tucker, I. Flow-induced effects in mixed surfactant mesophases. J. Phys. Chem. B 2007, 111, 9496–9503. [Google Scholar] [CrossRef] [PubMed]
- Raventos, M.; Lehmann, E.; Boin, M.; Morgano, M.; Hovind, J.; Harti, R.; Valsecchi, J.; Kaestner, A.; Carminati, C.; Boillat, P.; et al. A Monte Carlo approach for scattering correction towards quantitative neutron imaging of polycrystals. J. Appl. Cryst. Under review.
- Strobl, M.; Treimer, W.; Hilger, A. Small angle scattering signals for (neutron) computerized tomography. Appl. Phys. Lett. 2004, 85, 488–490. [Google Scholar] [CrossRef]
- Bonse, U.; Hart, M. Tailless X-ray single crystal reflection curves obtained by multiple reflection. Appl. Phys. Lett. 1965, 7, 238. [Google Scholar] [CrossRef]
- Andersson, R.; van Heijkamp, L.F.; de Schepper, I.M.; Bouwman, W.G. Analysis of spin-echo small-angle neutron scattering. J. Appl. Cryst. 2008, 41, 868–885. [Google Scholar] [CrossRef]
- Treimer, W.; Strobl, M.; Hilger, A.; Seifert, C.; Feye-Treimer, U. Refraction as imaging signal for computerized (neutron) tomography. Appl. Phys. Lett. 2003, 83, 398–400. [Google Scholar] [CrossRef]
- Strobl, M.; Treimer, W.; Hilger, A.; Feye-Treimer, U. Neutron tomography in double crystal diffractometers. Phys. B Condens. Matter 2004, 350, 155–158. [Google Scholar] [CrossRef]
- Strobl, M.; Treimer, W.; Hilger, A. First realisation of a three-dimensional refraction contrast computerised neutron tomography. Nucl. Instrum. Methods B 2004, 222, 653–658. [Google Scholar] [CrossRef]
- Gaehler, R. A Certain Class of Beam Modulation Techniques and Its Potential Applications; PNCMI Polarized Neutron School: Berlin, Germany, 2006. [Google Scholar]
- Pfeiffer, F.; Grünzweig, C.; Bunk, O.; Frei, G.; Lehmann, E.; David, C. Neutron phase imaging and tomography. Phys. Rev. Lett. 2006, 96, 215505. [Google Scholar] [CrossRef] [PubMed]
- Reimann, T.; Schulz, M.; Grünzweig, C.; Kaestner, A.; Bauer, A.; Böni, P.; Mühlbauer, S. Neutron Dark-Field Imaging of the Domain Distribution in the Intermediate State of Lead. J. Low Temp. Phys. 2016, 182, 107–116. [Google Scholar] [CrossRef]
- Reimann, T.; Mühlbauer, S.; Schulz, M.; Betz, B.; Kaestner, A.; Pipich, V.; Böni, P.; Grünzweig, C. Visualizing the morphology of vortex lattice domains in a bulk type-II superconductor. Nat. Commun. 2016, 6, 8813. [Google Scholar] [CrossRef] [PubMed]
- Betz, B.; Rauscher, P.; Harti, R.P.; Schäfer, R.; van Swygenhoven, H.; Kaestner, A.; Hovind, J.; Lehmann, E.; Grünzweig, C. In-situ visualization of stress-dependent bulk magnetic domain formation by neutron grating interferometry. Appl. Phys. Lett. 2016, 108, 012405. [Google Scholar] [CrossRef]
- Rauscher, P.; Betz, B.; Hauptmann, J.; Wetzig, A.; Beyer, E.; Grünzweig, C. The influence of laser scribing on magnetic domain formation in grain oriented electrical steel visualized by directional neutron dark-field imaging. Sci. Rep. 2016, 6, 38307. [Google Scholar] [CrossRef] [PubMed]
- Betz, B.; Rauscher, P.; Harti, R.P.; Schäfer, R.; Irastorza-Landa, A.; van Swygenhoven, H.; Kaestner, A.; Hovind, J.; Pomjakushina, E.; Lehmann, E.; et al. Magnetization Response of the Bulk and Supplementary Magnetic Domain Structure in High-Permeability Steel Laminations Visualized In Situ by Neutron Dark-Field Imaging. Phys. Rev. Appl. 2016, 6, 024023. [Google Scholar] [CrossRef]
- Betz, B.; Rauscher, P.; Harti, R.P.; Schäfer, R.; van Swygenhoven, H.; Kaestner, A.; Hovind, J.; Lehmann, E.; Grünzweig, C. Frequency-Induced Bulk Magnetic Domain-Wall Freezing Visualized by Neutron Dark-Field Imaging. Phys. Rev. Appl. 2016, 6, 024024. [Google Scholar] [CrossRef]
- Grünzweig, C.; Siebert, R.; Betz, B.; Rauscher, P.; Schäfer, R.; Lehmann, E. Determination of Bulk Magnetic Volume Properties by Neutron Dark-Field Imaging. Phys. Procedia. 2015, 69, 413–419. [Google Scholar] [CrossRef]
- Grünzweig, C.; David, C.; Bunk, O.; Kohlbrecher, J.; Lehmann, E.; Lai, Y.W.; Schäfer, R.; Roth, S.; Lejcek, P.; Kopecek, J.; et al. Visualizing the propagation of volume magnetization in bulk ferromagnetic materials by neutron grating interferometry. J. Appl. Phys. 2010, 107, 09D308. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, K.; Kwon, O.Y.; Kardjilov, N.; Dawson, M.; Hilger, A.; Manke, I. Observation of Magnetic Domains in Insulation-Coated Electrical Steels by Neutron Dark-Field Imaging. Appl. Phys. Express 2010, 3, 10. [Google Scholar] [CrossRef]
- Manke, I.; Kardjilov, N.; Schäfer, R.; Hilger, A.; Strobl, M.; Dawson, M.; Grünzweig, C.; Behr, G.; Hentschel, M.; David, C.; et al. Three-dimensionl imaging of magnetic domains. Nat. Commun. 2010, 1, 125. [Google Scholar] [CrossRef] [PubMed]
- Grünzweig, C.; David, C.; Bunk, O.; Dierolf, M.; Frei, G.; Kühne, G.; Schäfer, R.; Pofahl, S.; Rønnow, H.; Pfeiffer, F. Bulk magnetic domain structures visualized by neutron dark-field imaging. Appl. Phys. Lett. 2008, 93, 112504. [Google Scholar] [CrossRef]
- Grünzweig, C.; David, C.; Bunk, O.; Dierolf, M.; Frei, G.; Kühne, G.; Kohlbrecher, J.; Schäfer, R.; Lejcek, P.; Rønnow, H.; et al. Neutron decoherence imaging for visualizing bulk magnetic domain structures. Phys. Rev. Lett. 2008, 101, 025504. [Google Scholar] [CrossRef] [PubMed]
- Mezei, F.; Gutberlet, T. (Eds.) Neutron Spin Echo Spectroscopy; Springer Verlag: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Bouwman, W.G.; Duif, C.P.; Plomp, J.; Wiedenmann, A.; Gähler, R. Combined SANS–SESANS, from 1 nm to 0.1 mm in one instrument. Phys. B Condens. Matter 2011, 406, 2357. [Google Scholar] [CrossRef]
- Strobl, M.; Tremsin, A.S.; Hilger, A.; Wieder, F.; Kardjilov, N.; Manke, I.; Bouwman, W.G.; Plomp, J. TOF-SEMSANS—Time-of-flight spin-echo modulated small-angle neutron scattering. J. Appl. Phys. 2012, 112, 014503. [Google Scholar] [CrossRef]
- Strobl, M.; Bouwman, W.G.; Wieder, F.; Duiff, C.; Hilger, A.; Kardjilov, N.; Manke, I. Using a grating analyser for SEMSANS investigations in the very small angle range. Phys. B Condens. Matter 2012, 407, 4132–4135. [Google Scholar] [CrossRef]
- Strobl, M.; Sales, M.; Plomp, J.; Bouwman, W.G.; Tremsin, A.S.; Kaestner, A.; Pappas, C.; Habicht, K. Quantitative Neutron Dark-field Imaging through Spin-Echo Interferometry. Sci. Rep. 2015, 5, 16576. [Google Scholar] [CrossRef] [PubMed]
- Sales, M.; Plomp, J.; Habicht, K.; Strobl, M. Investigating time-of-flight spin-echo modulation for small-angle neutron scattering through experiments and simulation. J. Appl. Cryst. 2015, 48, 92–96. [Google Scholar] [CrossRef]
- Sales, M.; Plomp, J.; Bouwman, W.G.; Tremsin, A.S.; Habicht, K.; Strobl, M. On the analysis of time-of-flight spin-echo modulated dark-field imaging data. J. Phys. Conf. Ser. 2017, 862, 012026. [Google Scholar] [CrossRef]
- Strobl, M.; Grünzweig, C.; Hilger, A.; Manke, I.; Kardjilov, N.; David, C.; Pfeiffer, F. Neutron dark-field tomography. Phys. Rev. Lett. 2008, 101, 123902. [Google Scholar] [CrossRef] [PubMed]
- Bech, M.; Bunk, O.; Donath, T.; Feidenhans’l, R.; David, C.; Pfeiffer, F. Quantitative X-ray dark-field computed tomography. Phys. Med. Biol. 2010, 55, 5529–5539. [Google Scholar] [CrossRef] [PubMed]
- Gruenzweig, C.; Kopecek, J.; Betz, B.; Kaestner, A.; Jefimovs, K.; Kohlbrecher, J.; Gasser, U.; Bunk, O.; David, C.; Lehmann, E.; et al. Quantification of the neutron dark-field imaging signal in grating interferometry. Phys. Rev. B 2013, 88, 125104. [Google Scholar] [CrossRef]
- Hilger, A.; Kardjilov, N.; Kandemir, T.; Manke, I.; Banhart, J.; Penumadu, D.; Manescu, A.; Strobl, M. Revealing micro-structural inhomogeneities with dark-field neutron imaging. J. Appl. Phys. 2010, 107, 036101. [Google Scholar] [CrossRef]
- Brooks, A.J.; Ge, J.; Kirka, M.M.; Dehoff, R.R.; Bilheux, H.Z.; Kardjilov, N.; Manke, I.; Butler, L.G. Porosity detection in electron beam-melted Ti-6Al-4V using high-resolution neutron imaging and grating-based interferometry. Prog. Addit. Manuf. 2017, 2, 125–132. [Google Scholar] [CrossRef]
- Strobl, M. General solution for quantitative dark-field contrast imaging with grating interferometers. Sci. Rep. 2014, 4, 7243. [Google Scholar] [CrossRef] [PubMed]
- Kohlbrecher, J.; Studer, A. Transformation cycle between the spherically symmetric correlation function, projected correlation function and differential cross section as implemented in SASfit. J. Appl. Cryst. 2017, 50, 1395–1403. [Google Scholar] [CrossRef]
- Strobl, M.; Betz, B.; Harti, R.P.; Hilger, A.; Kardjilov, N.; Manke, I.; Gruenzweig, C. Wavelength dispersive dark-field contrast: Micrometer structure resolution in neutron imaging with gratings. J. Appl. Cryst. 2016, 49, 569–573. [Google Scholar] [CrossRef]
- Reimann, T.; Mühlbauer, S.; Horisberger, M.; Betz, B.; Böni, P.; Schulz, M. The new neutron grating interferometer at the ANTARES beamline: Design, principles and applications. J. Appl. Cryst. 2016, 49, 1488–1500. [Google Scholar] [CrossRef]
- Harti, R.P.; Strobl, M.; Betz, B.; Jefimovs, K.; Kagias, M.; Gruenzweig, C. Sub-pixel correlation length neutron imaging: Spatially resolved scattering information of microstructures on a macroscopic scale. Sci. Rep. 2017, 7, 44588. [Google Scholar] [CrossRef] [PubMed]
- Strobl, M.; Grazzi, F. From Scattering in Imaging to Prospects at Pulsed Sources. Neutron News 2015, 2, 23–26. [Google Scholar] [CrossRef]
- Betz, B.; Harti, R.P.; Strobl, M.; Hovind, J.; Kaestner, A.; Lehmann, E.; van Swygenhoven, H.; Grünzweig, C. Quantification of the sensitivity range in neutron dark-field imaging. Rev. Sci. Instrum. 2015, 86, 123704. [Google Scholar] [CrossRef] [PubMed]
- Woracek, R.; Santisteban, J.; Fedrigo, A.; Strobl, M. Diffraction in neutron imaging—A review. Nucl. Instrum. Meth. A 2017, in press. [Google Scholar] [CrossRef]
- Harti, R.; Strobl, M.; Morgano, M.; Valsecchi, J.; Grünzweig, C. Statistical uncertainty in the dark-field and transmission signal of grating interferometry. Rev. Sci. Instrum. 2017, 88, 103704. [Google Scholar] [CrossRef] [PubMed]
- Harti, R.; Kottler, C.; Valsecchi, J.; Jefimovs, K.; Kagias, M.; Strobl, M.; Grünzweig, C. Visibility simulation of realistic grating interferometers including grating geometries and energy spectra. Opt. Express 2017, 25, 1019–1029. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Zhou, Y.; Zhou, T.; Jiang, M.; Kim, J.; Ahn, C.W.; Louis, A.K. Visibility studies of grating-based neutron phase contrast and dark-field imaging by using partial coherence theory. J. Korean Phys. Soc. 2013, 63, 2093–2097. [Google Scholar] [CrossRef]
- Hussey, D.S.; Miao, H.; Yuan, G.; Pushin, D.A.; Sarenac, D.; Huber, M.G.; Jacobson, D.L.; LaManna, J.M.; Wen, H. Demonstration of a white beam far-field neutron interferometer for spatially resolved small angle neutron scattering. arXiv, 2016; arXiv:1606.03054. [Google Scholar]
- Li, F.; Parnell, S.R.; Bai, H.; Yang, W.; Hamilton, W.A.; Maranville, B.B.; Ashkar, R.; Baxter, D.V.; Cremer, J.T.; Pynn, R. Spin echo modulated small-angle neutron scattering using superconducting magnetic Wollaston prisms. J. Appl. Crystallogr. 2016, 49, 55–63. [Google Scholar] [CrossRef]
- Woracek, R.; Hoffmann, T.; Bullat, M.; Sales, M.; Habicht, K.; Andersen, K.; Strobl, M. The testbeamline of the European Spallation Source—Instrumentation development and wavelength frame multiplication. Nucl. Instr. Methods A. 2016, in press. [Google Scholar] [CrossRef]
- Rekveldt, M.T.; Plomp, J.; Bouwman, W.G.; Kraan, W.H.; Grigoriev, S.; Blaauw, M. Spin-echo small angle neutron scattering in Delft. Rev. Sci. Instrum. 2005, 76, 033901. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Vallerga, J.V.; McPhate, J.B.; Siegmund, O.H.W.; Feller, W.B.; Crow, L.; Cooper, R.G. On the possibility to image thermal and cold neutron with sub-15 mm spatial resolution. Nucl. Instrum. Methods Phys. Res. A 2008, 592, 374. [Google Scholar] [CrossRef]
- Sales, M.; Plomp, J.; Habicht, K.; Tremsin, A.S.; Bouwman, W.G.; Strobl, M. Wavelength-Independent Constant Period Spin-Echo Modulated Small Angle Neutron Scattering. Rev. Sci. Instrum. 2016, 87, 063907. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Jun, Y.K.; Kwon, O.Y. A Neutron Dark-field Imaging Experiment with a Neutron Grating Interferometer at a Thermal Neutron Beam Line at HANARO. J. Korean Phys. Soc. 2011, 58, 730–734. [Google Scholar]
- Lee, S.W.; Hussey, D.S.; Jacobson, D.L.; Sim, C.M.; Arif, M. Development of the Grating Phase Neutron Interferometer at a Monochromatic Beam Line. Nucl. Instrum. Methods Phys. Res. A 2009, 605, 16–20. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.W.; Gyuseong, C. Visibility evaluation of a neutron grating interferometer operated with a polychromatic thermal neutron beam. Nucl. Instrum. Methods Phys. Res. A 2014, 746, 26–32. [Google Scholar] [CrossRef]
- Shinohara, T.; Kai, T.; Oikawa, K.; Segawa, M.; Harada, M.; Nakatani, T.; Ooi, M.; Aizawa, K.; Sato, H.; Kamiyama, T.; et al. Final design of the Energy-Resolved Neutron Imaging System “RADEN” at J-PARC. J. Phys. Conf. Ser. 2016, 746, 012007. [Google Scholar] [CrossRef]
- Seki, Y.; Shinohara, T.; Parker, J.D.; Yashiro, W.; Momose, A.; Kato, K.; Kato, H.; Sadeghilaridjani, M.; Otake, Y.; Kiyanagi, Y. Development of Multi-colored Neutron Talbot–Lau Interferometer with Absorption Grating Fabricated by Imprinting Method of Metallic Glass. J. Phys. Soc. Jpn. 2017, 86, 044001. [Google Scholar] [CrossRef]
- Minniti, T.; Kockelmann, W.; Burca, G.; Kelleher, J.F.; Kabra, S.; Zhang, S.Y.; Pooley, D.E.; Schooneveld, E.M.; Mutamba, Q.; Sykora, J. Materials analysis opportunities on the new neutron imaging facility IMAT@ISIS. J. Instrum. 2016, 11, C03014. [Google Scholar] [CrossRef]
- Impression of LARMOR Instrument in SESANS Mode. Available online: https://larmor.weblog.tudelft.nl/ (accessed on 6 November 2017).
- Strobl, M. The Scope of the Imaging Instrument Project ODIN at ESS. Phys. Procedia 2015, 69, 18–26. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strobl, M.; Harti, R.P.; Gruenzweig, C.; Woracek, R.; Plomp, J. Small Angle Scattering in Neutron Imaging—A Review. J. Imaging 2017, 3, 64. https://doi.org/10.3390/jimaging3040064
Strobl M, Harti RP, Gruenzweig C, Woracek R, Plomp J. Small Angle Scattering in Neutron Imaging—A Review. Journal of Imaging. 2017; 3(4):64. https://doi.org/10.3390/jimaging3040064
Chicago/Turabian StyleStrobl, Markus, Ralph P. Harti, Christian Gruenzweig, Robin Woracek, and Jeroen Plomp. 2017. "Small Angle Scattering in Neutron Imaging—A Review" Journal of Imaging 3, no. 4: 64. https://doi.org/10.3390/jimaging3040064
APA StyleStrobl, M., Harti, R. P., Gruenzweig, C., Woracek, R., & Plomp, J. (2017). Small Angle Scattering in Neutron Imaging—A Review. Journal of Imaging, 3(4), 64. https://doi.org/10.3390/jimaging3040064





