Mereotopological Correction of Segmentation Errors in Histological Imaging ^†

Abstract

In this paper we describe mereotopological methods to programmatically correct image segmentation errors, in particular those that fail to fulfil expected spatial relations in digitised histological scenes. The proposed approach exploits a spatial logic called discrete mereotopology to integrate a number of qualitative spatial reasoning and constraint satisfaction methods into imaging procedures. Eight mereotopological relations defined on binary region pairs are represented as nodes in a set of 20 directed graphs, where the node-to-node graph edges encode the possible transitions between the spatial relations after set-theoretic and discrete topological operations on the regions are applied. The graphs allow one to identify sequences of operations that applied to regions of a given relation, and enables one to resegment an image that fails to conform to a valid histological model into one that does. Examples of the methods are presented using images of H&E-stained human carcinoma cell line cultures.

1. Introduction

This paper is an extended version of the work presented at the 21st Conference on Medical Image Understanding and Analysis (MIUA 2017) [1] where we describe an application of mereotopological model-based methods for the algorithmic correction of segmentation errors. In this approach, qualitative spatial reasoning (QSR) and constraint-satisfaction methods are integrated into image processing routines to create context-based histological imaging algorithms. (See our project page at http://www.mecourse.com/landinig/software/intellimic.html.) The “context” referred to here arises from: (i) an ontological stand whereby image regions instead of pixels are considered to be the principal carriers of histological information; and (ii) an explicit representation of the topological, and in particular, relational information present in the histological images. The analysis and model-based constraints are provided by a spatial logic called discrete meterotopology (DM) [2,3], which is used here to enhance classical imaging techniques and mathematical morphology (MM) operations. This is achieved by explicitly encoding a number of binary relations such as contact, overlap, and the part–whole relation on pairs of image regions. These mereotopological relations are then used to model the domain and, furthermore, act as constraints that can be exploited to firstly detect “faulty” segmentation results and secondly to guide algorithms in the choice of processing operators to apply potential corrections so the region relations conform to the requirements of valid or expected histological models.

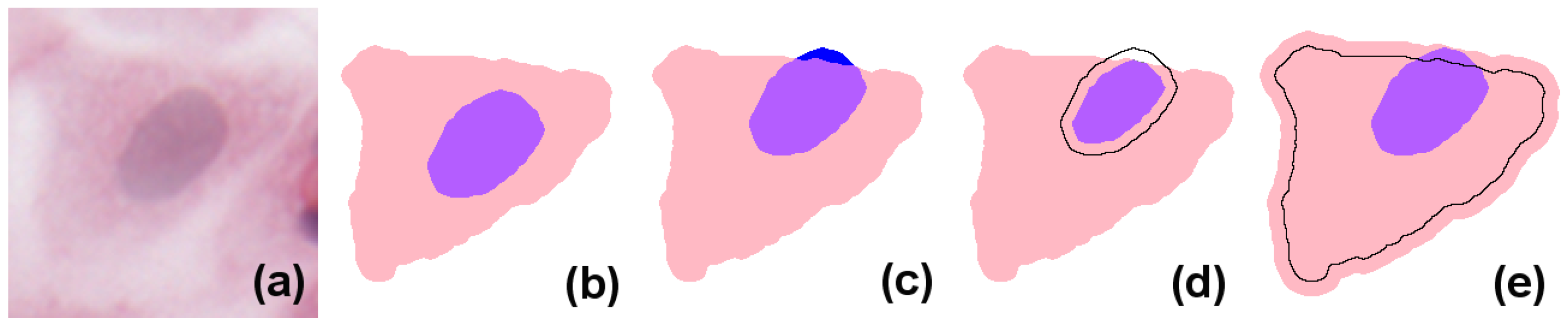
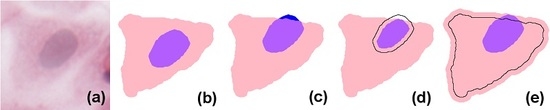
In simple terms, eukaryote cells have an organised nucleus included in a body of cytoplasm, which in turn is surrounded by a cellular membrane (for simplicity, we will not consider the cell membrane or multi-nucleated cells in the models presented here). Nucleus and cytoplasm are in contact but do not overlap; instead, the nucleus can be considered to exactly fill a cavity space within the cytoplasm. In H&E (haematoxylin and eosin)-stained images, due to the differential staining of cellular components, and to the projection of the cellular structure on the two-dimensional imaging sensor, the cytoplasmic region appears as a simply connected whole, lacking a cavity, and the nucleus forms a proper part of this (see the idealised image in Figure 1b). However, in many practical applications, cell and nucleus segmentation are achieved independently of each other, and this can result in imperfect relations (e.g., with a nucleus region partially overlapping the cytoplasm, as in Figure 1c). Errors like this can—to a certain degree—be corrected by a process called resegmentation, where component regions are processed with, for example, MM operators or deformable models so that the expected spatial relation between them holds. In Figure 1d this is accomplished by eroding the nuclear region; in (e), by dilating the cytoplasm.

The method described in this paper may be summarised as follows. We use discrete mereotopology to jointly define exhaustive pair-wise disjoint sets of binary relations defined on arbitrary sets of pixels, which we call regions. These relations capture the modes of overlap or connection between regions; a smaller set of five relations only handles relations definable in terms of parts and wholes; a larger set of eight additionally handles relations definable in terms of contact. A further set of set-theoretic and discrete topological operators are defined, and both the relations and operators are implemented using the ImageJ image processing platform. We use the relations and operators to define a set of 20 neighbourhood graphs, where each node represents a member of the eight-element relation set, and a directed edge connecting two nodes (“neighbours”) represents a possible transition from one relation to another achieved through the application of the operator encoded by the graph. Node–node paths through the graphs can be modelled as sequences of operations on regions, which enables one to define segmentation corrections satisfying an assumed histological model. The graphs cover the standard set of set-theoretic and topological operators defined on a discrete space. Examples of segmented H400 H&E-stained images are given to show how the underlying logic can be used both to model the domain and to algorithmically quantify and correct segmentation errors. The advantage of the method is that the underlying topology is made explicit, where subsets of segmented regions can be extracted and their associated relations reconstructed. The method also enables one to to integrate extra-logical empirical constraints relating to region morphology and geometry or staining patterns into segmentation algorithms.

While the potential of spatial reasoning in imaging has been suggested before (e.g., [4]), the novel aspects of our contribution are firstly on the role of mereotopology to enable systematic context-based processing of regions and their relations, and secondly their application to quantitative histological imaging where a systematic hierarchy of ontological levels [5] is essential to enable an in-depth interpretation of histological scene contents.

2. Related Work

This paper builds on previous works that apply DM to the interpretation and analysis of histological images [6,7,8,9]. DM first appeared in [2] as a discrete domain counterpart of the mereotopological region connection calculus (RCC) defined on a continuous space and its well-known eight-element relation set RCC8 [10]. An alternative way to model the discrete domain using mereotopology is the generalised region connection calculus) [11]. In the biological domain, mereotopology was used to model spatio-temporal cellular processes such as phagocytosis and exocytosis [12], and an example of DM used in a constraint-based graph traversal problem is given in [13]. In general, however, while RCC8 has been used extensively in the development of efficient constraint-based algorithms (for deciding the consistency of a set of constraints), the algorithms are typically restricted to operations on symbolic state–state models and not grounded in interpreted digital images as done here. A introduction to QSR and its methods is given in [14].

This paper extends the method that was originally reported in [9] and developed in [1]. Specifically, eight graphs are added to the twelve defined in [1] to cover the set theoretic operators: $\mathsf{sum}$, $\mathsf{prod}$, $\mathsf{diff}$, $\mathsf{compl}$, $\mathsf{xor}$ (denoting union, intersection, relative difference, complement, and symmetric difference) and the discrete topological operators ${\mathsf{int}}_D$, ${\mathsf{cl}}_D$, ${\mathsf{ext}}_D$, and ${\mathsf{bndry}}_D$ (denoting the discrete interior, closure, exterior, and boundary). The method is generic and does not favour any one particular image segmentation method over another, and all that is assumed is that pairs of regions can be represented as instances of binary relations. Those relations can be used to test whether or not the segmented regions conform to a histological model. Where they fail to conform to a histological model, they may either be rejected completely, or corrected by applying one of several operations on the regions in question. This approach goes beyond the use of gold-standard images used to compare and analyse results (though of course this could be done). We discuss this further below by considering a set of possible topological segmentations satisfying an assumed histological model. While there is a large body of literature on evaluation methods (e.g., [15,16]), none of those frameworks adopt the topological framework assumed here, nor do they address systematic methods of resegmentation to bring the results of initial segmentation into line with the expectations of histological theory, which is the main focus of the present paper.

3. Discrete Mereotopology (DM)

While different variants of DM have been proposed, we adopt that described in [2,9]. The domain is a set of possibly empty regions which are defined as sets of pixels. Regions are denoted by lower-case letters ($x,y,\dots$); pixels are denoted $\widehat{x},\widehat{y},\dots$. Set inclusion is defined in the standard way, the part–whole relation (Part) defined as inclusion restricted to non-null regions, and overlap ($\mathsf{O}$) between regions restricted to regions sharing a part in common. Adjacency between pixels is axiomatised as a reflexive symmetric relation. This is used to define the contact relation ($\mathsf{C}$) between regions. The set of all pixels is defined as the universal region u and the null set as ∅. Singleton pixel-sized regions are treated as atoms. The neighbourhood $N(\widehat{x})$ of pixel $\widehat{x}$ is defined as the set of pixels in u that are adjacent to $\widehat{x}$. In our application domain, u is a rectangular pixel array, and $N(\widehat{x})$ a 3 × 3 pixel array centred on $\widehat{x}$. Implemented in MM, the function $N(\widehat{x})$ maps to a morphological 3 × 3-pixel, 8-connected structuring element which we now assume by default.

As is common practice in QSR when developing these spatial logics and algebras, subsets of dyadic relations forming jointly exhaustive and pairwise disjoint (JEPD) sets are singled out. In DM, two JEPD relation sets are used: first, the eight-element set RCC8 comprising $\mathsf{DC}$, $\mathsf{EC}$, $\mathsf{PO}$, $\mathsf{TPP}$, $\mathsf{NTPP}$, $\mathsf{TPPi}$, $\mathsf{NTPPi}$ and $\mathsf{EQ}$, respectively disconnection, external connection, partial overlap, tangential proper part, non-tangential proper part, with their inverses, and equality, and second, the five-element relation set RCC5 comprising the relations $\mathsf{DR}$ (=$\mathsf{DC}|\mathsf{EC}$), $\mathsf{PO}$, $\mathsf{PP}$ (=$\mathsf{TPP}|\mathsf{NTPP}$), $\mathsf{PPi}$ (=$\mathsf{TPPi}|\mathsf{NTPPi}$), and $\mathsf{EQ}$ respectively disjoint, partial overlap, proper part, and inverse proper part and equality. Here the symbol “|” signifies disjunction; e.g., $\mathsf{DR}(x,y)\leftrightarrow \mathsf{DC}(x,y)\vee \mathsf{EC}(x,y)$. These respectively form the eight and five base relations of two relational subsumption lattices with top and bottom elements interpreted as the universal and null dyadic relations. Given that RCC8 is predicated on a continuous embedding space and DM on a discrete one, the relations sharing the same name are strictly not identical. For this reason, DM’s JEPD relation sets are identified in the text by the suffix “D” as in “RCC8D”. This same notation is used to mark the same distinction between the standard set of topological operators predicated on a continuous space and a set of discrete topological operators defined in DM; e.g., ${\mathsf{int}}_D$ denoting in this instance the discrete interior operator—see immediately following.

In [9], the discrete interior (${\mathsf{int}}_D$) and closure (${\mathsf{cl}}_D$) are pseudo-topological operators defined on regions, and they share some but not all of the usual properties of the interior and closure operators in standard treatments of topology. For example, in discrete space, the discrete interior and closure operators are not idempotent, and while both the standard and the discrete exterior, boundary, and interior operations defined on a region partition the embedding space u into three mutually exhaustive sets, the discrete boundary operator—unlike its standard counterpart—maps to a region of the same co-dimension.

The definitions for the discrete topological operators ${\mathsf{int}}_D,{\mathsf{cl}}_D,{\mathsf{ext}}_D$, and ${\mathsf{bndry}}_D$ are as follows:

$${\mathsf{int}}_D(x){=}_{\mathrm{def}}\left\{\widehat{x}\right|\mathsf{P}(N(\widehat{x}),x)\}$$

(1)

$${\mathsf{cl}}_D(x){=}_{\mathrm{def}}\left\{\widehat{x}\right|\mathsf{O}(N(\widehat{x}),x)\}$$

(2)

$${\mathsf{ext}}_D(x){=}_{\mathrm{def}}\left\{\widehat{x}\right|\mathsf{DR}(N(\widehat{x}),x)\}$$

(3)

$${\mathsf{bndry}}_D(x){=}_{\mathrm{def}}\left\{\widehat{x}\right|\mathsf{O}(N(\widehat{x}),x)\wedge \mathsf{O}(N(\widehat{x}),\mathsf{compl}(x)\}$$

(4)

The discrete interior contains those pixels whose immediate neighbourhoods lie within x, and the discrete exterior those pixels whose immediate neighbourhoods are disjoint from x; from which it can be inferred that the exterior is the interior of the complement. The discrete closure of x comprises all the pixels whose immediate neighbourhoods overlap x, while the discrete boundary of x contains those pixels whose immediate neighbourhoods overlap both x and the complement of x.

In our case where the canonical model is a (finite) $n\times m$ regular square pixel lattice, the discrete boundary of a region x typically maps to a two-pixel-wide non-null region, though four-pixel wide boundary regions can arise. This means that the discrete exterior of x is separated from x, as is the discrete interior of x from the complement of x.

A map between the ${\mathsf{int}}_D$ and ${\mathsf{cl}}_D$ operators and the MM operations erosion and dilation [8] enables one to define a notion of approximate equality that underpins transitions encoded in DM’s conceptual neighbourhood graphs, and it also enables the RCC8D relation set to be easily implemented in any image-processing programs featuring standard MM libraries. Other properties of regions can be defined in DM—for example, regions with or without an interior, regular regions (i.e., those without pixel-wide spikes and fissures), self-connected regions, and connected components.

In the histological domain, cells and their parts, groups of cells forming tissues and compartments, and the background of a digitised histological preparation can all be modelled using DM. Simple regions and arbitrary sets of pixels forming regions which may or may not be spatially contiguous all yield potential models. If a histological preparation is thresholded as a single binary image, then segmented regions of interest will form connected components, so that in any one image, the only possible relations between pairs of regions are $\mathsf{DC}$ and $\mathsf{EQ}$. However, the methods presented here assume that independent imaging modalities are used—for example, separating out the contribution of the different dyes in stained sections (as in Figure 1) or confocal microscopy channels. In this case, pairs of regions segmented from each channel can be compared, with all RCC5D and RCC8D relations now being possible.

3.1. Conceptual Neighbourhood Graphs, Continuity and Change, and Composition Tables

In [2,9], a set of conceptual neighbourhood diagrams (CNDs), or graphs, were defined on dyadic relations. In RCC8, relation $R^{\prime }$ is a conceptual neighbour of relation R if some pair of regions related by R can be continuously deformed so that R changes to $R^{\prime }$ with no other relation holding during that deformation. In the discrete setting of DM, continuous deformation is recast in terms of minimal change. In [2], this was defined using the discrete interior (${\mathsf{int}}_D$) and closure (${\mathsf{cl}}_D$) operators; here we extend this to include changes to regions produced using the set theoretic operators $\mathsf{sum}$, $\mathsf{prod}$, $\mathsf{diff}$, $\mathsf{compl}$, $\mathsf{xor}$ (denoting union, intersection, relative difference, complement, and symmetric difference) and the discrete topological operators ${\mathsf{int}}_D$, ${\mathsf{cl}}_D$, ${\mathsf{ext}}_D$, and ${\mathsf{bndry}}_D$ (denoting the discrete interior, closure, exterior, and boundary). The universal region u—representing the image—is assumed to be self-connected (i.e., $\mathsf{SC}(u)$).

In general, an RCC8D conceptual neighbourhood of a binary relation R can be defined as

$${\mathsf{nbhd}}_{\langle \alpha ,\beta \rangle }(R)=\{R^{\prime }\in \mathrm{RCC}8\mathrm{D}|\exists x,y(R(x,y)\wedge R^{\prime }(\alpha ,\beta ))\}$$

(5)

where $\alpha$ and $\beta$ are designated functions of the region variables x, y. The elements of ${\mathsf{nbhd}}_{\langle \alpha ,\beta \rangle }(R)$ are called the $\langle \alpha ,\beta \rangle$-neighbours of R. They are all the possible relations that can hold after regions x and y are modified in accordance with $\alpha ,\beta$. Given a segmented image, by a resegmentation we understand the replacement of a set S of regions in the image by a new set $S^{\prime }$ defined from S using some sequence of conceptual neighbourhood transitions. Such a resegmentation is chosen in order to correct anomalous relations in the original segmentation so that it satisfies the constraints of the domain being modelled.

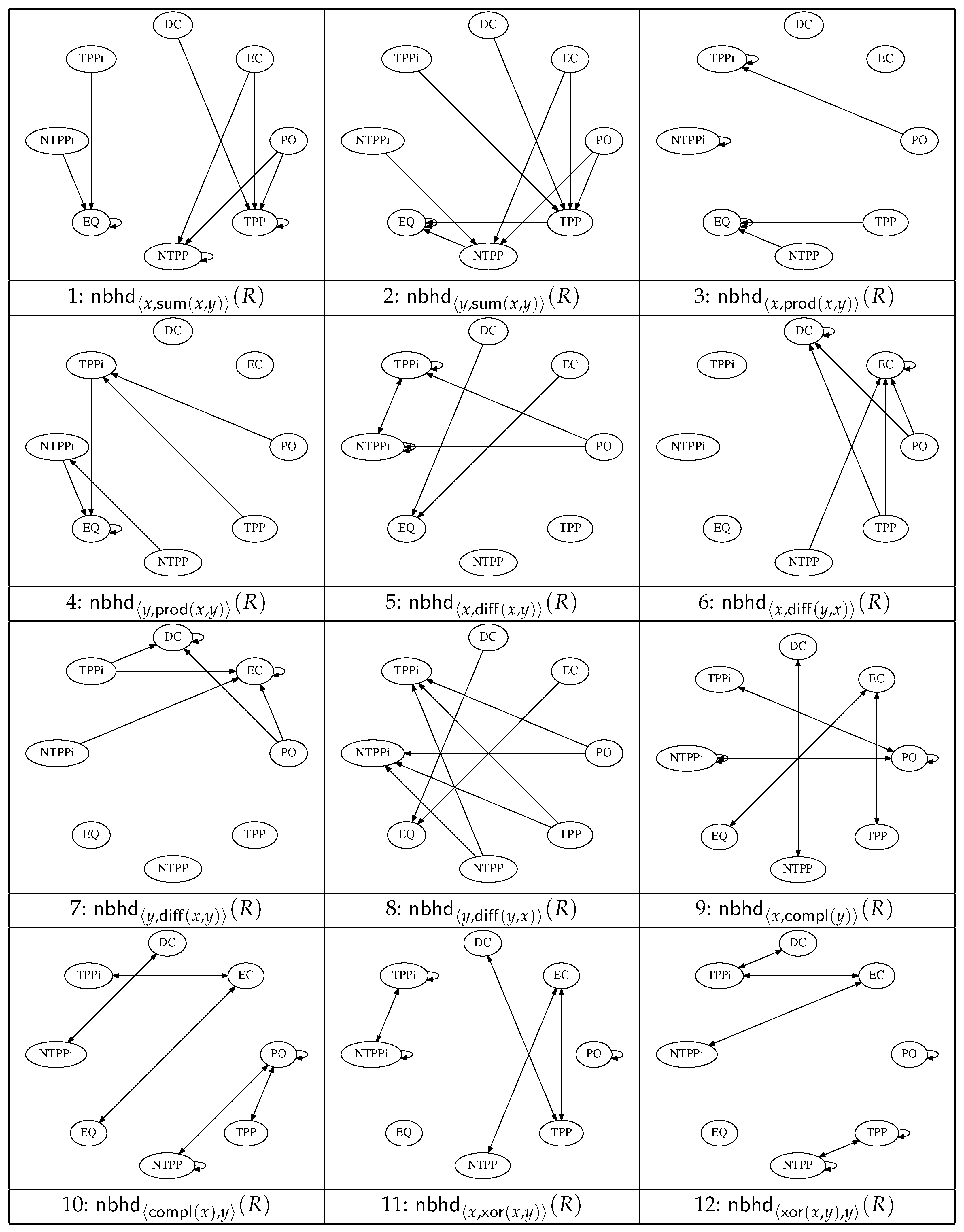
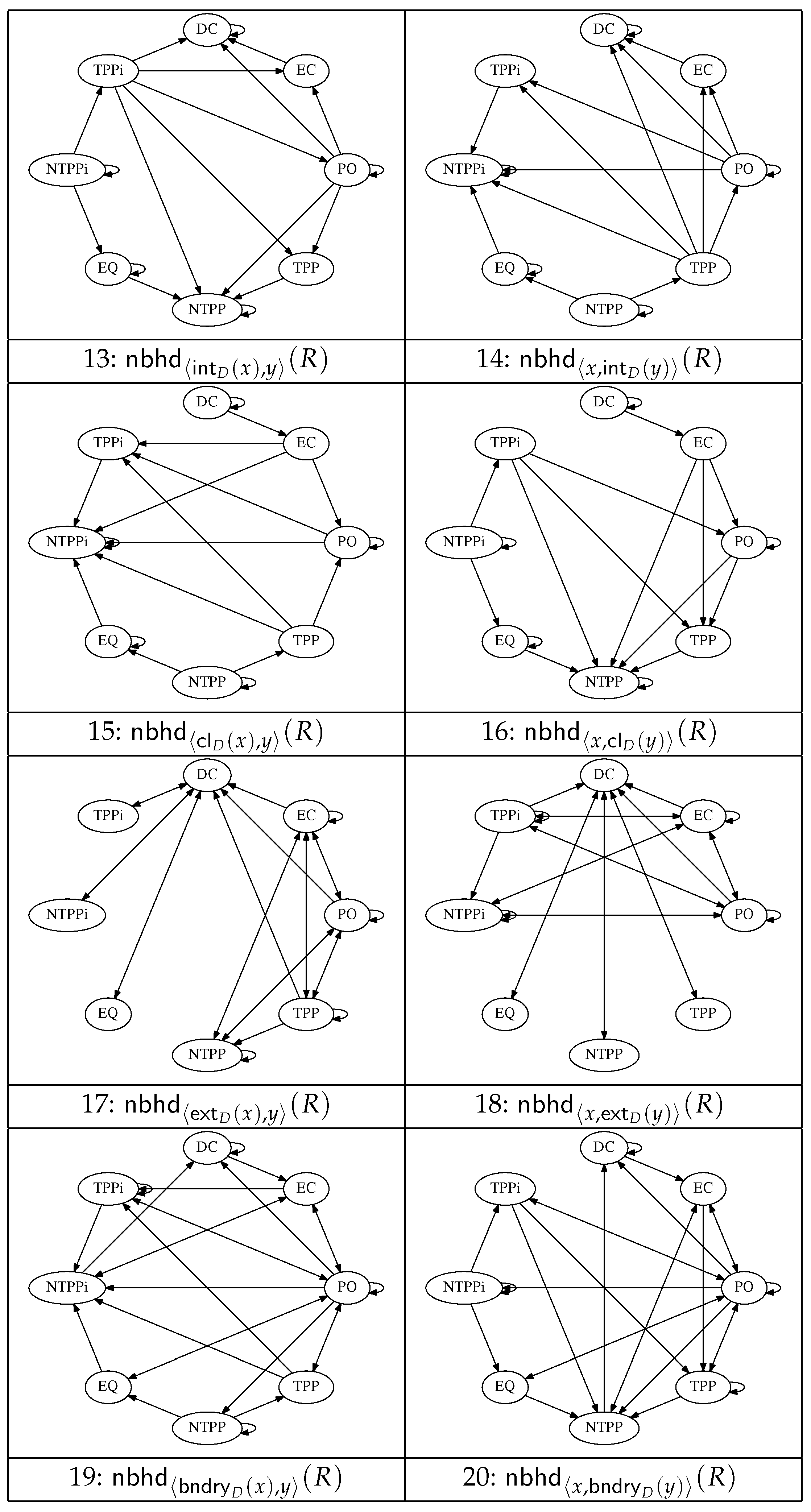
Figure 2 and Figure 3 show a set of 20 graphs that encode the conceptual neighbourhood relations defined in terms of the operators $\mathsf{sum},\mathsf{prod},\mathsf{diff},\mathsf{compl},\mathsf{xor}$ (Figure 2), and the quasi-topological operators ${\mathsf{int}}_D,{\mathsf{cl}}_D,{\mathsf{ext}}_D$, and ${\mathsf{bndry}}_D$ (Figure 3). Not all these operators yield resegmentations with obvious applications in the histological domain, but we include them here for completeness in view of the fact that all the operators arise in many formal descriptions of space. A subset of these operators are used in the resegmentations depicted in Figure 4 and Figure 5.

In the first graph, for example, showing

$${\mathsf{nbhd}}_{\langle x,\mathsf{sum}(x,y)\rangle }(R)=\{R^{\prime }\in \mathrm{RCC}8\mathrm{D}|\exists x,y(R(x,y)\wedge R^{\prime }(x,\mathsf{sum}(x,y))\}$$

(6)

the arrow from $\mathsf{DC}$ to $\mathsf{TPP}$ represents the case ${\mathsf{nbhd}}_{\langle x,\mathsf{sum}(x,y)\rangle }(\mathsf{DC})=\left\{\mathsf{TPP}\right\}$, meaning that if $\mathsf{DC}(x,y)$ holds then we must have $\mathsf{TPP}(x,\mathsf{sum}(x,y))$. In this case, only one resegmentation exists; other cases, such as ${\mathsf{nbhd}}_{\langle x,\mathsf{sum}(x,y)\rangle }(\mathsf{PO})=\{\mathsf{TPP},\mathsf{NTPP}\}$, may allow more than one. Loops in the CND indicate where a change to a region of a designated pair does not necessarily result in a corresponding change of relation. Isolated nodes or nodes without outgoing edges arise where an operator returns null (e.g., $\mathsf{diff}(x,y)$ where $\mathsf{PP}(x,y)$).

While 20 graphs are depicted here in the interests of clarity, these could theoretically be reduced to a minimal set of three from which all the others may be derived. One such set encodes the operators $\mathsf{sum}$, $\mathsf{compl}$, and ${\mathsf{int}}_D$ as primitive graphs. This property is a direct consequence of the definitions for $\mathsf{sum}$, $\mathsf{compl}$, and ${\mathsf{int}}_D$ from which all the other set-theoretic and topological operators can be defined—see Appendix A.1.

For graph number n (Figure 2 and Figure 3), the outgoing edges from the vertex labelled with relation R are designated with the mnemonic $n_R$; for example, in the case of the pair of outgoing edges from $\mathsf{PO}$ to $\mathsf{TPP}$ and $\mathsf{NTPP}$ in graph 1, this is denoted as $1_{\mathsf{PO}}$. Note that four of the RCC8D relations are self-inverse (i.e., $R(x,y)$ implies $R(y,x)$); these are $\mathsf{DC}$, $\mathsf{EC}$, $\mathsf{PO}$, and $\mathsf{EQ}$. The other four relations form two mutually inverse pairs: $\mathsf{TPPi}(x,y)$ if and only if $\mathsf{TPP}(y,x)$, and $\mathsf{NTPPi}(x,y)$ if and only if $\mathsf{NTPP}(y,x)$. These inverse relations will sometimes be exploited in our reasoning. In graph 4, for example, we see that $\mathsf{PO}(x,y)$ implies $\mathsf{TPPi}(y,\mathsf{prod}(x,y))$; sometimes we will find it more convenient to rewrite this as $\mathsf{TPP}(\mathsf{prod}(x,y),y)$, in which case we would cite the graph operation as $4_{\mathsf{PO}}^{\prime }$. An example of this is seen later in

Table 1. Resegmentation details for Figure 4. Here CT refers to the RCC8D composition table.

Figure	Initial Relation	Relation after Resegmentation	Graph Operation
(g)	$\mathsf{PO}(n,c)$	$\mathsf{TPP}({\mathsf{int}}_D^5(n),c)$	${13}_{\mathsf{PO}}$
(h)	$\mathsf{PO}(n,c)$	$\mathsf{TPP}(n,{\mathsf{cl}}_D^6(c))$	${16}_{\mathsf{PO}}$
(i)	$\mathsf{PO}(n,c)$	$\mathsf{TPP}(n,\mathsf{sum}(n,c))$	$1_{\mathsf{PO}}$
(j)	$\mathsf{PO}(n,c)$	$\mathsf{TPP}(\mathsf{prod}(n,c),c)$	$4_{\mathsf{PO}}^{\prime }$
(l) $\left\{\begin{array}{c}\phantom{(}\hfill \\ \phantom{(}\hfill \end{array}\right.$	$\begin{array}{c}\mathsf{PO}(n^{\prime },c_1)\hfill \\ \mathsf{PO}(n^{\prime },c_2)\hfill \end{array}$	$\left.\begin{array}{c}\mathsf{TPP}(\mathsf{prod}(n^{\prime },c_1),c_1)\hfill \\ \mathsf{TPP}(\mathsf{prod}(n^{\prime },c_2),c_2)\hfill \end{array}\right\}$	$4_{\mathsf{PO}}^{\prime }$
(m)	$\mathsf{PO}(n^{\prime },c_1)$	$\mathsf{TPP}(n^{\prime },\mathsf{sum}(n^{\prime },c_1))$	$1_{\mathsf{PO}}$
(n) $\left\{\begin{array}{c}\phantom{(}\hfill \\ \phantom{(}\hfill \end{array}\right.$	$\begin{array}{c}\mathsf{PO}(n^{\prime },c_1)\hfill \\ \mathsf{PO}(n^{\prime },c_2)\hfill \end{array}$	$\begin{array}{c}\mathsf{TPP}(n^{\prime },\mathsf{sum}(n^{\prime },c_1))\hfill \\ \mathsf{DC}(n^{\prime },\mathsf{diff}(c_2,{\mathsf{cl}}_D(n^{\prime })))\hfill \end{array}$	$\begin{array}{c}{1}_{\mathsf{PO}}\\ {15}_{\mathsf{PO}},6_{\mathsf{PO}},{16}_{\mathsf{EQ}},\mathrm{CT}\end{array}$
(o) $\left\{\begin{array}{c}\phantom{(}\hfill \\ \phantom{(}\hfill \end{array}\right.$	$\begin{array}{c}\mathsf{PO}(n^{\prime },c_1)\\ \mathsf{PO}(n^{\prime },c_2)\end{array}$	$\begin{array}{c}\mathsf{NTPP}(n^{\prime },\mathsf{sum}({\mathsf{cl}}_D(n^{\prime }),c_1))\hfill \\ \mathsf{DC}(n^{\prime },\mathsf{diff}(c_2,{\mathsf{cl}}_D^2(n^{\prime }))\hfill \end{array}$	$\begin{array}{c}{15}_{\mathsf{PO}},1_{\mathsf{PO}},{16}_{\mathsf{EQ}},\mathrm{CT}\\ {15}_{\mathsf{PO}},6_{\mathsf{PO}},{16}_{\mathsf{EQ}},{16}_{\mathsf{NTPP}},\mathrm{CT}\end{array}$

. Note that the graphs exclude edges marking transitions of relations to DC as a direct consequence of one of the relata passing to null (e.g., as arises when a region without interior is eroded).

We also use RCC8D’s composition table (RCC8D-CT). The notion of composition is well-known in AI, as it provides an efficient inference mechanism for many QSR constraint satisfaction programs, where it is typically implemented as a simple look-up table. Following [17], weak composition of DM’s JEPD relation sets is defined as follows. Given relation set $\Sigma$, the weak composition RCC8D-CT(R,S), where $R,S\in \Sigma$, is defined to be the smallest subset $\left\{T_i\right\}\subseteq \Sigma$ such that $\mathrm{DM}\models \forall x,y,z((R(x,y)\wedge S(y,z))\to T_1(x,z)\vee \cdots \vee T_n(x,z))$. The elements of RCC8D-CT defined on non-null regions agree identically with those of RCC8’s composition table entailed by RCC. This was mechanically proved using the sorted theorem prover SPASS [18] to verify that all entailments of the above form were included in the composition table; and constructing a set of graphical models satisfying each $T_i(x,z)$ disjunct. The same method was used to verify the sets of directed edges of the graphs depicted in Figure 2 and Figure 3.

3.2. Implementation

All the relations and functions described above were implemented on the ImageJ (IJ) image processing platform. Two variants of the RCC5/8D relation sets were implemented: one that restricts the indexed region pairs to simple (self-connected) regions, while the other relaxes this constraint by allowing a labelled region to consist of disjoint connected components. In the case where multiple regions arise in an image, paired images were processed by computing the Cartesian Product defined on pairs of connected components with the $n\times m$ relations stored in an $n\times m$ matrix. A raster scan encoding of the segmented regions in each image and the matrix enables images to be queried and specific relations and regions to be reconstructed. These matrices are encoded and stored as an 8-bit colour-coded $n\times m$ image which we call an RCC table.

The set-theoretic operators ($\mathsf{sum}$, $\mathsf{prod}$, $\mathsf{diff}$, $\mathsf{compl}$, $\mathsf{xor}$) were respectively mapped to IJ’s default set of operators (OR, AND, Subtract, Invert, Difference). Of the discrete topological operators, ${\mathsf{int}}_D$ and ${\mathsf{cl}}_D$ were mapped to IJ’s dilation and erosion operators (Erode, Dilate), respectively, while ${\mathsf{ext}}_D$ and ${\mathsf{bndry}}_D$ were defined and implemented in terms of these. The universal region denoted as u in DM maps to the image itself.

To provide an idea of the computation involved, our implementation of RCC8D in the ImageJ platform (Java 1.8.0) processes an image of 2048 × 1546 pixels containing 898 nuclear regions and 1007 cytoplasmic regions (total number of possible relations is 903,286) in 162 s using an Intel i7 CPU running at 3.3 GHz under the Linux operating system. The CPU processing the RCC table depends on a number of factors: the number of regions in each image, the types of relations held (some are quicker to compute than others), and the size of the image. With the RCC table precomputed, the time it takes the algorithm to get from the steps depicted in Figure 5b–f is 8.7 s (this is for the entire 2048 × 1536 pixel image with 548 nuclear and 1012 regions of cytoplasm).

4. Examples

This section presents two examples to illustrate the method using a H400 dataset. In the first example we show how we need a sequence of changes in the relations in order to get a sequence of changes in the regions. Several alternative re-segmentation solutions are constructed and verified by the underlying logic. A detailed example is given of one such correction to show a path through the graph network from a start to a goal state. The second example shows how the method can be extended to cover other morphological operations on region pairs not defined by the set-theoretic and discrete topological operators, or their compositions assumed here. It is additionally shown how the same model-based method provides a mereotopological method to quantify, evaluate, and correct segmentation errors.

4.1. Example 1: Segmenting Cells in Culture Using Set-Theoretic and Discrete Topological Operators

Figure 4a depicts a crop of an H&E-stained culture image of H400 cells grown on glass. Various image pre-processing operations are performed. First, a Gaussian filter (kernel radius 2) is applied to the original image to remove noise and reduce the fragmentation artefacts near the region boundaries. Next, colour deconvolution [19] is used to unmix the dye contributions and identify cell nuclei (H-stain, image (b)) from the rest of the cell bodies (E-stain, image (c)). Several standard image processing operations then follow (k-means clustering on the H,E stain images using three clusters, Boolean compositions of thresholded clusters, binary watershed separation), which are used to generate the two binary images of cell nuclei and their associated cell bodies (images (d) and (e), respectively). The colour composite merge depicted in (f) illustrates the extent of conformity to the assumed histological constraints; binary segmented nuclei (d) are mapped to green, cytoplasm (e) to magenta, and overlap between the two to white. Where a nucleus forms a proper part ($\mathsf{PP}$) of its cytoplasm, the latter appears as magenta surrounding a white nucleus; in less common cases where $\mathsf{EQ}$ holds, the whole cell appears white.

First we test the RCC8D relation between cell nuclei and cytoplasm, where each typed set of spatially disjoint regions is treated as a mereological whole (regions n and c, respectively). In the case illustrated, we obtain $\mathsf{PO}(n,c)$, as indicated by the presence of green regions in image (f). As this fails the test of conformity (which requires nuclei to fall within their associated cytoplasm), the task is to repair the segmentation. In (f) two candidate nuclei partially overlap ($\mathsf{PO}$) cytoplasm regions.

Using the directed graphs, we look for resegmentation operations on candidate nucleus/cytoplasm pairs that take us from $\mathsf{PO}$ to $\mathsf{PP}$. Consider the top cell in Figure 4f, where candidate nucleus (call it n) is $\mathsf{PO}$ to cytoplasm component (c) (by “candidate nucleus”, we mean image segments which to a first approximation correspond to the parts of the image derived from actual cell nuclei in the sample as defined in [5]). One possible solution (image (g)) successively erodes n (i.e., replaces it by its discrete interior) until it becomes $\mathsf{PP}$ to c; this requires five successive erosions. Another (image (h)) replaces c by its discrete closure (dilation) until the same result is achieved. This uses a dilate-no-merge operation to avoid the dilated cytoplasm region merging with adjacent cytoplasm regions, and requires six successive dilations. In (i) we extend c to cover all of n so that once again the nucleus is $\mathsf{PP}$ to its cytoplasm. In (j) we achieve the same result by subtracting from n the part that lies outside c.

Image (k) shows an example where a nucleus $n^{\prime }$ partially overlaps two cytoplasm components $c_1$ and $c_2$. One correction (image (l)) splits the nucleus into two by taking its intersections with $c_1$ and $c_2$. Each nuclear component is now $\mathsf{PP}$ to one cytoplasm component. In (m), the cytoplasm on the left, (component $c_2$), is extended to cover the whole of $n^{\prime }$. However, this has the effect of merging two cytoplasm components; to compensate for this, the rightmost component ($c_1$) is reduced by subtracting from it the closure of $n^{\prime }$ (image (n)). Finally, in (o), the nucleus is completely surrounded by cytoplasm; this is achieved by extending $c_2$ to cover not just $n^{\prime }$ but its closure; the compensatory reduction of $c_1$ must now subtract the closure of the closure of $n^{\prime }$ in order to ensure complete separation from the extended $c_2$.

These resegmentations, associated graphs, and inferences used to generate them are summarised in Table 1.

In detail, the steps for $c_1$ in (o), for example, are as follows:

• Start with $\mathsf{PO}(n^{\prime },c_1)$.
• By 15${}_{\mathsf{PO}}$ this gives $\mathsf{PO}\left|\mathsf{NTPPi}\right|\mathsf{TPPi}({\mathsf{cl}}_D(n^{\prime }),c_1)$.
• By 1${}_{\mathsf{PO}\left|\mathsf{NTPPI}\right|\mathsf{TPPI}}$ this gives $\mathsf{EQ}\left|\mathsf{NTPP}\right|\mathsf{TPP}({\mathsf{cl}}_D(n^{\prime }),\mathsf{sum}({\mathsf{cl}}_D(n^{\prime }),c_1))$.
• Next, from $\mathsf{EQ}(n^{\prime },n^{\prime })$ and 16${}_{\mathsf{EQ}}$ we have $\mathsf{EQ}|\mathsf{NTPP}(n^{\prime },{\mathsf{cl}}_D(n^{\prime }))$.
• The RCC8D weak composition $\mathsf{EQ}|\mathsf{NTPP}\circ \mathsf{EQ}|\mathsf{NTPP}|\mathsf{TPP}$ is $\mathsf{EQ}\left|\mathsf{NTPP}\right|\mathsf{TPP}$.
• Hence from 3 and 4 using 5 we have $\mathsf{EQ}\left|\mathsf{NTPP}\right|\mathsf{TPP}(n^{\prime },\mathsf{sum}({\mathsf{cl}}_D(n^{\prime }),c_1))$.

In step 2, we apply graph 1 to each disjunct of $\mathsf{PO}\left|\mathsf{TPPi}\right|\mathsf{NTPPi}$ separately to generate the new disjunction $\mathsf{EQ}\left|\mathsf{TPP}\right|\mathsf{NTPP}$ in step 3: here $\mathsf{PO}$ and $\mathsf{TPPi}$ ($\mathsf{NTPPi}$) are mapped to $\mathsf{TPP}|\mathsf{NTPP}$ and $\mathsf{EQ}$ by $1_{\mathsf{PO}}$ and $1_{\mathsf{TPPi}}$ ($1_{\mathsf{NTPPi}}$), respectively; the combined operation is notated as $1_{\mathsf{PO}\left|\mathsf{TPPi}\right|\mathsf{NTPPi}}$ (other disjunctions are handled similarly). The soundness and completeness of the inference procedures ensure not only that steps 1–4 encode the DM theorem $\mathsf{PO}(x,y)\to \mathsf{EQ}\left|\mathsf{TPP}\right|\mathsf{NTPP}(x,\mathsf{sum}({\mathsf{cl}}_D(x),y))$, but also that the disjunctive relation $\mathsf{EQ}\left|\mathsf{TPP}\right|\mathsf{NTPP}$ is the strongest obtainable.

4.2. Example 2: Segmenting Cells in Culture: Adding Other Morphological Operators

Morphological operators other than those that directly implement the set-theoretic and discrete topological ones described above can be exploited using the same method. In the example below, a binary geodesic dilate without merging operation is combined with the $\mathsf{sum}$ operator to resolve cases such as those depicted in Figure 4k, where the cytoplasm regions are repartitioned to resolve multiple merged cells with partially overlapping nuclei (Figure 5).

Several model-based constraints are exploited in this example: (1) morphology: nuclear shape and size tends to be more uniform than those of their host cells; (2) stain uptake: the haematoxylin staining is greater and relatively uniform in the nucleus compared to the cytoplasm, while the rest of the cell stains more prominently with the eosin dye; and (3) topology: a valid histological model of a cell requires the nucleus to be part of its associated body of cytoplasm. All three constraints are implemented as follows: first, using an image gradient method to segment nuclei based on circularity and size and a histogram method to extract the cytoplasmic regions, secondly, placing a priority on the resegmentation of the cytoplasm over the segmented nuclei, and thirdly assessing the model part–whole condition on the mereotopological relationship between nuclear and cytoplasmic regions that enables us to either accept, reject, or modify the segmentation results.

The proposed procedure is summarised as follows. Figure 5a depicts a cropped image of an H&E-stained culture of H400 cells grown on glass. For the nuclear regions, colour deconvolution [19] is used to separate the colour image information into haematoxylin-only and eosin-only images. A regional gradient and circularity and size constraints algorithm [20] is applied twice to the haematoxylin image. The first pass identifies fairly circular nuclear regions (with circularity ≥0.6), within a range of expected sizes (minimum and maximum areas of 400 and 3600 pixels, respectively, all determined empirically). A second pass is applied to the same image but modified so that the nuclei found in the first pass are masked with the background intensity (and so they are not detected) and the algorithm is set to accept lower circularity results (≥0.3) to find elliptical and clustered nuclear regions. After smoothing with opening and closing (kernel radius = 4 pixels), a binary watershed separation operation splits the clustered nuclei and these are merged with those detected in the first pass (Figure 5b). The cytoplasmic regions are segmented from the greyscale version of the original H&E image (as this has contributions of both dyes). Initially, a local contrast-limited adaptive histogram equalization [21] is applied to increase the contrast between cells and background and mitigate residual effects of uneven illumination that can still appear in background-corrected images. The image is then binarised using the histogram minimum method [22] followed by median filtering (kernel radius = 2 pixels) to smooth boundaries (Figure 5c). Finally, a binary watershed separation operation splits the entire cytoplasm region into tentative cell parts (seen in Figure 5d).

Since both segmentation results are obtained through independent processes, an assessment of the relations held between the two object types is necessary to evaluate the consistency of the results in terms of spatial relations with the biological reality (i.e., real cells). We note that the position of watershed split-lines is to some degree sensitive to the geometry of the regions, and can result in unintended separation of whole nuclei into parts and inadequately separated cells (Figure 5d). Investigation of the RCC5D relations existing between nuclear and cytoplasmic regions can help in identifying and correcting such artefacts. In the original uncropped image, 548 segmented nuclei and 1012 cytoplasmic regions were obtained using the procedure above. The frequency count of the different RCC5D relations was: $\mathsf{DR}$ = 553,778, $\mathsf{PO}$ = 490, $\mathsf{PP}$ = 308, $\mathsf{EQ}$ = 0, and $\mathsf{PPi}$ = 0. As the segmentation target is to generate model cells (i.e., pairs of nuclear and cytoplasmic regions satisfying a part–whole relation and a one-to-one mapping between nucleus and cytoplasm) of the mereotopological relations, the 490 $\mathsf{PO}$ counts enable the quantification of the number of relations not fulfilling the cell model, while the number of $\mathsf{PP}$ counts indicate those that do.

Interestingly, this provides a quality control measure of the segmentation results. The artefactual $\mathsf{PO}$ instances could arise either from cytoplasmic mis- or over-partitioning (where nuclei partially overlap across cytoplasmic split lines), from under-sized cytoplasmic regions (therefore the nucleus “spilling out” of the cell), or from oversized nuclei. To resolve these $\mathsf{PO}$ cases, the cytoplasm regions were re-merged by means of binary closing (which fills the 1 pixel- wide watershed lines) and repartitioned using the binary dilation without merging operation of the nuclei (considered here as seeds) on the merged cytoplasmic regions (the mask)—Figure 5e,f. Note that this procedure might leave the other $\mathsf{PO}$ instances unmodified. Indeed, a further RCC5D analysis revealed eight remaining $\mathsf{PO}$ instances due to nuclear spilling or cytoplasmic shortage. Inspection of $1_{\mathsf{PO}}$ in Figure 2 shows that the $\mathsf{sum}$ operator points to the sought-after resolution of $\mathsf{PO}$ into $\mathsf{PP}$ (either $\mathsf{TPP}$ or $\mathsf{NTPP}$) relations This is equivalent to forcing the space occupied by nuclear pixels not forming part of the cytoplasm to become so.

The re-segmentation method so far ensures that the repartitioning of the cytoplasm of the $\mathsf{PO}$ cases with respect to their associated segmented nuclei necessarily generates model cells; however, a $\mathsf{PP}$ relation (that only gives a necessary condition of being a model-cell) does not. Where this is required, the RCC-table that exhaustively enumerates the segmented RCC5/8D relation pairs is interrogated and used to test for one–one mappings. Those regions of cytoplasm and their overlapping nuclei that fail this test are factored out and the cytoplasm repartitioned using the binary dilation without merging operation of the nuclei (considered here as seeds) on the cytoplasmic regions (the masks). The final resegmentation of the subset of $\mathsf{PO}$ relations is shown in Figure 5g, while Figure 5h,i respectively show the resegmentation of $\mathsf{PO}$ cases from the initial watershed partition assumed in Figure 5d to the cytoplasm merge and resegmentation using a binary dilation without merging operation.

While this particular example might appear obvious, the neighbourhood diagrams and their graphs are essential to identify which paths exist for different operations that result in the search for specific models. In turn, the method provides a guide of which segmentation algorithms may or may not be suitable for a particular application. Additionally, note that the two strategies used here result in different modifications of the image regions. These depend on the nature of the $\mathsf{PO}$ occurrences (i.e., depending on the nature of the segmentation artefacts) while retaining unchanged those objects that were originally correctly segmented.

5. Discussion

While theoretically any one of the RCC8D relations is possible given a pair of segmented regions, when applied to histological images, morphological, geometric, and other empirical constraints on models will tend to favour some relations over others. One such example is the prevalence of the $\mathsf{PO}$ relation between segmented nuclei and regions of cytoplasm, and another is the histological part–whole relation $\mathsf{P}$ or the proper-part relation $\mathsf{PP}$ associated with model cells, which we now turn our attention to.

The 20 graphs reveal six resegmentation operations that take us directly from $\mathsf{PO}$ to $\mathsf{PP}$ (i.e., $\mathsf{TPP}|\mathsf{NTPP}$), hence guaranteeing the transition to $\mathsf{PP}$ (namely $1_{\mathsf{PO}}$, $2_{\mathsf{PO}}$, $3_{\mathsf{PO}}^{\prime }$, $4_{\mathsf{PO}}^{\prime }$, $5_{\mathsf{PO}}^{\prime }$, and $8_{\mathsf{PO}}^{\prime }$) and another ten that merely allow that possibility (namely, $9_{\mathsf{PO}}^{\prime }$, ${10}_{\mathsf{PO}}$, ${13}_{\mathsf{PO}}$, ${14}_{\mathsf{PO}}^{\prime }$, ${15}_{\mathsf{PO}}^{\prime }$, ${16}_{\mathsf{PO}}$, ${17}_{\mathsf{PO}}$, ${18}_{\mathsf{PO}}^{\prime }$, ${19}_{\mathsf{PO}}$, and ${20}_{\mathsf{PO}}$; in these cases the predicted models include $\mathsf{PP}$, but $\mathsf{PP}$ is not entailed). The number (and complexity) of potential resegmentations increases when several graphs are combined and node–node paths through these networks of length $n>2$ are considered, as in the segmentation operations used to generate the cell depicted in Figure 4o.

Strategies for selecting optimal resegmentations would be relatively straightforward if the segmented cells were widely separated from each other, but in Figure 4 this is not so, since several cells are separated by a pixel-width distance and in (f) and (k) nuclei overlap more than one cytoplasm component (these pixel-wide boundaries arise where neighbouring individual regions of a given type are represented in a single binary image). Hence, when applying ${16}_{\mathsf{PO}}$ to (f) to generate (h), or applying $1_{\mathsf{PO}}$ to (k) to generate (m), hitherto separated cytoplasm components can merge. As we have seen, one way to avoid this is to restrict the discrete closure operation so as to prevent merging with a neighbouring component:

$${\mathsf{cl}}_D^{-}(x,y){=}_{\mathrm{def}}\left\{\widehat{x}\right|\mathsf{O}(N(\widehat{x}),x)\wedge \neg \mathsf{O}(N(\widehat{x}),y)\}.$$

(7)

This picks out those pixels whose immediate neighbourhoods overlap x but are disjoint from y, giving the largest subset of ${\mathsf{cl}}_D(x)$ not connected to y. It cannot be applied carte blanche, however, since histological domain constraints may require some regions (e.g., fragmented nuclei) to be merged.

Within DM proper, different classes of regions operate as filters (e.g., atoms, regions without interiors, regular regions lacking spikes or fissures, or connected components), and all these give rise to varying constraints on the mereotopological relations defined on them. At the image scales typically used in digital microscopy, most segmented regions mapping to histological objects have interiors, and very few are atomic, but restricting these topological properties will constrain the possible segmentation models and relations that can be defined on them. Constraints other than those defined directly within DM can also be used to reduce the number of segmentation models. A simple example is where the range of sizes of histological objects can be used as a filter, either using MM granulometry methods or filtering by morphological thickness [2], enabling us to rule out the segmentation models with cell bodies too large or nuclear regions being too small.

Another extra-logical constraint that can be used exploits empirical information about the histological stains and their known selectivity in dye take-up with respect to targeted tissues and their parts. Given that the H-stain offers a potentially more reliable segmentation for nuclei than the eosin counter-stain does for cytoplasm, resegmentations could be ranked to favour those that minimize the changes to nuclei. Other assumed empirical and ontological dependencies can also be exploited. For example, depending on microscope resolution, each cell nucleus should fall wholly within some cytoplasm component, whether this is segmentable from the original image or not; in DM this can be captured by adding the histological domain axiom $Nuc(x)\to \exists y(Cell(y)\wedge P(x,y))$. This constraint also justifies the assumption underlying the transition $1_{\mathsf{PO}}$, where a cytoplasm component partially overlapping a nucleus is extended to cover the nucleus so that it forms part of that cell. The correspondence between histological features and stain selectivity can also be incorporated algorithmically: given a $\mathsf{PO}$ relation defined on a poorly segmented nucleus and its host cytoplasm, we favour ${16}_{\mathsf{PO}}$ (dilating the cytoplasm) over ${13}_{\mathsf{PO}}$ (eroding the nucleus). It is also worth noting that the boundaries of histological objects in grayscale images tend to exhibit intensity gradients, so if thresholding is used for segmentation, subsequent erosion and dilation-based resegmentations are more likely to follow gray-scale intensity levels in the original image than blind set-theoretic operations on the same binary images. This observation highlights a potential limitation of the underlying method, which is that once a target histological object is segmented, subsequent changes applied to it may not conform to the available information in the original image. However, in some cases, restricting oneself to information in an image may not—even in principle—lead to a histological model. For example, uneven staining may fail to reveal the full extent of the cytoplasm in the sample; in which case a model-based resegmentation solution can be used to factor out those regions in an image that need to be treated differently from the rest.

It is also perhaps useful here to give at least some indication of empirical methods and metrics envisaged for quantifying, validating, and measuring our segmentation solutions. For example, given that segmentation of cell nuclei appears to be more reliable than that of regions of cytoplasm, these can be used as a standard reference to measure how well the segmented cytoplasm conforms to the histological model. In this case, a necessary condition would be that a segmented nucleus forms part of some overlapping body of cytoplasm, so one possible quantitative measure is the proportion of region pairs that form a part–whole relation out of all possible overlap cases. These simple examples show (i) that the underlying physical model should guide the abstraction and (ii) the danger of abstracting and working with generic cases too quickly, where empirical constraints restricting valid resegmentations may be missed.

The methods presented so far address the correction of histological models. In [5] we proposed that deriving consistent histological models from tissue images can be seen as a progression through a number of ontological levels, each one consisting of distinctive classes of entities related in systematic ways to entities at other levels. According to [5], histological models are level 3 ontologies, and their correction assumes that the procedures used for obtaining candidate nuclear and cytoplasm regions (level 2 ontologies: nuclei, cytoplasm) are valid. The accuracy of such procedures to generate initial segmentations is therefore essential, and often involves ground truth sets or gold standards. However, this goes beyond the scope of the level 3 methods presented here. Furthermore, how accurately the level 2 segments represent biological reality cannot be directly addressed by the mereotopological approaches presented (because they address level 3 ontologies). Despite this, the frequency and magnitude of the corrections needed to be applied to obtain valid models could serve as additional indicators of a lack of correctness in the initial segmentation as an artefact detector operating at a higher ontological level than the original segmentation.

6. Conclusions

We have shown how DM provides the means to model cellular structure in digitised histological images. Segmentation and resegmentation satisfying a histological model can be achieved by a set of operations on regions that satisfy a set of constraints on pairs of regions. These constraints can be encoded as a set of graphs in which topological and set-theoretic operators lead from one vertex to another. The method is generic and can be applied to any domain where it is required to segment digitised images into regions satisfying specific sets of mereotopological relations.

Several directions for future work can be suggested. We have already discussed empirical validation methods using a set of gold-standard images. Secondly, the set of operators and associated graphs can be extended to cover morphological operators other than the topological and set-theoretic operators used here. In order to generate graphs encoding all possible relation transitions, each operator needs to be defined together with a proof that the models constructed are exhaustive. However, this can be an onerous task when encoding all but the simplest of morphological-based operators, such as opening and closing, or implementing alternate sequential smoothing operations [23]. Thirdly, various different metrics can be defined on the conceptual neighbourhoods and their graphs, allowing optimisation of segmentation models and prediction of the most likely path to take through the graphs from a given state to a segmentation goal. These could be based on what proportion of JEPD relations reached at each step can lead to a valid model, or probability measures determined from a statistical analysis of the data sets, taking into account a priori and empirically-derived properties such as cell type and morphological shape and size.