Alpha Channel Fragile Watermarking for Color Image Integrity Protection

Abstract

This paper presents a fragile watermarking algorithm`m for the protection of the integrity of color images with alpha channel. The system is able to identify modified areas with very high probability, even with small color or transparency changes. The main characteristic of the algorithm is the embedding of the watermark by modifying the alpha channel, leaving the color channels untouched and introducing a very small error with respect to the host image. As a consequence, the resulting watermarked images have a very high peak signal-to-noise ratio. The security of the algorithm is based on a secret key defining the embedding space in which the watermark is inserted by means of the Karhunen–Loève transform (KLT) and a genetic algorithm (GA). Its high sensitivity to modifications is shown, proving the security of the whole system.

1. Introduction

Due to the large diffusion of multimedia data as a result of the widespread use of networks, it has become important to protect digital data from fraudulent or unauthorized use. Illegal copies of movies, forged images and tampered audio files are examples of such illegitimate manipulations [1]. Thus, appropriate techniques must be devised to protect data against such attacks. Among the available techniques, message authentication codes (MACs) may help in some contexts; digital signatures are also a powerful method for protecting data integrity and authenticating their origin. Nonetheless, these methods produce bit strings that must be appended to the data, and their removal destroys the intended protection.

In order to allow the integration of security data into a digital object to be protected, watermarking techniques are used. A watermark is a signal which is embedded into the digital object and lives with the object itself. The kind of watermark and algorithm used strongly depends on the objective of the application.

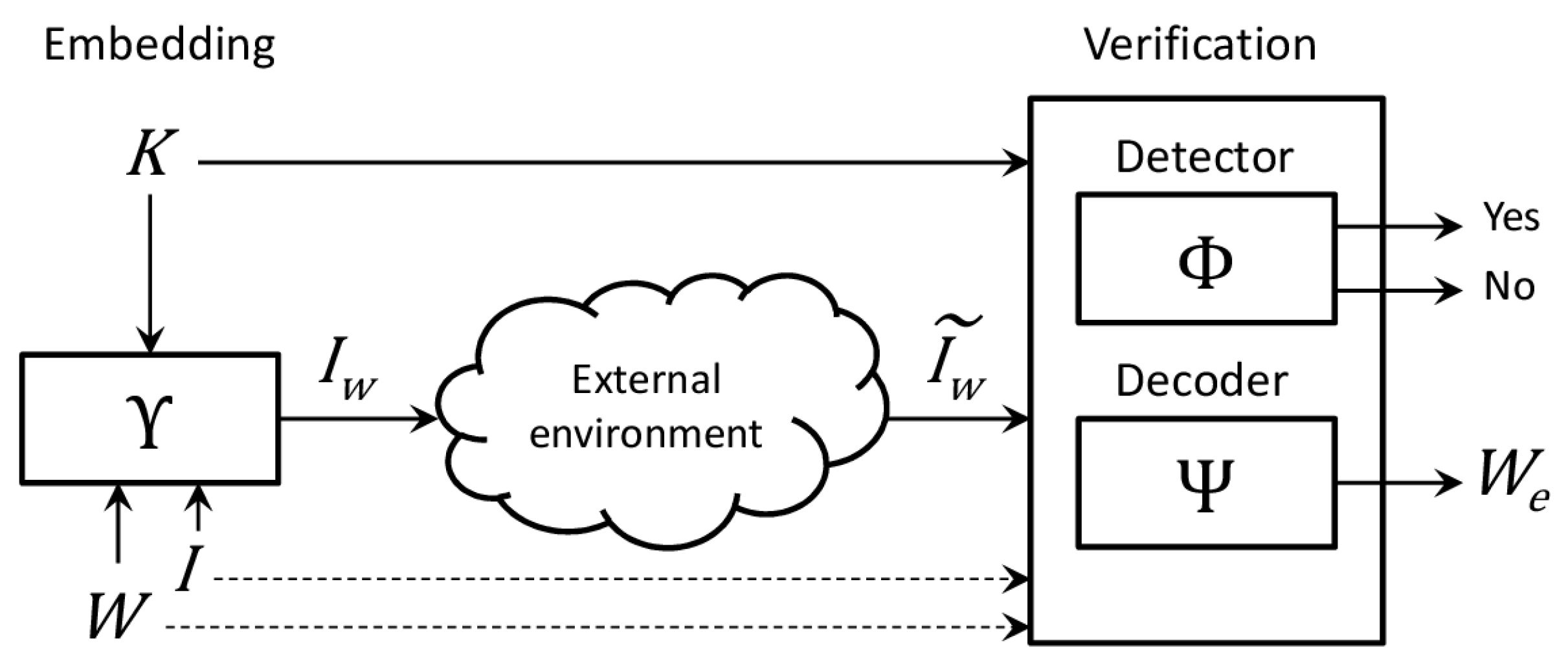
The watermarking procedure is composed of two different phases: the first is the embedding, which produces a watermarked object, and the second is the verification. Between the two phases the watermarked object is stored or transferred in an uncontrolled and possibly hostile environment and may undergo attacks aimed at its modification (Figure 1).

The embedding phase is defined by a function $\mathrm{{\rm Y}}$ taking as input a host signal $I$ (in our context, an image), a watermark $W$ and possibly a secret key $K$ (to improve the security of the method), and produces a watermarked object $I_W$.

The verification phase is composed of two functions, namely detector and decoder. The detector is a two-valued function $\mathrm{\Phi }$ which tells if the watermark is present in the watermarked object; its inputs are a possibly altered object $\widetilde{I_W}$ and $K$. The decoder is a function $\mathrm{\Psi }$ which extracts a candidate watermark $W_e$ from $\widetilde{I_W}$ possibly using the secret key. Note that some algorithms may also require the host signal $I$, the watermark $W$ or both.

A watermarking algorithm whose verification functions need the host object $I$ is called informed or non-blind, otherwise it is called blind.

Depending on the context of application, watermarks (and their respective algorithms) may be developed to be fragile or robust. A fragile watermark is designed to be altered as long as the object containing it is modified, even minimally; a typical application is content integrity protection. On the other hand, a robust watermark must resist and be detectable even if the object is modified: the main application is copyright protection, where the owner of an object’s copyright wants its watermark to resist any attempt aimed at its removal.

Another characteristic of watermarking algorithms is reversibility. If the host object may be restored from the watermarked object, then the algorithm is said to be reversible. This property is required in some application domains, typically related to the medical field.

The watermark is embedded by modifying features of the image. These features may be the pixels of the image or frequency components obtained by linear transformations such as discrete Fourier transform (FFT), wavelet transform (DWT) or discrete cosine transform (DCT). In the former case, the watermarking is said to take place in the spatial domain, like least significant bit (LSB) embedding, in the latter case it is said to be inserted in the frequency domain. Other features exploited by some watermarking algorithms are the singular values and vectors of singular value decomposition (SVD), and the various types of moment-based transformations, such as Zernike moments [2] or radial harmonic Fourier moments [3].

In this work, we present a blind fragile watermarking algorithm developed for color images that embed a watermark in the frequency domain, computed by applying the Karhunen–Loève transform (KLT). This choice is based on the fact that we want to have a higher degree of security with respect to the traditional transform, such as DCT, because the frequency domain derived by KLT depends on a secret set of eigenvectors. Moreover, as we are considering a fragile watermarking task, geometric invariant transformations, such as those based on moments, are not adequate for the problem at hand, as in this case the watermark should not be robust to the slightest modification of the image.

The main characteristics and novelties of the method are that:

• it can extract the watermark without using the original image;
• it does not modify the RGB channels of the image but the alpha channel only: in this sense the algorithm may be considered as reversible for the RGB components;
• it uses an optimal embedding strategy, which generates the smallest modifications to the alpha channel (maximum one intensity level per pixel), resulting in watermarked images with a very high peak signal-to-noise (PSNR) ratio;
• it may cope with any kind of alpha channel already present in the image or added for the purpose of watermark embedding; no constraints on the values of the alpha channel pixels are posed;
• the tamper localization ability is at block level, the size of which may be selected as one of the main parameters of the algorithm.

The paper is organized as follows: Section 2 recalls some related works; Section 3 gives an overview of the main tools used to implement the proposed algorithm, which is presented in Section 4. Section 5 shows the experimental results obtained by applying the method to a set of color images and in Section 6 some conclusions are presented.

2. Related Works

A central task in watermarking is to find representative features to insert the watermark [4]. The current tendency of fragile schemes calls for constraining the embedding changes to LSBs of the image features. We report some references to works inserting the watermark in the spatial and frequency domains focusing on papers considering the fragile watermarking of images with the alpha channel.

The method presented in [5] and improved in [6] is an efficient fragile watermarking method in the spatial domain that produces watermarked images with the highest theoretical quality. This method can be used to watermark each channel separately (including the alpha channel).

In [7], the watermark is stored in the DCT middle frequencies, while [8] uses DCT to store recovered information in the three LSBs of every pixel. In [9], the DCT domain is used along with fractal coding to improve the efficiency of encoding.

Many approaches make use of the Karhunen–Loève transform (KLT) to watermark image data. The methods presented in [10,11,12] perform robust watermarking using the coefficients computed from the KLT, while [13] hides authentication data in secret coefficients defined by a KLT. The KLT has also been used in [14,15] to fragile watermark web pages.

In [16], the authors investigate the issue of ensuring the authenticity of digital media in a cloud sharing scenario. In order to preserve confidential information in the cloud, a secure watermark detection is proposed, which makes use of a sparse low-dimensional representation of the host signal and the multiparty computation protocol.

In [17], the security of watermarking schemes based on embedding in the transformed domain of singular value decomposition is analyzed. Therein some attacks are proposed, showing that great attention should be paid to security aspects when devising novel methods of data protection in transformed domains.

An adaptive watermarking scheme for drug images displayed by online medical suppliers was introduced in [18]. The content-dependent watermark is merged with the host image through the alpha channel and alpha blending methods. The logo watermark characteristics are determined by the size and color distribution of the drug image. The experiments ran on a dataset of 265 drug images to confirm the performance of the proposed method.

In [19], the authors developed an image authentication method which combines Shamir secret sharing (S3) and alpha-channel embedding. The integrity signal is computed from each block of the host image which afterwards is broken into several shares (which actually are the authentication watermarks) using the S3 scheme. The shares are additively embedded into the alpha channel of the host image, by mapping their values to the maximum range value of the alpha channel. To detect if a tamper has occurred, a two-step process is employed: firstly, the shares are extracted from each block of the alpha channel, and secondly the authentication information generated from the host image blocks is compared to the one extracted from the shares inserted into the alpha channel. A similar alpha-channel embedding approach is used in [20] to authenticate color images. Another very similar approach that embeds into the two LSBs of an alpha channel is reported in [21].

Genetic algorithms (GAs) are employed for data hiding due to their ability to search for an optimal solution to a non-linear problem. Using an approach directly in the spatial domain, [22] proposes a method for hiding data in the LSB planes of an image, minimizing the distortion through the use of a GA. In [23], a DCT-based fragile watermarking technique is enhanced by applying different methods of intelligent optimization (i.e., particle swarm, genetic algorithm, differential evolution and clonal selection): the watermark is embedded into the LSBs of some of the image DCT coefficients and the authors use intelligent optimization techniques to deal with alterations of the LSBs after pixel rounding to an integer.

3. Background

3.1. Notation

In the following, column vectors will be represented with lowercase italic boldface letters ($\mathit{x}$), matrices are indicated with capital italic letters ($K$), sets or vector spaces are denoted as capital boldface letters ($X$) and $\mathbb{E}\left\{\right\}$ is the expected value operator.

3.2. The Karhunen–Loève Transform

A linear mapping, or linear transformation, between two vector spaces $\mathit{R}$ and $\mathit{S}$ having same dimension $d$, is defined by a matrix $A$ called the kernel of the transformation. The matrix $A$ has size $d\times d$ and maps a vector $\mathit{x}\in \mathit{R}$ to a vector $\mathit{y}\in \mathit{S}$ with

$$\mathit{y}=A\mathit{x}$$

(1)

It is possible to obtain the original vector $\mathit{x}$ from $\mathit{y}$ by using the inverse mapping (i.e., inverse transform)

$$\mathit{x}=A^{-1}\mathit{y}$$

(2)

There exist many linear transformations defined by fixed (for each vector space dimension) kernels, such as the discrete cosine transform (DCT), the discrete Fourier transform (DFT), the Hadamard transform or the Haar transform.

The Karhunen–Loève transform (KLT) has the characteristic that the kernel is not fixed but is computed from a set of vectors $X=\left\{{\mathit{x}}_1,{\mathit{x}}_2,\dots {\mathit{x}}_n\right\}$. It is possible to compute the mean vector of the set

$${\mathit{m}}_X=\mathbb{E}\left\{{\mathit{x}}_i\right\},{\mathit{x}}_i\in X$$

(3)

and the covariance of the centered vectors ${\mathit{x}}_i-{\mathit{m}}_X$

$$C_X=\mathbb{E}\left\{\left({\mathit{x}}_i-{\mathit{m}}_X\right){\left({\mathit{x}}_i-{\mathit{m}}_X\right)}^{\prime }\right\},{\mathit{x}}_i\in X$$

(4)

The $d$ eigenvectors ${\mathit{e}}_i$ of $C_X$ may be computed and arranged as rows of the matrix $A$: to give an order to the eigenvectors, they are sorted in non-increasing order of their associated eigenvalues ${\lambda }_i$.

Then, the KLT of a vector $\mathit{x}$ is calculated as

$$\mathit{y}=A\left(\mathit{x}-{\mathit{m}}_X\right)$$

(5)

and the inverse transform is obtained from

$$\mathit{x}=A^{-1}\mathit{y}+{\mathit{m}}_X$$

(6)

The elements of $\mathit{y}$ are the transform coefficients. In this context, the eigenvectors ${\mathit{e}}_i$ are called basis images, because they can be interpreted as images and are used to perform an analysis of the complex frequencies present in $\mathit{x}$.

3.3. Genetic Algorithms

Genetic algorithms (GAs) are a computing paradigm that simulates the evolution of biological beings. The objective is to find an optimal solution to a problem by coding the input parameters into individuals (in general, randomly initialized) and evolving a population of these individuals by mating and mutating them, as happens in nature. Individuals may be assimilated to chromosomes, where each input parameter plays the role of a gene.

In order to evolve the best individuals, the GA uses a fitness function, which measures how much an individual fits the desired solution. The fitness function may take a value proportional to the quality of the solution represented by the individual, or a value inversely proportional to it (i.e., the smaller the value the better the solution); in the following discussion the latter case is considered.

It is possible to describe the processing of a GA through the following high-level description:

• CREATE POPULATION
• solution_found = FALSE
• WHILE NOT solution_found AND NOT REACHED MAXIMUM NUMBER OF EPOCHS
•   CREATE NEW INDIVIDUALS THROUGH SELECTION AND CROSSOVER
•   MUTATE INDIVIDUALS
•   EVALUATE FITNESS OF EVERY INDIVIDUAL
•   IF BEST(FITNESS IN POPULATION) < threshold
•       THEN solution_found = TRUE;
•       ELSE UPDATE POPULATION
• END WHILE
• RETURN INDIVIDUAL HAVING BEST FITNESS;

Starting from an initial population of individuals, created randomly or using some information about the desired solution which could help convergence, a series of cycles (named epochs) is begun.

In each epoch, reproduction and mutation operators are applied a certain amount of times to evolve the actual population. The reproduction selects two individuals (each one with many possible strategies, like tournament selection) and operates with probability $p_c$, a crossover exchanging random genes, in homologous positions, of the chromosomes. Tournament selection randomly takes pairs of individuals and selects the one with best fitness. After reproduction has taken place, each individual is mutated with probability $p_m$: mutation modifies one gene of the individual with a random value, with the objective of creating individuals that may explore other parts of the solution space and avoid local minima.

Each individual of the population is then evaluated by means of the fitness function and the smaller one is considered as a viable solution if it is below a specified threshold: the individual with the best fitness is the output and the process terminates. If no acceptable solution is found, then the population is updated and a new epoch is started over. The update may take place replacing the whole old population with the new offspring, or the new individuals may replace the worst ones in the old population, or tournament selection may be performed to select the individuals from the new population.

To avoid cycling infinitely, a maximum number of epochs is defined; if no solution is found within a specified number of cycles, the process terminates signaling the failure and possibly returns the best solution found up to that point.

In our algorithm, the GA examines one subimage at a time and evolves a population of individuals each composed of pixel modifications (namely values in the set $\left\{-2,-1,0,1,2\right\}$); the fitness function takes into account two aspects: the final modified subimage must contain the watermark (embedded in the subimage KLT coefficients), and the squared error w.r.t. of the original subimage should be as small as possible. The use of the GA solves the problem of storing the correct watermark and minimizes the distortion by finding a (quasi) optimal solution.

4. The Proposed Algorithm

4.1. Overview

The proposed algorithm works on color images with an alpha channel (RGBA images).

The characteristics and properties of the presented algorithm are:

• good localization ability;
• high security against attacks and modifications to the watermarked images;
• only the modification of the alpha channel necessary to store the watermark, leaving unaltered the RGB channels;
• a high peak signal-to-noise ratio (more than 66 dB) for the watermarked images.

The host image is divided into contiguous non-overlapping blocks (i.e., subimages) of size $n\times n$: we call each block a smallest localization block (SLB). Each SLB is composed of $n\times n\times 4$ pixels because the image has four channels; therefore, an image of size $N\times M$ will be made up of $NM/n^2$ SLBs (we assume $N$ and $M$ to be a multiple of $n$ to simplify the description of the algorithm; it is possible to define various methods in order to deal with non-multiple dimensions).

To perform the watermarking operation, $b$ watermark bits are stored (hidden) in each SLB; in this case we say that the payload is $b$ bits-per-block (bpb). Thus the total watermark length will be $bNM/n^2$ bits.

During the embedding phase, the pixels in the alpha channel of each SLB are modified in such a way that the respective $b$ bits are stored in the coefficients of the SLB KLT. The rule used to extract the watermark bit values from the coefficients is presented in the following.

In order to verify the integrity of the watermarked image, a watermark verification step is performed on each SLB, as described in detail in Section 4.5 below.

4.2. Application of the KLT

The KLT is applied independently to each SLB. There are many ways in which the SLB pixels may be transformed by the KLT; in the present algorithm we use a weighted channel combination extended to comprise the alpha channel.

Let us call $p_R$, $p_G$, $p_B$ and $p_A$ the values of each pixel in the red, green, blue and alpha channels respectively; the linear combination with the respective weights $w_R$, $w_G$, $w_B$ and $w_A$ produces the value

$$q=w_R{p}_R+w_G{p}_G+w_B{p}_B+w_A{p}_A$$

(7)

Note that this is just an arbitrary linear combination of pixel values, that transforms a four-channel image block into a greyscale image block. This can be applied to any color model (RGBA, YCbCr, YIQ, etc.) without influencing the localization ability and the resulting image quality of the method.

Ordering these values in a raster scan order of the pixels and arranging them in a column vector leads to vectors of the size $n^2$ representing an SLB:

$$\overrightarrow{\mathit{q}}={\left[\begin{array}{ccc}{q}^{\left(1\right)}& q^{\left(2\right)}& \begin{array}{cc}\dots & q^{\left(n^2\right)}\end{array}\end{array}\right]}^{\prime }$$

(8)

The vectors derived from the SLBs of an image may be considered as a set from which to compute a KLT basis of size $n^2$ and may also be linearly transformed using a KLT basis (not necessarily the one computed using the vectors themselves).

The embedding algorithm is composed of two steps: the first one, called key generation, is performed once to generate a secret KLT kernel basis. This basis is used many times to watermark many host images. The second step, called integrity protection, is performed every time a host image must be watermarked in order to be protected.

4.3. Key Generation

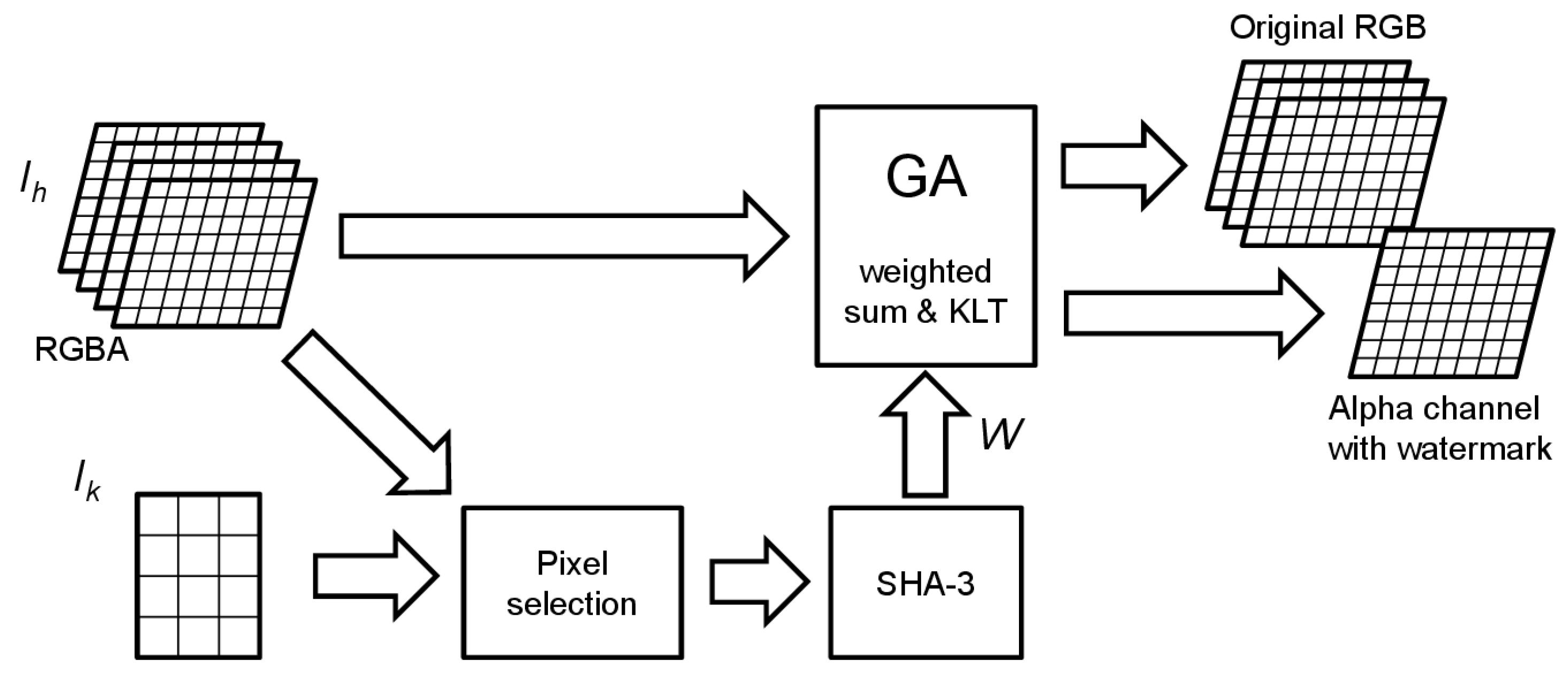
In this step, an image $I_k$ (gray scale or color) is used to create a KLT basis of $n^2$ basis images of size $n\times n$ using its SLBs. This image must be kept secret to ensure the security of the method, because it defines the space in which the watermark lays.

The secret image is divided into contiguous non-overlapping subimages of size $n\times n$ (in the case of color images the channels are considered separately, creating a larger set of vectors, or the channels may be linearly combined as in Equation (1) to obtain $n^2$ values and from them a KLT basis and mean vector are computed, as explained in the Background section and depicted in Figure 2.

The basis and the mean vector are employed both during watermark embedding and verification.

4.4. Integrity Protection

In this section we present the steps involved in the fragile watermarking of a host image. They are the generation of the watermark (made dependent on both the key $I_k$ and host $I_h$ images), the watermark embedding (to deliver the image that will be protected and that may be published) and the watermark verification (which checks and locate possible forgeries or alterations to the image).

4.4.1. Watermark Generation

When a host image $I_h$ must be protected against unauthorized modifications, it is embedded with a watermark $W$, dependent on $I_k$ and $I_h$, to cope with copy-and-paste attacks and transplantation attacks [24]. The set of pixels in $I_h$ used to create $W$ must not be altered during embedding; otherwise, during verification, it will not be possible to extract the correct $W$ and the watermarked image will be detected as forged even if it is not.

Note also that an attack modifying at least one of the pixels used in creating $W$ will completely alter the watermark built during verification: this will result in the detection of almost all subimages as forged. In this case the attack is revealed, but the localization capability is lost; to contrast this eventuality, we suggest keeping the set of pixels used in $I_h$ as small as possible (typically four pixels).

The selected pixels are used to initialize a secure cryptographic hash function, like SHA-3, and to produce a bit-string sequence of the required length (Figure 3 depicts a sketch of this procedure).

4.4.2. Watermark Embedding

The host image $I_h$ is divided into SLBs and each of them, for example in raster scan order, is assigned consecutive $b$ bits of $W$. Then, the respective bits are stored in each SLB by means of a genetic algorithm (GA) (see Figure 4).

The idea behind the embedding of the watermark into a SLB is based on the following two principles:

Embedding strategy: The GA looks for a modification of the SLB pixel values such that the watermark bits are contained in the KLT coefficients of the SLB.

Embedding rule: A KLT coefficient $c$ is said to contain a bit with value $t$ in position $p$ if and only if in its binary representation the $p$-th bit has value $t$, i.e.,

$$c\mathrm{stores}t\iff t=integer\left(c·2^{-p}\right)\mathrm{mod}2$$

(9)

Thus, $b$ consecutive KLT coefficients are selected to store $b$ bits in an SLB. We experimentally found that apart from the first two coefficients, whose modification could lead to a low PSNR, all the other coefficients are available for embedding; therefore, we used $b$ consecutive coefficients starting from the third.

The GA evolves a population of individuals coding pixel modifications: each individual is applied to the alpha channel values only (leaving the RGB channels unaltered), then the weighted Equation (1) is computed for all pixels producing a vector of $n^2$ elements; these values are then transformed using the secret KLT basis and mean computed in the key generation phase (see Figure 5). The GA fitness function evaluates

• if the $b$ coefficients contain the watermark bits, and
• the PSNR of the modified SLB

and the population is evolved looking for the best individual satisfying the first constraint with the highest PSNR. When it finds a viable solution, the modification is applied to the original SLB, producing a watermarked SLB.

When the embedding process is completed for all the SLBs in the host image, the result is the watermarked image $I_w$.

4.5 Watermark Verification

The verification (Figure 6) is performed to locate possible alterations and forgeries of a watermarked image $I_w$.

Firstly, the key image $I_k$ and the watermarked image $I_w$ are used to compute the expected watermark string. Then $I_w$ is divided into SLBs, and each one is transformed, after computing the weighted Equation (1), with the KLT, using the mean and the basis derived from $I_k$. From the resulting coefficients, which depend on all the pixel values in the four RGBA channels, the embedded $b$ bits in each SLB are decoded and compared with the corresponding bits in the watermark. Any bit difference evidences an SLB as forged, localizing the modification (trivially, xor-ing the two bit strings, the one valued bits of the result evidence differences).

5. Experimental Results

In this section we report and analyze the results of applying the proposed algorithm to a set of images.

The algorithm was evaluated according to the following parameters:

• Peak signal-to-noise ratio (PSNR), which for eight bit-per-channel images is computed as

  $$\mathrm{PSNR}=10{\log }_{10}\frac{{255}^2}{MSE}$$

  (10)

  where $MSE$ represents the mean squared error, that is the average of the squared error between the host and the watermarked images, involving the difference between pixel channel (RGBA) values in homologous positions;
• Mean absolute error (MAE), which is the average absolute difference between the host and the watermarked images, considering the difference between pixel channel (RGBA) values in homologous positions;
• Sensitivity: as in [13] we define the sensitivity of level $D$ as the fraction of tampered blocks detected by the algorithm when a single pixel in one of the block channels (RGBA) is altered by $D$ levels (positive or negative).

The weighting coefficients in (1) were set to $w_R=1.13$, $w_G=1.97$, $w_B=2.93$ and $w_A=3.93$, but other values are possible given that their function is to linearly combine four values into one.

The settings for the GA were the following: population size $=100$, $p_c=0.9$, $p_m=0.06$, maximum generations $=2000$. This setting was found optimal from a large experiment aimed at speed of convergence, the ability to find a viable solution and the quality of the resulting image.

In the presented tests, the block size was set to $n=8$ (i.e., the blocks were composed of $8\times 8\times 4$ pixels). We also conducted tests with $n=4$ to improve the localization capability, and we found that the values of the performance parameters did not change significantly; nonetheless we feel that the used block size (along with the resulting detection capability) may be considered sufficient for a large part of all applications.

We first watermarked a set of $29$ PNG sticker RGBA images of the Telegram application [25,26], which were publicly available and had a non-trivial alpha channel. The results are reported in

Table 1. The performance of the proposed algorithm on a set of RGBA images publicly available.

Payload (bpb)	PSNR (dB)	WPSNR (dB)	MAE	Sensitivity ± 1 (%)	Sensitivity ± 2 (%)
8	66.61 ± 0.14	73.72 ± 0.18	0.057 ± 0.0018	78.78 ± 0.81	91.37 ± 0.31
12	64.81 ± 0.06	71.49 ± 0.08	0.086 ± 0.001	84.90 ± 0.36	96.16 ± 0.12

, for two different values of payload. It is worth noting that the reported (W) PSNR is computed considering all RGBA channels, being $\infty$ if computed on RGB channels only, as the algorithm does not modify any RGB pixel values. As concerns running times, watermark embedding takes an average of 23.66 ± 1.75 s with a payload of 8 bpb, and 33.55 ± 2.21 s with a payload of 12 bpb on a Dell XPS with an Intel(R) Core(TM) i7-3517U CPU @ 1.90GHz (Dell Inc., Round Rock, TX, USA). Watermark verification is much faster as it takes less than 0.05 s on average per image.

Moreover, Table 1 (sensitivity columns) reports the percentage of SLBs the algorithm detects as tampered when a single pixel in the block has been modified by ±1 or ±2 grey levels, respectively. It should be pointed out that this kind of tampering is the smallest possible alteration an attacker can perform on the watermarked image, and if an algorithm can detect this, it surely can detect larger modifications, as those derived from JPEG compression, distortion, and other image processing operations. When an attacker modifies more than one pixel in several SLBs, the probability of not recognizing a tampered image decreases exponentially in the number of actually-tampered SLBs.

To our knowledge, there are not many watermarking algorithms used for integrity protection of images with alpha channel. We compare with [20], which proposes a data-hiding method with an application to data authentication, and with [21], which inserts a watermark into the two LSBs of the alpha channel. Both settings are different from ours because they assume that the image is RGB and add the alpha channel to save the data integrity information. Our algorithm, instead, slightly modifies an existing alpha channel, and thus has a wider range of applications to images of any kind. The advantage of [20] is an authentication at the pixel level, whilst ours, as well as [21], is at the block level: nonetheless, when [20] uses three bits to authenticate every single pixel, the probability of not detecting an attack to a pixel is $12.5\%$ (i.e., $1/2^3$).

By comparing the performance of the proposed algorithm with [20,21], we found that apart from an $\infty$ PSNR when computed on the three RGB channels only (because both algorithms do not modify them), the values of the MAE for the alpha channel computed by the proposed algorithm, reported in

Table 2. Comparison of MAE values for some images.

Image	MAE
	Lee et al. [20]	Bandyopadhyay et al. [21]	Proposed Algorithm
Baboon	0.723	~1.5	0.0560
Lena	0.720	~1.5	0.0558
F-16	0.721	~1.5	0.0561
Tiffany	0.721	~1.5	0.0558

, are one order of magnitude smaller than those in [20]. As concerns [21], the MAE is ~ 1.5 (we can only estimate this value by saying that on average every pixel in the alpha channel is modified by 1.5 grey levels, because the authors do not report any measurements in the alpha channel).

The images used in the comparison were obtained, as in [20,21], from the original RGB images (of size $512\times 512$ pixels) by adding a completely opaque alpha channel (i.e., having pixel values equal to $255$).

We performed tests on a larger set of 500 images comprising those in Table 2 and the average value of MAE for our algorithm was $0.056$ with a standard deviation of $0.0005$, not only proving the high quality of the watermarked images but also the stability of the results independently of the image. Moreover, the low impact of the proposed algorithm on the alpha channel w.r.t. the modifications induced by [20,21] can be seen.

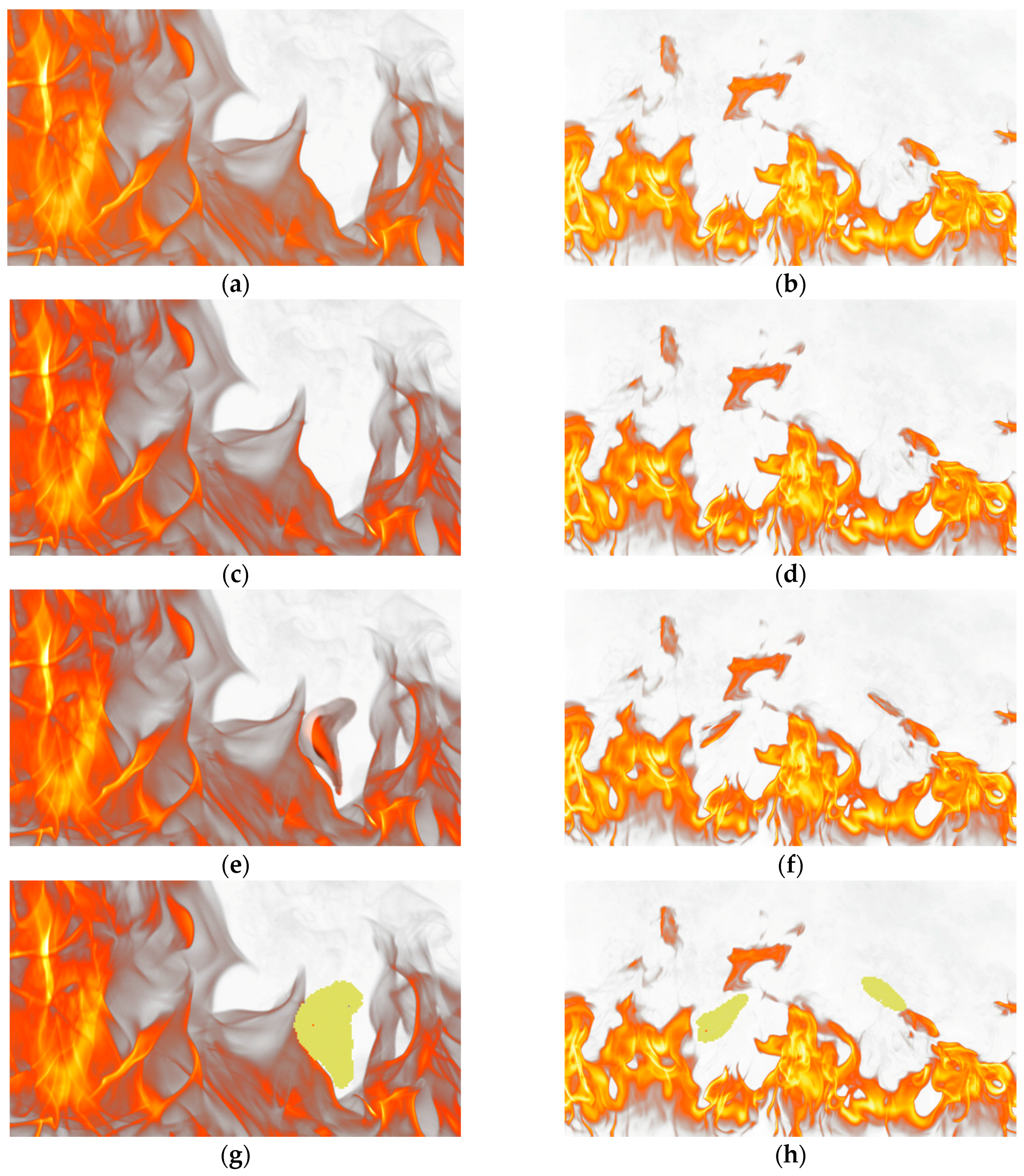
Figure 7 shows an example of the watermarking and detection process on two images. Figure 7a,b are the host images, while Figure 7c,d are the watermarked images. Figure 7e,f are tampered images, to which we added a couple of flames, and Figure 7g,h show the results of the detection process. Due to the very high PSNR (the RGB channels are untouched), it is impossible to notice any difference between the host and watermarked images.

6. Security Considerations and Conclusions

The algorithm presented may be used to fragile watermark images with an alpha channel: it may operate in two ways, namely by modifying the pixel values of the four channels or of a single channel, in particular the alpha channel.

In the present embodiment, we only modified the transparency channel, both to leave the color information unaltered, and to make a comparison with existing data-hiding algorithms [20,21].

The advantage of the proposed algorithm is that it may deal with an existing alpha channel by performing very small modifications to it, as may be inferred from the tables reported in the experimental section.

The method is flexible and the localization capability may be improved by reducing the SLB size to $4\times 4$ pixels.

The proposed method is secure due to the secrecy of the key image and to the use of the KLT.

First of all, the watermark is a secret bit-string, because it is produced by a cryptographic hash function initialized by secret data depending on the secret key image $I_k$. Secondly, the watermark is embedded into a secret space defined by a linear transformation kernel computed from $I_k$. Thus, the watermark cannot be extracted without the key image, so an attacker cannot modify an SLB and re-embed the correct watermark.

Making the watermark also dependent on the host image avoids copy-and-paste attacks, because SLBs of two different host images in the same position will, with high probability, embed different watermarks, thus they cannot be interchanged without being unnoticed in the verification step.

Strictly related to the previous consideration is the possibility that the substitution of a random SLB may go undetected. If the payload is $b$ bpb, then there is a probability of $1/2^b$ that a randomly-chosen SLB may be substituted for the correct one without being detected. This probability rapidly decreases as $b$ increases. Moreover, the probability that in an image the random substitution of $m$ SLBs goes undetected for all of them is $1/2^{mb}$, which exponentially decreases as $m$ increases.

To cope with crop attacks, or any other attack that may change the dimensions of the watermarked image, the size of the host image may also be used in the initialization of the cryptographic hash function for the watermark generation: in the case of such attacks the watermark computed during verification will be different from the original one and almost all SLBs will be flagged as forged.

As a last consideration, considering a modification involving a pixel used in the watermark generation will reveal the attack but will vanish the localization capability, because almost all SLBs will be marked as forged. In any case, making the watermark dependent on a small set of pixels reduces this eventuality and will also provide a hint as to where the attack was probably performed when almost all SLBs are flagged as tampered.