Color Texture Image Retrieval Based on Local Extrema Features and Riemannian Distance
Abstract
1. Introduction
2. Local Texture Representation and Description Using Local Extrema Features
2.1. Approach
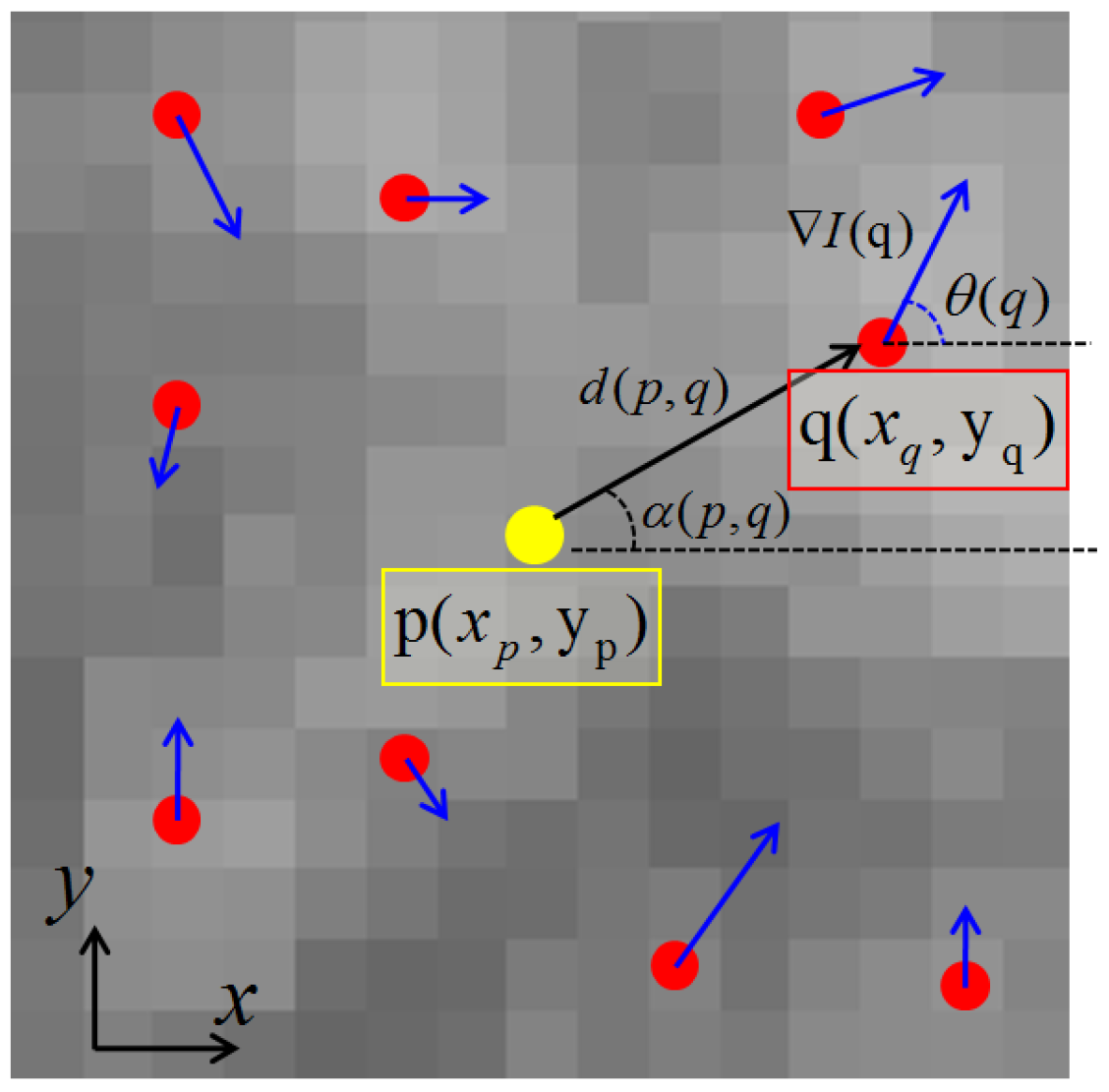
2.2. Generation of Local Extrema-Based Descriptor (LED)
- fix the number (N) of nearest local maxima and nearest local minima for each one;
- or, fix a window size around each keypoint; then, all local maxima and minima inside that window are considered.
- Mean and variance of three color channels:where represents the three color components and is the cardinality of the set .
- Mean and variance of spatial distances from each local maximum to point p:where is the spatial distance between two points p and q on the image plane. We remind readers that and .
- Circular variance [38] of angles of geometric vectors formed by each local maximum and point p:where
- Mean and variance of gradient magnitudes:where is the gradient magnitude image obtained by applying the Sobel filter on the gray-scale version of the image.
3. Proposed Framework for Texture and Color Image Retrieval
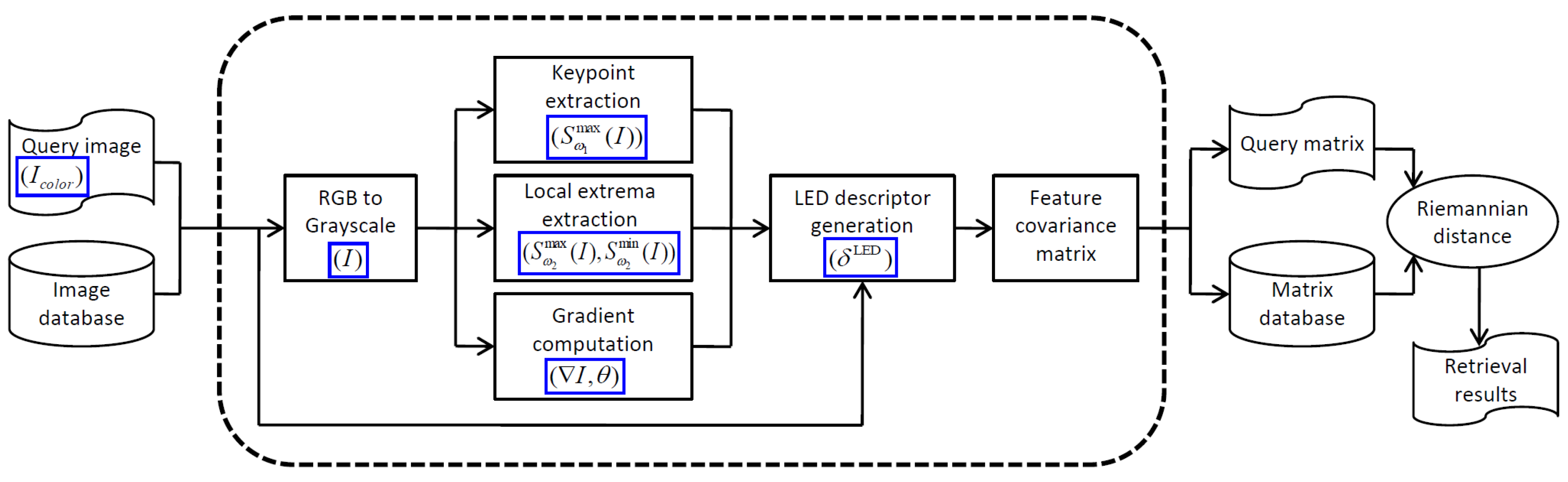
3.1. LED Feature Extraction
3.2. Dissimilarity Measure for Retrieval
3.3. Proposed Retrieval Framework
- Load the query color image .
- Convert the image to grayscale I.
- Compute gradient images from I:
- +
- () for the 27D version,
- +
- () for the enhanced 33D version.
- Extract the keypoint set and the two local extrema sets from I:
- +
- keypoint set: ,
- +
- extrema sets: and .
- Generate LED descriptors for all keypoints:
- +
- , extract as (12).
- Estimate the feature covariance matrice for these LED descriptors.
- Compute the Riemannian distance (15) between the query and the other images from the database.
- Sort these distance measures and produce the best matches as the final retrieval result for the query.
4. Experimental Study
4.1. Image Databases
4.2. Evaluation Criteria
4.3. Results and Discussion
4.3.1. Performance in Retrieval Accuracy
4.3.2. Computation Time
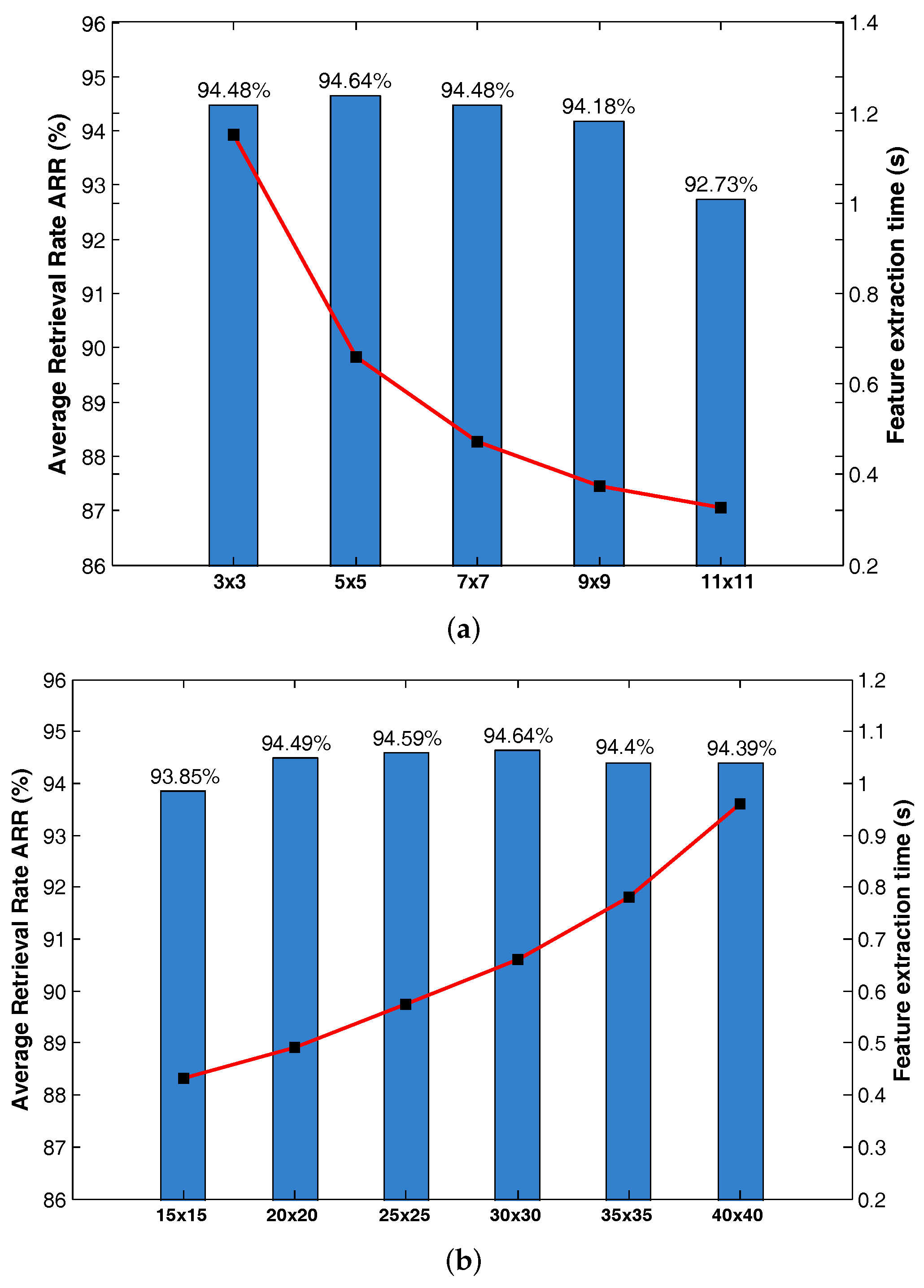
4.3.3. Sensitivity Analysis
4.3.4. Sensitivity to Distance Measure
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Alzu’bi, A.; Amira, A.; Ramzan, N. Semantic content-based image retrieval: A comprehensive study. J. Vis. Commun. Image Represent. 2015, 32, 20–54. [Google Scholar] [CrossRef]
- Dharani, T.; Aroquiaraj, I.L. A survey on content based image retrieval. In Proceedings of the 2013 International Conference on Pattern Recognition, Informatics and Mobile Engineering (PRIME), Salem, India, 21–22 February 2013; pp. 485–490. [Google Scholar]
- Veltkamp, R.; Burkhardt, H.; Kriegel, H.P. State-of-the-Art in Content-Based Image and Video Retrieval; Springer Science & Business Media: New York, NY, USA, 2013; Volume 22. [Google Scholar]
- Do, M.N.; Vetterli, M. Wavelet-based texture retrieval using generalized Gaussian density and Kullback- Leibler distance. IEEE Trans. Image Process. 2002, 11, 146–158. [Google Scholar] [CrossRef] [PubMed]
- Kokare, M.; Biswas, P.K.; Chatterji, B.N. Texture image retrieval using new rotated complex wavelet filters. IEEE Trans. Syst. Man Cybern., Part B Cybern. 2005, 35, 1168–1178. [Google Scholar] [CrossRef]
- Kwitt, R.; Uhl, A. Image similarity measurement by Kullback-Leibler divergences between complex wavelet subband statistics for texture retrieval. In Proceedings of the 15th IEEE International Conference on Image Processing, ICIP 2008, San Diego, CA, USA, 12–15 October 2008; pp. 933–936. [Google Scholar]
- Kwitt, R.; Uhl, A. Lightweight probabilistic texture retrieval. IEEE Trans. Image Process. 2010, 19, 241–253. [Google Scholar] [CrossRef] [PubMed]
- Choy, S.K.; Tong, C.S. Statistical wavelet subband characterization based on generalized gamma density and its application in texture retrieval. IEEE Trans. Image Process. 2010, 19, 281–289. [Google Scholar] [CrossRef] [PubMed]
- Lasmar, N.E.; Berthoumieu, Y. Gaussian copula multivariate modeling for texture image retrieval using wavelet transforms. IEEE Trans. Image Process. 2014, 23, 2246–2261. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Huang, Y.; Zhu, L. Color texture image retrieval based on Gaussian copula models of Gabor wavelets. Pattern Recognit. 2017, 64, 118–129. [Google Scholar] [CrossRef]
- Verdoolaege, G.; De Backer, S.; Scheunders, P. Multiscale colour texture retrieval using the geodesic distance between multivariate generalized Gaussian models. In Proceedings of the 15th IEEE International Conference on Image Processing, ICIP 2008, San Diego, CA, USA, 12–15 October 2008; pp. 169–172. [Google Scholar]
- Kwitt, R.; Meerwald, P.; Uhl, A. Efficient texture image retrieval using copulas in a Bayesian framework. IEEE Trans. Image Process. 2011, 20, 2063–2077. [Google Scholar] [CrossRef] [PubMed]
- Ojala, T.; Pietikäinen, M.; Mäenpää, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Zhang, B.; Gao, Y.; Zhao, S.; Liu, J. Local derivative pattern versus local binary pattern: face recognition with high-order local pattern descriptor. IEEE Trans. Image Process. 2010, 19, 533–544. [Google Scholar] [CrossRef] [PubMed]
- Subrahmanyam, M.; Maheshwari, R.; Balasubramanian, R. Local maximum edge binary patterns: A new descriptor for image retrieval and object tracking. Signal Process. 2012, 92, 1467–1479. [Google Scholar] [CrossRef]
- Tan, X.; Triggs, B. Enhanced local texture feature sets for face recognition under difficult lighting conditions. IEEE Trans. Image Process. 2010, 19, 1635–1650. [Google Scholar] [PubMed]
- Murala, S.; Maheshwari, R.; Balasubramanian, R. Local tetra patterns: A new feature descriptor for content- based image retrieval. IEEE Trans. Image Process. 2012, 21, 2874–2886. [Google Scholar] [CrossRef] [PubMed]
- Verma, M.; Raman, B. Local tri-directional patterns: A new texture feature descriptor for image retrieval. Digit. Signal Process. 2016, 51, 62–72. [Google Scholar] [CrossRef]
- Murala, S.; Wu, Q.J.; Balasubramanian, R.; Maheshwari, R. Joint histogram between color and local extrema patterns for object tracking. In Proceedings of the IS&T/SPIE Electronic Imaging, International Society of Optics and Photonics, Burlingame, CA, USA, 19 March 2013. [Google Scholar]
- Jacob, I.J.; Srinivasagan, K.; Jayapriya, K. Local oppugnant color texture pattern for image retrieval system. Pattern Recognit. Lett. 2014, 42, 72–78. [Google Scholar] [CrossRef]
- Verma, M.; Raman, B.; Murala, S. Local extrema co-occurrence pattern for color and texture image retrieval. Neurocomputing 2015, 165, 255–269. [Google Scholar] [CrossRef]
- Qiu, G. Color image indexing using BTC. IEEE Trans. Image Process. 2003, 12, 93–101. [Google Scholar] [PubMed]
- Gahroudi, M.R.; Sarshar, M.R. Image retrieval based on texture and color method in BTC-VQ compressed domain. In Proceedings of the 9th International Symposium on Signal Processing and Its Applications, ISSPA 2007, Sharjah, United Arab Emirates, 12–15 February 2007; pp. 1–4. [Google Scholar]
- Yu, F.X.; Luo, H.; Lu, Z.M. Colour image retrieval using pattern co-occurrence matrices based on BTC and VQ. Electron. Lett. 2011, 47, 100–101. [Google Scholar] [CrossRef]
- Guo, J.M.; Prasetyo, H.; Su, H.S. Image indexing using the color and bit pattern feature fusion. J. Vis. Commun. Image Represent. 2013, 24, 1360–1379. [Google Scholar] [CrossRef]
- Guo, J.M.; Prasetyo, H. Content-based image retrieval using features extracted from halftoning-based block truncation coding. IEEE Trans. Image Process. 2015, 24, 1010–1024. [Google Scholar] [PubMed]
- Guo, J.M.; Prasetyo, H.; Chen, J.H. Content-based image retrieval using error diffusion block truncation coding features. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 466–481. [Google Scholar]
- Guo, J.M.; Prasetyo, H.; Wang, N.J. Effective Image Retrieval System Using Dot-Diffused Block Truncation Coding Features. IEEE Trans. Multimedia 2015, 17, 1576–1590. [Google Scholar] [CrossRef]
- Li, C.; Duan, G.; Zhong, F. Rotation Invariant Texture Retrieval Considering the Scale Dependence of Gabor Wavelet. IEEE Trans. Image Process. 2015, 24, 2344–2354. [Google Scholar]
- Pham, M.T.; Mercier, G.; Michel, J. Pointwise graph-based local texture characterization for very high resolution multispectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1962–1973. [Google Scholar] [CrossRef]
- Pham, M.T.; Mercier, G.; Michel, J. PW-COG: An effective texture descriptor for VHR satellite imagery using a pointwise approach on covariance matrix of oriented gradients. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3345–3359. [Google Scholar] [CrossRef]
- Pham, M.T.; Mercier, G.; Regniers, O.; Michel, J. Texture Retrieval from VHR Optical Remote Sensed Images using the Local Extrema Descriptor with Application to Vineyard Parcel Detection. Remote Sens. 2016, 8, 368. [Google Scholar] [CrossRef]
- Pham, M.T.; Mercier, G.; Michel, J. Textural features from wavelets on graphs for very high resolution panchromatic Pléiades image classification. Revue française de photogrammétrie et de télédétection 2014, 208, 131–136. [Google Scholar]
- Pham, M.T.; Mercier, G.; Michel, J. Change detection between SAR images using a pointwise approach and graph theory. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2020–2032. [Google Scholar] [CrossRef]
- Pham, M.T.; Mercier, G.; Regniers, O.; Bombrun, L.; Michel, J. Texture retrieval from very high resolution remote sensing images using local extrema-based descriptors. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; IEEE: Beijing, China, 2016; pp. 1839–1842. [Google Scholar]
- Förstner, W.; Moonen, B. A metric for covariance matrices. In Geodesy-The Challenge of the 3rd Millennium; Springer: Berlin, Germany, 2003; pp. 299–309. [Google Scholar]
- Vision Texture. MIT Vision and Modeling Group. Available online: http://vismod.media.mit.edu/pub/VisTex/ (accessed on 1 October 2017).
- Mardia, K.V.; Jupp, P.E. Directional Statistics; John Wiley and Sons, Ltd.: Chichester, UK, 2000. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. SURF: Speeded up robust features. In Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Tuytelaars, T.; Mikolajczyk, K. Local invariant feature detectors: A survey. Found. Trends Comput. Graph. Vis. 2008, 3, 177–280. [Google Scholar] [CrossRef]
- Dryden, I.L.; Koloydenko, A.; Zhou, D. Non-Euclidean statistics for covariance matrices, with applications to diffusion tensor imaging. Ann. Appl. Stat. 2009, 3, 1102–1123. [Google Scholar] [CrossRef]
- Frery, A.C.; Nascimento, A.D.; Cintra, R.J. Analytic expressions for stochastic distances between relaxed complex Wishart distributions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1213–1226. [Google Scholar] [CrossRef]
- Kwitt, R.; Meerwald, P. Salzburg Texture Image Database. Available online: http://www.wavelab.at/sources/STex/ (accessed on 1 October 2017).
- Abdelmounaime, S.; Dong-Chen, H. New Brodatz-Based Image Databases for Grayscale Color and Multiband Texture Analysis. ISRN Mach. Vis. 2013, 2013. [Google Scholar] [CrossRef]
- USPTex dataset (2012). Scientific Computing Group. Available online: http://fractal.ifsc.usp.br/dataset/USPtex.php (accessed on 1 October 2017).
- Outex Texture Database. University of Oulu. Available online: http://www.outex.oulu.fi/index.php?page=classificationOutexTC00013 (accessed on 1 October 2017).
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, Preprint. arXiv:1409.1556. [Google Scholar]
- Cusano, C.; Napoletano, P.; Schettini, R. Evaluating color texture descriptors under large variations of controlled lighting conditions. JOSA A 2016, 33, 17–30. [Google Scholar] [CrossRef] [PubMed]
- Napoletano, P. Hand-Crafted vs Learned Descriptors for Color Texture Classification. In Proceedings of the International Workshop on Computational Color Imaging, Milan, Italy, 29–31 March 2017; Springer: Berlin, Germany, 2017; pp. 259–271. [Google Scholar]
- Subrahmanyam, M.; Wu, Q.J.; Maheshwari, R.; Balasubramanian, R. Modified color motif co-occurrence matrix for image indexing and retrieval. Comput. Electr. Eng. 2013, 39, 762–774. [Google Scholar] [CrossRef]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary robust invariant scalable keypoints. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 3–13 November 2011; pp. 2548–2555. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary robust independent elementary features. In Computer Vision–ECCV 2010; Springer: Berlin, Germany, 2010; pp. 778–792. [Google Scholar]
- Southam, P.; Harvey, R. Texture classification via morphological scale-space: Tex-Mex features. J. Electron. Imag. 2009, 18, 043007. [Google Scholar] [CrossRef]
- Desai, A.; Lee, D.J.; Ventura, D. Matching affine features with the SYBA feature descriptor. In International Symposium on Visual Computing; Springer: Berlin, Germany, 2014; pp. 448–457. [Google Scholar]
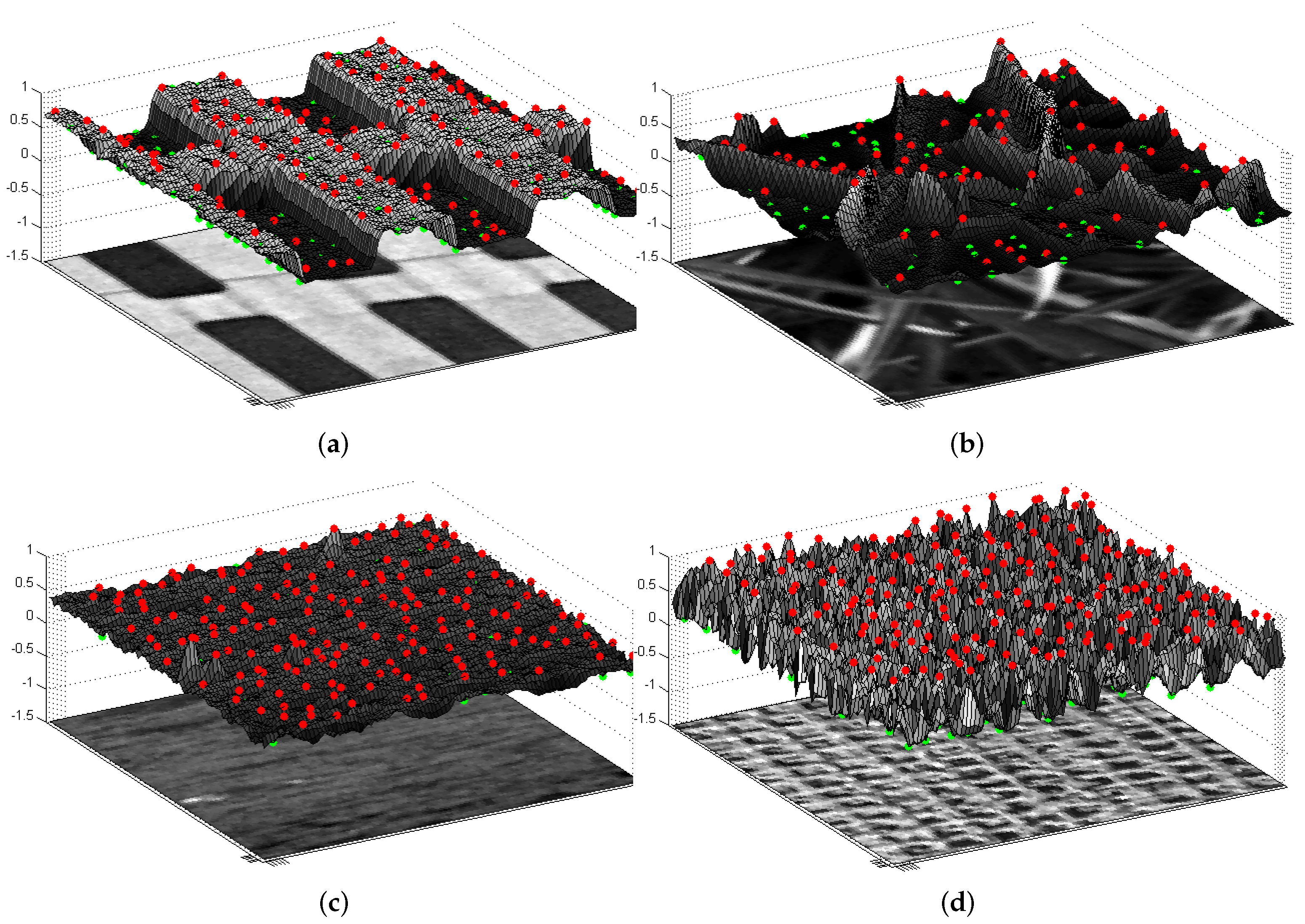


| Database | Number of Classes | Number of Images/Class | Total Number |
|---|---|---|---|
| Vistex-640 | 40 | 16 | 640 |
| Stex-7616 | 476 | 16 | 7616 |
| CBT-2800 | 112 | 25 | 2800 |
| USPtex-2292 | 191 | 12 | 2292 |
| Outex-1380 | 68 | 20 | 1380 |
| Method | Using Color | ARR (%) |
|---|---|---|
| GT+GGD+KLD [4] | - | 76.57 |
| DT-CWT [5] | - | 80.78 |
| DT-CWT+DT-RCWT [5] | - | 82.34 |
| MGG+Gaussian+KLD [11] | √ | 87.40 |
| MGG+Laplace+GD [11] | √ | 91.70 |
| DCT+MGMM [7] | - | 84.94 |
| Gaussian Copula+Gamma+ML [12] | √ | 89.10 |
| Gaussian Copula+Weibull+ML [12] | √ | 89.50 |
| Student-t Copula+GG+ML [12] | √ | 88.90 |
| LMEBP [15] | - | 87.77 |
| Gabor LMEBP [15] | - | 87.93 |
| LtrP [17] | - | 90.02 |
| Gabor LtrP [17] | - | 90.16 |
| LEP+colorhist [19] | √ | 82.65 |
| MCMCM+DBPSP [52] | √ | 86.17 |
| Gaussian Copula-MWbl [9] | - | 84.41 |
| ODBTC [26] | √ | 90.67 |
| Gaussian Copula+Gabor Wavelet [10] | √ | 92.40 |
| EDBTC [27] | √ | 92.55 |
| DDBTC [28] | √ | 92.65 |
| LECoP [21] | √ | 92.99 |
| ODII [25] | √ | 93.23 |
| CNN-AlexNet [51] | √ | 91.34 |
| CNN-VGG16 [51] | √ | 92.97 |
| CNN-VGG19 [51] | √ | 93.04 |
| Proposed LED+RD (27D) | √ | 94.64 |
| Proposed LED+RD (33D) | √ | 94.70 |
| Class | 27D | 33D | Class | 27D | 33D |
|---|---|---|---|---|---|
| Bark.0000 | 76.95 | 75.00 | Food.0008 | 100.00 | 100.00 |
| Bark.0006 | 98.05 | 98.05 | Grass.0001 | 94.53 | 93.36 |
| Bark.0008 | 83.20 | 84.38 | Leaves.0008 | 99.61 | 100.00 |
| Bark.0009 | 77.13 | 78.13 | Leaves.0010 | 100.00 | 100.00 |
| Brick.0001 | 100.00 | 99.22 | Leaves.0011 | 100.00 | 100.00 |
| Brick.0004 | 97.66 | 98.05 | Leaves.0012 | 55.86 | 56.25 |
| Brick.0005 | 100.00 | 100.00 | Leaves.0016 | 86.72 | 86.72 |
| Buildings.0009 | 100.00 | 100.00 | Metal.0000 | 98.83 | 99.61 |
| Fabric.0000 | 100.00 | 100.00 | Metal.0002 | 100.00 | 100.00 |
| Fabric.0004 | 76.95 | 77.34 | Misc.0002 | 100.00 | 100.00 |
| Fabric.0007 | 99.61 | 99.61 | Sand.0000 | 100.00 | 100.00 |
| Fabric.0009 | 100.00 | 100.00 | Stone.0001 | 82.42 | 82.42 |
| Fabric.0011 | 100.00 | 100.00 | Stone.0004 | 90.63 | 91.02 |
| Fabric.0014 | 100.00 | 100.00 | Terrain.0010 | 94.92 | 95.31 |
| Fabric.0015 | 100.00 | 100.00 | Tile.0001 | 91.80 | 89.45 |
| Fabric.0017 | 96.48 | 97.66 | Tile.0004 | 100.00 | 100.00 |
| Fabric.0018 | 98.83 | 100.00 | Tile.0007 | 100.00 | 100.00 |
| Flowers.0005 | 100.00 | 100.00 | Water.0005 | 100.00 | 100.00 |
| Food.0000 | 100.00 | 100.00 | Wood.0001 | 96.88 | 96.88 |
| Food.0005 | 99.22 | 99.22 | Wood.0002 | 88.28 | 90.23 |
| ARR | 94.64 | 94.70 |
| Method | Using Color | ARR (%) |
|---|---|---|
| GT+GGD+KLD [4] | - | 49.30 |
| DT-CWT+Weibull+KLD [6] | - | 58.80 |
| MGG+Laplace+GD [11] | √ | 71.30 |
| DWT+Gamma+KLD [8] | - | 52.90 |
| Gaussian Copula+Gamma+ML [12] | √ | 69.40 |
| Gaussian Copula+Weibull+ML [12] | √ | 70.60 |
| Student-t Copula+GG+ML [12] | √ | 65.60 |
| LEP+colorhist [19] | √ | 59.90 |
| DDBTC [28] | √ | 44.79 |
| LECoP [21] | √ | 74.15 |
| Gaussian Copula+Gabor Wavelet [10] | √ | 76.40 |
| CNN-AlexNet [51] | √ | 68.84 |
| CNN-VGG16 [51] | √ | 74.92 |
| CNN-VGG19 [51] | √ | 73.93 |
| Proposed LED+RD (27D) | √ | 79.95 |
| Proposed LED+RD (33D) | √ | 80.08 |
| Method | Using Color | ARR (%) |
|---|---|---|
| LBP [13] | - | 81.75 |
| LtrP [17] | - | 82.05 |
| LOCTP-YCbCr [20] | √ | 84.46 |
| LOCTP-HSV [20] | √ | 88.60 |
| LOCTP-LAB [20] | √ | 88.90 |
| LOCTP-RGB [20] | √ | 93.89 |
| CNN-AlexNet [51] | √ | 90.72 |
| CNN-VGG16 [51] | √ | 91.64 |
| CNN-VGG19 [51] | √ | 90.36 |
| Proposed LED+RD (27D) | √ | 99.06 |
| Proposed LED+RD (33D) | √ | 98.79 |
| Method | UPStex-2292 | Outex-1360 |
|---|---|---|
| DDBTC () [28] | 63.19 | 61.97 |
| DDBTC () [28] | 55.38 | 57.51 |
| DDBTC () [28] | 73.41 | 65.54 |
| DDBTC (Canberra) [28] | 74.97 | 66.82 |
| CNN-AlexNet [51] | 83.57 | 69.87 |
| CNN-VGG16 [51] | 85.03 | 72.91 |
| CNN-VGG19 [51] | 84.22 | 73.20 |
| Proposed LED+RD (27D) | 90.22 | 76.54 |
| Proposed LED+RD (33D) | 90.50 | 76.67 |
| Method | Feature Dimension |
|---|---|
| DT-CWT [4] | = 40 |
| DT-CWT+DT-RCWT [4] | = 80 |
| LBP [13] | 256 |
| LTP [16] | |
| LMEBP [15] | |
| Gabor LMEBP [15] | |
| LEP+colorhist [19] | |
| LECoP() [21] | |
| LECoP() [21] | |
| LECoP() [21] | |
| ODII [25] | 128 + 128 = 256 |
| CNN-AlexNet [51] | 4096 |
| CNN-VGG16 [51] | 4096 |
| CNN-VGG19 [51] | 4096 |
| Proposed LED+RD (27D) | 27 |
| Proposed LED+RD (33D) | 33 |
| Version | FE Time (s) | DM Time (s) | Total Time (s) | ARR (%) | |||
|---|---|---|---|---|---|---|---|
| 27D | 422.8 | 0.661 | 22.3 | 0.035 | 445.1 | 0.695 | 94.64 |
| 33D | 476.6 | 0.745 | 28.1 | 0.044 | 504.7 | 0.789 | 94.70 |
| Method | Feature Dimension | Extraction Time (ms) |
|---|---|---|
| SIFT [39] | 128 | 538.6 |
| SURF [40] | 64 | 162.2 |
| BRISK [53] | 64 | 8.2 |
| BRIEF [54] | 32 | 3.2 |
| Proposed LED (27D) | 27 | 1298.7 |
| Proposed LED (33D) | 33 | 1476.3 |
| Distance Measure | Formula | (s) | (ms) | ARR (%) |
|---|---|---|---|---|
| Taking into account mean feature vectors | ||||
| Simplified Mahalanobis | 40.51 | 63.30 | 90.48 | |
| Symmetric Kullback–Leibler | 47.10 | 73.59 | 91.82 | |
| Not accounting for mean feature vectors | ||||
| Log-euclidean | 20.21 | 31.58 | 72.65 | |
| Bartlett | 27.03 | 42.23 | 76.51 | |
| Wishart-like | 37.79 | 59.90 | 92.39 | |
| Riemannian | , where | 22.34 | 34.91 | 94.64 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, M.-T.; Mercier, G.; Bombrun, L. Color Texture Image Retrieval Based on Local Extrema Features and Riemannian Distance. J. Imaging 2017, 3, 43. https://doi.org/10.3390/jimaging3040043
Pham M-T, Mercier G, Bombrun L. Color Texture Image Retrieval Based on Local Extrema Features and Riemannian Distance. Journal of Imaging. 2017; 3(4):43. https://doi.org/10.3390/jimaging3040043
Chicago/Turabian StylePham, Minh-Tan, Grégoire Mercier, and Lionel Bombrun. 2017. "Color Texture Image Retrieval Based on Local Extrema Features and Riemannian Distance" Journal of Imaging 3, no. 4: 43. https://doi.org/10.3390/jimaging3040043
APA StylePham, M.-T., Mercier, G., & Bombrun, L. (2017). Color Texture Image Retrieval Based on Local Extrema Features and Riemannian Distance. Journal of Imaging, 3(4), 43. https://doi.org/10.3390/jimaging3040043






