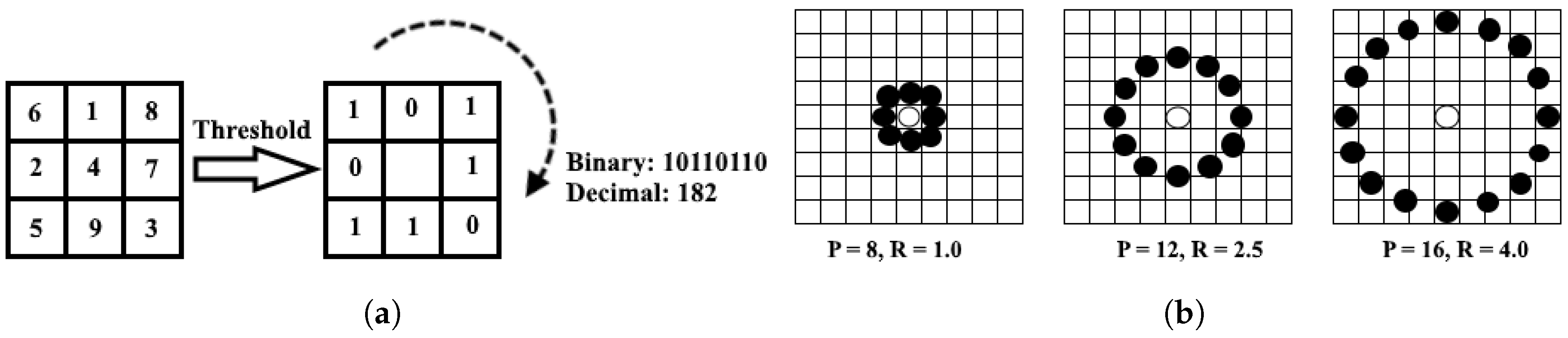
1. Introduction
Object recognition is a computer technology related to computer vision and image processing that deals with detecting and identifying humans, buildings, cars, etc., in digital images and video sequences. It is a huge domain including face recognition which basically has two different modes: verification and identification [
1]. In this paper, we focus on the identification basic mode.
A face is a typical multidimensional structure and needs good computational analysis for recognition. The overall problem is to be able to accurately recognize a person’s identity and take some actions based on the outcome of the recognition process. Recognizing a person’s identity is important mainly for security reasons, but it could also be used to obtain quick access to medical, criminal, or any type of records. Solving this problem is important because it could allow people to take preventive action, provide better service in the case of a doctor appointment, allow users access to a secure area, and so forth.
Face identification is the process of identifying a person in a digital image or video, and showing their authentication identity. Identification is a one-to-many matching process that compares a query face image against all the template images inside the face database in order to determine the identity of the query face. Identification mode allows both positive and negative recognition outcomes, but the results are much more computationally costly if the template database is large [
2,
3]. Now, our goal is to determine which person inside the gallery—if any—is represented by the query face. More precisely, when a particular query image is submitted to the recognition system, the resulting normal map is compressed in order to compute its feature indexes, which are subsequently used to reduce the search to a cluster of similar normal maps selected through a visit in the k-d-tree [
4].
In the past several years, academia and industry have developed many research works and practical approaches to overcome face recognition issues, specifically in pattern recognition and computer vision domains [
5]. Facial recognition is a difficult problem due to the morphology of the face that can vary easily under the influence of many factors, such as pose, illumination, and expression [
3]. In addition, faces have similar form and the same local parts (eyes, cheekbones, nose, lips, etc.). Therefore, to enhance the ability of a system to identify facial images, we need to apply an efficient algorithm that can describe the similarity representation and distinctive classification properties of diverse subject images.
As we mentioned above, local binary patterns (LBP) and k-nearest neighbor (K-NN) are among the famous proposed solutions available today.
For a decade, LBP was only used for texture classification; now it is also widely used to solve some of the common face recognition issues. LBP has many important properties, such as its robustness against any monotonic transformation of the gray scale, and its computational simplicity, which makes it possible to analyze images in challenging real-time settings [
6].
The greater accuracy of k-nearest neighbor (K-NN) in image classification problems is highlighted; it is commonly used for its easier interpretation and low calculation time [
7,
8]. The main aim of LBP and K-NN in this work is to extract features and classify different LBP histograms, respectively, in order to ensure good matching between the extracted features histograms and provide a greater identification rate.
This paper is organized as follows:
Section 2 elaborates on some prior works. In
Section 3, we present the fundamental background.
Section 4 details our proposed methodology.
Section 5 analyses our experiments and Results, and finally, we conclude in
Section 6.
2. Prior Works
Over the past decades, there have been many studies and algorithms proposed to deal with face identification issues. Basically, the identification face is marked by similarity; authors in [
9] measured the similarity between entire faces of multiple identities via Doppelganger List. It is claimed that the direct comparisons between faces are required only in similar imaging conditions, where they are actually feasible and informative. In the same way, Madeena et al. [
10] presents a novel normalization method to obtain illumination invariance. The proposed model can recognize face images regardless of the face variations using a small number of features.
In [
2], Sandra Mau et al. proposed a quick and widely applicable approach for converting biometric identification match scores to probabilistic confidence scores, resulting in increased discrimination accuracy. This approach works on 1-to-N matching of a face recognition system and builds on a confidence scoring approach for binomial distributions resulting from Hamming distances (commonly used in iris recognition).
In 2015, Pradip Panchal et al. [
11] proposed Laplacian of Gaussian (LoG) and local binary pattern as face recognition solutions. In this approach, the extracted features of each face region are enhanced using LoG. In fact, the main purpose of LoG is to make the query image more enhanced and noise free. In our opinion, authors should use a Gaussian filter before applying LoG, since the combination of these two algorithms would provide better results than the ones obtained. Following the same way, authors in [
12,
13] also used LBP technique. In [
12], the face recognition performance of LBP is investigated under different facial expressions, which are anger, disgust, fear, happiness, sadness, and surprise. Facial expression deformations are challenging for a robust face recognition system; thus, the study gives an idea about using LBP features to expression invariant. Further, authors in [
13] implemented LBP and SSR (single scale retinex) algorithms for recognizing face images. In this work, lighting changes were normalized and the illumination factor from the actual image was removed by implementing the SSR algorithm. Then, the LBP feature extraction histograms could correctly match with the most similar face inside the database. The authors claimed that applying SSR and LBP algorithms gave powerful performance for illumination variations in their face recognition system.
Bilel Ameur et al. [
14] proposed an approach where face recognition performance is significantly improved by combining Gabor wavelet and LBP for features extraction and, K-NN and SRC for classification. The best results are obtained in terms of time consumption and recognition rate; the proposed work also proved that the system efficiency depends on the size of the reduced vector obtained by the dimension reduction technique. However, Dhriti et al. [
7] revealed the higher performance and accuracy of K-NN in classification images. In the same way as [
7], authors in [
8] used K-NN as the main classification technique and bagging as the wrapping classification method. Based on the powerful obtained outcomes, the proposed model demonstrated the performance and capabilities of K-NN to classify images.
Nowadays, research is not only focalized on face recognition in constrained environments; many authors also are trying to resolve face recognition in unconstrained environments.
The works [
15,
16,
17] proposed a convolutional neural network (CNN) as a solution of the face recognition problem in unconstrained environments. Deep learning provides much more powerful capabilities to handle two types of variations; it is essential to learn such features by using two supervisory signals simultaneously (i.e., the face identification and verification signals), and the learned features are referred to as Deep IDentification-verification features (DeepID2) [
15]. The paper showed that the effect of the face identification and verification supervisory signals on deep feature representation coincide with the two aspects of constructing ideal features for face recognition (i.e., increasing inter-personal variations and reducing intra-personal variations), and the combination of the two supervisory signals led to significantly better features than either one of them individually. Guosheng Hu et al. [
16] presented a rigorous empirical evaluation of CNN based on face recognition systems. Authors quantitatively evaluated the impact of different CNN architectures and implementation choices on face recognition performances on common ground. The work [
17] proposed a new supervision signal called center loss for face recognition task; the proposed center loss is used to improve the discriminative power of the deeply learned features. Combining the center loss with the softmax loss to jointly supervise the learning of CNNs, the discriminative power of the deeply learned features can be highly enhanced for robust face recognition.
4. Proposed Approach
The proposed face identification system is based on the combination of the robust uniform local binary Ppattern and k-nearest neighbor. Face recognition is not a simple problem, since an unknown face image seen in the extraction phase is usually different from the face image seen in the classification phase. The main aim of this work is to solve the identification problem through face images which can vary easily under the influence of pose, illumination, and expression. The face image is divided into a grid of small non-overlapping regions, where the global LBP histogram of a particular face image is obtained by combining the histogram sequence of each non-overlapping region; explicitly, the global features are collected in single vector and therefore classified using the k-nearest neighbor algorithm. The Euclidean distance finds the minimum distance between histogram images. After comparing two individual histograms, if there is any similarity distance, it means they are related, and otherwise, not.
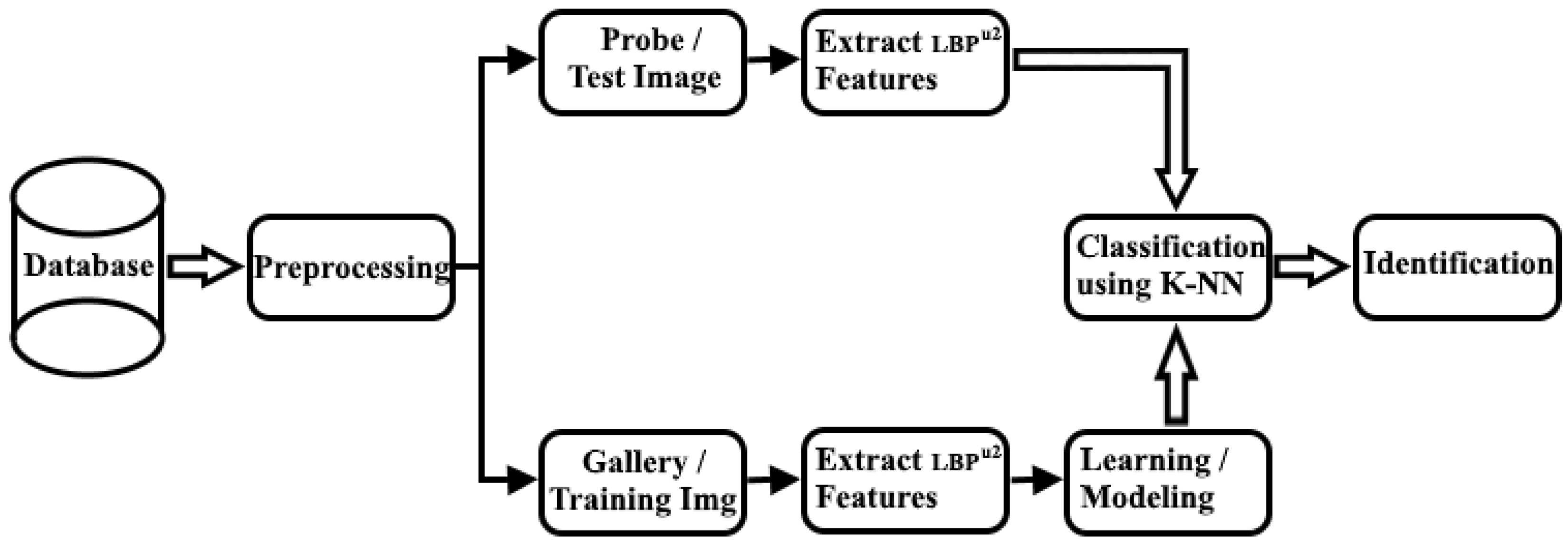
Figure 3 below displays our process diagram.
Our proposed system contains two principal stages before the junction:
Start:
Face database
Preprocessing
First stage:
Input gallery images (training images)
Collection of the extraction features using uniform LBP algorithm
Learning or modeling via the LBP histogram
Second stage:
Junction:
End:
4.1. Preprocessing Phase
Consists of registering all images inside the database. The main aim of this phase is to improve the image data by suppressing unwanted distortions or enhancing important image features for further processing. Sometimes images have many lacks in contrast and brightness due to different limitations of imaging sub-systems and illumination conditions while capturing the image; techniques to resolve these issues include: contrast stretching, noise filtering, and histogram modification. Only noise filtering is applied in our work, after image registration. In definition, noise filtering is used to remove the unnecessary information from the image while preserving the underlying structure and the original texture under diverse lightning conditions. There are various types of filters available today, such as low-pass, high-pass, mean, median, etc.
Gaussian Filters Used as Low Pass Filters
One of the major problems that face recognition has to deal with is variations in illumination. Many studies have been explored to reduce, normalize, and ameliorate the effect caused by illumination variations. A Gaussian filter used as a low-pass filter is an appropriate method for carrying out illumination reduction and remove the lighting changes; its main purpose is to suppress all noise in the image. Another important property of Gaussian filters is that they are non-negative everywhere; this is important because most 1D signals vary about
and can have either positive or negative values. Images are different in the sense that all values of one image are non-negative
. Thus, convolution with a Gaussian filter guarantees a non-negative result, so the function maps non-negative values to other non-negative values
; the result is always another valid image. Digital images are composed of two frequency components: low (illumination) and high (noise). The Gaussian mathematical function implemented in this work is:
where
is the Gaussian low-pass filter of size
x and
y, with standard deviation
(positive).
4.2. Feature Extraction Phase
The LBP algorithm is a method of damage reduction technology that represents a discrimination of an interesting part of the face image in a compact feature vector. When the pre-processing phase is achieved, the LBP algorithm is applied to the segments in order to obtain a specific feature histogram. A focus on the feature extraction phase is essential because it has an observable impact on recognition system efficiency. The selection of our feature extraction method is the single most important factor to achieve higher recognition performance; that is why we used uniform LBP to extract useful features as it generates a more precise recognition rate and makes the process simpler and more effective. Hence, the application of suitable neighbor-sets for different values of needs to be done with utmost care.
4.3. Learning or Modeling Phase
Learning or modeling via LBP histogram is used to fit a model of the appearance of face images in the gallery, so that we can be able to know the discrimination between the faces of different subjects inside the database. In order to improve processing time, the extracted distance vectors are sorted in increasing order. In our framework, the learning step forms tightly packed conglomerates of visual feature histograms at detailed scales. These are determined by a form of configuration feature set, implying that the processing part reveals the similarity between features histograms. The characteristics of the processing part will be made explicit during matching in the classification phase.
4.4. K-NN Classifier
K-NN is the simplest of all machine learning and classification algorithms, and stores all available cases and classifies new cases based on a similarity measure. Therefore, the value K is used to perform classification by computing the simple histogram similarities. In this context, our good K value is selected by applying a K-fold cross-validation approach in order to estimate the optimum K. Further, each image of a set of visual features will find the best matching feature set between the test and all the training images.
5. Experiments and Results
To verify the robustness and optimum of our method, experiments were carried out on two huge databases: CMU PIE and LFW. Our proposed Algorithm 1 was conducted on an Intel Core i5-2430M CPU 2.40 GHz Windows 10 machine with 6 GB memory, and implemented in MATLAB R2016b. The performance of our proposed algorithm showed a powerful identification rate on the CMU PIE dataset.
| Algorithm 1: Proposed Algorithm |
Initialize temp = 0 For each image I inside the database Apply Gaussian low pass filter (G) Divide the database into training and test sets For each image inside the sets Extract LBP features End For k-nearest neighbours (K value) are then found by analysing the Euclidean distance matrix Find similarity between LBP histograms The most common class label is then assigned to the successfully recognized image
|
Our face databases are very influential and common in studies of face recognition across pose, illumination, and expression variations. We used the image of the five nearly frontal poses (P05, P07, P09, P27, P29), a subset of 11,560 face images with 170 images per person on the CMU PIE dataset; and used around 6000 face images on the LFW dataset.
Firstly, we preprocessed our database due to the different illumination variations, and then applied the Gaussian filter before feature extractions in order to remove noises in the image to get a real LBP histogram of each image. Euclidian distance calculates the distance matrix between two images so that the image can be classified by a majority vote of its neighbors.
In our framework, we showed the performance of the Gaussian filter used as low-pass filter, which is an appropriate method for noise filtering. Here, the filter size used was different for each dataset. For the CMU PIE dataset we used
as the size with
, and
as the size with
for the LFW dataset. The higher filter size on LFW is due to the fact that it is an unconstrained or uncontrolled environment database and each image contains much more noise than images in a constrained or controlled environment (CMU PIE). Thus, the calculation and application of Gaussian parameters must be done with utmost care. After applying the filter, we obtain an enhanced image without noise; it is important to note that the Gaussian filter has the same role inside our databases. The filter size and
are the same for all images inside a specific database. For instance,
Figure 4 illustrates:
Figure 4a is the image before applying the Gaussian filter (Original image), associated with its corresponding
histogram;
Figure 4b is the image after applying the Gaussian filter (Filtered image), with the corresponding
histogram. The Gaussian filter removes all of the undesirable artifact (noise). Thus, we obtained an unmistakable image compared to
Figure 4a. Moreover, the histograms in
Figure 4a and
Figure 4b are different; in
Figure 4b, applying the filter is beneficial to get higher and more precise features (real histogram image without noise) than
Figure 4a. Therefore, Gaussian’s difference can increase the visibility of edges and other details present in a digital image.
Figure 5 reveals the identification results of four people across the pose, illumination, and expression variations and accessories (wearing glasses). As we can see, all the subjects were correctly matched. Particularly, the subject in
Figure 5a has a correct matching even in a reverse image, with incomplete face appearance and lighting change. Whereas, subjects in
Figure 5b–d, displayed correct matching with different facial expressions: blinking and wearing glasses, talking, and smiling with lighting change, respectively.
Finally, in
Figure 6, the incorrect matching is less distinguishable—especially for the subject in
Figure 6a,b, where the resemblance between probe image and gallery image (incorrectly matched) is extremely close. However, there are some cases where the failures are very blatant (
Figure 6b,c), since the displayed images are chosen randomly inside the different sets.
For overall results,
Table 1 describes the different outcomes obtained during the experiments. Maximum accuracy and powerful performance were achieved by implementing
on CMU PIE (99.26%) and
K = 4 on LFW (85.71%).
Table 2 and
Table 3 describe the comparison of our results against many existing ones in both controlled and unconstrained environments, respectively.
The novelty in this research effort is that the combination of LBP, K-NN algorithms, and Gaussian filter is applied to increase and enhance our face identification rate. Furthermore, our method proved that the performance of the proposed model can be validated using one controlled environment database (CMU PIE). In order to reinforce our experiments, we used one unconstrained database (i.e., LFW). The obtained result shows that our proposed algorithm compared to the innovative solutions produced approximatively the same results.