Deep Learning-Based Algorithm for the Classification of Left Ventricle Segments by Hypertrophy Severity
Abstract
1. Introduction
1.1. Motivation and Background
1.2. Objectives and Contributions
2. Related Research
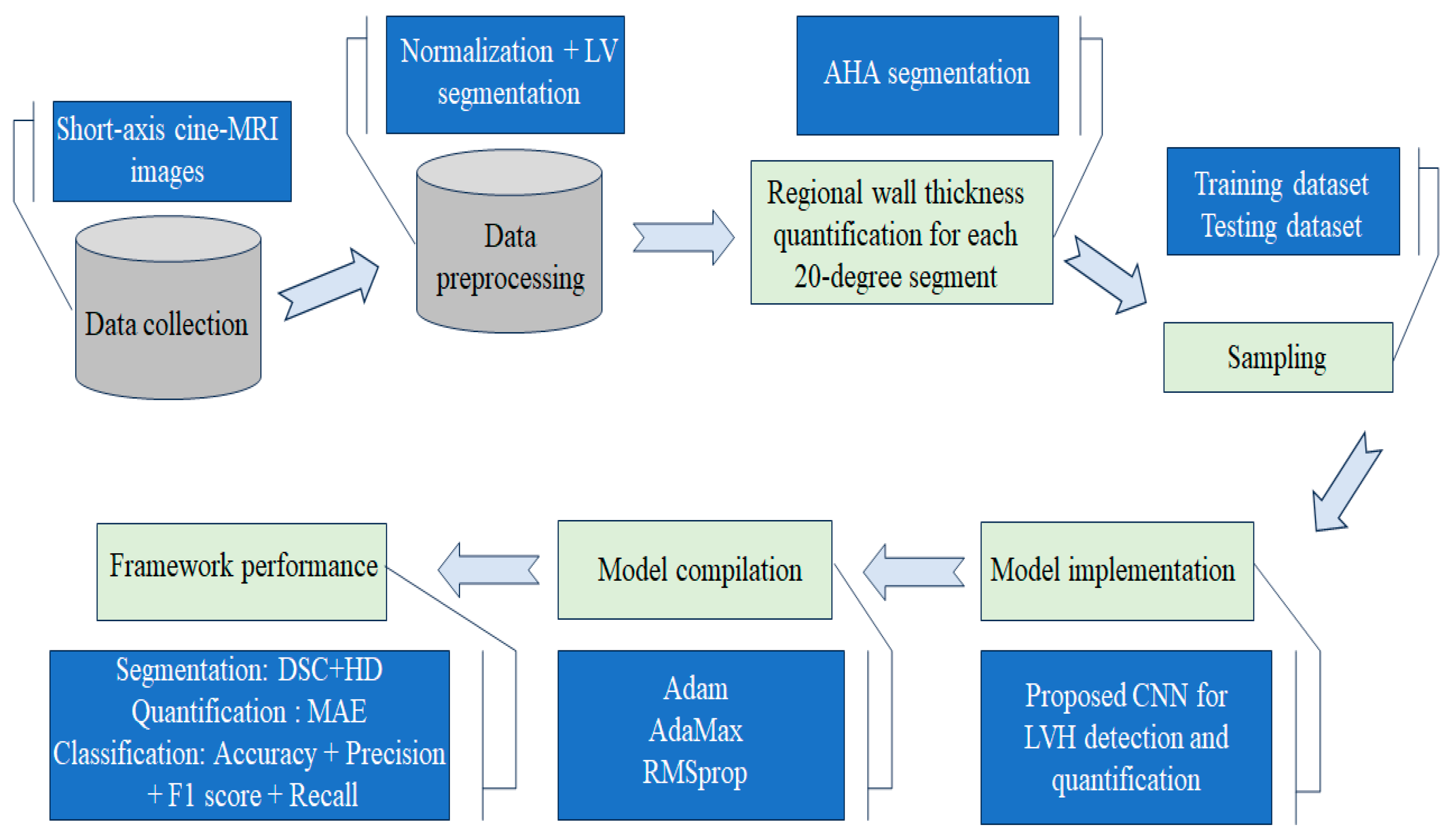
3. Materials and Methods
3.1. Study Design
3.2. Study Population and CMR Acquisition
3.3. Data Preprocessing
3.3.1. Min-Max Normalization
3.3.2. Automatic Segmentation of Short-Axis Cine-MR Images Using Deep Learning
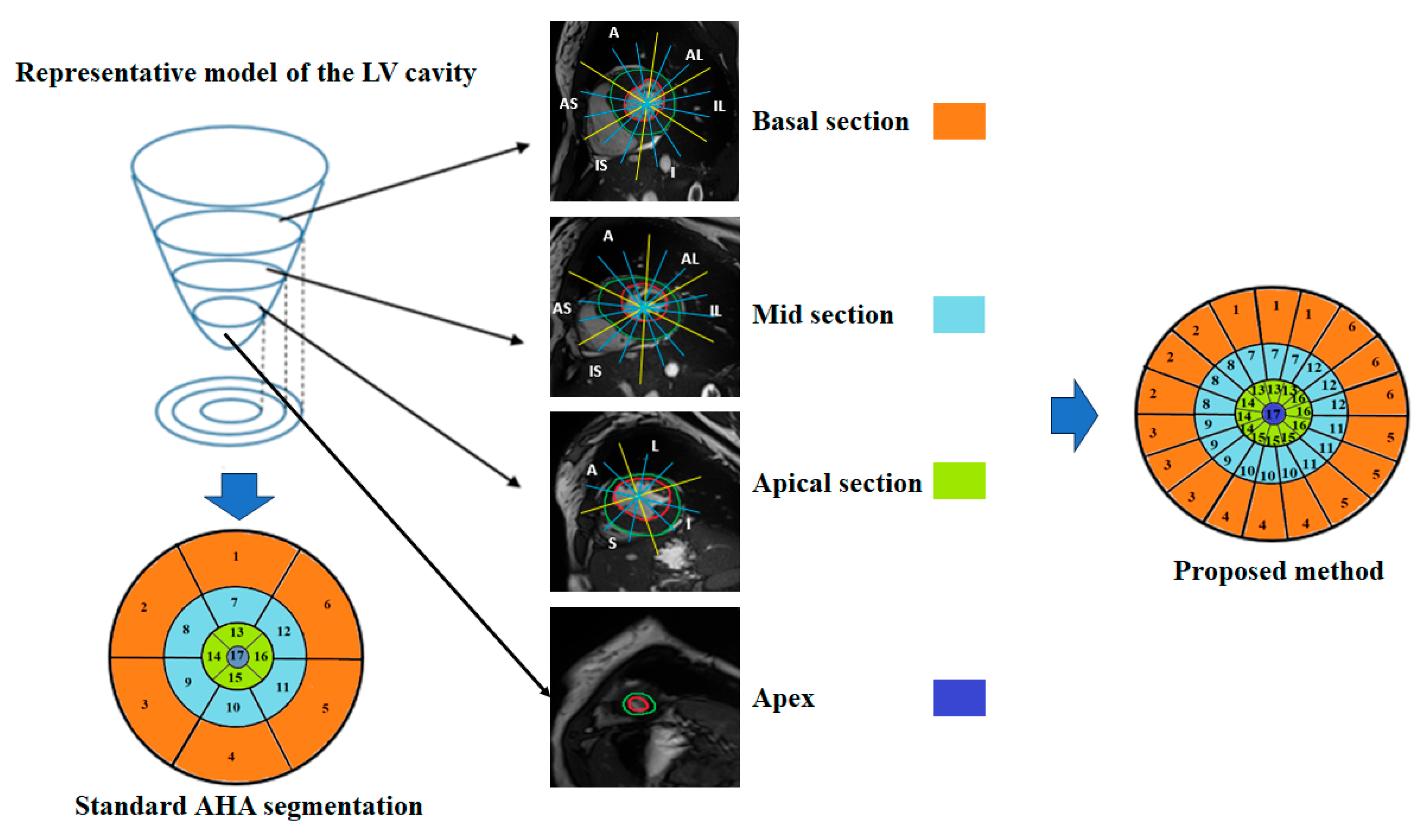
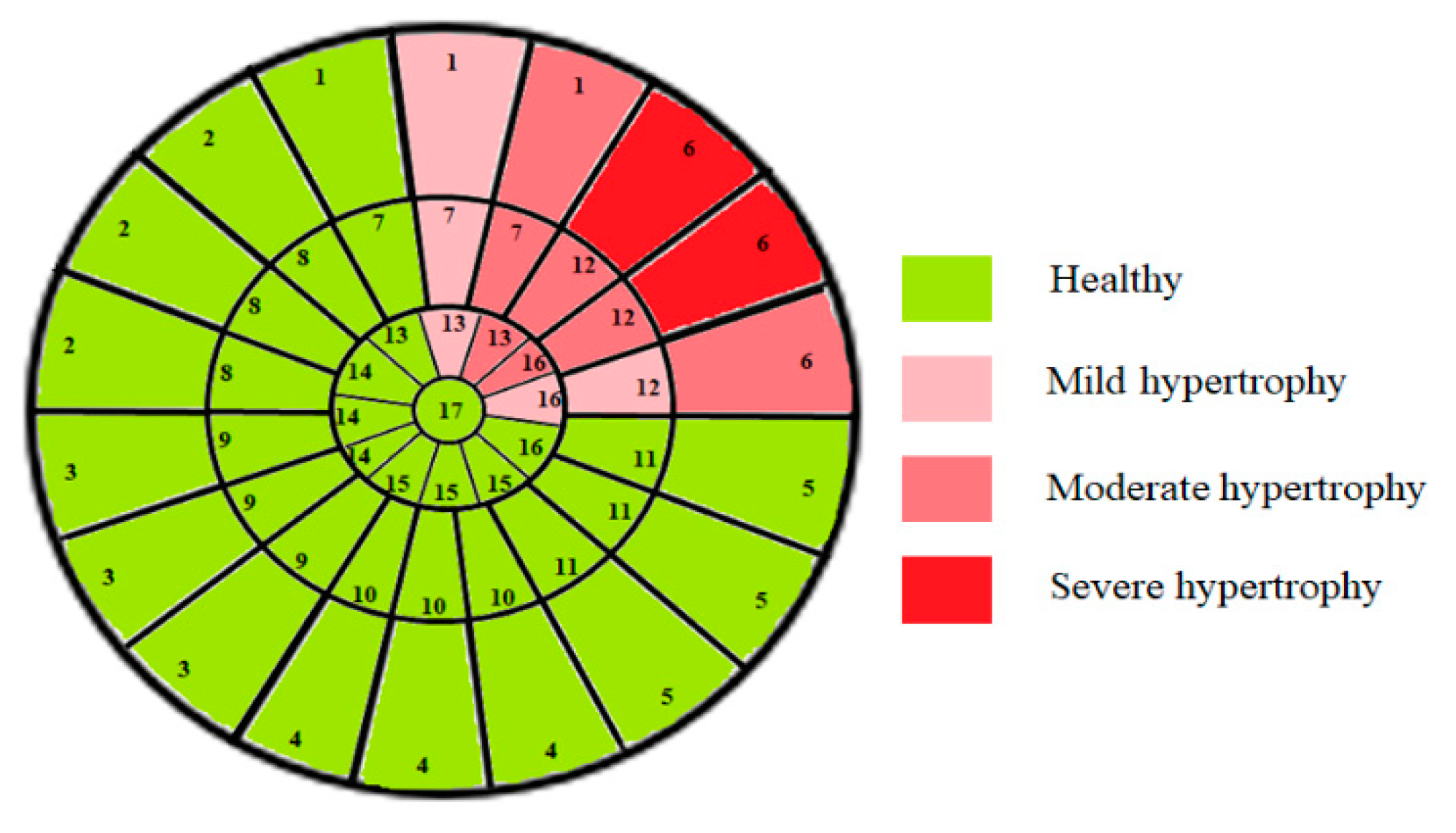
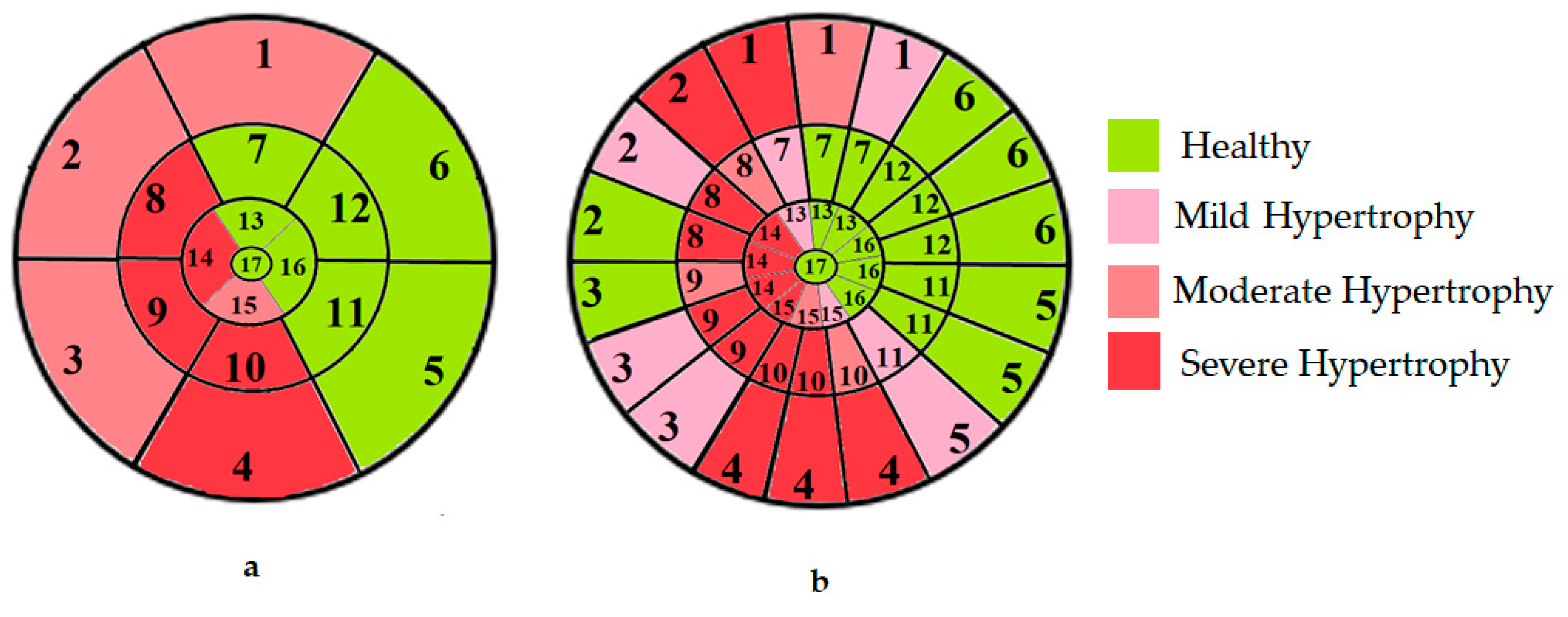
3.4. Automatic Regional Wall Thickness Quantification
3.5. Proposed Convolutional Neural Network for LVH Detection and Quantification
3.5.1. Ground Truth and Data Sampling
- Score 0 was assigned to healthy myocardial sub-segments characterized by a wall thickness < 15 mm.
- Score 1 was assigned to sub-segments with mild hypertrophy characterized by a wall thickness in the range [15 mm, 20 mm].
- Score 2 was assigned to sub-segments with moderate hypertrophy characterized by a wall thickness in the range [20 mm, 25 mm].
- Score 3 was assigned to sub-segments with severe hypertrophy characterized by a wall thickness > 25 mm.
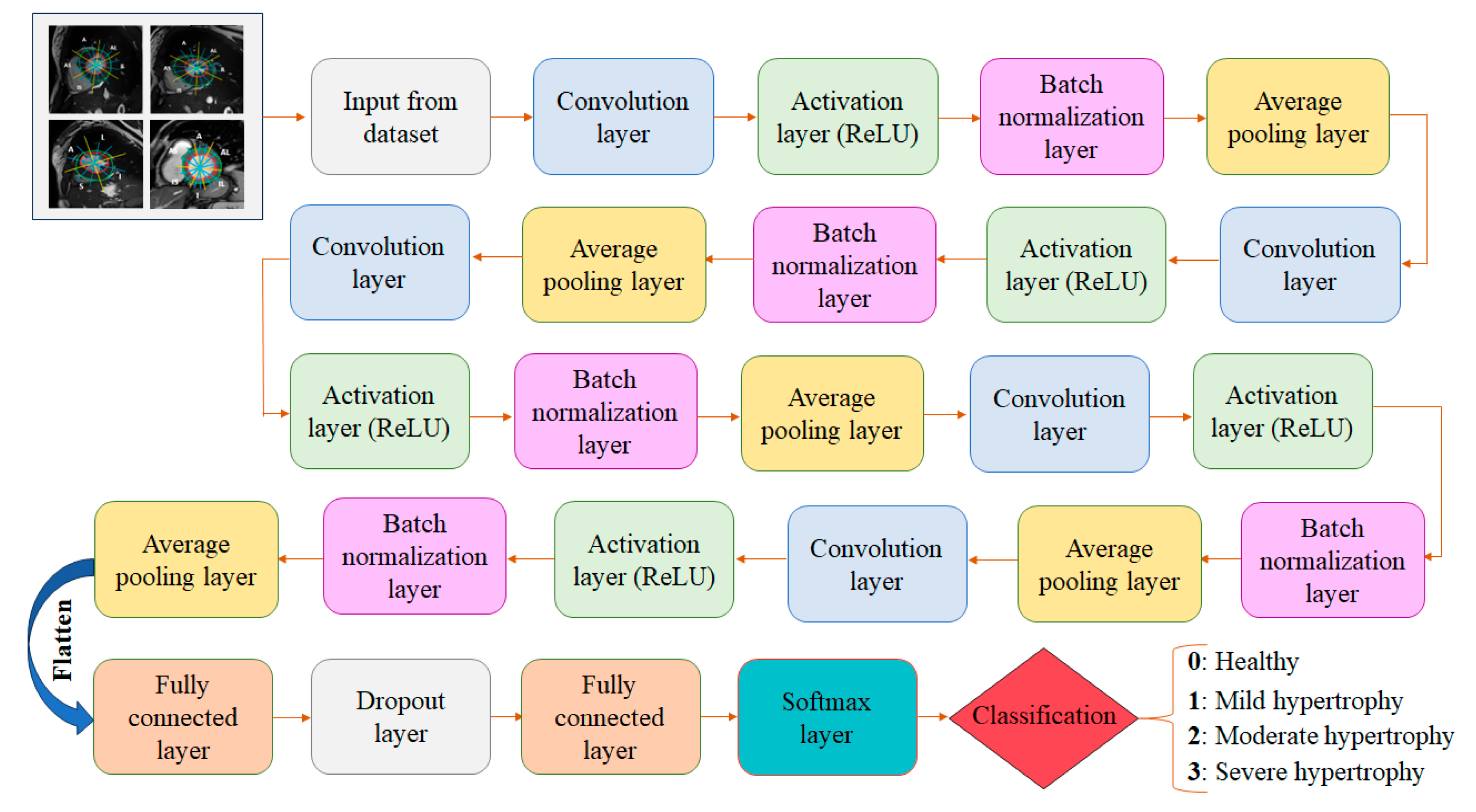
3.5.2. Detailed CNN Architecture
- The input layer: The initial layer receives the preprocessed dataset consisting of cine-MRI images acquired in the short-axis orientation. Each image has a size of 256 ×256 and the preprocessing includes several key steps: normalization to standardize pixel intensity values, segmentation of the LV contours, and the division of each myocardial segment into three equal sub-segments.
- Five convolutional layers: Convolutional layers are key components of a CNN responsible for automatically learning and extracting features from the dataset. These layers consist of applying convolutional filters (kernels) to the input images to create feature maps. These filters slide over the image, performing element-wise multiplication and summing the results to produce a single value in the feature map. In our case, with 2D input images and 2D filters, the convolution operation can be mathematically expressed as follows [28]:
- Five activation layers (ReLU): The output of the convolutional layers serves as the input to the activation layers. These layers introduce nonlinearity into the network, allowing it to learn complex patterns and relationships in the data. ReLU activates neurons by outputting the input value directly if it is positive, or zero otherwise. Mathematically, the ReLU function is expressed by the following equation [26].
- Five batch normalization layers: These are applied to improve the training and performance of the proposed neural network. By modifying and scaling the activations, it normalizes the output of an earlier activation layer. This stabilizes and accelerates the learning process.
- Five average pooling layers: These layers are integrated into our CNN architecture to reduce spatial resolution while preserving relevant structural information from the feature maps. Although max pooling is commonly used for its ability to emphasize dominant activations, we explored both pooling strategies during the hyperparameter tuning phase to determine which would better preserve clinically meaningful features, particularly in the context of classifying myocardial segments by hypertrophy severity. The results of this ablation study are presented in the Results section (Section 4.1). Based on the outcomes, we selected average pooling for the final architecture, as it consistently yielded slightly superior performance across all evaluation metrics. This choice reflects the specific needs of our task: capturing subtle but clinically relevant differences in myocardial morphology, which may be disregarded due to the selective nature of max pooling that emphasizes only the strongest activations. The average pooling operation computes the mean of the values within a 2 × 2 window and can be mathematically defined as follows [29]:
- Two fully connected layers (FC): Each neuron is connected to every neuron in the preceding layer. The FC layers combine and integrate the spatial features extracted by the convolutional and pooling layers using them to make predictions. This layer is used at the end of the proposed CNN to map the learned features into the final output, such as class scores. Mathematically, a fully connected layer uses n neurons to receive information from the preceding layer. Each neuron in the FC layers applies a weighted sum of the input values followed by an activation function to generate its output as described in Equation (4) [30]:
- Softmax layer: This converts the output of the fully connected layer into a probability distribution, assigning a probability to each class. In our case, the Softmax layer assigns each myocardial sub-segment a hypertrophy score (0, 1, 2, or 3) corresponding to the hypertrophy severity, with 0 indicating no hypertrophy and 3 representing the most severe level. Mathematically, the Softmax function can be expressed as follows [29]:
- Dropout layer: In our CNN, the dropout layer serves as regularization technique used to prevent overfitting in neural networks and improve the model’s ability to generalize to new data. It works by randomly deactivating a fraction of neurons during each training iteration, forcing the network to learn more robust features, which results in more reliable classification of myocardial sub-segments. A detailed overview of the architecture is provided in Table 1, outlining the configuration and parameters of each layer.
| Algorithm 1: Classification algorithm of myocardial sub-segments according to hypertrophy severity |
| ## INPUT 2D cine-MRI dataset; (1) Min-max normalization; (2) Automatic segmentation of left ventricle endocardial and epicardial contours using U-Net; RWT: Regional Wall Thickness; Score = [0,1,2,3] # Scores identifying the severity of hypertrophy; N = 49 #Total number of sub-segments per patient; ## OUTPUT Training
|
3.6. Performance Metric Evaluation
3.7. Expert-Driven Dataset Annotation and Validation Process
4. Experiments and Results
4.1. Hyperparameters Tuning
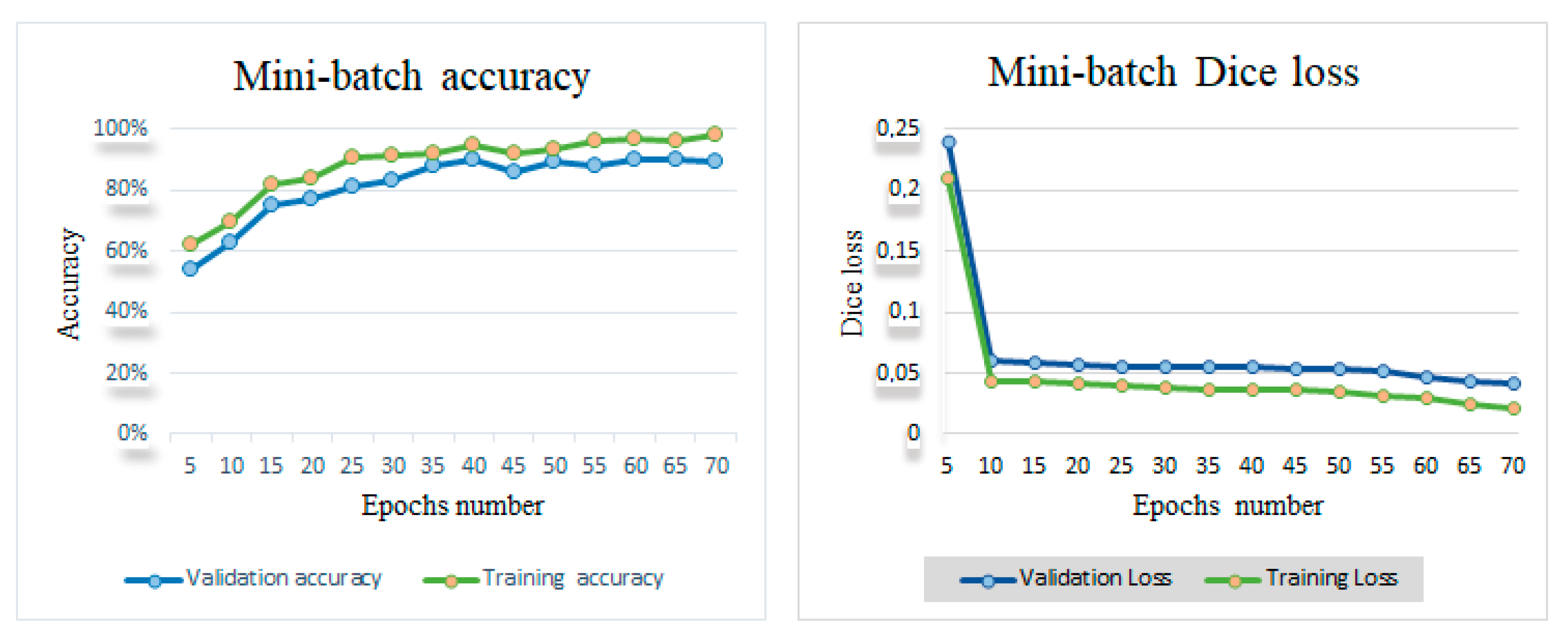
4.2. Results of Automatic Left Ventricle Contours’ Delineation
4.3. Outcomes of Automated Regional Wall Thickness Quantification
4.4. Clinical Relevance of the Proposed Approach for Classifying Myocardial Segments by Hypertrophy Severity
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AHA | American Heart Association |
| AI | Artificial Intelligence |
| CMRI | Cardiac Magnetic Resonance Imaging |
| CNN | Convolutional Neural Network |
| CVD | Cardiovascular Disease |
| DSC | Dice Similarity Coefficient |
| ECG | Electrocardiogram |
| HD | Hausdorff Distance |
| LV | Left Ventricle |
| LVH | Left Ventricle Hypertrophy |
| LVM | Left Ventricle Mass |
| MAE | Mean Absolute Error |
| RWT | Regional Wall Thickness |
References
- Roth, G.A.; Mensah, G.A.; Johnson, C.O.; Addolorato, G.; Ammirati, E.; Baddour, L.M.; Barengo, N.C.; Beaton, A.Z.; Benjamin, E.J.; Benziger, C.P.; et al. Global Burden of Cardiovascular Diseases Writing Group. Global burden of cardiovascular diseases and risk factors, 1990–2019: Update from the GBD 2019 study. J. Am. Coll. Cardiol. 2020, 76, 2982–3021. [Google Scholar] [CrossRef] [PubMed]
- Baptista, E.A.; Queiroz, B.L. Spatial analysis of cardiovascular mortality and associated factors around the world. BMC Public Health 2022, 22, 1556. [Google Scholar] [CrossRef] [PubMed]
- Budai, A.; Suhai, F.I.; Csorba, K.; Dohy, Z.; Szabo, L.; Merkely, B.; Vago, H. Automated classification of left ventricular hypertrophy on cardiac mri. Appl. Sci. 2022, 12, 4151. [Google Scholar] [CrossRef]
- Méndez, C.; Soler, R.; Rodríguez, E.; Barriales, R.; Ochoa, J.P.; Monserrat, L. Differential diagnosis of thickened myocardium: An illustrative MRI review. Insights Into Imaging 2018, 9, 695–707. [Google Scholar] [CrossRef] [PubMed]
- Parlati, A.L.M.; Nardi, E.; Marzano, F.; Madaudo, C.; Di Santo, M.; Cotticelli, C.; Agizza, S.; Abbellito, G.M.; Filardi, F.P.; Del Giudice, M.; et al. Advancing Cardiovascular Diagnostics: The Expanding Role of CMR in Heart Failure and Cardiomyopathies. J. Clin. Med. 2025, 14, 865. [Google Scholar] [CrossRef] [PubMed]
- Grajewski, K.G.; Stojanovska, J.; Ibrahim, E.-S.H.; Sayyouh, M.; Attili, A. Left ventricular hypertrophy: Evaluation with cardiac MRI. Curr. Probl. Diagn. Radiol. 2020, 49, 460–475. [Google Scholar] [CrossRef] [PubMed]
- Maron, B.J.; Kragel, A.H.; Roberts, W.C. Case 883 Sudden Death in Hypertrophic Cardiomyopathy with Normal Left Ventricular Mass. Case Reports in Cardiology: Cardiomyopathy. Br. Heart J. 1990, 63, 308–310. [Google Scholar] [CrossRef] [PubMed]
- Baccouch, W.; Hadidi, T.; Benameur, N.; Lahidheb, D.; Labidi, S. Convolution neural network for Objective Myocardial Viability Assessment based on Regional Wall Thickness Quantification from Cine-MR images. IEEE Access 2024, 12, 112381–112396. [Google Scholar] [CrossRef]
- Lundin, M.; Heiberg, E.; Nordlund, D.; Gyllenhammar, T.; Steding-Ehrenborg, K.; Engblom, H.; Carlsson, M.; Atar, D.; van der Pals, J.; Erlinge, D.; et al. Left ventricular mass and global wall thickness–prognostic utility and characterization of left ventricular hypertrophy. MedRxiv 2022, 3, 10–28. [Google Scholar] [CrossRef]
- Maanja, M.; Noseworthy, P.A.; Geske, J.B.; Ackerman, M.J.; Arruda-Olson, A.M.; Ommen, S.R.; Attia, Z.I.; Friedman, P.A.; Siontis, K.C. Tandem deep learning and logistic regression models to optimize hypertrophic cardiomyopathy detection in routine clinical practice. Cardiovasc. Digit. Health J. 2022, 3, 289–296. [Google Scholar] [CrossRef] [PubMed]
- Maanja, M.; Schlegel, T.T.; Kozor, R.; Lundin, M.; Wieslander, B.; Wong, T.C.; Schelbert, E.B.; Ugander, M. The electrical determinants of increased wall thickness and mass in left ventricular hypertrophy. J. Electrocardiol. 2020, 58, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Kokubo, T.; Kodera, S.; Sawano, S.; Katsushika, S.; Nakamoto, M.; Takeuchi, H.; Kimura, N.; Shinohara, H.; Matsuoka, R.; Nakanishi, K.; et al. Automatic detection of left ventricular dilatation and hypertrophy from electrocardiograms using deep learning. Int. Heart J. 2022, 63, 939–947. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Feng, Z.; Xiao, C.; Wu, Y.; Ye, W.; Zhang, F. The establishment of hypertrophic cardiomyopathy diagnosis model via artificial neural network and random decision forest method. Mediat. Inflamm. 2022, 2022, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Duffy, G.; Cheng, P.P.; Yuan, N.; He, B.; Kwan, A.C.; Shun-Shin, M.J.; Alexander, K.M.; Ebinger, J.; Lungren, M.P.; Rader, F.; et al. High-throughput precision phenotyping of left ventricular hypertrophy with cardiovascular deep learning. JAMA Cardiol. 2022, 7, 386–395. [Google Scholar] [CrossRef] [PubMed]
- Soto, J.T.; Hughes, J.W.; Sanchez, P.A.; Perez, M.; Ouyang, D.; A Ashley, E. Multimodal deep learning enhances diagnostic precision in left ventricular hypertrophy. Eur. Heart J.-Digit. Health 2022, 3, 380–389. [Google Scholar] [CrossRef] [PubMed]
- Jian, Z.; Wang, X.; Zhang, J.; Wang, X.; Deng, Y. Diagnosis of left ventricular hypertrophy using convolutional neural network. BMC Med. Inform. Decis. Mak. 2020, 20, 243. [Google Scholar] [CrossRef] [PubMed]
- Hwang, I.-C.; Choi, D.; Choi, Y.-J.; Ju, L.; Kim, M.; Hong, J.-E.; Lee, H.-J.; Yoon, Y.E.; Park, J.-B.; Lee, S.-P.; et al. Differential diagnosis of common etiologies of left ventricular hypertrophy using a hybrid CNN-LSTM model. Sci. Rep. 2022, 12, 20998. [Google Scholar] [CrossRef] [PubMed]
- Beneyto, M.; Ghyaza, G.; Cariou, E.; Amar, J.; Lairez, O. Development and validation of machine learning algorithms to predict posthypertensive origin in left ventricular hypertrophy. Arch. Cardiovasc. Dis. 2023, 116, 397–402. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Harvey, C.J.; DeBauge, A.; Shomaji, S.; Yao, Z.; Noheria, A. Machine learning to classify left ventricular hy-pertrophy using ECG feature extraction by variational autoencoder. MedRxiv 2024, 2024, 1–27. [Google Scholar] [CrossRef]
- Lim, D.Y.; Sng, G.; Ho, W.H.; Hankun, W.; Sia, C.-H.; Lee, J.S.; Shen, X.; Tan, B.Y.; Lee, E.C.; Dalakoti, M.; et al. Machine learning versus classical electrocardiographic criteria for echocardiographic left ventricular hypertrophy in a pre-participation cohort. Kardiol. Pol. 2021, 79, 654–661. [Google Scholar] [CrossRef] [PubMed]
- Kwon, J.-M.; Jeon, K.-H.; Kim, H.M.; Kim, M.J.; Lim, S.M.; Kim, K.-H.; Song, P.S.; Park, J.; Choi, R.K.; Oh, B.-H. Comparing the performance of artificial intelligence and conventional diagnosis criteria for detecting left ventricular hypertrophy using electrocardiography. EP Eur. 2020, 22, 412–419. [Google Scholar] [CrossRef] [PubMed]
- Khurshid, S.; Friedman, S.; Pirruccello, J.P.; Di Achille, P.; Diamant, N.; Anderson, C.D.; Ellinor, P.T.; Batra, P.; Ho, J.E.; Philippakis, A.A.; et al. Deep learning to predict cardiac magnetic resonance–derived left ventricular mass and hypertrophy from 12-lead ECGs. Circ. Cardiovasc. Imaging 2021, 14, e012281. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Li, L.; Liu, Z.; Zhao, K.; Chen, X.; Lu, M.; Yin, G.; Song, L.; Zhao, S.; Zheng, H.; et al. Deep learning algorithm to improve hypertrophic cardiomyopathy mutation prediction using cardiac cine images. Eur. Radiol. 2021, 31, 3931–3940. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-De-Vera, J.M.; Bernabé, G.; García, J.M.; Saura, D.; González-Carrillo, J. Left ventricular non-compaction cardiomyopathy automatic diagnosis using a deep learning approach. Comput. Methods Programs Biomed. 2022, 214, 106548. [Google Scholar] [CrossRef] [PubMed]
- Henderi, H.; Wahyuningsih, T.; Rahwanto, E. Comparison of Min-Max normalization and Z-Score Normalization in the K-nearest neighbor (kNN) Algorithm to Test the Accuracy of Types of Breast Cancer. Int. J. Inform. Inf. Syst. 2021, 4, 13–20. [Google Scholar] [CrossRef]
- Baccouch, W.; Oueslati, S.; Solaiman, B.; Lahidheb, D.; Labidi, S. Automatic Left Ventricle Segmentation from Short-Axis MRI Images Using U-Net with Study of the Papillary Muscles’ Removal Effect. J. Med. Biol. Eng. 2023, 43, 278–290. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015, Proceedings, Part III 18; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Zhu, X.; Meng, Q.; Ding, B.; Gu, L.; Yang, Y. Weighted pooling for image recognition of deep convolutional neural networks. Clust. Comput. 2019, 22, 9371–9383. [Google Scholar] [CrossRef]
- Sorour, S.E.; Wafa, A.A.; Abohany, A.A.; Hussien, R.M.; Rajamohan, V. A Deep Learning System for Detecting Cardiomegaly Disease Based on CXR Image. Int. J. Intell. Syst. 2024, 2024, 8997093. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef] [PubMed]
- Baccouch, W.; Oueslati, S.; Solaiman, B.; Lahidheb, D.; Labidi, S. Automatic left ventricle volume and mass quantification from 2D cine-MRI: Investigating papillary muscle influence. Med. Eng. Phys. 2024, 127, 104162. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-H.; Zhang, F.-Z.; Wu, J.-X.; Pai, N.-S.; Chen, P.-Y.; Pai, C.-C.; Kan, C.-D. Posteroanterior chest X-ray image classification with a multilayer 1D convolutional neural network-based classifier for cardiomegaly level screening. Electronics 2022, 11, 1364. [Google Scholar] [CrossRef]
- Wu, J.-X.; Pai, C.-C.; Kan, C.-D.; Chen, P.-Y.; Chen, W.-L.; Lin, C.-H. Chest X-ray image analysis with combining 2D and 1D convolutional neural network based classifier for rapid cardiomegaly screening. IEEE Access 2022, 10, 47824–47836. [Google Scholar] [CrossRef]
- Chen, L.; Mao, T.; Zhang, Q. Identifying cardiomegaly in chest X-rays using dual attention network. Appl. Intell. 2022, 52, 11058–11067. [Google Scholar] [CrossRef]
- Ajmera, P.; Kharat, A.; Gupte, T.; Pant, R.; Kulkarni, V.; Duddalwar, V.; Lamghare, P. Observer performance evaluation of the feasibility of a deep learning model to detect cardiomegaly on chest radiographs. Acta Radiol. Open 2022, 11, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, E.; Cardenas, D.A.C.; Krieger, J.E.; Gutierrez, M.A. Interpretable deep learning model for cardiomegaly detection with chest X-ray images. In Anais do XXIII Simp´osio Brasileiro de Computação Aplicada a Saude´; SBC: London, UK, 2023; pp. 340–347. [Google Scholar] [CrossRef]
- Innat, M.; Hossain, F.; Mader, K.; Kouzani, A.Z. A convolutional attention mapping deep neural network for classification and localization of cardiomegaly on chest X-rays. Sci. Rep. 2023, 13, 6247. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Li, X.; Li, X.; Wang, Z.; Deng, H.; Luo, X.; Yin, L.; Zhang, H. A Deep Learning-Driven Pipeline for Differentiating Hypertrophic Cardiomyopathy from Cardiac Amyloidosis Using 2D Multi-View Echocardiography. arXiv 2024, arXiv:2404.16522. [Google Scholar]
- Gomes, B.; Hedman, K.; Kuznetsova, T.; Cauwenberghs, N.; Hsu, D.; Kobayashi, Y.; Ingelsson, E.; Oxborough, D.; George, K.; Salerno, M.; et al. Defining left ventricular remodeling using lean body mass allometry: A UK Biobank study. Eur. J. Appl. Physiol. 2023, 123, 989–1001. [Google Scholar] [CrossRef] [PubMed]
- Sivalokanathan, S. The role of cardiovascular magnetic resonance imaging in the evaluation of hypertrophic cardiomyopathy. Diagnostics 2022, 12, 314. [Google Scholar] [CrossRef] [PubMed]
- Bukharovich, I.; Wengrofsky, P.; Akivis, Y. Cardiac multimodality imaging in hypertrophic cardiomyopathy: What to look for and when to image. Curr. Cardiol. Rev. 2023, 19, 1–18. [Google Scholar] [CrossRef] [PubMed]
- De la Garza-Salazar, F.; Romero-Ibarguengoitia, M.E.; Rodriguez-Diaz, E.A.; Azpiri-Lopez, J.R.; González-Cantu, A.; Ab Rahman, N.H. Improvement of electrocardiographic diagnostic accuracy of left ventricular hypertrophy using a Machine Learning approach. PLoS ONE 2020, 15, e0232657. [Google Scholar] [CrossRef] [PubMed]
| Layer Name | Layer Type | Kernal Size | Filters | Stride | Padding | Activation | Output Shape | Parameters |
|---|---|---|---|---|---|---|---|---|
| 1. Input | Input | - | - | - | - | - | 256 × 256 × 3 | 0 |
| 2. Convolutional | Conv 2D | 3 × 3 | 32 | 1 × 1 | Same | - | 256 × 256 × 32 | 896 |
| 3. Activation layer | Activation | - | - | - | - | ReLU | 256 × 256 × 32 | 0 |
| 4. BN | Batch normalization | - | - | - | - | - | 256 × 256 × 32 | 64 |
| 5. Average pooling | Average pooling 2D | 2 × 2 | - | 2 × 2 | - | - | 128 × 128 × 32 | 0 |
| 6. Convolutional | Conv 2D | 3 × 3 | 64 | 1 × 1 | 2 | - | 130 × 130 × 64 | 18,496 |
| 7. Activation layer | Activation | - | - | - | - | ReLU | 130 × 130 × 64 | 0 |
| 8. BN | Batch normalization | - | - | - | - | - | 130 × 130 × 64 | 128 |
| 9. Average pooling | Average pooling 2D | 2 × 2 | - | 2 × 2 | - | - | 65 × 65 × 64 | 0 |
| 10. Convolutional | Conv 2D | 3 × 3 | 128 | 1 × 1 | 2 | - | 67 × 67 × 128 | 73,856 |
| 11. Activation | Activation | - | - | - | - | ReLU | 67 × 67 × 128 | 0 |
| 12. BN | Batch normalization | - | - | - | - | - | 67 × 67 × 128 | 256 |
| 13. Average pooling | Average pooling 2D | 2 × 2 | - | 2 × 2 | - | - | 33 × 33 × 128 | 0 |
| 14. Convolutional | Conv 2D | 3 × 3 | 256 | 1 × 1 | 2 | - | 35 × 35 × 256 | 295,168 |
| 15. Activation | Activation | - | - | - | - | ReLU | 35 × 35 × 256 | 0 |
| 16. BN | Batch normalization | - | - | - | - | - | 35 × 35 × 256 | 512 |
| 17. Average pooling | Average pooling 2D | 2 × 2 | - | 2 × 2 | - | - | 17 × 17 × 256 | 0 |
| 18. Convolutional | Conv 2D | 3 × 3 | 512 | 1 × 1 | 2 | - | 19 × 19 × 512 | 1,181,160 |
| 19. Activation | Activation | - | - | - | - | ReLU | 19 × 19 × 512 | 0 |
| 20. BN | Batch normalization | - | - | - | - | - | 19 × 19 × 512 | 1024 |
| 21. Average pooling | Average pooling 2D | 2 × 2 | - | 2 × 2 | - | - | 9 ×9 ×512 | 0 |
| 22. FC layer | Dense 1 | - | - | - | - | ReLU | 128 | 5,308,544 |
| 23. Dropout layer | Dropout | Dropout rate = 0.3 | 128 | 0 | ||||
| 24. FC layer | Dense 2 | - | - | - | - | ReLU | 16 | 2064 |
| 25. Classification | Softmax classifier | - | - | - | - | Softmax | 4 | 0 |
| Parameters | Epochs | Batch-Size = 4 | Batch-Size = 8 | |||||
|---|---|---|---|---|---|---|---|---|
| Rmsprop | Adam | Adamax | Rmsprop | Adam | Adamax | |||
| LR | 10−1 | 10 | 51.43 | 53.12 | 54.34 | 49.44 | 52.67 | 52.61 |
| 20 | 54.67 | 56.24 | 58.63 | 52.09 | 53.18 | 54.29 | ||
| 30 | 61.44 | 63.71 | 68.92 | 58.25 | 62.14 | 63.48 | ||
| 40 | 63.56 | 67.81 | 70.41 | 62.15 | 66.43 | 68.17 | ||
| 50 | 70.91 | 74.26 | 82.74 | 68.22 | 71.61 | 77.02 | ||
| 60 | 76.13 | 81.67 | 87.15 | 73.43 | 79.25 | 82.45 | ||
| 70 | 81.07 | 90.24 | 91.02 | 79.16 | 82.77 | 89.27 | ||
| 10−2 | 10 | 52.14 | 53.99 | 54.67 | 51.32 | 52.89 | 53.23 | |
| 20 | 55.21 | 57.71 | 61.23 | 53.15 | 54.04 | 57.51 | ||
| 30 | 62.17 | 65.04 | 71.56 | 60.43 | 63.38 | 69.27 | ||
| 40 | 70.63 | 72.31 | 86.45 | 64.52 | 70.12 | 81.13 | ||
| 50 | 80.06 | 84.22 | 90.28 | 78.16 | 81.36 | 87.71 | ||
| 60 | 83.22 | 87.63 | 92.64 | 80.72 | 83.23 | 91.44 | ||
| 70 | 84.46 | 92.58 | 94.72 | 82.83 | 84.37 | 93.10 | ||
| 10−3 | 10 | 56.73 | 59.28 | 69.82 | 53.44 | 56.69 | 64.32 | |
| 20 | 59.40 | 61.13 | 74.56 | 56.03 | 58.23 | 60.17 | ||
| 30 | 64.31 | 72.23 | 86.33 | 60.38 | 64.78 | 70.42 | ||
| 40 | 73.60 | 83.88 | 91.56 | 71.04 | 80.47 | 86.65 | ||
| 50 | 86.44 | 87.21 | 93.03 | 82.56 | 85.09 | 89.21 | ||
| 60 | 90.45 | 92.19 | 96.72 | 87.22 | 89.13 | 91.52 | ||
| 70 | 92.03 | 94.15 | 98.10 | 90.82 | 92.62 | 94.63 | ||
| Metric | Average Pooling (Selected) | Max Pooling |
|---|---|---|
| Accuracy (%) | 98.19 | 97.41 |
| Precision (%) | 98.27 | 97.33 |
| Recall (%) | 99.23 | 98.02 |
| F1-Score (%) | 98.70 | 97.67 |
| Number of Blocks | Training DSC (%) | Validation DSC (%) | Test DSC (%) | Observation |
|---|---|---|---|---|
| 3 | 96.80 | 95.5 | 95.70 | Underfitting |
| 4 (Selected) | 98.10 | 97.90 | 97.85 | Best overall performance |
| 5 | 100 | 96.50 | 96.40 | Overfitting suspected |
| Metric | Group | 3 Blocks | 4 Blocks (Selected) | 5 Blocks |
|---|---|---|---|---|
| Mean DSC (%) | Endo-Healthy | 96.32 ± 3.5 | 98.05 ± 2.8 | 98.40 ± 1.9 |
| Endo-HCM | 95.90 ± 2.7 | 97.68 ± 1.6 | 97.20 ± 3.4 | |
| Epi-Healthy | 97.78 ± 4.5 | 99.23 ± 3.1 | 99.50 ± 2.2 | |
| Epi-HCM | 97.10 ± 5.0 | 98.47 ± 4.2 | 97.90 ± 5.8 | |
| Mean HD (mm) | Endo-Healthy | 6.89 ± 3.1 | 5.678 ± 2.6 | 5.45 ± 2.2 |
| Endo-HCM | 7.45 ± 3.9 | 6.345 ± 3.5 | 6.90 ± 3.8 | |
| Epi-Healthy | 5.91 ± 2.6 | 4.103 ± 1.4 | 4.00 ± 1.3 | |
| Epi-HCM | 6.39 ± 2.8 | 5.424 ± 2.2 | 5.90 ± 2.9 |
| Myocardial Section | Myocardial Segments | Mean Thickness Values for All Sub-Segments (mm) | MAE | ||||
|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 1st | 2nd | 3rd | ||
| Basal | 1 | 21.23 | 18.12 | 14.78 | 1.23 ± 0.5 | 1.44 ± 1.1 | 1.07 ± 1.3 |
| 2 | 7.84 | 7.63 | 6.51 | 1.42 ± 1.01 | 1.42 ± 1.02 | 1.21 ± 2.4 | |
| 3 | 6.57 | 7.2 | 6.22 | 1.18 ± 3.22 | 1.20 ± 1.23 | 1.25 ± 2.3 | |
| 4 | 8.2 | 10.44 | 7.99 | 1.32 ± 2.5 | 1.11 ± 2.91 | 1.24 ± 1.15 | |
| 5 | 9.32 | 12.67 | 8.71 | 1.24 ± 1.04 | 1.22 ± 1.01 | 1.22 ± 1.20 | |
| 6 | 25.61 | 26.08 | 22.77 | 1.01 ± 1.16 | 1.19 ± 0.81 | 1.23 ± 1.12 | |
| Median | 7 | 12.44 | 16.08 | 22.08 | 1.15 ± 1.12 | 1.27 ± 1.02 | 1.09 ± 1.22 |
| 8 | 11.50 | 10.34 | 9.17 | 1.03 ± 1.37 | 1.13 ± 1.04 | 1.21 ± 1.41 | |
| 9 | 13.21 | 11.72 | 11.13 | 1.31 ± 1.07 | 1.05 ± 1.22 | 1.28 ± 1.09 | |
| 10 | 13.82 | 13.40 | 12.61 | 1.27 ± 1.15 | 1.28 ± 0.87 | 1.25 ± 1.13 | |
| 11 | 12.47 | 13.12 | 14.55 | 1.23 ± 1.41 | 1.31 ± 1.09 | 1.13 ± 1.02 | |
| 12 | 23.54 | 21.91 | 15.89 | 1.23 ± 1.03 | 1.22. ±0.81 | 1.02 ± 0.43 | |
| Apical | 13 | 14.56 | 16.34 | 21.61 | 1.41 ± 1.2 | 1.28 ± 1.03 | 1.33 ± 0.98 |
| 14 | 12.28 | 13.49 | 13.01 | 1.29 ± 0.87 | 1.39 ± 1.52 | 1.28 ± 0.73 | |
| 15 | 9.13 | 10.32 | 10.75 | 1.39 ± 1.47 | 1.50 ± 1.31 | 1.28 ± 1.06 | |
| 16 | 11.93 | 16.61 | 21.18 | 1.37 ± 0.88 | 1.37 ± 0.9 | 1.42 ± 0.48 | |
| Apex | 17 | 5.31 | 1.28 ± 1.34 | ||||
| Hypertrophy Class | Model | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) |
|---|---|---|---|---|---|
| Normal | 17-segment | 95.42 | 94.81 | 95.92 | 96.22 |
| 49-sub-segment | 98.86 | 98.79 | 99.36 | 98.91 | |
| Mild Hypertrophy | 17-segment | 91.27 | 90.72 | 87.54 | 91.46 |
| 49-sub-segment | 95.92 | 96.81 | 95.91 | 96.55 | |
| Moderate Hypertrophy | 17-segment | 90.33 | 89.47 | 85.43 | 89.67 |
| 49-sub-segment | 94.54 | 96.96 | 94.18 | 97.14 | |
| Severe Hypertrophy | 17-segment | 94.66 | 94.12 | 94.17 | 94.62 |
| 49-sub-segment | 98.71 | 98.39 | 98.91 | 98.58 | |
| Average (All classes) | 17-segment | 92.92 | 92.28 | 90.76 | 92.99 |
| 49-sub-segment | 97.01 | 97.73 | 97.09 | 97.80 |
| Section | Segmented Cine-MRI | 17-Segment Model | Proposed 49-Sub-Segment Model | Number of Misclassifications |
|---|---|---|---|---|
| Basal section | 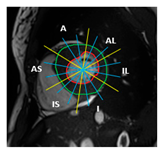 |  | 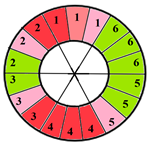 | 9 sub-segments (2 sub-segments of segment 1 + 3 sub-segments of segment 2 + 3 sub-segments of segment 3 + 1 sub-segment of segment 5) |
| Mid-section | 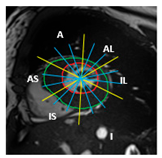 | 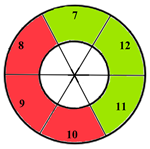 | 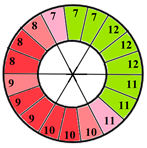 | 5 sub-segments (1 sub-segment of segment 7 + 1 sub-segment of segment 8 + 1 sub-segment of segment 9 + 1 sub-segment of segment 10 + 1 sub-segment of segment 11) |
| Apical section | 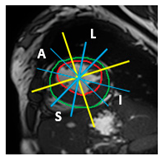 | 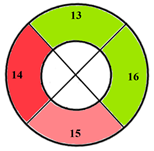 | 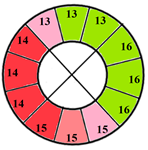 | 3 sub-segments (1 sub-segment of segment 13 + 2 sub-segments of segment 15) |
| Patients | 17-Segment Model | 49-Sub-Segment Model | Number of Misclassifications |
|---|---|---|---|
| Patient 1 | 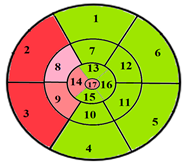 | 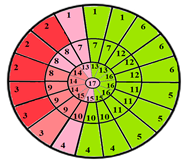 | 9 sub-segments |
| Patient 2 | 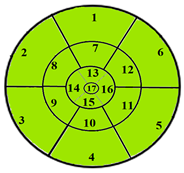 | 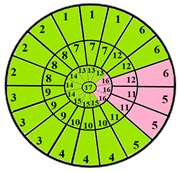 | 9 sub-segments |
| Patient 3 | 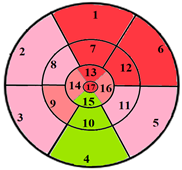 | 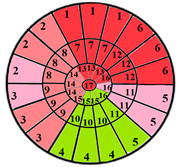 | 13 sub-segments |
| Performance Measures | Intra-Observer Variability | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Visual Analysis | Quantitative Analysis | ||||||||||
| Results | Acc | Pre | Re | F1-Score | Results | Acc | Pre | Re | F1-score | ||
| R1 | TP = 827 TN = 354 FP = 77 FN = 65 | 89.27 | 91.48 | 92.71 | 92 | TP = 847 TN = 423 FP = 32 FN = 21 | 95.99 | 96.36 | 97.58 | 97 | 6.72% |
| R2 | TP = 881 TN = 380 FP = 35 FN = 27 | 95.31 | 96.18 | 97.03 | 96.6 | TP = 910 TN = 389 FP = 16 FN = 8 | 98.19 | 98.27 | 99.13 | 98.7 | 2.88% |
| Inter-observer variability | 6.04% | 2.19% | - | ||||||||
| Reference | Year | Database | Performance Metrics | |||
| Accuracy | Precision | Recall | F1-Score | |||
| Budai et al. [3] | 2022 | CMR dataset 428 patients + 234 healthy subjects | - | 91 | 97 | 92 |
| Lim et al. [32] | 2022 | 300 patients | 98.00 | 97.80 | 98.20 | 97.99 |
| Wu et al. [33] | 2022 | National institutes of health (NIH) database | 98.40 | 97.60 | 99.20 | 98.38 |
| Chen et al. [34] | 2022 | NIH | 90.50 | - | 94.45 | 90.59 |
| Ajmera et al. [35] | 2022 | 1012 posteroanterior CXRs | - | 99.00 | 80.00 | 88.00 |
| Ribeiro et al. [36] | 2023 | VinDr-CXR | 91.80 | 74.00 | 87.00 | 79.80 |
| Innat et al. [37] | 2023 | NIH | 87.00 | - | 85.00 | 86.00 |
| E. Sorour et al. [29] | 2023 | NIH | 95.50 | 96.89 | 73.10 | 83.30 |
| Peng et al. [38] | 2024 | 442 patients | - | 90.5 | 90.5 | 90.4 |
| Proposed | 2025 | 133 patients | 98.19 | 98.27 | 99.13 | 98.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baccouch, W.; Hasnaoui, B.; Benameur, N.; Jemai, A.; Lahidheb, D.; Labidi, S. Deep Learning-Based Algorithm for the Classification of Left Ventricle Segments by Hypertrophy Severity. J. Imaging 2025, 11, 244. https://doi.org/10.3390/jimaging11070244
Baccouch W, Hasnaoui B, Benameur N, Jemai A, Lahidheb D, Labidi S. Deep Learning-Based Algorithm for the Classification of Left Ventricle Segments by Hypertrophy Severity. Journal of Imaging. 2025; 11(7):244. https://doi.org/10.3390/jimaging11070244
Chicago/Turabian StyleBaccouch, Wafa, Bilel Hasnaoui, Narjes Benameur, Abderrazak Jemai, Dhaker Lahidheb, and Salam Labidi. 2025. "Deep Learning-Based Algorithm for the Classification of Left Ventricle Segments by Hypertrophy Severity" Journal of Imaging 11, no. 7: 244. https://doi.org/10.3390/jimaging11070244
APA StyleBaccouch, W., Hasnaoui, B., Benameur, N., Jemai, A., Lahidheb, D., & Labidi, S. (2025). Deep Learning-Based Algorithm for the Classification of Left Ventricle Segments by Hypertrophy Severity. Journal of Imaging, 11(7), 244. https://doi.org/10.3390/jimaging11070244







