Noise Suppressed Image Reconstruction for Quanta Image Sensors Based on Transformer Neural Networks
Abstract
1. Introduction
- This study propose a reconstruction method that suppress photon shot noise during the QIS imaging process under a practical and acceptable temporal oversampling rate based on deep neural network instead of traditional denoising.
- The proposed neural network framework integrates CNN and Transformer to improve denoising performance. A hybrid structure combining serial and parallel is introduced in the network framework to enhance the strength and robustness of denoising. The serial module deeply explores the key information in image denoising, while the parallel module widely explores more relevant and complementary information between pixels from different angles, thereby enhancing the adaptability of the QIS-SPFT denoiser to complex scenes. In the network, a variance-stabilizing transformation is used to convert the high Poisson noise in QIS into Gaussian noise to enhance the performance as well.
2. Background
3. Method Description
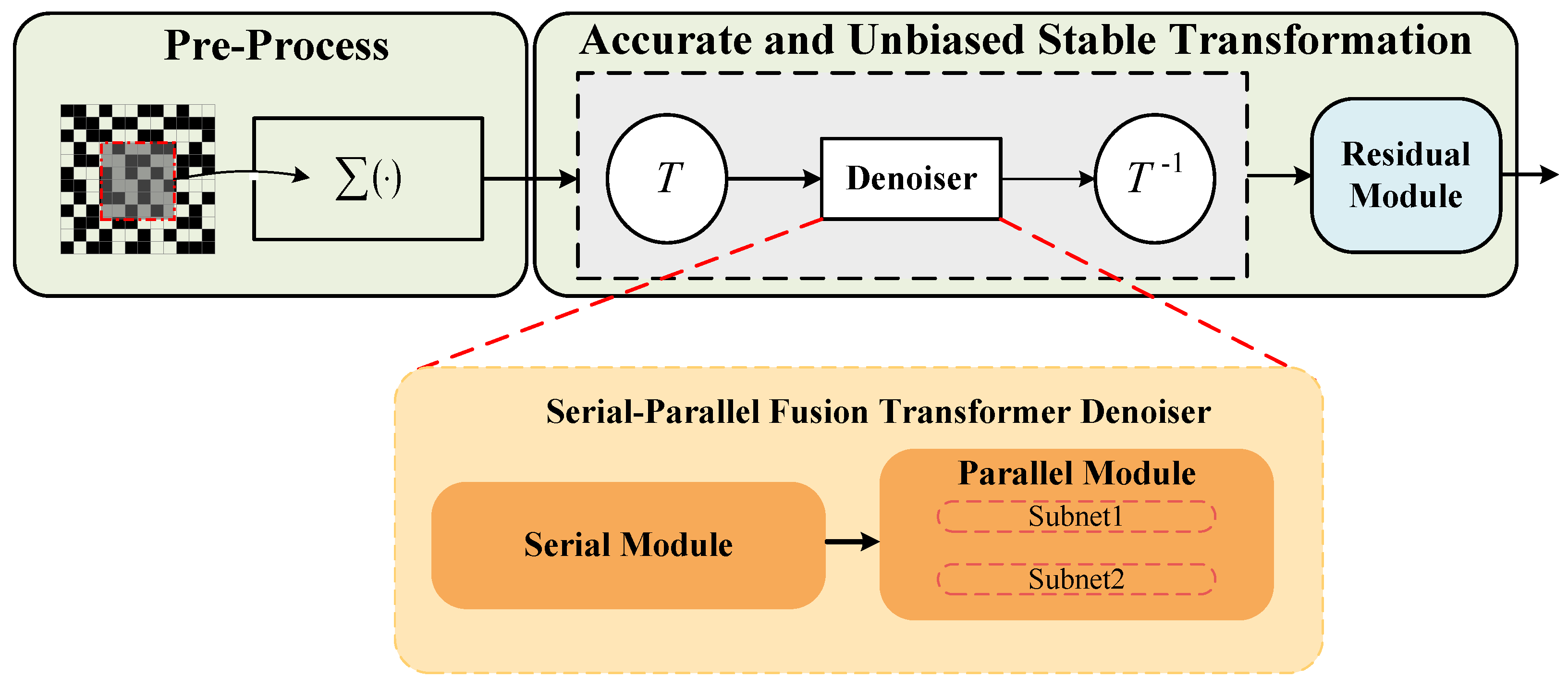
3.1. Architecture of the Proposed QIS Reconstruction Method
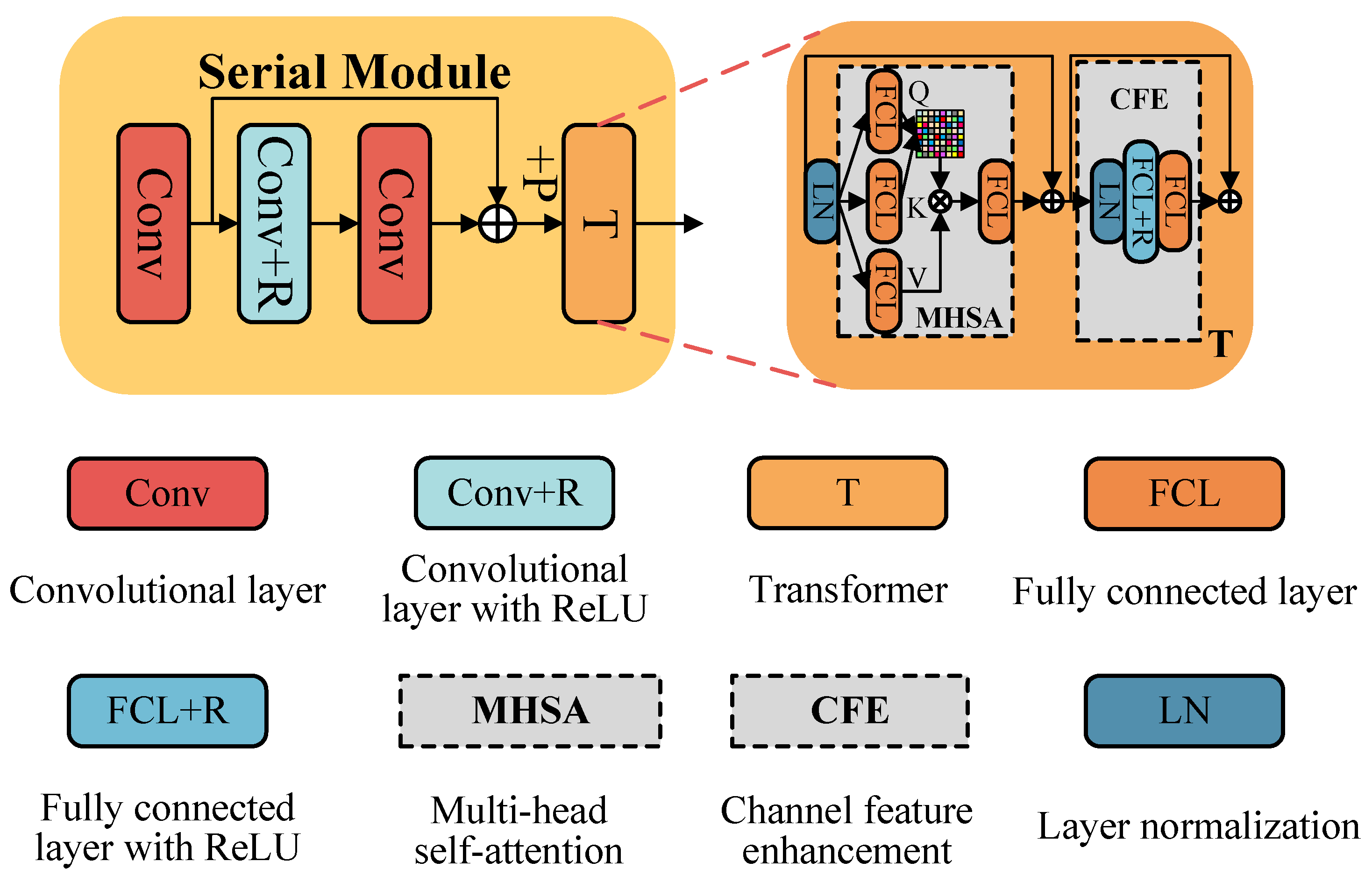
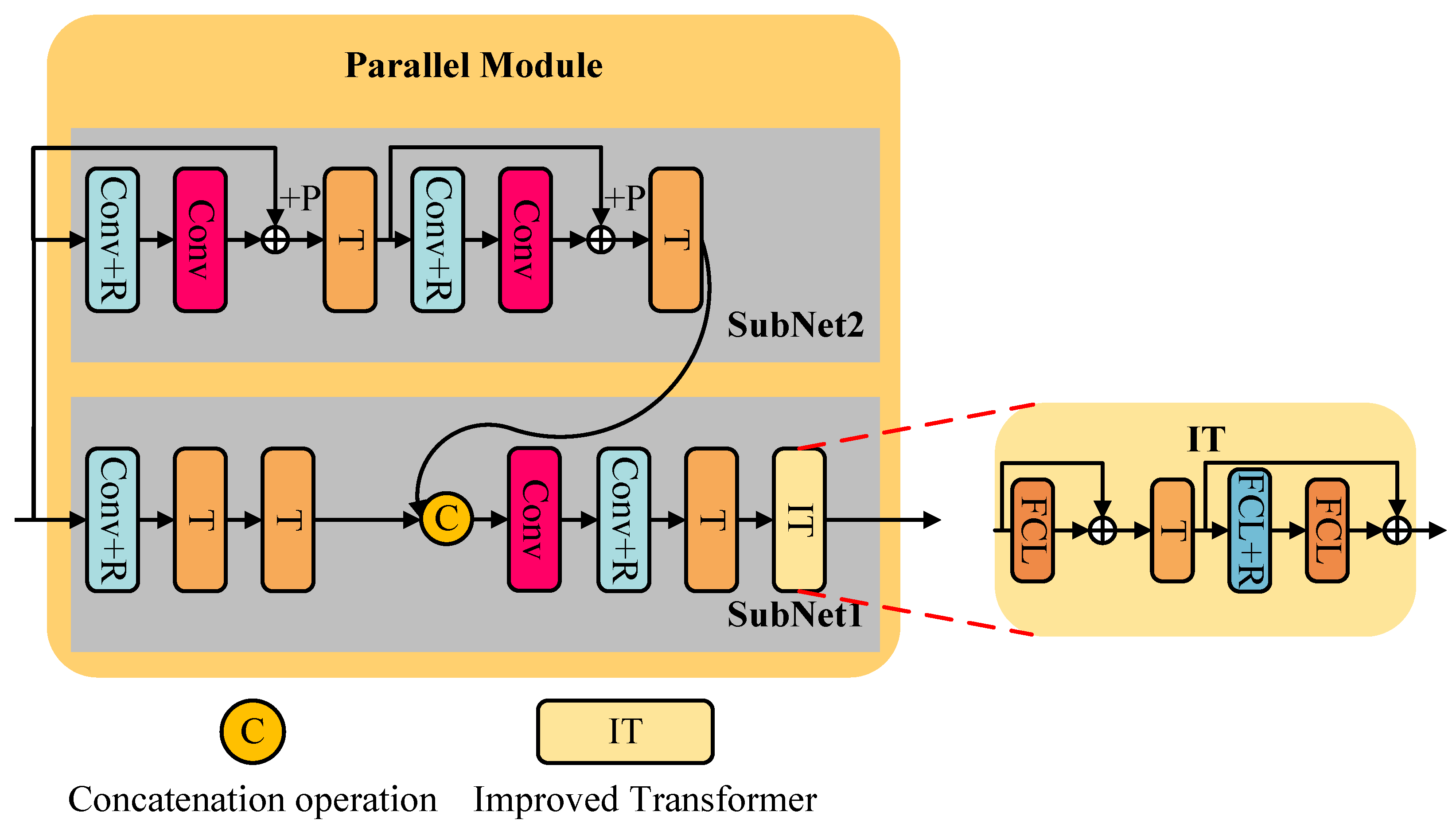
3.2. Detail of the QIS-SPFT Denoiser
4. Experimental Results
4.1. Network Analysis Experiments
4.2. Image Denoising Experimental Results
5. Discussion
- Loss of Image Texture: The proposed method is primarily designed to enhance image fidelity in the context of QIS reconstruction, where input signals are extremely noisy due to photon-limited conditions and sparse bit-plane encoding. In such scenarios, suppressing heavy noise and faithfully recovering the underlying image structure become the main objectives. As a result, our model is trained to minimize pixel-wise reconstruction error, which is well-reflected by metrics such as PSNR. However, this emphasis on fidelity can sometimes lead to a perceptual compromise. Specifically, the network exhibits a mild tendency toward over-smoothing, which may result in the suppression of some fine details, even when such details remain partially visible in the noisy input. This phenomenon stems from the inherent trade-off between aggressive noise suppression and texture preservation.To address this, our network architecture integrates modules for capturing local and global pixel correlations, which help preserve detailed structures to a certain extent. Nevertheless, the current design is still biased toward achieving higher fidelity scores, rather than optimizing for perceptual quality. To further improve the balance between these two aspects, future extensions of this work will consider introducing perceptual-oriented loss functions and incorporating structural attention mechanisms. These improvements are expected to enhance the retention of fine details and visual textures, particularly in important regions, while maintaining strong denoising performance under extreme noise conditions.
- Image Degradation: While the proposed QIS-SPFT framework demonstrates strong performance for photon shot noise suppression in QIS image reconstruction, it is specifically designed for binary bit-plane data under low-light conditions. Its generalization to other degradation types—such as motion blur [32] or haze [33]—has not been explored in this work. The blur degradation is a convolution of the Poisson process of imaging and require additional pre-processing or architectural adaptations. Equation (5) now can be described as:where represents the blur kernel. The haze degradation follows the atmospheric scattering model. Future work may consider extending the framework to incorporate deblurring or dehazing modules to broaden its applicability.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fossum, E.R. Some Thoughts on Future Digital Still Cameras. In Image Sensors and Signal Processing for Digital Still Cameras; CRC Press: Boca Raton, FL, USA, 2017; pp. 305–314. ISBN 9781315221083. [Google Scholar]
- Fossum, E.R. What to do with sub-diffraction-limit (SDL) pixels?—A proposal for a gigapixel digital film sensor (DFS). In Proceedings of the IEEE Workshop on Charge-Coupled Devices and Advanced Image Sensors, Nagano, Japan, 9–11 June 2005; pp. 214–217. [Google Scholar]
- Fossum, E.R. The quanta image sensor (QIS): Concepts and challenges. In Proceedings of the Imaging and Applied Optics, Toronto, ON, Canada, 10–14 July 2011. [Google Scholar]
- Ma, J.; Zhang, D.; Elgendy, O.A.; Masoodian, S. A 0.19 e-rms read noise 16.7 Mpixel stacked quanta image sensor with 1.1 μm-pitch backside illuminated pixels. IEEE Electron. Device Lett. 2021, 42, 891–894. [Google Scholar] [CrossRef]
- Ma, J.; Chan, S.; Fossum, E.R. Review of quanta image sensors for ultralow-light imaging. IEEE Trans. Electron. Devices 2022, 69, 2824–2839. [Google Scholar] [CrossRef]
- Li, C.; Qu, X.; Gnanasambandam, A.; Elgendy, O.A.; Ma, J.; Chan, S.H. Photon-Limited Object Detection Using Non-Local Feature Matching and Knowledge Distillation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCVW), Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Gnanasambandam, A.; Chan, S.H. HDR Imaging with Quanta Image Sensors: Theoretical Limits and Optimal Reconstruction. IEEE Trans. Comput. Imaging 2020, 6, 1571–1585. [Google Scholar] [CrossRef]
- Gyongy, I.; Dutton, N.A.; Henderson, R.K. Single-Photon Tracking for High-Speed Vision. Sensors 2018, 18, 323. [Google Scholar] [CrossRef] [PubMed]
- Elgendy, O.A.; Chan, S.H. Color Filter Arrays for Quanta Image Sensors. IEEE Trans. Comput. Imaging 2020, 6, 652–665. [Google Scholar] [CrossRef]
- Chen, S.; Ceballos, A.; Fossum, E.R. Digital integration sensor. In Proceedings of the International Image Sensor Workshop, Snowbird, UT, USA, 12–16 June 2013. [Google Scholar]
- Fossum, E.R.; Ma, J.; Masoodian, S. Quanta image sensor: Concepts and progress. In Proceedings of the Advanced Photon Counting Techniques X, Baltimore, MD, USA, 5 May 2016. [Google Scholar]
- Fossum, E.R. Modeling the Performance of Single-Bit and Multi-Bit Quanta Image Sensors. IEEE J. Electron. Devices Soc. 2013, 1, 166–174. [Google Scholar] [CrossRef]
- Fossum, E.R. Photon Counting Error Rates in Single-Bit and Multi-Bit Quanta Image Sensors. IEEE J. Electron. Devices Soc. 2016, 4, 136–143. [Google Scholar] [CrossRef]
- Gnanasambandam, A.; Chan, S.H. Exposure-Referred Signal-to-Noise Ratio for Digital Image Sensors. IEEE Trans. Comput. Imaging 2022, 8, 561–575. [Google Scholar] [CrossRef]
- Yang, F.; Lu, Y.M.; Sbaiz, L.; Vetterli, M. Bits from Photons: Oversampled Image Acquisition Using Binary Poisson Statistics. IIEEE Trans. Image Process. 2012, 21, 1421–1436. [Google Scholar] [CrossRef] [PubMed]
- Chan, S.H.; Lu, Y.M. Efficient Image Reconstruction for Gigapixel Quantum Image Sensors. In Proceedings of the 2014 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Atlanta, GA, USA, 3–5 December 2014. [Google Scholar]
- Chan, S.H.; Elgendy, O.A.; Wang, X. Images from Bits: Non-Iterative Image Reconstruction for Quanta Image Sensors. Sensors 2016, 16, 1961. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.H.; Elgendy, O.A.; Chan, S.H. Image Reconstruction for Quanta Image Sensors Using Deep Neural Networks. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Tian, C.; Fei, L.; Zheng, W.; Xu, Y.; Zuo, W.; Lin, C.W. Deep Learning on Image Denoising: An Overview. Neural Netw. 2020, 131, 251–275. [Google Scholar] [CrossRef] [PubMed]
- Buades, A.; Coll, B.; Morel, J.M. Image Denoising Methods. A New Nonlocal Principle. SIAM Rev. 2010, 52, 113–147. [Google Scholar] [CrossRef]
- Andriyanov, N.; Belyanchikov, A.; Vasiliev, K.; Dementiev, V. Restoration of Spatially Inhomogeneous Images Based on Doubly Stochastic Filters. In Proceedings of the 2022 IEEE International Conference on Information Technologies (ITNT), Moscow, Russia, 18–20 May 2022. [Google Scholar] [CrossRef]
- Krasheninnikov, V.; Kuvayskova, Y.; Subbotin, A. Pseudo-gradient Algorithm for Identification of Doubly Stochastic Cylindrical Image Model. In Proceedings of the 2020 International Conference on Information Technology and Nanotechnology (ITNT), Samara, Russia, 23–27 May 2020. [Google Scholar] [CrossRef]
- Jiang, B.; Li, J.; Lu, Y.; Cai, Q.; Song, H.; Lu, G. Efficient Image Denoising Using Deep Learning: A Brief Survey. Inf. Fusion 2025, 118, 103013. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, X.; Han, L.; Nie, K.; Xu, L.; Ma, J. Effect of the Transition Points Mismatch on Quanta Image Sensors. Sensors 2018, 18, 4357. [Google Scholar] [CrossRef] [PubMed]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A Database of Human Segmented Natural Images and Its Application to Evaluating Segmentation Algorithms and Measuring Ecological Statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001. [Google Scholar]
- Agustsson, E.; Timofte, R. NTIRE 2017 Challenge on Single Image Super-Resolution: Dataset and Study. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Timofte, R.; Agustsson, E.; Van Gool, L.; Yang, M.H.; Zhang, L. NTIRE 2017 Challenge on Single Image Super-Resolution: Methods and Results. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ma, K.; Duanmu, Z.; Wu, Q.; Wang, Z.; Yong, H.; Li, H.; Zhang, L. Waterloo Exploration Database: New Challenges for Image Quality Assessment Models. IEEE Trans. Image Process. 2016, 26, 1004–1016. [Google Scholar] [CrossRef] [PubMed]
- Roth, S.; Black, M.J. Fields of Experts: A Framework for Learning Image Priors. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Franzen, R. Kodak Lossless True Color Image Suite. 1999, Volume 2. Available online: http://r0k.us/graphics/kodak (accessed on 18 March 2023).
- Zhang, K.; Zuo, W.; Zhang, L.; Zhang, D. Plug-and-Play Image Restoration with Deep Denoiser Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 6360–6376. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, C.; Xu, J. Motion Deblurring Method of Quanta Image Sensor Based on Spatial Correlation and Frequency Domain Characteristics. Opt. Eng. 2024, 63, 083102. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Hu, E.; Wang, A.; Shiri, B.; Lin, W. VNDHR: Variational Single Nighttime Image Dehazing for Enhancing Visibility in Intelligent Transportation Systems via Hybrid Regularization. IEEE Trans. Intell. Transp. Syst. 2025, 1–15. [Google Scholar] [CrossRef]
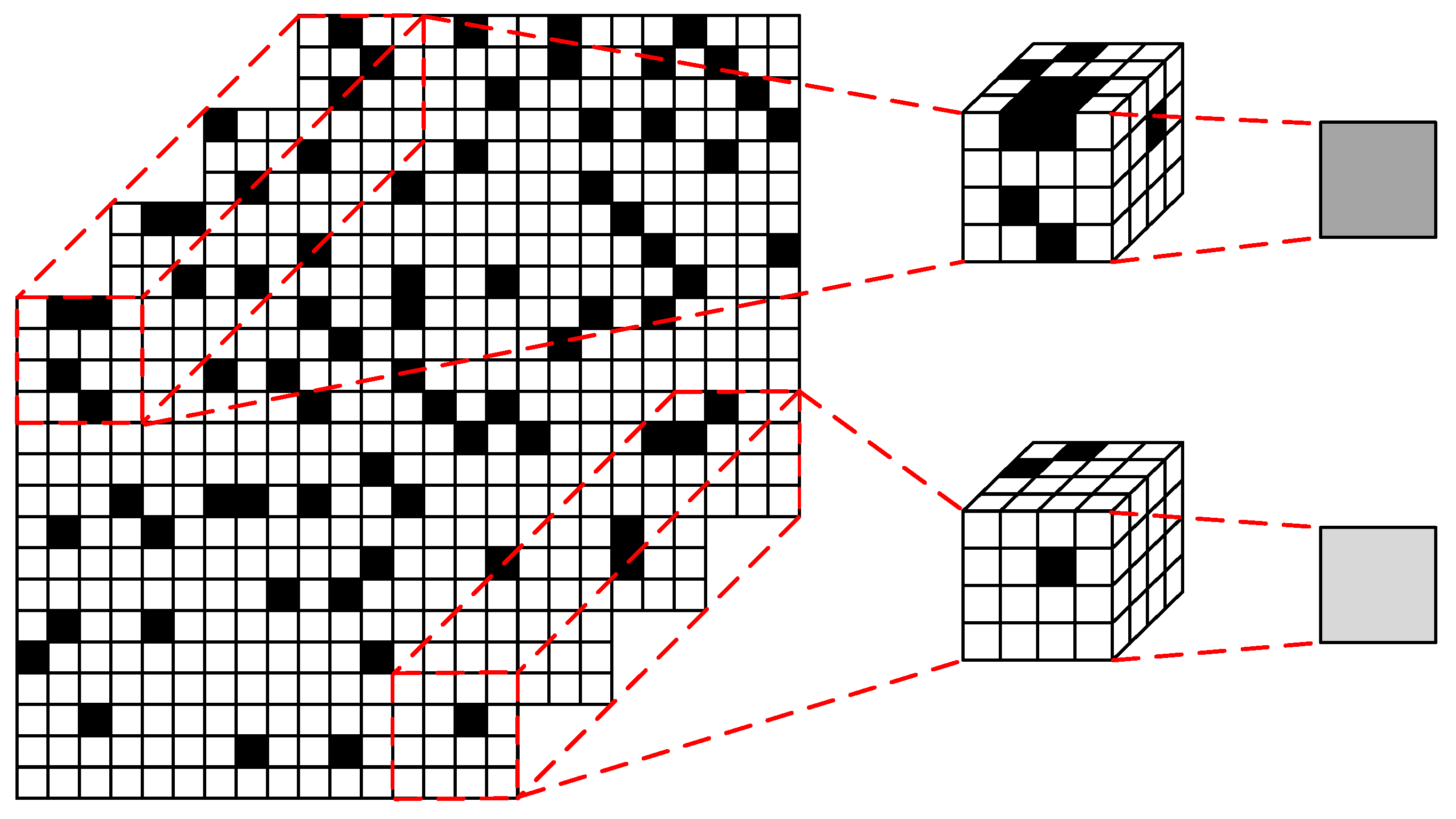






| Method | PSNR (dB) |
|---|---|
| QIS-SPFT without Anscombe, without IT | 28.214 |
| QIS-SPFT without Anscombe, with IT | 28.253 |
| QIS-SPFT with Anscombe, without IT | 28.221 |
| QIS-SPFT with Anscombe, with IT | 28.269 |
| Methods | Noise Level 1 | Noise Level 2 | Noise Level 3 | Noise Level 4 |
|---|---|---|---|---|
| MLE [15] | 20.32 | 19.98 | 19.65 | 13.84 |
| TD-BM3D [17] | 28.89 | 28.76 | 27.86 | 23.66 |
| QISNet [18] | 29.31 | 29.01 | 28.32 | 24.32 |
| DPIR [31] | 30.01 | 29.33 | 28.79 | 25.42 |
| QIS-SPFT (proposed) | 30.32 | 29.78 | 29.13 | 25.85 |
| Images | Cameraman | House | Pepper | Starfish | Monarch | Parrot |
|---|---|---|---|---|---|---|
| Noise level 1 | ||||||
| MLE [15] | 19.72 | 22.11 | 20.92 | 19.76 | 19.74 | 18.88 |
| TD-BM3D [17] | 29.21 | 33.32 | 31.44 | 30.31 | 29.34 | 29.04 |
| QISNet [18] | 29.74 | 33.77 | 31.91 | 30.89 | 29.83 | 29.64 |
| DPIR [31] | 30.43 | 34.42 | 32.63 | 31.52 | 30.62 | 30.31 |
| QIS-SPFT (proposed) | 30.77 | 34.75 | 32.80 | 31.95 | 30.91 | 30.75 |
| Noise level 2 | ||||||
| MLE [15] | 18.21 | 21.42 | 18.91 | 18.43 | 19.22 | 17.84 |
| TD-BM3D [17] | 28.77 | 31.64 | 30.21 | 29.02 | 29.88 | 28.44 |
| QISNet [18] | 29.33 | 32.12 | 30.84 | 29.54 | 30.34 | 29.01 |
| DPIR [31] | 29.72 | 33.53 | 31.23 | 30.30 | 30.77 | 29.33 |
| QIS-SPFT (proposed) | 30.07 | 33.92 | 31.71 | 30.65 | 31.02 | 29.84 |
| Noise level 3 | ||||||
| MLE [15] | 18.19 | 21.34 | 18.94 | 18.88 | 18.26 | 18.66 |
| TD-BM3D [17] | 27.22 | 31.24 | 28.34 | 27.21 | 27.84 | 27.34 |
| QISNet [18] | 28.41 | 31.86 | 28.91 | 27.86 | 28.52 | 27.88 |
| DPIR [31] | 29.66 | 32.91 | 30.64 | 29.15 | 29.72 | 28.81 |
| QIS-SPFT (proposed) | 29.90 | 33.24 | 30.89 | 29.46 | 30.13 | 29.16 |
| Noise level 4 | ||||||
| MLE [15] | 13.23 | 15.44 | 14.10 | 12.98 | 13.32 | 13.58 |
| TD-BM3D [17] | 23.91 | 25.71 | 23.32 | 23.11 | 23.97 | 24.23 |
| QISNet [18] | 24.32 | 26.15 | 23.91 | 23.74 | 24.51 | 24.72 |
| DPIR [31] | 25.88 | 27.02 | 26.41 | 24.97 | 26.24 | 26.58 |
| QIS-SPFT (proposed) | 26.10 | 28.34 | 26.85 | 25.35 | 26.62 | 26.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Gao, Z. Noise Suppressed Image Reconstruction for Quanta Image Sensors Based on Transformer Neural Networks. J. Imaging 2025, 11, 160. https://doi.org/10.3390/jimaging11050160
Wang G, Gao Z. Noise Suppressed Image Reconstruction for Quanta Image Sensors Based on Transformer Neural Networks. Journal of Imaging. 2025; 11(5):160. https://doi.org/10.3390/jimaging11050160
Chicago/Turabian StyleWang, Guanjie, and Zhiyuan Gao. 2025. "Noise Suppressed Image Reconstruction for Quanta Image Sensors Based on Transformer Neural Networks" Journal of Imaging 11, no. 5: 160. https://doi.org/10.3390/jimaging11050160
APA StyleWang, G., & Gao, Z. (2025). Noise Suppressed Image Reconstruction for Quanta Image Sensors Based on Transformer Neural Networks. Journal of Imaging, 11(5), 160. https://doi.org/10.3390/jimaging11050160





