A Transfer Learning-Based VGG-16 Model for COD Detection in UV–Vis Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset Acquisition
2.1.1. Water Sample Collection
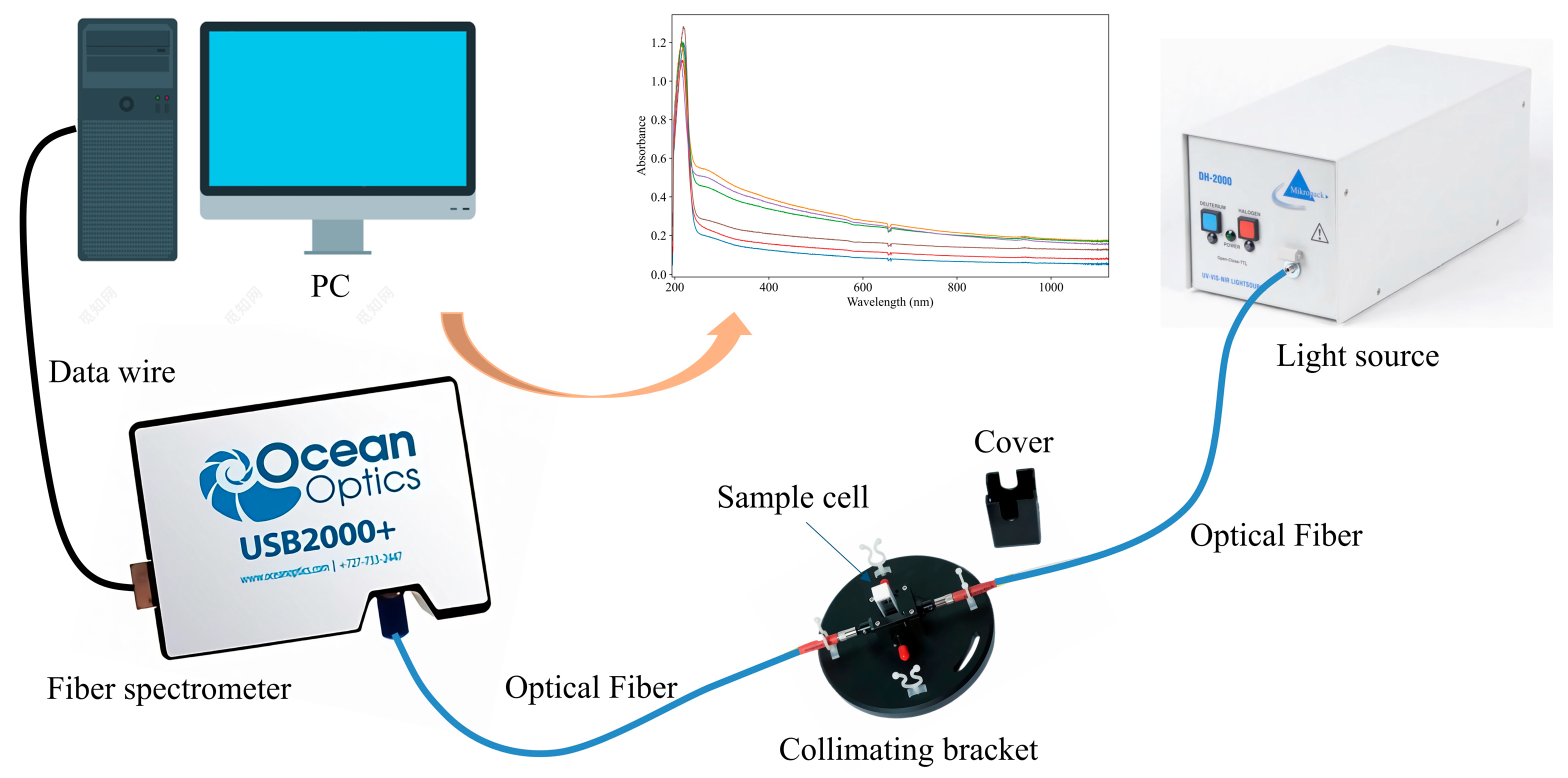
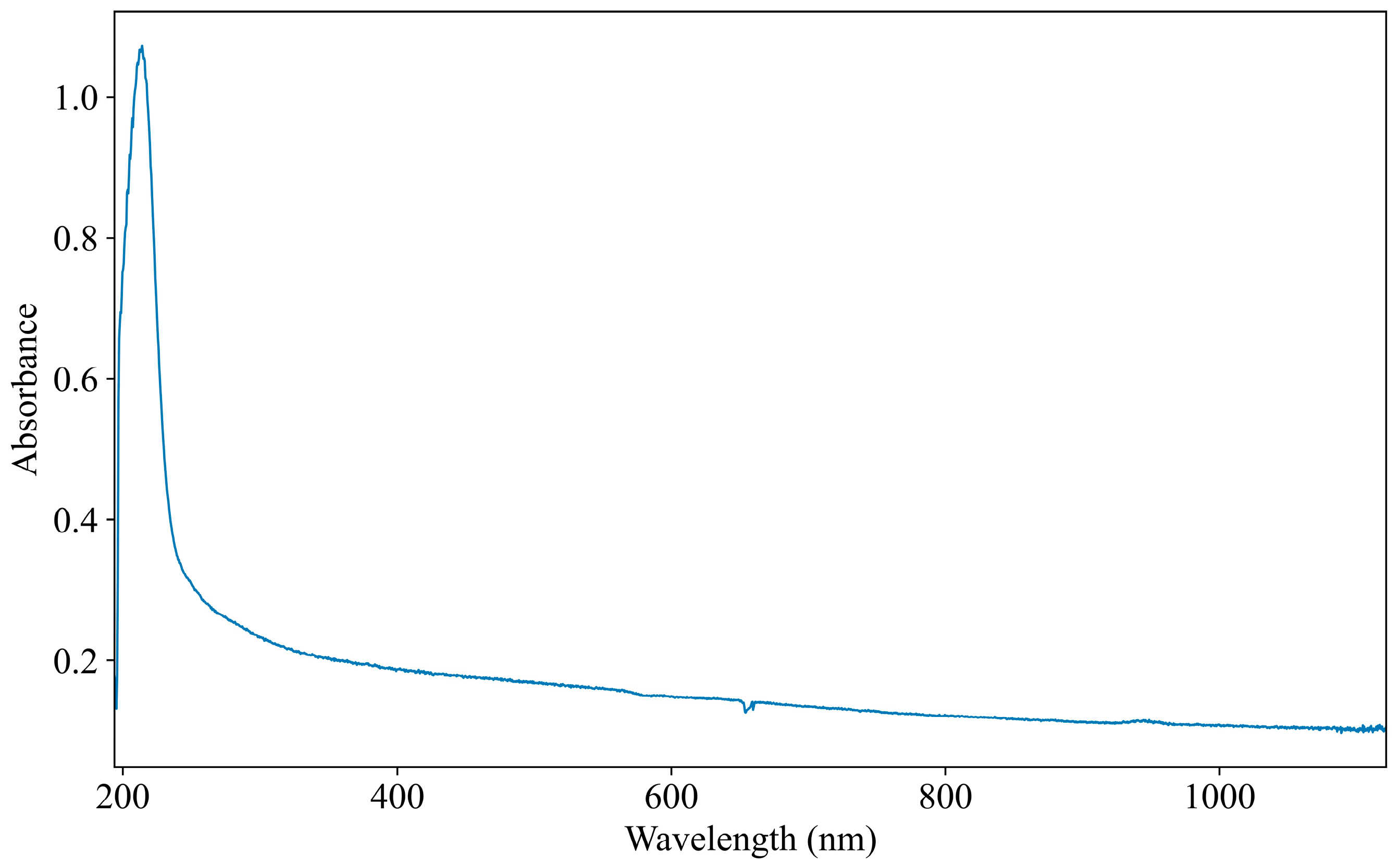
2.1.2. Spectral Acquisition
2.1.3. COD Standard Value Measurement
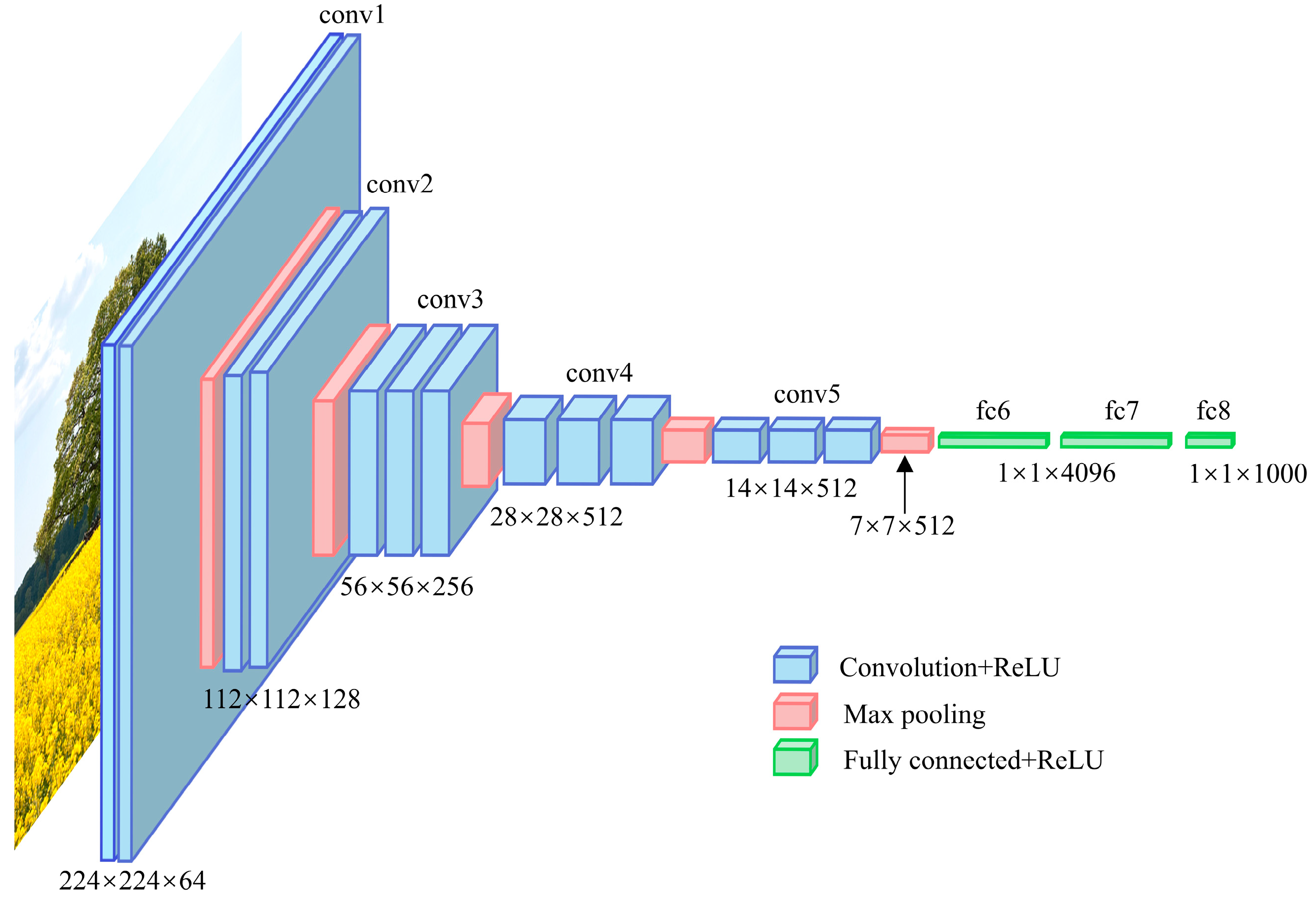
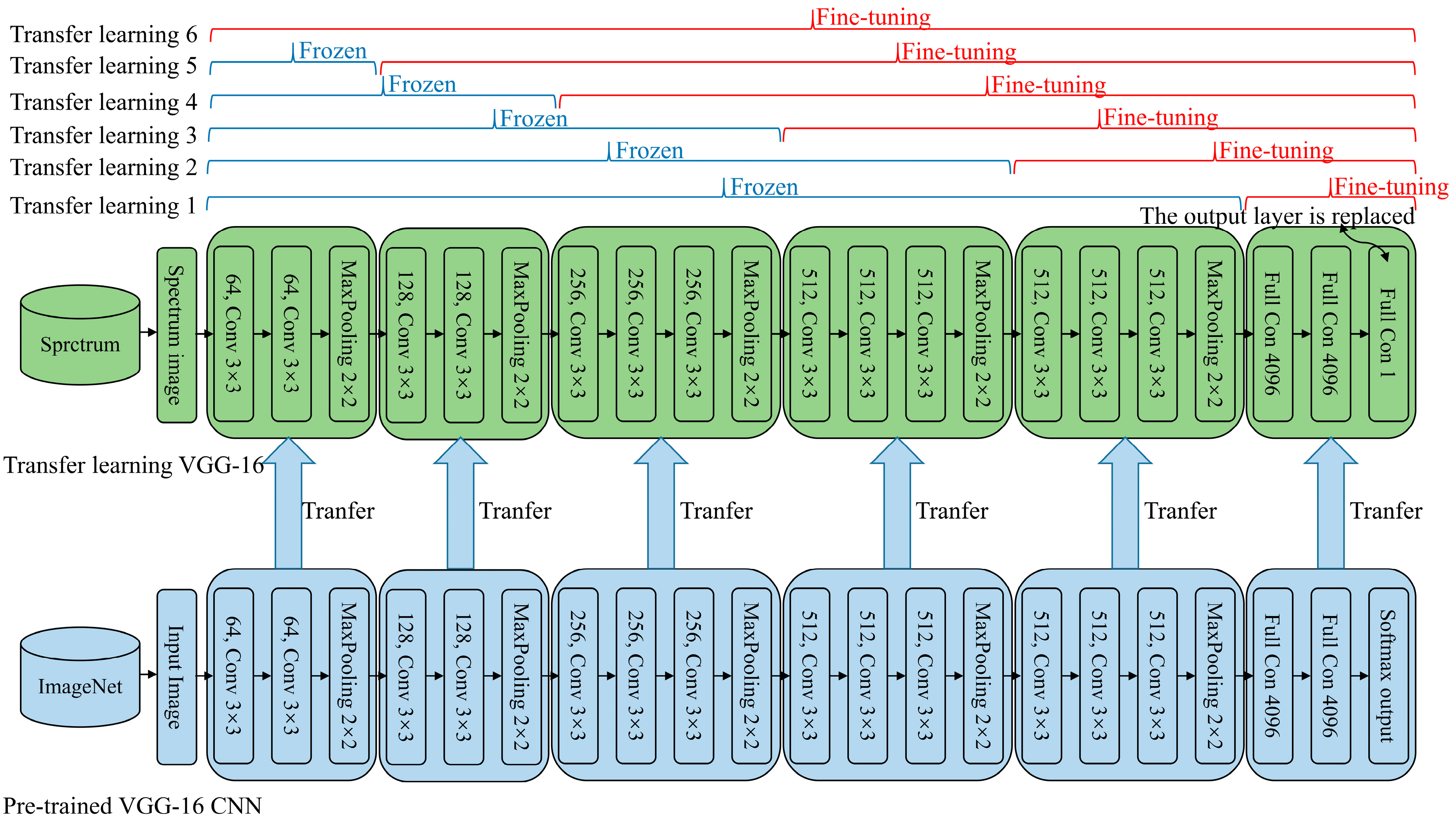
2.2. VGG-16 Architecture
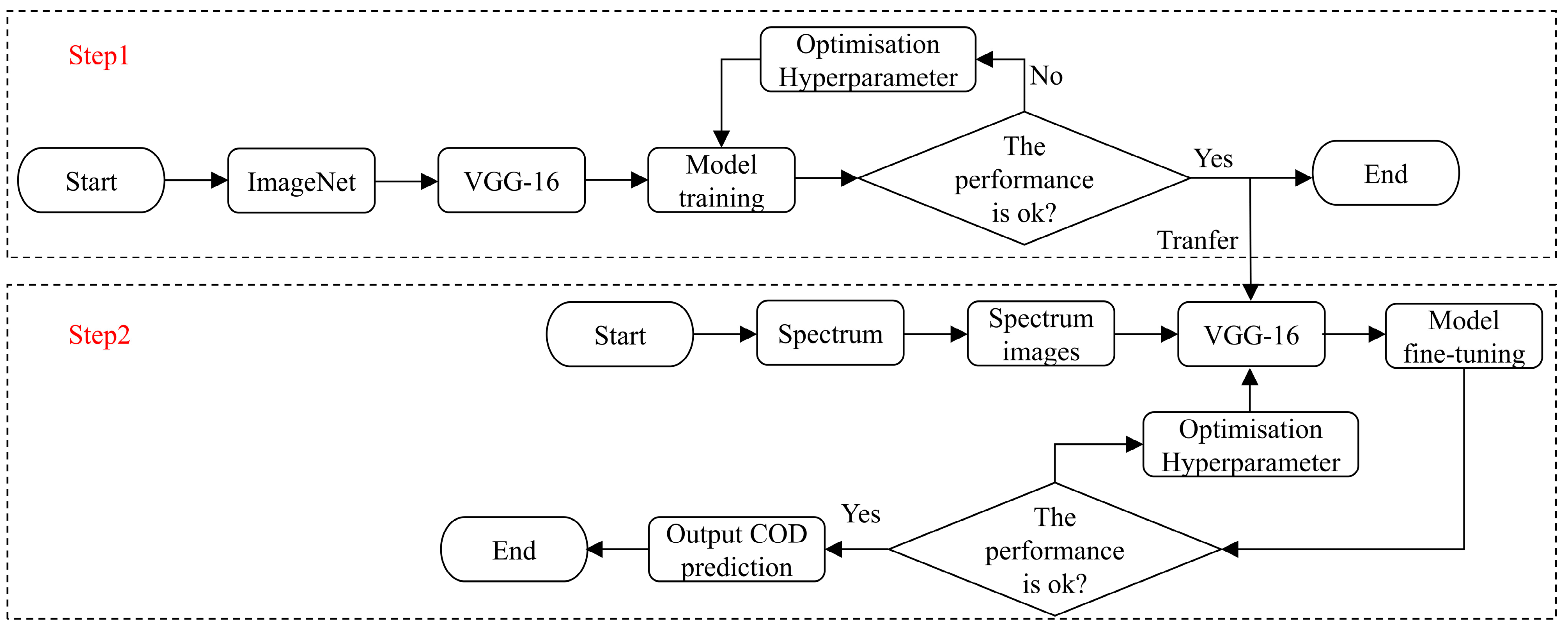
2.3. The Proposed Method
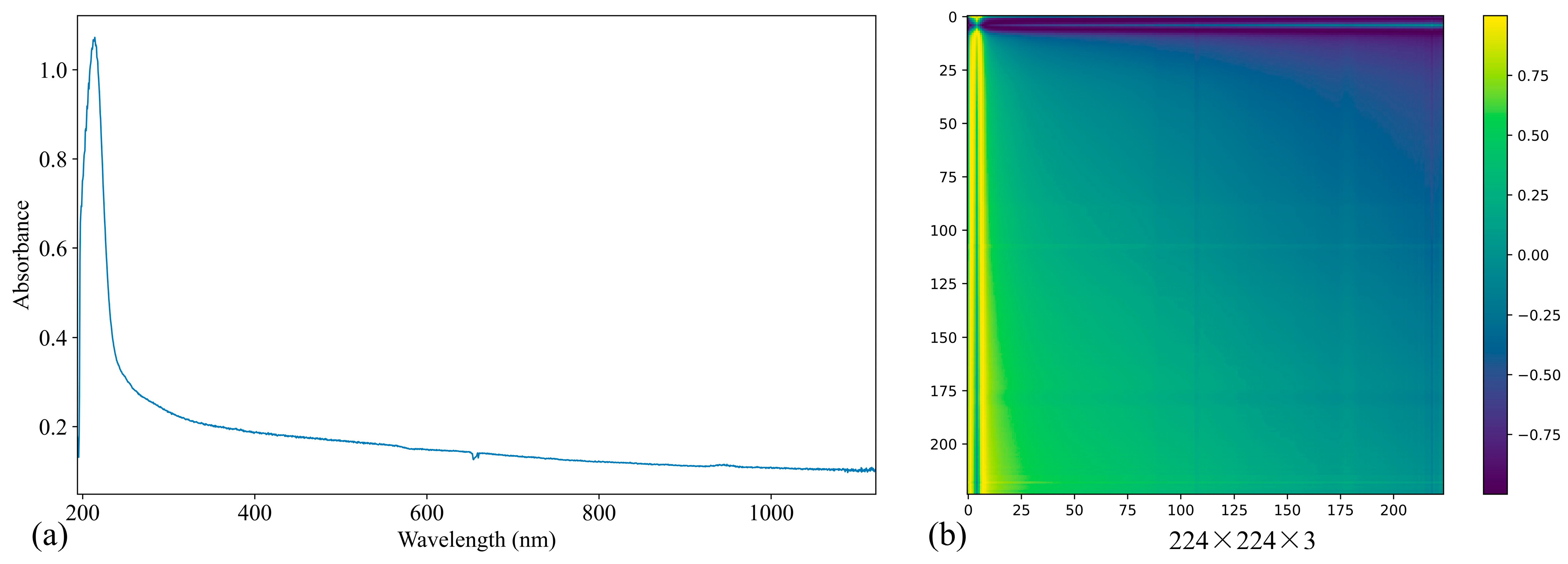
2.3.1. Spectrum Pre-Processing Based GAF
2.3.2. Transfer Learning
2.3.3. Fine-Tuning
2.4. COD Prediction Process of the Proposed Method
2.5. Performance Indices
3. Experiments and Results Analysis
3.1. Selection of Model
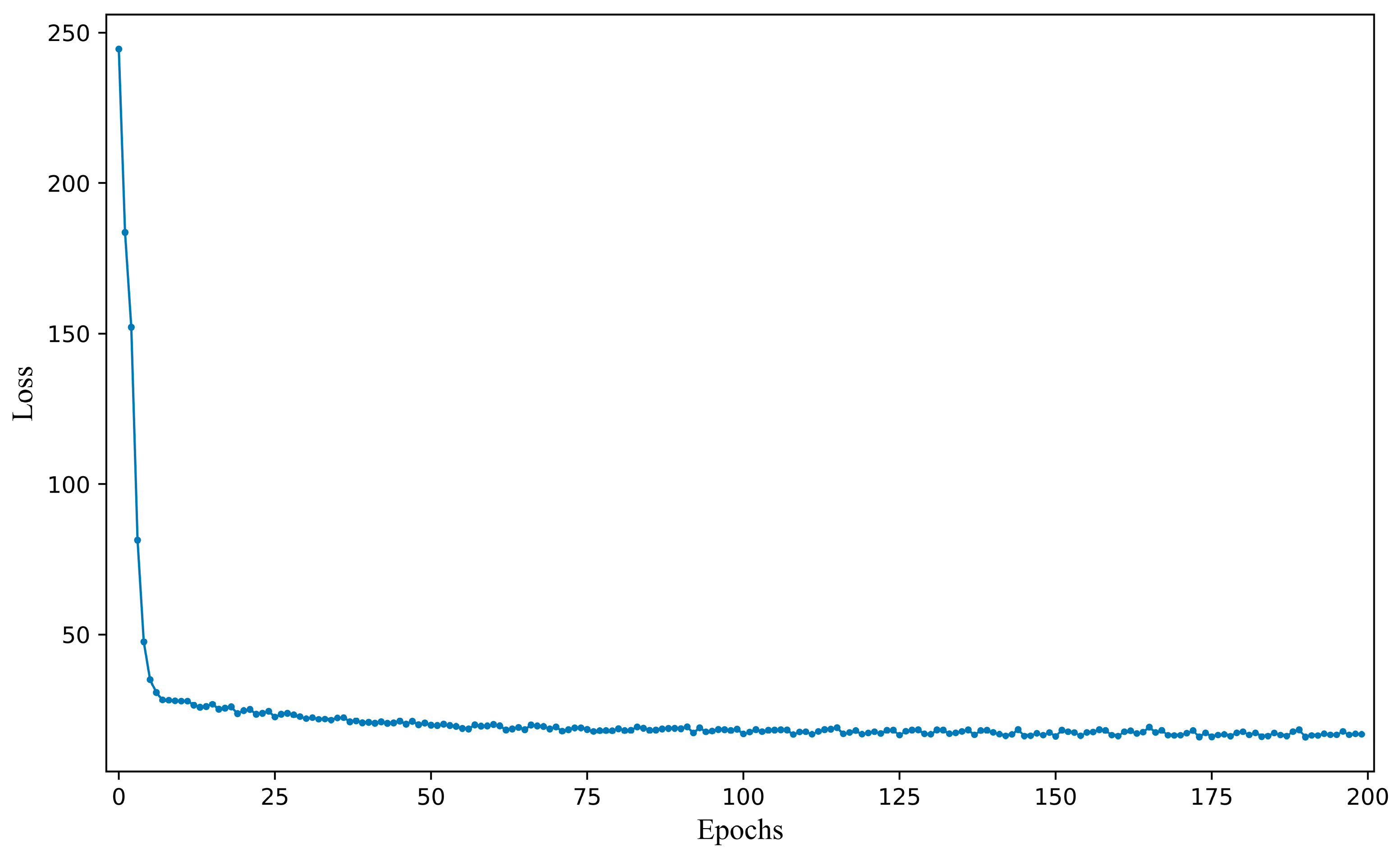
3.2. Selection of Hyperparameters
3.3. Fine-Tuning Procedure
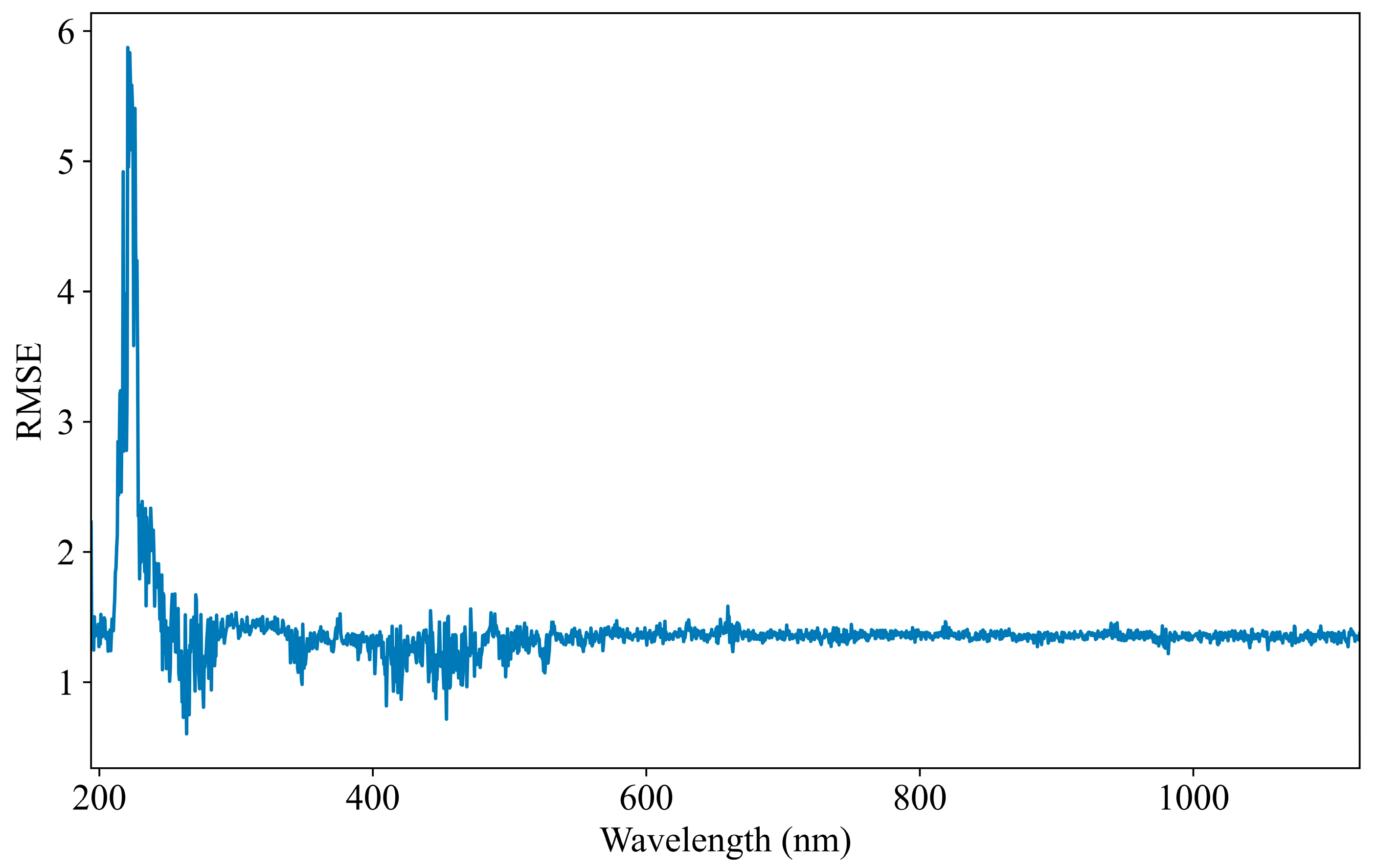
3.4. Visualization of Feature Importance
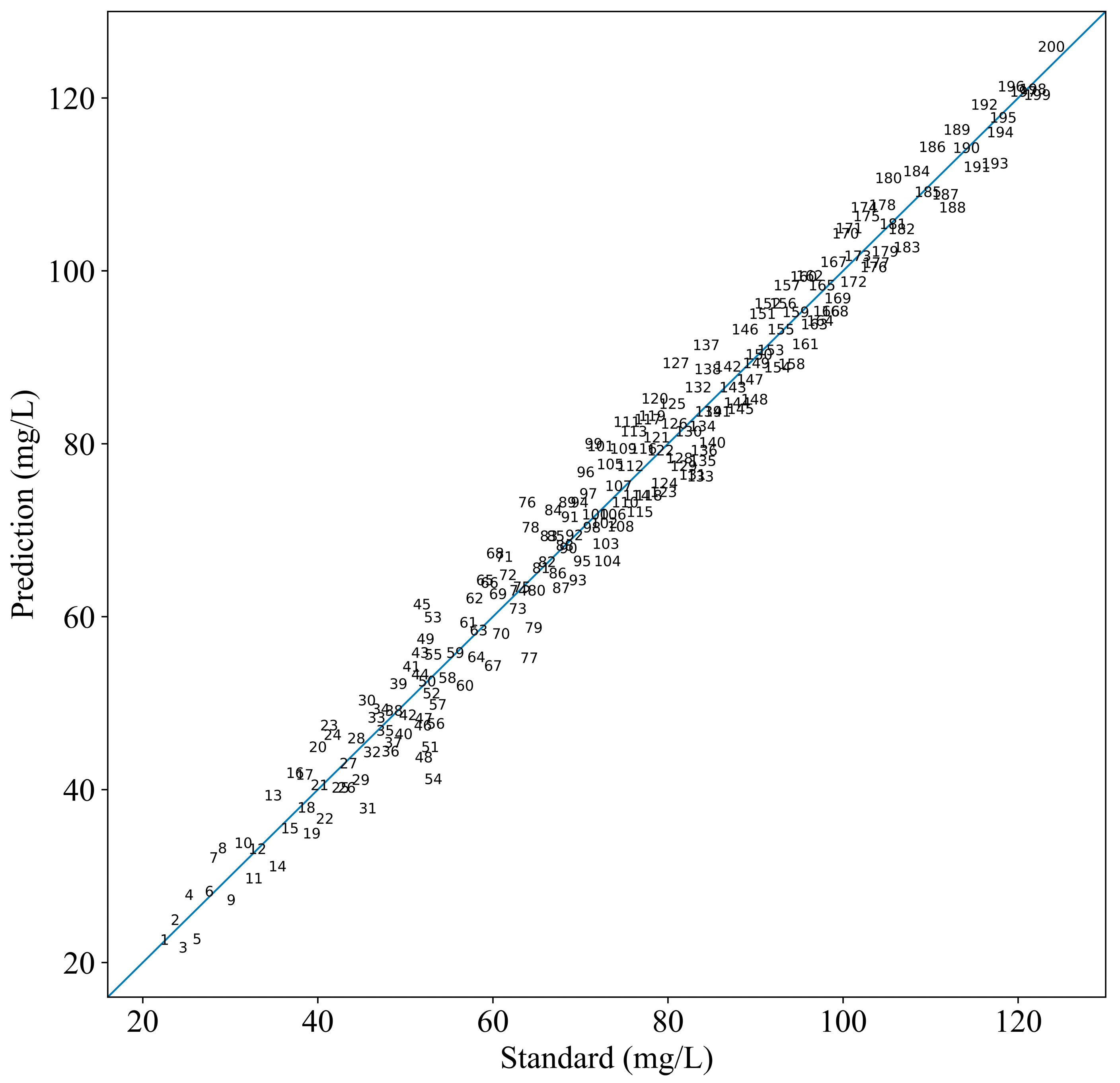
3.5. Model Performance Analysis
3.6. Comparison with Other Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Zhu, Y.; Guo, G.; An, L.; Fang, W.; Tan, Y.; Jiang, J.; Bing, X.; Song, Q.; Zhou, Q.; et al. A comprehensive risk assessment of microplastics in soil, water, and atmosphere: Implications for human health and environmental safety. Ecotox. Environ. Safe. 2024, 285, 117154. [Google Scholar] [CrossRef] [PubMed]
- Abdallah, S.M.; Muhammed, R.E.; Mohamed, R.E.; Daous, H.E.; Saleh, D.M.; Ghorab, M.A.; Chen, S.; El-Sayyad, G.S. Assessment of biochemical biomarkers and environmental stress indicators in some freshwater fish. Environ. Geochem. Health 2024, 46, 1–19. [Google Scholar] [CrossRef]
- Bansal, S.; Geetha, G. A Machine Learning Approach towards Automatic Water Quality Monitoring. J. Water Chem. Technol. 2020, 42, 321–328. [Google Scholar] [CrossRef]
- Pansa-Ngat, P.; Jedsukontorn, T.; Hunsom, M. Optimal Hydrogen Production Coupled with Pollutant Removal from Biodiesel Wastewater Using a Thermally Treated TiO2 Photocatalyst (P25): Influence of the Operating Conditions. Nanomaterials 2018, 8, 96. [Google Scholar] [CrossRef]
- Waras, M.N.; Zabidi, M.A.; Ismail, Z.; Sangaralingam, M.; Gazzali, A.M.; Harun, M.S.R.; Aziz, M.Y.; Mohamed, R.; Najib, M.N.M. Comparative analysis of water quality index and river classification in Kereh River, Penang, Malaysia: Impact of untreated swine wastewater from Kampung Selamat pig farms. Water Environ. Res. 2024, 96, e11095. [Google Scholar] [CrossRef]
- Nica, A.V.; Olaru, E.A.; Bradu, C.; Dumitru, A.; Avramescu, S.M. Catalytic Ozonation of Ibuprofen in Aqueous Media over Polyaniline–Derived Nitrogen Containing Carbon Nanostructures. Nanomaterials 2022, 12, 3468. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, C.; Ye, R.; Duan, Q. Advances on Water Quality Detection by UV-Vis Spectroscopy. Appl. Sci. 2020, 10, 6874. [Google Scholar] [CrossRef]
- Huang, J.; Chow, C.W.K.; Shi, Z.; Fabris, R.; Mussared, A.; Hallas, G.; Monis, P.; Jin, B.; Saint, C.P. Stormwater monitoring using on-line UV-Vis spectroscopy. Environ. Sci. Pollut. Res. 2022, 29, 19530–19539. [Google Scholar] [CrossRef] [PubMed]
- Hossain, S.; Chow, C.W.K.; Hewa, G.A.; Cook, D.; Harris, M. Spectrophotometric Online Detection of Drinking Water Disinfectant: A Machine Learning Approach. Sensors 2020, 20, 1–29. [Google Scholar] [CrossRef]
- Qin, X.; Gao, F.; Chen, G. Wastewater quality monitoring system using sensor fusion and machine learning techniques. Water Res. 2012, 46, 1133–1144. [Google Scholar] [CrossRef]
- Cao, H.; Qu, W.; Yang, X. A rapid determination method for chemical oxygen demand in aquaculture wastewater using the ultraviolet absorbance spectrum and chemometrics. Anal. Methods 2014, 6, 3799–3803. [Google Scholar] [CrossRef]
- Li, P.; Qu, J.; He, Y.; Bo, Z.; Pei, M. Global calibration model of UV-Vis spectroscopy for COD estimation in the effluent of rural sewage treatment facilities. RSC Adv. 2020, 10, 20691–20700. [Google Scholar] [CrossRef]
- Lyu, Y.; Zhao, W.; Kinouchi, T.; Nagano, T.; Tanaka, S. Development of statistical regression and artificial neural network models for estimating nitrogen, phosphorus, COD, and suspended solid concentrations in eutrophic rivers using UV–Vis spectroscopy. Environ. Monit. Assess. 2023, 195, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Wang, J.; Li, J.; Fan, A.; Zhang, Y.; Xu, C.; Qin, H.; Mu, F.; Xu, T. Research on COD measurement method based on UV-Vis absorption spectra of transmissive and reflective detection systems. Front. Environ. Sci. 2023, 11, 1–12. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, J. Simultaneous measurement of chemical oxygen demand and turbidity in water based on broad optical spectra using backpropagation neural network. Chemometr. Intell. Lab. Syst. 2023, 237, 104830. [Google Scholar] [CrossRef]
- Moon, J.; Suh, S.; Jung, S.; Baek, S.; Pyo, J. Deep learning-based mapping of total suspended solids in rivers across South Korea using high resolution satellite imagery. GIsci. Remote Sens. 2024, 61, 1–27. [Google Scholar] [CrossRef]
- Hou, T.; Li, J. Application of mask R-CNN for building detection in UAV remote sensing images. Heliyon 2024, 10, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Abdulsalam, W.H.; Mashhadani, S.; Hussein, S.S.; Hashim, A.A. Artificial Intelligence Techniques to Identify Individuals through Palm Image Recognition. Int. J. Math. Comput. Sci. 2025, 20, 165–171. [Google Scholar] [CrossRef]
- Jia, W.; Zhang, H.; Ma, J.; Liang, G.; Wang, J.; Liu, X. Study on the Predication Modeling of COD for Water Based on UV-VIS Spectroscopy and CNN Algorithm of Deep Learning. Spectrosc. Spect. Anal. 2020, 40, 2981–2988. [Google Scholar]
- Ye, B.; Cao, X.; Liu, H.; Wang, Y.; Tang, B.; Chen, C.; Chen, Q. Water chemical oxygen demand prediction model based on the CNN and ultraviolet-visible spectroscopy. Front. Environ. Sci. 2022, 10, 1–16. [Google Scholar] [CrossRef]
- Xia, M.; Yang, R.; Zhao, N.; Chen, X.; Dong, M.; Chen, J. A Method of Water COD Retrieval Based on 1D CNN and 2D Gabor Transform for Absorption–Fluorescence Spectra. Micromachines 2023, 14, 1128. [Google Scholar] [CrossRef] [PubMed]
- Guan, L.; Zhou, Y.; Yang, S. An improved prediction model for COD measurements using UV-Vis spectroscopy. RSC Adv. 2024, 14, 193–205. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Hu, X. Effective distributed convolutional neural network architecture for remote sensing images target classification with a pre-training approach. J. Syst. Eng. Electron. 2019, 30, 238–244. [Google Scholar]
- Li, H.; Liu, T.; Fu, Y.; Li, W.; Zhang, M.; Yang, X.; Song, D.; Wang, J.; Wang, Y.; Huang, M. Rapid classification of copper concentrate by portable laser-induced breakdown spectroscopy combined with transfer learning and deep convolutional neural network. Chin. Opt. Lett. 2023, 21, 043001. [Google Scholar] [CrossRef]
- Basha, S.H.S.; Tula, D.; Vinakota, S.K.; Dubey, S.R. Target aware network architecture search and compression for efficient knowledge transfer. Multimed. Syst. 2024, 30, 1–13. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, C.; Xie, M.; Cao, B. Classification Method of Composite Insulator Surface Image Based on GAN and CNN. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 2242–2251. [Google Scholar] [CrossRef]
- Li, W.; Guo, E.; Zhao, H.; Li, Y.; Miao, L.; Liu, C.; Sun, W. Evaluation of transfer ensemble learning-based convolutional neural network models for the identification of chronic gingivitis from oral photographs. BMC Oral Health 2024, 24, 1–12. [Google Scholar] [CrossRef]
- Bansal, K.; Singh, A. Development of VGG-16 Transfer Learning Framework for Geographical Landmark Recognition. Intell. Decis. Technol. 2023, 17, 799–810. [Google Scholar] [CrossRef]
- Prasshanth, C.V.; Venkatesh, S.N.; Mahanta, T.K.; Sakthivel, N.R.; Sugumaran, V. Fault diagnosis of monoblock centrifugal pumps using pre-trained deep learning models and scalogram images. Eng. Appl. Artif. Intel. 2024, 136, 1–12. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Balderas, L.; Lastra, M.; Benitez, J.M. Optimizing Convolutional Neural Network Architectures. Mathematics 2024, 12, 1–19. [Google Scholar] [CrossRef]
- Meir, Y.; Tzach, Y.; Hodassman, S.; Tevet, O.; Kanter, I. Towards a universal mechanism for successful deep learning. Sci. Rep. 2024, 14, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Guan, H.; Qiu, W.; Shen, L.; Liu, H.; Tian, L.; Hou, D.; Zhang, G. Quantitative detection of hepatocyte mixture based on terahertz time-domain spectroscopy using spectral image analysis methods. Spectrochim. Acta A 2025, 326, 125235. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Chen, X.; Wang, Y.; Bai, Y.; Pu, Z. Exploiting graph neural network with one-shot learning for fault diagnosis of rotating machinery. Int. J. Mach. Learn. Cyb. 2024, 15, 5279–5290. [Google Scholar] [CrossRef]
- Balaji, E.; Elumalai, V.K.; Sandhiya, D.; Priya, R.M.S.; Shantharajah, S.P. Parkinson’s disease detection and stage classification: Quantitative gait evaluation through variational mode decomposition and DCNN architecture. Connect. Sci. 2024, 36, 1–26. [Google Scholar]
- Jat, T.; Patil, N.; Bhat, P. Detection of heart arrhythmia with electrocardiography. Netw. Model. Anal. Health Inform. Bioinformatics 2024, 13, 1–13. [Google Scholar]
- Li, X.; Zhang, J.; Xiao, B.; Zeng, Y.; Lv, S.; Qian, J.; Du, Z. Fault Diagnosis of Hydropower Units Based on Gramian Angular Summation Field and Parallel CNN. Energies 2024, 17, 3084. [Google Scholar] [CrossRef]
- Huang, P.; Huang, J.; Huang, Y.; Yang, M.; Kong, R.; Sun, H.; Han, J.; Guo, H.; Wang, S. Optimization and evaluation of facial recognition models for Williams-Beuren syndrome. Eur. J. Pediatr. 2024, 183, 3797–3808. [Google Scholar] [CrossRef]
- Ikechukwu, A.V. Leveraging Transfer Learning for Efficient Diagnosis of COPD Using CXR Images and Explainable AI Techniques. Intel. Artific. 2024, 24, 133–151. [Google Scholar]
- Boiger, R.; Churakov, S.V.; Llagaria, I.B.; Kosakowski, G.; Wüst, R.; Prasianakis, N.I. Direct mineral content prediction from drill core images via transfer learning. Swiss. J. Geosci. 2024, 117, 1–26. [Google Scholar] [CrossRef]
- Alves, E.M.; Rodrigues, R.J.; Corrêa, C.D.; Fidemann, T.; Rocha, J.C.; Buzzo, J.L.L.; Neto, P.D.; Núñez, E.G.F. Use of ultraviolet–visible spectrophotometry associated with artificial neural networks as an alternative for determining the water quality index. Environ. Monit. Assess. 2018, 190, 319. [Google Scholar] [CrossRef] [PubMed]
| Sample Set | Samples | Mean (mg/L) | Minimum (mg/L) | Maximum (mg/L) | Standard Deviation (mg/L) |
|---|---|---|---|---|---|
| Training set | 800 | 67.86 | 23.1 | 128.4 | 27.59 |
| Testing set | 200 | 67.42 | 24.3 | 126.2 | 27.12 |
| All | 1000 | 67.57 | 23.1 | 128.4 | 27.41 |
| Method. | μ | σ |
|---|---|---|
| Transfer learning mode 1 | 8.3619 | 0.1661 |
| Transfer learning mode 2 | 7.5197 | 0.1689 |
| Transfer learning mode 3 | 5.6497 | 0.1685 |
| Transfer learning mode 4 | 4.3801 | 0.1656 |
| Transfer learning mode 5 | 5.0113 | 0.1755 |
| Transfer learning mode 6 | 6.2498 | 0.1717 |
| Learning Rate | Batch Size | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 16 | 32 | 64 | 128 | ||||||
| μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | |
| 0.00005 | 4.6412 | 0.1924 | 4.5679 | 0.1547 | 4.3935 | 0.1539 | 4.2818 | 0.1620 | 4.7392 | 0.1608 |
| 0.0001 | 5.3089 | 0.1743 | 4.4464 | 0.1672 | 4.2318 | 0.1528 | 4.5026 | 0.1542 | 5.1408 | 0.1535 |
| 0.0005 | 5.4709 | 0.1937 | 5.9191 | 0.1643 | 4.7652 | 0.1542 | 4.4704 | 0.1535 | 5.7828 | 0.1596 |
| 0.001 | 6.1552 | 0.1734 | 4.3801 | 0.1656 | 5.1627 | 0.1643 | 5.0266 | 0.1673 | 5.0808 | 0.1658 |
| 0.003 | 6.5127 | 0.2038 | 5.3841 | 0.1734 | 5.1104 | 0.1618 | 4.8098 | 0.1595 | 4.8264 | 0.1729 |
| 0.005 | 5.7071 | 0.1967 | 6.1594 | 0.2172 | 6.1593 | 0.1706 | 5.3534 | 0.1632 | 4.7859 | 0.1794 |
| 0.01 | 6.3373 | 0.2126 | 6.5447 | 0.2237 | 5.3286 | 0.1943 | 5.1603 | 0.1741 | 5.1867 | 0.1672 |
| Method | Calibration Set | Prediction Set | ||
|---|---|---|---|---|
| R2 | RMSEC | R2 | RMSEP | |
| Proposed method | 0.9783 | 3.8834 | 0.9751 | 4.1662 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Tauqeer, I.M.; Shao, Z.; Yu, H. A Transfer Learning-Based VGG-16 Model for COD Detection in UV–Vis Spectroscopy. J. Imaging 2025, 11, 159. https://doi.org/10.3390/jimaging11050159
Li J, Tauqeer IM, Shao Z, Yu H. A Transfer Learning-Based VGG-16 Model for COD Detection in UV–Vis Spectroscopy. Journal of Imaging. 2025; 11(5):159. https://doi.org/10.3390/jimaging11050159
Chicago/Turabian StyleLi, Jingwei, Iqbal Muhammad Tauqeer, Zhiyu Shao, and Haidong Yu. 2025. "A Transfer Learning-Based VGG-16 Model for COD Detection in UV–Vis Spectroscopy" Journal of Imaging 11, no. 5: 159. https://doi.org/10.3390/jimaging11050159
APA StyleLi, J., Tauqeer, I. M., Shao, Z., & Yu, H. (2025). A Transfer Learning-Based VGG-16 Model for COD Detection in UV–Vis Spectroscopy. Journal of Imaging, 11(5), 159. https://doi.org/10.3390/jimaging11050159







