Investigation of the Robustness and Transferability of Adversarial Patches in Multi-View Infrared Target Detection
Abstract
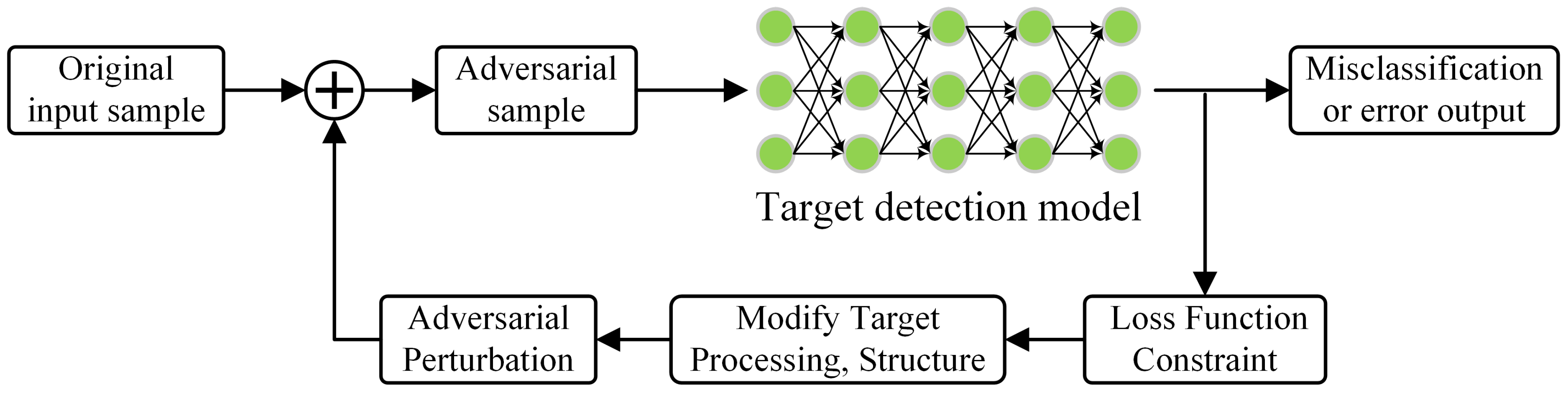
1. Introduction
- (1)
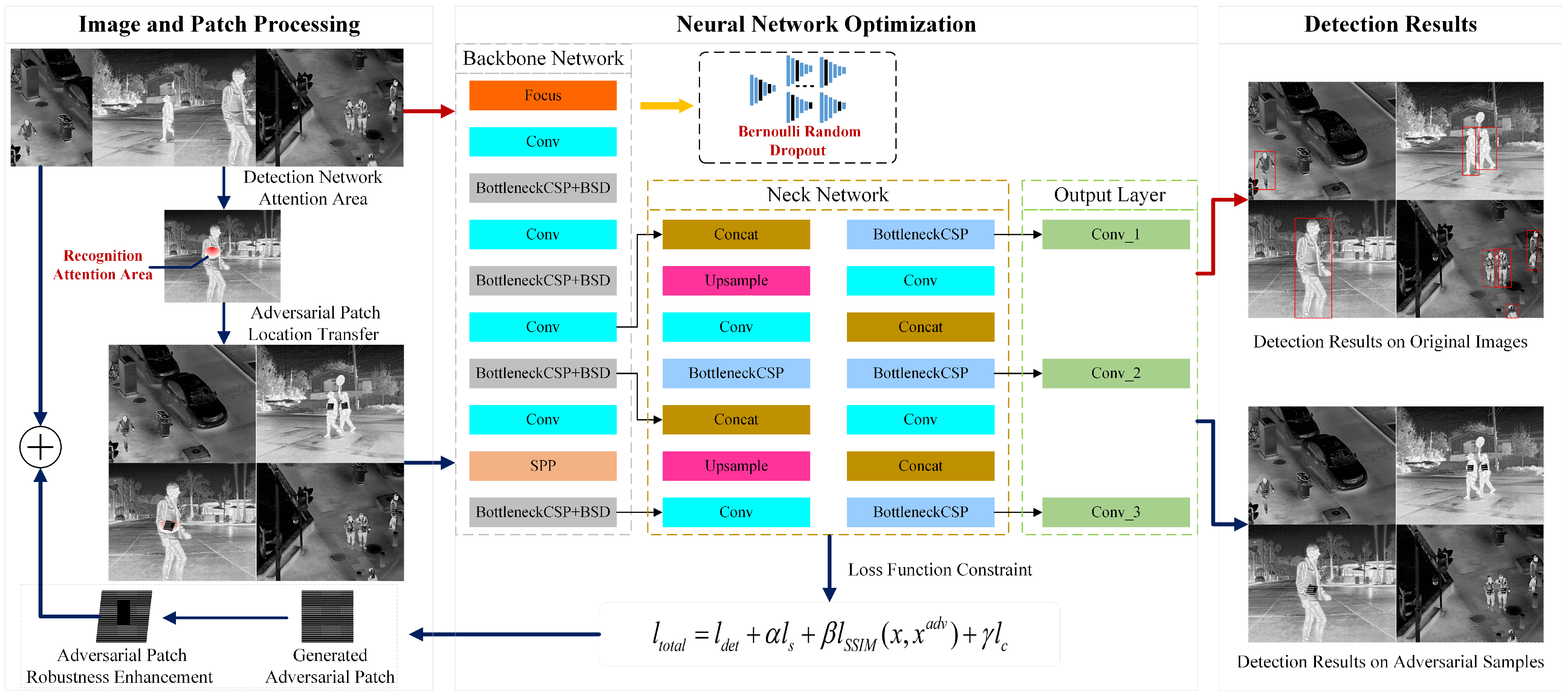
- We introduce a Bernoulli Stochastic Dropout (BSD) mechanism [21,22] during the patch generation process. By randomly discarding partial residual modules in the key feature-extraction stages of the backbone network, BSD simulates diverse feature distributions across different models. This strategy mitigates overfitting to a single detection model and significantly enhances the transferability of adversarial patches across different models. Compared with multi-model ensemble training, BSD does not substantially increase computational overhead while maintaining feature diversity and preserving detection accuracy.
- (2)
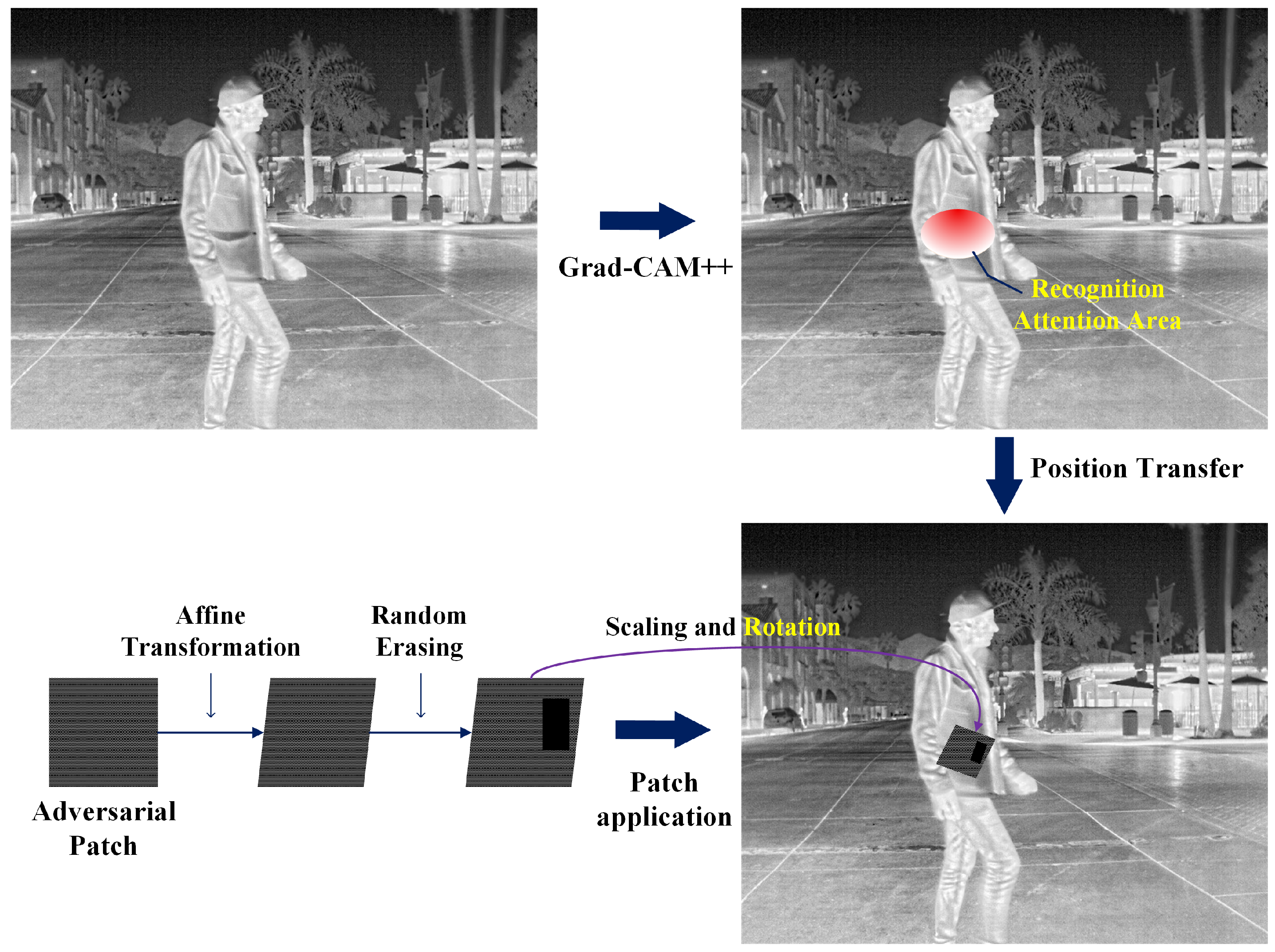
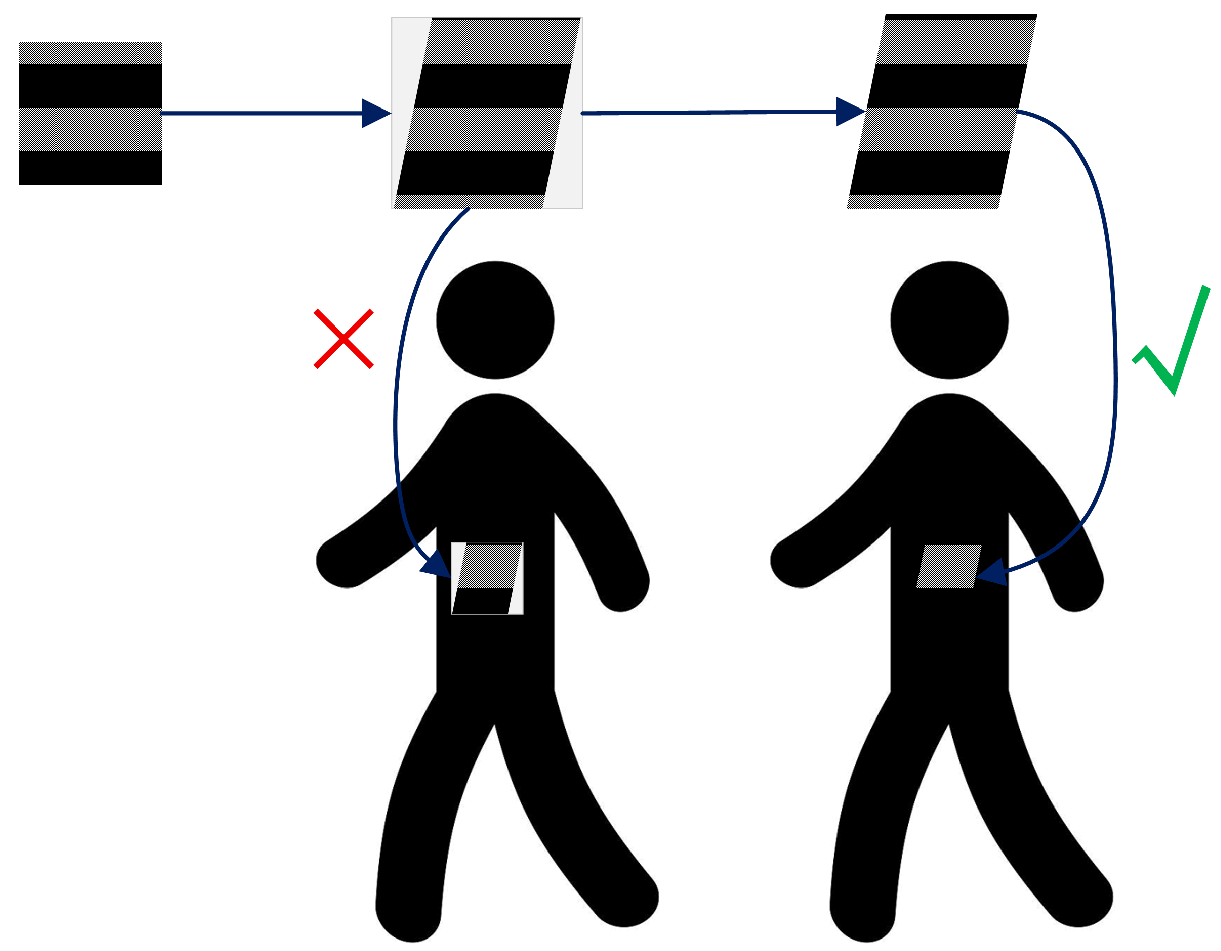
- To address the challenges of physical deployment in infrared scenarios, we incorporate region constraints and robustness enhancement strategies. Specifically, we leverage Grad-CAM [23] to extract high-attention regions of the model and apply adversarial patches precisely to the decision-critical areas of the detector, thereby maximizing attack effectiveness within a limited perturbation range. Furthermore, we integrate data augmentation techniques such as affine transformations, scaling, and random erasing to simulate real infrared imaging conditions under varying viewing angles, distance changes, and partial occlusions. These strategies improve the adaptability of adversarial patches to complex scenarios such as drone-based aerial imaging and ground surveillance.
- (3)
- In terms of loss function design, we construct a joint optimization objective comprising multiple constraints, including object-hiding loss, texture-smoothing loss, local structural similarity loss, and pixel-value constraint loss. This design not only ensures attack effectiveness but also enhances the naturalness and feasibility of the generated patches in infrared images. By reducing isolated noise points and maintaining plausible thermal radiation characteristics, the patches become more practical for real-world physical deployment.
- (1)
- This paper proposes a novel adversarial patch generation algorithm, GADP, which combines the Bernoulli Stochastic Dropout mechanism, loss function design, and robustness optimization strategies. The proposed method effectively attacks infrared image-based deep learning target detection models and demonstrates high robustness.
- (2)
- By incorporating the random dropout technique, the transferability of adversarial patches across different target detection models is significantly improved. This reduces reliance on specific model architectures and enhances the general applicability and reliability of the attack.
- (3)
- A loss function is designed that comprehensively considers object-hiding, smoothness, and structural similarity. This addition introduces quality constraints for the generated adversarial patches, ensuring their visual naturalness and effectiveness while minimizing the confidence of the target detector.
- (4)
- By combining the Grad-CAM algorithm to identify critical regions and introducing affine transformations and random erasing strategies, the overfitting of patches to specific detection models is reduced. These strategies enhance the precision of adversarial attacks and improve the adaptability of the patches in varying environmental conditions.
2. Related Work
3. Method
3.1. Adversarial Attack Framework
| Algorithm 1: GADP Adversarial Attack Algorithm |
|
Input: Original input sample images: , , …, , The target infrared object detection model D, number of iterations E, batch size B, initial patch Output: Optimized adversarial patch Initialize the value of patch as For do: Input the batch of original infrared images into model D, obtaining the target bounding box positions and confidence scores; Identify the neural network attention regions corresponding to the target in the infrared image; Apply the transformed adversarial patch to the original infrared image, incorporating the attention regions, generating the adversarial sample ; Apply Bernoulli random dropout to the backbone network of model D; Obtain the target bounding box confidence and location information for the adversarial sample in model D; Compute the loss function value; Update the adversarial patch using the Adam optimizer based on the gradient of the loss function: Perform affine transformation and random erasing on the adversarial patch; Obtain the transformed adversarial patch; End for Obtain the transformed adversarial patch. |
3.2. Optimization Problem Formulation
3.3. Adversarial Patch Transferability and Enhanced Strategies
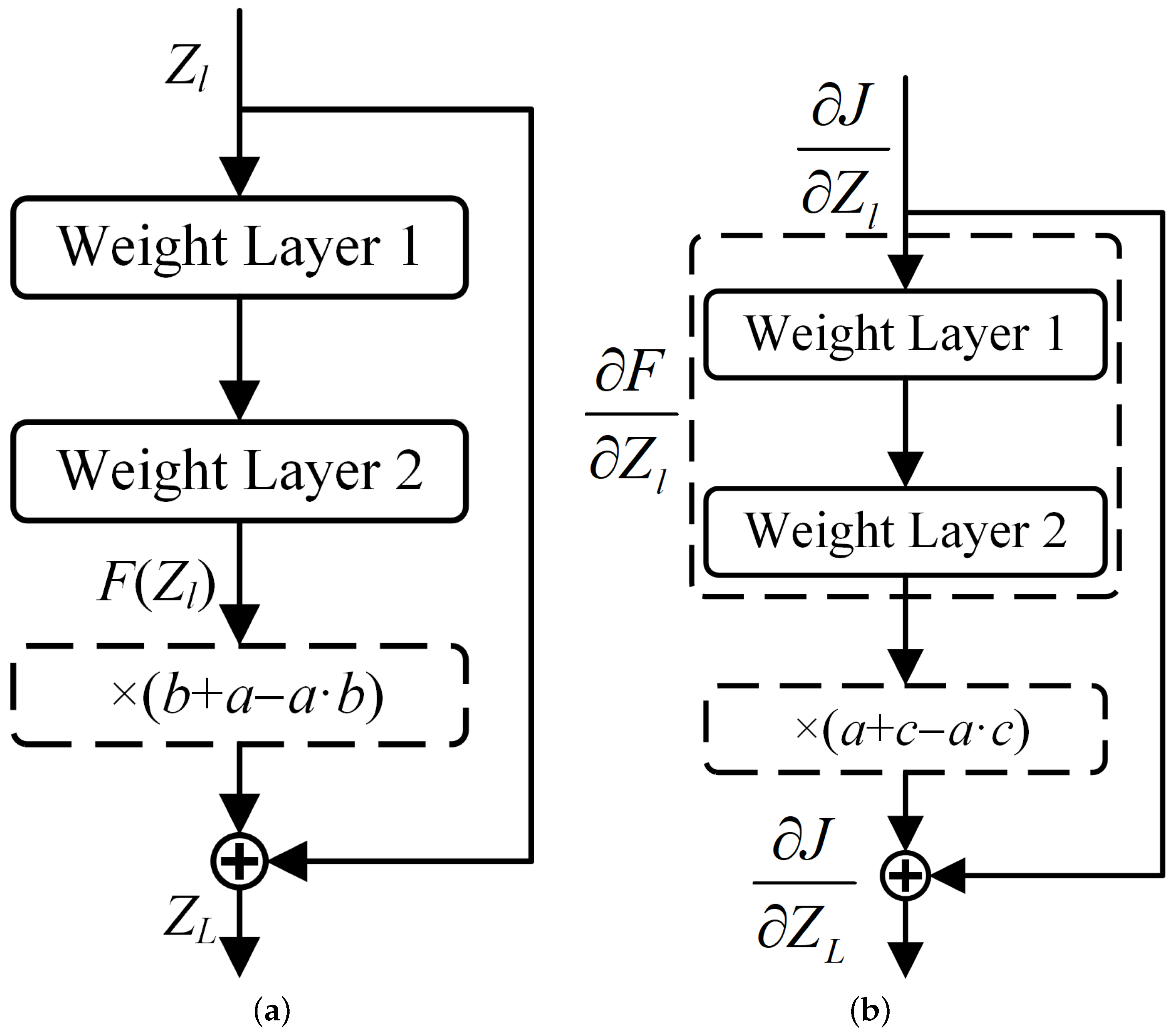
3.3.1. Theoretical Foundation of Transferability
3.3.2. Bernoulli Stochastic Dropout
3.4. Loss Function for Adversarial Attack Algorithm
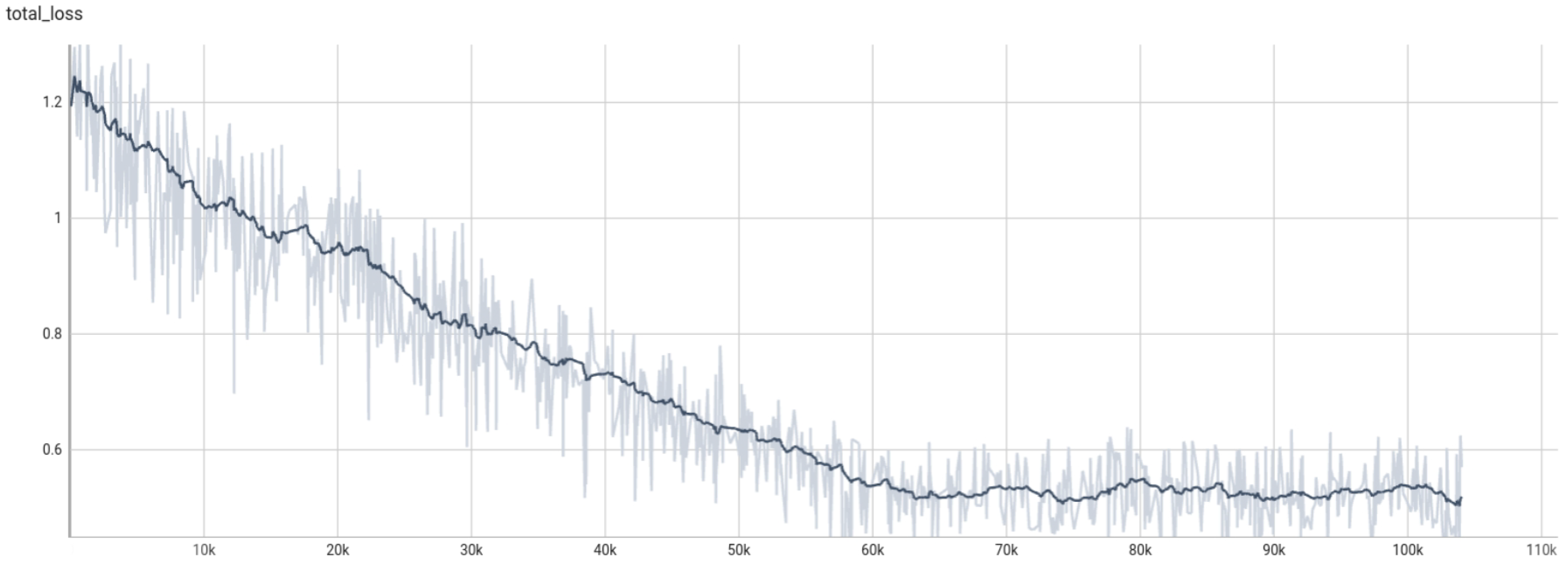
3.4.1. Total Loss Function
3.4.2. Detailed Definition of Each Loss Term
3.4.3. Magnitude-Level Analysis of Loss Terms
3.4.4. Analysis of Weight Coefficients
3.5. Optimization Strategy
3.6. Adversarial Patch Region Constraints and Robustness Enhancement
4. Experiments
4.1. Datasets and Hardware Configuration
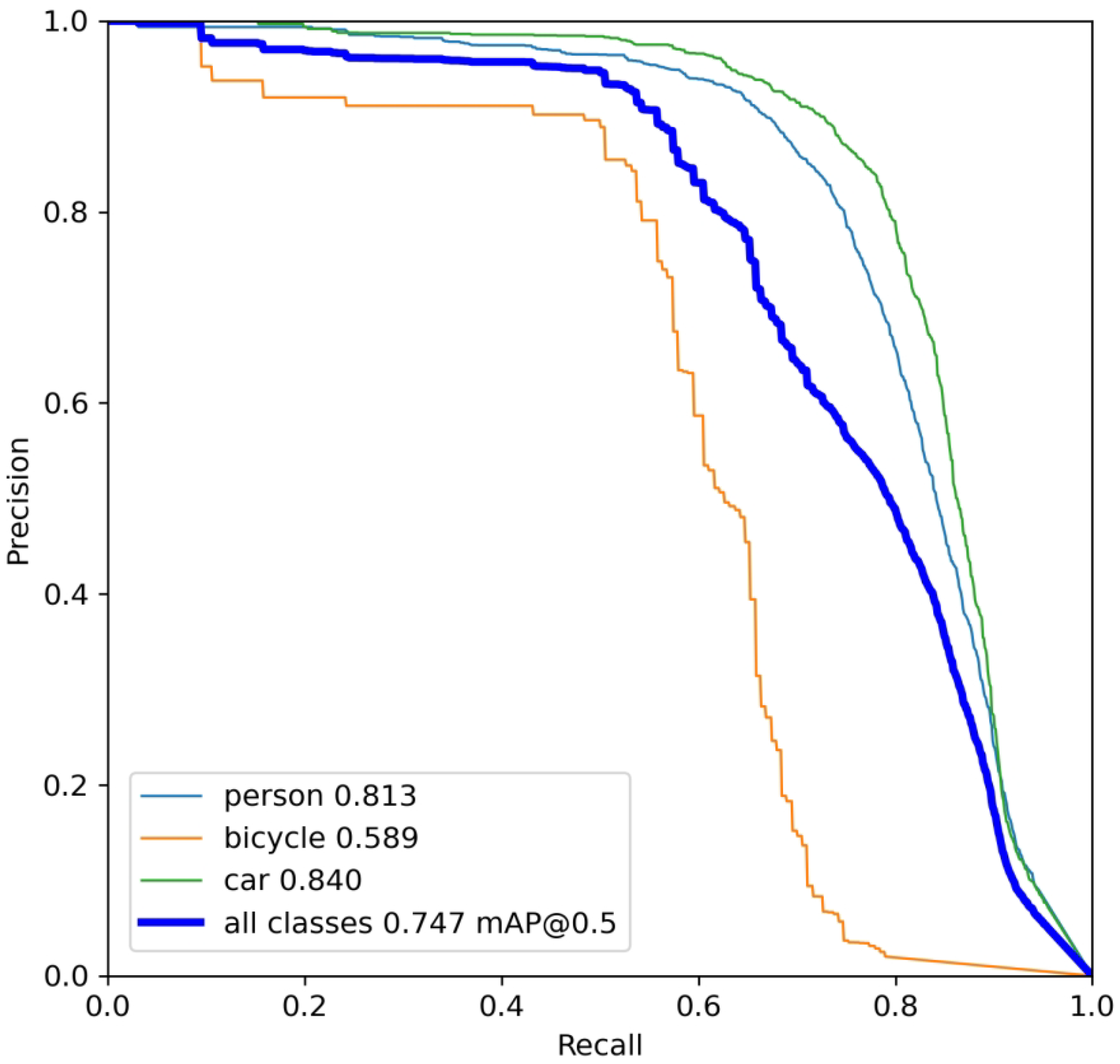
4.2. Evaluation Metrics for Adversarial Attack Effectiveness
4.3. Target Recognition Model and Adversarial Patch Training
4.3.1. Target Recognition Model Initialization Training
4.3.2. Attention Heatmaps of the Target Recognition Model
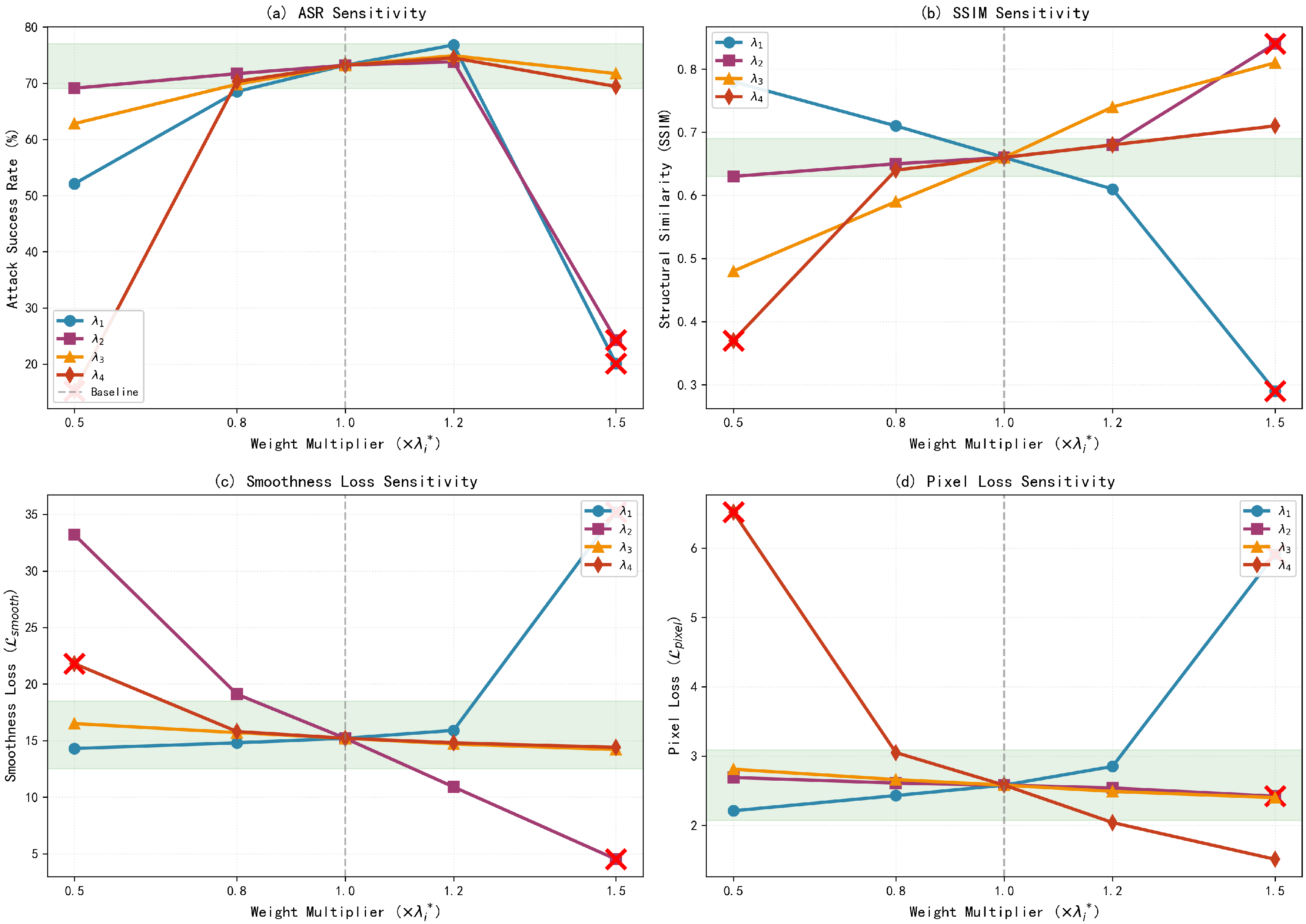
4.3.3. Sensitivity Analysis of Loss Weight Coefficients
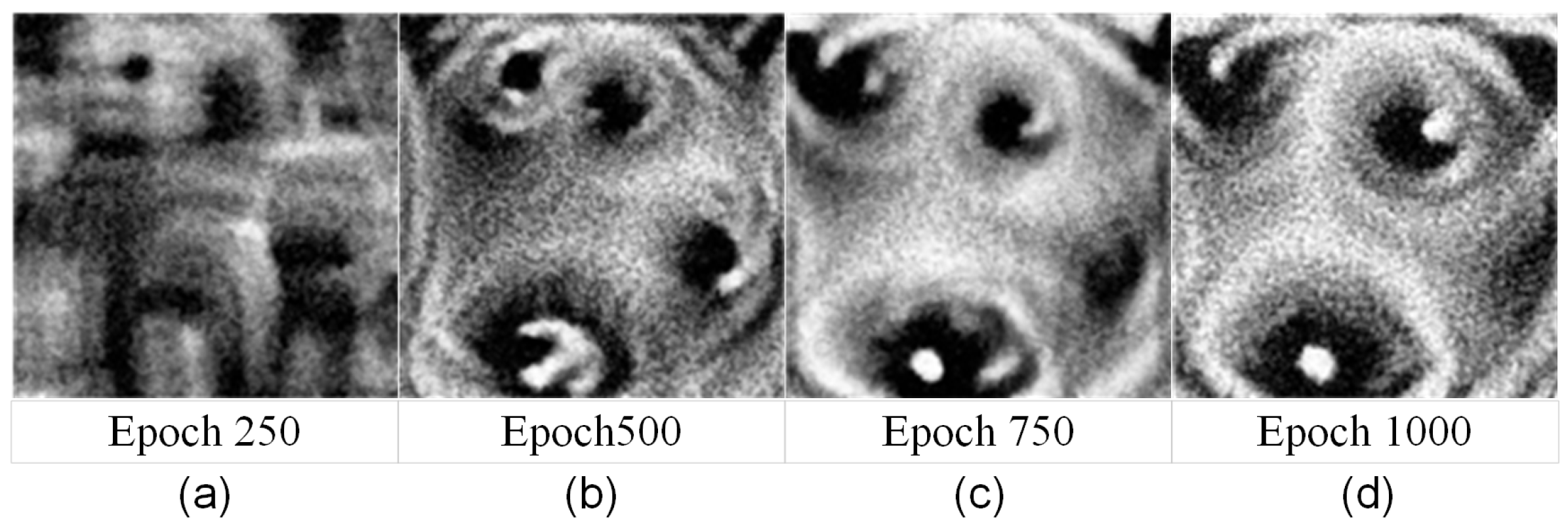
4.3.4. YOLOv5s + GADP Algorithm Adversarial Patch Training Process
4.3.5. Adversarial Patch Generation for Other Detection Algorithms Using GADP
4.3.6. Complexity Analysis of the GADP Training Algorithm
4.4. Adversarial Patch Application Results
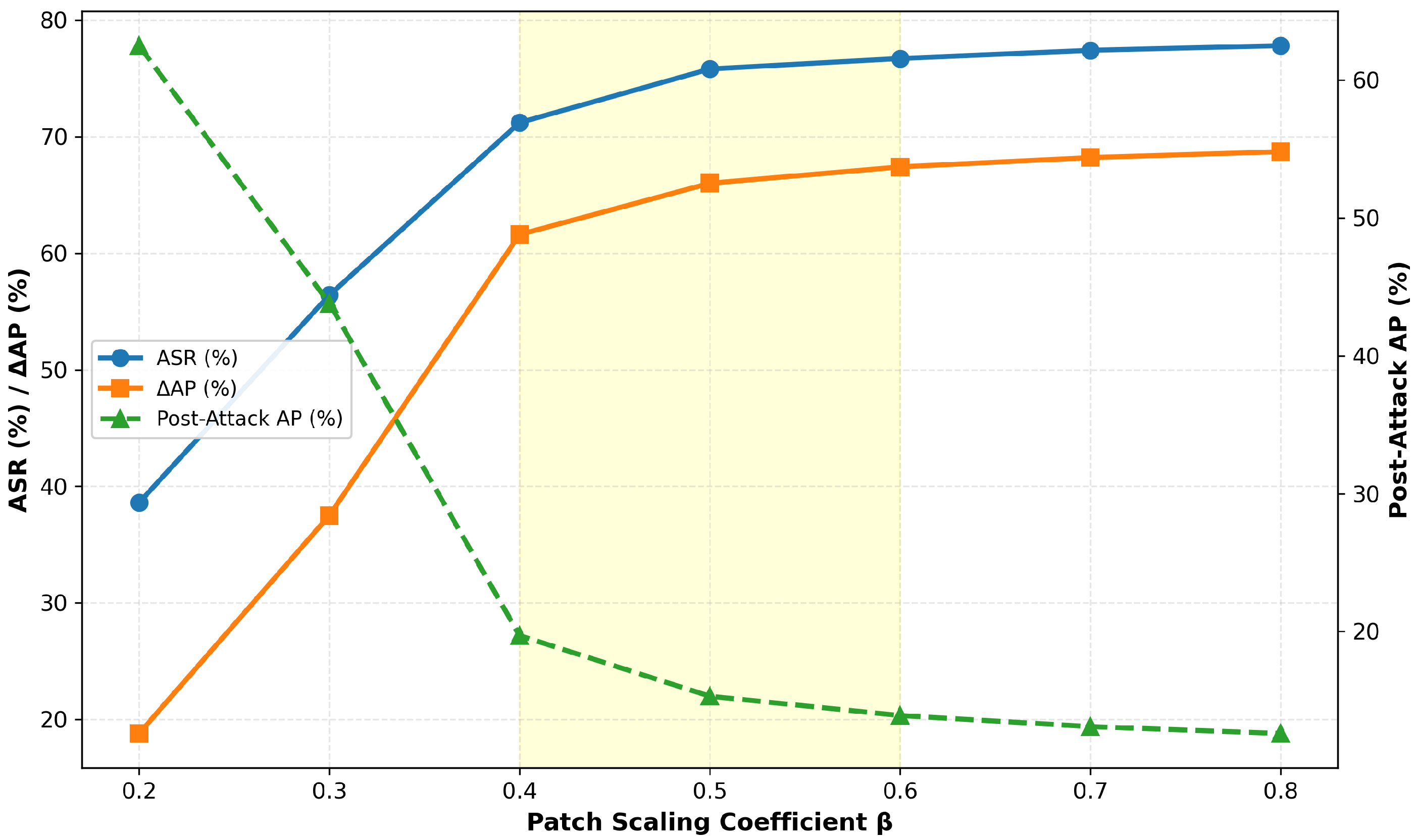
4.5. Adaptive Scaling of Patch Size and Performance Analysis
4.6. Transferability of Adversarial Attack Methods
4.6.1. Model Similarity Analysis
4.6.2. Transfer Attack Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Li, Y.; Li, Y.; Li, M.; Xu, X. Yolo-firi: Improved yolov5 for infrared image object detection. IEEE Access 2021, 9, 141861–141875. [Google Scholar] [CrossRef]
- Jiang, C.; Ren, H.; Ye, X.; Zhu, J.; Zeng, H.; Nan, Y.; Sun, M.; Ren, X.; Huo, H. Object detection from UAV thermal infrared images and videos using YOLO models. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102912. [Google Scholar] [CrossRef]
- Costa, J.C.; Roxo, T.; Proença, H.; Inácio, P.R. How deep learning sees the world: A survey on adversarial attacks & defenses. IEEE Access 2024, 12, 61113–61136. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Qi, J.; Bin, K.; Wen, H.; Tong, X.; Zhong, P. Adversarial patch attack on multi-scale object detection for UAV remote sensing images. Remote Sens. 2022, 14, 5298. [Google Scholar] [CrossRef]
- Li, Y.; Fan, X.; Sun, S.; Lu, Y.; Liu, N. Categorical-Parallel Adversarial Defense for Perception Models on Single-Board Embedded Unmanned Vehicles. Drones 2024, 8, 438. [Google Scholar] [CrossRef]
- Kim, H.; Hyun, J.; Yoo, H.; Kim, C.; Jeon, H. Adversarial Attacks for Deep Learning-Based Infrared Object Detection. J. Korea Inst. Mil. Sci. Technol. 2021, 24, 591–601. [Google Scholar] [CrossRef]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Liu, J.; Levine, A.; Lau, C.P.; Chellappa, R.; Feizi, S. Segment and complete: Defending object detectors against adversarial patch attacks with robust patch detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 14973–14982. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Hu, Z.; Huang, S.; Zhu, X.; Sun, F.; Zhang, B.; Hu, X. Adversarial texture for fooling person detectors in the physical world. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 13307–13316. [Google Scholar]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Artificial Intelligence Safety and Security; Chapman and Hall/CRC: Boca Raton, FL, USA; CRC: Boca Raton, FL, USA, 2018; pp. 99–112. [Google Scholar]
- Tarchoun, B.; Alouani, I.; Khalifa, A.B.; Mahjoub, M.A. Adversarial attacks in a multi-view setting: An empirical study of the adversarial patches inter-view transferability. In Proceedings of the 2021 International Conference on Cyberworlds (CW), Caen, France, 28–30 September 2021; pp. 299–302. [Google Scholar]
- Zhu, Z.; Chen, H.; Wang, X.; Zhang, J.; Jin, Z.; Choo, K.-K.R.; Shen, J.; Yuan, D. GE-AdvGAN: Improving the transferability of adversarial samples by gradient editing-based adversarial generative model. In Proceedings of the 2024 SIAM International Conference on Data Mining (SDM), Houston, TX, USA, 18–20 April 2024; pp. 706–714. [Google Scholar]
- Zhu, R.; Ma, S.; He, L.; Ge, W. Ffa: Foreground feature approximation digitally against remote sensing object detection. Remote Sens. 2024, 16, 3194. [Google Scholar] [CrossRef]
- Carlini, N.; Wagner, D. Towards evaluating the robustness of neural networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (sp), San Jose, CA, USA, 22–26 May 2017; pp. 39–57. [Google Scholar]
- Liu, H.; Ge, Z.; Zhou, Z.; Shang, F.; Liu, Y.; Jiao, L. Gradient correction for white-box adversarial attacks. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 18419–18430. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Chang, X.; Rodríguez, R.J.; Wang, J. Di-aa: An interpretable white-box attack for fooling deep neural networks. Inf. Sci. 2022, 610, 14–32. [Google Scholar] [CrossRef]
- Zhang, H.; Shao, W.; Liu, H.; Ma, Y.; Luo, P.; Qiao, Y.; Zhang, K. Avibench: Towards evaluating the robustness of large vision-language model on adversarial visual-instructions. arXiv 2024, arXiv:2403.09346. [Google Scholar] [CrossRef]
- Mahmood, K.; Mahmood, R.; Rathbun, E.; van Dijk, M. Back in black: A comparative evaluation of recent state-of-the-art black-box attacks. IEEE Access 2021, 10, 998–1019. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Zhou, S.; Deng, W.; Wu, Z.; Qiu, S. Efficient Ensemble Adversarial Attack for a Deep Neural Network (DNN)-Based Unmanned Aerial Vehicle (UAV) Vision System. Drones 2024, 8, 591. [Google Scholar] [CrossRef]
- Huang, G.; Sun, Y.; Liu, Z.; Sedra, D.; Weinberger, K.Q. Deep networks with stochastic depth. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part IV. pp. 646–661. [Google Scholar]
- Nie, A. Stochastic Dropout: Activation-Level Dropout to Learn Better Neural Language Models; Stanford University: Stanford, CA, USA, 2016. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Xiao, C.; Li, B.; Zhu, J.-Y.; He, W.; Liu, M.; Song, D. Generating adversarial examples with adversarial networks. arXiv 2018, arXiv:1801.02610. [Google Scholar]
- Moosavi-Dezfooli, S.-M.; Fawzi, A.; Frossard, P. Deepfool: A simple and accurate method to fool deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2574–2582. [Google Scholar]
- Moosavi-Dezfooli, S.-M.; Fawzi, A.; Fawzi, O.; Frossard, P. Universal adversarial perturbations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1765–1773. [Google Scholar]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar]
- Bubeck, S.; Cherapanamjeri, Y.; Gidel, G.; Tachet des Combes, R. A single gradient step finds adversarial examples on random two-layers neural networks. Adv. Neural Inf. Process. Syst. 2021, 34, 10081–10091. [Google Scholar]
- Dong, Y.; Liao, F.; Pang, T.; Su, H.; Zhu, J.; Hu, X.; Li, J. Boosting adversarial attacks with momentum. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9185–9193. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; pp. 1139–1147. [Google Scholar]
- Liu, X.; Yang, H.; Liu, Z.; Song, L.; Li, H.; Chen, Y. Dpatch: An adversarial patch attack on object detectors. arXiv 2018, arXiv:1806.02299. [Google Scholar]
- Xie, C.; Wang, J.; Zhang, Z.; Zhou, Y.; Xie, L.; Yuille, A. Adversarial examples for semantic segmentation and object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1369–1378. [Google Scholar]
- Athalye, A.; Engstrom, L.; Ilyas, A.; Kwok, K. Synthesizing robust adversarial examples. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 284–293. [Google Scholar]
- Sharif, M.; Bhagavatula, S.; Bauer, L.; Reiter, M.K. Accessorize to a crime: Real and stealthy attacks on state-of-the-art face recognition. In Proceedings of the 2016 ACM Sigsac Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 1528–1540. [Google Scholar]
- Thys, S.; Van Ranst, W.; Goedemé, T. Fooling automated surveillance cameras: Adversarial patches to attack person detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Zhu, X.; Hu, Z.; Huang, S.; Li, J.; Hu, X. Infrared invisible clothing: Hiding from infrared detectors at multiple angles in real world. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 13317–13326. [Google Scholar]
- Eykholt, K.; Evtimov, I.; Fernandes, E.; Li, B.; Rahmati, A.; Xiao, C.; Prakash, A.; Kohno, T.; Song, D. Robust physical-world attacks on deep learning visual classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1625–1634. [Google Scholar]
- Jia, E.; Xu, Y.; Zhang, Z.; Zhang, F.; Feng, W.; Dong, L.; Hui, T.; Tao, C. An adaptive adversarial patch-generating algorithm for defending against the intelligent low, slow, and small target. Remote Sens. 2023, 15, 1439. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Zhong, Z.; Zheng, L.; Kang, G.; Li, S.; Yang, Y. Random erasing data augmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, Singapore, 20–27 January 2026; pp. 13001–13008. [Google Scholar]
- Wang, C.-Y.; Bochkovskiy, A.; Liao, H.-Y.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 7464–7475. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 21–37. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28, 1137–1149. [Google Scholar] [CrossRef] [PubMed]







| Method | Advantages | Disadvantages |
|---|---|---|
| GAN-based adversarial attack methods | Good transferability; effective for image classification tasks | Training instability; slow convergence |
| Decision boundary-based adversarial attack methods | Fast computation; small perturbations | Difficult to formulate decision boundaries for complex models |
| Gradient optimization-based adversarial attacks | High success rate, simple implementation, suitable for white-box scenarios | Requires knowledge of the network’s gradient |
| Gradient-based adversarial attack methods | High Attack Success Rate; simple to implement | Requires access to model gradients; high computational cost |
| Patch-based adversarial attack methods | Easy to generate; efficient interference; practical for real-world deployment | Limited robustness |
| Perturbation Setting | ASR (%) | SSIM | ||||||
|---|---|---|---|---|---|---|---|---|
| Baseline (1.0×) | 22 | 0.4 | 5 | 2 | 73.2 | 0.66 | 15.2 | 2.58 |
| 11 | 0.4 | 5 | 2 | 52.1 | 0.78 | 14.3 | 2.21 | |
| 26.4 | 0.4 | 5 | 2 | 76.8 | 0.61 | 15.9 | 2.85 | |
| 33 | 0.4 | 5 | 2 | 20.1 | 0.29 | 35.2 | 5.91 | |
| 22 | 0.6 | 5 | 2 | 24.3 | 0.84 | 4.5 | 2.42 | |
| 22 | 0.4 | 2.5 | 2 | 62.8 | 0.48 | 16.5 | 2.81 | |
| 22 | 0.4 | 6 | 2 | 74.9 | 0.74 | 14.7 | 2.49 | |
| 22 | 0.4 | 5 | 1 | 15.2 | 0.37 | 21.8 | 6.52 | |
| 22 | 0.4 | 5 | 2.4 | 74.5 | 0.68 | 14.8 | 2.04 |
| Adversarial Attack Methods | Pre-Attack AP(%) | Post-Attack ASR (%) | Post-Attack AP (%) | AP(%) |
|---|---|---|---|---|
| White Square Patch | 6.5 | 75.6 | 5.7 | |
| Random Noise Patch | 8.7 | 74.9 | 6.4 | |
| QR Patch | 81.3 | 74.6 | 16.3 | 65.0 |
| advYOLO Patch | 69.2 | 16.8 | 64.5 | |
| GADP (Our Method) | 75.9 | 15.1 | 66.2 |
| Model Combination | YOLOv5s vs. YOLOv7 | YOLOv5s vs. SSD | YOLOv5s vs. Faster R-CNN | YOLOv7 vs. SSD | YOLOv7 vs. Faster R-CNN | SSD vs. Faster R-CNN |
|---|---|---|---|---|---|---|
| KL Divergence | 0.18 | 0.32 | 0.55 | 0.30 | 0.51 | 0.40 |
| Object Detection Models Used in Adversarial Patch Training | Adversarial Attack Methods | Post-Attack Average Precision (AP, %) of Object Detection Models | |||
|---|---|---|---|---|---|
| White-Box Adversarial Attack | Transferable Adversarial Attack | ||||
| YOLOv5s | YOLOv7 | SSD | Faster R-CNN | ||
| YOLOv5s | No Attack | 81.3 | 88.3 | 70.8 | 74.3 |
| advYOLO Patch | 15.6 | 47.4 | 49.6 | 46.1 | |
| QR Patch | 15.3 | 49.6 | 51.2 | 48.3 | |
| GADP (Our Method) | 14.8 | 45.3 | 49.1 | 45.2 | |
| Object Detection Models Used in Adversarial Patch Training | Adversarial Attack Methods | Post-Attack Average Precision (AP, %) of Object Detection Models | |||
|---|---|---|---|---|---|
| White-Box Adversarial Attack | Transferable Adversarial Attack | ||||
| YOLOv7 | YOLOv5s | SSD | Faster R-CNN | ||
| YOLOv7 | No Attack | 88.3 | 81.3 | 70.8 | 74.3 |
| advYOLO Patch | 13.7 | 37.6 | 39.1 | 40.5 | |
| QR Patch | 14.3 | 36.8 | 40.7 | 39.2 | |
| GADP (Our Method) | 11.5 | 35.8 | 38.2 | 37.4 | |
| Object Detection Models Used in Adversarial Patch Training | Adversarial Attack Methods | Post-Attack Average Precision (AP, %) of Object Detection Models | |||
|---|---|---|---|---|---|
| White-Box Adversarial Attack | Transferable Adversarial Attack | ||||
| SSD | YOLOv5s | YOLOv7 | Faster R-CNN | ||
| SSD | No Attack | 70.8 | 81.3 | 88.3 | 74.3 |
| advYOLO Patch | 14.7 | 46.3 | 50.4 | 46.6 | |
| QR Patch | 15.2 | 47.8 | 48.2 | 46.3 | |
| GADP (Our Method) | 13.8 | 44.9 | 47.3 | 45.2 | |
| Object Detection Models Used in Adversarial Patch Training | Adversarial Attack Methods | Post-Attack Average Precision (AP, %) of Object Detection Models | |||
|---|---|---|---|---|---|
| White-Box Adversarial Attack | Transferable Adversarial Attack | ||||
| Faster R-CNN | YOLOv5s | YOLOv7 | SSD | ||
| Faster R-CNN | No Attack | 74.3 | 81.3 | 88.3 | 70.8 |
| advYOLO Patch | 11.4 | 45.3 | 41.8 | 40.5 | |
| QR Patch | 12.9 | 44.5 | 41.6 | 41.3 | |
| GADP (Our Method) | 10.1 | 43.7 | 40. | 38.1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Zhou, Z.; Zhang, Z.; Luo, W.; Xiao, F.; Xia, S.; Zhu, C.; Wang, L. Investigation of the Robustness and Transferability of Adversarial Patches in Multi-View Infrared Target Detection. J. Imaging 2025, 11, 378. https://doi.org/10.3390/jimaging11110378
Zhou Q, Zhou Z, Zhang Z, Luo W, Xiao F, Xia S, Zhu C, Wang L. Investigation of the Robustness and Transferability of Adversarial Patches in Multi-View Infrared Target Detection. Journal of Imaging. 2025; 11(11):378. https://doi.org/10.3390/jimaging11110378
Chicago/Turabian StyleZhou, Qing, Zhongchen Zhou, Zhaoxiang Zhang, Wei Luo, Feng Xiao, Sijia Xia, Chunjia Zhu, and Long Wang. 2025. "Investigation of the Robustness and Transferability of Adversarial Patches in Multi-View Infrared Target Detection" Journal of Imaging 11, no. 11: 378. https://doi.org/10.3390/jimaging11110378
APA StyleZhou, Q., Zhou, Z., Zhang, Z., Luo, W., Xiao, F., Xia, S., Zhu, C., & Wang, L. (2025). Investigation of the Robustness and Transferability of Adversarial Patches in Multi-View Infrared Target Detection. Journal of Imaging, 11(11), 378. https://doi.org/10.3390/jimaging11110378






