Dynamic Fractional Flow Reserve from 4D-CTA: A Novel Framework for Non-Invasive Coronary Assessment
Abstract
1. Introduction
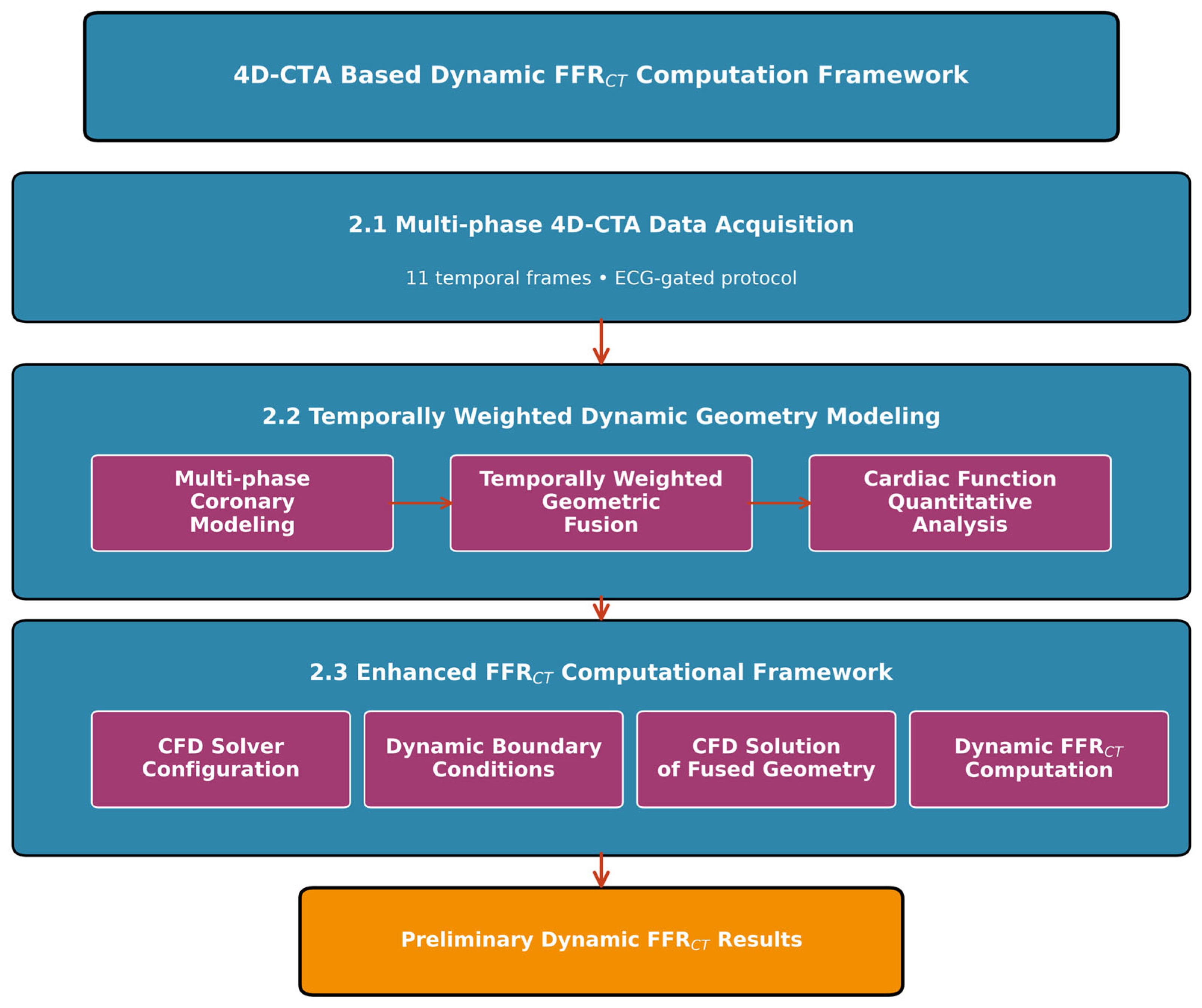
2. Materials and Methods
2.1. Patient Data Acquisition
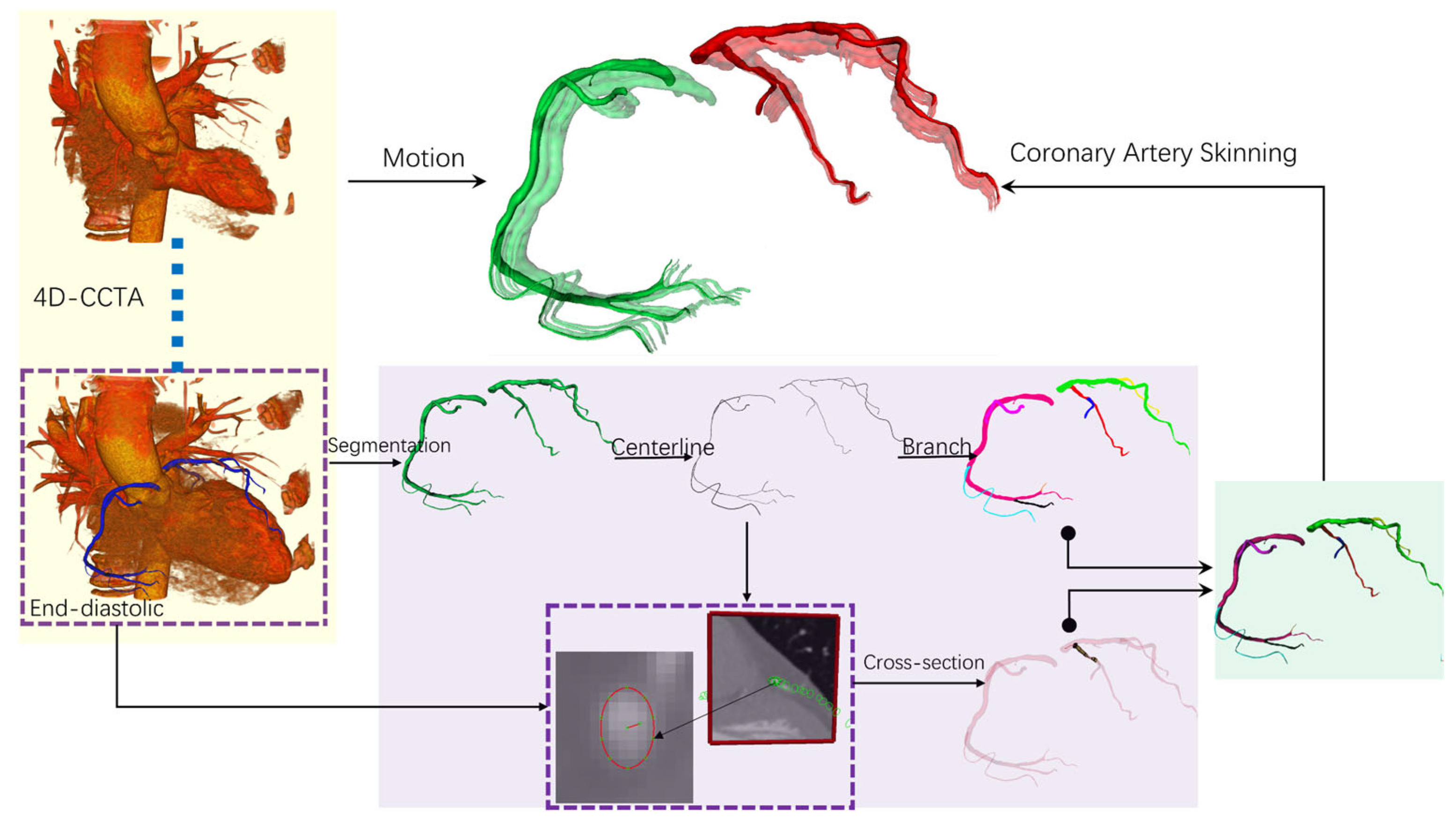
2.2. Temporally Weighted Dynamic Coronary Geometry Modeling
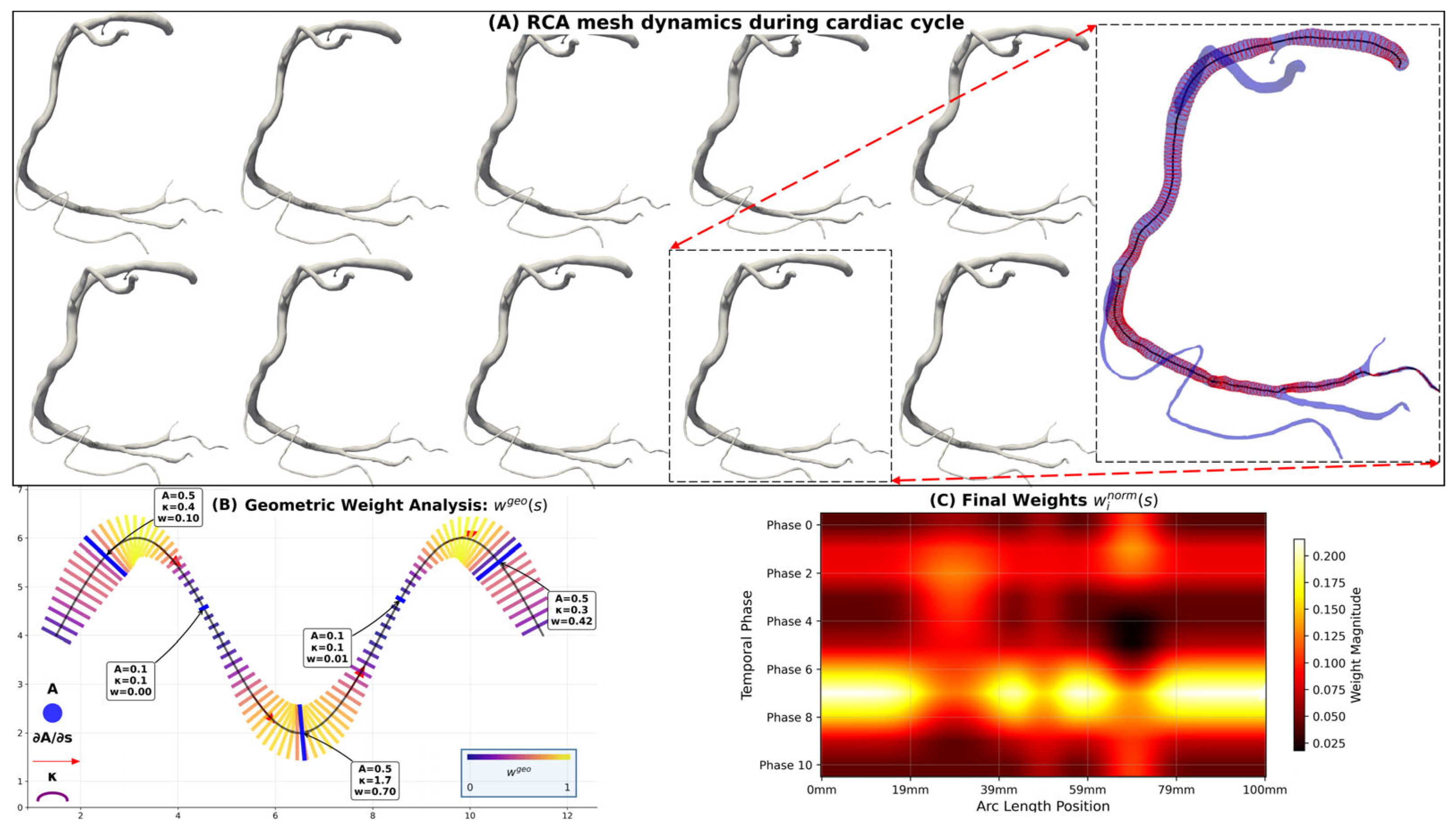
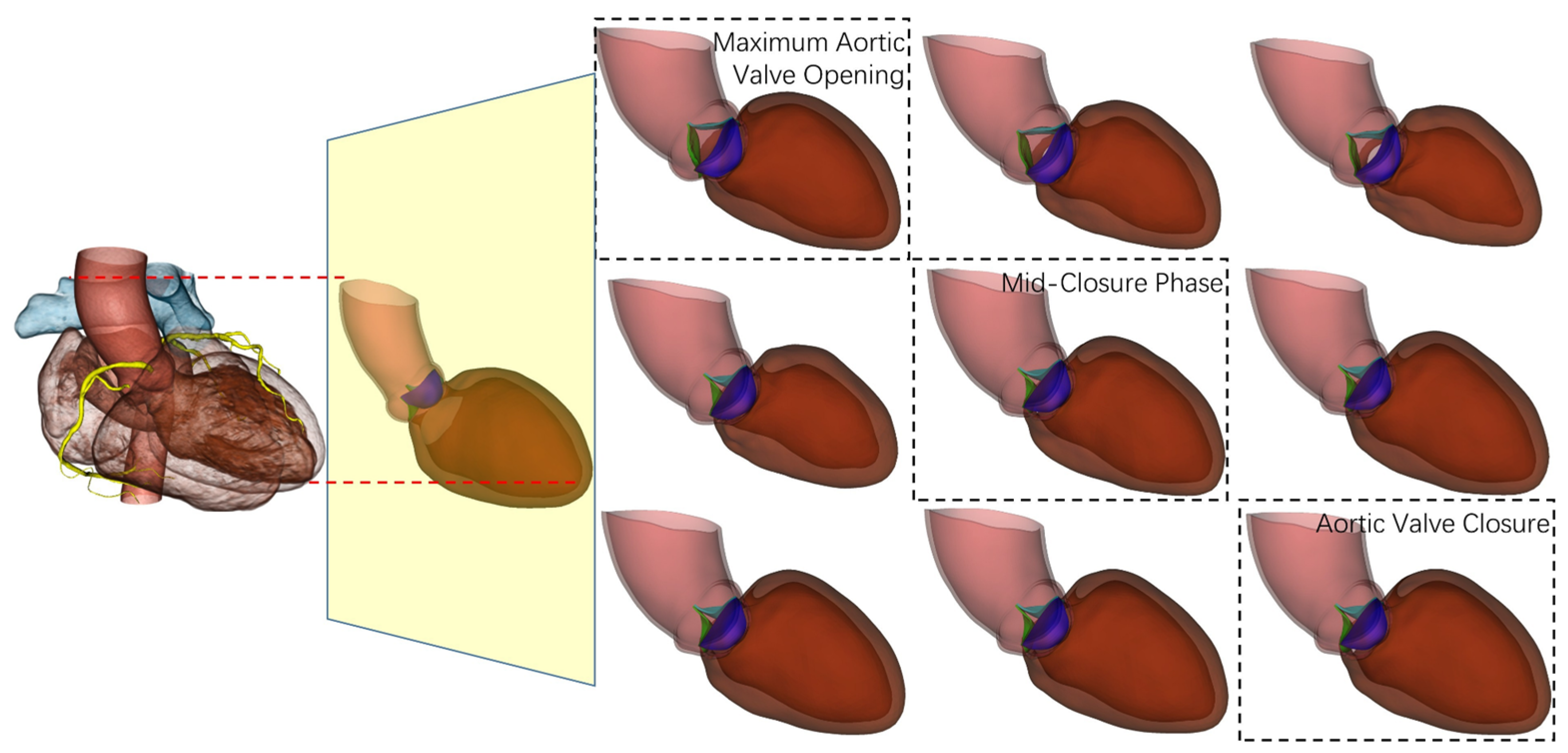
2.2.1. Dynamic Multi-Phase Coronary Modeling
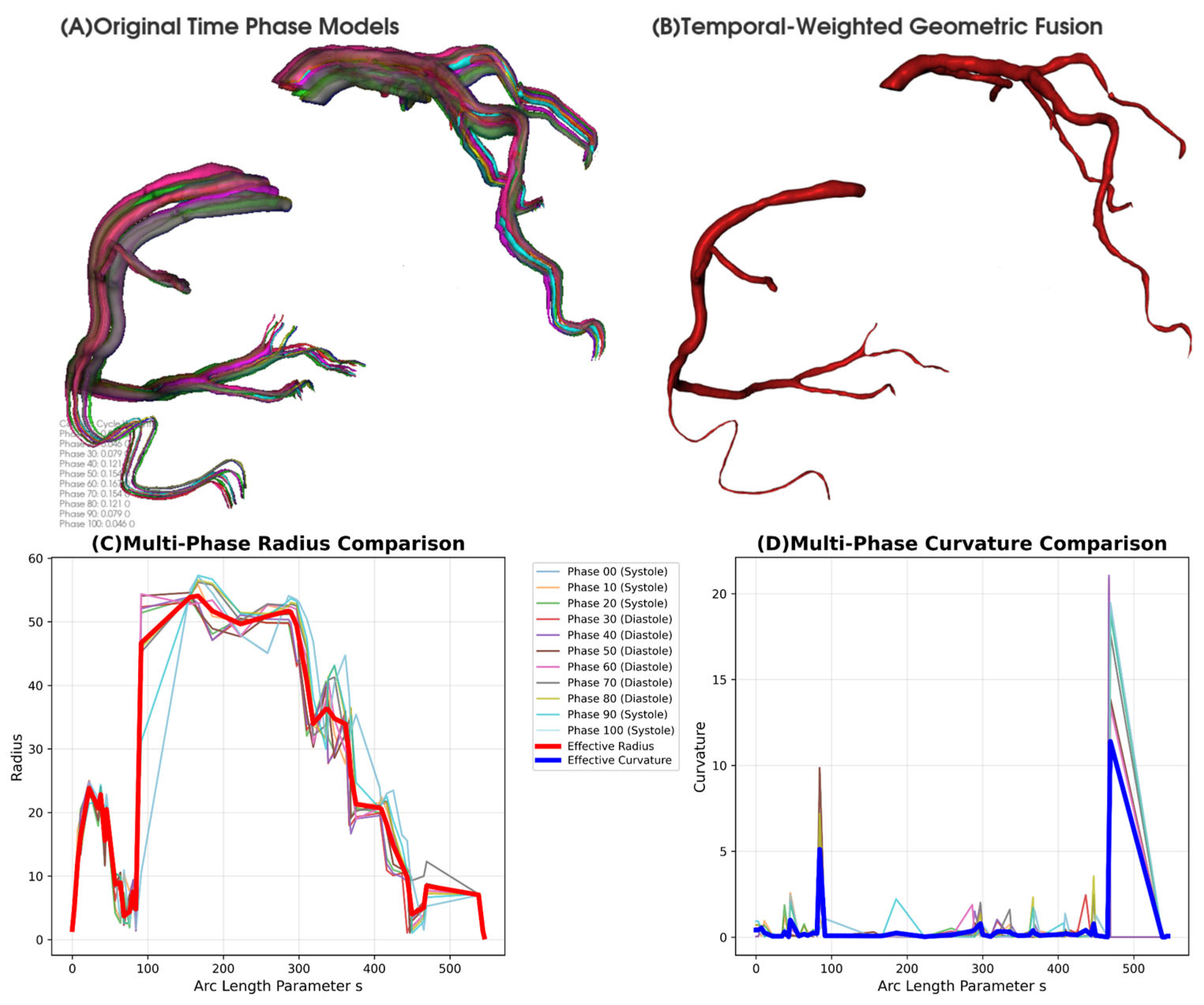
2.2.2. Temporally Weighted Geometric Fusion Algorithm
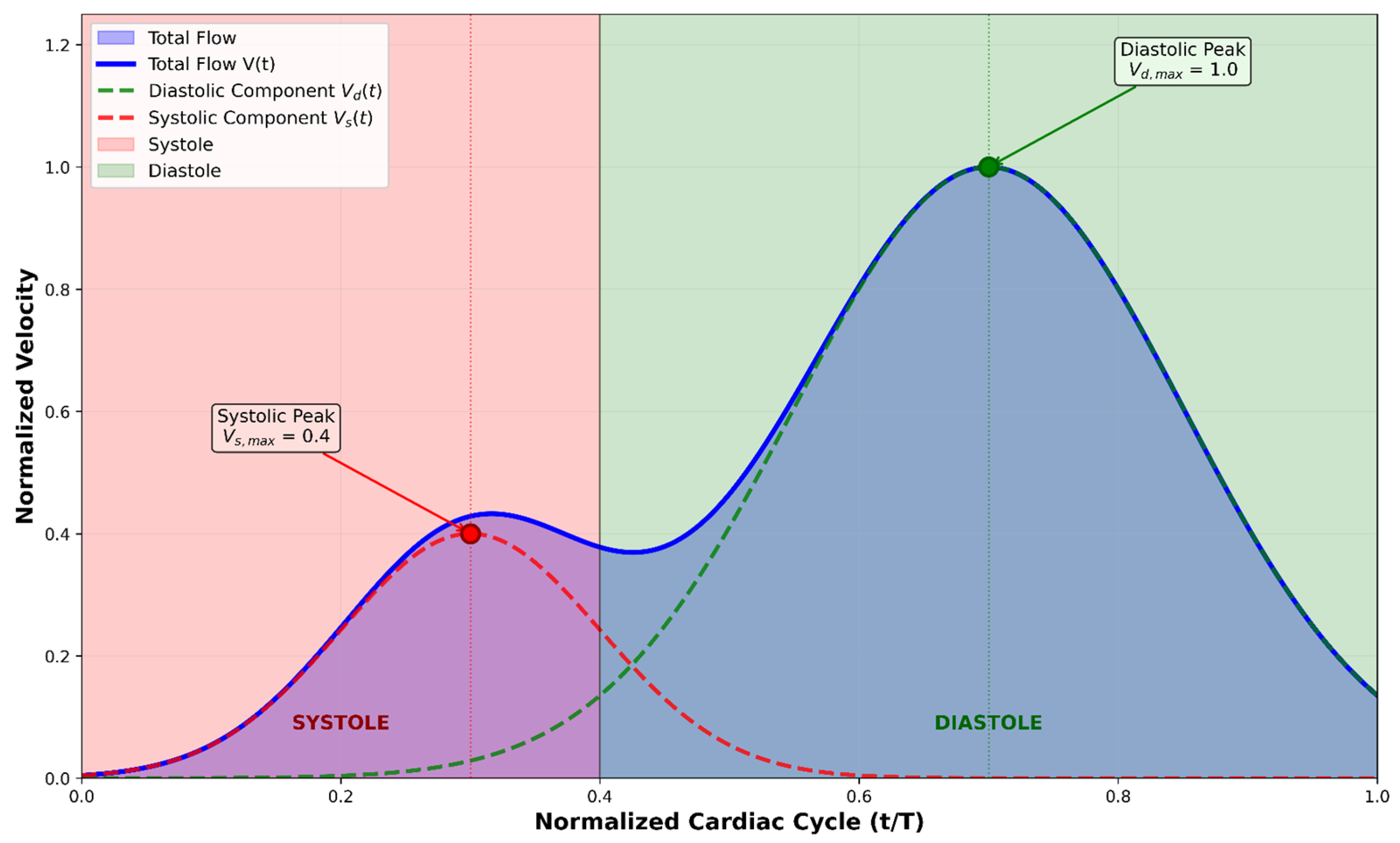
2.2.3. Cardiac Function Quantitative Analysis
2.3. Enhanced FFRCT Computational Framework
2.3.1. Computational Fluid Dynamics Solver Configuration
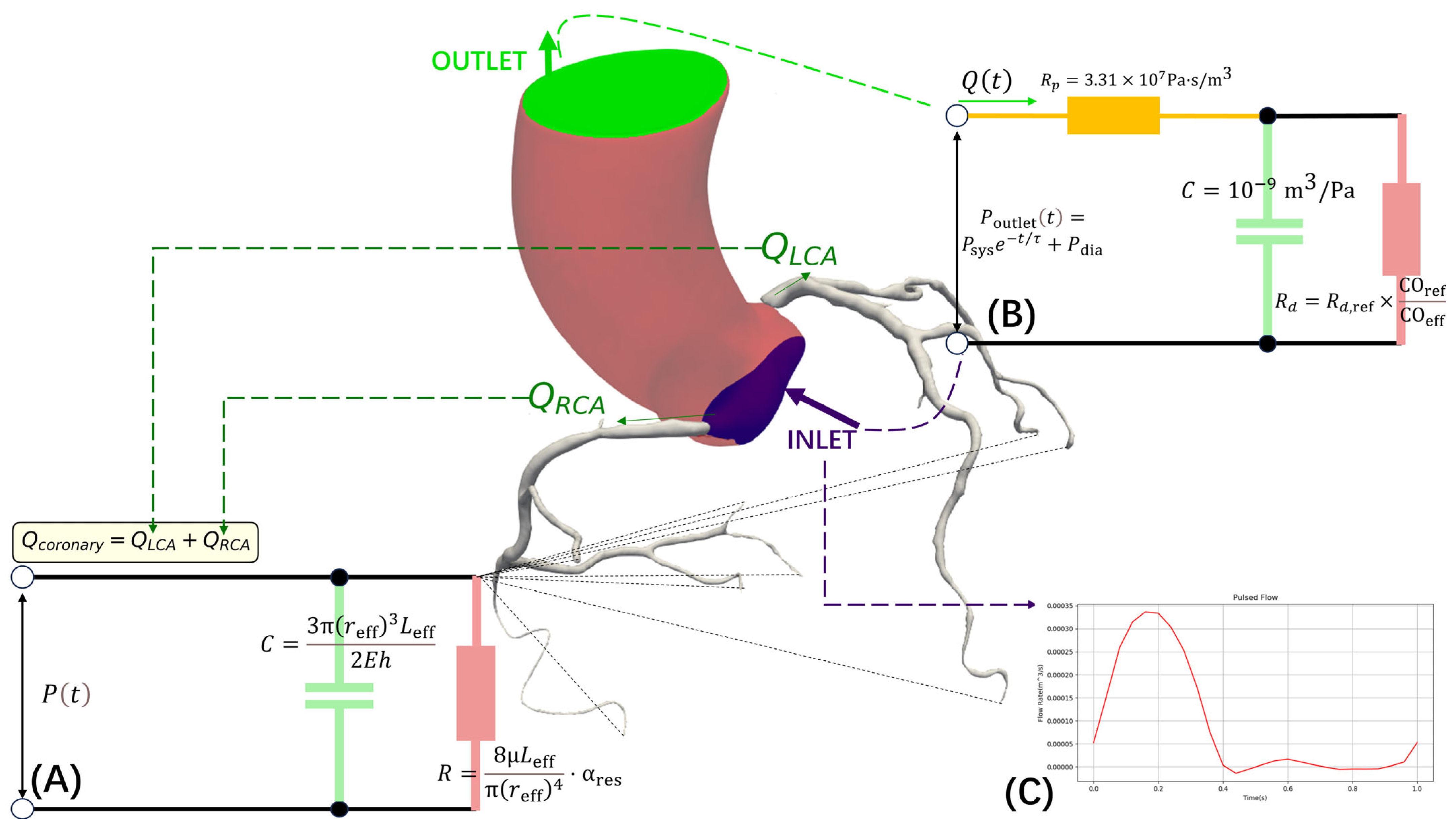
2.3.2. Dynamic Boundary Condition Configuration
2.3.3. CFD Implementation of Temporally Weighted Geometry
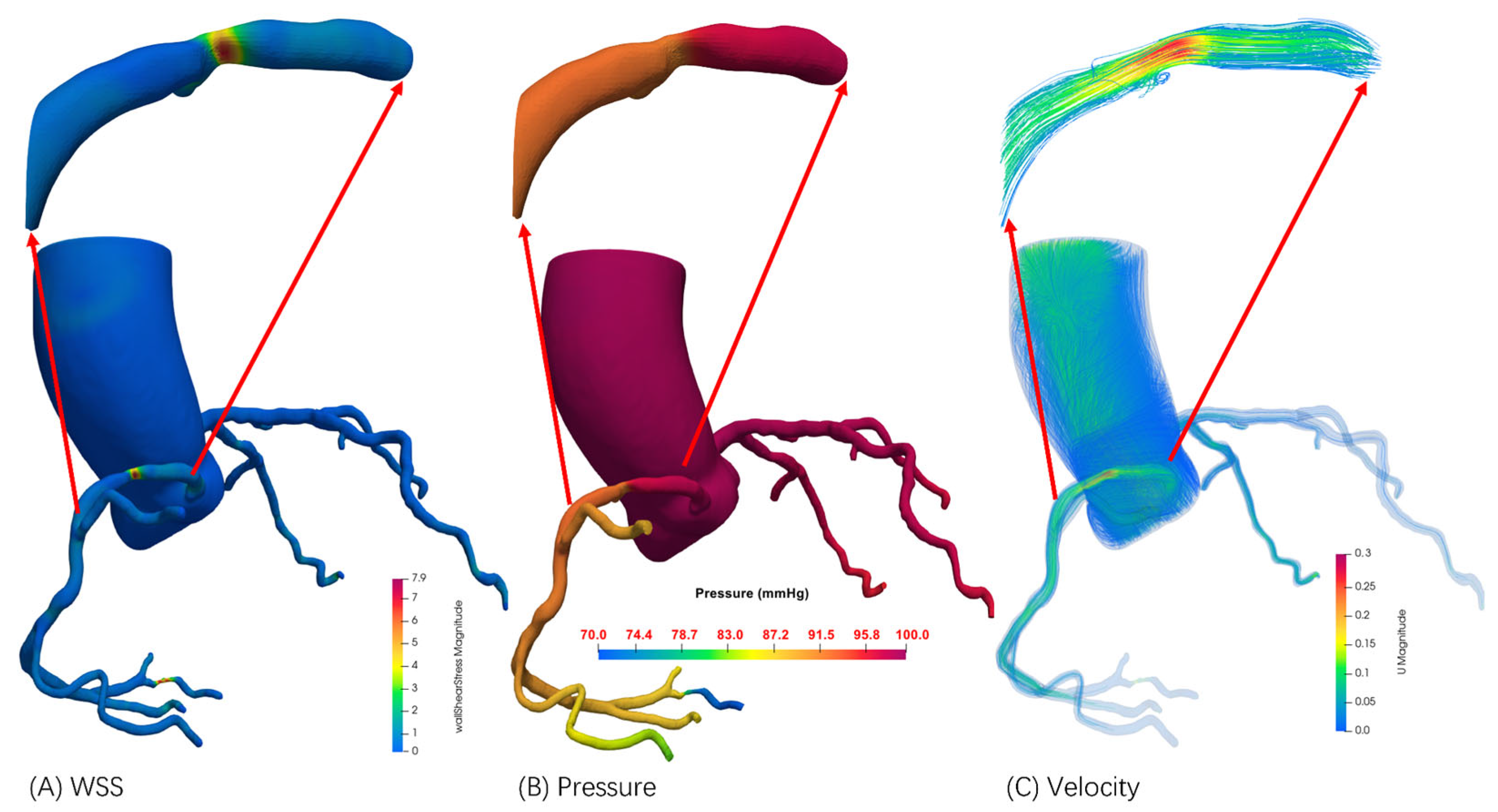
2.3.4. Enhanced FFR Computation Framework
3. Results
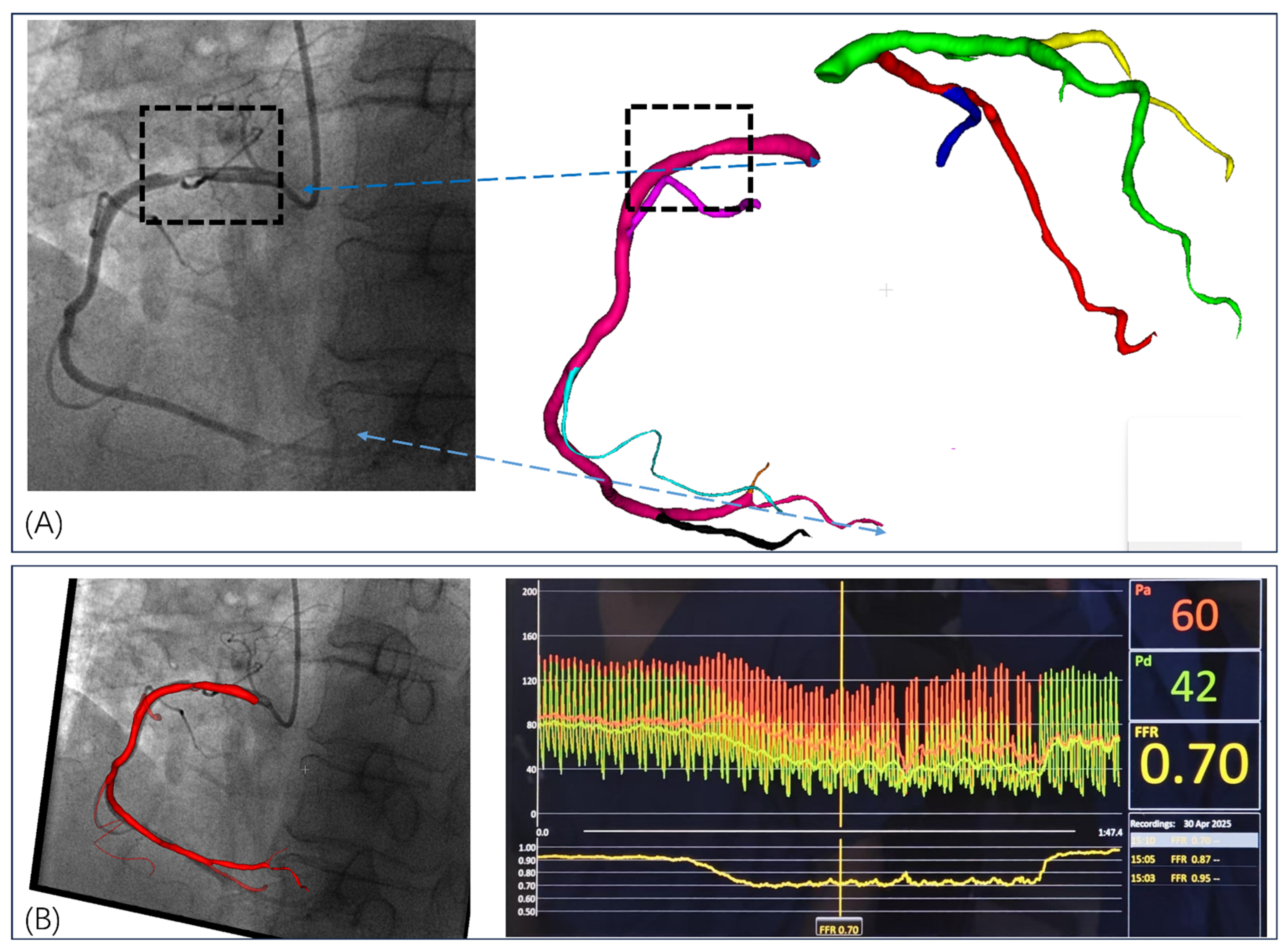
3.1. Invasive FFR Assessment
3.2. FFRCT Computational Results
3.3. Comparative Validation Results
3.3.1. Patient Demographics and Clinical Characteristics
3.3.2. Computational Methodologies
3.3.3. Validation Results
4. Discussion
4.1. Technical Innovation and Clinical Significance
4.2. Methodological Advantages
4.3. Study Limitations and Future Directions
4.4. Clinical Implementation Considerations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 4D-CTA | Four-dimensional computed tomography angiography |
| CAD | Coronary artery disease |
| CCTA | Coronary computed tomography angiography |
| CFD | Computational Fluid Dynamics |
| CVDs | Cardiovascular diseases |
| EDV | End-diastolic volume |
| ESV | End-systolic volume |
| FFR | Fractional Flow Reserve |
| FFRCT | FFR derived from CCTA |
| QFR | Quantitative Flow Ratio |
| vFFR | Virtual FFR |
Appendix A
References
- Di Cesare, M.; Perel, P.; Taylor, S.; Kabudula, C.; Bixby, H.; Gaziano, T.A.; McGhie, D.V.; Mwangi, J.; Pervan, B.; Narula, J.; et al. The heart of the world. Glob. Heart 2024, 19, 11. [Google Scholar] [CrossRef]
- Fernandes, M.; Sousa, L.C.; António, C.C.; Silva, S.; Pinto, S.I.S. A review of computational methodologies to predict the fractional flow reserve in coronary arteries with stenosis. J. Biomech. 2025, 178, 112299. [Google Scholar] [CrossRef] [PubMed]
- Dell’Aversana, S.; Ascione, R.; Vitale, R.A.; Cavaliere, F.; Porcaro, P.; Basile, L.; Napolitano, G.; Boccalatte, M.; Sibilio, G.; Esposito, G.; et al. CT Coronary Angiography: Technical Approach and Atherosclerotic Plaque Characterization. J. Clin. Med. 2023, 12, 7615. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Hashim, M.J.; Mustafa, H.; Baniyas, M.Y.; Al Suwaidi, S.K.B.M.; AlKatheeri, R.; Alblooshi, F.M.K.; Almatrooshi, M.E.A.H.; Alzaabi, M.E.H.; Al Darmaki, R.S.; et al. Global epidemiology of ischemic heart disease: Results from the global burden of disease study. Cureus 2020, 12, e9349. [Google Scholar] [CrossRef] [PubMed]
- Soulis, J.V.; Giannoglou, G.D.; Chatzizisis, Y.S.; Seralidou, K.V.; Parcharidis, G.E.; Louridas, G.E. Non-Newtonian models for molecular viscosity and wall shear stress in a 3D reconstructed human left coronary artery. Med. Eng. Phys. 2008, 30, 9–19. [Google Scholar] [CrossRef]
- Updegrove, A.; Wilson, N.M.; Merkow, J.; Lan, H.; Marsden, A.L.; Shadden, S.C. SimVascular: An open source pipeline for cardiovascular simulation. Ann. Biomed. Eng. 2017, 45, 525–541. [Google Scholar] [CrossRef]
- Khlebnikov, R.; Figueroa, C.A. CRIMSON: An open-source software framework for cardiovascular integrated modelling and simulation. PLoS Comput. Biol. 2016, 12, e1004981. [Google Scholar]
- Pijls, N.H.; De Bruyne, B.; Peels, K.; Van Der Voort, P.H.; Bonnier, H.J.; Bartunek, J.K.J.; Koolen, J.J. Measurement of fractional flow reserve to assess the functional severity of coronary-artery stenoses. N. Engl. J. Med. 1996, 334, 1703–1708. [Google Scholar] [CrossRef]
- Mastoi, Q.U.; Wah, T.Y.; Gopal Raj, R.; Iqbal, U. Automated diagnosis of coronary artery disease: A review and workflow. Cardiol. Res. Pract. 2018, 2018, 2016282. [Google Scholar] [CrossRef]
- Koo, B.K.; Erglis, A.; Doh, J.H.; Daniels, D.V.; Jegere, S.; Kim, H.S.; Dunning, A.; DeFrance, T.; Lansky, A.; Leipsic, J.; et al. Diagnosis of ischemia-causing coronary stenoses by noninvasive fractional flow reserve computed from coronary computed tomographic angiograms: Results from the prospective multicenter DISCOVER-FLOW study. J. Am. Coll. Cardiol. 2011, 58, 1989–1997. [Google Scholar] [CrossRef]
- Nørgaard, B.L.; Leipsic, J.; Gaur, S.; Seneviratne, S.; Ko, B.S.; Ito, H.; Jensen, J.M.; Mauri, L.; De Bruyne, B.; Bezerra, H.; et al. Diagnostic performance of noninvasive fractional flow reserve derived from coronary computed tomography angiography in suspected coronary artery disease: The NXT trial. J. Am. Coll. Cardiol. 2014, 63, 1145–1155. [Google Scholar] [CrossRef]
- Tu, S.; Westra, J.; Yang, J.; von Birgelen, C.; Ferrara, A.; Pellicano, M.; Nef, H.; Tebaldi, M.; Murasato, Y.; Lansky, A.; et al. Diagnostic accuracy of fast computational approaches to derive fractional flow reserve from diagnostic coronary angiography: The international multicenter FAVOR pilot study. JACC Cardiovasc. Interv. 2016, 9, 2024–2035. [Google Scholar] [CrossRef]
- Budoff, M.J.; Dowe, D.; Jollis, J.G.; Gitter, M.; Sutherland, J.; Halamert, E.; Scherer, M.; Bellinger, R.; Martin, A.; Benton, R.; et al. Diagnostic performance of 64-multidetector row coronary computed tomographic angiography for evaluation of coronary artery stenosis in individuals without known coronary artery disease: Results from the prospective multicenter ACCURACY trial. J. Am. Coll. Cardiol. 2008, 52, 1724–1732. [Google Scholar] [CrossRef]
- Miller, J.M.; Rochitte, C.E.; Dewey, M.; Arbab-Zadeh, A.; Niinuma, H.; Gottlieb, I.; Paul, N.; Clouse, M.E.; Shapiro, E.P.; Hoe, J.; et al. Diagnostic performance of coronary angiography by 64-row CT. N. Engl. J. Med. 2008, 359, 2324–2336. [Google Scholar] [CrossRef] [PubMed]
- Motoyama, S.; Sarai, M.; Harigaya, H.; Anno, H.; Inoue, K.; Hara, T.; Naruse, H.; Ishii, J.; Hishida, H.; Wong, N.D.; et al. Computed tomographic angiography characteristics of atherosclerotic plaques subsequently resulting in acute coronary syndrome. J. Am. Coll. Cardiol. 2009, 54, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Nørgaard, B.L.; Terkelsen, C.J.; Mathiassen, O.N.; Grove, E.L.; Bøtker, H.E.; Parner, E.; Leipsic, J.; Steffensen, F.H.; Riis, A.H.; Pedersen, K.; et al. Coronary CT angiographic and flow reserve-guided management of patients with stable chest pain. J. Am. Coll. Cardiol. 2019, 73, 2718–2728. [Google Scholar]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ library for complex physics simulations. In Proceedings of the International Workshop on Coupled Methods in Numerical Dynamics, Dubrovnik, Croatia, 19–21 September 2007; Volume 1000, pp. 1–20. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Greenshields, C.J. OpenFOAM User Guide; OpenFOAM Foundation Ltd.: London, UK, 2015. [Google Scholar]
- Franjo, J. cfMesh User Guide; Creative Fields: Zagreb, Croatia, 2014. [Google Scholar]
- Itu, L.; Rapaka, S.; Passerini, T.; Georgescu, B.; Schwemmer, C.; Schoebinger, M.; Flohr, T.; Sharma, P.; Comaniciu, D. A machine-learning approach for computation of fractional flow reserve from coronary computed tomography. J. Appl. Physiol. 2016, 121, 42–52. [Google Scholar] [CrossRef]
- Tian, F.B.; Zhu, L.; Fok, P.W.; Lu, X.Y. Simulation of a pulsatile non-Newtonian flow past a stenosed 2D artery with an immersed boundary method. Comput. Biol. Med. 2013, 43, 1098–1113. [Google Scholar] [CrossRef]
- Dewey, M.; Siebes, M.; Kachelrieß, M.; Kofoed, K.F.; Maurovich-Horvat, P.; Nikolaou, K.; Sarwar, A.; Schlett, C.L.; Scholtz, J.E.; Schoepf, U.J.; et al. Clinical quantitative cardiac imaging for the assessment of myocardial ischaemia. Nat. Rev. Cardiol. 2020, 17, 427–450. [Google Scholar] [CrossRef]
- Pontone, G.; Baggiano, A.; Andreini, D.; Guaricci, A.I.; Guglielmo, M.; Muscogiuri, G.; Fusini, L.; Soldi, M.; Del Torto, A.; Mushtaq, S.; et al. Dynamic stress computed tomography perfusion with a whole-heart coverage scanner in addition to coronary computed tomography angiography and fractional flow reserve computed tomography derived. JACC Cardiovasc. Imaging 2019, 12, 2460–2471. [Google Scholar] [CrossRef]
- Wang, S.; Ren, T.; Cheng, N.; Wang, R.; Zhang, L. Time-Varying Coronary Artery Deformation: A Dynamic Skinning Framework for Coronary Intervention Planning and Training. Preprints 2025, 2025052914. [Google Scholar] [CrossRef]
- Frangi, A.F.; Niessen, W.J.; Vincken, K.L.; Viergever, M.A. Multiscale vessel enhancement filtering. Med. Image Comput. Comput. Assist. Interv. 1998, 1496, 130–137. [Google Scholar]
- Zhou, Y.; Kassab, G.S.; Molloi, S. On the design of the coronary arterial tree: A generalization of Murray’s law. Phys. Med. Biol. 1999, 44, 2929–2945. [Google Scholar] [CrossRef]
- Pontone, G.; Baggiano, A.; Andreini, D.; Guaricci, A.I.; Guglielmo, M.; Muscogiuri, G.; Fusini, L.; Fazzari, F.; Mushtaq, S.; Conte, E.; et al. Stress computed tomography perfusion versus fractional flow reserve CT derived in suspected coronary artery disease: The PERFECTION study. JACC Cardiovasc. Imaging 2019, 12, 1487–1497. [Google Scholar]
- Hoffman, J.I.E.; Spaan, J.A.E. Pressure-flow relations in coronary circulation. Physiol. Rev. 1990, 70, 331–390. [Google Scholar] [CrossRef] [PubMed]
- Westerhof, N.; Bovendeerd, P.H.; Mollema, S.A.; van der Velde, E.T. Cross-talk between cardiac muscle and coronary vasculature. Physiol. Rev. 2006, 86, 1263–1308. [Google Scholar] [CrossRef] [PubMed]
- Kamada, H.; Nakamura, M.; Ota, H.; Higuchi, S.; Takase, K. Blood flow analysis with computational fluid dynamics and 4D-flow MRI for vascular diseases. J. Cardiol. 2022, 80, 386–396. [Google Scholar] [CrossRef]
- Kundu, P.K.; Cohen, I.M.; Dowling, D.R.; Capecelatro, J. Fluid Mechanics, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Steinman, D.A.; Taylor, C.A. Flow imaging and computing: Large artery hemodynamics. Ann. Biomed. Eng. 2005, 33, 1704–1709. [Google Scholar] [CrossRef]
- Klabunde, R. Cardiovascular Physiology Concepts, 2nd ed.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2011. [Google Scholar]
- Nichols, W.W.; O’Rourke, M.; Edelman, E.R.; Vlachopoulos, C. McDonald’s Blood Flow in Arteries: Theoretical, Experimental and Clinical Principles, 7th ed.; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Westerhof, N.; Lankhaar, J.W.; Westerhof, B.E. The arterial windkessel. Med. Biol. Eng. Comput. 2009, 47, 131–141. [Google Scholar] [CrossRef]
- Taylor, C.A.; Fonte, T.A.; Min, J.K. Computational fluid dynamics applied to cardiac computed tomography for noninvasive quantification of fractional flow reserve: Scientific basis. J. Am. Coll. Cardiol. 2013, 61, 2233–2241. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, Y. CoronaryHemodynamics: An Automated Simulation Framework for Coronary Artery Hemodynamics Using OpenFOAM. arXiv 2025, arXiv:2501.08340. [Google Scholar]
- Marcus, M.L.; Chilian, W.M.; Kanatsuka, H.; Dellsperger, K.C.; Eastham, C.L.; Lamping, K.G. Understanding the coronary circulation through studies at the microvascular level. Circulation 1990, 82, 1–7. [Google Scholar] [CrossRef]
- Ku, D.N. Blood flow in arteries. Annu. Rev. Fluid Mech. 1997, 29, 399–434. [Google Scholar] [CrossRef]
- Karimi, A.; Navidbakhsh, M.; Shojaei, A.; Faghihi, S. Measurement of the uniaxial mechanical properties of healthy and atherosclerotic human coronary arteries. Mater. Sci. Eng. C 2013, 33, 2550–2554. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Stadler, M.; Schulze-Bauer, C.A. A layer-specific three-dimensional model for the simulation of balloon angioplasty using magnetic resonance imaging and mechanical testing. Ann. Biomed. Eng. 2002, 30, 753–767. [Google Scholar] [CrossRef]
- Larsson, J.; Kawai, S.; Bodart, J.; Bermejo-Moreno, I. Large eddy simulation with modeled wall-stress: Recent progress and future directions. Mech. Eng. Rev. 2016, 3, 15-00418. [Google Scholar] [CrossRef]
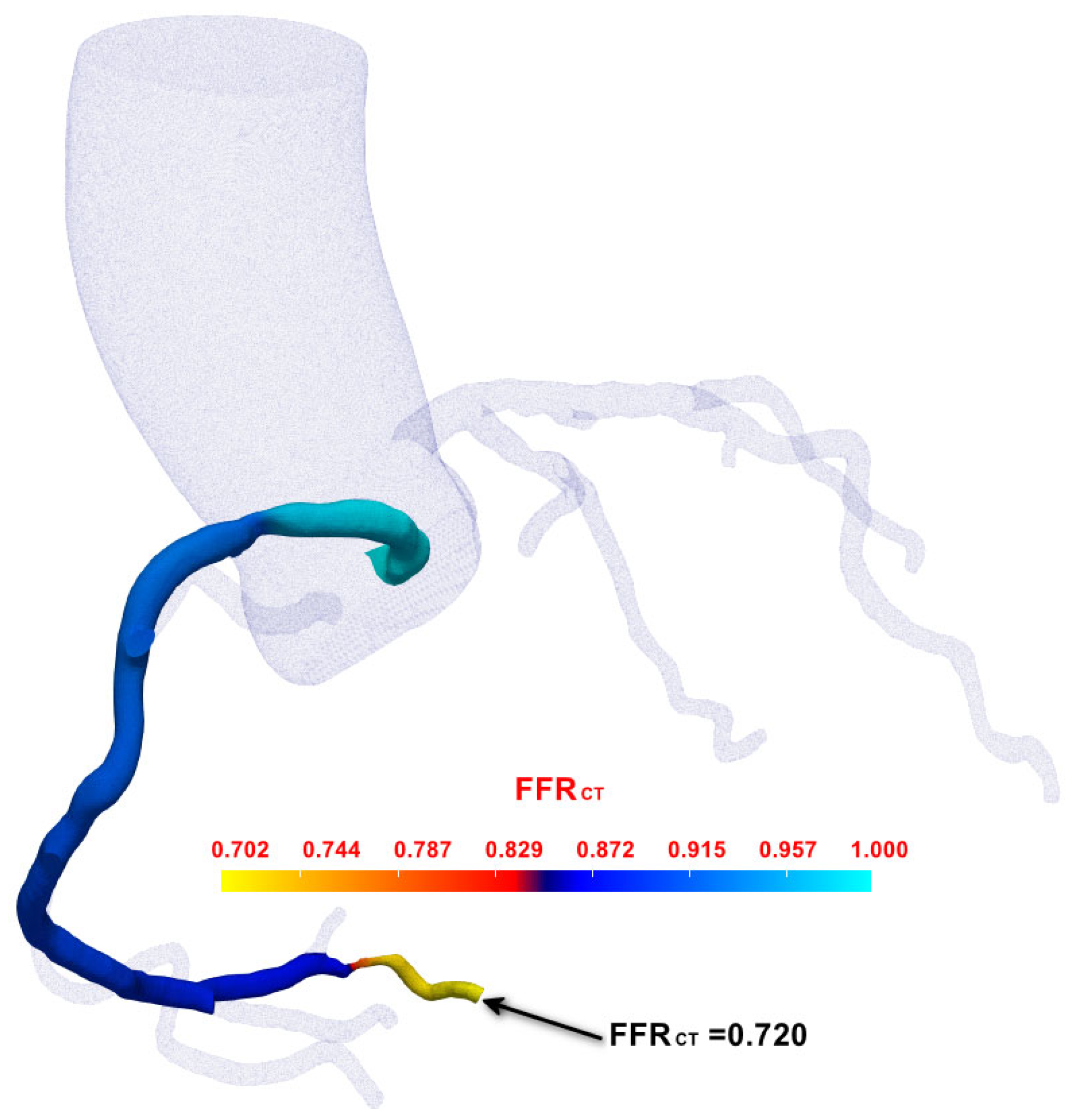
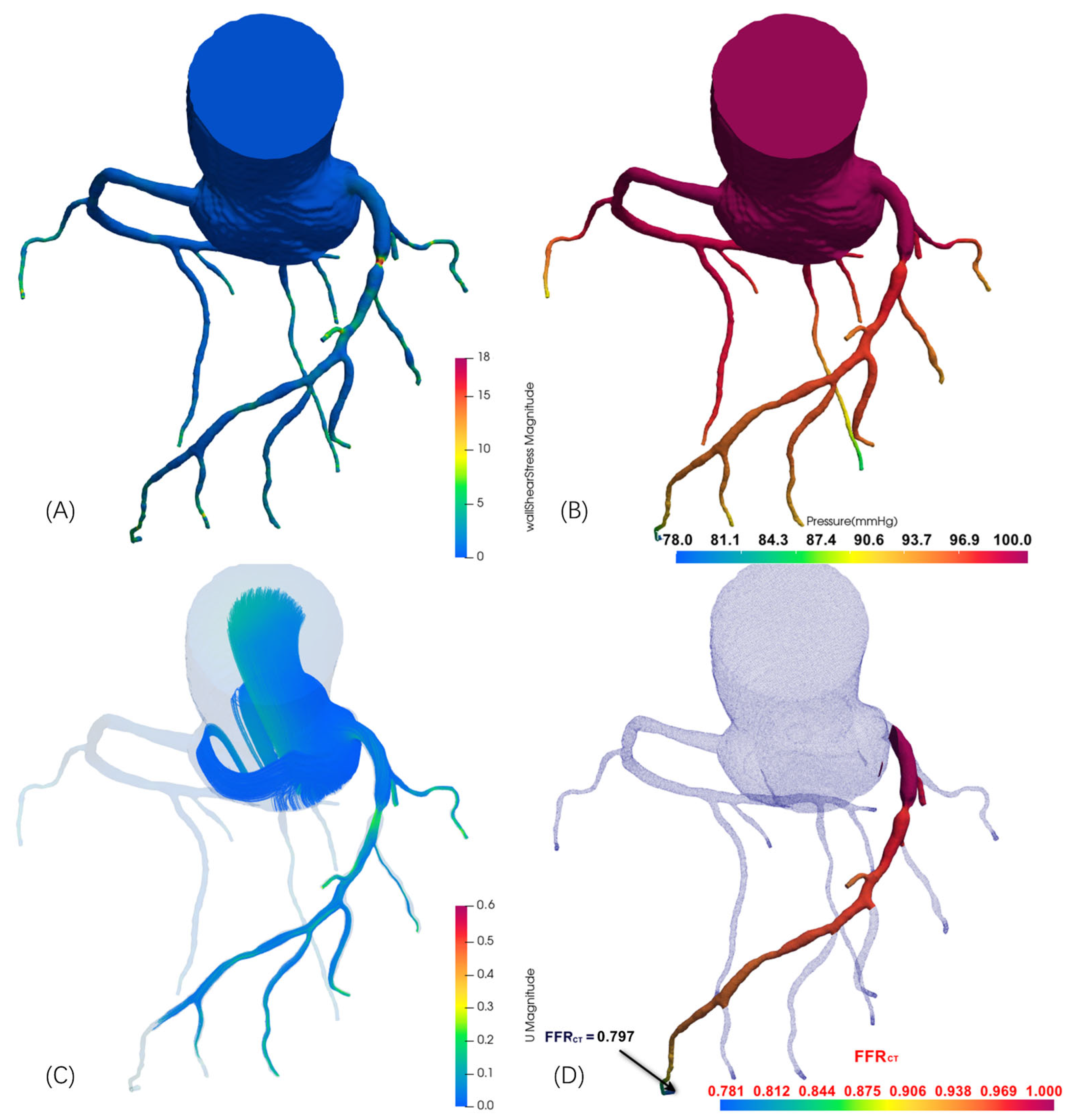
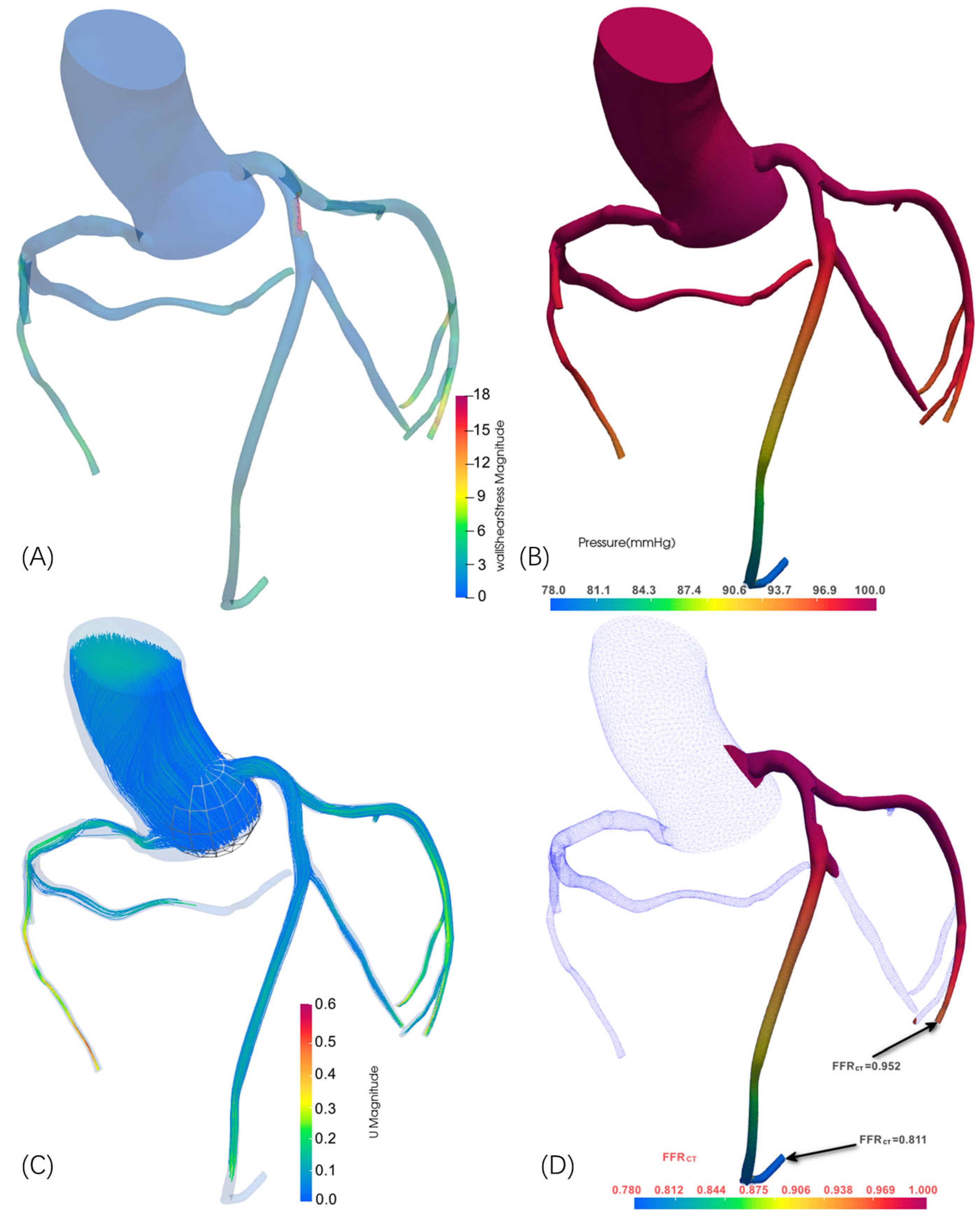
| Case | Vessel | Invasive FFR | Static FFRCT | Dynamic FFRCT |
|---|---|---|---|---|
| 1 | RCA | 0.70 | 0.742 | 0.720 |
| 2 | LAD | 0.78 | 0.825 | 0.797 |
| 3a | LAD | 0.78 | 0.818 | 0.811 |
| 3b | LCX | 0.94 | 0.961 | 0.952 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Liu, R.; Zhang, L. Dynamic Fractional Flow Reserve from 4D-CTA: A Novel Framework for Non-Invasive Coronary Assessment. J. Imaging 2025, 11, 330. https://doi.org/10.3390/jimaging11100330
Wang S, Liu R, Zhang L. Dynamic Fractional Flow Reserve from 4D-CTA: A Novel Framework for Non-Invasive Coronary Assessment. Journal of Imaging. 2025; 11(10):330. https://doi.org/10.3390/jimaging11100330
Chicago/Turabian StyleWang, Shuo, Rong Liu, and Li Zhang. 2025. "Dynamic Fractional Flow Reserve from 4D-CTA: A Novel Framework for Non-Invasive Coronary Assessment" Journal of Imaging 11, no. 10: 330. https://doi.org/10.3390/jimaging11100330
APA StyleWang, S., Liu, R., & Zhang, L. (2025). Dynamic Fractional Flow Reserve from 4D-CTA: A Novel Framework for Non-Invasive Coronary Assessment. Journal of Imaging, 11(10), 330. https://doi.org/10.3390/jimaging11100330







