A Fast Nonlinear Sparse Model for Blind Image Deblurring
Abstract
1. Introduction
- We propose a novel nonlinear sparse regularization () that nonlinearly couples the norm with the norm.
- An Adaptive Generalized Soft-Thresholding (AGST) algorithm is developed to optimize the regularization problem.
- Building upon -regularization, we design a novel nonlinear sparse model for blind deblurring and develop an efficient optimization algorithm based on AGST and HQS.
2. Related Work
2.1. Optimization-Based Methods
2.2. Learning-Based Methods
3. Proposed Method
3.1. Definition of Nonlinear Sparse Regularization
| Algorithm 1: The Adaptive Generalized Soft-Thresholding algorithm |
| input: , , , p, J if else for t = 1, 2, …, J end end Output: |
3.2. Deblurring Model and Optimization
3.2.1. Updating Latent Image
| Algorithm 2: Latent image estimation |
| Input Blurred image , initialized from the coarser level. , , repeat Calculating using Equation (22) Calculating using Equation (23) Calculating using Equation (20) λ1←2λ1 λ2←2λ2 until λ1 >αmax Output Intermediate latent image . |
3.2.2. Updating Blur Kernel k
| Algorithm 3: Blur kernel estimation |
| Input Blurred image Initialized from the previous level of the image pyramid. while do Estimate using Algorithm 2 Estimate using Equation (25) Output Blur kernel |
4. Experimental Results
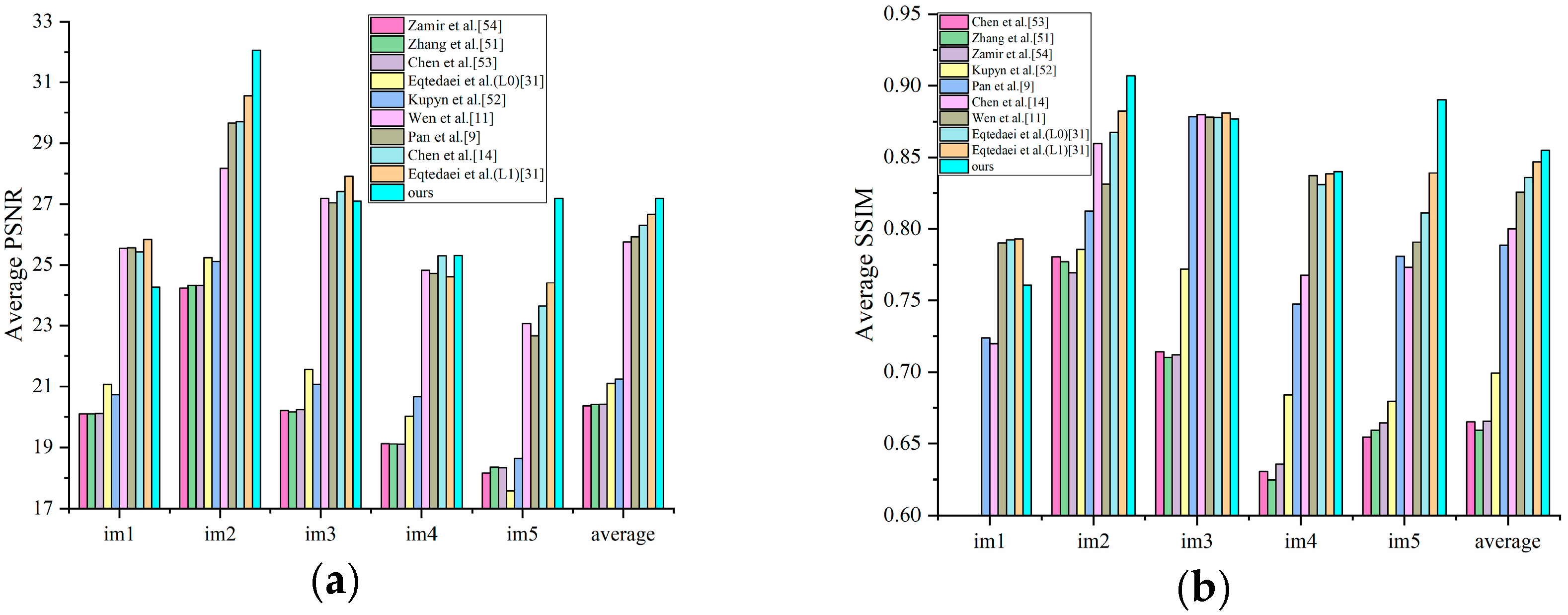
4.1. Natural Images
4.1.1. Levin’s Dataset
4.1.2. Sun’s Dataset
4.2. Specific Images
4.2.1. Human Face Images
4.2.2. Text Images
4.3. Comparison Against Deep Learning Methods
4.4. Real-World Images
5. Analysis and Discussion
5.1. The Effectiveness of the Fast Nonlinear Sparse Model
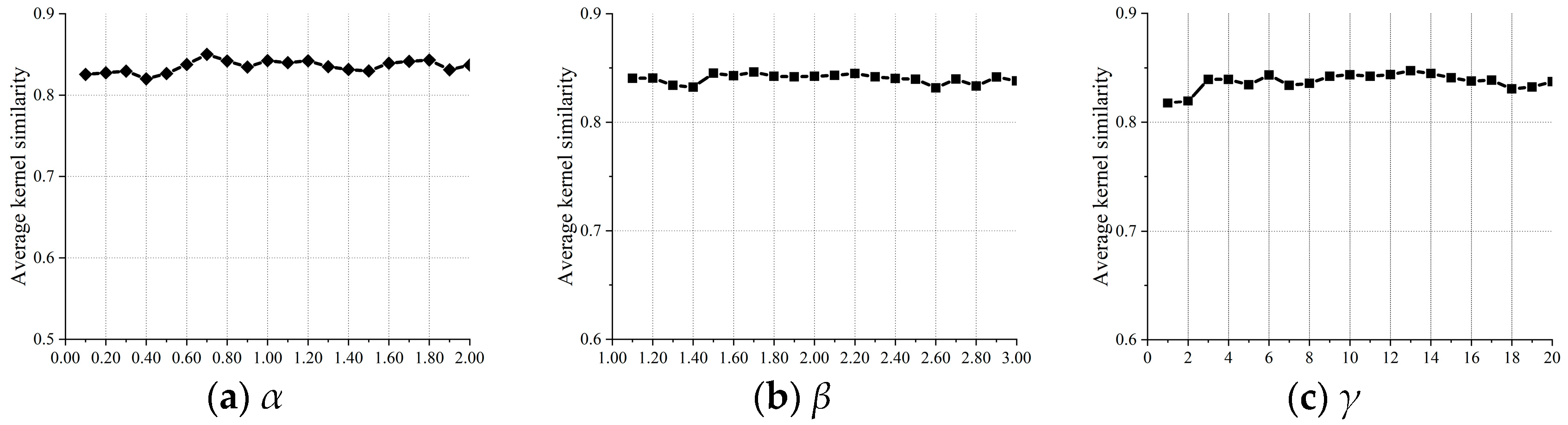
5.2. Effect of Main Parameters
5.3. Runtime Analysis
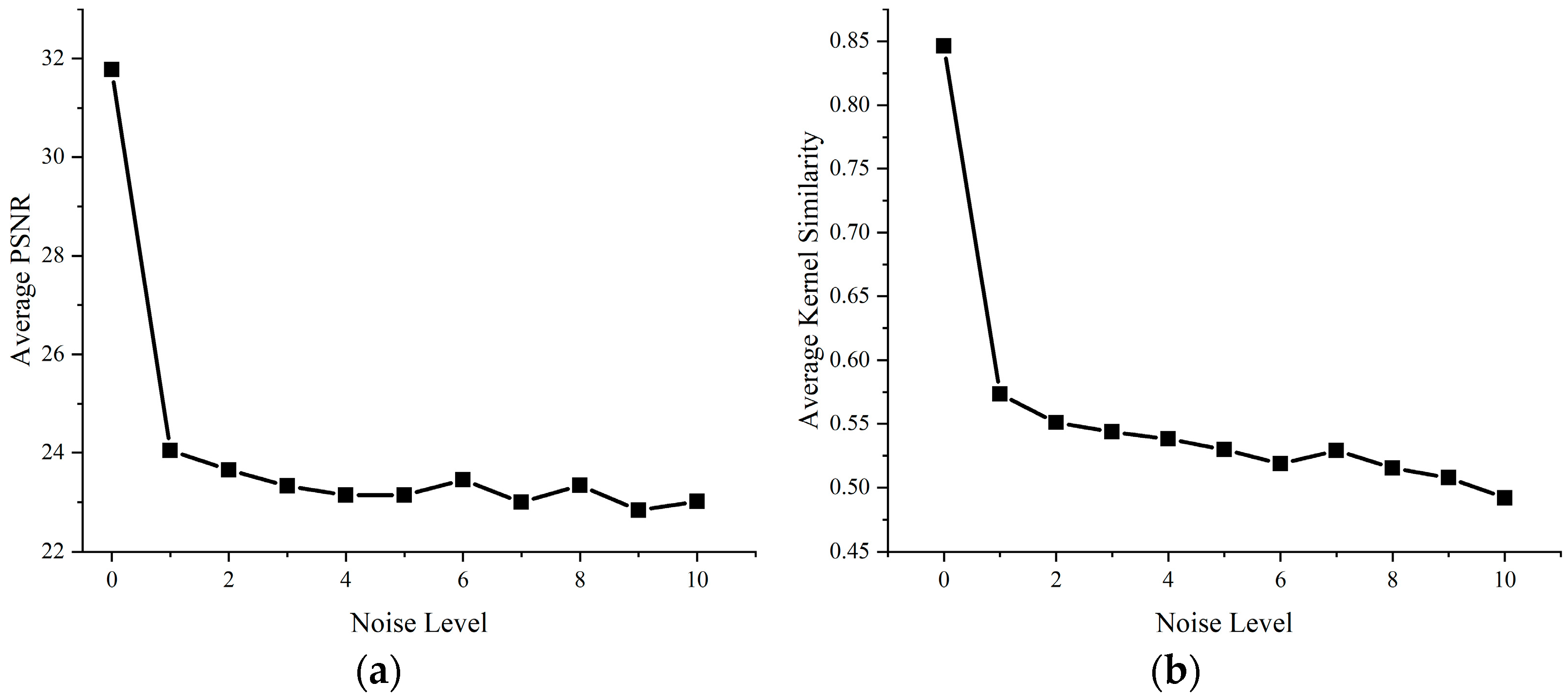
5.4. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, L.; Lu, C.; Xu, Y.; Jia, J. Image smoothing via L0 gradient minimization. In Proceedings of the 2011 SIGGRAPH Asia Conference, Hong Kong, China, 12–15 December 2011. [Google Scholar]
- Xu, L.; Zheng, S.; Jia, J. Unnatural L0 Sparse Representation for Natural Image Deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Wang, J.; Ma, Q. The variant of the iterative shrinkage-thresholding algorithm for minimization of the 1 over ∞ norms. Signal Process. 2023, 211, 109104. [Google Scholar] [CrossRef]
- Wang, C.; Yan, M.; Yu, J. Sorted L1/L2 Minimization for Sparse Signal Recovery. J. Sci. Comput. 2023, 99, 32. [Google Scholar] [CrossRef]
- Wang, H.; Hu, C.; Qian, W.; Wang, Q. RT-Deblur: Real-time image deblurring for object detection. Vis. Comput. 2023, 40, 2873–2887. [Google Scholar] [CrossRef]
- Wang, C.; Tao, M.; Nagy, J.; Lou, Y. Limited-angle CT reconstruction via the L1/L2 minimization. arXiv 2020, arXiv:2006.00601. [Google Scholar]
- Wang, J. A wonderful triangle in compressed sensing. Inf. Sci. 2022, 611, 95–106. [Google Scholar] [CrossRef]
- Levin, A.; Weiss, Y.; Durand, F.; Freeman, W.T. Understanding and evaluating blind deconvolution algorithms. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1964–1971. [Google Scholar]
- Pan, J.; Sun, D.; Pfister, H.; Yang, M.H. Blind Image Deblurring Using Dark Channel Prior. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Chen, L.; Fang, F.; Wang, T.; Zhang, G. Blind Image Deblurring with Local Maximum Gradient Prior. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Wen, F.; Ying, R.; Liu, Y.; Liu, P.; Truong, T.K. A Simple Local Minimal Intensity Prior and an Improved Algorithm for Blind Image Deblurring. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 2923–2937. [Google Scholar] [CrossRef]
- Feng, X.; Tan, J.; Ge, X.; Liu, J.; Hu, D. Blind Image Deblurring via Weighted Dark Channel Prior. Circuits Syst. Signal Process. CSSP 2023, 42, 5478–5499. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, H.; Li, Z. Fast blind deconvolution using a deeper sparse patch-wise maximum gradient prior. Signal Process. Image Commun. 2021, 90, 116050. [Google Scholar] [CrossRef]
- Chen, L.; Fang, F.; Lei, S.; Li, F.; Zhang, G. Enhanced Sparse Model for Blind Deblurring. In Proceedings of the 16th European Conference Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Richardson, W.H. Bayesian-Based Iterative Method of Image Restoration. J. Opt. Soc. Am. 1972, 62, 55–59. [Google Scholar] [CrossRef]
- Lucy, L.B. An Iterative Technique for the Rectification of Observed Distributions. Astron. J. 1974, 79, 745. [Google Scholar] [CrossRef]
- Fergus, R.; Singh, B.; Hertzmann, A.; Roweis, S.; Freeman, W. Removing camera shake from a single photograph. ACM Trans. Graph. 2006, 25, 787–794. [Google Scholar] [CrossRef]
- Cho, S.; Lee, S. Fast Motion Deblurring. ACM Trans. Graph. 2009, 28, 1–8. [Google Scholar] [CrossRef]
- Yang, A.Y.; Zhou, Z.; Ganesh, A.; Sastry, S.S.; Ma, Y. Fast L1-Minimization Algorithms For Robust Face Recognition. IEEE Trans. Image Process. 2010, 22, 3234–3246. [Google Scholar] [CrossRef] [PubMed]
- Candès, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing Sparsity by Reweighted 1 Minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Perrone, D.; Diethelm, R.; Favaro, P. Blind Deconvolution via Lower-Bounded Logarithmic Image Priors. In Energy Minimization Methods in Computer Vision and Pattern Recognition. EMMCVPR 2015; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Gasso, G.; Rakotomamonjy, A.; Canu, S. Recovering sparse signals with a certain family of non-convex penalties and DC programming. IEEE Trans. Signal Process. 2009, 57, 4686–4698. [Google Scholar] [CrossRef]
- Zou, H.; Li, R. One-step sparse estimates in nonconcave penalized likelihood models. Ann. Stat. 2008, 36, 1509–1533. [Google Scholar]
- Rao, B.D.; Kreutz-Delgado, K. An affine scaling methodology for best basis selection. IEEE Trans. Signal Process. 1999, 47, 187–200. [Google Scholar] [CrossRef]
- She, Y. Thresholding-based Iterative Selection Procedures for Model Selection and Shrinkage. Electron. J. Stat. 2009, 3, 384–415. [Google Scholar] [CrossRef]
- Zuo, W.; Meng, D.; Zhang, L.; Feng, X.; Zhang, D. A generalized iterated shrinkage algorithm for non-convex sparse coding. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Zuo, W.; Ren, D.; Zhang, D.D.; Gu, S.; Zhang, L. Learning Iteration-wise Generalized Shrinkage–Thresholding Operators for Blind Deconvolution. IEEE Trans. Image Process. 2016, 25, 1751–1764. [Google Scholar] [CrossRef]
- Pan, J.; Hu, Z.; Su, Z.; Yan, M.H. L0—Regularized Intensity and Gradient Prior for Deblurring Text Images and Beyond. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 342–355. [Google Scholar] [CrossRef]
- Li, J.; Lu, W. Blind image motion deblurring with L 0 -regularized priors. J. Vis. Commun. Image Represent. 2016, 40, 14–23. [Google Scholar] [CrossRef]
- Yan, Y.; Ren, W.; Guo, Y.; Wang, R.; Cao, X. Image Deblurring via Extreme Channels Prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Eqtedaei, A.; Ahmadyfard, A. Blind image deblurring using both L0 and L1 regularization of Max-min prior. Neurocomputing 2024, 592, 127727. [Google Scholar] [CrossRef]
- Joshi, N.; Szeliski, R.; Kriegman, D.J. PSF estimation using sharp edge prediction. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Xu, L.; Jia, J. Two-Phase Kernel Estimation for Robust Motion Deblurring. In Proceedings of the Computer Vision—ECCV 2010 11th European Conference on Computer Vision, Crete, Greece, 5–11 September 2010. [Google Scholar]
- Pan, J.; Liu, R.; Su, Z.; Gu, X. Kernel Estimation from Salient Structure for Robust Motion Deblurring. Signal Process. Image Commun. 2013, 28, 1156–1170. [Google Scholar] [CrossRef]
- Liu, J.; Yan, M.; Zeng, T. Surface-Aware Blind Image Deblurring. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 1041–1055. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.Q.; Wu, T.; Chan, J.C.W. Tensor Convolution-Like Low-Rank Dictionary for High-Dimensional Image Representation. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 13257–13270. [Google Scholar] [CrossRef]
- Wu, T.; Gao, B.; Fan, J.; Xue, J.; Woo, W.L. Low-Rank Tensor Completion Based on Self-Adaptive Learnable Transforms. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 8826–8838. [Google Scholar] [CrossRef]
- Bu, Y.; Zhao, Y.; Xue, J.; Yao, J.; Chan, J.C.W. Transferable Multiple Subspace Learning for Hyperspectral Image Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2024, 21, 5501005. [Google Scholar] [CrossRef]
- Sun, J.; Cao, W.; Xu, Z.; Ponce, J. Learning a Convolutional Neural Network for Non-uniform Motion Blur Removal. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Chakrabarti, A. A Neural Approach to Blind Motion Deblurring. In Proceedings of the Computer Vision—ECCV 2016 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Gong, D.; Yang, J.; Liu, L.; Zhang, Y.; Reid, I.; Shen, C.; Hengel, A.V.D.; Shi, Q. From Motion Blur to Motion Flow: A Deep Learning Solution for Removing Heterogeneous Motion Blur. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ren, D.; Zhang, K.; Wang, Q.; Hu, Q.; Zuo, W. Neural Blind Deconvolution Using Deep Priors. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 3338–3347. [Google Scholar]
- Feng, Z.; Zhang, J.; Ran, X.; Li, D.; Zhang, C. Ghost-Unet: Multi-stage network for image deblurring via lightweight subnet learning. Vis. Comput. 2025, 41, 141–155. [Google Scholar] [CrossRef]
- Mao, X.; Liu, Y.; Shen, W.; Li, Q.; Wang, Y. Deep Residual Fourier Transformation for Single Image Deblurring. arXiv 2021, arXiv:2111.11745. [Google Scholar]
- Mou, C.; Wang, Q.; Zhang, J. Deep Generalized Unfolding Networks for Image Restoration. arXiv 2022, arXiv:2204.13348. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Chen, J.; Wang, L. Hybrid Deblur Net: Deep Non-uniform Deblurring with Event Camera. IEEE Access 2020, 8, 148075–148083. [Google Scholar] [CrossRef]
- Kong, L.; Dong, J.; Li, M.; Ge, J.; Pan, J.-s. Efficient Frequency Domain-based Transformers for High-Quality Image Deblurring. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 5886–5895. [Google Scholar]
- Khler, R.; Hirsch, M.; Mohler, B.; Schlkopf, B.; Harmeling, S. Recording and Playback of Camera Shake: Benchmarking Blind Deconvolution with a Real-World Database. In Proceedings of the Computer Vision—ECCV 2012 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Sun, L.; Cho, S.; Wang, J.; Hays, J. Edge-based blur kernel estimation using patch priors. In Proceedings of the IEEE International Conference on Computational Photography (ICCP), Cambridge, MA, USA, 19–21 April 2013. [Google Scholar]
- Lai, W.S.; Huang, J.B.; Hu, Z.; Ahuja, N.; Yang, M.H. A Comparative Study for Single Image Blind Deblurring. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zhang, H.; Dai, Y.; Li, H.; Koniusz, P. Deep Stacked Hierarchical Multi-patch Network for Image Deblurring. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Kupyn, O.; Martyniuk, T.; Wu, J.; Wang, Z. DeblurGAN-v2: Deblurring (Orders-of-Magnitude) Faster and Better. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 7 October–2 November 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Chen, L.; Lu, X.; Zhang, J.; Chu, X.; Chen, C. HINet: Half Instance Normalization Network for Image Restoration. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Multi-Stage Progressive Image Restoration. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Krishnan, D.; Tay, T.; Fergus, R. Blind deconvolution using a normalized sparsity measure. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011. [Google Scholar]
- Levin, A.; Weiss, Y.; Durand, F.; Freeman, W.T. Efficient Marginal Likelihood Optimization in Blind Deconvolution. In Proceedings of the 24th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011. [Google Scholar]
- Zoran, D.; Weiss, Y. From learning models of natural image patches to whole image restoration. In Proceedings of the International Conference on Computer Vision, Tokyo, Japan, 25–27 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 479–486. [Google Scholar]
- Fang, Z.; Wu, F.; Dong, W.; Li, X.; Wu, J.; Shi, G. Self-supervised Non-uniform Kernel Estimation with Flow-based Motion Prior for Blind Image Deblurring. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 18105–18114. [Google Scholar]
- Liu, C.X.; Wang, X.; Xu, X.; Tian, R.; Li, S.; Qian, X.; Yang, M.H. Motion-Adaptive Separable Collaborative Filters for Blind Motion Deblurring. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 25595–25605. [Google Scholar]
- Mao, X.; Li, Q.; Wang, Y. AdaRevD: Adaptive Patch Exiting Reversible Decoder Pushes the Limit of Image Deblurring. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 25681–25690. [Google Scholar]










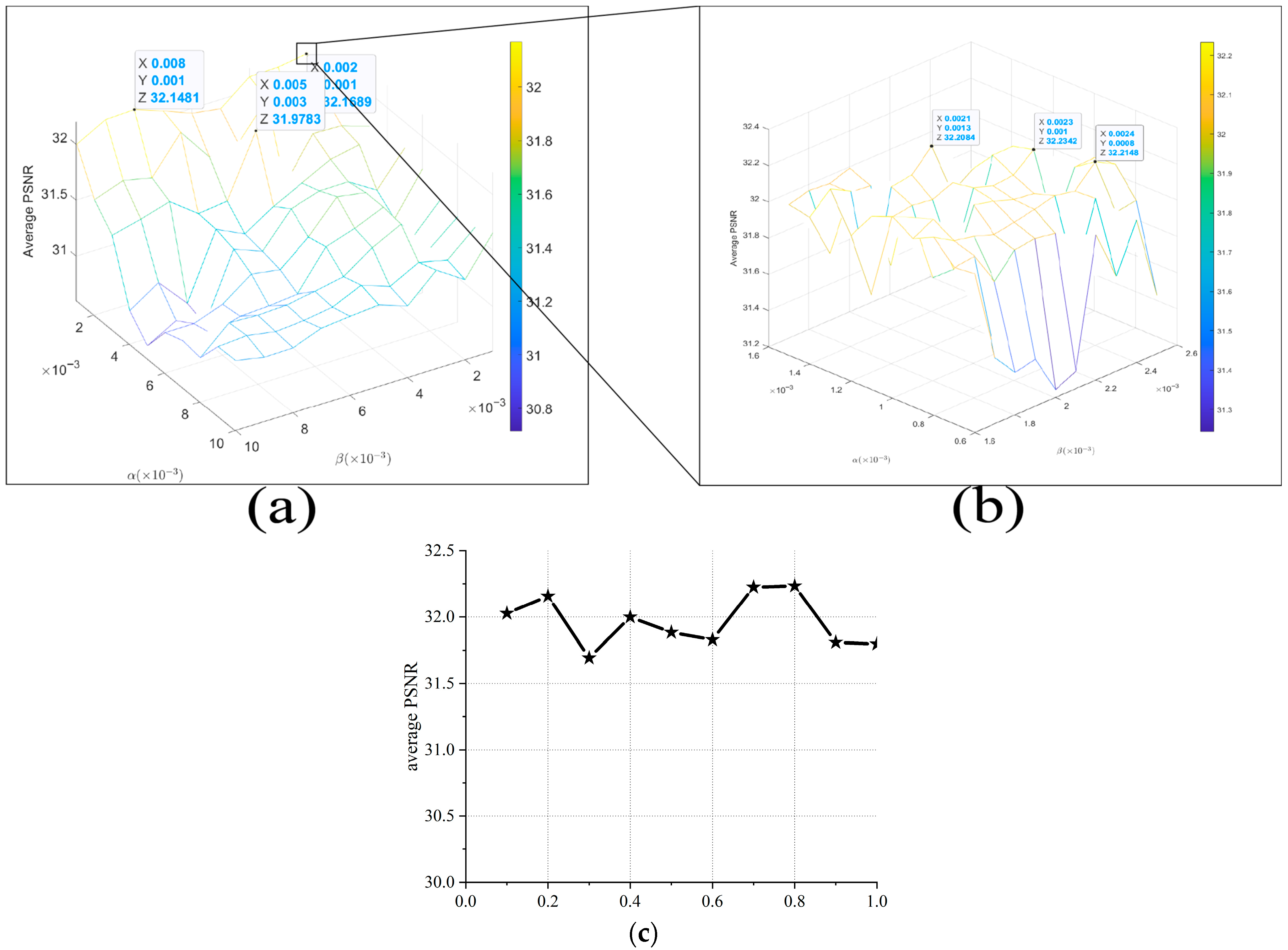



| Average PSNR | 28.481 | 30.829 | 31.420 | 31.555 | 31.739 | 31.646 | 32.234 |
| Average SSIM | 0.811 | 0.884 | 0.894 | 0.889 | 0.895 | 0.895 | 0.909 |
| 255 × 255 | 600 × 600 | 800 × 800 | |
|---|---|---|---|
| Pan et al. [9] | 63.652 | 327.051 | 659.056 |
| Wen et al. [11] | 10.229 | 22.034 | 59.721 |
| Xu et al. [13] | 9.321 | 35.021 | 82.246 |
| Chen et al. [10] | 33.041 | 179.554 | 327.993 |
| Eqtedaei et al. [31] | 27.079 | 114.625 | 198.729 |
| Ours | 4.657 | 20.871 | 35.443 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Guo, Z.; Xu, Z.; Chen, H.; Wang, C.; Song, Y.; Lai, J.; Ji, Y.; Li, Z. A Fast Nonlinear Sparse Model for Blind Image Deblurring. J. Imaging 2025, 11, 327. https://doi.org/10.3390/jimaging11100327
Zhang Z, Guo Z, Xu Z, Chen H, Wang C, Song Y, Lai J, Ji Y, Li Z. A Fast Nonlinear Sparse Model for Blind Image Deblurring. Journal of Imaging. 2025; 11(10):327. https://doi.org/10.3390/jimaging11100327
Chicago/Turabian StyleZhang, Zirui, Zheng Guo, Zhenhua Xu, Huasong Chen, Chunyong Wang, Yang Song, Jiancheng Lai, Yunjing Ji, and Zhenhua Li. 2025. "A Fast Nonlinear Sparse Model for Blind Image Deblurring" Journal of Imaging 11, no. 10: 327. https://doi.org/10.3390/jimaging11100327
APA StyleZhang, Z., Guo, Z., Xu, Z., Chen, H., Wang, C., Song, Y., Lai, J., Ji, Y., & Li, Z. (2025). A Fast Nonlinear Sparse Model for Blind Image Deblurring. Journal of Imaging, 11(10), 327. https://doi.org/10.3390/jimaging11100327






