Individual Contrast Preferences in Natural Images
Abstract
1. Introduction
2. Background
 |  |  |  |  | |
| RMS Contrast | 0.05 | 0.06 | 0.21 | 0.35 | 0.37 |
 |  |  |  |  | |
| Busyness | 0.08 | 0.16 | 51.27 | 99.93 | 99.95 |
 |  |  |  |  | |
| Colorfulness | 0.008 | 2.1 | 18.04 | 45.14 | 45.45 |
 |  |  |  |  | |
| Lightness | 4.83 | 8.06 | 52.8 | 90.11 | 93.4 |
 |  |  |  |  | |
| Complexity | 0.06 | 0.07 | 1.15 | 3.84 | 3.88 |
3. Experiment
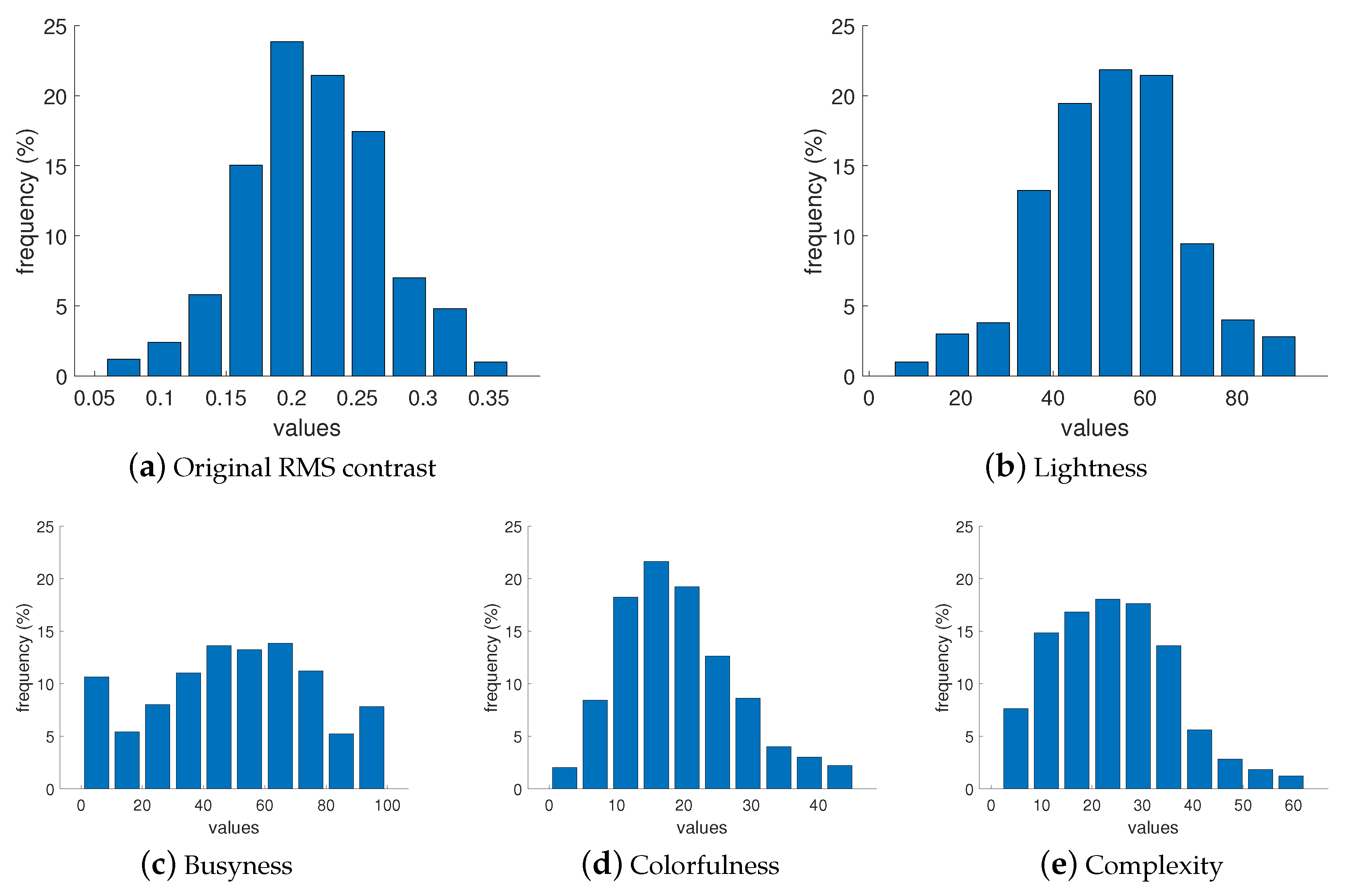
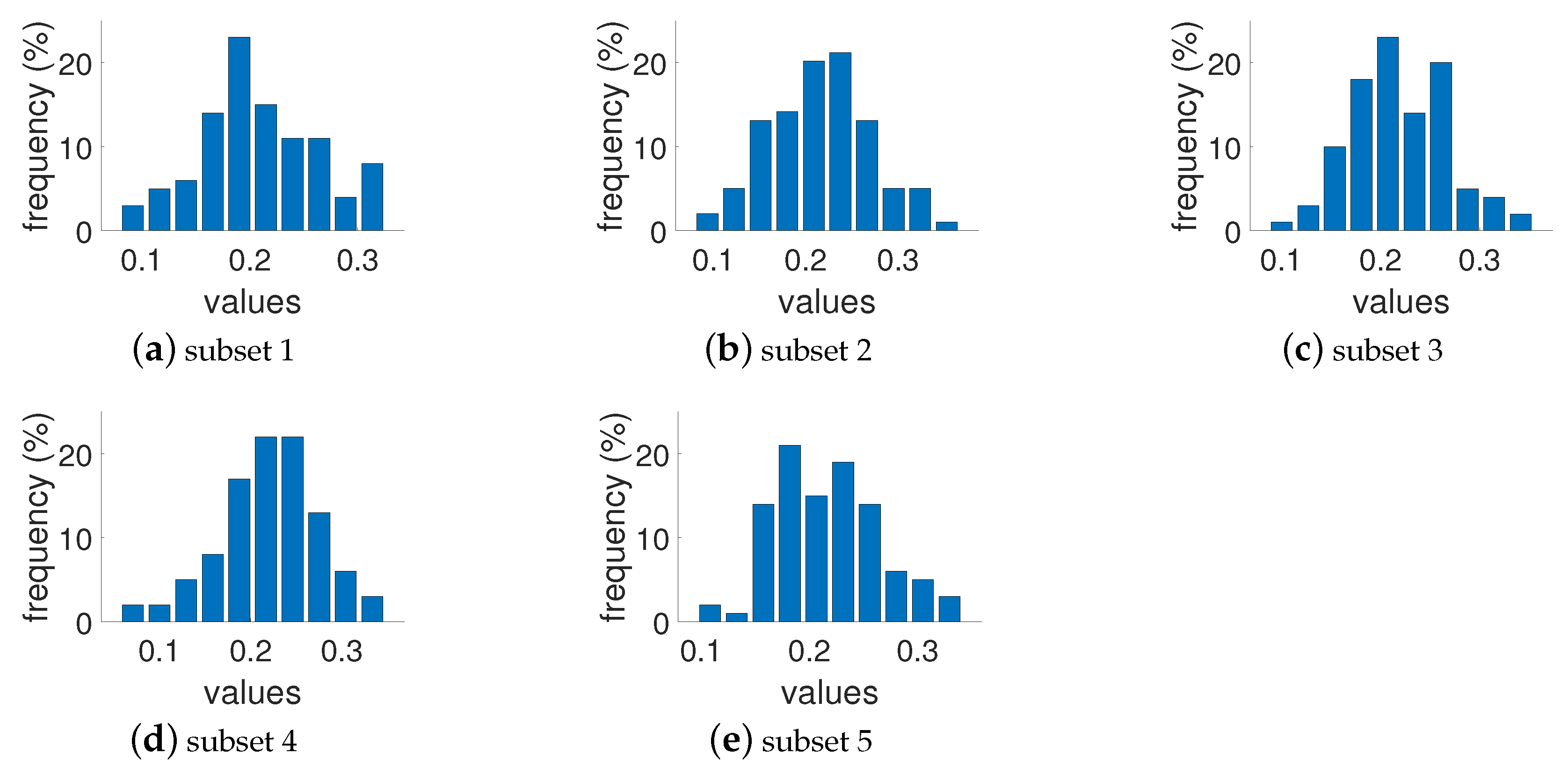
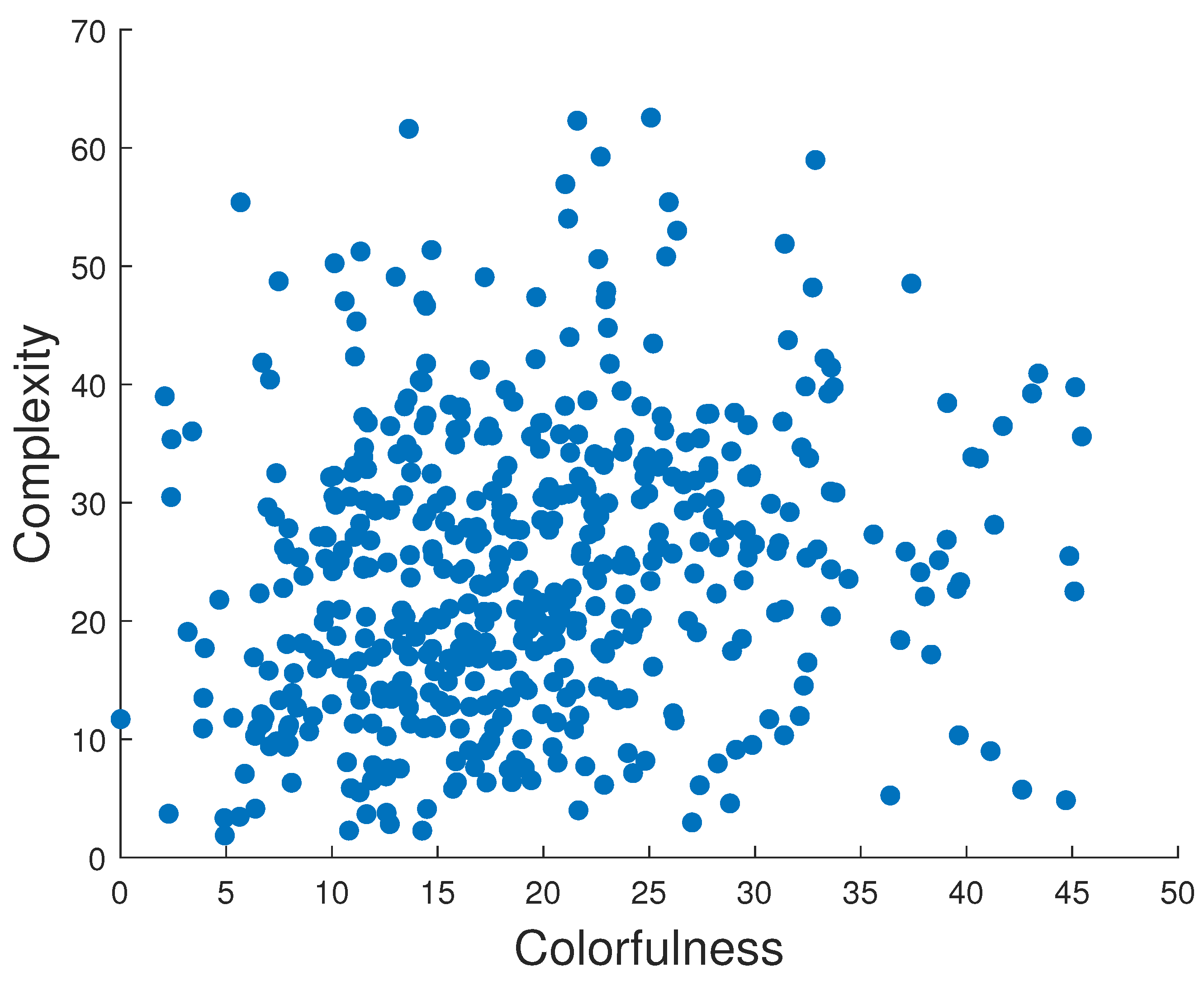
3.1. Dataset Preparation
3.2. Experimental Design
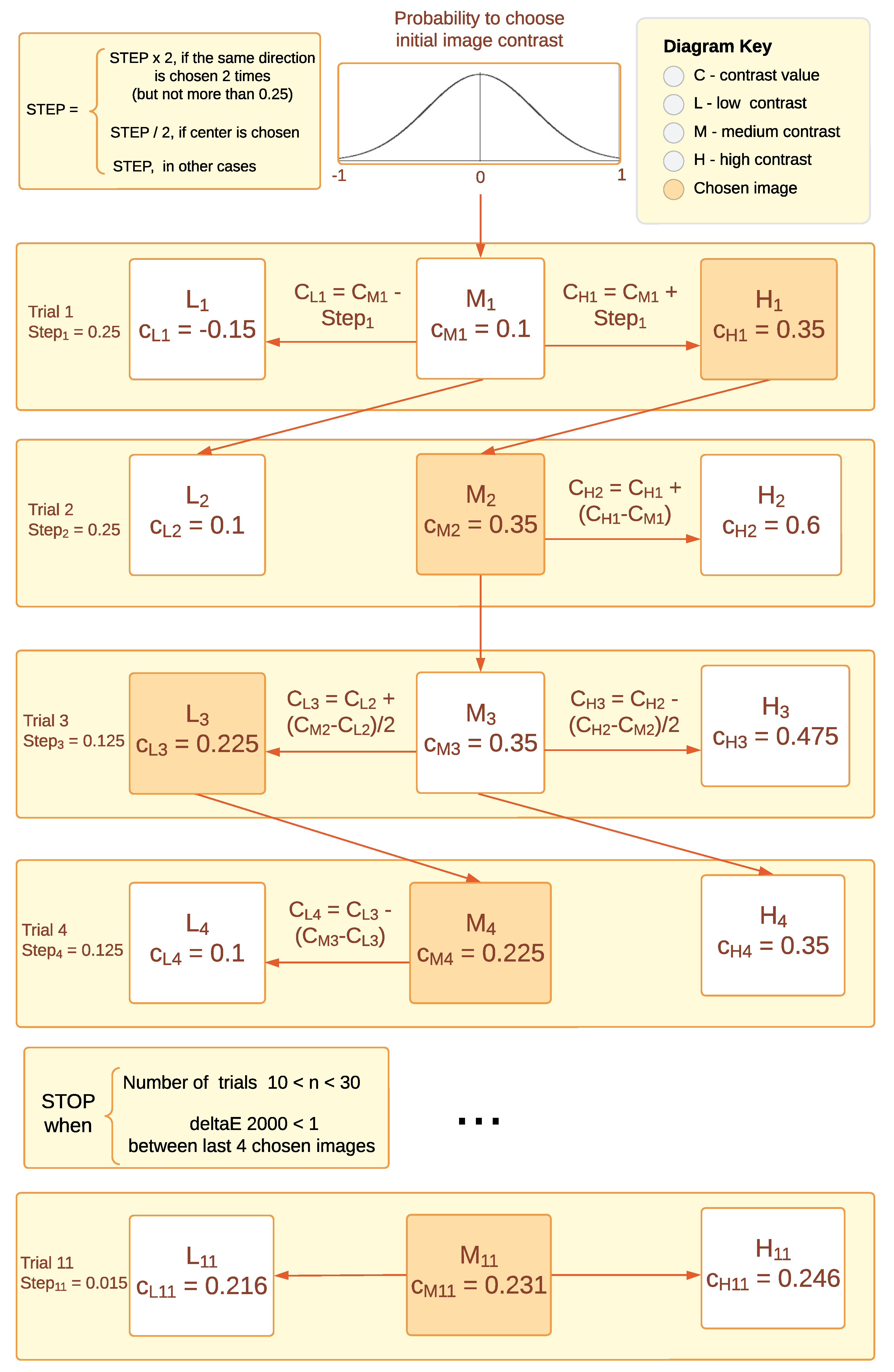
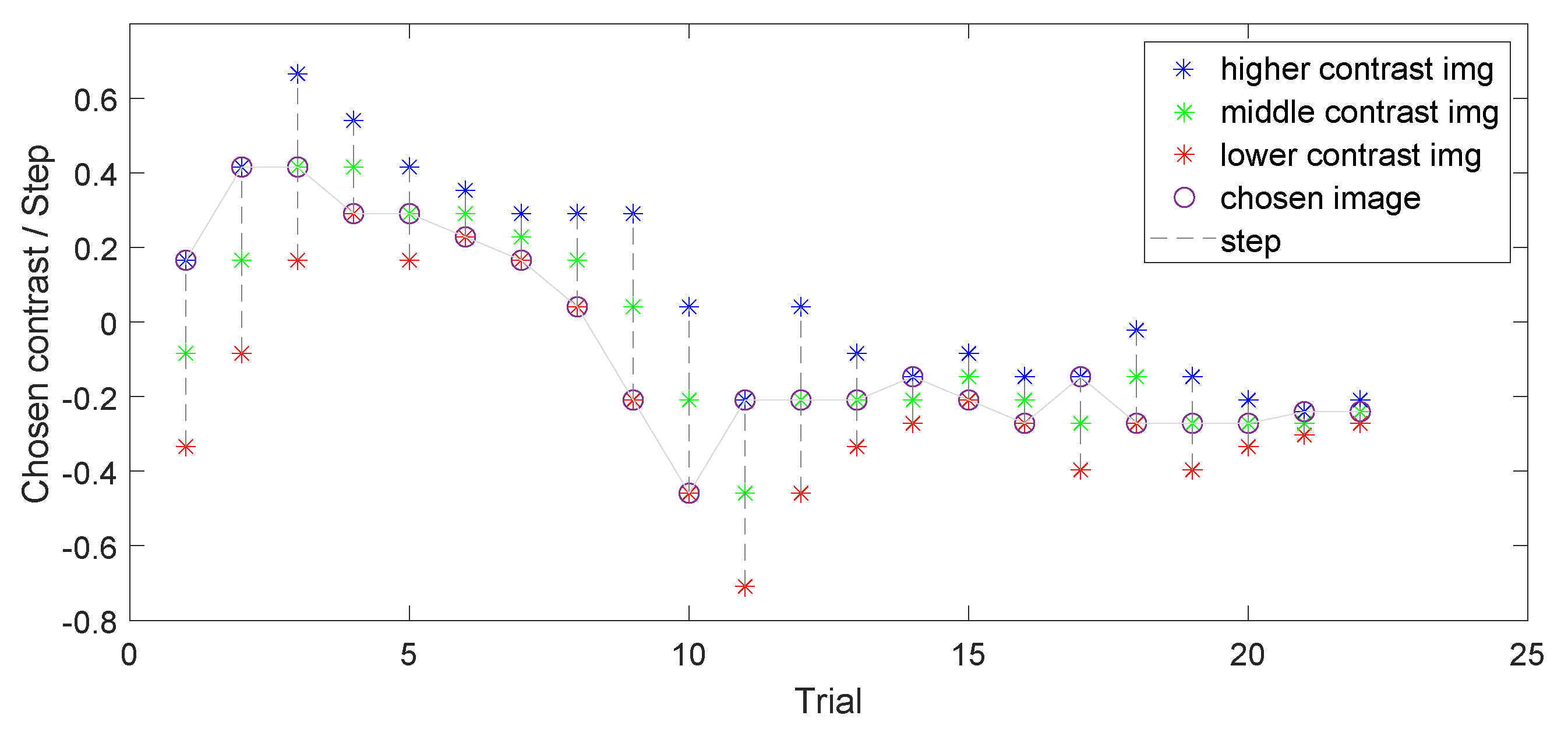
3.3. Experimental Procedure
4. Results and Discussion
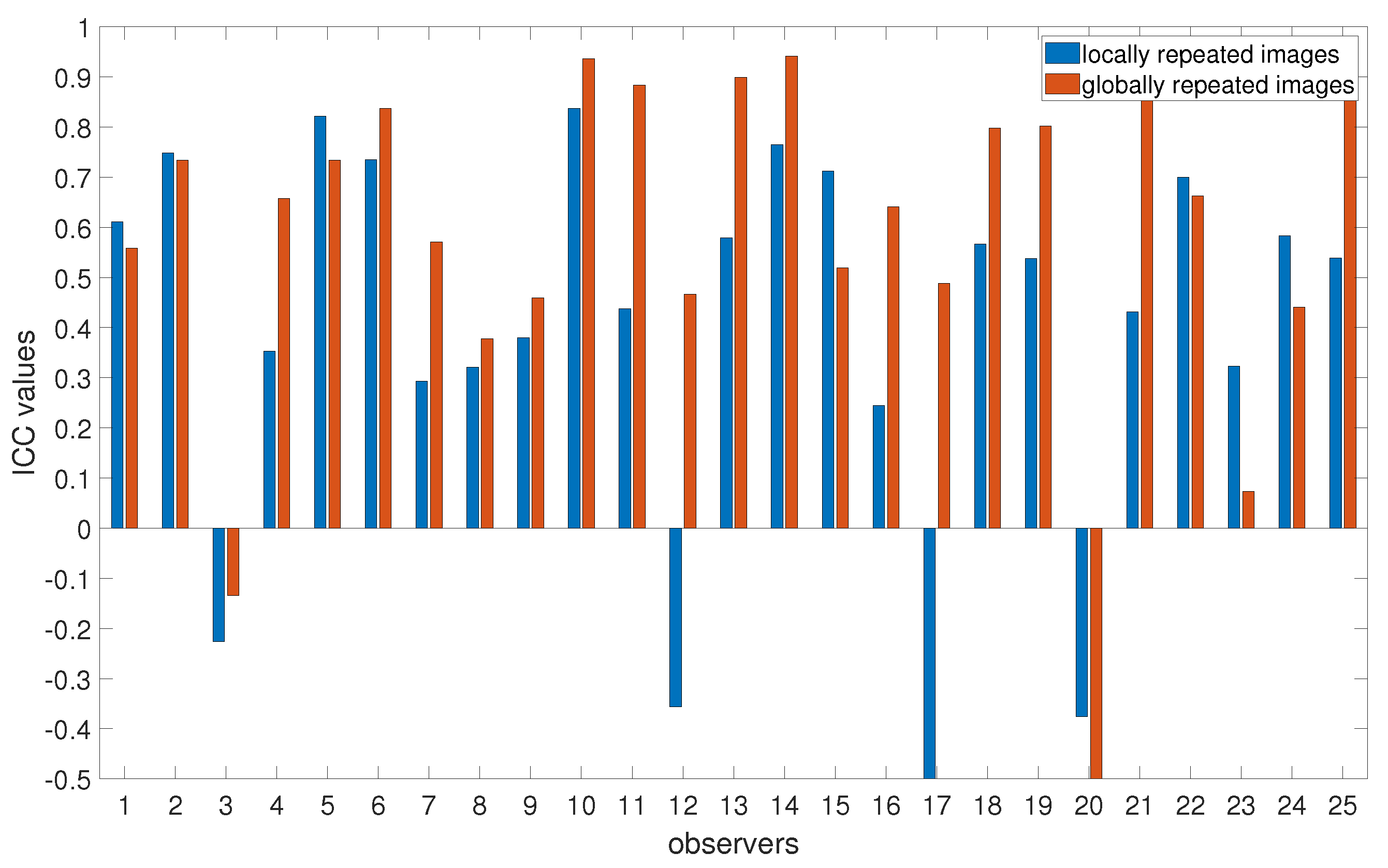
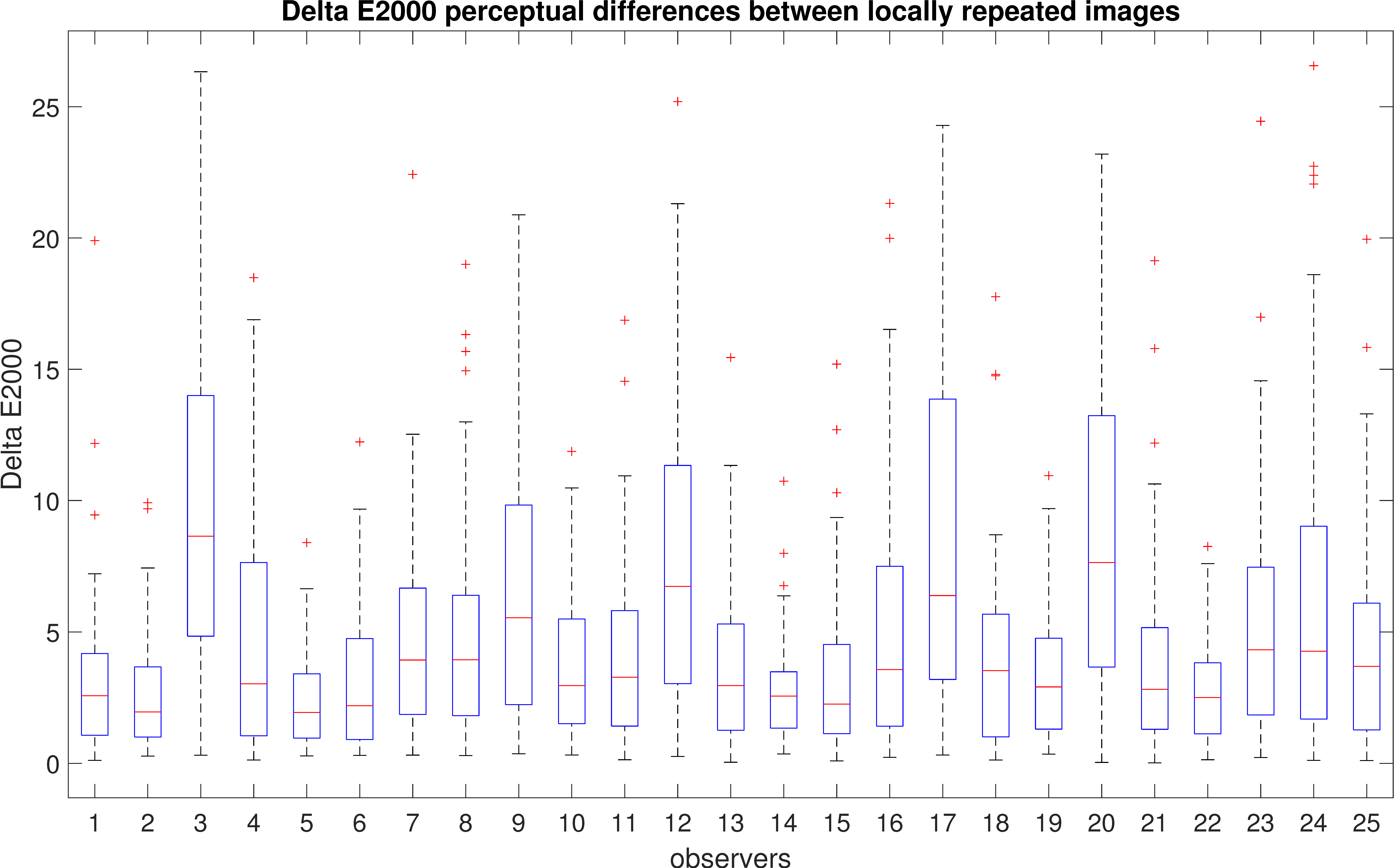
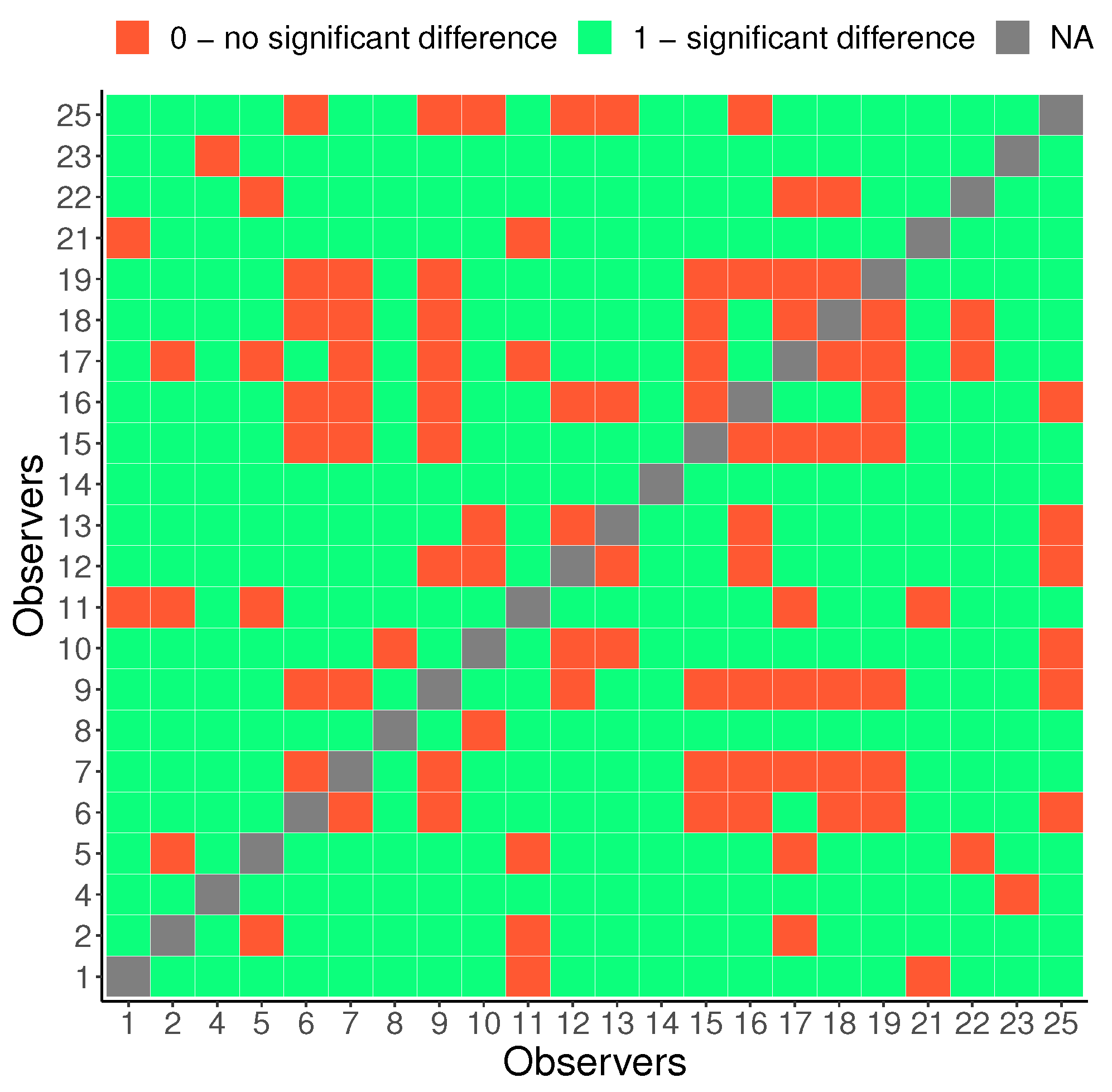
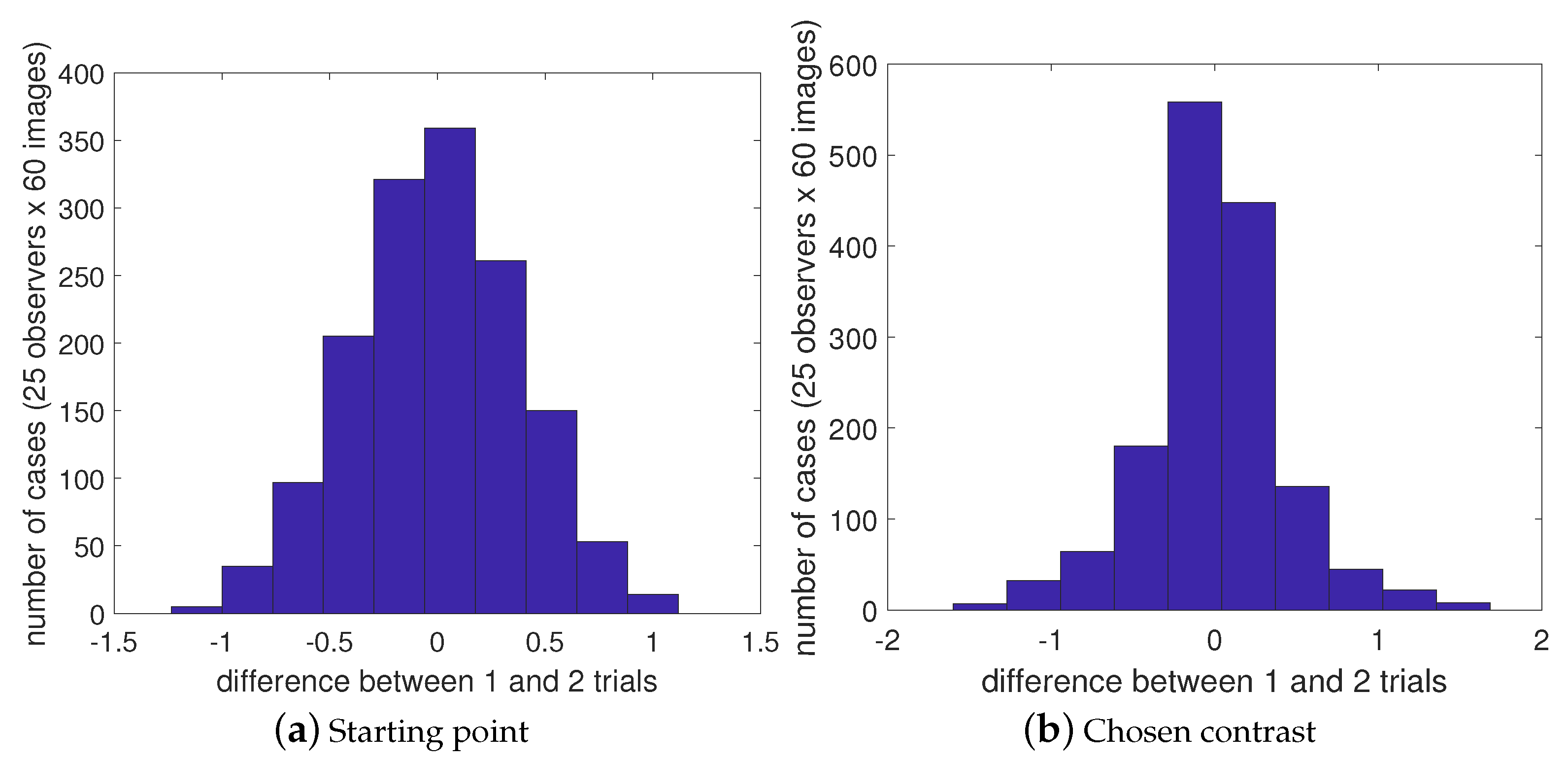
4.1. Intra-Observer Reliability
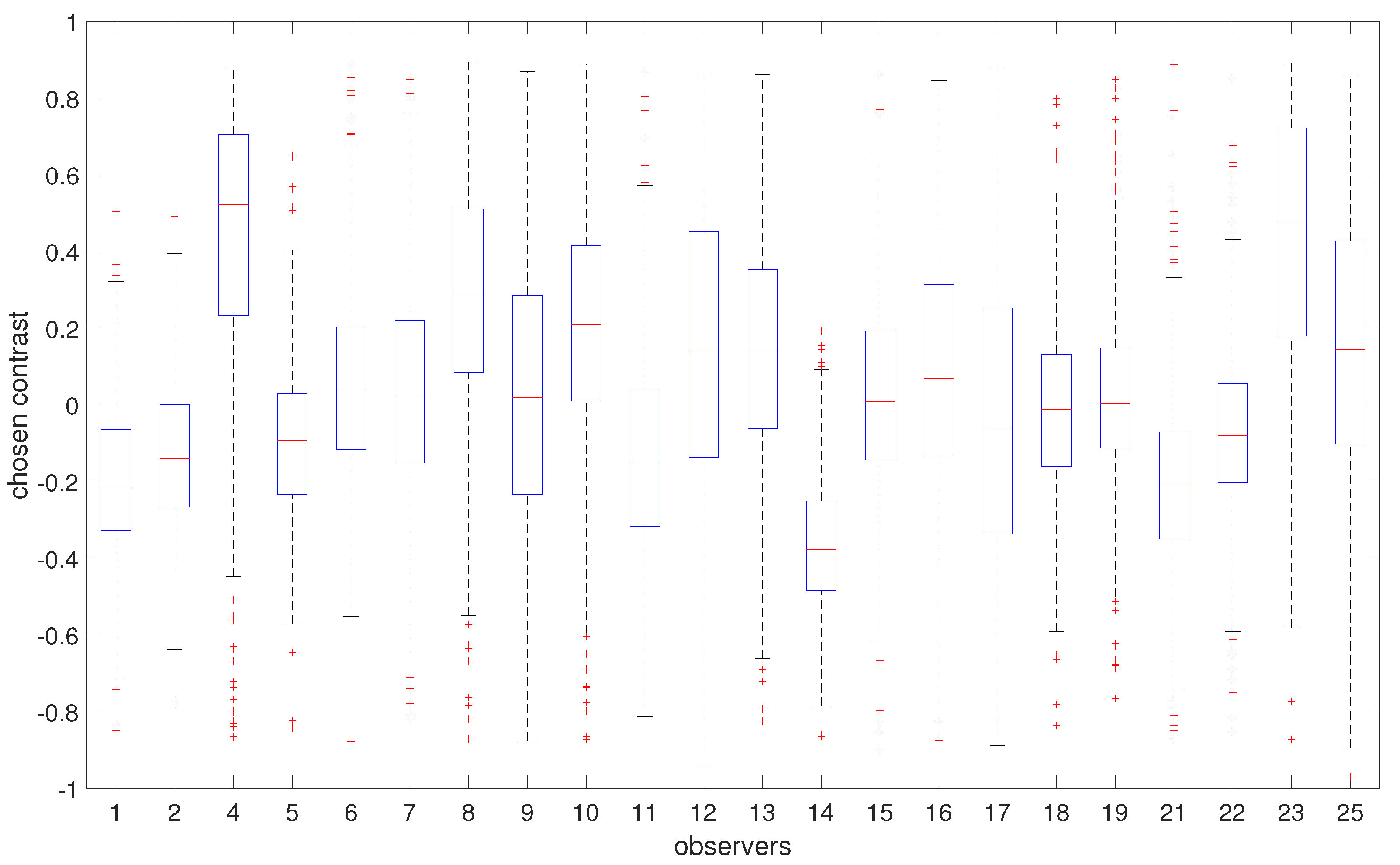
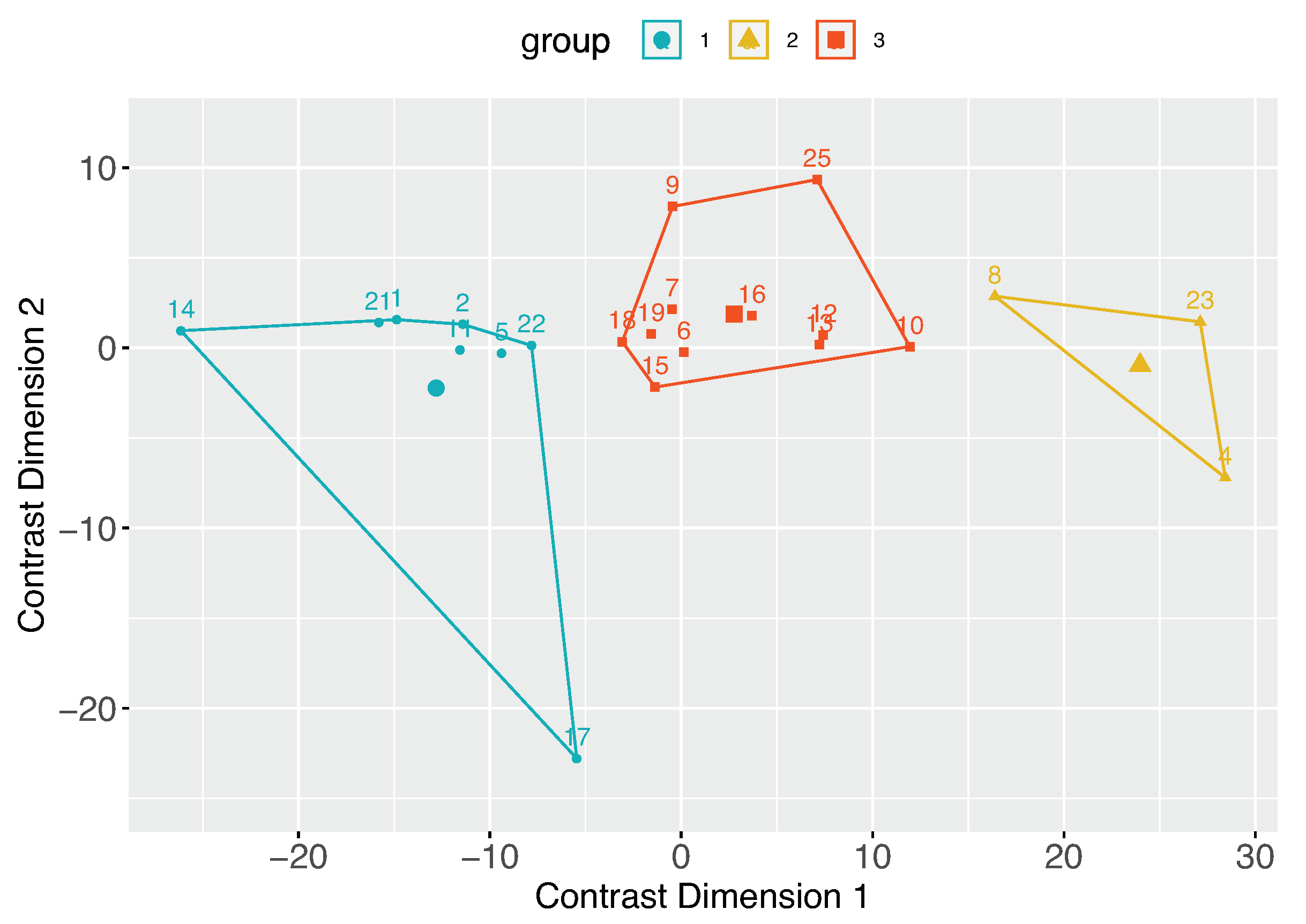
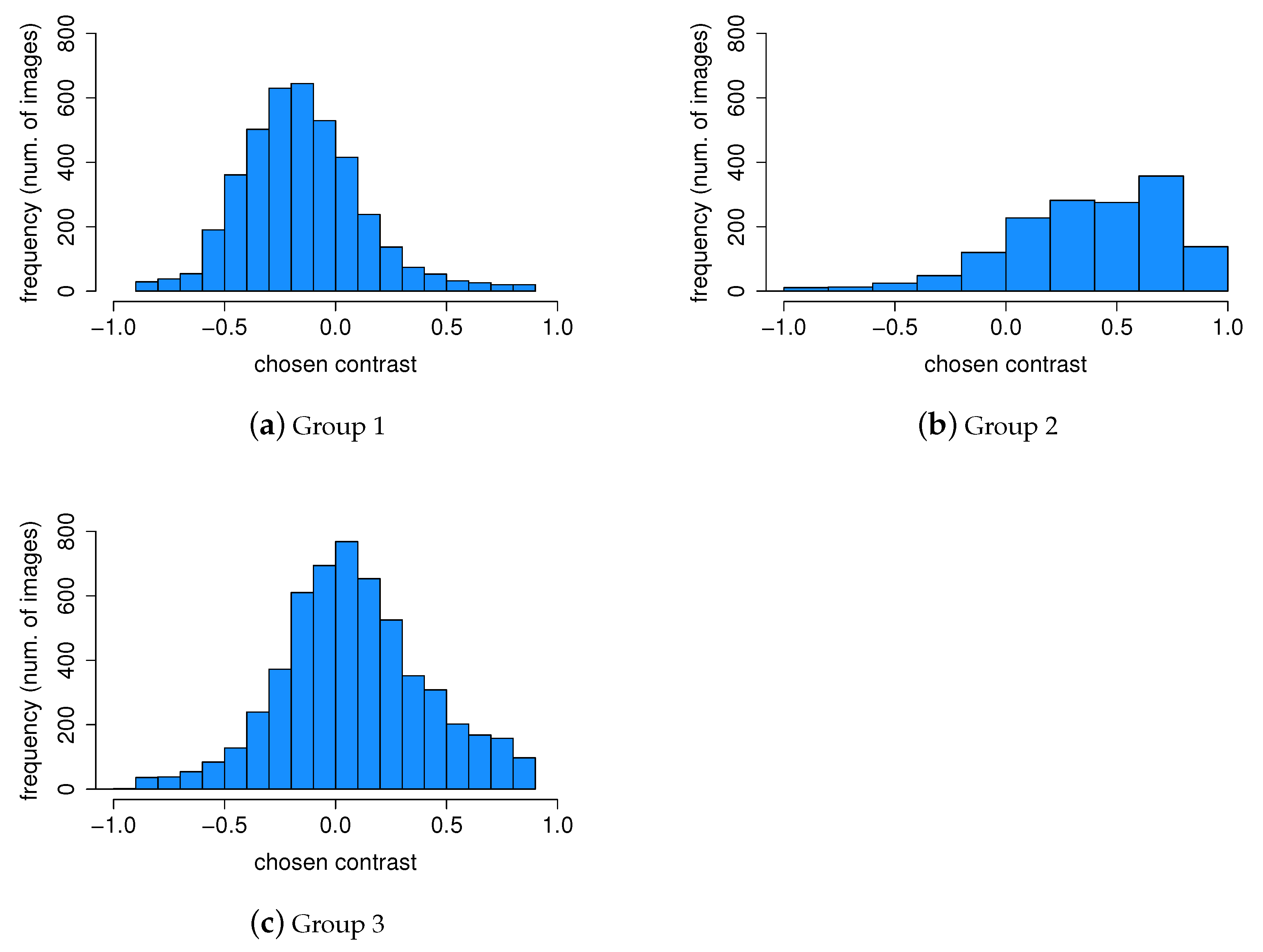
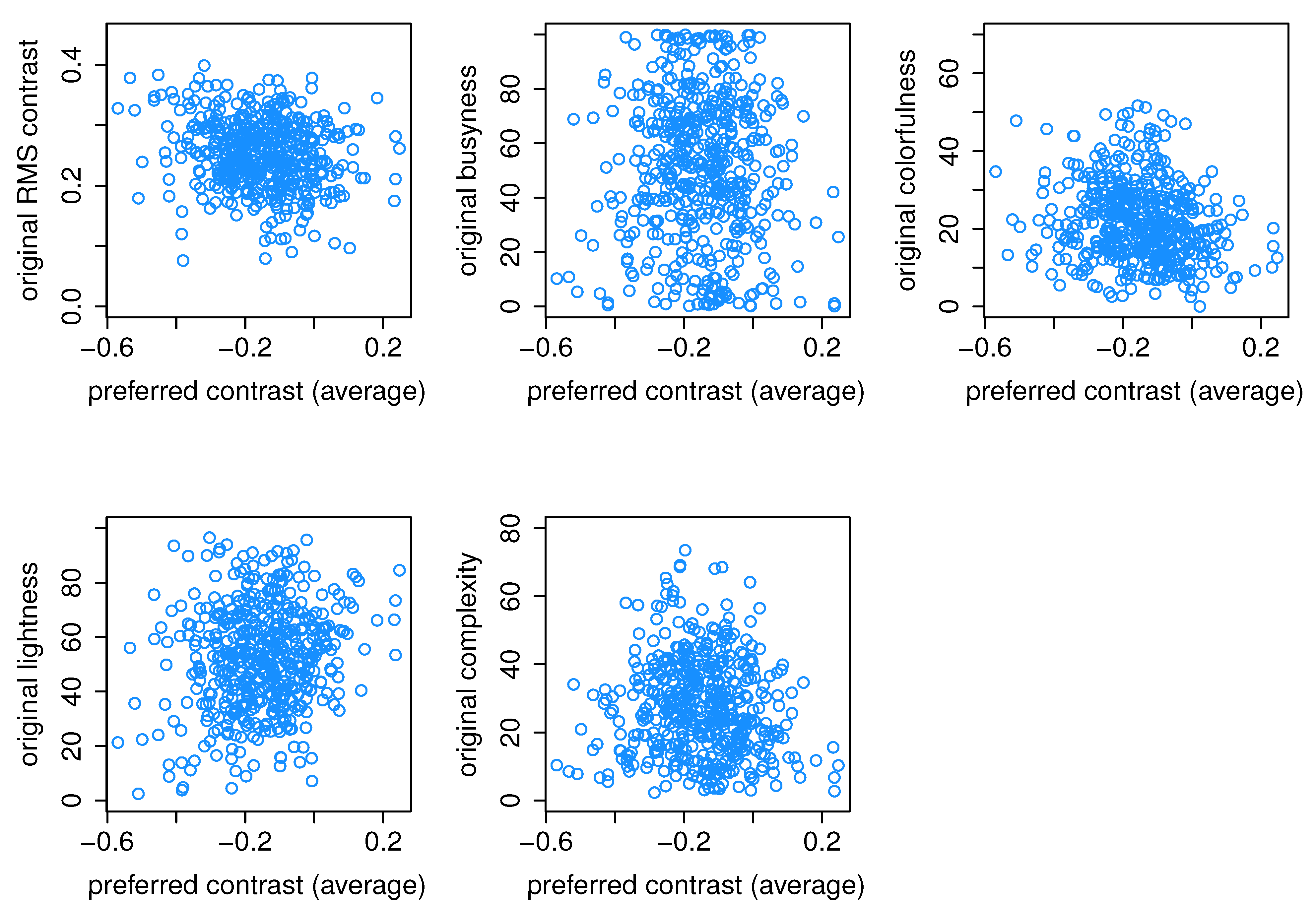
4.2. Personal Contrast Preferences
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IQA | Image Quality Assessment |
| IQM | Image Quality Metric |
| MOS | Mean Opinion Score |
| 3-AFC | Three-Alternative Forced Choice |
| JND | Just-Noticeable Difference |
| ICC | Intraclass Correlation Coefficient |
References
- Cherepkova, O.; Amirshahi, S.A.; Pedersen, M. Analyzing the Variability of Subjective Image Quality Ratings for Different Distortions. In Proceedings of the 2022 Eleventh International Conference on Image Processing Theory, Tools and Applications (IPTA), Salzburg, Austria, 19–22 April 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Ren, J.; Shen, X.; Lin, Z.; Mech, R.; Foran, D.J. Personalized image aesthetics. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 638–647. [Google Scholar]
- ITU. Vocabulary for Performance, Quality of Service and Quality of Experience; ITU: Geneva, Switzerland, 2017. [Google Scholar]
- CIE. Guidelines for the evaluation of gamut mapping algorithms. Publ.-Comm. Int. Eclair. Cie 2003, 153, D8-6. [Google Scholar]
- ITU. Methods for the Subjective Assessment of Video Quality Audio Quality and Audiovisual Quality of Internet Video and Distribution Quality Television in any Environment; Series P: Terminals and Subjective and Objective Assessment Methods; ITU: Geneva, Switzerland, 2016. [Google Scholar]
- Field, G.G. Test image design guidelines for color quality evaluation. In Color and Imaging Conference; Society for Imaging Science and Technology: Springfield, VA, USA, 1999; Volume 1999, pp. 194–196. [Google Scholar]
- Lin, H.; Hosu, V.; Saupe, D. KADID-10k: A large-scale artificially distorted IQA database. In Proceedings of the 2019 Eleventh International Conference on Quality of Multimedia Experience (QoMEX), Berlin, Germany, 5–7 June 2019; pp. 1–3. Available online: http://database.mmsp-kn.de/kadid-10k-database.html (accessed on 1 November 2021).
- Ghadiyaram, D.; Bovik, A.C. Massive online crowdsourced study of subjective and objective picture quality. IEEE Trans. Image Process. 2015, 25, 372–387. [Google Scholar]
- Ponomarenko, N.; Jin, L.; Ieremeiev, O.; Lukin, V.; Egiazarian, K.; Astola, J.; Vozel, B.; Chehdi, K.; Carli, M.; Battisti, F.; et al. Image database TID2013: Peculiarities, results and perspectives. Signal Process. Image Commun. 2015, 30, 57–77. [Google Scholar] [CrossRef]
- Partos, T.R.; Cropper, S.J.; Rawlings, D. You don’t see what I see: Individual differences in the perception of meaning from visual stimuli. PLoS ONE 2016, 11, e0150615. [Google Scholar] [CrossRef]
- Owsley, C.; Sekuler, R.; Siemsen, D. Contrast sensitivity throughout adulthood. Vis. Res. 1983, 23, 689–699. [Google Scholar] [CrossRef]
- Cornsweet, T. Visual Perception; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Roufs, J.; Goossens, I. The effect of gamma on perceived image quality. In Proceedings of the Conference Record of the 1988 International Display Research Conference, San Diego, CA, USA, 4–6 October 1988; pp. 27–31. [Google Scholar] [CrossRef]
- Beghdadi, A.; Qureshi, M.A.; Amirshahi, S.A.; Chetouani, A.; Pedersen, M. A Critical Analysis on Perceptual Contrast and Its Use in Visual Information Analysis and Processing. IEEE Access 2020, 8, 156929–156953. [Google Scholar] [CrossRef]
- Cherepkova, O.; Amirshahi, S.A.; Pedersen, M. Analysis of individual quality scores of different image distortions. In Color and Imaging Conference (CIC); Society for Imaging Science and Technology: Springfield, VA, USA, 2022; pp. 124–129. [Google Scholar]
- Azimian, S.; Torkamani-Azar, F.; Amirshahi, S.A. How good is too good? A subjective study on over enhancement of images. In Color and Imaging Conference (CIC); Society for Imaging Science and Technology: Springfield, VA, USA, 2021; pp. 83–88. [Google Scholar]
- Azimian, S.; Amirshahi, S.A.; Azar, F.T. Preventing Over-Enhancement Using Modified ICSO Algorithm. IEEE Access 2023, 17, 51296–51306. [Google Scholar] [CrossRef]
- Roufs, J.A.; Koselka, V.J.; van Tongeren, A.A. Global brightness contrast and the effect on perceptual image quality. In Proceedings of the Human Vision, Visual Processing, and Digital Display V, San Jose, CA, USA, 8–10 February 1994; Volume 2179, pp. 80–89. [Google Scholar]
- Varga, D. No-reference image quality assessment with global statistical features. J. Imaging 2021, 7, 29. [Google Scholar] [CrossRef]
- Chen, S.D. A new image quality measure for assessment of histogram equalization-based contrast enhancement techniques. Digit. Signal Process. 2012, 22, 640–647. [Google Scholar] [CrossRef]
- Ziaei Nafchi, H.; Cheriet, M. Efficient No-Reference Quality Assessment and Classification Model for Contrast Distorted Images. IEEE Trans. Broadcast. 2018, 64, 518–523. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X. No-Reference Quality Assessment for Contrast-Distorted Images. IEEE Access 2020, 8, 84105–84115. [Google Scholar] [CrossRef]
- Fang, Y.; Ma, K.; Wang, Z.; Lin, W.; Fang, Z.; Zhai, G. No-Reference Quality Assessment of Contrast-Distorted Images Based on Natural Scene Statistics. IEEE Signal Process. Lett. 2015, 22, 838–842. [Google Scholar] [CrossRef]
- Michelson, A. Studies in Optics; The University of Chicago Press: Chicago, IL, USA, 1927. [Google Scholar]
- Attneave, F. Some informational aspects of visual perception. Psychol. Rev. 1954, 61, 183. [Google Scholar] [PubMed]
- Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Haralick, R.M.; Shapiro, L.G. Image segmentation techniques. Comput. Vision, Graph. Image Process. 1985, 29, 100–132. [Google Scholar] [CrossRef]
- Calabria, A.J.; Fairchild, M.D. Perceived image contrast and observer preference II. Empirical modeling of perceived image contrast and observer preference data. J. Imaging Sci. Technol. 2003, 47, 494–508. [Google Scholar]
- Kadyrova, A.; Pedersen, M.; Ahmad, B.; Mandal, D.J.; Nguyen, M.; Zimmermann, P. Image enhancement dataset for evaluation of image quality metrics. In IS&T International Symposium on Electronic Imaging Science and Technology; Society for Imaging Science and Technology: Springfield, VA, USA, 2022; pp. 317-1–317-6. [Google Scholar]
- Orfanidou, M.; Triantaphillidou, S.; Allen, E. Predicting image quality using a modular image difference model. In Proceedings of the Image Quality and System Performance V, San Jose, CA, USA, 28–30 January 2008; SPIE: Bellingham, WA, USA, 2008; Volume 6808, pp. 132–143. [Google Scholar]
- Hasler, D.; Suesstrunk, S.E. Measuring colorfulness in natural images. In Proceedings of the Human Vision and Electronic Imaging VIII, Santa Clara, CA, USA, 21–24 January 2003; SPIE: Bellingham, WA, USA, 2003; Volume 5007, pp. 87–95. [Google Scholar]
- Redies, C.; Amirshahi, S.A.; Koch, M.; Denzler, J. PHOG-derived aesthetic measures applied to color photographs of artworks, natural scenes and objects. In Proceedings of the Computer Vision–ECCV 2012. Workshops and Demonstrations, Florence, Italy, 7–13 October 2012; Proceedings, Part I 12. Springer: Berlin/Heidelberg, Germany, 2012; pp. 522–531. [Google Scholar]
- Amirshahi, S.A. Aesthetic Quality Assessment of Paintings. Ph.D. Thesis, Verlag Dr. Hut GmbH, München, Germany, 2015. [Google Scholar]
- Amirshahi, S.A.; Hayn-Leichsenring, G.U.; Denzler, J.; Redies, C. Jenaesthetics subjective dataset: Analyzing paintings by subjective scores. Lect. Notes Comput. Sci. 2015, 8925, 3–19. [Google Scholar]
- Li, J.; Datta, R.; Joshi, D.; Wang, J. Studying aesthetics in photographic images using a computational approach. Lect. Notes Comput. Sci. 2006, 3953, 288–301. [Google Scholar]
- Ke, Y.; Tang, X.; Jing, F. The design of high-level features for photo quality assessment. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2006), New York, NY, USA, 17–22 June 2006; Volume 1, pp. 419–426. [Google Scholar]
- Dhar, S.; Ordonez, V.; Berg, T.L. High level describable attributes for predicting aesthetics and interestingness. In Proceedings of the 2011 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2011), Colorado Springs, CO, USA, 20–25 June 2011; pp. 1657–1664. [Google Scholar]
- Segalin, C.; Perina, A.; Cristani, M.; Vinciarelli, A. The pictures we like are our image: Continuous mapping of favorite pictures into self-assessed and attributed personality traits. IEEE Trans. Affect. Comput. 2016, 8, 268–285. [Google Scholar] [CrossRef]
- Lovato, P.; Bicego, M.; Segalin, C.; Perina, A.; Sebe, N.; Cristani, M. Faved! biometrics: Tell me which image you like and I’ll tell you who you are. IEEE Trans. Inf. Forensics Secur. 2014, 9, 364–374. [Google Scholar] [CrossRef]
- Li, L.; Zhu, H.; Zhao, S.; Ding, G.; Lin, W. Personality-assisted multi-task learning for generic and personalized image aesthetics assessment. IEEE Trans. Image Process. 2020, 29, 3898–3910. [Google Scholar] [CrossRef]
- Bhandari, U.; Chang, K.; Neben, T. Understanding the impact of perceived visual aesthetics on user evaluations: An emotional perspective. Inf. Manag. 2019, 56, 85–93. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, L.; Li, L.; Qie, N.; Li, Y.; Zhang, P.; Guo, Y. Personalized image aesthetics assessment with rich attributes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 19861–19869. [Google Scholar]
- Zhu, H.; Zhou, Y.; Shao, Z.; Du, W.; Wang, G.; Li, Q. Personalized Image Aesthetics Assessment via Multi-Attribute Interactive Reasoning. Mathematics 2022, 10, 4181. [Google Scholar]
- Park, K.; Hong, S.; Baek, M.; Han, B. Personalized image aesthetic quality assessment by joint regression and ranking. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 1206–1214. [Google Scholar]
- Zhu, H.; Li, L.; Wu, J.; Zhao, S.; Ding, G.; Shi, G. Personalized image aesthetics assessment via meta-learning with bilevel gradient optimization. IEEE Trans. Cybern. 2020, 52, 1798–1811. [Google Scholar]
- Lv, P.; Fan, J.; Nie, X.; Dong, W.; Jiang, X.; Zhou, B.; Xu, M.; Xu, C. User-guided personalized image aesthetic assessment based on deep reinforcement learning. IEEE Trans. Multimed. 2021, 25, 736–749. [Google Scholar]
- Cui, C.; Yang, W.; Shi, C.; Wang, M.; Nie, X.; Yin, Y. Personalized image quality assessment with social-sensed aesthetic preference. Inf. Sci. 2020, 512, 780–794. [Google Scholar]
- Kim, H.U.; Koh, Y.J.; Kim, C.S. PieNet: Personalized image enhancement network. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XXX 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 374–390. [Google Scholar]
- Kang, S.B.; Kapoor, A.; Lischinski, D. Personalization of image enhancement. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1799–1806. [Google Scholar] [CrossRef]
- Bianco, S.; Cusano, C.; Piccoli, F.; Schettini, R. Personalized image enhancement using neural spline color transforms. IEEE Trans. Image Process. 2020, 29, 6223–6236. [Google Scholar]
- Caicedo, J.C.; Kapoor, A.; Kang, S.B. Collaborative personalization of image enhancement. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 249–256. [Google Scholar] [CrossRef]
- Gigilashvili, D.; Thomas, J.B.; Pedersen, M.; Hardeberg, J.Y. Perceived glossiness: Beyond surface properties. In Proceedings of the Color and Imaging Conference. Society for Imaging Science and Technology, Chiba, Japan, 27–29 March 2019; Volume 1, pp. 37–42. [Google Scholar]
- Engelke, U.; Pitrey, Y.; Le Callet, P. Towards an inter-observer analysis framework for multimedia quality assessment. In Proceedings of the 2011 Third International Workshop on Quality of Multimedia Experience, Mechelen, Belgium, 7–9 September 2011; pp. 183–188. [Google Scholar]
- Zhang, B.; Allebach, J.P.; Pizlo, Z. An investigation of perceived sharpness and sharpness metrics. In Proceedings of the Image Quality and System Performance II, San Jose, CA, USA, 18–20 January 2005; SPIE: Bellingham, WA, USA, 2005; Volume 5668, pp. 98–110. [Google Scholar]
- Pixabay. Available online: https://pixabay.com (accessed on 13 October 2023).
- Achanta, R.; Hemami, S.; Estrada, F.; Susstrunk, S. Frequency-tuned salient region detection. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1597–1604. [Google Scholar]
- Leek, M.R. Adaptive procedures in psychophysical research. Percept. Psychophys. 2001, 63, 1279–1292. [Google Scholar] [CrossRef]
- Lu, Z.L.; Dosher, B. Adaptive Psychophysical Procedures. In Visual Psychophysics: From Laboratory to Theory; MIT Press: Cambridge, MA, USA, 2013; Chapter 11; pp. 351–384. [Google Scholar]
- Hall, J.L. Hybrid adaptive procedure for estimation of psychometric functions. J. Acoust. Soc. Am. 1981, 69, 1763–1769. [Google Scholar] [CrossRef]
- Watson, A.B.; Pelli, D.G. QUEST: A Bayesian adaptive psychometric method. Percept. Psychophys. 1983, 33, 113–120. [Google Scholar]
- Mantiuk, R.K.; Tomaszewska, A.; Mantiuk, R. Comparison of four subjective methods for image quality assessment. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2012; Volume 31, pp. 2478–2491. [Google Scholar]
- Shelton, B.; Scarrow, I. Two-alternative versus three-alternative procedures for threshold estimation. Percept. Psychophys. 1984, 35, 385–392. [Google Scholar]
- Schlauch, R.S.; Rose, R.M. Two-, three-, and four-interval forced-choice staircase procedures: Estimator bias and efficiency. J. Acoust. Soc. Am. 1990, 88, 732–740. [Google Scholar] [CrossRef]
- Sharma, G.; Wu, W.; Dalal, E.N. The CIEDE2000 color-difference formula: Implementation notes, supplementary test data, and mathematical observations. Color Res. Appl. 2005, 30, 21–30. [Google Scholar]
- Karma, I.G.M. Determination and Measurement of Color Dissimilarity. Int. J. Eng. Emerg. Technol. 2020, 5, 67. [Google Scholar] [CrossRef]
- Bt Recommendation ITU-R. Methodology for the Subjective Assessment of the Quality of Television Pictures; International Telecommunication Union: Geneva, Switzerland, 2002. [Google Scholar]
- McGraw, K.O.; Wong, S.P. Forming inferences about some intraclass correlation coefficients. Psychol. Methods 1996, 1, 30. [Google Scholar]
- Salarian, A. Intraclass Correlation Coefficient (ICC). 2023. Available online: https://www.mathworks.com/matlabcentral/fileexchange/22099-intraclass-correlation-coefficient-icc (accessed on 28 March 2023).
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 59–174. [Google Scholar] [CrossRef]
- Girard, J.M. MATLAB Functions for Computing Inter-Observer Reliability. 2016–2021. Available online: https://www.mathworks.com/matlabcentral/fileexchange/64602-matlab-functions-for-computing-inter-observer-reliability (accessed on 15 March 2023).
- Schuessler, Z. Delta E 101. 2016. Available online: http://zschuessler.github.io/DeltaE/learn/ (accessed on 28 March 2023).
- Lehmann, E.L.; D’Abrera, H.J. Nonparametrics: Statistical Methods Based on Ranks; Holden-Day: Toronto, ON, Canada, 1975. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Smirnov, N.V. Estimate of deviation between empirical distribution functions in two independent samples. Bull. Mosc. Univ. 1939, 2, 3–16. [Google Scholar]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Litchfield, J.J.; Wilcoxon, F. A simplified method of evaluating dose-effect experiments. J. Pharmacol. Exp. Ther. 1949, 96, 99–113. [Google Scholar]



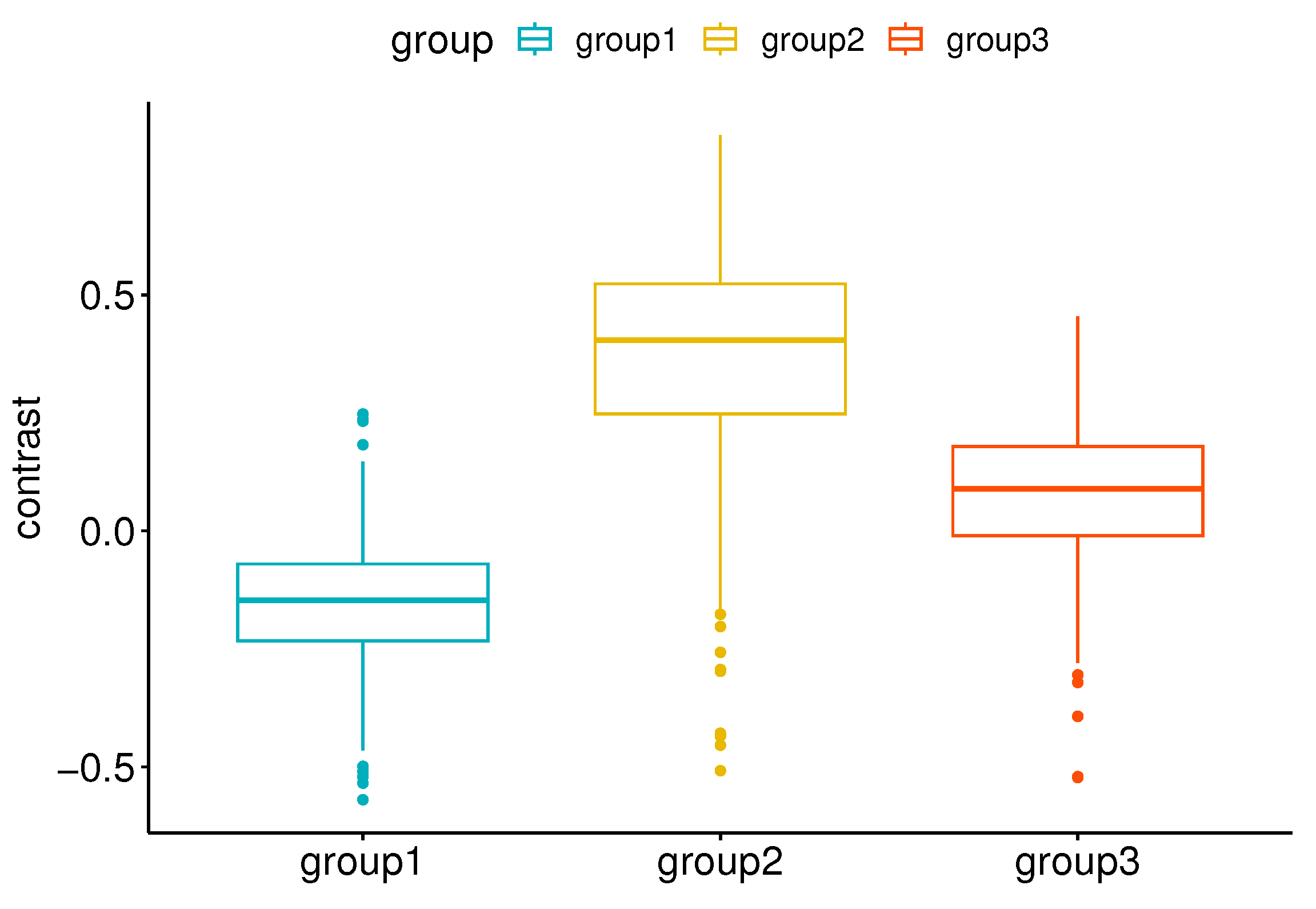

| Delta-E 2000 | Perception |
|---|---|
| ≤1.0 | Not perceptible by human eyes. |
| 1–2 | Perceptible through close observation. |
| 2–10 | Perceptible at a glance. |
| 11–49 | Colors are more similar than opposite. |
| 100 | Colors are exact opposite. |
| Group | Group | n1 | n2 | p | p.adj | p.adj.signif | |
|---|---|---|---|---|---|---|---|
| 1 | Group 1 | Group 2 | 499 | 499 | <0.01 | <0.01 | **** |
| 2 | Group 1 | Group 3 | 499 | 499 | <0.01 | <0.01 | **** |
| 3 | Group 2 | Group 3 | 499 | 499 | <0.01 | <0.01 | **** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cherepkova, O.; Amirshahi, S.A.; Pedersen, M. Individual Contrast Preferences in Natural Images. J. Imaging 2024, 10, 25. https://doi.org/10.3390/jimaging10010025
Cherepkova O, Amirshahi SA, Pedersen M. Individual Contrast Preferences in Natural Images. Journal of Imaging. 2024; 10(1):25. https://doi.org/10.3390/jimaging10010025
Chicago/Turabian StyleCherepkova, Olga, Seyed Ali Amirshahi, and Marius Pedersen. 2024. "Individual Contrast Preferences in Natural Images" Journal of Imaging 10, no. 1: 25. https://doi.org/10.3390/jimaging10010025
APA StyleCherepkova, O., Amirshahi, S. A., & Pedersen, M. (2024). Individual Contrast Preferences in Natural Images. Journal of Imaging, 10(1), 25. https://doi.org/10.3390/jimaging10010025











