Convolutional Neural Network Approaches in Median Nerve Morphological Assessment from Ultrasound Images
Abstract
1. Introduction
2. Materials and Methods
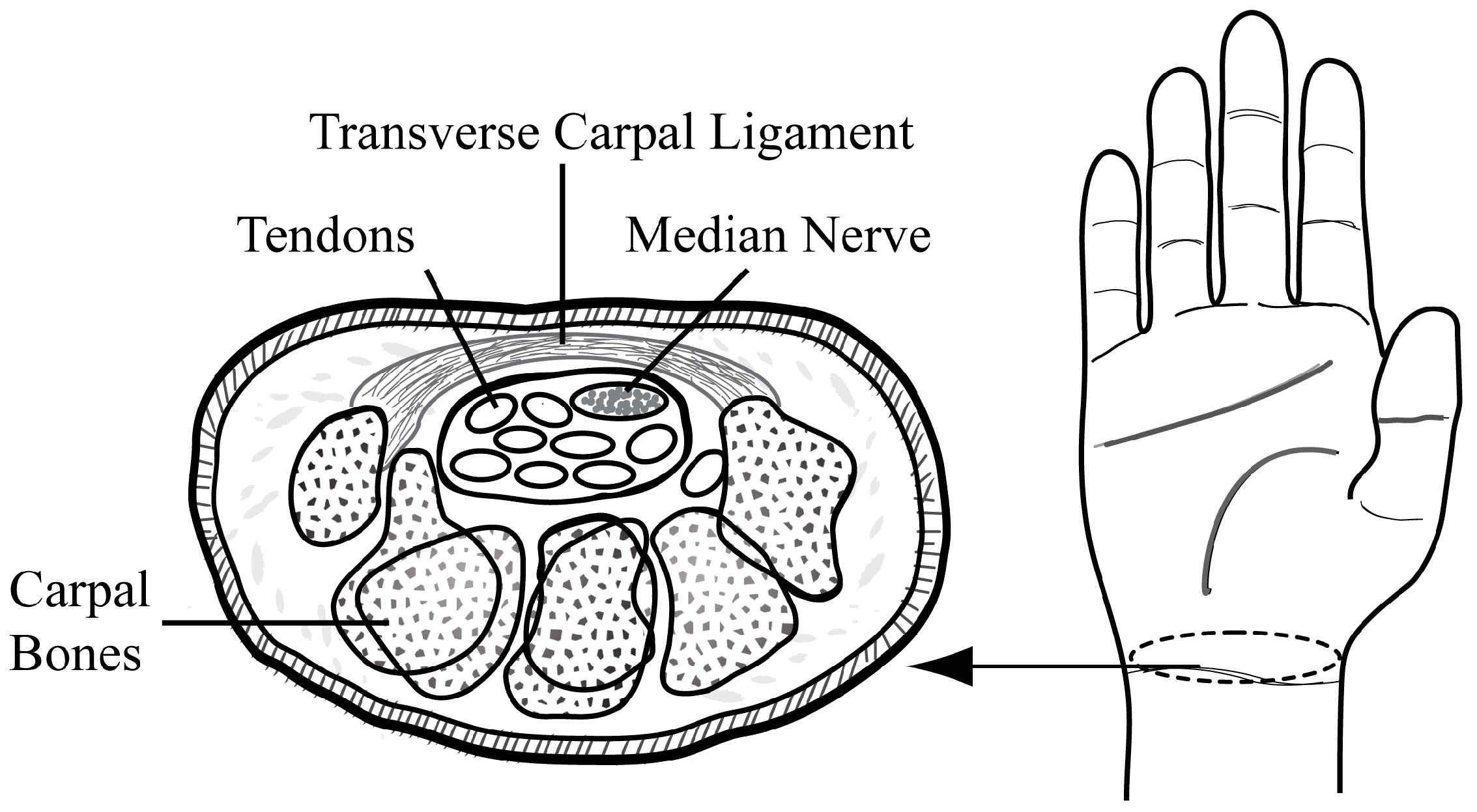
2.1. Ultrasound Image Acqusition and Dataset Preparation
2.2. Manual Annotation of the Median Nerve
2.3. Deep Learning Estimation of the Median Nerve
2.4. Statistical Analysis
3. Results
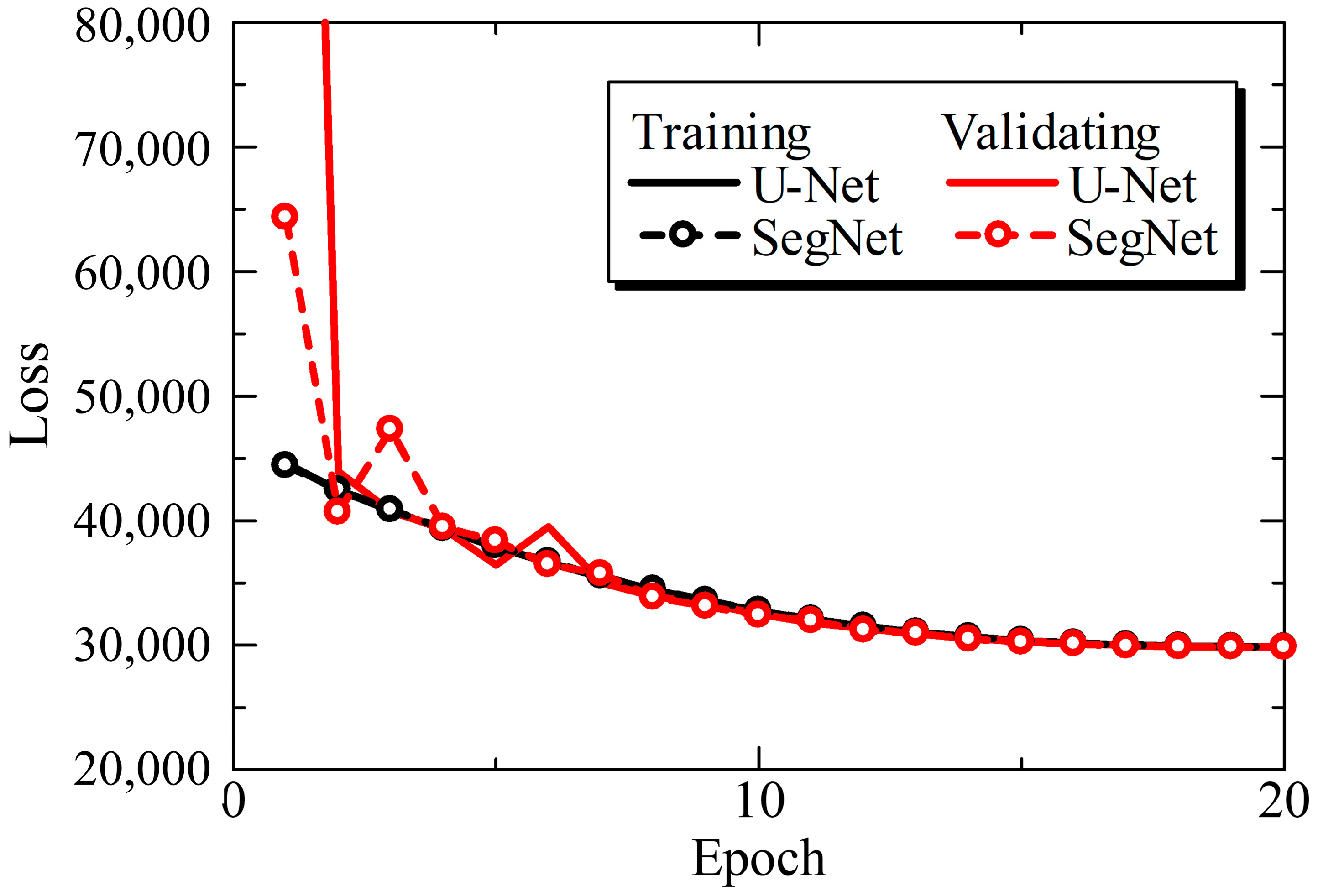
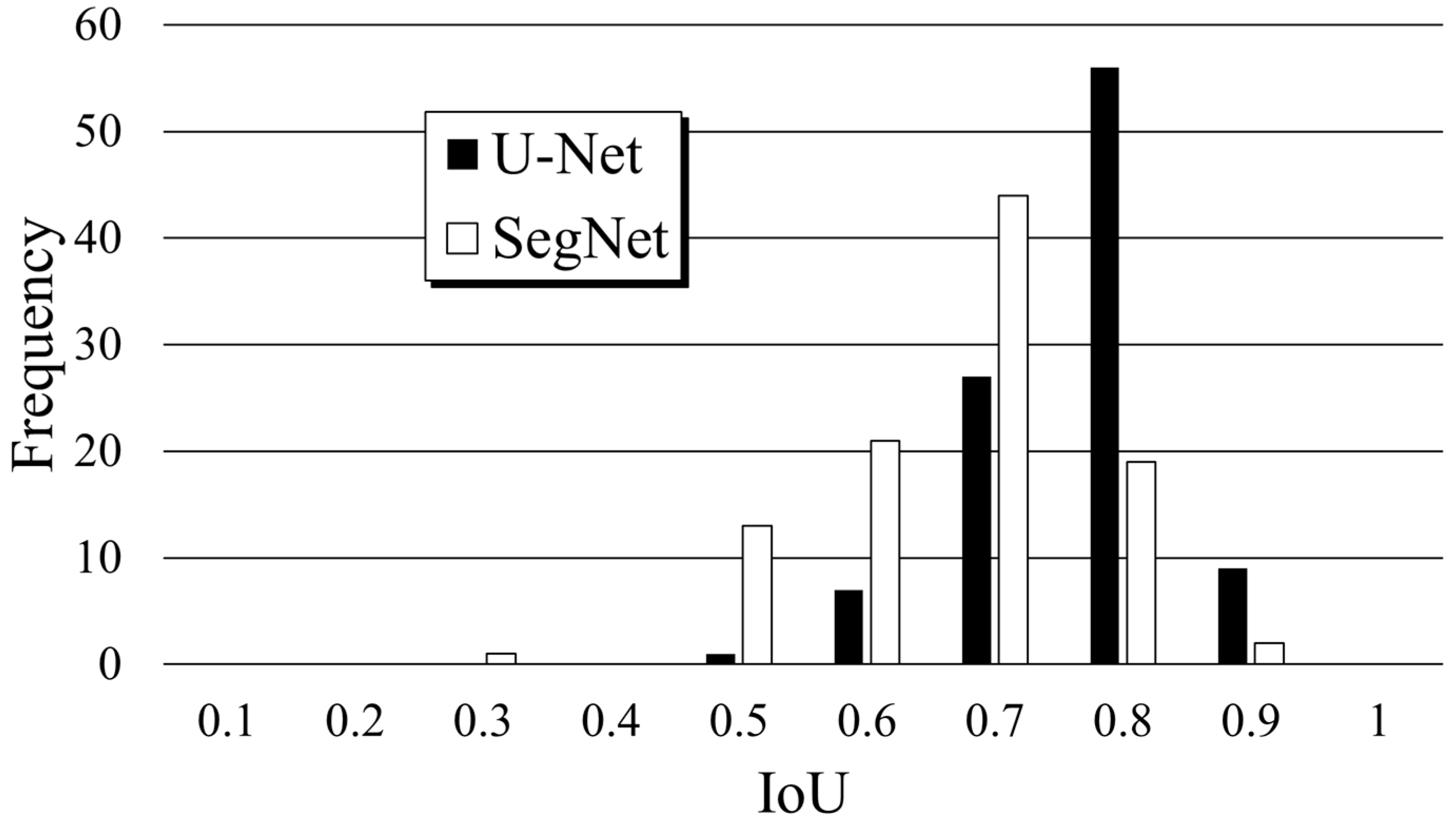
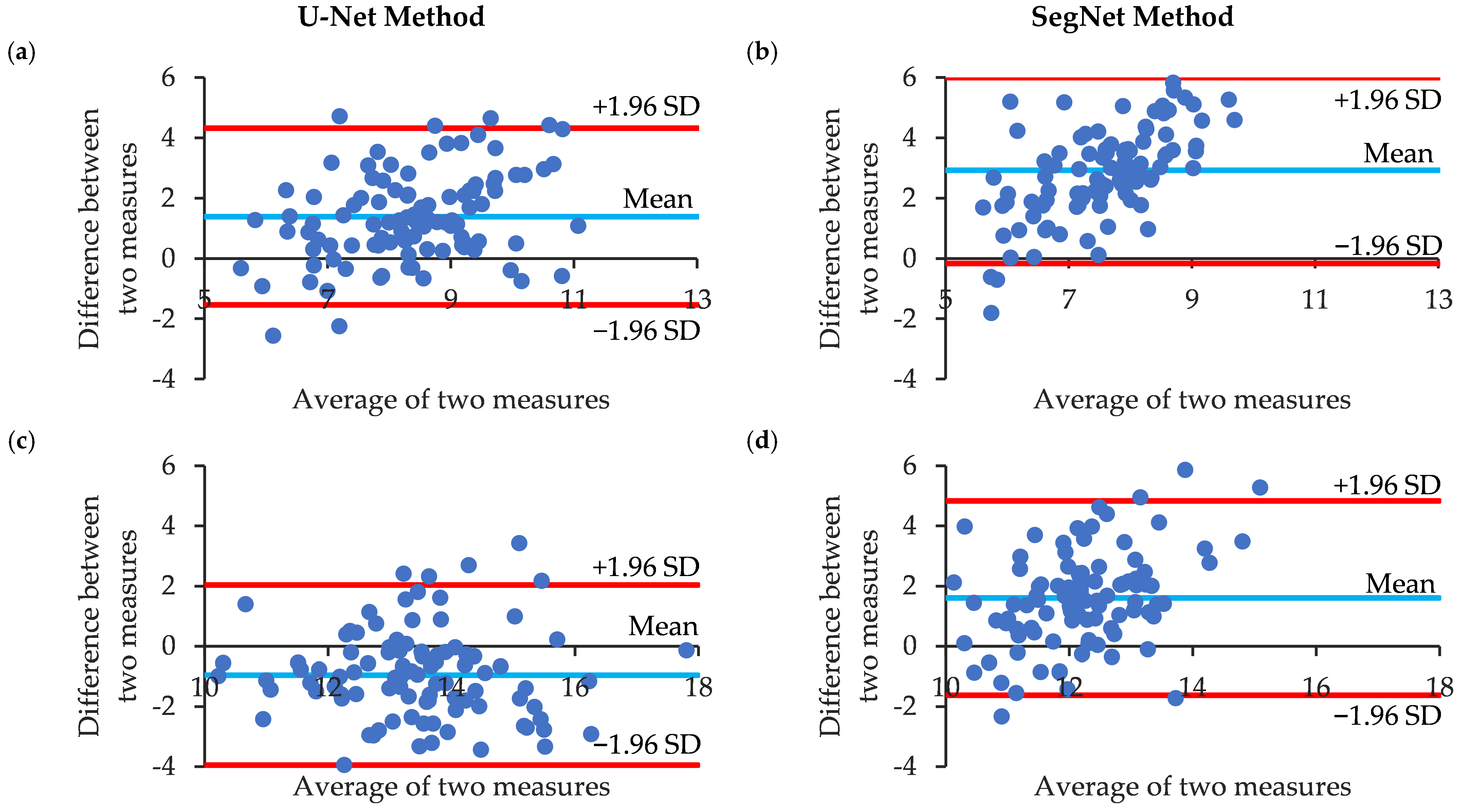
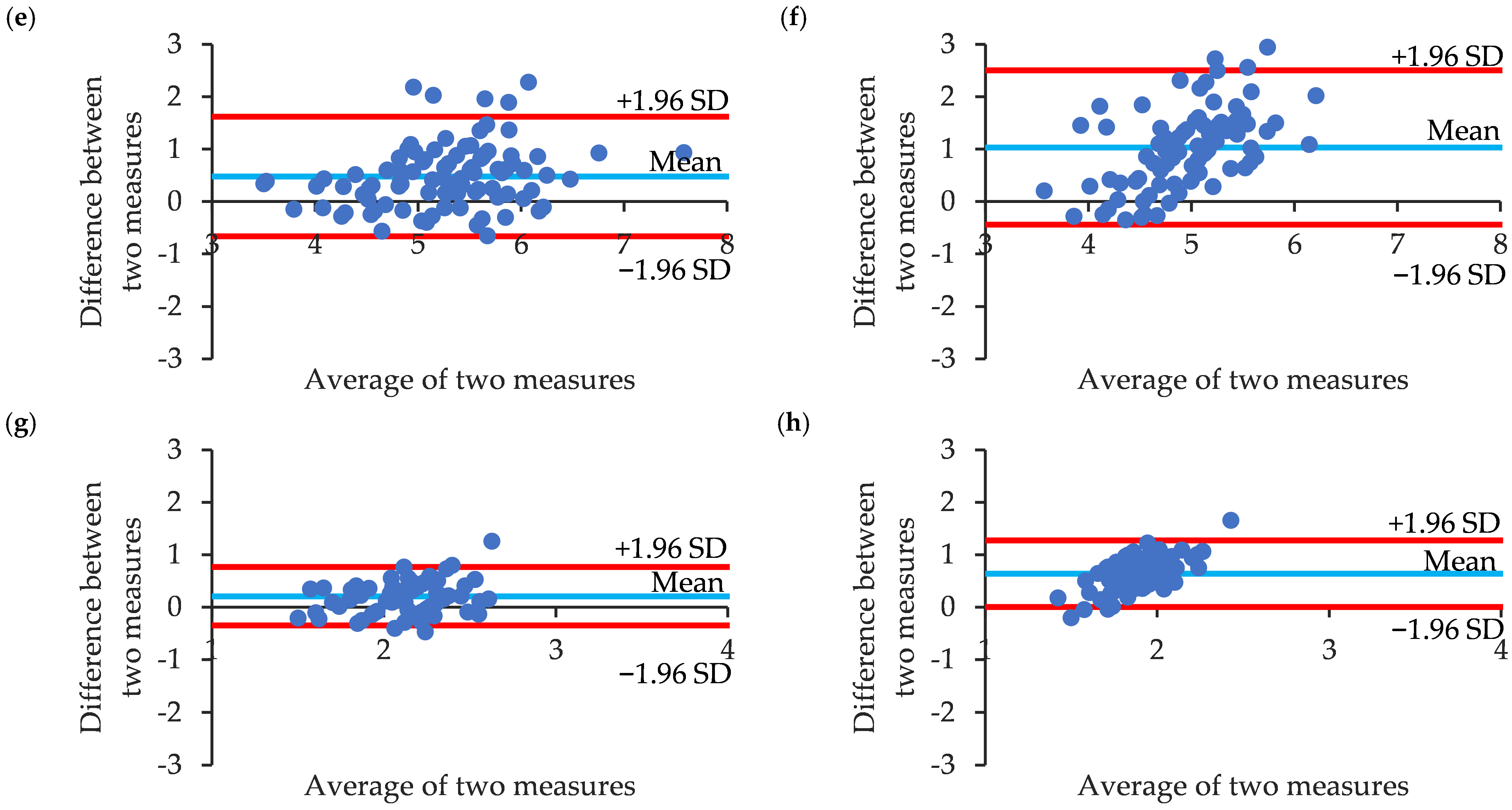
3.1. U-Net and SegNet Analysis
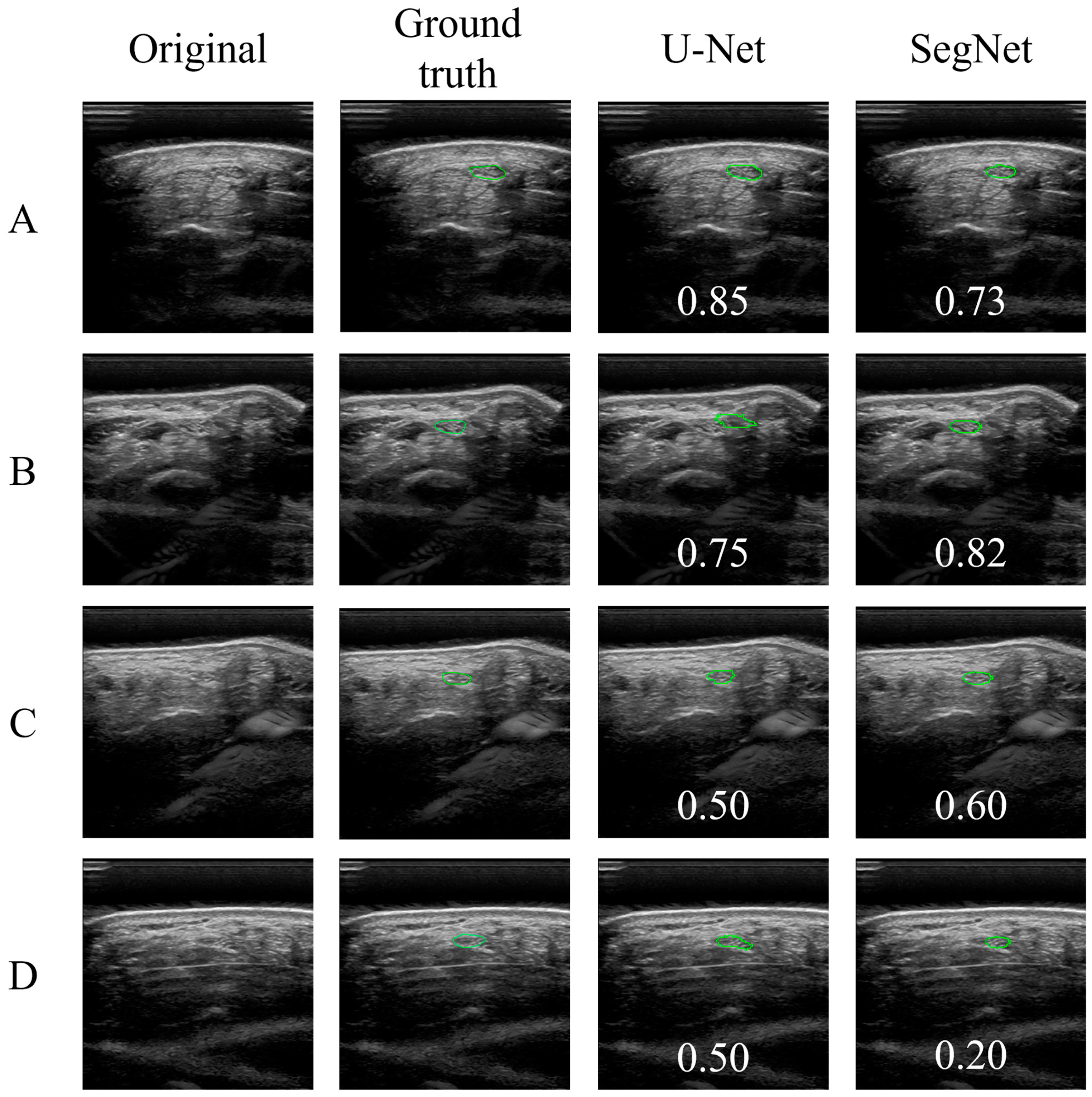
3.2. Correlation and Agreement of Manual Annotation and CNN
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. U-Net and SegNet Architectures
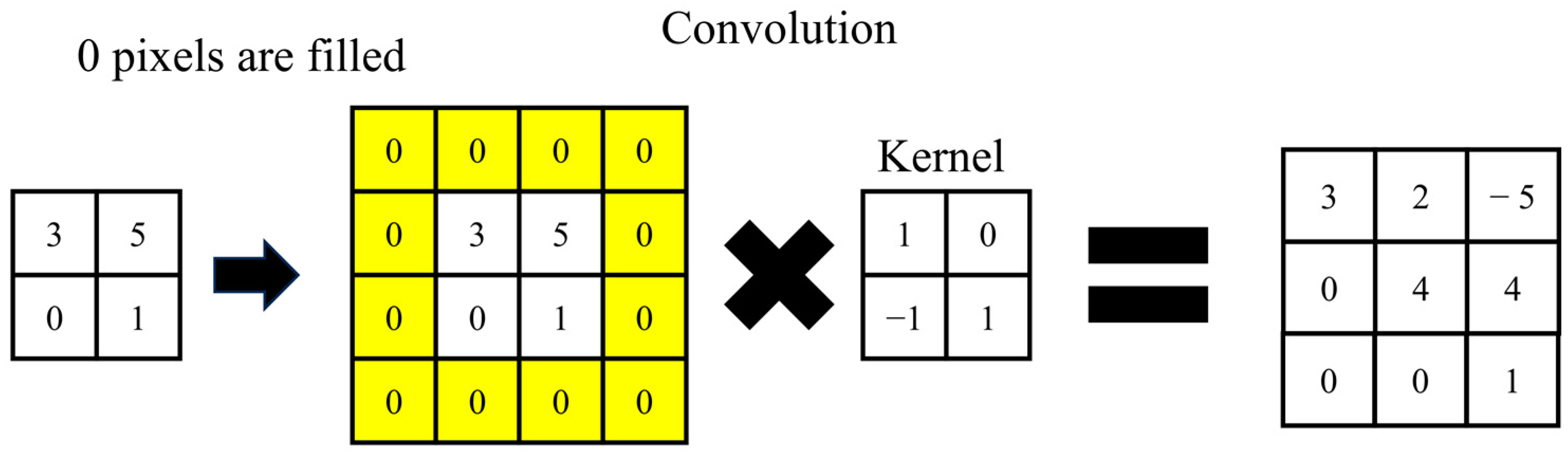
- Convolution

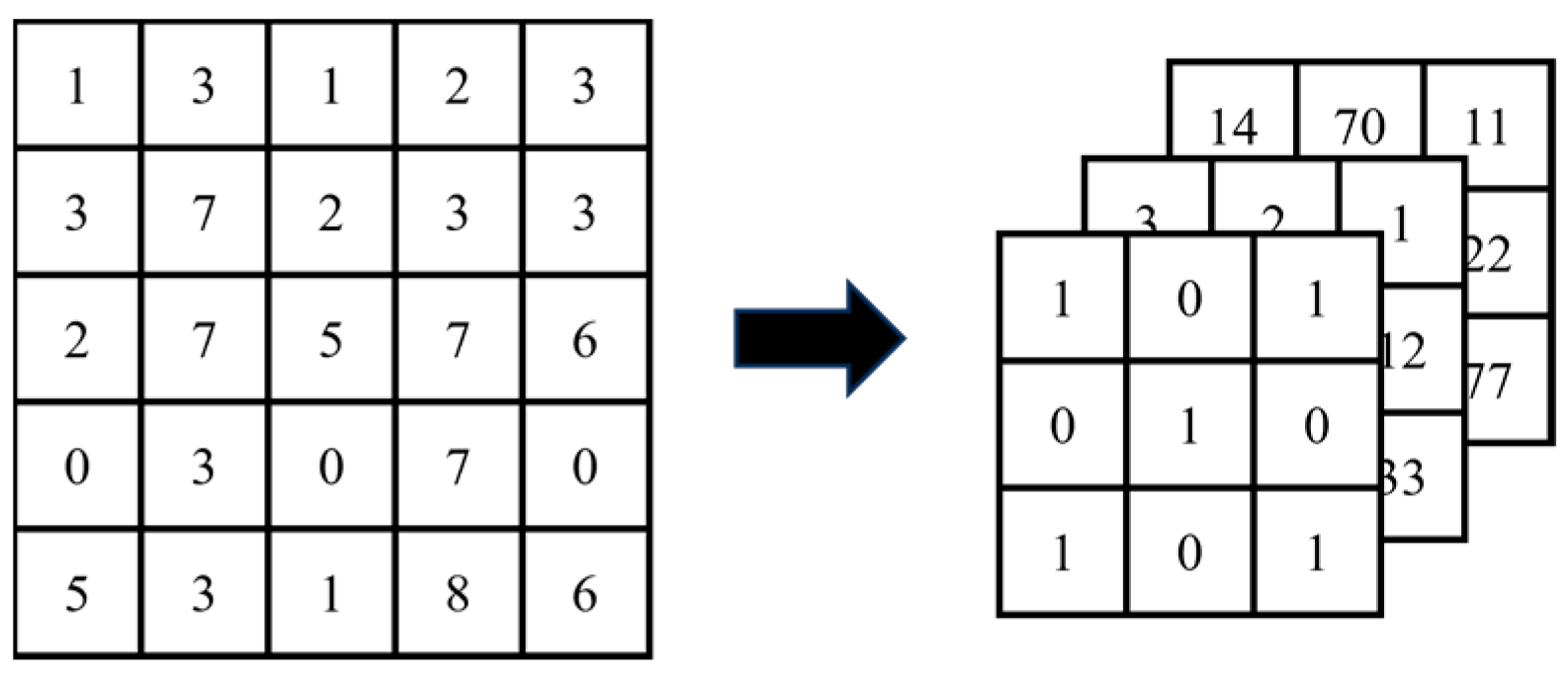
- 2.
- Pooling
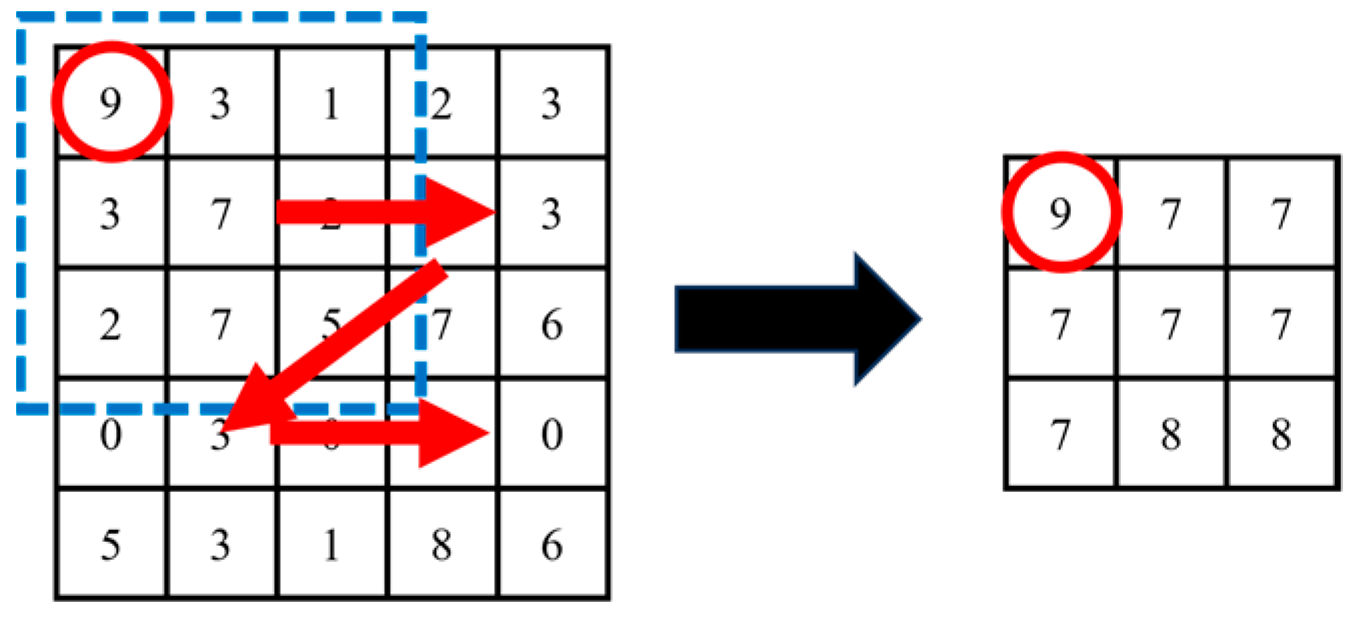
- 3.
- Deconvolution and unpooling
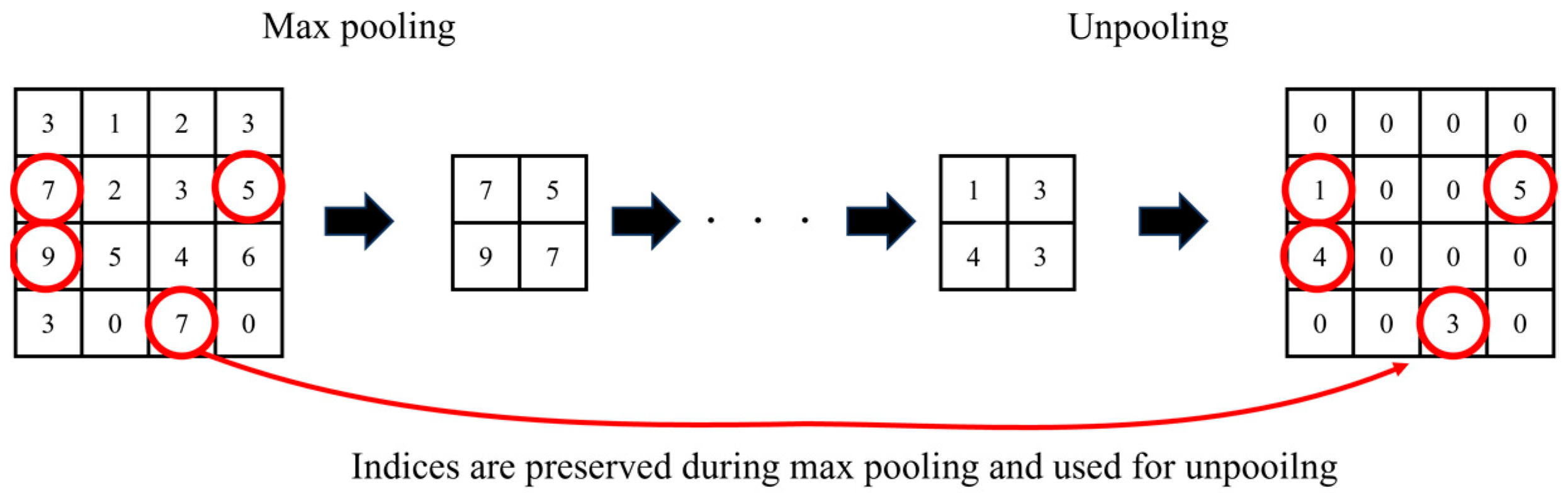
- 4.
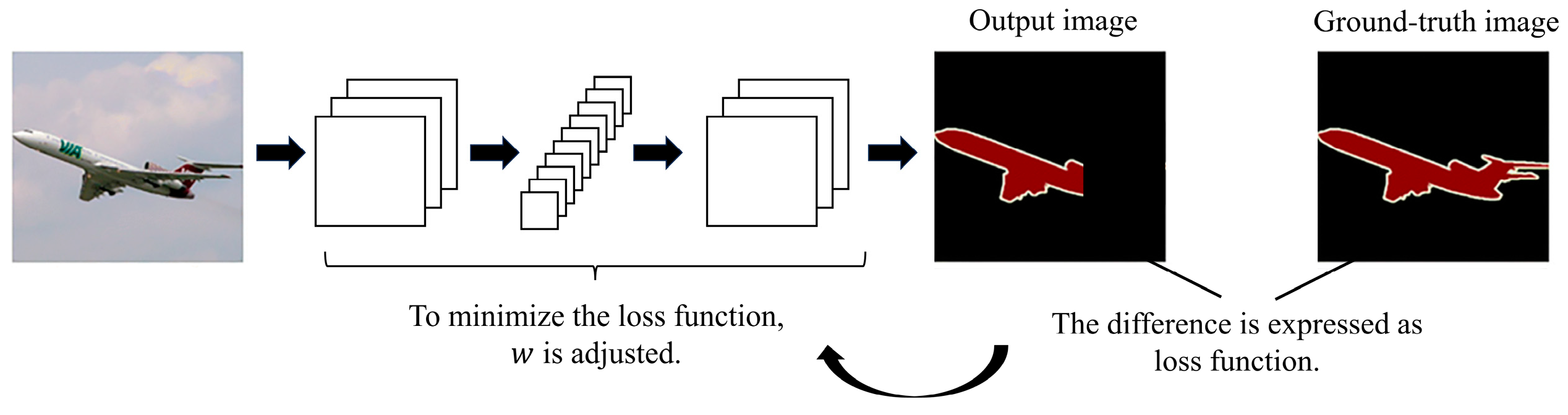
- Semantic segmentation

- 5.
- Encoder–decoder
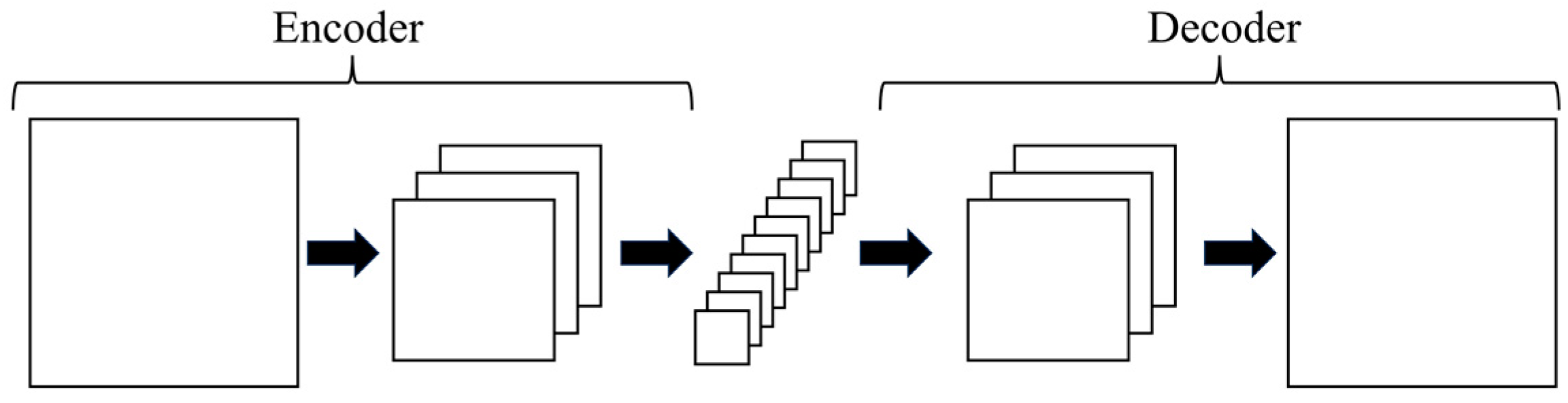
- 6.
- U-Net
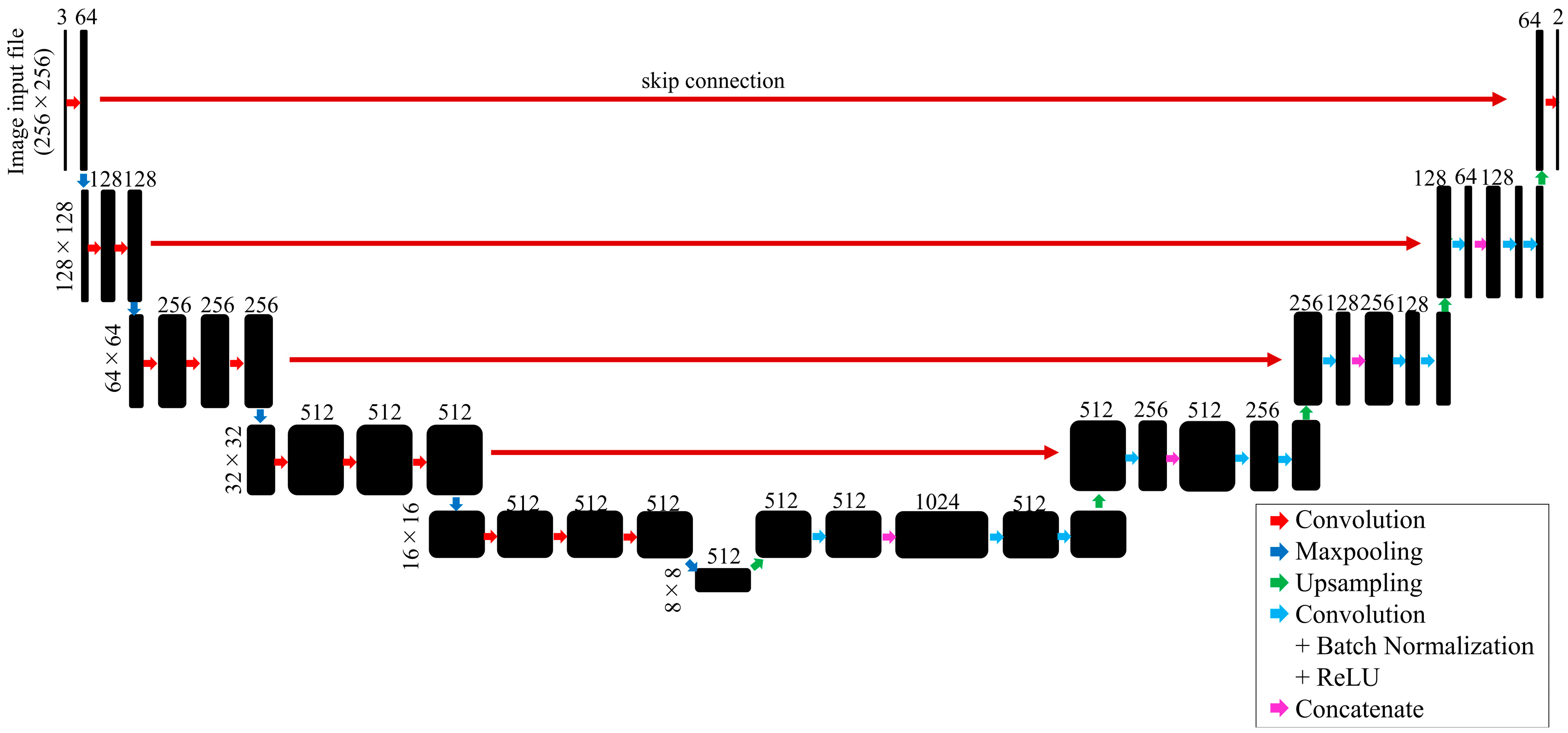
- 7.
- SegNet
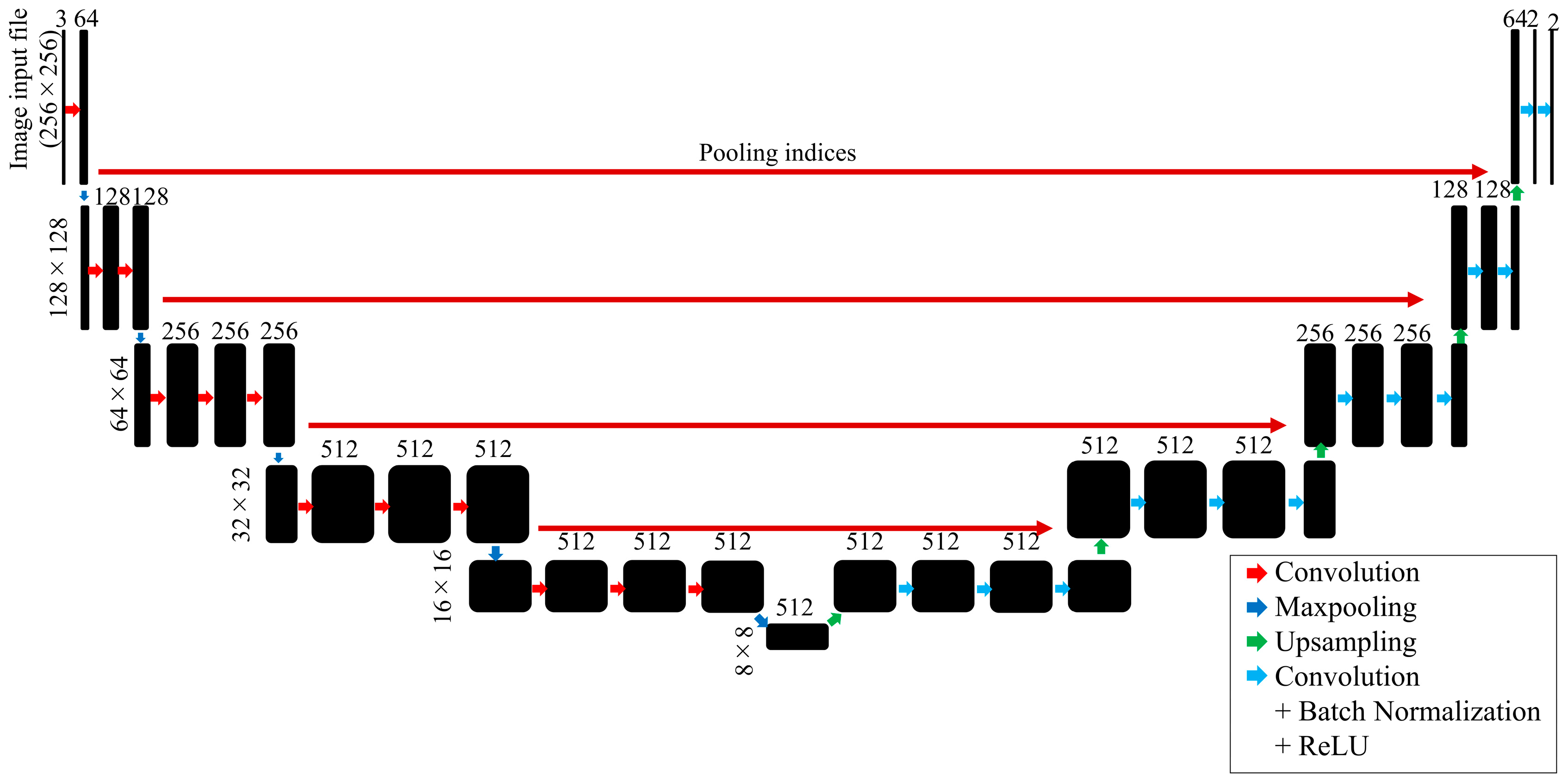
- 8.
- Binary cross-entropy

- 9.
- ReLU and Adams
References
- Keith, M.W.; Masear, V.; Chung, K.C.; Amadio, P.C.; Andary, M.; Barth, R.W.; Maupin, K.; Graham, B.; Watters, W.C., III; Turkelson, C.M.; et al. American Academy of Orthopedic Surgeons Clinical Practice Guidelines on Diagnosis of Carpal Tunnel Syndrome. Am. Acad. Orthop. Surg. 2007, 92, 218. [Google Scholar]
- van Doesburg, M.H.; Yoshii, Y.; Villarraga, H.R.; Henderson, J.; Cha, S.S.; An, K.N.; Amadio, P.C. Median Nerve Deformation and Displacement in the Carpal Tunnel during Index Finger and Thumb Motion. J. Orthop. Res. 2010, 28, 1387–1390. [Google Scholar] [CrossRef] [PubMed]
- van Doesburg, M.H.; Henderson, J.; Yoshii, Y.; van der Molen, A.B.M.; Cha, S.S.; An, K.N.; Amadio, P.C. Median Nerve Deformation in Differential Finger Motions: Ultrasonographic Comparison of Carpal Tunnel Syndrome Patients and Healthy Controls. J. Orthop. Res. 2012, 30, 643–648. [Google Scholar] [CrossRef] [PubMed]
- Loh, P.Y.; Nakashima, H.; Muraki, S. Metacarpophalangeal Joint Flexion and the Deformation of Median Nerve Median Nerve. In Proceedings of the 57th Conference of Japan Ergonomics Society (JES), Hyogo, Japan, 5–6 June 2014. [Google Scholar]
- Loh, P.Y.; Yeoh, W.L.; Nakashima, H.; Muraki, S. Deformation of the Median Nerve at Different Finger Postures and Wrist Angles. PeerJ 2018, 6, e5406. [Google Scholar] [CrossRef] [PubMed]
- Aleman, L.; Berna, J.D.; Reus, M. Reproducibility of Sonographic Measurements of the Median Nerve. J. Ultrasound Med. 2008, 27, 193–197. [Google Scholar] [CrossRef] [PubMed]
- Duymuş, M.; Ulaşli, A.M.; Yilmaz, Ö.; Asal, N.; Kacar, M.; Nacir, B.; Eerdem, H.R.; Koşar, U. Measurement of Median Nerve Cross Sectional Area with Ultrasound and MRI in Idiopathic Carpal Tunnel Syndrome Patients. J. Neurol. Sci.-Turk. 2013, 30, 59–71. [Google Scholar]
- Ko, C.; Brown, T.D. A Fluid-Immersed Multi-Body Contact Finite Element Formulation for Median Nerve Stress in the Carpal Tunnel. Comput. Methods Biomech. Biomed. Engin. 2007, 10, 343–349. [Google Scholar] [CrossRef]
- Jarvik, J.G.; Yuen, E.; Haynor, D.R.; Bradley, C.M.; Fulton-Kehoe, D.; Smith-Weller, T.; Wu, R.; Kliot, M.; Kraft, G.; Wang, L.; et al. MR Nerve Imaging in a Prospective Cohort of Patients with Suspected Carpal Tunnel Syndrome. Neurology 2002, 58, 1597–1602. [Google Scholar] [CrossRef]
- Jarvik, J.G.; Yuen, E.; Kliot, M. Diagnosis of Carpal Tunnel Syndrome: Electrodiagnostic and MR Imaging Evaluation. Neuroimaging Clin. N. Am. 2004, 14, 93–102. [Google Scholar] [CrossRef]
- Pasternack, I.I.; Malmivaara, A.; Tervahartiala, P.; Forsberg, H.; Vehmas, T. Magnetic Resonance Imaging Findings in Respect to Carpal Tunnel Syndrome. Scand. J. Work. Environ. Health 2003, 29, 189–196. [Google Scholar] [CrossRef][Green Version]
- Shah, R.; Li, Z.M. Ligament and Bone Arch Partition of the Carpal Tunnel by Three-Dimensional Ultrasonography. J. Biomech. Eng. 2020, 142, 091008. [Google Scholar] [CrossRef] [PubMed]
- Shah, R.; Li, Z.M. Three-Dimensional Carpal Arch Morphology Using Robot-Assisted Ultrasonography. IEEE Trans. Biomed. Eng. 2021, 69, 894–898. [Google Scholar] [CrossRef] [PubMed]
- Jordan, D.; Zhang, H.; Li, Z.M. Spatial Relationship of the Median Nerve and Transverse Carpal Ligament in Asymptomatic Hands. J. Biomech. Eng. 2023, 145, 031003. [Google Scholar] [CrossRef] [PubMed]
- Cartwright, M.S.; Passmore, L.V.; Yoon, J.S.; Brown, M.E.; Caress, J.B.; Walker, F.O. Cross-Sectional Area Reference Values for Nerve Ultrasonography. Muscle Nerve 2008, 37, 566–571. [Google Scholar] [CrossRef] [PubMed]
- Greening, J.; Lynn, B.; Leary, R.; Warren, L.; O’Higgins, P.; Hall-Craggs, M. The Use of Ultrasound Imaging to Demonstrate Reduced Movement of the Median Nerve during Wrist Flexion in Patients with Non-Specific Arm Pain. J. Hand Surg. Br. 2001, 26, 401–408. [Google Scholar] [CrossRef] [PubMed]
- Hobson-Webb, L.D.; Massey, J.M.; Juel, V.C.; Sanders, D.B. The Ultrasonographic Wrist-to-Forearm Median Nerve Area Ratio in Carpal Tunnel Syndrome. Clin. Neurophysiol. 2008, 119, 1353–1357. [Google Scholar] [CrossRef]
- Hough, A.D.; Moore, A.P.; Jones, M.P. Reduced Longitudinal Excursion of the Median Nerve in Carpal Tunnel Syndrome. Arch. Phys. Med. Rehabil. 2007, 88, 569–576. [Google Scholar] [CrossRef]
- Korstanje, J.W.H.; Schreuders, T.R.; van der Sijde, J.; Hovius, S.E.R.; Bosch, J.G.; Selles, R.W. Ultrasonographic Assessment of Long Finger Tendon Excursion in Zone V During Passive and Active Tendon Gliding Exercises. J. Hand Surg. Am. 2010, 35, 559–565. [Google Scholar] [CrossRef]
- Walker, F.O.; Cartwright, M.S.; Wiesler, E.R.; Caress, J. Ultrasound of Nerve and Muscle. Clin. Neurophysiol. 2004, 115, 495–507. [Google Scholar] [CrossRef]
- Yao, Y.; Grandy, E.; Evans, P.J.; Seitz, W.H.; Li, Z.M. Location-Dependent Change of Median Nerve Mobility in the Carpal Tunnel of Patients with Carpal Tunnel Syndrome. Muscle Nerve 2019, 62, 522–527. [Google Scholar] [CrossRef]
- Lakshminarayanan, K.; Shah, R.; Li, Z.M. Morphological and Positional Changes of the Carpal Arch and Median Nerve Associated with Wrist Deviations. Clin. Biomech. 2020, 71, 133–138. [Google Scholar] [CrossRef] [PubMed]
- Toosi, K.K.; Impink, B.G.; Baker, N.A.; Boninger, M.L. Effects of Computer Keyboarding on Ultrasonographic Measures of the Median Nerve. Am. J. Ind. Med. 2011, 54, 826–833. [Google Scholar] [CrossRef] [PubMed]
- Toosi, K.K.; Hogaboom, N.S.; Oyster, M.L.; Boninger, M.L. Computer Keyboarding Biomechanics and Acute Changes in Median Nerve Indicative of Carpal Tunnel Syndrome. Clin. Biomech. 2015, 30, 546–550. [Google Scholar] [CrossRef] [PubMed]
- Loh, P.Y.; Yeoh, W.L.; Nakashima, H.; Muraki, S. Impact of Keyboard Typing on the Morphological Changes of the Median Nerve. J. Occup. Health 2017, 59, 408–417. [Google Scholar] [CrossRef] [PubMed]
- Di Cosmo, M.; Chiara Fiorentino, M.; Villani, F.P.; Frontoni, E.; Smerilli, G.; Filippucci, E.; Moccia, S. A Deep Learning Approach to Median Nerve Evaluation in Ultrasound Images of Carpal Tunnel Inlet. Med. Biol. Eng. Comput. 2022, 60, 3255–3264. [Google Scholar] [CrossRef]
- Kuroiwa, T.; Jagtap, J.; Starlinger, J.; Lui, H.; Akkus, Z.; Erickson, B.; Amadio, P. Deep Learning Estimation of Median Nerve Volume Using Ultrasound Imaging in a Human Cadaver Model. Ultrasound Med. Biol. 2022, 48, 2237–2248. [Google Scholar] [CrossRef]
- Yeh, C.L.; Wu, C.H.; Hsiao, M.Y.; Kuo, P.L. Real-Time Automated Segmentation of Median Nerve in Dynamic Ultrasonography Using Deep Learning. Ultrasound Med. Biol. 2023, 49, 1129–1136. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, Y.; Georgiou, T.; Lew, M.S. A Review of Semantic Segmentation Using Deep Neural Networks. Int. J. Multimed. Inf. Retr. 2018, 7, 87–93. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Handa, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Robust Semantic Pixel-Wise Labelling. arXiv 2015, arXiv:1505.07293. [Google Scholar]
- Xin, C.; Li, B.; Wang, D.; Chen, W.; Yue, S.; Meng, D.; Qiao, X.; Zhang, Y. Deep Learning for the Rapid Automatic Segmentation of Forearm Muscle Boundaries from Ultrasound Datasets. Front. Physiol. 2023, 14, 1166061. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, Z.; Li, N.; Raj, A.N.J.; Mahesh, V.G.V.; Qiu, S. An RDAU-NET Model for Lesion Segmentation in Breast Ultrasound Images. PLoS ONE 2019, 14, e0221535. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.K.; Rashwan, H.A.; Abdel-Nasser, M.; Mostafa, M.; Sarker, K.; Akram, F.; Pandey, N.; Romani, S.; Puig, D. An Efficient Solution for Breast Tumor Segmentation and Classification in Ultrasound Images Using Deep Adversarial Learning. arXiv 2019, arXiv:1907.00887. [Google Scholar]
- Vianna, P.; Farias, R.; de Albuquerque Pereira, W.C. U-Net and SegNet Performances on Lesion Segmentation of Breast Ultrasonography Images. Res. Biomed. Eng. 2021, 37, 171–179. [Google Scholar] [CrossRef]
- Duncan, I.; Sullivan, P.; Lomas, F. Sonography in the Diagnosis of Carpal Tunnel Syndrome. AJR Am. J. Roentgenol. 1999, 173, 681–684. [Google Scholar] [CrossRef]
- Fowler, J.R.; Hirsch, D.; Kruse, K. The Reliability of Ultrasound Measurements of the Median Nerve at the Carpal Tunnel Inlet. J. Hand Surg. Am. 2015, 40, 1992–1995. [Google Scholar] [CrossRef]
- Loh, P.Y.; Muraki, S. Effect of Wrist Angle on Median Nerve Appearance at the Proximal Carpal Tunnel. PLoS ONE 2015, 10, e0117930. [Google Scholar] [CrossRef]

| U-Net | SegNet | |
|---|---|---|
| Precision | 0.811 ± 0.095 | 0.677 ± 0.114 |
| Recall | 0.869 ± 0.077 | 0.897 ± 0.084 |
| DICE | 0.833 ± 0.053 | 0.765 ± 0.081 |
| IoU | 0.717 ± 0.074 | 0.625 ± 0.099 |
| CNN | ||
|---|---|---|
| Measurements | U-Net | SegNet |
| Median nerve cross-sectional area (MNCSA) | rs (98) = 0.517, p < 0.001 | rs (98) = 0.337, p = 0.001 |
| Circumference | rs (98) = 0.424, p < 0.001 | rs (98) = 0.233, p = 0.020 |
| Diameter (Longitudinal, D1) | rs (98) = 0.606, p < 0.001 | rs (98) = 0.317, p = 0.001 |
| Diameter (Vertical, D2) | rs (98) = 0.440, p < 0.001 | rs (98) = 0.061, p = 0.546 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ando, S.; Loh, P.Y. Convolutional Neural Network Approaches in Median Nerve Morphological Assessment from Ultrasound Images. J. Imaging 2024, 10, 13. https://doi.org/10.3390/jimaging10010013
Ando S, Loh PY. Convolutional Neural Network Approaches in Median Nerve Morphological Assessment from Ultrasound Images. Journal of Imaging. 2024; 10(1):13. https://doi.org/10.3390/jimaging10010013
Chicago/Turabian StyleAndo, Shion, and Ping Yeap Loh. 2024. "Convolutional Neural Network Approaches in Median Nerve Morphological Assessment from Ultrasound Images" Journal of Imaging 10, no. 1: 13. https://doi.org/10.3390/jimaging10010013
APA StyleAndo, S., & Loh, P. Y. (2024). Convolutional Neural Network Approaches in Median Nerve Morphological Assessment from Ultrasound Images. Journal of Imaging, 10(1), 13. https://doi.org/10.3390/jimaging10010013






