Determination of Quantitative Ratios (Mechanical and Dissolved) of Copper, Gold and Silver Losses in Vanyukov Furnace Slags Under the Conditions of the Balkhash Copper Smelter in Kazakhstan
Abstract
1. Introduction
- (1)
- A study of the material composition of slags from the VF siphon was carried out in order to determine the forms of occurrence of metals, including precious metals.
- (2)
- The effect of slag composition on the redistribution of metals between matte and slag in the process of melting copper raw materials of complex composition in the Vanyukov furnace was investigated.
- (3)
- Quantitative ratios of dissolved and mechanical losses of copper and precious metals with slag have been determined and recommendations for the development of a technology for the complex extraction of metals from slag have been formulated.
- (4)
- Mathematical models have been created to predict the distribution of metals during smelting.
2. Materials and Methods
- The existence of a linear relationship between the predictors and the target variable;
- Lack of relationship between residuals (difference between observed and model values);
- Uniformity of residue dispersion regardless of the values of predictor variables;
- Normal distribution of residues.
- (a)
- Evaluate the effect of matte and slag composition on the recovery of Cu, Au and Ag into matte or slag;
- (b)
- Determine the optimal matte and slag compositions for maximum recovery of valuable metals;
- (c)
- Predict metal losses in slag when the composition of smelting products or process parameters changes;
- (d)
- Optimize smelting parameters to increase the recovery of valuable metals and minimize losses.
3. Results and Discussion
3.1. Mineralogy and Morphology of Hardened Industrial Slags
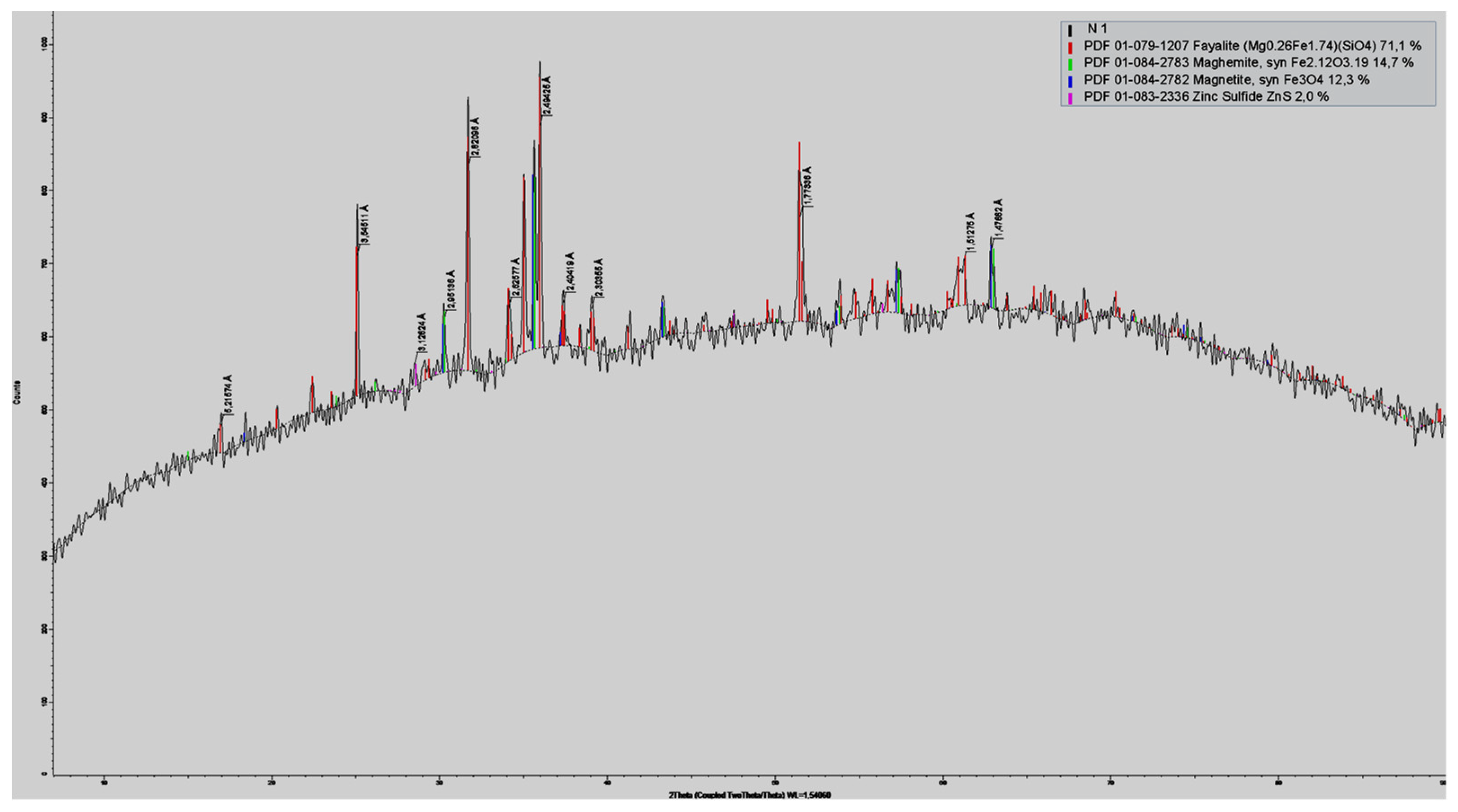
3.2. Forms of Copper and Associated Metals in Slags
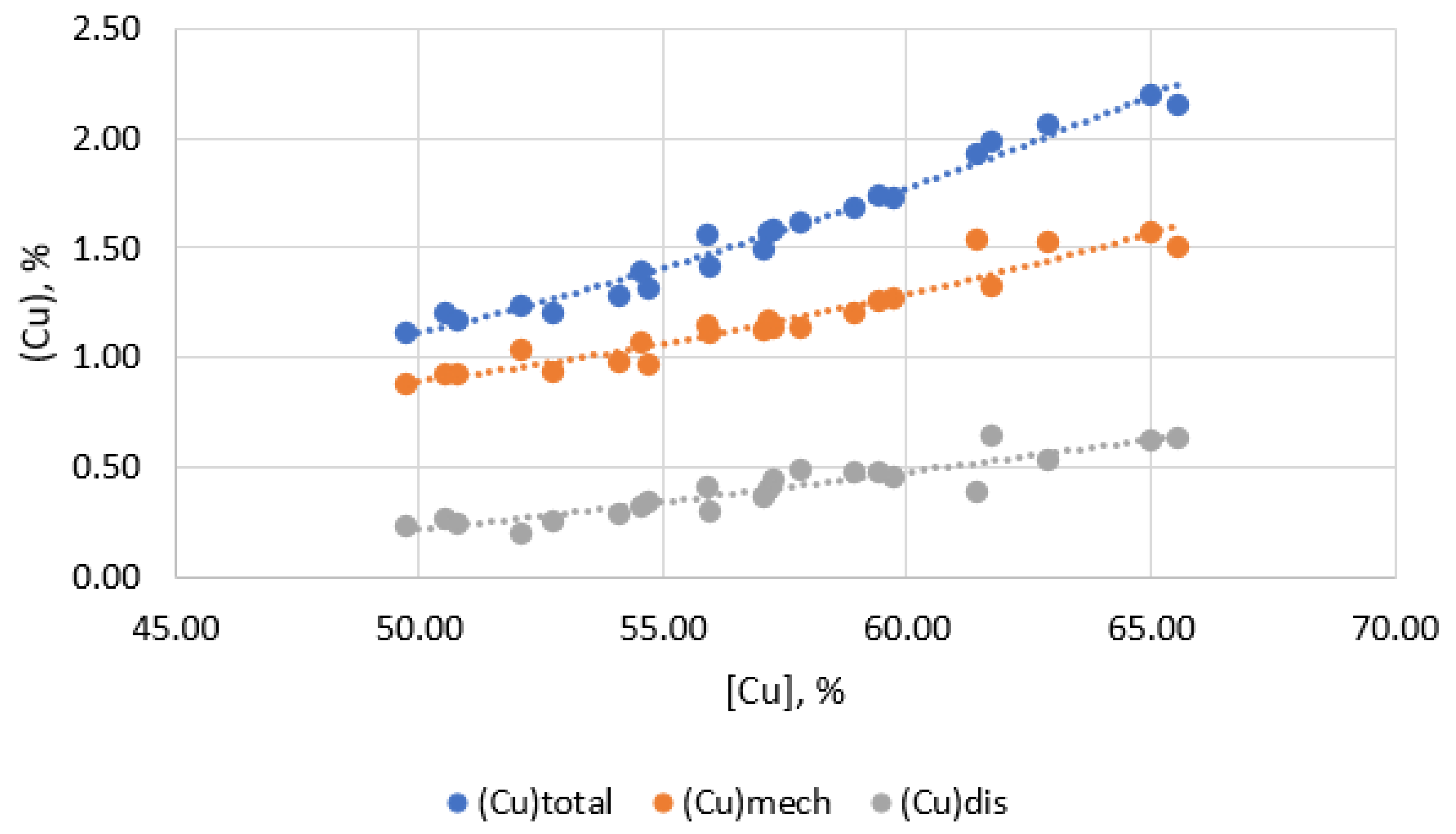
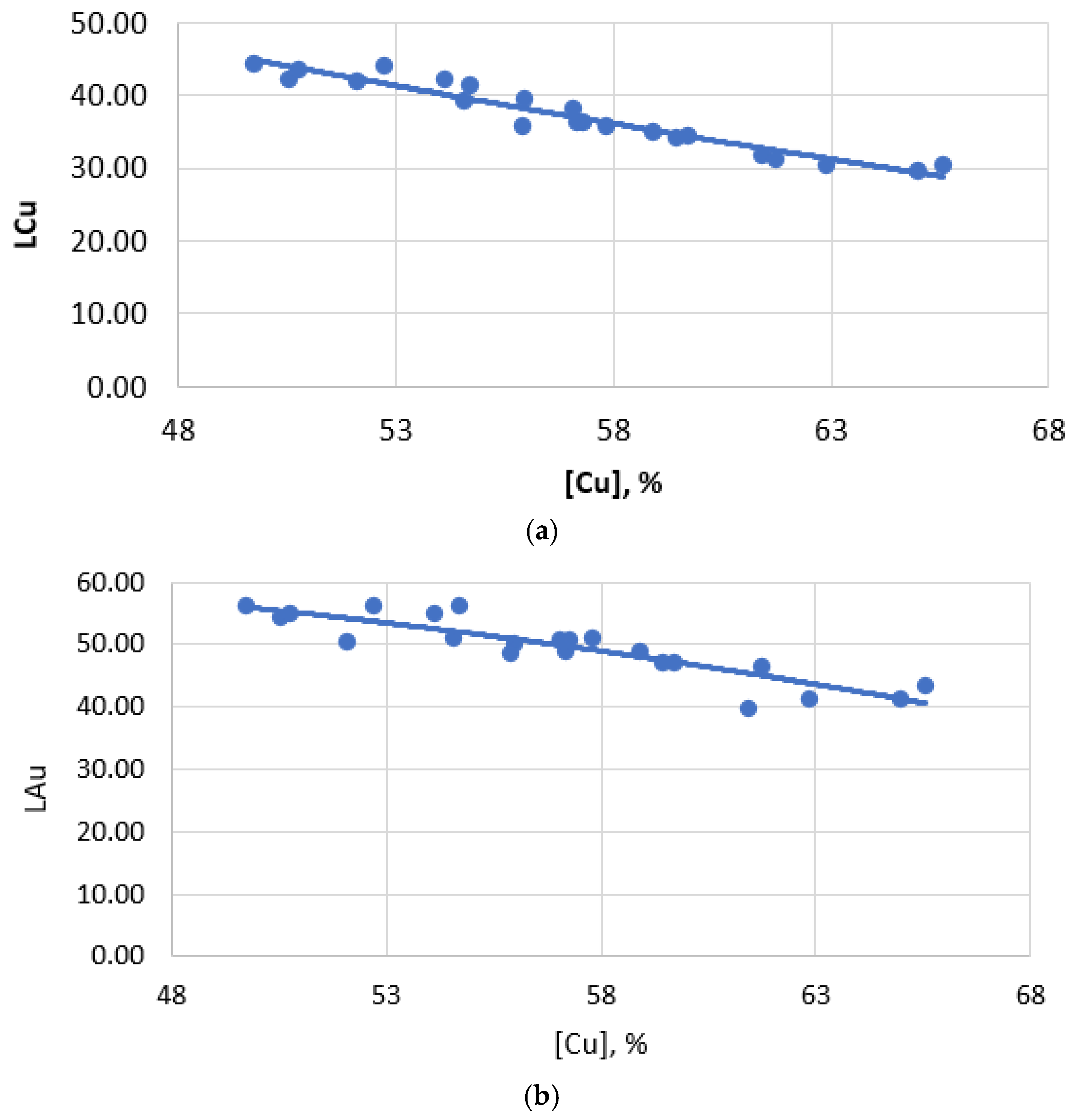
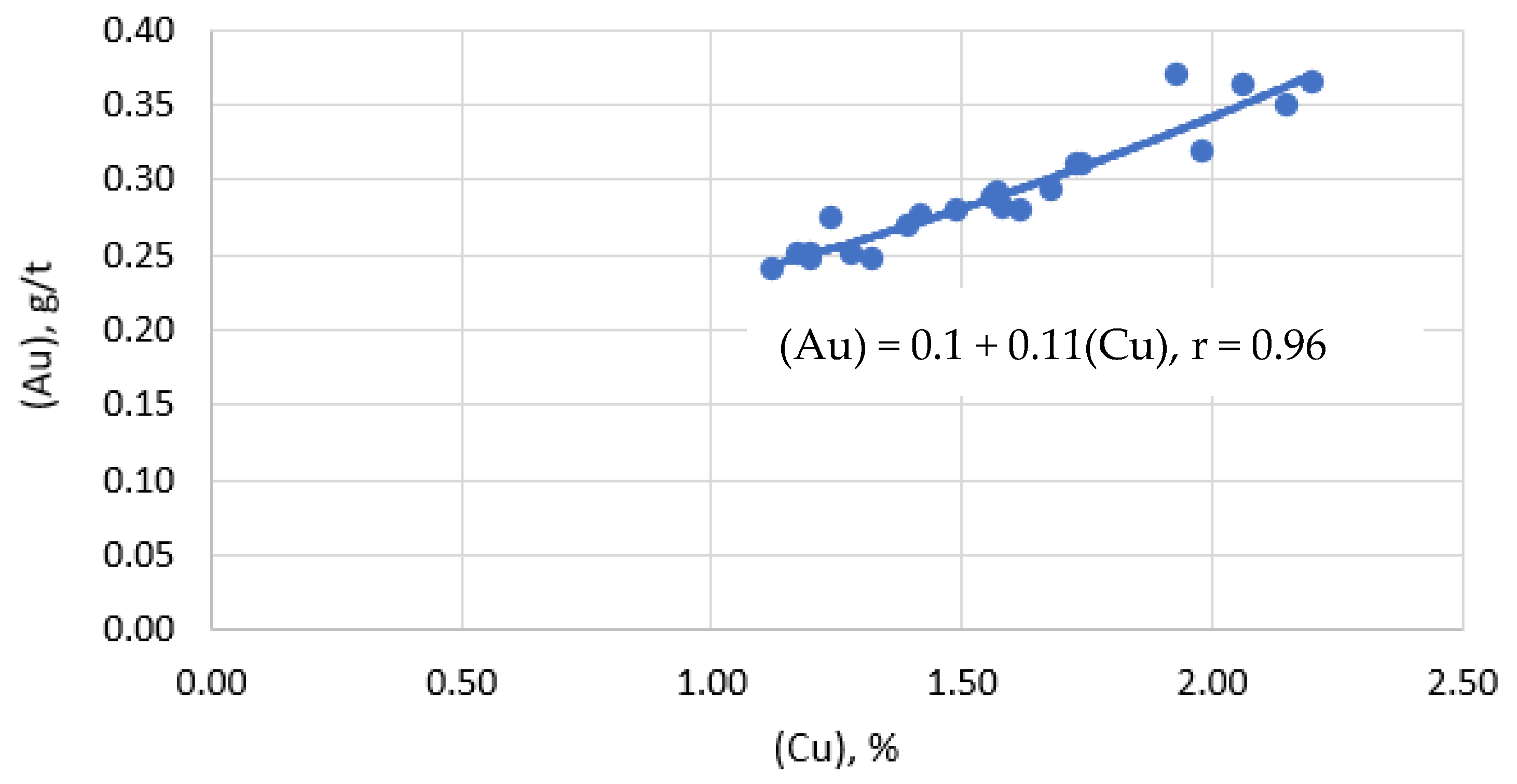
3.3. Estimation of Losses of Copper, Lead and Precious Metals with Slag
4. Conclusions
- (1)
- Optimize phase separation in the electric sedimentation tank by intensifying the processes of selective extraction of copper into the bottom matte phase with the concentration of Au and Ag, and deep sublimation of impurities (Pb, Zn, As) into dust.
- (2)
- Develop fundamentally new solutions to increase the productivity of the depletion of slags and the selective extraction of valuable metals and impurities into targeted products.
- Benefits:
- Increased copper recovery by reducing mechanical copper losses in slag (up to 75–80%) and optimizing furnace hydrodynamics and feed granulometry control. This will lead to higher output of marketable copper and, consequently, increased revenue.
- Improved gold and silver recovery by reducing mechanical copper losses and lowering lead content in slags, which will positively impact the extraction of these valuable metals and further increase revenue.
- Reduced volume of waste slags due to more efficient extraction of valuable components from the feed, resulting in lower volumes of waste slags, reduced storage and disposal costs, and decreased negative environmental impact.
- Improved environmental performance by reducing the content of lead and other harmful impurities in slags and dust, which will enhance the environmental situation around the facility and lower environmental protection costs.
- Processing of additional slags through the development of new technology will allow for the treatment of converter and accumulated solid slags, generating additional profit.
- 2.
- Costs:
- Implementation of technological improvements will require modernization of existing equipment, including electric furnaces, tuyeres, air supply systems, and process control and management systems.
- Development and implementation of new technologies, such as selective fluxes and X-ray fluorescence analysis systems, will require significant investment.
- Optimization of furnace hydrodynamics: costs for designing and implementing changes to tuyere construction, regulating air supply rates, and optimizing furnace geometry.
- Development of new slag processing technologies will require additional research and development, including labor costs for scientific staff and the purchase of equipment and materials.
- Implementation of new technologies will require personnel training, which will also incur costs.
- During the implementation period of new technologies, there may be a temporary decrease in productivity.
- The cost of implementing each proposed technological improvement.
- The forecasted increase in copper, gold, and silver recovery resulting from each proposed technological improvement.
- Current prices for copper, gold, and silver.
- The cost of storage and disposal of waste slags.
- Costs for electricity, fluxes, and other consumables.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ash, C.; Borůvka, L.; Tejnecký, V.; Šebek, O.; Nikodem, A.; Drábek, O. Temporal dissolution of potentially toxic elements from silver smelting slag by synthetic environmental solutions. J. Environ. Manag. 2013, 129, 157–163. [Google Scholar] [CrossRef] [PubMed]
- Radojevic, A.A.; Serbula, S.M.; Kalinovic, T.S.; Kalinovic, J.V.; Steharnik, M.M.; Petrovic, J.V. Metal/metalloid content in plant parts and soils of Corylus spp. influenced by mining–metallurgical production of copper. Environ. Sci. Pollut. Res. 2017, 24, 10326–10340. [Google Scholar] [CrossRef] [PubMed]
- Rönnlund, I.; Reuter, M.; Horn, S.; Aho, J.; Aho, M.; Päällysaho, M.; Ylimäki, L.; Pursula, T. Eco-efficiency indicator framework implemented in the metallurgical industry: Part 2—A case study from the copper industry. Int. J. Life Cycle Assess 2016, 21, 1719–1748. [Google Scholar] [CrossRef]
- Shi, C.; Meyer, C.; Behnood, A. Utilization of copper slag in cement and concrete. Resour. Conserv. Recycl. 2008, 52, 1115–1120. [Google Scholar] [CrossRef]
- Coursol, P.; Valencia, N.C.; Mackey, P.; Bell, S.; Davis, B. Minimization of copper losses in copper smelting slag during electric furnace treatment. JOM 2012, 64, 1305–1313. [Google Scholar] [CrossRef]
- Demetrio, S.; Ahumada, S.A.J.; Durán, M.Á.; Mast, E.; Rojas, U.; Sanhueza, J.; Reyes, P.; Morales, E. Slag cleaning: The Chilean copper smelter experience. JOM 2000, 52, 20–25. [Google Scholar] [CrossRef]
- Vanyukov, A.V.; Zaitsev, V.Y. Slags and Mattes of Non-Ferrous Metallurgy; Metallurgy: Moscow, Russia, 1969. [Google Scholar]
- Esin, O.A.; Geld, P.V. Physical Chemistry of Pyrometallurgical Processes; Metallurgy: Moscow, Russia, 1965; Part 2. [Google Scholar]
- Medikhanov, D.G. Involvement of technogenic deposits of BGMK in the processing of raw materials. In Proceedings of Scientific Works on the Problems of the BGMK, Dedicated to the 10th Anniversary of the Independence of the Republic of Kazakhstan; BGTI: Balkhash, Kazakhstan, 2001; pp. 137–142. [Google Scholar]
- Kvyatkovsky, A.N.; Bobrov, V.M.; Sitko, E.A. Search for ways to increase the complexity of the use of raw materials of the Kazakhmys Corporation. In Proceedings of Scientific Works on the Problems of the BGMK, Dedicated to the 10th Anniversary of the Independence of the Republic of Kazakhstan; BGTI: Balkhash, Kazakhstan, 2001; pp. 19–23. [Google Scholar]
- Karyaev, V.I.; Komkov, A.A.; Kuznetsov, A.V.; Plotnikov, I.P.; Sokolykh, V.A. Study of the microstructure of industrial copper-containing slags. Metallurgist 2020, 9, 90–99. [Google Scholar]
- Lukavy, S.L.; Fedorov, A.N.; Khabiev, R.P.; Min, M.G. Study of the dynamic viscosity of high-copper slag melts. Non-Ferr. Met. 2012, 2, 32–35. [Google Scholar]
- Vanyukov, A.V.; Bystrov, V.P.; Vaskevich, A.D.; Bruek, V.N. Flash Smelting; Metallurgiya: Moscow, Russia, 1988. [Google Scholar]
- Kaplan, V.A.; Vaskevich, A.D.; Zaitsev, V.Y. Study of equilibrium in the system of matte–slag–gas phase. Metals 1982, 2, 31–34. [Google Scholar]
- Swinbourne, D.R.; Kho, T.S. Computational thermodynamics modeling of minor element distributions during copper flash converting. Metall. Mater. Trans. B 2012, 43, 823–829. [Google Scholar] [CrossRef]
- Sarfo, P.; Das, A.; Wyss, G.; Young, C. Recovery of metals values from copper slag and reuse of residual secondary slag. Waste Manag. 2017, 70, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Dosmukhamedov, N.; Egizekov, M.; Zholdasbay, E.; Kaplan, V. Metal Recovery from converter slags using a sulfiding agent. JOM 2018, 70, 2400–2406. [Google Scholar] [CrossRef]
- Vaskevich, A.D.; Sorokin, M.L. General thermodynamic model of copper solubility in slags. Non-Ferr. Met. 1982, 10, 22–26. [Google Scholar]
- Ruddle, R.W.; Taylor, B.; Bates, A.P. The solubility of copper in iron silicate slags. Trans. Inst. Min. Met. 1966, 75, 1–12. [Google Scholar]
- Toguri, J.M.; Santander, N.H. The solubility of copper in fayalite slags at 1300 °C. Can. Metall. Q. 1969, 8, 167–171. [Google Scholar] [CrossRef]
- Toguri, J.M.; Santander, N.H. Distribution of copper between Cu-Au alloys and silica-saturated fayalite slags. Can. Metall. Q. 1972, 3, 586–588. [Google Scholar] [CrossRef]
- Altman, R.; Kellog, H.H. Thermodynamics of FeO-MnO-TiO2 melts saturated with iron at 1475 °C. Trans. Inst. Min. Met. 1972, 81, 163–175. [Google Scholar]
- Nagamori, M.; Mackey, P.J.; Tarassoff, P. The distribution of As, Sb, Bi, Se, and Te between molten copper and white metal. Metall. Trans. B 1975, 6, 295–301. [Google Scholar] [CrossRef]
- Taylor, J.P.; Jeffes, I.H.E. Activity of cuprous oxide in iron silicate slags of various compositions. Trans. Inst. Min. Met. 1975, 84, 18–24. [Google Scholar]
- Nagamori, M. Metal loss to slag: Part I. Sulfidic and oxidic dissolution of copper in fayalite slag from low grade matte. Metall. Trans. B 1974, 5, 531–538. [Google Scholar] [CrossRef]
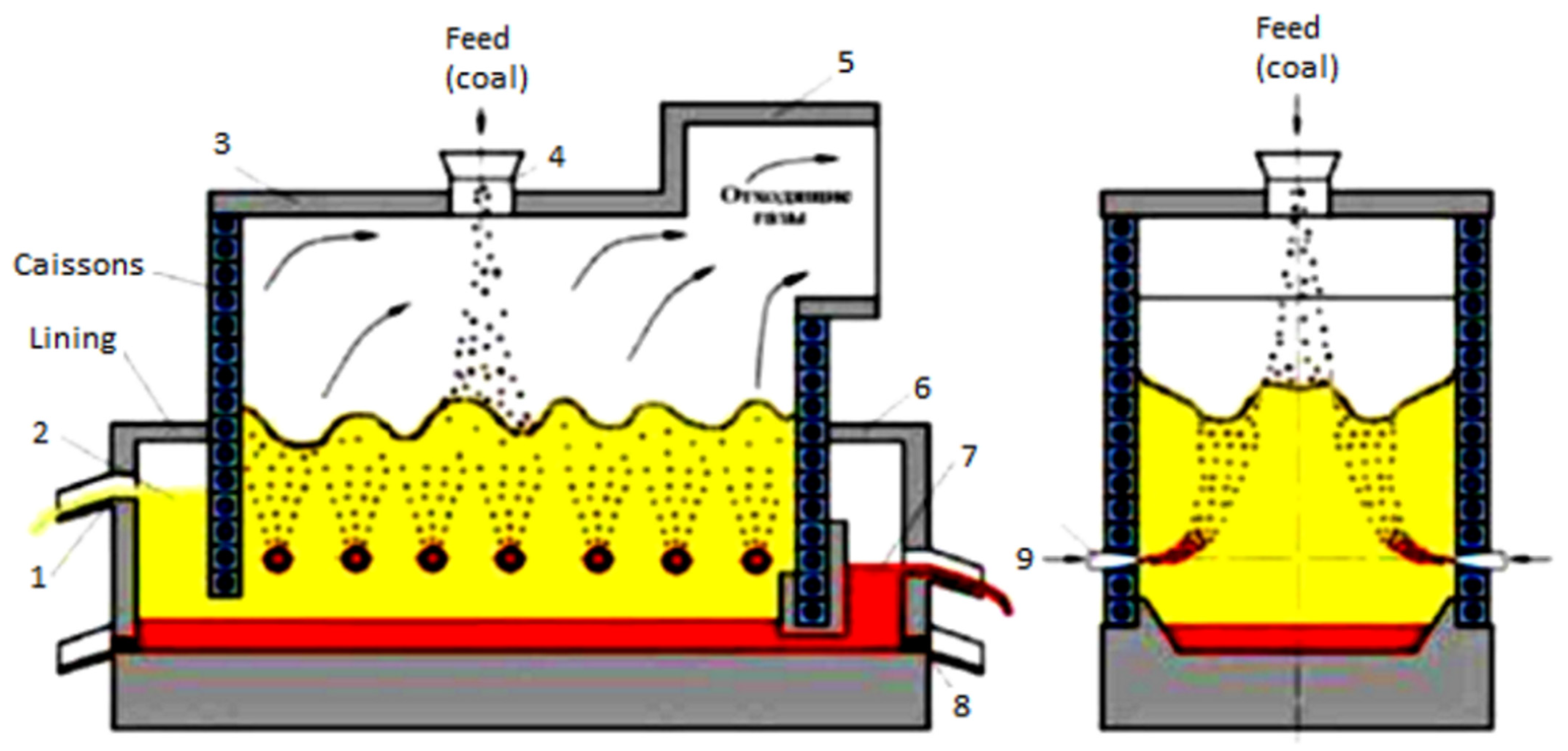
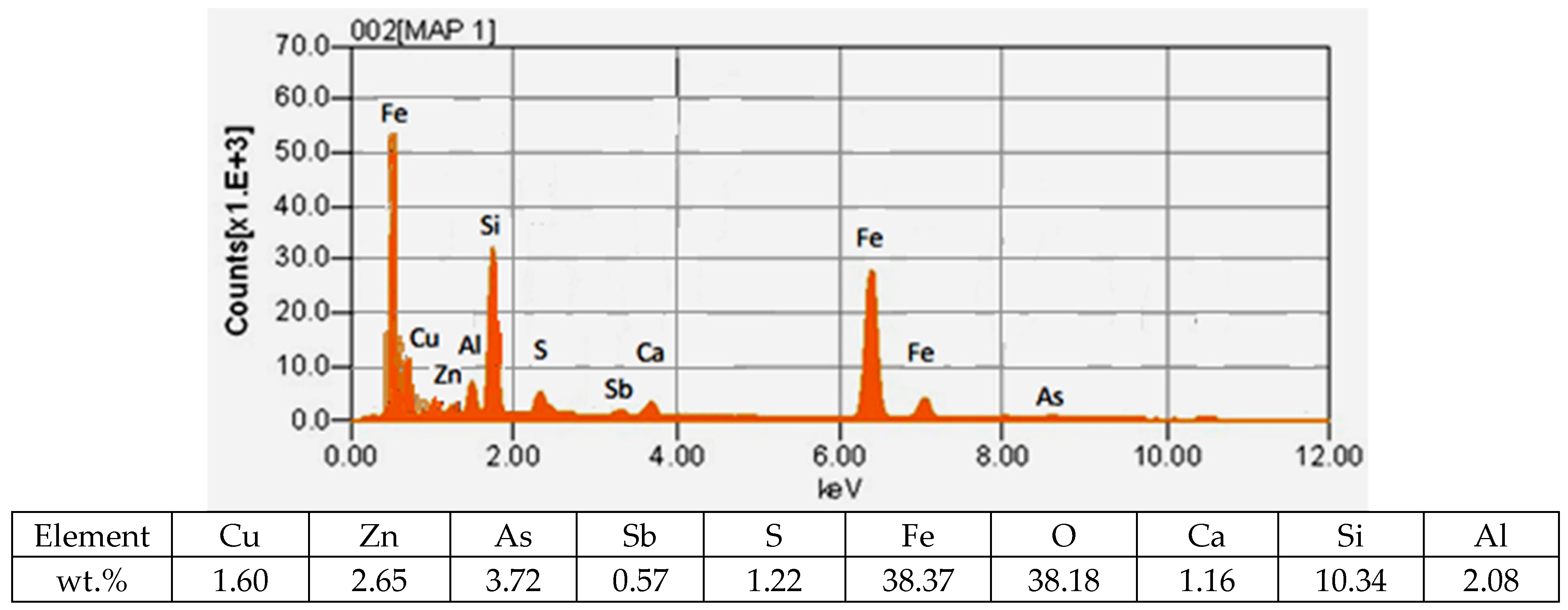
| # | Matte Composition. wt.% | Slag Composition. wt.% | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [Cu] | [Pb] | [Zn] | [Fe] | [S] | [Au] * | [Ag] * | Cu | Pb | ZnO | SiO2 | FeO | CaO | Au * | Ag * | |
| 1 | 55.90 | 1.27 | 0.13 | 17.83 | 22.45 | 13.99 | 213.57 | 1.56 | 0.66 | 2.61 | 23.48 | 55.44 | 2.51 | 0.29 | 7.58 |
| 2 | 54.67 | 1.43 | 0.12 | 19.81 | 23.33 | 13.90 | 214.11 | 1.31 | 0.60 | 2.43 | 22.38 | 56.49 | 1.96 | 0.25 | 7.02 |
| 3 | 52.67 | 1.43 | 0.19 | 20.31 | 23.45 | 13.75 | 213.89 | 1.25 | 0.52 | 2.38 | 23.66 | 55.11 | 1.87 | 0.24 | 7.22 |
| 4 | 59.33 | 1.28 | 0.10 | 16.87 | 22.16 | 14.44 | 214.12 | 1.69 | 0.75 | 2.78 | 22.96 | 55.93 | 2.11 | 0.33 | 7.19 |
| 5 | 51.74 | 1.13 | 0.17 | 22.94 | 23.77 | 14.08 | 213.36 | 1.18 | 0.42 | 2.24 | 24.75 | 55.12 | 1.96 | 0.27 | 7.22 |
| 6 | 58.99 | 1.08 | 0.10 | 16.17 | 22.04 | 14.66 | 214.13 | 1.69 | 0.78 | 2.40 | 22.56 | 56.26 | 1.78 | 0.34 | 7.87 |
| 7 | 65.39 | 1.06 | 0.10 | 11.21 | 20.44 | 14.12 | 213.37 | 2.12 | 0.92 | 2.57 | 22.30 | 57.01 | 1.91 | 0.28 | 7.19 |
| 8 | 65.37 | 1.06 | 0.10 | 12.08 | 19.58 | 15.16 | 215.13 | 2.20 | 0.92 | 2.78 | 23.41 | 56.37 | 3.42 | 0.37 | 8.24 |
| 9 | 59.02 | 1.18 | 0.15 | 17.43 | 22.25 | 14.73 | 213.13 | 1.55 | 0.69 | 2.51 | 23.22 | 56.11 | 2.08 | 0.35 | 7.32 |
| 10 | 57.28 | 1.09 | 0.17 | 16.97 | 22.18 | 14.22 | 213.54 | 1.58 | 0.73 | 2.32 | 23.59 | 56.16 | 1.79 | 0.28 | 6.60 |
| 11 | 62.01 | 0.90 | 0.12 | 14.09 | 21.05 | 13.63 | 214.16 | 1.96 | 0.83 | 2.61 | 23.24 | 57.11 | 2.04 | 0.25 | 7.33 |
| 12 | 50.82 | 1.15 | 0.24 | 22.56 | 23.59 | 13.90 | 214.34 | 1.19 | 0.57 | 2.20 | 23.68 | 55.68 | 1.86 | 0.29 | 7.46 |
| 13 | 61.05 | 1.09 | 0.14 | 16.38 | 21.46 | 13.91 | 215.13 | 1.76 | 0.70 | 2.68 | 22.26 | 57.48 | 2.03 | 0.29 | 8.69 |
| 14 | 56.70 | 1.18 | 0.15 | 17.43 | 22.25 | 14.72 | 213.05 | 1.46 | 0.69 | 2.51 | 23.22 | 56.11 | 2.08 | 0.35 | 6.28 |
| 15 | 62.87 | 1.11 | 0.10 | 12.93 | 20.09 | 15.01 | 214.87 | 2.06 | 0.81 | 2.74 | 23.14 | 55.74 | 3.42 | 0.36 | 8.10 |
| 16 | 57.20 | 1.12 | 0.15 | 17.23 | 22.31 | 14.46 | 213.29 | 1.57 | 0.70 | 2.54 | 23.37 | 56.07 | 1.88 | 0.30 | 7.04 |
| 17 | 57.17 | 1.12 | 0.15 | 17.23 | 22.31 | 14.28 | 213.80 | 1.57 | 0.70 | 2.54 | 23.37 | 56.07 | 1.88 | 0.29 | 7.66 |
| 18 | 53.42 | 1.53 | 0.21 | 19.43 | 23.16 | 14.81 | 213.05 | 1.34 | 0.56 | 2.39 | 23.08 | 54.78 | 1.79 | 0.34 | 6.35 |
| 19 | 50.78 | 1.15 | 0.24 | 22.56 | 23.59 | 13.75 | 213.10 | 1.17 | 0.57 | 2.20 | 23.68 | 55.68 | 1.86 | 0.25 | 6.22 |
| 20 | 57.03 | 1.18 | 0.15 | 17.43 | 22.25 | 15.04 | 213.05 | 1.47 | 0.69 | 2.51 | 23.22 | 56.11 | 2.08 | 0.37 | 6.26 |
| 21 | 53.60 | 1.34 | 0.28 | 20.13 | 23.18 | 13.96 | 215.10 | 1.21 | 0.58 | 2.23 | 23.48 | 56.89 | 1.73 | 0.27 | 8.25 |
| 22 | 65.57 | 1.06 | 0.10 | 12.08 | 19.58 | 14.45 | 215.13 | 2.20 | 0.92 | 2.78 | 23.41 | 56.37 | 3.42 | 0.33 | 8.19 |
| 23 | 59.71 | 0.73 | 0.12 | 15.81 | 22.30 | 14.59 | 214.22 | 1.73 | 0.78 | 2.44 | 22.77 | 56.37 | 1.97 | 0.31 | 7.21 |
| 24 | 58.97 | 1.08 | 0.10 | 16.17 | 22.04 | 13.61 | 213.07 | 1.65 | 0.78 | 2.40 | 22.56 | 56.26 | 1.78 | 0.24 | 6.90 |
| 25 | 58.07 | 1.28 | 0.10 | 16.87 | 22.16 | 13.70 | 213.09 | 1.60 | 0.75 | 2.78 | 22.96 | 55.93 | 2.11 | 0.25 | 6.33 |
| 26 | 55.37 | 1.53 | 0.21 | 19.43 | 23.16 | 14.27 | 213.12 | 1.40 | 0.56 | 2.39 | 23.08 | 54.78 | 1.79 | 0.31 | 6.51 |
| 27 | 57.81 | 1.28 | 0.10 | 16.87 | 22.16 | 14.33 | 214.00 | 1.62 | 0.75 | 2.78 | 22.96 | 55.93 | 2.11 | 0.28 | 7.06 |
| 28 | 56.10 | 1.33 | 0.14 | 18.52 | 22.94 | 13.59 | 213.15 | 1.42 | 0.42 | 2.60 | 22.59 | 56.82 | 2.16 | 0.24 | 6.39 |
| 29 | 60.80 | 0.90 | 0.12 | 14.09 | 21.05 | 13.90 | 213.18 | 1.92 | 0.83 | 2.61 | 23.24 | 57.11 | 2.04 | 0.25 | 6.38 |
| 30 | 59.99 | 0.73 | 0.12 | 15.81 | 22.30 | 14.96 | 213.20 | 1.74 | 0.78 | 2.44 | 22.77 | 56.37 | 1.97 | 0.35 | 6.22 |
| 31 | 52.05 | 1.15 | 0.24 | 22.56 | 23.59 | 14.66 | 213.21 | 1.20 | 0.57 | 2.20 | 23.68 | 55.68 | 1.86 | 0.33 | 6.43 |
| 32 | 53.07 | 1.43 | 0.19 | 20.31 | 23.45 | 14.37 | 213.24 | 1.24 | 0.52 | 2.38 | 23.66 | 55.11 | 1.87 | 0.32 | 6.47 |
| 33 | 50.98 | 1.43 | 0.19 | 20.31 | 23.45 | 14.23 | 213.25 | 1.21 | 0.52 | 2.38 | 23.66 | 55.11 | 1.87 | 0.31 | 6.74 |
| 34 | 54.55 | 1.53 | 0.21 | 19.43 | 23.16 | 13.79 | 213.33 | 1.39 | 0.56 | 2.39 | 23.08 | 54.78 | 1.79 | 0.27 | 7.33 |
| 35 | 55.27 | 1.37 | 0.20 | 19.04 | 22.88 | 15.02 | 213.30 | 1.33 | 0.46 | 2.32 | 23.26 | 55.36 | 1.85 | 0.36 | 6.56 |
| 36 | 60.61 | 0.73 | 0.12 | 15.81 | 22.30 | 13.56 | 213.31 | 1.73 | 0.78 | 2.44 | 22.77 | 56.37 | 1.97 | 0.24 | 6.55 |
| 37 | 56.42 | 1.18 | 0.15 | 17.43 | 22.25 | 13.83 | 213.33 | 1.50 | 0.69 | 2.51 | 23.22 | 56.11 | 2.08 | 0.25 | 6.45 |
| 38 | 54.51 | 1.53 | 0.21 | 19.43 | 23.16 | 14.52 | 213.36 | 1.37 | 0.56 | 2.39 | 23.08 | 54.78 | 1.79 | 0.35 | 6.72 |
| 39 | 54.49 | 1.43 | 0.12 | 19.81 | 23.33 | 14.56 | 213.37 | 1.30 | 0.60 | 2.43 | 22.38 | 56.49 | 1.96 | 0.35 | 6.70 |
| 40 | 52.51 | 1.43 | 0.19 | 20.31 | 23.45 | 13.67 | 213.40 | 1.27 | 0.52 | 2.38 | 23.66 | 55.11 | 1.87 | 0.25 | 6.73 |
| 41 | 50.94 | 1.11 | 0.18 | 22.29 | 23.73 | 13.53 | 213.42 | 1.19 | 0.56 | 2.34 | 24.22 | 55.05 | 1.84 | 0.25 | 6.58 |
| 42 | 50.34 | 1.11 | 0.18 | 22.29 | 23.73 | 14.07 | 213.44 | 1.17 | 0.56 | 2.34 | 24.22 | 55.05 | 1.84 | 0.27 | 6.84 |
| 43 | 52.10 | 1.43 | 0.19 | 20.31 | 23.45 | 13.88 | 213.16 | 1.24 | 0.52 | 2.38 | 23.66 | 55.11 | 1.87 | 0.28 | 7.23 |
| 44 | 55.96 | 1.37 | 0.20 | 19.04 | 22.88 | 13.72 | 213.48 | 1.34 | 0.46 | 2.32 | 23.26 | 55.36 | 1.85 | 0.25 | 6.81 |
| 45 | 57.17 | 1.18 | 0.15 | 17.43 | 22.25 | 14.21 | 213.50 | 1.51 | 0.69 | 2.51 | 23.22 | 56.11 | 2.08 | 0.30 | 7.00 |
| 46 | 61.55 | 0.90 | 0.12 | 14.09 | 21.05 | 13.62 | 213.52 | 1.93 | 0.83 | 2.61 | 23.24 | 57.11 | 2.04 | 0.27 | 6.69 |
| 47 | 50.56 | 1.15 | 0.24 | 22.56 | 23.59 | 13.61 | 213.54 | 1.14 | 0.57 | 2.20 | 23.68 | 55.68 | 1.86 | 0.26 | 6.76 |
| 48 | 53.88 | 1.34 | 0.28 | 20.13 | 23.18 | 13.67 | 213.56 | 1.23 | 0.58 | 2.23 | 23.48 | 56.89 | 1.73 | 0.24 | 6.85 |
| 49 | 54.01 | 1.43 | 0.19 | 20.31 | 23.45 | 14.24 | 213.58 | 1.31 | 0.52 | 2.38 | 23.66 | 55.11 | 1.87 | 0.28 | 6.81 |
| 50 | 60.00 | 1.09 | 0.14 | 16.38 | 21.46 | 15.13 | 213.60 | 1.73 | 0.70 | 2.68 | 22.26 | 57.48 | 2.03 | 0.37 | 6.73 |
| 51 | 61.74 | 1.26 | 0.10 | 13.42 | 21.24 | 15.05 | 214.21 | 1.98 | 0.87 | 2.67 | 23.38 | 57.16 | 1.76 | 0.36 | 8.11 |
| 52 | 56.55 | 1.27 | 0.13 | 17.83 | 22.45 | 14.25 | 213.64 | 1.57 | 0.66 | 2.61 | 23.48 | 55.44 | 2.51 | 0.28 | 6.83 |
| 53 | 62.85 | 0.90 | 0.12 | 14.09 | 21.05 | 14.34 | 213.66 | 1.94 | 0.83 | 2.61 | 23.24 | 57.11 | 2.04 | 0.32 | 7.01 |
| 54 | 56.81 | 1.27 | 0.13 | 17.83 | 22.45 | 13.83 | 213.69 | 1.61 | 0.66 | 2.61 | 23.48 | 55.44 | 2.51 | 0.27 | 6.90 |
| 55 | 65.57 | 1.06 | 0.10 | 12.08 | 19.58 | 14.00 | 213.70 | 2.20 | 0.92 | 2.78 | 23.41 | 56.37 | 3.42 | 0.25 | 7.18 |
| 56 | 54.02 | 1.34 | 0.28 | 20.13 | 23.18 | 13.73 | 213.72 | 1.21 | 0.58 | 2.23 | 23.48 | 56.89 | 1.73 | 0.25 | 6.95 |
| 57 | 59.43 | 1.09 | 0.14 | 16.38 | 21.46 | 14.67 | 214.24 | 1.74 | 0.70 | 2.68 | 22.26 | 57.48 | 2.03 | 0.31 | 8.19 |
| 58 | 55.57 | 1.37 | 0.20 | 19.04 | 22.88 | 14.29 | 213.76 | 1.34 | 0.46 | 2.32 | 23.26 | 55.36 | 1.85 | 0.31 | 7.17 |
| 59 | 62.18 | 1.26 | 0.10 | 13.42 | 21.24 | 13.75 | 213.78 | 2.01 | 0.87 | 2.67 | 23.38 | 57.16 | 1.76 | 0.26 | 6.85 |
| 60 | 54.66 | 1.53 | 0.21 | 19.43 | 23.16 | 15.06 | 213.80 | 1.37 | 0.56 | 2.39 | 23.08 | 54.78 | 1.79 | 0.37 | 7.15 |
| 61 | 49.72 | 1.13 | 0.17 | 22.94 | 23.77 | 13.55 | 213.82 | 1.12 | 0.42 | 2.24 | 24.75 | 55.12 | 1.96 | 0.24 | 7.29 |
| 62 | 51.49 | 1.15 | 0.24 | 22.56 | 23.59 | 13.80 | 213.85 | 1.17 | 0.57 | 2.20 | 23.68 | 55.68 | 1.86 | 0.26 | 6.77 |
| 63 | 65.57 | 1.06 | 0.10 | 12.08 | 19.58 | 13.89 | 213.87 | 2.20 | 0.92 | 2.78 | 23.41 | 56.37 | 3.42 | 0.27 | 6.87 |
| 64 | 51.21 | 1.13 | 0.17 | 22.94 | 23.77 | 14.76 | 213.89 | 1.17 | 0.42 | 2.24 | 24.75 | 55.12 | 1.96 | 0.33 | 7.26 |
| 65 | 55.83 | 1.37 | 0.20 | 19.04 | 22.88 | 14.33 | 213.91 | 1.35 | 0.46 | 2.32 | 23.26 | 55.36 | 1.85 | 0.31 | 7.34 |
| 66 | 56.83 | 1.09 | 0.17 | 16.97 | 22.18 | 14.82 | 213.93 | 1.57 | 0.73 | 2.32 | 23.59 | 56.16 | 1.79 | 0.35 | 7.15 |
| 67 | 59.07 | 1.28 | 0.10 | 16.87 | 22.16 | 14.89 | 213.94 | 1.63 | 0.75 | 2.78 | 22.96 | 55.93 | 2.11 | 0.37 | 7.16 |
| 68 | 50.53 | 1.11 | 0.18 | 22.29 | 23.73 | 13.68 | 213.11 | 1.20 | 0.56 | 2.34 | 24.22 | 55.05 | 1.84 | 0.25 | 7.23 |
| 69 | 55.97 | 1.33 | 0.14 | 18.52 | 22.94 | 13.87 | 213.34 | 1.42 | 0.42 | 2.60 | 22.59 | 56.82 | 2.16 | 0.28 | 7.5 |
| 70 | 61.53 | 1.11 | 0.10 | 12.93 | 20.09 | 14.97 | 214.01 | 2.02 | 0.81 | 2.74 | 23.14 | 55.74 | 3.42 | 0.37 | 7.40 |
| 71 | 58.91 | 1.08 | 0.10 | 16.17 | 22.04 | 14.37 | 214.17 | 1.68 | 0.78 | 2.40 | 22.56 | 56.26 | 1.78 | 0.29 | 7.76 |
| 72 | 52.72 | 1.34 | 0.28 | 20.13 | 23.18 | 13.89 | 213.34 | 1.20 | 0.58 | 2.23 | 23.48 | 56.89 | 1.73 | 0.25 | 6.25 |
| 73 | 52.18 | 1.43 | 0.19 | 20.31 | 23.45 | 13.80 | 214.07 | 1.26 | 0.52 | 2.38 | 23.66 | 55.11 | 1.87 | 0.27 | 7.47 |
| 74 | 57.43 | 1.18 | 0.15 | 17.43 | 22.25 | 14.37 | 214.09 | 1.48 | 0.69 | 2.51 | 23.22 | 56.11 | 2.08 | 0.32 | 7.10 |
| 75 | 57.44 | 1.18 | 0.15 | 17.43 | 22.25 | 14.78 | 214.11 | 1.50 | 0.69 | 2.51 | 23.22 | 56.11 | 2.08 | 0.35 | 7.42 |
| 76 | 54.71 | 1.37 | 0.20 | 19.04 | 22.88 | 13.95 | 213.54 | 1.32 | 0.46 | 2.32 | 23.26 | 55.36 | 1.85 | 0.25 | 7.54 |
| 77 | 52.66 | 1.43 | 0.19 | 20.31 | 23.45 | 14.50 | 214.15 | 1.25 | 0.52 | 2.38 | 23.66 | 55.11 | 1.87 | 0.34 | 7.60 |
| 78 | 65.52 | 1.06 | 0.10 | 12.08 | 19.58 | 14.93 | 214.17 | 2.20 | 0.92 | 2.78 | 23.41 | 56.37 | 3.42 | 0.36 | 7.45 |
| 79 | 56.38 | 1.12 | 0.15 | 17.23 | 22.31 | 14.97 | 214.19 | 1.52 | 0.70 | 2.54 | 23.37 | 56.07 | 1.88 | 0.37 | 7.46 |
| 80 | 58.28 | 1.09 | 0.17 | 16.97 | 22.18 | 14.07 | 214.21 | 1.62 | 0.73 | 2.32 | 23.59 | 56.16 | 1.79 | 0.31 | 7.52 |
| 81 | 50.45 | 1.13 | 0.17 | 22.94 | 23.77 | 14.00 | 214.23 | 1.14 | 0.42 | 2.24 | 24.75 | 55.12 | 1.96 | 0.28 | 7.73 |
| 82 | 57.74 | 1.18 | 0.15 | 17.43 | 22.25 | 14.54 | 214.25 | 1.50 | 0.69 | 2.51 | 23.22 | 56.11 | 2.08 | 0.35 | 7.79 |
| 83 | 59.08 | 1.09 | 0.14 | 16.38 | 21.46 | 13.93 | 214.27 | 1.76 | 0.70 | 2.68 | 22.26 | 57.48 | 2.03 | 0.26 | 7.60 |
| 84 | 55.31 | 1.43 | 0.12 | 19.81 | 23.33 | 14.54 | 214.29 | 1.28 | 0.60 | 2.43 | 22.38 | 56.49 | 1.96 | 0.32 | 7.82 |
| 85 | 65.57 | 1.06 | 0.10 | 11.21 | 20.44 | 14.19 | 214.31 | 2.13 | 0.92 | 2.57 | 22.30 | 57.01 | 1.91 | 0.27 | 7.78 |
| 86 | 56.77 | 1.12 | 0.15 | 17.23 | 22.31 | 15.13 | 214.33 | 1.54 | 0.70 | 2.54 | 23.37 | 56.07 | 1.88 | 0.37 | 7.85 |
| 87 | 50.12 | 1.13 | 0.17 | 22.94 | 23.77 | 14.47 | 214.36 | 1.14 | 0.42 | 2.24 | 24.75 | 55.12 | 1.96 | 0.31 | 7.99 |
| 88 | 56.86 | 1.37 | 0.20 | 19.04 | 22.88 | 14.48 | 214.38 | 1.35 | 0.46 | 2.32 | 23.26 | 55.36 | 1.85 | 0.31 | 7.79 |
| 89 | 52.88 | 1.34 | 0.28 | 20.13 | 23.18 | 13.84 | 214.40 | 1.23 | 0.58 | 2.23 | 23.48 | 56.89 | 1.73 | 0.28 | 7.76 |
| 90 | 55.34 | 1.53 | 0.21 | 19.43 | 23.16 | 14.14 | 214.42 | 1.40 | 0.56 | 2.39 | 23.08 | 54.78 | 1.79 | 0.27 | 7.77 |
| 91 | 63.79 | 1.06 | 0.10 | 12.08 | 19.58 | 14.66 | 214.44 | 2.20 | 0.92 | 2.78 | 23.41 | 56.37 | 3.42 | 0.33 | 7.80 |
| 92 | 53.33 | 1.43 | 0.12 | 19.81 | 23.33 | 13.96 | 214.46 | 1.28 | 0.60 | 2.43 | 22.38 | 56.49 | 1.96 | 0.26 | 7.90 |
| 93 | 60.57 | 1.08 | 0.10 | 16.17 | 22.04 | 14.62 | 214.48 | 1.73 | 0.78 | 2.40 | 22.56 | 56.26 | 1.78 | 0.33 | 7.97 |
| 94 | 58.45 | 1.09 | 0.17 | 16.97 | 22.18 | 15.14 | 214.50 | 1.61 | 0.73 | 2.32 | 23.59 | 56.16 | 1.79 | 0.37 | 7.99 |
| 95 | 53.41 | 1.43 | 0.12 | 19.81 | 23.33 | 14.10 | 214.52 | 1.27 | 0.60 | 2.43 | 22.38 | 56.49 | 1.96 | 0.30 | 8.07 |
| 96 | 65.57 | 1.06 | 0.10 | 12.08 | 19.58 | 14.42 | 214.54 | 2.20 | 0.92 | 2.78 | 23.41 | 56.37 | 3.42 | 0.33 | 8.01 |
| 97 | 57.29 | 1.33 | 0.14 | 18.52 | 22.94 | 13.71 | 214.55 | 1.45 | 0.42 | 2.60 | 22.59 | 56.82 | 2.16 | 0.26 | 8.18 |
| 98 | 58.27 | 1.12 | 0.15 | 17.23 | 22.31 | 15.07 | 214.58 | 1.59 | 0.70 | 2.54 | 23.37 | 56.07 | 1.88 | 0.37 | 8.03 |
| 99 | 59.86 | 1.08 | 0.10 | 16.17 | 22.04 | 14.12 | 214.60 | 1.71 | 0.78 | 2.40 | 22.56 | 56.26 | 1.78 | 0.29 | 8.37 |
| 100 | 59.18 | 1.28 | 0.10 | 16.87 | 22.16 | 14.22 | 214.62 | 1.66 | 0.75 | 2.78 | 22.96 | 55.93 | 2.11 | 0.30 | 8.17 |
| 101 | 65.44 | 1.06 | 0.10 | 12.08 | 19.58 | 14.91 | 214.64 | 2.19 | 0.92 | 2.78 | 23.41 | 56.37 | 3.42 | 0.37 | 8.04 |
| 102 | 56.72 | 1.28 | 0.10 | 16.87 | 22.16 | 13.79 | 214.66 | 1.62 | 0.75 | 2.78 | 22.96 | 55.93 | 2.11 | 0.27 | 8.04 |
| 103 | 54.07 | 1.53 | 0.21 | 19.43 | 23.16 | 13.68 | 214.68 | 1.38 | 0.56 | 2.39 | 23.08 | 54.78 | 1.79 | 0.24 | 8.23 |
| 104 | 63.53 | 1.11 | 0.10 | 12.93 | 20.09 | 15.01 | 214.70 | 2.09 | 0.81 | 2.74 | 23.14 | 55.74 | 3.42 | 0.37 | 8.18 |
| 105 | 61.42 | 0.90 | 0.12 | 14.09 | 21.05 | 14.75 | 214.72 | 1.93 | 0.83 | 2.61 | 23.24 | 57.11 | 2.04 | 0.37 | 7.81 |
| 106 | 60.07 | 1.08 | 0.10 | 16.17 | 22.04 | 14.03 | 214.74 | 1.70 | 0.78 | 2.40 | 22.56 | 56.26 | 1.78 | 0.29 | 8.30 |
| 107 | 57.05 | 1.18 | 0.15 | 17.43 | 22.25 | 14.20 | 213.19 | 1.49 | 0.69 | 2.51 | 23.22 | 56.11 | 2.08 | 0.28 | 7.09 |
| 108 | 65.57 | 1.06 | 0.10 | 11.21 | 20.44 | 13.75 | 215.13 | 2.15 | 0.92 | 2.57 | 22.30 | 57.01 | 1.91 | 0.25 | 8.54 |
| 109 | 56.36 | 1.33 | 0.14 | 18.52 | 22.94 | 13.56 | 214.80 | 1.40 | 0.42 | 2.60 | 22.59 | 56.82 | 2.16 | 0.24 | 8.17 |
| 110 | 60.18 | 0.73 | 0.12 | 15.81 | 22.30 | 14.87 | 214.82 | 1.72 | 0.78 | 2.44 | 22.77 | 56.37 | 1.97 | 0.36 | 8.30 |
| 111 | 52.68 | 1.15 | 0.24 | 22.56 | 23.59 | 14.87 | 214.84 | 1.20 | 0.57 | 2.20 | 23.68 | 55.68 | 1.86 | 0.36 | 8.46 |
| 112 | 63.05 | 1.11 | 0.10 | 12.93 | 20.09 | 14.63 | 214.87 | 2.03 | 0.81 | 2.74 | 23.14 | 55.74 | 3.42 | 0.34 | 8.42 |
| 113 | 61.23 | 0.90 | 0.12 | 14.09 | 21.05 | 15.05 | 214.88 | 1.91 | 0.83 | 2.61 | 23.24 | 57.11 | 2.04 | 0.37 | 8.29 |
| 114 | 61.77 | 1.26 | 0.10 | 13.42 | 21.24 | 14.39 | 214.91 | 1.99 | 0.87 | 2.67 | 23.38 | 57.16 | 1.76 | 0.30 | 8.47 |
| 115 | 55.60 | 1.53 | 0.21 | 19.43 | 23.16 | 14.60 | 214.92 | 1.39 | 0.56 | 2.39 | 23.08 | 54.78 | 1.79 | 0.32 | 8.51 |
| 116 | 61.86 | 1.26 | 0.10 | 13.42 | 21.24 | 14.52 | 214.94 | 1.97 | 0.87 | 2.67 | 23.38 | 57.16 | 1.76 | 0.31 | 8.40 |
| 117 | 63.20 | 1.26 | 0.10 | 13.42 | 21.24 | 15.15 | 214.97 | 2.02 | 0.87 | 2.67 | 23.38 | 57.16 | 1.76 | 0.37 | 8.53 |
| 118 | 64.99 | 1.06 | 0.10 | 12.08 | 19.58 | 15.11 | 215.04 | 2.20 | 0.92 | 2.78 | 23.41 | 56.37 | 3.42 | 0.37 | 8.22 |
| 119 | 65.57 | 1.06 | 0.10 | 12.08 | 19.58 | 14.15 | 215.01 | 2.20 | 0.92 | 2.78 | 23.41 | 56.37 | 3.42 | 0.31 | 8.45 |
| 120 | 58.32 | 1.28 | 0.10 | 16.87 | 22.16 | 14.32 | 215.03 | 1.63 | 0.75 | 2.78 | 22.96 | 55.93 | 2.11 | 0.30 | 8.63 |
| 121 | 65.57 | 1.06 | 0.10 | 11.21 | 20.44 | 14.90 | 215.05 | 2.16 | 0.92 | 2.57 | 22.30 | 57.01 | 1.91 | 0.37 | 8.68 |
| 122 | 54.12 | 1.43 | 0.12 | 19.81 | 23.33 | 13.75 | 213.38 | 1.28 | 0.60 | 2.43 | 22.38 | 56.49 | 1.96 | 0.25 | 6.94 |
| 123 | 49.72 | 1.13 | 0.17 | 22.94 | 23.77 | 14.02 | 213.05 | 1.12 | 0.42 | 2.24 | 24.75 | 55.12 | 1.96 | 0.26 | 6.53 |
| 124 | 54.64 | 1.37 | 0.20 | 19.04 | 22.88 | 14.10 | 215.11 | 1.31 | 0.46 | 2.32 | 23.26 | 55.36 | 1.85 | 0.27 | 8.54 |
| 125 | 59.72 | 1.08 | 0.10 | 16.17 | 22.04 | 14.85 | 215.13 | 1.71 | 0.78 | 2.40 | 22.56 | 56.26 | 1.78 | 0.37 | 8.61 |
| Matte Composition, wt.% | ||||||||
| Statistics | [Cu] | [Pb] | [Zn] | [Fe] | [S] | [Au] * | [Ag] * | |
| Average | 57.46 | 1.20 | 0.15 | 17.42 | 22.23 | 14.30 | 214.02 | |
| Maximum | 65.57 | 1.53 | 0.28 | 22.94 | 23.77 | 15.16 | 215.13 | |
| Minimum | 49.72 | 0.73 | 0.10 | 11.21 | 19.58 | 13.53 | 213.05 | |
| Standard Deviation | 4.41 | 0.18 | 0.05 | 3.23 | 1.22 | 0.48 | 0.64 | |
| Slag composition, wt.% | ||||||||
| Statistics | Cu | Pb | ZnO | SiO2 | FeO | CaO | Au * | Ag * |
| Average | 1.58 | 0.67 | 2.49 | 23.23 | 56.06 | 2.10 | 0.30 | 7.44 |
| Maximum | 2.24 | 0.92 | 2.78 | 24.75 | 57.48 | 3.42 | 0.37 | 8.69 |
| Minimum | 1.12 | 0.42 | 2.21 | 22.26 | 54.78 | 1.73 | 0.24 | 6.22 |
| Standard Deviation | 0.33 | 0.15 | 0.18 | 0.56 | 0.74 | 0.49 | 0.04 | 0.69 |
| # | Composition of Matte, wt.% | Composition of Slag, wt.% | LMe | dmech | ddis | Cudis, wt.% | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [Cu] | [Au] * | [Ag] * | (Cu)total | (Au) * | (Ag) * | LCu | LAu | LAg | ||||
| 1 | 59.71 | 14.59 | 214.22 | 1.73 | 0.31 | 7.21 | 34.51 | 47.06 | 4.27 | 0.73 | 0.27 | 0.47 |
| 2 | 61.42 | 14.75 | 214.72 | 1.93 | 0.37 | 7.31 | 31.82 | 39.86 | 4.10 | 0.80 | 0.20 | 0.38 |
| 3 | 65.57 | 15.21 | 215.13 | 2.15 | 0.35 | 8.54 | 30.50 | 43.46 | 4.17 | 0.70 | 0.30 | 0.65 |
| 4 | 58.91 | 14.37 | 214.17 | 1.68 | 0.29 | 7.76 | 35.07 | 49.04 | 4.30 | 0.71 | 0.29 | 0.49 |
| 5 | 57.28 | 14.22 | 213.54 | 1.58 | 0.28 | 6.60 | 36.25 | 50.60 | 4.39 | 0.72 | 0.28 | 0.44 |
| 6 | 61.74 | 14.88 | 214.21 | 1.98 | 0.32 | 8.11 | 31.18 | 46.50 | 4.27 | 0.67 | 0.33 | 0.65 |
| 7 | 54.71 | 13.95 | 213.54 | 1.32 | 0.25 | 7.54 | 41.45 | 56.25 | 4.49 | 0.74 | 0.26 | 0.34 |
| 8 | 49.72 | 13.55 | 213.05 | 1.12 | 0.24 | 6.53 | 44.39 | 56.22 | 4.58 | 0.79 | 0.21 | 0.24 |
| 9 | 50.53 | 13.68 | 213.11 | 1.20 | 0.25 | 7.43 | 42.11 | 54.35 | 4.40 | 0.77 | 0.23 | 0.28 |
| 10 | 52.1 | 13.88 | 213.16 | 1.24 | 0.28 | 7.23 | 42.02 | 50.44 | 4.42 | 0.83 | 0.17 | 0.21 |
| 11 | 57.17 | 14.28 | 213.80 | 1.57 | 0.29 | 7.66 | 36.41 | 49.04 | 4.31 | 0.74 | 0.26 | 0.41 |
| 12 | 50.78 | 13.75 | 213.10 | 1.17 | 0.25 | 6.22 | 43.40 | 54.95 | 4.51 | 0.79 | 0.21 | 0.25 |
| 13 | 57.81 | 14.33 | 214.00 | 1.62 | 0.28 | 7.06 | 35.69 | 51.05 | 4.36 | 0.70 | 0.30 | 0.49 |
| 14 | 55.97 | 13.87 | 213.34 | 1.42 | 0.28 | 7.50 | 39.42 | 50.02 | 4.49 | 0.79 | 0.21 | 0.3 |
| 15 | 54.12 | 13.75 | 213.38 | 1.28 | 0.25 | 6.94 | 42.28 | 54.95 | 4.55 | 0.77 | 0.23 | 0.29 |
| 16 | 54.55 | 13.79 | 213.33 | 1.39 | 0.27 | 7.33 | 39.24 | 51.19 | 4.51 | 0.77 | 0.23 | 0.32 |
| 17 | 59.43 | 14.67 | 214.24 | 1.74 | 0.31 | 8.69 | 34.16 | 47.17 | 4.23 | 0.72 | 0.28 | 0.49 |
| 18 | 52.72 | 13.89 | 213.34 | 1.20 | 0.25 | 6.25 | 43.93 | 56.16 | 4.42 | 0.78 | 0.22 | 0.26 |
| 19 | 55.9 | 13.99 | 213.57 | 1.56 | 0.29 | 7.58 | 35.83 | 48.58 | 4.31 | 0.74 | 0.26 | 0.41 |
| 20 | 62.87 | 15.01 | 214.87 | 2.06 | 0.36 | 8.10 | 30.52 | 41.24 | 4.12 | 0.74 | 0.26 | 0.54 |
| 21 | 64.99 | 15.11 | 215.04 | 2.20 | 0.37 | 8.22 | 29.54 | 41.40 | 4.04 | 0.71 | 0.29 | 0.64 |
| 22 | 57.05 | 14.20 | 213.19 | 1.49 | 0.28 | 7.09 | 38.29 | 50.71 | 4.26 | 0.75 | 0.25 | 0.37 |
| # | LCu | LAu | LAg | dmech | ddis |
|---|---|---|---|---|---|
| 1 | 34.51 ± 1.55 | 47.06 ± 1.03 | 4.27 ± 0.09 | 0.73 ± 0.03 | 0.27 ± 0.02 |
| 2 | 31.82 ± 1.43 | 39.86 ± 0.88 | 4.10 ± 0.09 | 0.80 ± 0.04 | 0.20 ± 0.02 |
| 3 | 30.50 ± 1.37 | 43.46 ± 0.96 | 4.17 ± 0.09 | 0.70 ± 0.03 | 0.30 ± 0.02 |
| 4 | 35.07 ± 1.58 | 49.04 ± 1.08 | 4.30 ± 0.09 | 0.71 ± 0.04 | 0.29 ± 0.02 |
| 5 | 36.25 ± 1.63 | 50.60 ± 1.11 | 4.39 ± 0.10 | 0.72 ± 0.04 | 0.28 ± 0.02 |
| 6 | 31.18 ± 1.40 | 46.50 ± 1.02 | 4.27 ± 0.09 | 0.67 ± 0.03 | 0.33 ± 0.02 |
| 7 | 41.45 ± 1.87 | 56.25 ± 1.24 | 4.49 ± 0.10 | 0.74 ± 0.04 | 0.26 ± 0.02 |
| 8 | 44.39 ± 2.00 | 56.22 ± 1.24 | 4.58 ± 0.10 | 0.79 ± 0.04 | 0.21 ± 0.02 |
| 9 | 42.11 ± 1.89 | 54.35 ± 1.19 | 4.40 ± 0.10 | 0.77 ± 0.04 | 0.23 ± 0.02 |
| 10 | 42.02 ± 1.89 | 50.44 ± 1.11 | 4.42 ± 0.10 | 0.83 ± 0.04 | 0.17 ± 0.01 |
| 11 | 36.41 ± 1.64 | 49.04 ± 1.08 | 4.31 ± 0.09 | 0.74 ± 0.04 | 0.26 ± 0.02 |
| 12 | 43.40 ± 1.95 | 54.95 ± 1.21 | 4.51 ± 0.10 | 0.79 ± 0.04 | 0.21 ± 0.02 |
| 13 | 35.69 ± 1.61 | 51.05 ± 1.12 | 4.36 ± 0.10 | 0.70 ± 0.04 | 0.30 ± 0.02 |
| 14 | 39.42 ± 1.77 | 50.02 ± 1.10 | 4.49 ± 0.10 | 0.79 ± 0.04 | 0.21 ± 0.02 |
| 15 | 42.28 ± 1.90 | 54.95 ± 1.21 | 4.55 ± 0.10 | 0.77 ± 0.04 | 0.23 ± 0.02 |
| 16 | 39.24 ± 1.77 | 51.19 ± 1.13 | 4.51 ± 0.10 | 0.77 ± 0.04 | 0.23 ± 0.02 |
| 17 | 34.16 ± 1.54 | 47.17 ± 1.04 | 4.23 ± 0.09 | 0.72 ± 0.04 | 0.28 ± 0.02 |
| 18 | 43.93 ± 1.98 | 56.16 ± 1.24 | 4.42 ± 0.10 | 0.78 ± 0.04 | 0.22 ± 0.02 |
| 19 | 35.83 ± 1.61 | 48.58 ± 1.07 | 4.31 ± 0.09 | 0.74 ± 0.04 | 0.26 ± 0.02 |
| 20 | 30.52 ± 1.37 | 41.24 ± 0.91 | 4.12 ± 0.09 | 0.74 ± 0.04 | 0.26 ± 0.02 |
| 21 | 29.54 ± 1.33 | 41.40 ± 0.91 | 4.04 ± 0.09 | 0.71 ± 0.04 | 0.29 ± 0.02 |
| 22 | 38.29 ± 1.72 | 50.71 ± 1.12 | 4.26 ± 0.09 | 0.75 ± 0.04 | 0.25 ± 0.02 |
| Values | Au | Ag |
|---|---|---|
| MAE | 1.776 | 1.232 |
| RMSE | 2.114 | 1.354 |
| R2 | 0.844 | 0.783 |
| Fold | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| R2 | 0.842 | 0.792 | 0.866 | 0.784 | 0.845 |
| Fold | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| R2 | 0.805 | 0.807 | 0.794 | 0.796 | 0.824 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dosmukhamedov, N.; Shambulayev, B.; Dityatovskiy, L.; Zholdasbay, Y.; Argyn, A. Determination of Quantitative Ratios (Mechanical and Dissolved) of Copper, Gold and Silver Losses in Vanyukov Furnace Slags Under the Conditions of the Balkhash Copper Smelter in Kazakhstan. Recycling 2025, 10, 181. https://doi.org/10.3390/recycling10050181
Dosmukhamedov N, Shambulayev B, Dityatovskiy L, Zholdasbay Y, Argyn A. Determination of Quantitative Ratios (Mechanical and Dissolved) of Copper, Gold and Silver Losses in Vanyukov Furnace Slags Under the Conditions of the Balkhash Copper Smelter in Kazakhstan. Recycling. 2025; 10(5):181. https://doi.org/10.3390/recycling10050181
Chicago/Turabian StyleDosmukhamedov, Nurlan, Bakhtiyar Shambulayev, Leonid Dityatovskiy, Yerzhan Zholdasbay, and Aidar Argyn. 2025. "Determination of Quantitative Ratios (Mechanical and Dissolved) of Copper, Gold and Silver Losses in Vanyukov Furnace Slags Under the Conditions of the Balkhash Copper Smelter in Kazakhstan" Recycling 10, no. 5: 181. https://doi.org/10.3390/recycling10050181
APA StyleDosmukhamedov, N., Shambulayev, B., Dityatovskiy, L., Zholdasbay, Y., & Argyn, A. (2025). Determination of Quantitative Ratios (Mechanical and Dissolved) of Copper, Gold and Silver Losses in Vanyukov Furnace Slags Under the Conditions of the Balkhash Copper Smelter in Kazakhstan. Recycling, 10(5), 181. https://doi.org/10.3390/recycling10050181





