Environmental Performance Assessment of a Decentralized Network of Recyclable Waste Sorting Facilities: Case Study in Montreal
Abstract
1. Introduction
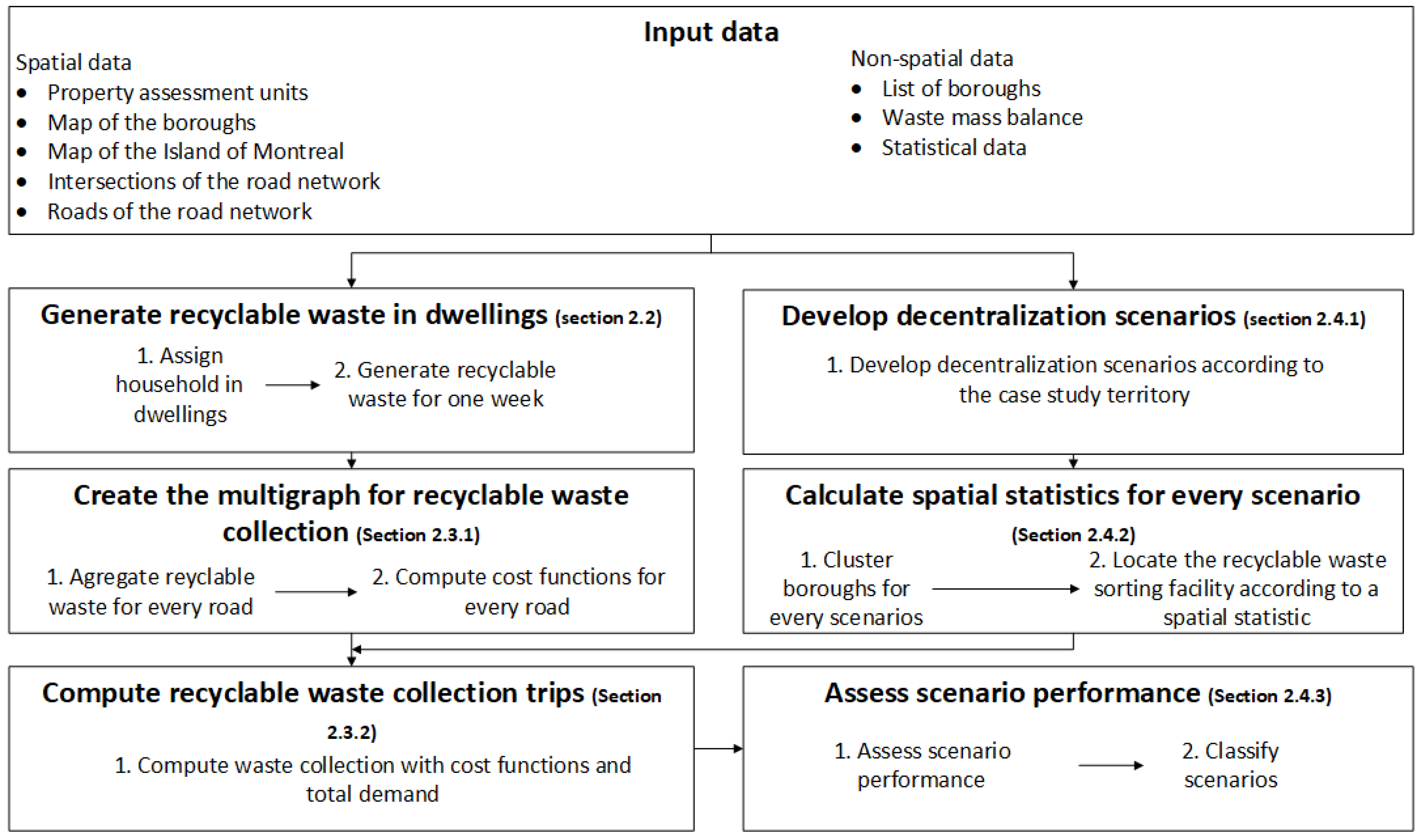
2. Materials and Methods
2.1. Case Study
2.2. Waste Generation Model
| Algorithm 1. Household assignment to buildings | ||||
| Procedure PopulationAssignment () For reach | ||||
| For | ||||
| While | ||||
| If | ||||
- : recyclable waste generation rate of one building (kg/week);
- : recyclable waste generation rate for one person in a given borough (kg/capita/year);
- : number of residents in a building.
- : mass of recycling waste for a building for a given week (kg);
- : monthly coefficient.
2.3. Waste Collection Model
2.3.1. Construction of the Road Network Multigraph
- : average time between two stops (s);
- : number of stops;
- : number of buildings on the edge (s);
- : walking time from the truck to the building (s).
- : average distance between stops (m);
- : maximum achievable speed by a truck between two stops (km/h);
- : speed coefficient;
- : unit conversion coefficient from km/h to m/s.
- : walking distance (m);
- : number of dwellings inside the building.
2.3.2. Algorithmic Application of Waste Collection
2.4. Performance Assessment of Recyclable Waste Sorting Facility Decentralization Scenarios
2.4.1. Decentralization Scenarios
2.4.2. Location of Recyclable Waste Sorting Facilities
- : degree matrix of the graph;
- : adjacency matrix of the graph.
2.4.3. Scenario Assessment
- : hourly cost of trucks (CAD/hour);
- : time the truck is on the road (h);
- : fuel consumed on the road (L);
- : fuel cost (CAD/L).
- : molar mass (g/mol);
- : emission for a road (g);
- : density of diesel (kg/L).
- : roads inside a trip (deadheading and collection);
- : hot emissions emitted during the trip (g);
- : cold emissions emitted at the start of a trip (g).
- : hot emission factor for a pollutant (g/km);
- : length of the road (km).
- , , , , , , , , , , , and : constants for a pollutant;
- : speed of the truck on the road (km/h);
- : relative load of the truck on the road.
- : costs for the scenario (CAD);
- : the costs of the baseline scenario (CAD);
- : CO2 emissions for the baseline scenario (kg);
- : CO2 emissions for the scenario (kg).
3. Results
3.1. Spatialized Recyclable Waste Generation
3.2. Recyclable Waste Collection Simulation
3.2.1. Road Network Multigraph
3.2.2. Waste Collection Trips
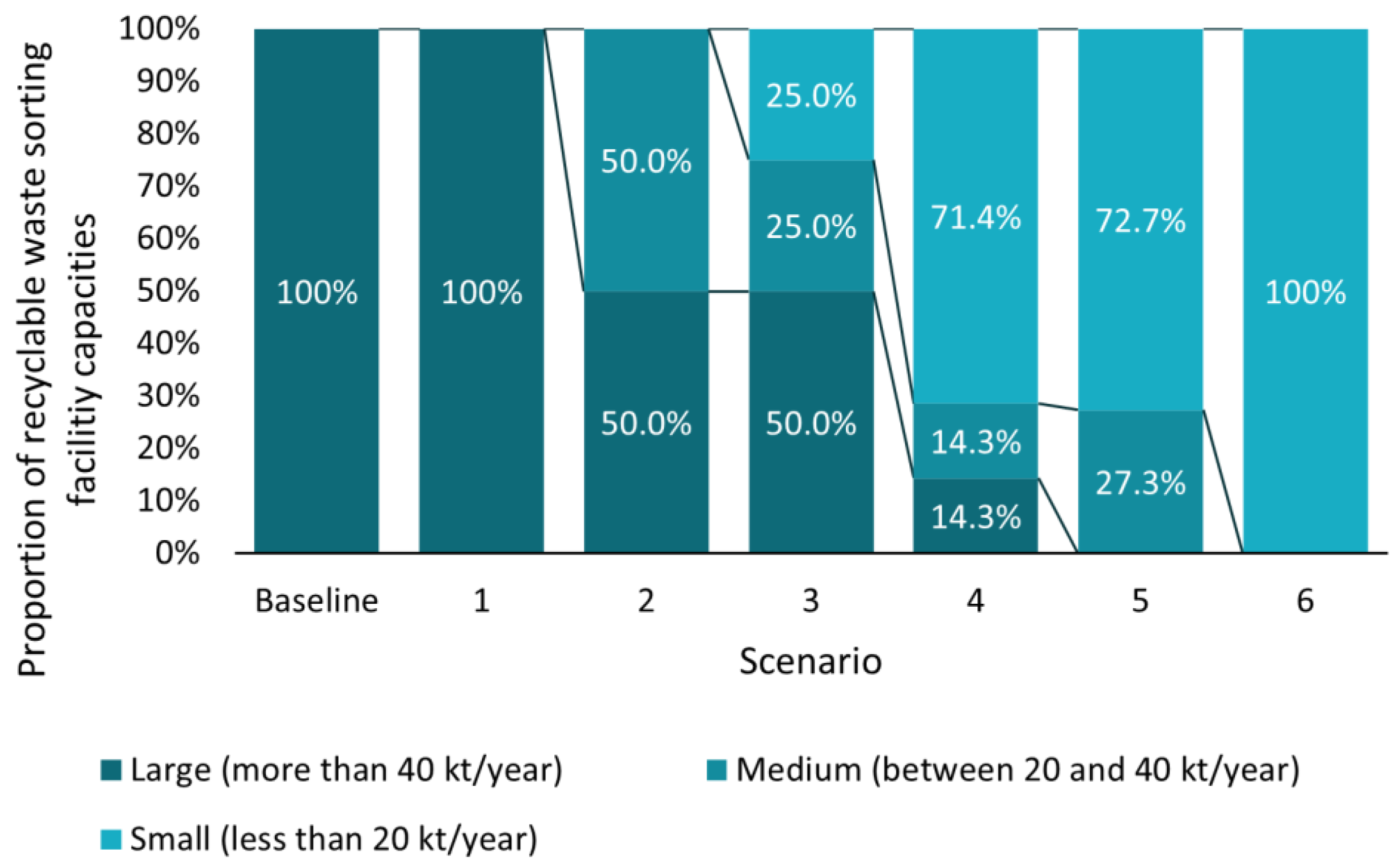
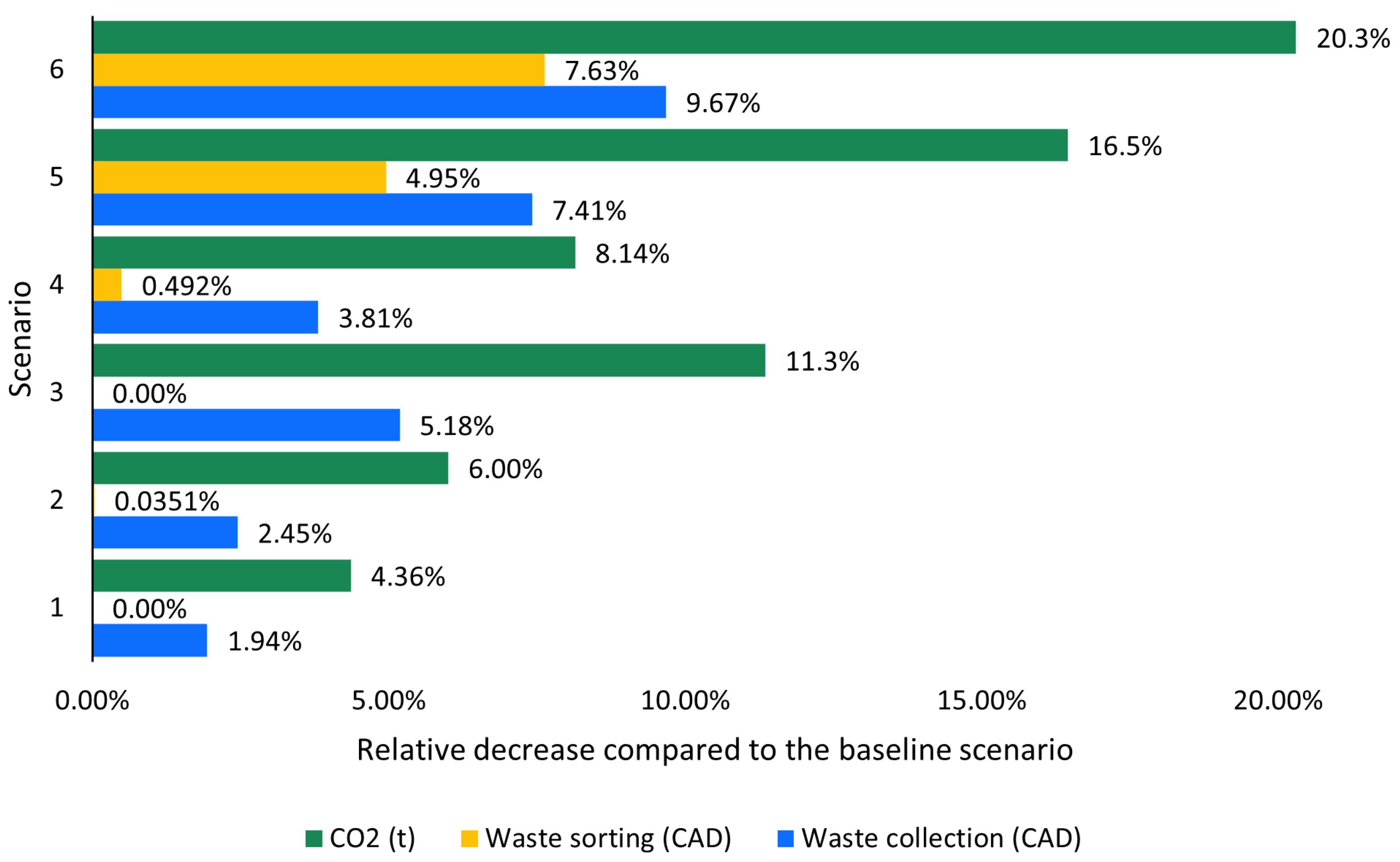
3.3. Decentralization Performance Assessment
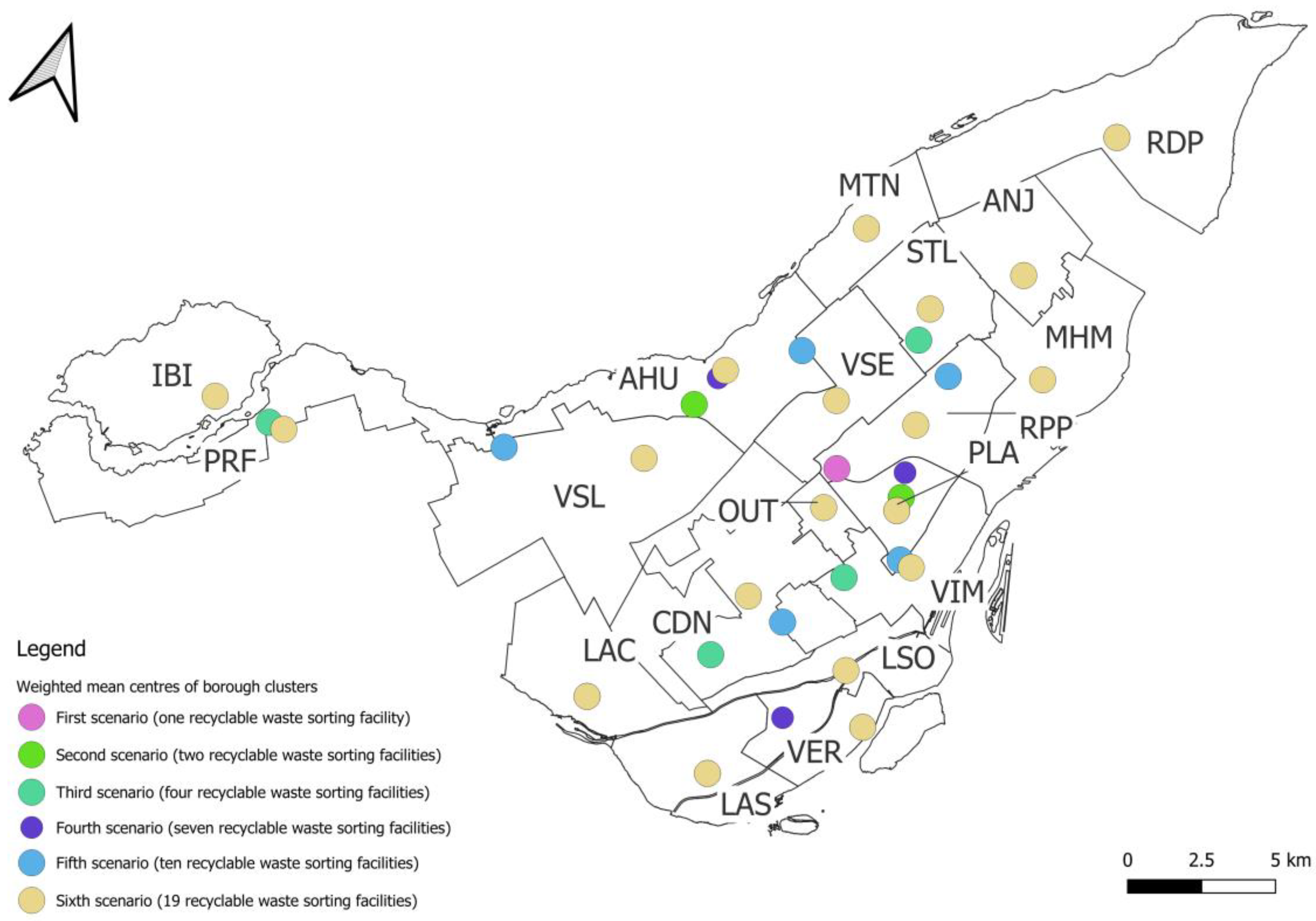
3.3.1. Location of Recyclable Waste Sorting Facilities
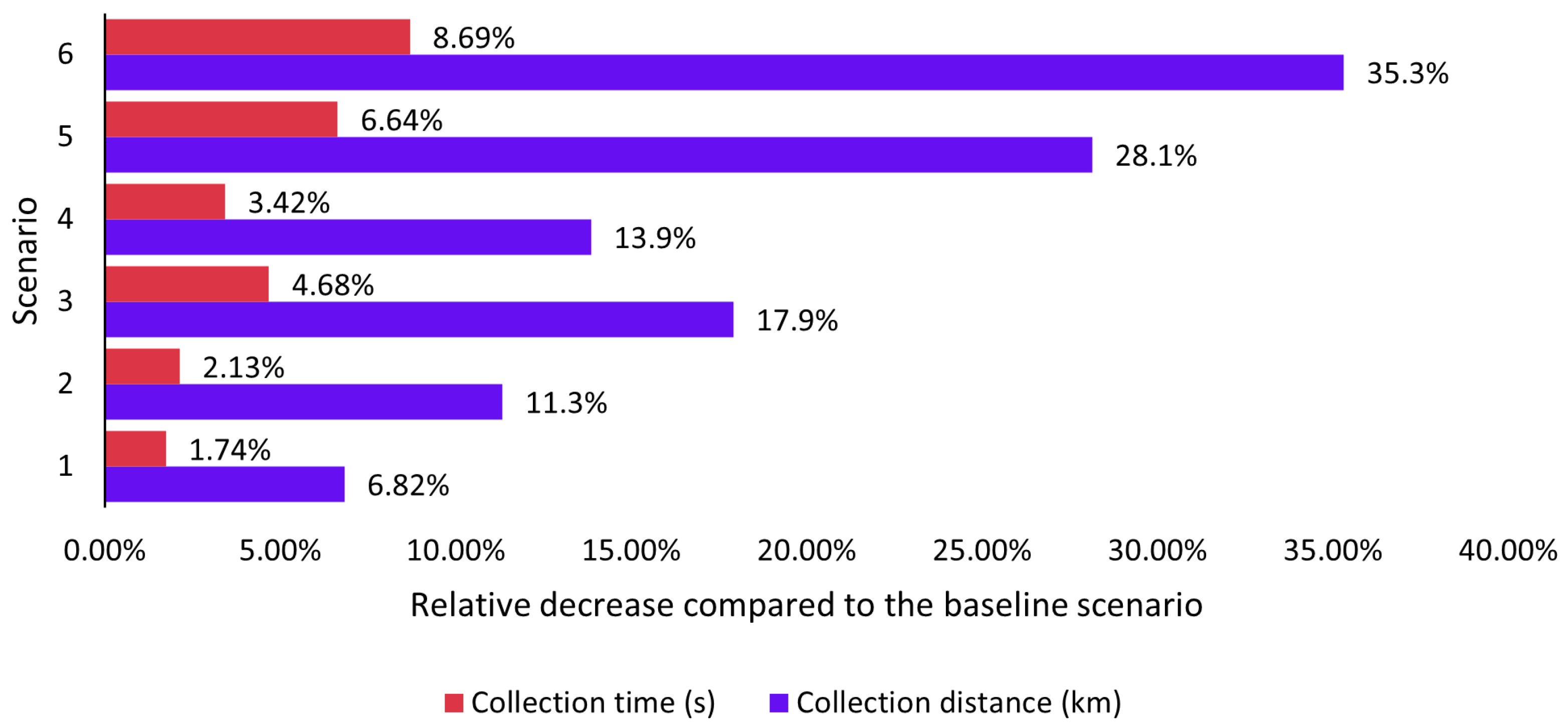
3.3.2. Decentralization Scenario Performance
4. Discussion
4.1. Overview of the Decentralization Approach
4.2. Operationalization of Decentralization Approach
4.3. Modelling Perspectives
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Heuristic Adaptations to the Waste Collection Model
| Algorithm A1. Split procedure, adapted from [51] | ||||
| Function Split | ||||
| For | ||||
| While | ||||
| If | ||||
| Else | ||||
| Else | ||||
| While | ||||
| Inverse | ||||
| For | ||||
| If | ||||
| , | ||||
| Return | ||||
References
- RECYC-QUÉBEC Lexique. Available online: https://www.recyc-quebec.gouv.qc.ca/haut-de-page/lexique (accessed on 28 October 2020).
- RECYC-QUÉBEC Bilan 2021 de la Gestion des Matières Résiduelles au Québec. 2023. Available online: https://www.recyc-quebec.gouv.qc.ca/actualite/recyc-quebec-diffuse-les-resultats-du-bilan-2021-de-la-gestion-des-matieres-residuelles-au-quebec-bilan-gmr/ (accessed on 27 November 2023).
- ADEME; Devauze, C.; Koite, A.; Chretien, A.; Monier, V. Bilan National du Recyclage 2010–2019—Évolutions du Recyclage en France de Différents Matériaux: Métaux Ferreux et non Ferreux, Papiers-Cartons, Verre, Plastiques, Inertes du BTP et Bois. 2022. Available online: https://librairie.ademe.fr/dechets-economie-circulaire/5233-bilan-national-du-recyclage-bnr-2010-2019.html#/44-type_de_produit-format_electronique (accessed on 11 March 2022).
- Kuznetsova, E.; Cardin, M.-A.; Diao, M.; Zhang, S. Integrated Decision-Support Methodology for Combined Centralized-Decentralized Waste-to-Energy Management Systems Design. Renew. Sustain. Energy Rev. 2019, 103, 477–500. [Google Scholar] [CrossRef]
- Weitz, K.A.; Thorneloe, S.A.; Nishtala, S.R.; Yarkosky, S.; Zannes, M. The Impact of Municipal Solid Waste Management on Greenhouse Gas Emissions in the United States. J. Air Waste Manag. Assoc. 2002, 52, 1000–1011. [Google Scholar] [CrossRef] [PubMed]
- Bureau D’audiences Publiques sur L’environnement Déchets D’hier, Ressources de Demain; Québec, 1997. Available online: https://www.bape.gouv.qc.ca/fr/dossiers/dechets-hier-ressources-demain/ (accessed on 9 September 2021).
- Madden, B.; Florin, N.; Mohr, S.; Giurco, D. Spatial Modelling of Municipal Waste Generation: Deriving Property Lot Estimates with Limited Data. Resour. Conserv. Recycl. 2021, 168, 105442. [Google Scholar] [CrossRef]
- Bocken, N.M.P.; de Pauw, I.; Bakker, C.; van der Grinten, B. Product Design and Business Model Strategies for a Circular Economy. J. Ind. Prod. Eng. 2016, 33, 308–320. [Google Scholar] [CrossRef]
- United Nations Sustainable Development Sustainable Consumption and Production. Available online: https://www.un.org/sustainabledevelopment/sustainable-consumption-production/ (accessed on 13 March 2025).
- Hoornweg, D.; Bhada-Tata, P. What a Waste: A Global Review of Solid Waste Management; World Bank: Washington, DC, USA, 2012. [Google Scholar]
- Kaza, S.; Yao, L.C.; Bhada-Tata, P.; Van Woerden, F. What a Waste 2.0: A Global Snapshot of Solid Waste Management to 2050; World Bank: Washington, DC, USA, 2018; ISBN 978-1-4648-1329-0. [Google Scholar]
- Ma, Y.; Zhang, W.; Feng, C.; Lev, B.; Li, Z. A Bi-Level Multi-Objective Location-Routing Model for Municipal Waste Management with Obnoxious Effects. Waste Manag. 2021, 135, 109–121. [Google Scholar] [CrossRef]
- United Nations Environment Programme. Global Waste Management Outlook 2024: Beyond an Age of Waste—Turning Rubbish into a Resource; United Nations Environment Programme: Nairobi, Kenya, 2024. [Google Scholar]
- Eurostat Municipal Waste Statistics. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Municipal_waste_statistics (accessed on 11 March 2025).
- Duzgun, H.S.; Uskay, S.O.; Aksoy, A. Parallel Hybrid Genetic Algorithm and GIS-Based Optimization for Municipal Solid Waste Collection Routing. J. Comput. Civ. Eng. 2016, 30, 04015037. [Google Scholar] [CrossRef]
- Lou, X.F.; Nair, J. The Impact of Landfilling and Composting on Greenhouse Gas Emissions—A Review. Bioresour. Technol. 2009, 100, 3792–3798. [Google Scholar] [CrossRef]
- Tanguy, A.; Villot, J.; Glaus, M.; Laforest, V.; Hausler, R. Service Area Size Assessment for Evaluating the Spatial Scale of Solid Waste Recovery Chains: A Territorial Perspective. Waste Manag. 2017, 64, 386–396. [Google Scholar] [CrossRef]
- Strange, K. Overview of Waste Management Options: Their Efficacy and Acceptability Page. In Environmental and Health Impact of Solid Waste Management Activities; Royal Society of Chemistry (RSC): London, UK, 2002; pp. 1–51. ISBN 978-0-85404-285-2. [Google Scholar]
- Ministère des Affaires Municipales et de l’Habitation Rapport Du Ministère Des Affaires Municipales et de L’habitation Présenté à La Commission d’enquête Sur l’état Des Lieux et La Gestion Des Résidus Ultimes. 2021. Available online: https://voute.bape.gouv.qc.ca/dl/?id=00000235537 (accessed on 5 October 2021).
- Aziz, H.A.; Abu Amr, S.S. Introduction to Solid Waste and Its Management. In Waste Management—Concepts, Methodologies, Tools, and Applications; Information Resources Management Association, Ed.; IGI Global: Hershey, PA, USA, 2020; pp. 1–24. ISBN 978-1-79981-210-4. [Google Scholar]
- Environment and Climate Change Canada National Inventory Report 1990–2022: Greenhouse Gas Sources and Sinks in Canada. 2024. Available online: https://www.canada.ca/en/environment-climate-change/services/climate-change/greenhouse-gas-emissions/inventory.html (accessed on 12 March 2025).
- Ministère de l’Environnement, de la Lutte Contre les Changements Climatiques, de la Faune et des Parcs Inventaire Québécois des Émissions de Gaz à Effet de Serre en 2021 et Leur Évolution Depuis 1990. 2023. Available online: https://www.environnement.gouv.qc.ca/changements/ges/2021/inventaire-ges-1990-2021.pdf (accessed on 12 March 2025).
- Smith, A.; Brown, K.; Ogilvie, S.; Rushton, K.; Bates, J. Waste Management Options and Climate Change. 2011. Available online: https://ec.europa.eu/environment/pdf/waste/studies/climate_change.pdf (accessed on 17 January 2025).
- Gouvernement du Québec Loi sur la Qualité de L’environnement. 2021. Available online: http://legisquebec.gouv.qc.ca/fr/ShowDoc/cs/Q-2 (accessed on 11 August 2021).
- RECYC-QUÉBEC Bilan 2018 de la Gestion des Matières Résiduelles au Québec. 2020. Available online: https://www.recyc-quebec.gouv.qc.ca/sites/default/files/documents/bilan-gmr-2018-complet.pdf (accessed on 11 March 2022).
- Éco Entreprises Québec; RECYC-QUÉBEC Caractérisation des Matières Sortantes des Centres de Tri. 2020. Available online: https://www.recyc-quebec.gouv.qc.ca/sites/default/files/documents/caracterisation-matieres-sortantes-centres-de-tri-2018-2020.pdf (accessed on 28 March 2025).
- Ville de Montréal Complexe Environnemental de Saint-Michel. Available online: https://montreal.ca/lieux/complexe-environnemental-de-saint-michel (accessed on 21 March 2022).
- Montréal en Statistiques Annuaire Statistique de l’Agglomération de Montréal—2021. Available online: https://ville.montreal.qc.ca/portal/page?_pageid=6897,68149701&_dad=portal&_schema=PORTAL (accessed on 11 January 2023).
- Sytcom Centres de Tri. Available online: https://www.syctom-paris.fr/les-installations/centres-de-tri.html (accessed on 11 March 2025).
- Institut National de la Statistique et des Études Économiques Population Estimates—All—Ville de Paris 2024. Available online: https://www.insee.fr/en/statistiques/serie/001760155 (accessed on 11 March 2025).
- Höke, M.C.; Yalcinkaya, S. Municipal Solid Waste Transfer Station Planning through Vehicle Routing Problem-Based Scenario Analysis. Waste Manag. Res. 2021, 39, 185–196. [Google Scholar] [CrossRef]
- Tanguy, A.; Glaus, M.; Laforest, V.; Villot, J.; Hausler, R. A Spatial Analysis of Hierarchical Waste Transport Structures under Growing Demand. Waste Manag. Res. 2016, 34, 1064–1073. [Google Scholar] [CrossRef]
- Kosai, S.; Kurogi, D.; Kozaki, K.; Yamasue, E. Distributed Recycling System with Microwave-Based Heating for Obsolete Alkaline Batteries. Resour. Environ. Sustain. 2022, 9, 100071. [Google Scholar] [CrossRef]
- Rallo, H.; Sánchez, A.; Canals, L.; Amante, B. Battery Dismantling Centre in Europe: A Centralized vs Decentralized Analysis. Resour. Conserv. Recycl. Adv. 2022, 15, 200087. [Google Scholar] [CrossRef]
- Abed Al Ahad, M.; Chalak, A.; Fares, S.; Mardigian, P.; Habib, R.R. Decentralization of Solid Waste Management Services in Rural Lebanon: Barriers and Opportunities. Waste Manag. Res. 2020, 38, 639–648. [Google Scholar] [CrossRef] [PubMed]
- de Souza, L.C.G.; Drumond, M.A. Decentralized Composting as a Waste Management Tool Connect with the New Global Trends: A Systematic Review. Int. J. Environ. Sci. Technol. 2022, 19, 12679–12700. [Google Scholar] [CrossRef]
- Python 3.9; Python Software Foundation: Wilmington, DE, USA, 2019; Available online: https://www.python.org/ (accessed on 15 August 2022).
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Jordahl, K.; den Bossche, J.V.; Fleischmann, M.; McBride, J.; Wasserman, J.; Richards, M.; Badaracco, A.G.; Gerard, J.; Snow, A.D.; Tratner, J.; et al. Geopandas v0.11.1. 2022. Available online: https://zenodo.org/record/6894736 (accessed on 9 September 2022).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- QGIS 3.20.1; QGIS Development Team: Laax, Switzerland, 2021; Available online: https://qgis.org (accessed on 16 April 2021).
- Arrondissement de la Ville de Montréal—Liste. Ville de Montréalé. 2013. Available online: https://donnees.montreal.ca/ville-de-montreal/arros-liste (accessed on 19 February 2021).
- Lavergne, Inc. Contactez-Nous. Available online: https://lavergne.ca/fr/ (accessed on 20 June 2022).
- Loubert, A. Évaluation de l’Effet de la Spatialité sur la Performance Environnementale du Recyclage des Bouteilles de PET. Master’s Thesis, École de Technologie Supérieure, Montreal, QC, Canada, 2022. [Google Scholar]
- Limites Administratives de l’Agglomération de Montréal (Arrondissements et Villes Liées). Ville de Montréal. 2022. Available online: https://donnees.montreal.ca/dataset/limites-administratives-agglomeration (accessed on 21 May 2023).
- Unités d’Évaluation Foncière. Ville de Montréal. 2017. Available online: https://donnees.montreal.ca/ville-de-montreal/unites-evaluation-fonciere (accessed on 28 October 2020).
- Matières Résiduelles—Bilan Massique. Ville de Montréal. 2013. Available online: https://donnees.montreal.ca/ville-de-montreal/matieres-residuelles-bilan-massique (accessed on 28 October 2020).
- Géobase—Nœuds. Ville de Montréal. 2019. Available online: https://donnees.montreal.ca/ville-de-montreal/geobase-noeud (accessed on 12 August 2021).
- Géobase—Réseau Routier. Ville de Montréal. 2013. Available online: https://donnees.montreal.ca/ville-de-montreal/geobase (accessed on 31 March 2021).
- Rhyner, C.R. Monthly Variations in Solid Generation. Waste Manag. Res. 1992, 10, 67–71. [Google Scholar] [CrossRef]
- Lacomme, P.; Prins, C.; Ramdane-Cherif, W. Competitive Memetic Algorithms for Arc Routing Problems. Ann. Oper. Res. 2004, 131, 159–185. [Google Scholar] [CrossRef]
- Rahman, M.S. (Ed.) Basic Graph Terminologies. In Basic Graph Theory; Undergraduate Topics in Computer Science; Springer International Publishing: Cham, Switzerland, 2017; pp. 11–29. ISBN 978-3-319-49475-3. [Google Scholar]
- Cormen, T.H. Introduction to Algorithms, 3rd ed.; MIT Press: Cambridge, MA, USA, 2009; ISBN 978-0-262-27083-0. [Google Scholar]
- Laguna, M.; Martí, R. Heuristics. In Encyclopedia of Operations Research and Management Science; Gass, S.I., Fu, M.C., Eds.; Springer: Boston, MA, USA, 2013; pp. 695–703. ISBN 978-1-4419-1153-7. [Google Scholar]
- Everett, J.W.; Maratha, S.; Dorairaj, R.; Riley, P. Curbside Collection of Recyclables I: Route Time Estimation Model. Resour. Conserv. Recycl. 1998, 22, 177–192. [Google Scholar] [CrossRef]
- Ville de Montréal Chartre du Piéton—Document de Consultation; Ville de Montréal, 2006. Available online: https://ville.montreal.qc.ca/portal/page?_pageid=6877,63217598&_dad=portal&_schema=PORTAL (accessed on 26 March 2025).
- Belenguer, J.M.; Benavent, E. The Capacitated Arc Routing Problem 2003. Available online: https://www.uv.es/belengue/carp.html (accessed on 16 February 2022).
- Strang, G. 35. Finding Clusters in Graphs. Available online: https://www.youtube.com/watch?v=cxTmmasBiC8 (accessed on 20 July 2022).
- Liu, J.; Han, J. Spectral Clustering. In Data Clustering; Chapman and Hall/CRC: Boca Raton, FL, USA, 2014; ISBN 978-1-315-37351-5. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. K-Means++: The Advantages of Careful Seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; pp. 1027–1035. [Google Scholar]
- Aloise, D.; Deshpande, A.; Hansen, P.; Popat, P. NP-Hardness of Euclidean Sum-of-Squares Clustering. Mach. Learn. 2009, 75, 245–248. [Google Scholar] [CrossRef]
- Aggarwal, C.C. An Introduction to Cluster Analysis. In Data Clustering; Chapman and Hall/CRC: Boca Raton, FL, USA, 2014; ISBN 978-1-315-37351-5. [Google Scholar]
- ESRI Esri Support GIS Dictionary. Available online: https://support.esri.com/en/other-resources/gis-dictionary/term/5d54a903-1839-4687-bb77-92441e72a209 (accessed on 12 August 2022).
- Cheniti, H.; Cheniti, M.; Brahamia, K. Use of GIS and Moran’s I to Support Residential Solid Waste Recycling in the City of Annaba, Algeria. Environ. Sci. Pollut. Res. 2021, 28, 34027–34041. [Google Scholar] [CrossRef]
- Langlois-Blouin, S.; Fontaine, C.I.; Boies, M.; Turgeon, N. Diagnostic des Centres de tri du Québec. 2021. Available online: https://www.recyc-quebec.gouv.qc.ca/sites/default/files/documents/rapport-cric-diagnostic-centres-de-tri.pdf (accessed on 11 August 2022).
- Zsigraiova, Z.; Semiao, V.; Beijoco, F. Operation Costs and Pollutant Emissions Reduction by Definition of New Collection Scheduling and Optimization of MSW Collection Routes Using GIS. The Case Study of Barreiro, Portugal. Waste Manag. 2013, 33, 793–806. [Google Scholar] [CrossRef]
- Yalcinkaya, S. A Spatial Modeling Approach for Siting, Sizing and Economic Assessment of Centralized Biogas Plants in Organic Waste Management. J. Clean. Prod. 2020, 255, 120040. [Google Scholar] [CrossRef]
- Éco Entreprises Québec. RECYC-QUÉBEC Allocation des coûts par Activité—Résultats 2016. 2016. Available online: https://www.recyc-quebec.gouv.qc.ca/sites/default/files/documents/allocation-couts-activite-2016.pdf (accessed on 11 August 2022).
- Transport Research Laboratory; Hickman, J.; Hassel, D.; Joumard, R.; Samaras, Z.; Sorenson, S. Methodology for Calculating Transport Emissions and Energy Consumption. 1999. Available online: https://trimis.ec.europa.eu/sites/default/files/project/documents/meet.pdf (accessed on 4 March 2022).
- Speight, J.G. 2—Production, Properties and Environmental Impact of Hydrocarbon Fuel Conversion. In Advances in Clean Hydrocarbon Fuel Processing; Khan, M.R., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Sawston, UK, 2011; pp. 54–82. ISBN 978-1-84569-727-3. [Google Scholar]
- Jaunich, M.K.; Levis, J.W.; DeCarolis, J.F.; Gaston, E.V.; Barlaz, M.A.; Bartelt-Hunt, S.L.; Jones, E.G.; Hauser, L.; Jaikumar, R. Characterization of Municipal Solid Waste Collection Operations. Resour. Conserv. Recycl. 2016, 114, 92–102. [Google Scholar] [CrossRef]
- Nguyen, T.T.T.; Wilson, B.G. Fuel Consumption Estimation for Kerbside Municipal Solid Waste (MSW) Collection Activities. Waste Manag. Res. 2010, 28, 289–297. [Google Scholar] [CrossRef]
- Franco González, J.; Gallardo Izquierdo, A.; Commans, F.; Carlos, M. Fuel-Efficient Driving in the Context of Urban Waste-Collection: A Spanish Case Study. J. Clean. Prod. 2021, 289, 125831. [Google Scholar] [CrossRef]
- Morency, C.; Verreault, H.; Demers, M. Identification of the Minimum Size of the Shared-Car Fleet Required to Satisfy Car-Driving Trips in Montreal. Transportation 2015, 42, 435–447. [Google Scholar] [CrossRef]
- Sun, S.; Ertz, M. Contribution of Bike-Sharing to Urban Resource Conservation: The Case of Free-Floating Bike-Sharing. J. Clean. Prod. 2021, 280, 124416. [Google Scholar] [CrossRef]
- Doré, G. De nouveaux lieux d’innovation en France à travers la mutualisation de services. Rev. Organ. Territ. 2021, 30, 141–157. [Google Scholar] [CrossRef]
- Office de la Consultation Publique de Montréal Centres de Traitement des Matières Organiques. Montréal, 2012. Available online: https://ocpm.qc.ca/fr/consultation-publique/traitement-matieres-organiques (accessed on 27 January 2023).
- Ville de Montréal Secteurs Info-Collectes 2013. Available online: https://donnees.montreal.ca/ville-de-montreal/info-collectes (accessed on 8 May 2021).
- Communauté Métropolitaine de Montréal Plan Métropolitain D’aménagement et de Développement. 2012. Available online: https://cmm.qc.ca/planification/plan-metropolitain-damenagement-et-de-developpement-pmad/ (accessed on 8 November 2022).
- Office de la Consultation Publique de Montréal Centre de Traitement des Matières Organiques—Secteur EST—RDP-PAT. Montréal, 2015. Available online: https://ocpm.qc.ca/fr/consultation-publique/implantation-dun-centre-compostage-dans-secteur-est (accessed on 27 January 2023).
- Xue, W.; Cao, K. Optimal Routing for Waste Collection: A Case Study in Singapore. Int. J. Geogr. Inf. Sci. 2016, 30, 554–572. [Google Scholar] [CrossRef]
- Éco Entreprises Québec; RECYC-QUÉBEC Caractérisation des Matières Résiduelles du Secteur Municipal 2015–2018. 2021. Available online: https://www.recyc-quebec.gouv.qc.ca/sites/default/files/documents/caracterisation-secteur-municipal-2015-2018.pdf (accessed on 6 July 2022).
- Dijkstra, E.W. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Jolliet, O.; Saadé, M.; Crettaz, P. Analyse du Cycle de Vie: Comprendre et Réaliser un Écobilan; EPFL Press: Lausanne, Switzerland, 2010; ISBN 978-2-88074-886-9. [Google Scholar]



| Dataset | References | Initial Input Data |
|---|---|---|
| Boroughs with geographic boundaries | [42,45] | Seven boroughs |
| Property assessment units | [46] | 79,500 property assessment units and 350,000 dwellings |
| Population statistical data | [28] | 645,000 inhabitants and 320,000 households |
| Waste mass balance | [47] | 83.6 kg/capita on average for the seven boroughs |
| Road network data | [48,49] | 28,400 roads totaling 1300 km |
| Scenario Number | Number of Recyclable Waste Sorting Facilities | Representation of Territory Division |
|---|---|---|
| 1 | 1 | One recyclable waste sorting facility for Montreal (19 boroughs) |
| 2 | 2 | One recyclable waste sorting facility per ten boroughs |
| 3 | 4 | One recyclable waste sorting facility per five boroughs |
| 4 | 7 | One recyclable waste sorting facility per three boroughs |
| 5 | 10 | One recyclable waste sorting facility per two boroughs |
| 6 | 19 | One recyclable waste facility per borough |
| Chemical Component | Molar Mass |
|---|---|
| CO2 | 28 |
| CO | 44 |
| PM | 12 |
| HC | 14 |
| Diesel | 14 |
| Pollutant | Cold Emission Factor |
|---|---|
| CO2 | 300 |
| CO | 6.00 |
| PM | 0.600 |
| HC | 2.00 |
| Pollutant | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CO2 | 765 | −7.04 | 0 | 6.32 × 10−4 | 8.83 × 103 | 0 | 0 | 1.27 | 0 | 0 | 0 | −0.483 |
| CO | 1.53 | 0 | 0 | 0 | 60.6 | 117 | 0 | 1.17 | 0 | 0 | 0 | −0.755 |
| PM | 0.184 | 0 | 0 | 1.72 × 10−7 | 15.2 | 0 | 0 | 1.24 | 0 | 0 | 0 | −1.06 |
| HC | 0.207 | 0 | 0 | 0 | 58.3 | 0 | 0 | 1.01 | 8.89 × 10−4 | 0 | −2.54 × 10−7 | 0 |
| Boroughs | Vacancy Rate (%) |
|---|---|
| ANJ | 6.84 |
| PLA | 11.9 |
| OUT | 10.9 |
| RPP | 6.16 |
| STL | 7.22 |
| VIM | 13.6 |
| VSE | 6.52 |
| Average for the seven boroughs | 9.10 |
| Boroughs | Reference Population 1 | Adjusted Reference Population 2 | Simulated Population 3 | Error 4 (%) |
|---|---|---|---|---|
| ANJ | 43,200 | 46,000 | 46,400 | −0.0840 |
| PLA | 106,000 | 120,000 | 120,000 | −0.200 |
| OUT | 24,600 | 27,600 | 27,500 | −0.492 |
| RPP | 142,000 | 151,000 | 151,000 | 0.177 |
| STL | 79,500 | 85,700 | 85,300 | −0.501 |
| VIM | 105,000 | 122,000 | 122,000 | 0.0908 |
| VSE | 145,000 | 155,000 | 156,000 | 0.510 |
| Average for the seven boroughs | 645,000 | 701,000 | 708,000 | 0.0461 |
| Boroughs | Adjusted Reference of Generated Recyclable Waste (kt/year) | Simulated Generated Recyclable Waste (kt/year) | Error (%) |
|---|---|---|---|
| ANJ | 3.11 | 3.11 | 0.00343 |
| PLA | 11.3 | 11.3 | −0.0750 |
| OUT | 2.63 | 2.62 | −0.383 |
| RPP | 14.3 | 14.3 | 0.284 |
| STL | 5.89 | 5.87 | −0.396 |
| VIM | 12.7 | 12.7 | 0.176 |
| VSE | 9.45 | 9.51 | 0.612 |
| Average for the seven boroughs | 59.4 | 59.5 | 0.133 |
| Statistic | Deadheading Cost (s) | Collection Cost (s) | Demand (kg) |
|---|---|---|---|
| Mean | 11.9 | 84.2 | 129 |
| Median | 8.74 | 57.9 | 55.1 |
| Standard deviation | 10.7 | 73.9 | 228 |
| Minimum | 0.440 | 25.9 | 0.940 |
| Maximum | 209 | 2010 | 7680 |
| Statistic | Time (h) | Waste Collected (t) |
|---|---|---|
| Mean | 1.86 | 8.42 |
| Median | 1.74 | 8.77 |
| Standard deviation | 0.574 | 0.862 |
| Minimum | 0.795 | 3.64 |
| Maximum | 4.10 | 8.99 |
| Absolute Distances (km) | Relative Distances (%) | ||||
|---|---|---|---|---|---|
| Statistic | Total | Waste Collection | Deadheading | Waste Collection | Deadheading |
| Mean | 23.1 | 8.21 | 14.9 | 37.0 | 63.0 |
| Median | 21.5 | 7.05 | 14.0 | 37.5 | 62.5 |
| Standard deviation | 9.08 | 4.91 | 8.03 | 17.7 | 17.7 |
| Minimum | 8.59 | 0.327 | 3.34 | 1.91 | 23.4 |
| Maximum | 70.4 | 25.9 | 65.8 | 76.6 | 98.1 |
| Cluster | |||||
|---|---|---|---|---|---|
| Scenario Number | 2 | 3 | 4 | 5 | |
| Number of Recyclable Waste Sorting Facilities | 2 | 4 | 7 | 10 1 | |
| Cluster Range | A–B | A–D | A–G | A–J | |
| Boroughs | AHU | B | A | A | A |
| ANJ | A | A | F | F | |
| CDN | A | C | F | J | |
| IBI | B | D | D | F | |
| LAC | B | B | B | B | |
| LAS | A | B | E | E | |
| LSO | A | C | E | J | |
| MHM | A | A | F | F | |
| MTN | B | A | A | A | |
| OUT | A | C | F | H | |
| PLA | A | C | F | I | |
| PRF | B | D | A | D | |
| RDP | A | A | G | G | |
| RPP | A | A | F | F | |
| STL | A | A | F | F | |
| VER | A | B | C | G | |
| VIM | A | C | F | H | |
| VSE | B | A | A | A | |
| VSL | B | B | A | D | |
| Waste Collection | Deadheading | Delivery | ||||
|---|---|---|---|---|---|---|
| Category | Abs. | % | Abs. | % | Abs. | % |
| CO2 emissions (kg) | 2200 | 57.7 | 1600 | 41.9 | 16.1 | 0.422 |
| Fuel consumption (L) | 845 | 58.0 | 607 | 41.6 | 6.13 | 0.420 |
| Cost Category | Weekly Cost (K CAD) | Percentage |
|---|---|---|
| Investment | 50.9 | 42.2 |
| Waste collection | 22.9 | 19.0 |
| Waste sorting | 46.9 | 38.8 |
| Delivery | 0.0363 | 0.0301 |
| Total | 121 | 100 |
| Scenario | Emitted CO2 (t) | Total Costs (K CAD) | (CAD/kg of Avoided CO2) |
|---|---|---|---|
| Baseline | 3.82 | 120.7 | N/A |
| 1 | 3.82 | 120.3 | −2.59 |
| 2 | 3.65 | 157.3 | 160 |
| 3 | 3.59 | 207.6 | 201 |
| 4 | 3.51 | 242.5 | 392 |
| 5 | 3.19 | 306.1 | 295 |
| 6 | 3.04 | 621.2 | 646 |
| Scenario | Operating Costs (K CAD) | (CAD/kg of Avoided CO2) |
|---|---|---|
| Baseline | 69.79 | N/A |
| 1 | 69.36 | −2.59 |
| 2 | 69.26 | −2.31 |
| 3 | 68.62 | −2.71 |
| 4 | 68.74 | −3.38 |
| 5 | 66.26 | −5.64 |
| 6 | 64.18 | −7.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anglehart-Nunes, J.; Glaus, M. Environmental Performance Assessment of a Decentralized Network of Recyclable Waste Sorting Facilities: Case Study in Montreal. Recycling 2025, 10, 58. https://doi.org/10.3390/recycling10020058
Anglehart-Nunes J, Glaus M. Environmental Performance Assessment of a Decentralized Network of Recyclable Waste Sorting Facilities: Case Study in Montreal. Recycling. 2025; 10(2):58. https://doi.org/10.3390/recycling10020058
Chicago/Turabian StyleAnglehart-Nunes, Jessy, and Mathias Glaus. 2025. "Environmental Performance Assessment of a Decentralized Network of Recyclable Waste Sorting Facilities: Case Study in Montreal" Recycling 10, no. 2: 58. https://doi.org/10.3390/recycling10020058
APA StyleAnglehart-Nunes, J., & Glaus, M. (2025). Environmental Performance Assessment of a Decentralized Network of Recyclable Waste Sorting Facilities: Case Study in Montreal. Recycling, 10(2), 58. https://doi.org/10.3390/recycling10020058






