SOC Estimation Methods for Lithium-Ion Batteries without Current Monitoring

Abstract

State of charge (SOC) estimation is an important part of a battery management system (BMS). As for small portable devices powered by lithium-ion batteries, no current sensor will be configured in BMS, which presents a challenge to traditional current-based SOC estimation algorithms. In this work, an electrochemical model is developed for lithium batteries, and three methods, including the incremental seeking method, dichotomous method, and extended Kalman filter algorithm (EKF), are separately developed to establish the framework of current and SOC estimation simultaneously. The results show that the EKF algorithm performs better than the other two methods in terms of estimation accuracy and convergence speed. In addition, the estimation error of the EKF algorithm is within ±2%, which demonstrates its feasibility.

1. Introduction

In recent years, the sustainable development of the environmental ecosystem has become a pressing issue due to the increasingly prevalent problems of environmental pollution. In this case, it is essential to focus on the efficient use of energy and resources. Lithium-ion batteries are a popular choice as energy storage components for small electronics and large electric vehicles due to their high energy density, long cycle life, no memory effect, and low self-discharge [1]. However, overcharging or over-discharging a lithium battery can lead to capacity degradation, shortened battery life, and even explosion.

In order to guarantee the safe and secure use of lithium-ion batteries and to extend their cycle life, a battery management system (BMS) is critical, which can effectively manage the performance of lithium-ion batteries in a comprehensive, efficient, and refined manner [2]. It is necessary to ensure optimal battery performance and longevity in various applications.

The reliability of the BMS depends on the precision of the state of charge (SOC) estimation of lithium-ion batteries. SOC indicates the remaining capacity and provides an indication of whether the battery needs to be charged or discharged. The variation characteristics of SOC are a critical performance indicator for assessing the status of lithium-ion batteries. Therefore, accurate SOC estimation is a core function of BMS [3], and it is a prerequisite to achieve additional functions such as safety control, battery equalization, and troubleshooting.

However, SOC is an internal state of the battery and cannot be directly measured. It can only be estimated based on the relationship between voltage, current, temperature, and the aging of the battery [4]. Therefore, it is crucial to develop reliable SOC estimation algorithms that consider all relevant factors to ensure optimal performance and safety of lithium-ion batteries in various applications.

In automobiles, robots, and energy storage systems, current measurement is usually achieved using shunt resistors or Hall-effect current sensors. While shunt resistors have inherent power losses and require isolation circuitry, Hall-effect sensors are typically expensive. In low-cost portable applications, such as microphones and hearing aids, the current sensor is often not equipped, considering the size and cost of the device. Therefore, it is practical to design a current sensorless SOC estimation method for low-cost portable applications.

Common SOC estimation algorithms include the open-circuit voltage method, ampere-hour integral method, electrochemical impedance spectroscopy, adaptive filtering method, and data-driven neural network method [5]. The open circuit voltage method takes a long time to collect data and is difficult to apply in practice [6], while the ampere-hour integral method is affected by the initial charge state and current stability. The electrochemical impedance spectroscopy method is only used for laboratory research [7]. In addition, the adaptive filtering method has a complex algorithm and long calculation cycle, which includes nonlinear Kalman filter, particle filter, specifically including extended Kalman filter, traceless Kalman filter, and other methods [8,9,10,11,12]. In neural network methods [13,14,15] and support vector machine methods [16,17,18,19], the SOC estimation of a battery is viewed as a regression problem, using multiple inputs (e.g., voltage, current, and environmental variables) to predict the SOC. These methods usually require a large quantity of experimental data to train the neural network and use various optimization techniques to improve precision and robustness. Ignoring the internal mechanism of the battery, the model accuracy depends on the quality of the sample data. In addition, in the field of fast charging, Xuejiao Xu et al. [20] created their own three-electrode system so as to measure the anode/cathode potential and estimate the SOC.

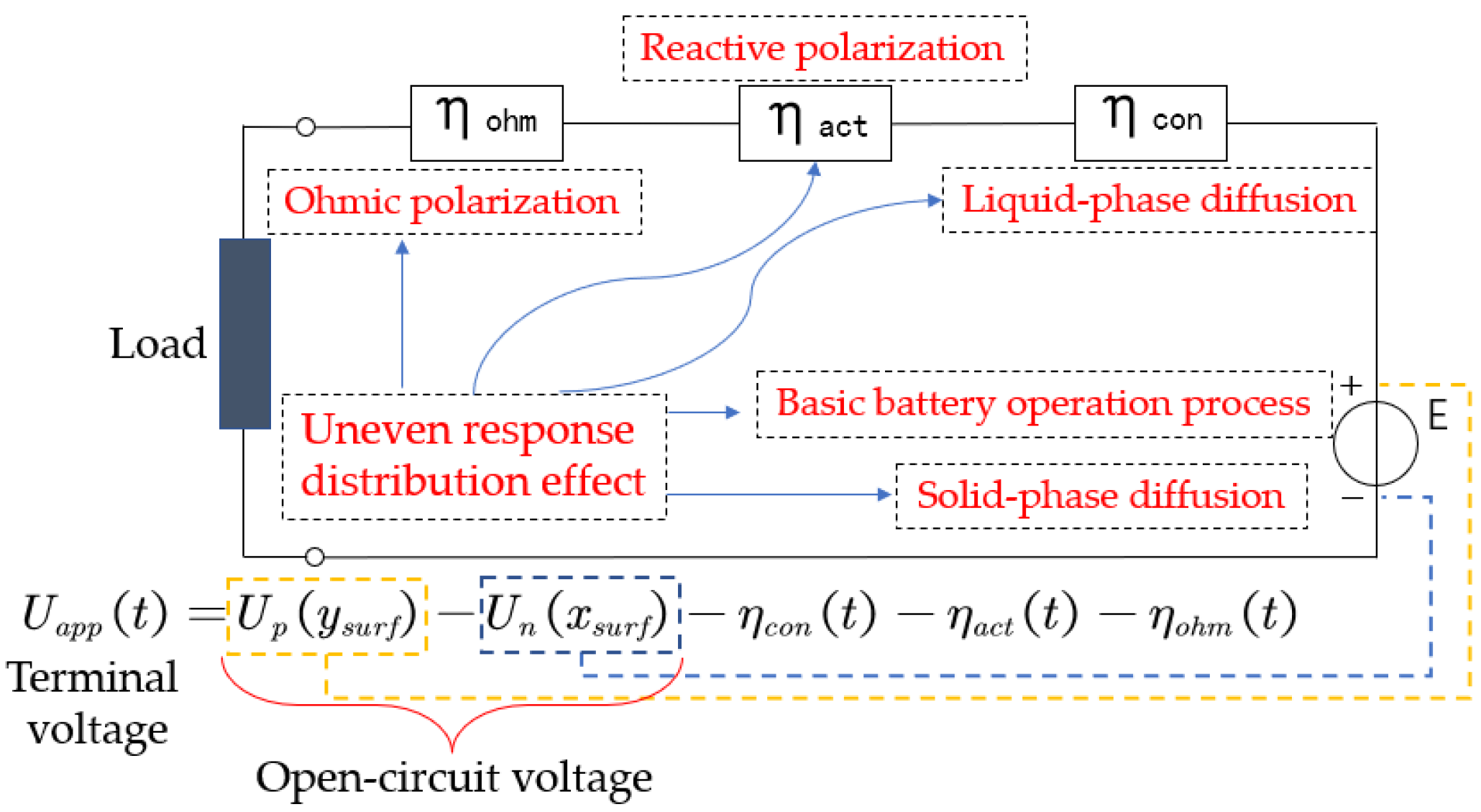
A battery model, which includes equivalent circuit models (ECM) [21] and electrochemical models, provides high simulation accuracy and reflects the external characteristics of the battery. The electrochemical model parameters have physical meanings and act as a bridge between the external characteristics of the battery and the internal electrochemical reaction mechanism of the battery [22,23,24]. In order to achieve accurate SOC estimation, the BMS requires current measurements as input to the estimator.

For the current sensorless SOC estimation method, Cambron and Cramer [25] estimated the current by an unknown input observer, and Putra et al. [26] created a new method to accomplish current estimation on the basis of Thevenin ECM. Chun et al. [27] obtained the open circuit voltage (OCV) and current information from the terminal voltages and then calculated the SOC using the ampere-hour integral method. However, these methods either used a linear relationship between OCV and SOC or utilized an overly simple battery model that led to a decrease in the accuracy of the model.

To avoid the above problems, Jing Hou et al. [28] used the variational Bayesian extended Kalman filter method to achieve simultaneous estimation of SOC and current. Experimental results showed that the mean absolute errors (MAEs) and the root mean square errors (RMSEs) of the SOC estimations of the proposed variational Bayes-based unscented Kalman filter (VB-UKF) were less than ±3%.

In this work, three methods are proposed to estimate SOC in the absence of current sensors based on the electrochemical model of lithium-ion batteries, which include the incremental seeking method, the dichotomous method, and the improved extended Kalman filter algorithm. The remainder of this work is organized as follows: (1) In Section 2, the electrochemical model of lithium-ion batteries is established to mathematically express the mechanisms in the charging and discharging process, and the relationship function between voltage and SOC is obtained. The principles of the three methods are described; (2) In Section 3, the data test of LCO lithium-ion batteries is conducted to obtain the voltage and current data under different working conditions; (3) In Section 4, the estimation of SOC under no current monitoring by three methods is completed compared with the reference value. In addition, the effects of inaccurate initial values of SOC and different levels of voltage noise on the accuracy of the estimation results are also explored.

2. Lithium-Ion Battery Model and Algorithm Principle

2.1. Simplified Electrochemical Model

The structure of a lithium-ion battery is divided into three areas: the positive electrode, the negative electrode, and the diaphragm. The cathode material typically uses lithium ferrous phosphate (LFP), lithium cobalt oxide (LCO), lithium-nickel-cobalt-manganese oxide (LNCM), etc., while the anode material is usually graphite, and the electrolyte is mostly LiPF6 alkyl carbonate with polymer materials. During the process of charging and discharging, lithium ions are de-embedded and transferred between the positive and negative electrodes [29].

The classical electrochemical model of lithium-ion batteries is based on ten control equations in the form of partial differential equations. These equations describe the solid-phase diffusion within the particles, liquid-phase diffusion in the electrolyte, solid-phase potential equilibrium, and liquid-phase potential equilibrium in the positive, diaphragm, and negative regions. The model structure is shown in Figure 1.

In this work, the internal processes of the cell were described using algebraic equations. These equations encompassed various aspects of the cell’s functioning, such as the basic working process, solid-phase diffusion process, concentration polarization effect, reaction polarization effect, ohmic polarization effect, and the calculation of the terminal voltage [30]. The equations involved in the model are presented in

Table 1. Electrochemical model equations for lithium batteries.

Correlation Mechanism	Equations
Terminal voltage	$U_{\mathit{app}}(k) = E_{\mathit{ocv}}(k) - {\eta }_{\mathit{con}}(k) - {\eta }_{\mathit{act}}(k) - {\eta }_{\mathit{ohm}}(k)$
Open circuit potential correction	$E_{\mathit{ocv}}(k) = { E}_{\mathit{ocv}}^{\mathit{ref}}(k) + (T(k) - T_{\mathit{ref}})\frac{\mathrm{d}{E}_{\mathit{ocv}}}{\mathrm{d}T}$
Basic working principle	$x_{\mathit{avg}}(k) = x_0 - {\int }_{{\mathrm{t}}_1}^{{\mathrm{t}}_{\mathrm{k}}}I\mathrm{d}t/Q_n$, $x_{\mathit{surf}}(k) = x_{\mathit{avg}}(k) - ∆x(k)$, $∆x(k) = ∆x_1(k) + \frac{2}{7}{\tau }_{n}I(k)/Q_n$, $y_{\mathit{avg}}(k) = { y}_0 + {\int }_{{\mathrm{t}}_1}^{{\mathrm{t}}_{\mathrm{k}}}I\mathrm{d}t/Q_p$, $y_{\mathit{surf}}(k) = y_{\mathit{avg}}(k) + ∆y(k)$, $∆y(k) = ∆y_1(k) + \frac{2}{7}{\tau }_{p}I(k)/Q_p$, $E_{\mathit{ocv}}(k) = U_p\left[y_{\mathit{surf}}(k)\right] - U_n\left[x_{\mathit{surf}}(k)\right]$
Solid diffusion	$∆x_1(k + 1) = ∆x_1(k) + \frac{1}{{\tau }_n}[\frac{12{\tau }_{n}I(k)}{{7Q}_n} - ∆x_1(k)]∆t, ∆y_1(k + 1) = ∆y_1(k) + \frac{1}{{\tau }_p}[\frac{12{\tau }_{p}I(k)}{{7Q}_p} - ∆y_1(k)]∆t$
Liquid-phase diffusion	$∆c_n(k + 1) = ∆c_n(k) + \frac{1}{{\tau }_e}\left[P_{\mathit{conn}}I(k) - ∆c_n(k)\right]∆t, ∆c_p(k + 1) = ∆c_p(k) + \frac{1}{{\tau }_e}\left[P_{\mathit{conp}} - ∆c_p(k)\right]∆t,$ ${\eta }_{\mathit{con}}(k)=\frac{2\mathit{RT}(k)}{F}\left(1 - t_{+}\right)\ln \left[\frac{c_0 + ∆c_p(k)}{c_0 - ∆c_n(k)}\right]$
Reactive polarization	${\eta }_{\mathit{act}}(k) = \frac{2\mathit{RT}(k)}{F}[\ln (\sqrt{m_n^2(k) + 1} + m_n(k)) - \ln (\sqrt{m_p^2(k) + 1} + m_p(k))]$ $m_p(k) = \frac{1}{6Q_p{c}_0^{0.5}}\frac{1}{{(1 - y_{\mathit{surf}}(k))}^{0.5}{(y_{\mathit{surf}}(k))}^{0.5}}{P}_{\mathit{act}}I(k)$,$m_n = \frac{1}{6Q_n{c}_0^{0.5}}\frac{1}{{(1 - x_{\mathit{surf}}(k))}^{0.5}{(x_{\mathit{surf}}(k))}^{0.5}}{P}_{\mathit{act}}I(k)$
Ohmic polarization	${\eta }_{\mathit{ohm}} = R_{\mathit{ohm}}I (k)$

. The meanings of the parameters involved in the above model are shown in

Table 2. Meaning of related parameters.

Parameters	Physical Meaning
$U_{\mathit{app}}$	Terminal voltage (V)
$E_{\mathit{ocv}}$	Electromotive force (V)
${\eta }_{\mathit{con}}$	Concentration polarization overpotential (V)
${\eta }_{\mathit{act}}$	Reaction polarization overpotential (V)
${\eta }_{\mathit{ohm}}$	Ohmic polarization overpotential (V)
$y_{\mathit{avg}}$, $x_{\mathit{avg}}$	Solid-phase average stoichiometric number of positive and negative electrodes (-)
$y_{\mathit{surf}}$, $x_{\mathit{surf}}$	Solid-phase surface stoichiometric number of positive and negative electrodes (-)
$∆y$	Deviations between ysurf and yavg (-)
$∆x$	Deviations between xsurf and xavg (-)
$∆y_1$	Intermediate variable of $∆y$ (-)
$∆x_1$	Intermediate variable of $∆x$ (-)
T	Battery internal temperature (K)
R	Ideal gas constant (J mol−1 K−1)
y0, x0	Initial lithium intercalation concentration fraction of positive and negative electrodes (-)
c0	Initial lithium ion concentration in electrolyte (mol m−3)
Qp, Qn	Total capacity of positive and negative electrodes (A s)
Qall	Total capacity of the battery (A s)
τp, τn	Solid diffusion time constants of positive and negative electrodes (s)
Dx, Dy	Lithium embedding rate of positive and negative electrodes (-)
Pact	Reaction polarization coefficient (m−1.5 mol0.5 s)
Pcon	Proportional coefficient of liquid phase diffusion (mol m−3 A−1)
Rohm	Ohm internal resistance (Ω)
yofs	Embedded lithium offset (-)
τe	Liquid phase diffusion time constant (s)

.

2.2. Identification of Model Parameters

The intrinsic characteristics of the battery parameters remain constant and can be obtained by consulting the manufacturer or references. However, the variables to be identified in the electrochemical model include the initial lithium intercalation in the cathode, cathode capacity, offset of the lithium intercalation, and more [31]. The parameters involved can be obtained by analyzing the intrinsic connection between the cell terminal voltage change, the open-circuit voltage, and each part of the overpotential under the designed identification conditions with different forms of current excitation.

The parameter identification method referred to an excitation response analysis developed in [30]. Based on the simplified electrochemical model, using the input data of current and the corresponding response data of voltage, the relationship between the internal mechanisms and external behaviors was established quantitatively, and the parameters in the model were fitted during this process.

The parameters obtained by identification are shown in

Table 3. Battery parameters.

Parameters	Value
y0, x0	0.7941, 0.4538
c0	1000
Qp, Qn	19,859.04, 11,888.64
τp, τn	184.7533, 2.5501
Dx, Dy	0.7922, 0.4743
Pact	271,780
Pcon	955.1863
Rohm	0.0686
yofs	0.0708
τe	62.2686

.

2.3. Principle of SOC Estimation Algorithm under No Current Monitoring

The three SOC estimation algorithms utilized in this study were based on the simplified electrochemical model. However, the model function inputs did not take into account the temperature of the battery. The inputs solely consisted of the SOC and current, while the output was limited to the cell terminal voltage.

2.3.1. Incremental Seeking Method

This solution was based on the idea of enumeration to achieve current estimation and SOC prediction. The approach involves gradually increasing the current within fixed boundary conditions and then inputting the current into the model to calculate the voltage to identify the current values that meet the necessary requirements. Once the appropriate current value is determined, the SOC can be estimated using the ampere-hour integral method. The corresponding flowchart illustrating this method is depicted in Figure 2.

The specific scheme was as follows: Firstly, the measured voltage was compared with the previous second’s voltage to determine whether the battery was being charged or discharged. Then, the current sign was initialized, and upper and lower search boundaries were set. An initial current value of 0 was assumed. A voltage simulation was carried out using the assumed current, and the simulated voltage was compared to the measured voltage. If the error between the measured voltage and simulated voltage exceeded an acceptable range, the current value was increased based on the error until the error was within an acceptable range. The current corresponding to the simulated voltage was considered the current, and the SOC was predicted using the ampere-hour integration method.

2.3.2. Dichotomous Method

As shown in Figure 3, this scheme used the dichotomy method for current estimation and SOC prediction. The basic principle of the dichotomy method involved continuously dividing the search range into two parts within fixed boundary conditions to find the number that meets certain requirements.

The specific scheme is as follows: firstly, the measured voltage was compared with that of the previous second to determine the charging and discharging state at this time. Then, the current was initialized, and the upper and lower search boundaries were assumed. The voltage simulation was carried out based on the assumed current, and the corresponding simulation voltage was compared with the measured voltage. If the error is greater than the acceptable range, the current value is adjusted according to the error until the error between the measured voltage and the simulated voltage is in the acceptable range. At this point, the current corresponding to the simulated voltage was considered as the current at that moment. Finally, the SOC prediction was carried out by the ampere-hour integration method.

2.3.3. Extended Kalman Filter

The solution utilized a modified extended Kalman filter to achieve SOC estimation. Based on the simplified electrochemical model, the load current was taken as the unknown input, and the system state equation and the measurement equation were established. In addition, the current estimation was achieved using the modified extended Kalman filter method. Finally, the SOC estimation was completed by the ampere-hour integral method. The flow chart is shown in Figure 4.

To implement this solution, an update of state variables and observation updates was required, which meant that the priori SOC estimation, succession of current values, and covariance matrix calculations were carried out. The gain matrix was then calculated, and the currents were corrected according to voltage errors. Finally, the accurate SOC estimation for a single cell was obtained by the ampere-hour integration method.

3. Battery Testing Process and Results

Different lithium cobaltate battery monoblocks from the same batch with a standard capacity of 800 mAh were selected. Charging and discharging tests were performed using Neware’s battery test system to simulate the battery operating conditions at different charge and discharge multipliers. The data sampling frequency was 1 s. The specific current configurations were as follows:

The specific current configuration for the DST operating conditions test is described as follows:

(1)

The lithium-ion battery was fully charged by constant current and constant voltage charging.

(2)

The battery was rested in a constant temperature chamber for 1 h.

(3)

The battery was discharged at a constant discharge rate of 0.25 C for 30 s, discharged at 0.5 C for 12 s, and charged at 0.25 C for 10 s.

(4)

Step (3) was repeated three times.

(5)

The battery was charged successively at a constant charge rate of 0.25 C for 35 s, 2 C for 10 s, and 1.25 C for 25 s.

(6)

The battery was charged at a constant charge rate of 0.5 C for 10 s, discharged at 0.5 C for 30 s, and charged at 1 C for 10 s.

(7)

The battery was rested for 50 s.

(8)

Steps (3)–(7) were repeated until the voltage decreased to 3.7 V. Then, the battery was discharged at a constant discharge rate of 0.5 C until the voltage was 2.5 V to stop the experiment.

The HPPC condition test with the specific current configuration was conducted as follows:

(1)

The lithium-ion battery was fully charged by constant current and constant voltage charging.

(2)

The battery was rested in a constant temperature chamber for 1 h.

(3)

The battery was discharged at 1 C for 8 min and was rested for 30 min.

(4)

The battery was discharged at 3 C for 10 s and rested for 3 min.

(5)

The battery was charged at 1.5 C for 10 s and rested for 2 min.

(6)

Steps (3)–(5) were repeated once.

(7)

The current in (4) and (5) was modified to 1.875 C. Steps (3)–(5) were repeated until the resting voltage dropped to 3.6 V.

(8)

The battery was discharged at 0.9 C until the voltage was 2.5 V to stop the experiment.

4. Results and Discussion

It is worth noting that all three methods of SOC estimation without current monitoring include the ampere-hour integration method, and the estimation accuracy is greatly influenced by the initial SOC accuracy and noise. The effects of different initial SOCs and random voltage noise on the algorithm estimation results were shown and discussed as follows, respectively.

4.1. Effect of Different Initial SOC on Estimation Results

The initial SOC of the test data was set as 100%, 70%, and 90%, respectively. The estimated results were as follows.

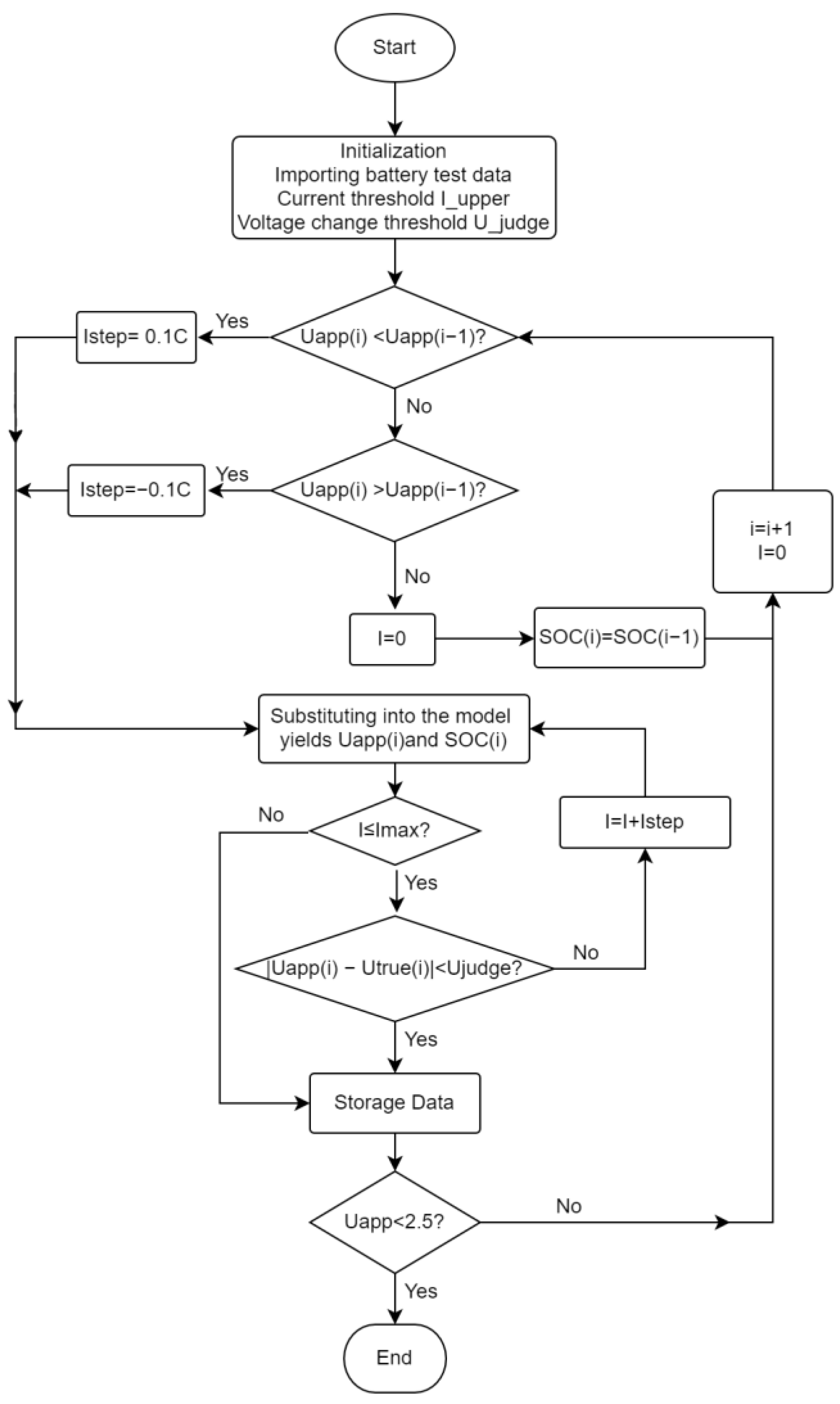
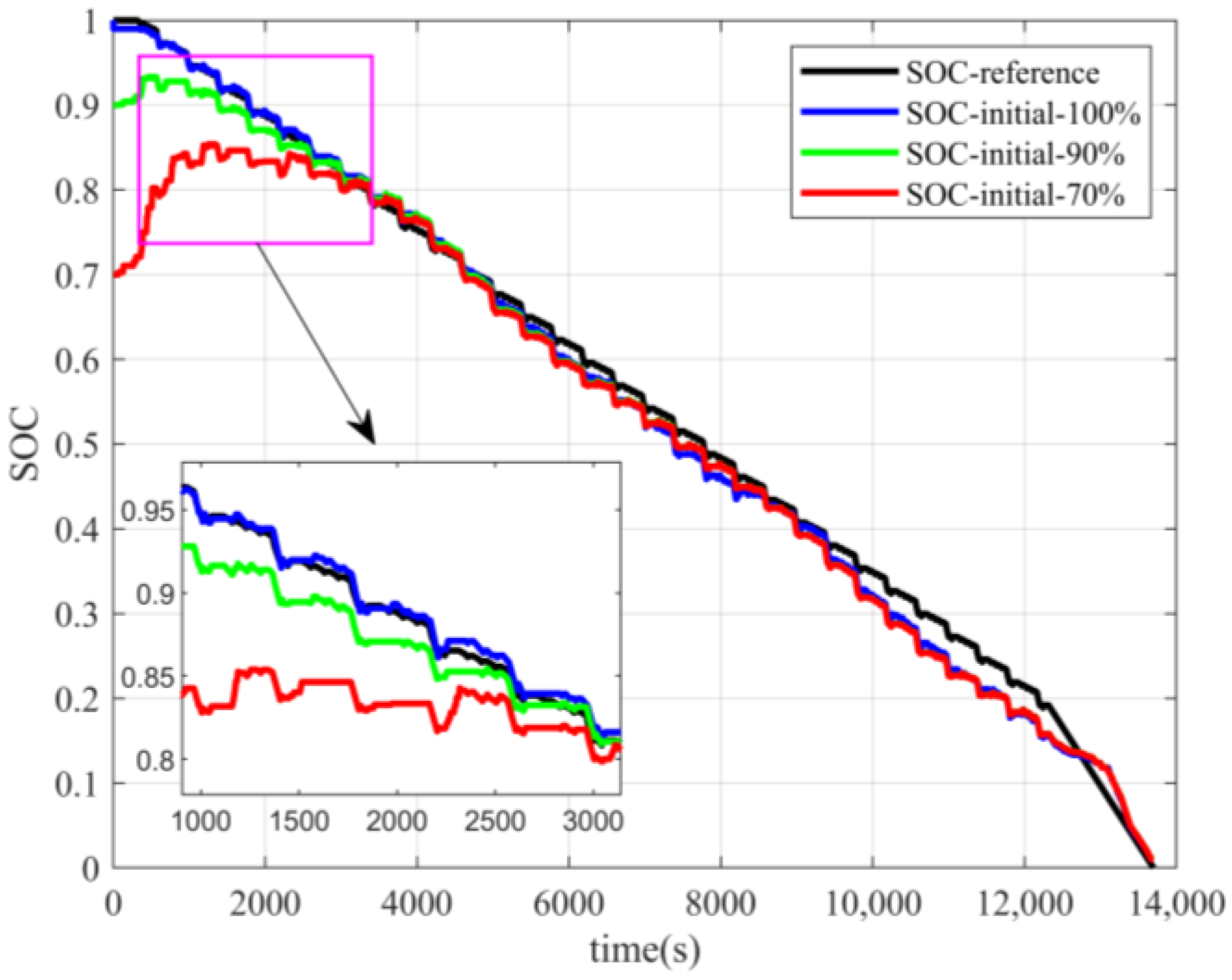
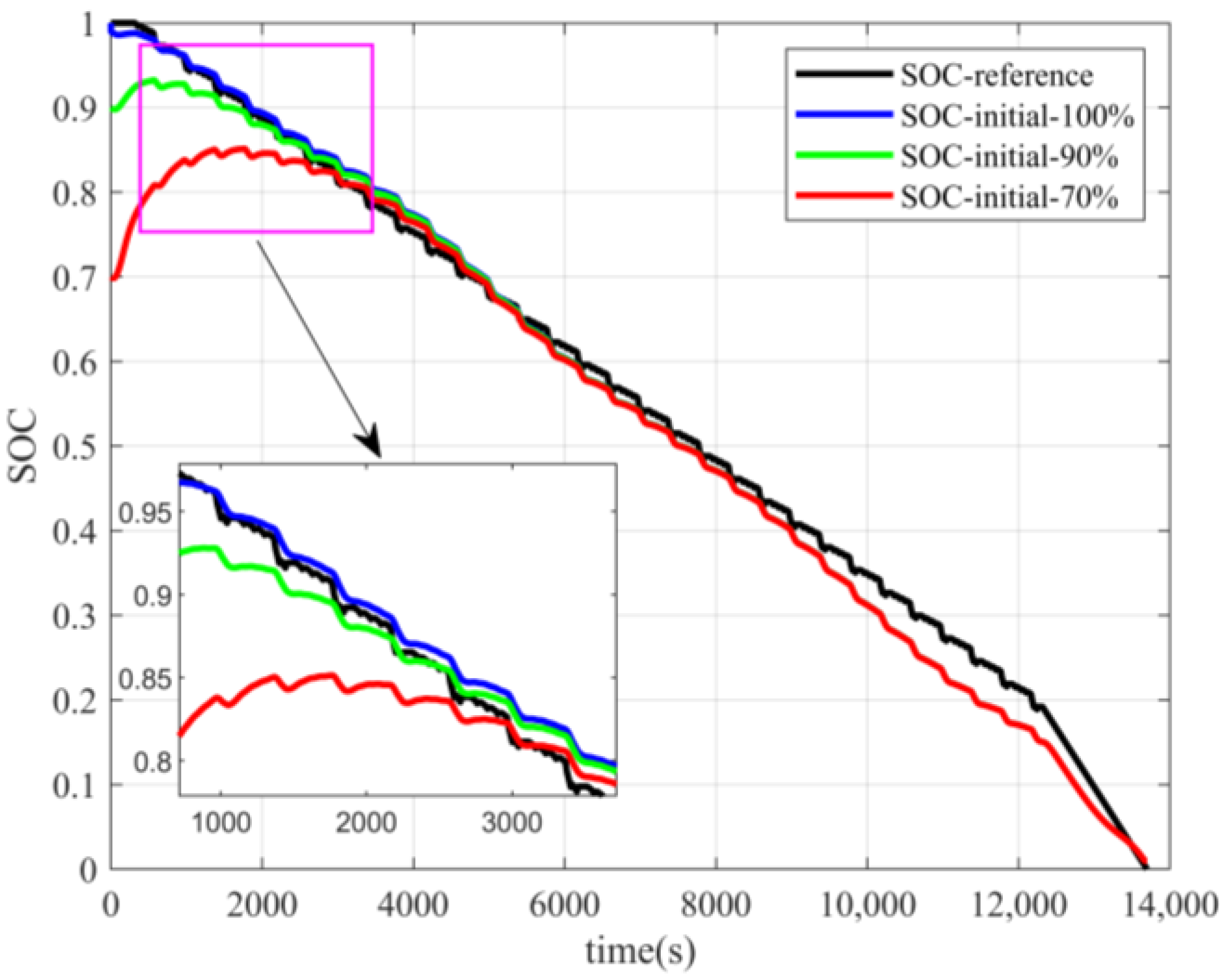
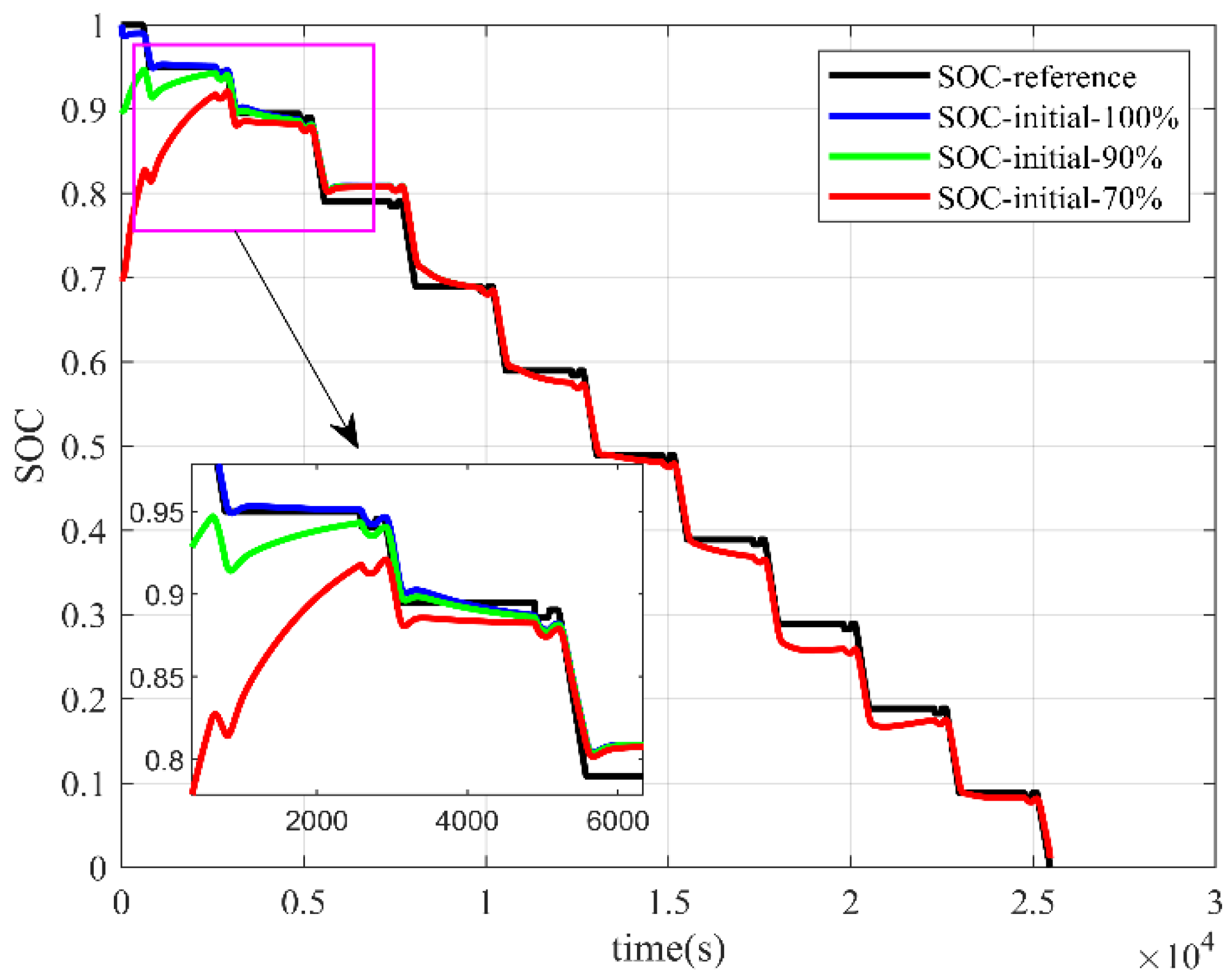
4.1.1. Incremental Seeking Method

The estimation results using the incremental seeking method for different initial SOC states are shown in Figure 5 and Figure 6.

The estimated trend obtained by the incremental seeking method was consistent with the actual reference value, and the estimated results varied with the battery charge and discharge state. For example, under DST conditions, SOC decreased along a wave line until 12,500 s and then decreased along a straight line. Under HPPC conditions, SOC decreased along a step.

However, the difference between the estimation results with initial SOC values of 100%, 90%, and 70% was significant under the HPPC condition. The error was largest when the initial SOC was accurate, illustrating the instability of the algorithm. When the initial SOC state was inaccurate, the incremental seeking method converged when the SOC dropped to nearly 80%, and the convergence process was often accompanied by a large abrupt change. After convergence was completed, the initial SOC value had a large impact on the estimation results.

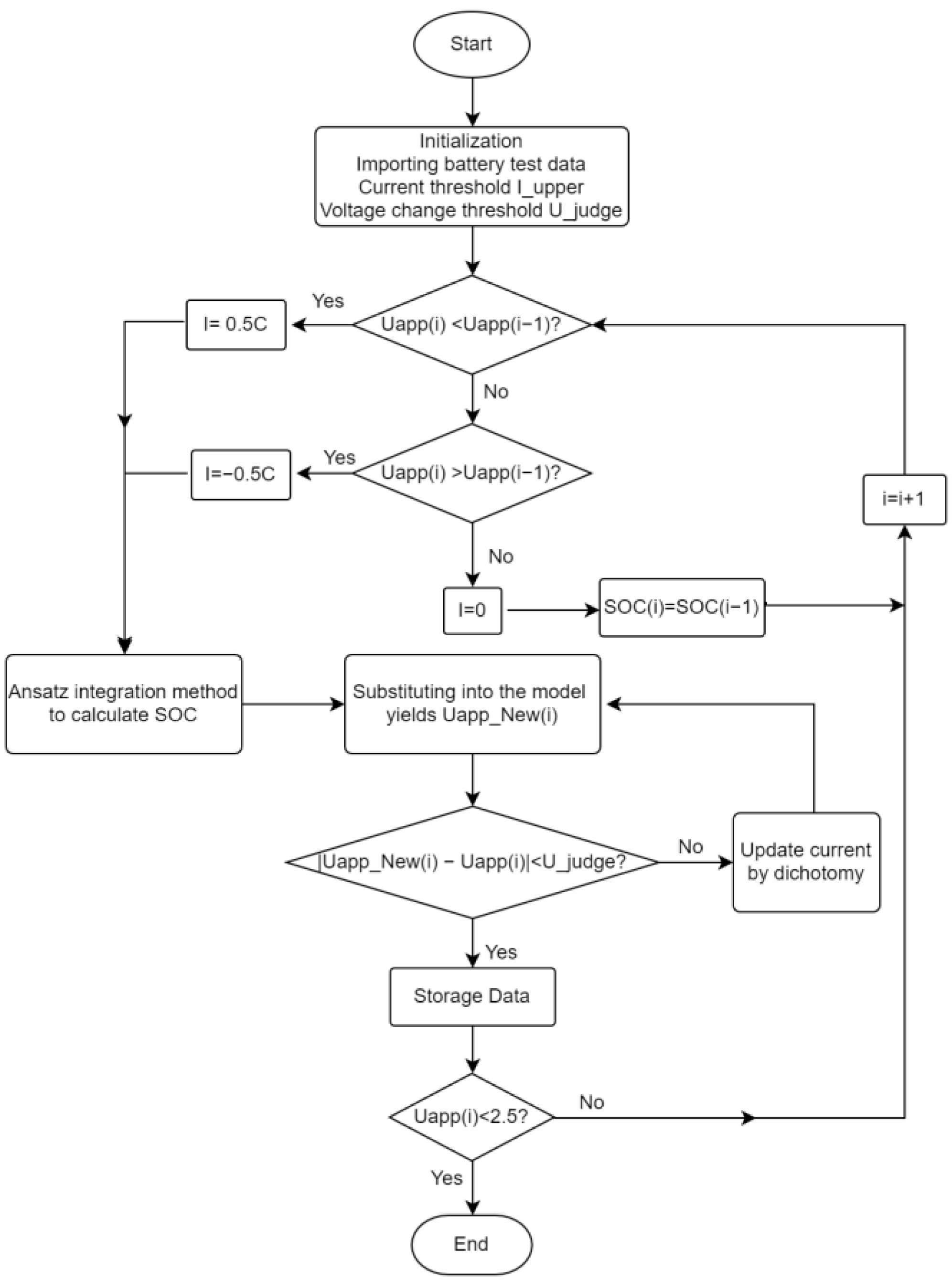
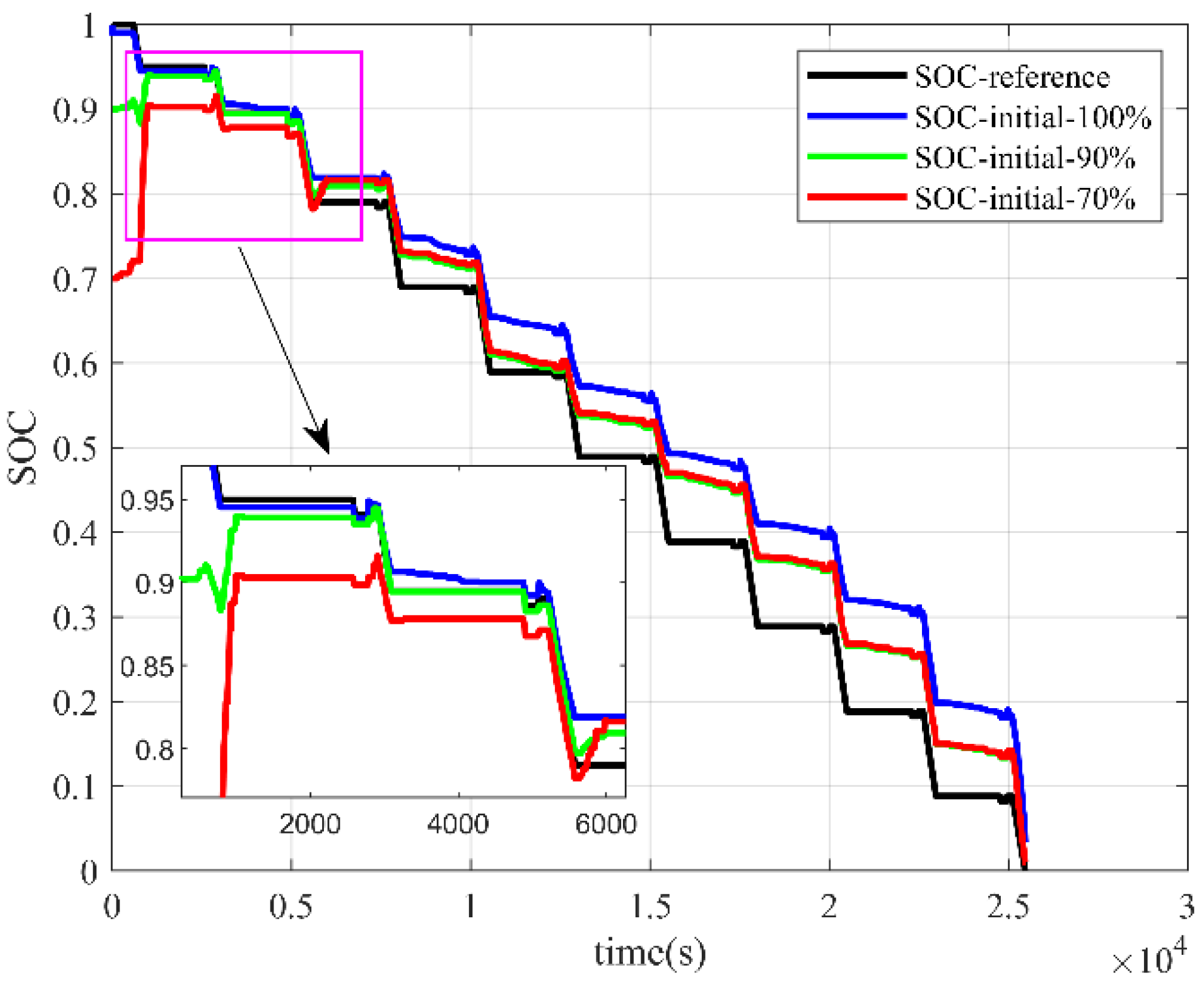
4.1.2. Dichotomous Method

The estimation results using the dichotomous method for different initial SOC states are shown in Figure 7 and Figure 8.

When applying the dichotomy method, the overall estimation trend was consistent with the actual reference value, and the algorithmic estimation results captured the same change phenomenon as the charging and discharging state of the battery varied.

From the overall viewpoint, the dichotomous SOC estimation error was large, especially under HPPC conditions, and significant estimation bias could be seen in Figure 8. When the initial SOC state was inaccurate, if the initial SOC was 90%, it completed convergence when the SOC decreased to around 85%. In addition, if the initial SOC was 70%, it completed convergence when the SOC decreased to around 75%. The convergence process had a great degree of abrupt change, but it was less than the incremental seeking method. Inaccurate initial SOC had a small impact on the estimation results after the convergence of the algorithm.

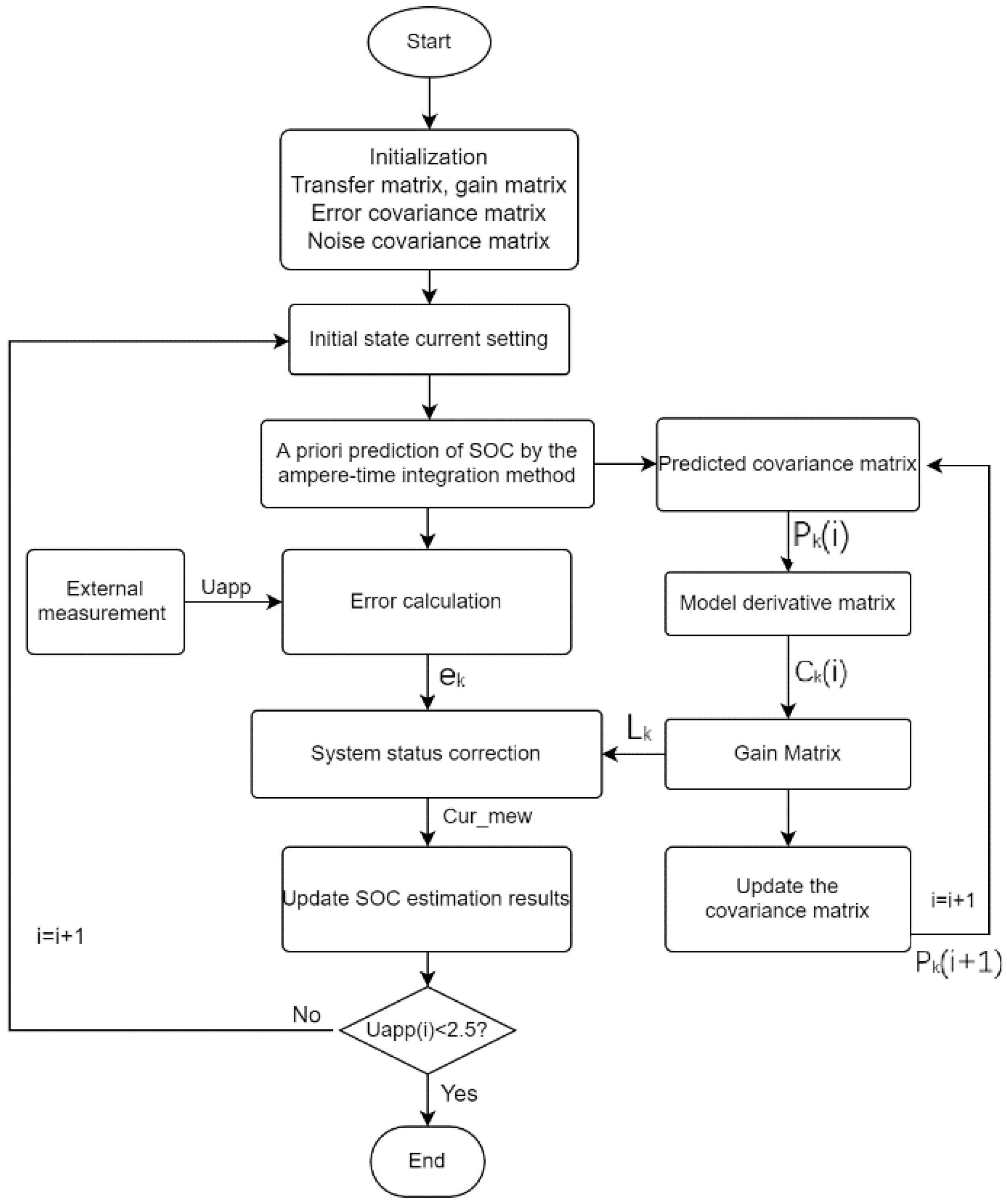
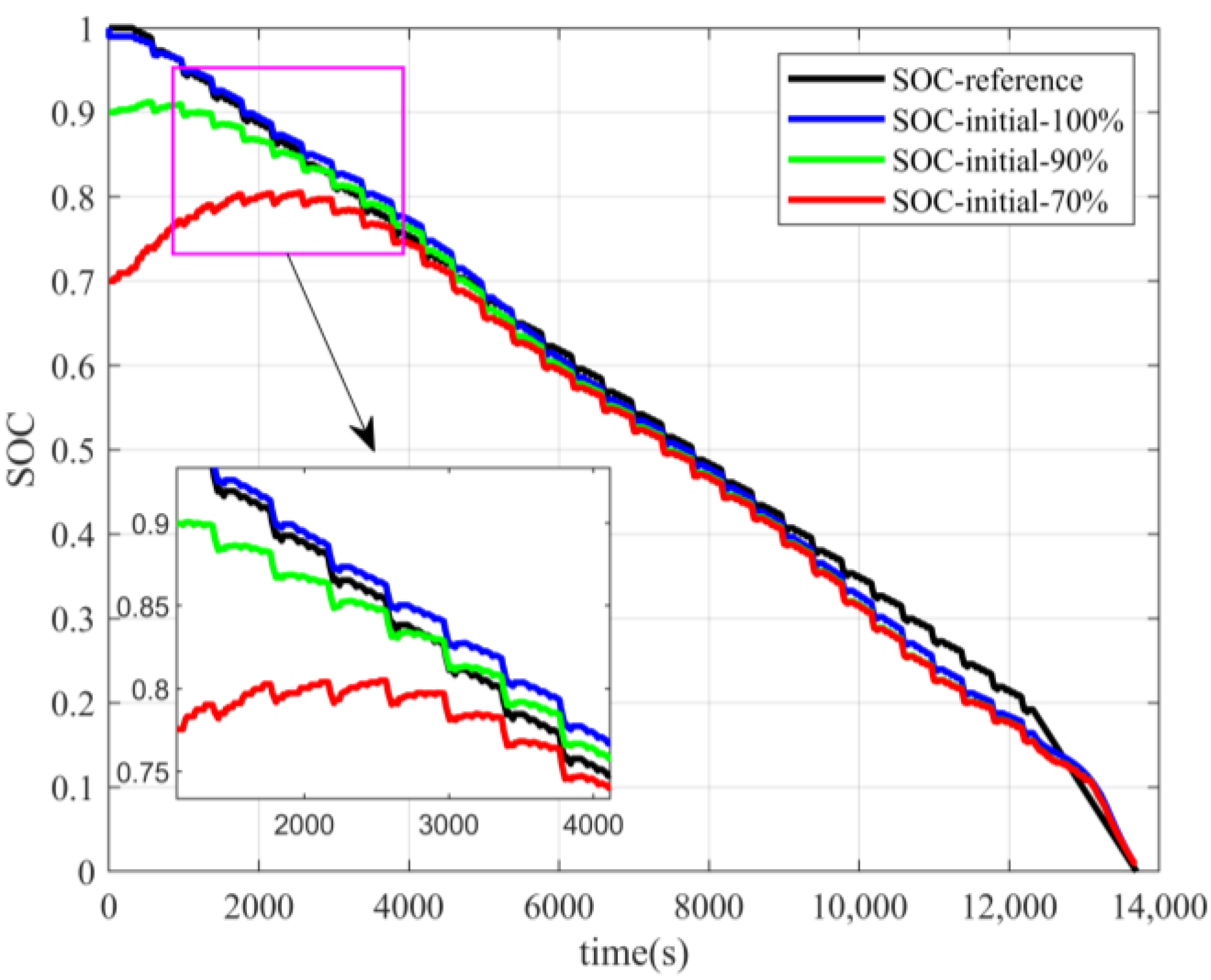
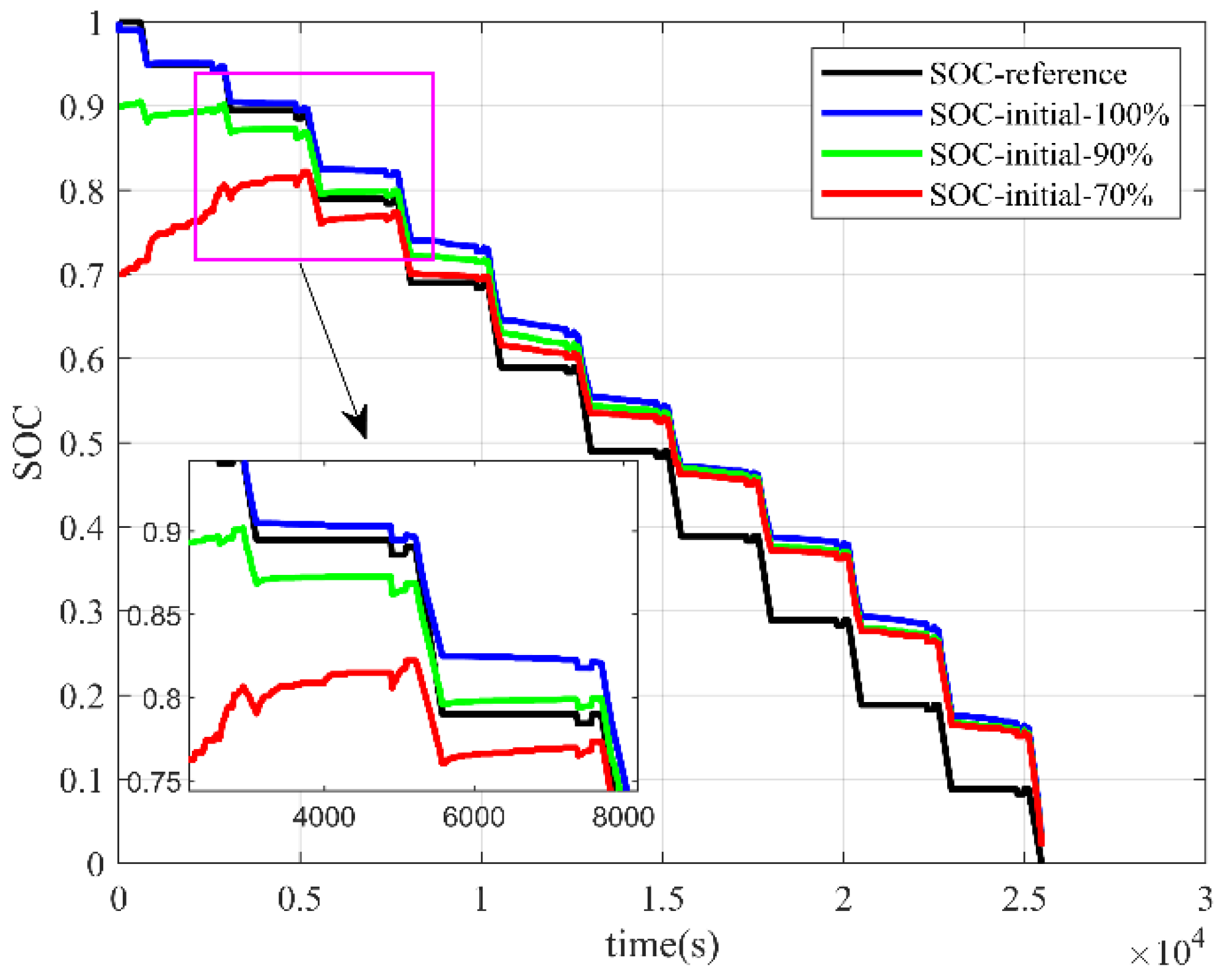
4.1.3. EKF

The estimation results using the EKF algorithm for different initial SOC states are shown in Figure 9 and Figure 10.

The overall estimation trend obtained using the EKF algorithm was consistent with the actual reference value, and the algorithm estimation results reflected the same variation phenomenon as the battery charge and discharge state change.

As a whole, the SOC estimation error of the EKF algorithm was small, and the average errors for the two operating conditions when the initial SOC was accurate were 1.94% and 1.13%, respectively. When the initial SOC was inaccurate, the algorithm converged quickly except for the DST condition where the initial SOC is 70%. Convergence was achieved when the SOC decreased to about 85~90%. The convergence process was smooth, and the convergence estimates were largely consistent with the reference values and almost independent of the initial SOC.

The estimation errors of the three methods for different initial SOC states are shown in

Table 4. Estimation error at different initial SOC states.

		Accurate Initial SOC		Initial SOC 0.9		Initial SOC 0.7
Incremental seeking method		soc	Voltage	soc	Voltage	soc	Voltage
DST	Average value	3.58%	0.042 V	3.60%	0.035 V	5.08%	0.043 V
	Maximum value	12.76%	0.300 V	11.42%	0.450 V	30%	0.659 V
HPPC	Average value	7.62%	0.025 V	7.80%	0.028 V	9.10%	0.035 V
	Maximum value	15.13%	0.373 V	15.20%	0.372 V	30%	0.669 V
Dichotomous method		soc	Voltage	soc	Voltage	soc	Voltage
DST	Average value	1.87%	0.014 V	2.58%	0.016 V	4.17%	0.084 V
	Maximum value	5.02%	0.416 V	10.00%	0.416 V	30%	0.495 V
HPPC	Average value	4.51%	0.028 V	4.43%	0.030 V	6.37%	0.044 V
	Maximum value	8.82%	0.352 V	10.00%	0.296 V	30%	0.288 V
EKF		soc	Voltage	soc	Voltage	soc	Voltage
DST	Average value	1.94%	0.034 V	2.36%	0.035 V	3.82%	0.036 V
	Maximum value	5.27%	0.414 V	10.21%	0.414 V	30.15%	0.414 V
HPPC	Average value	1.13%	0.0098 V	1.41%	0.010 V	2.33%	0.011 V
	Maximum value	3.69%	0.3872 V	10.20%	0.387 V	30.14%	0.387 V

.

In terms of overall SOC estimation performance, the EKF algorithm performed the best and met the actual demand. The dichotomy method was the second-best and could accurately estimate SOC when the initial state was reliable. However, the incremental seeking method had the worst performance, with the highest error, failing to meet the actual demand and requiring further improvement.

Regarding the impact of different initial SOC states on algorithm estimation, the EKF algorithm was highly resistant to interference and almost unaffected. The dichotomy method was less affected, while the incremental seeking method was the most unstable. Inaccurate initial states had a significant impact on the results of the incremental seeking method.

Concerning the convergence of algorithms under different initial SOC states, the EKF converged fast and seamlessly, while the dichotomy method converged slightly slower than the EKF. In contrast, the incremental seeking method had the slowest convergence rate, with a sudden change in the convergence process caused by the algorithm’s principle.

If the initial SOC error was too large, there was a significant increase in the error for all three methods. This indicates that the error correction capability of the three methods is limited due to the lack of current input. However, it is worth noting that the initial SOC error is usually not so large in portable devices. Furthermore, the SOC error can be calibrated gradually during the rest mode.

Jing Hou et al. [24] conducted pulse discharge experiments to validate their proposed VB-UKF method. The average absolute errors of the two methods, VB-UKF and the unscented recursive three-step filter (URTSF), were 1.52% and 2.65% when the initial SOC was accurate. When the initial SOC was 80%, the errors of the two methods were 1.67% and 2.28%, respectively. When the initial SOC was 60%, the errors of the two methods were 2.16% and 2.58%, respectively. It can be seen that the estimation effect of the EKF algorithm is perfectly acceptable.

4.2. Effect of Different Voltage Noise on Algorithm Estimation Results

The test data was free of voltage noise, and random Gaussian noise with the mean of 0 and 3σ of 10 mV, 50 mV, and 100 mV was superimposed, respectively. The estimated results are shown below.

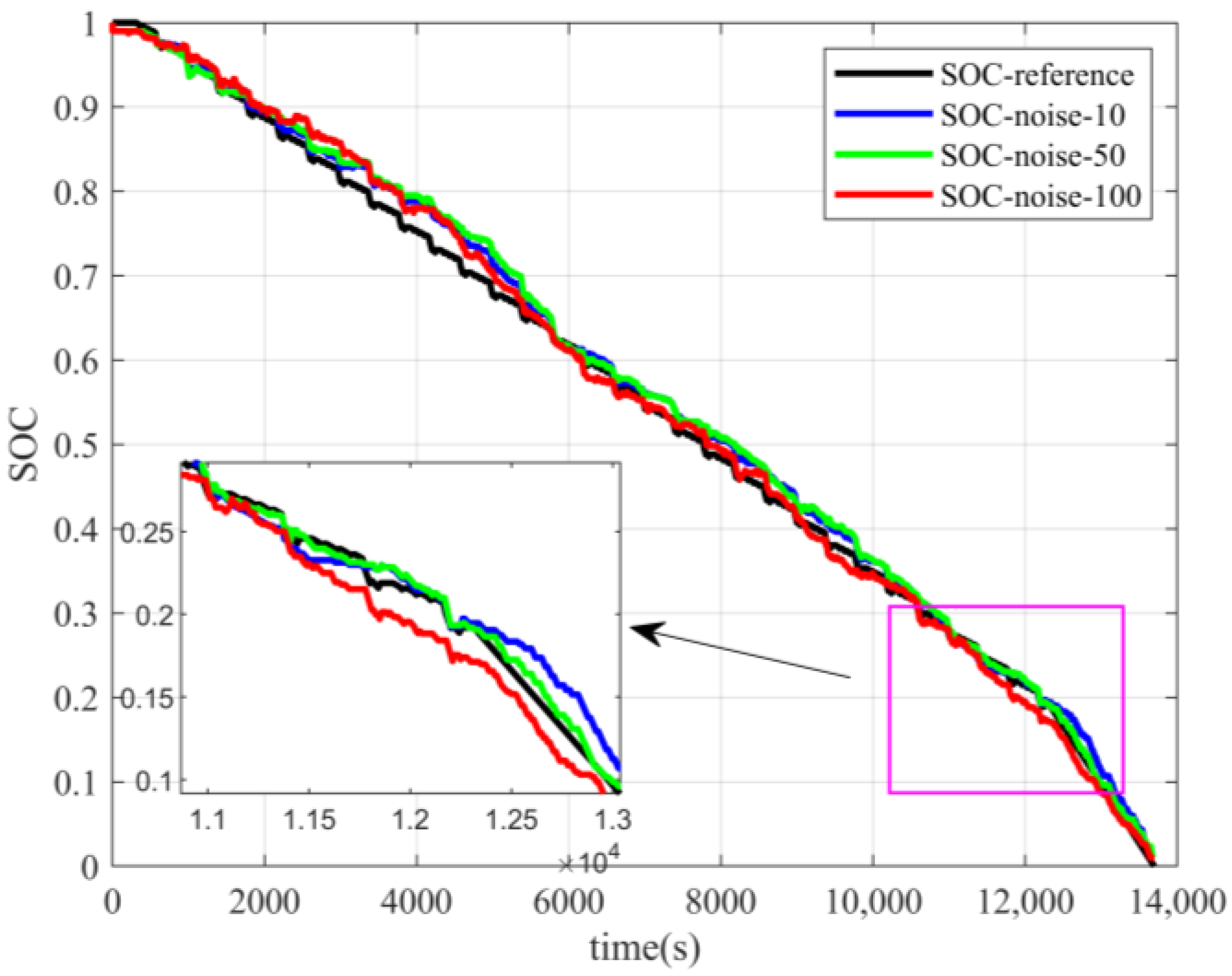
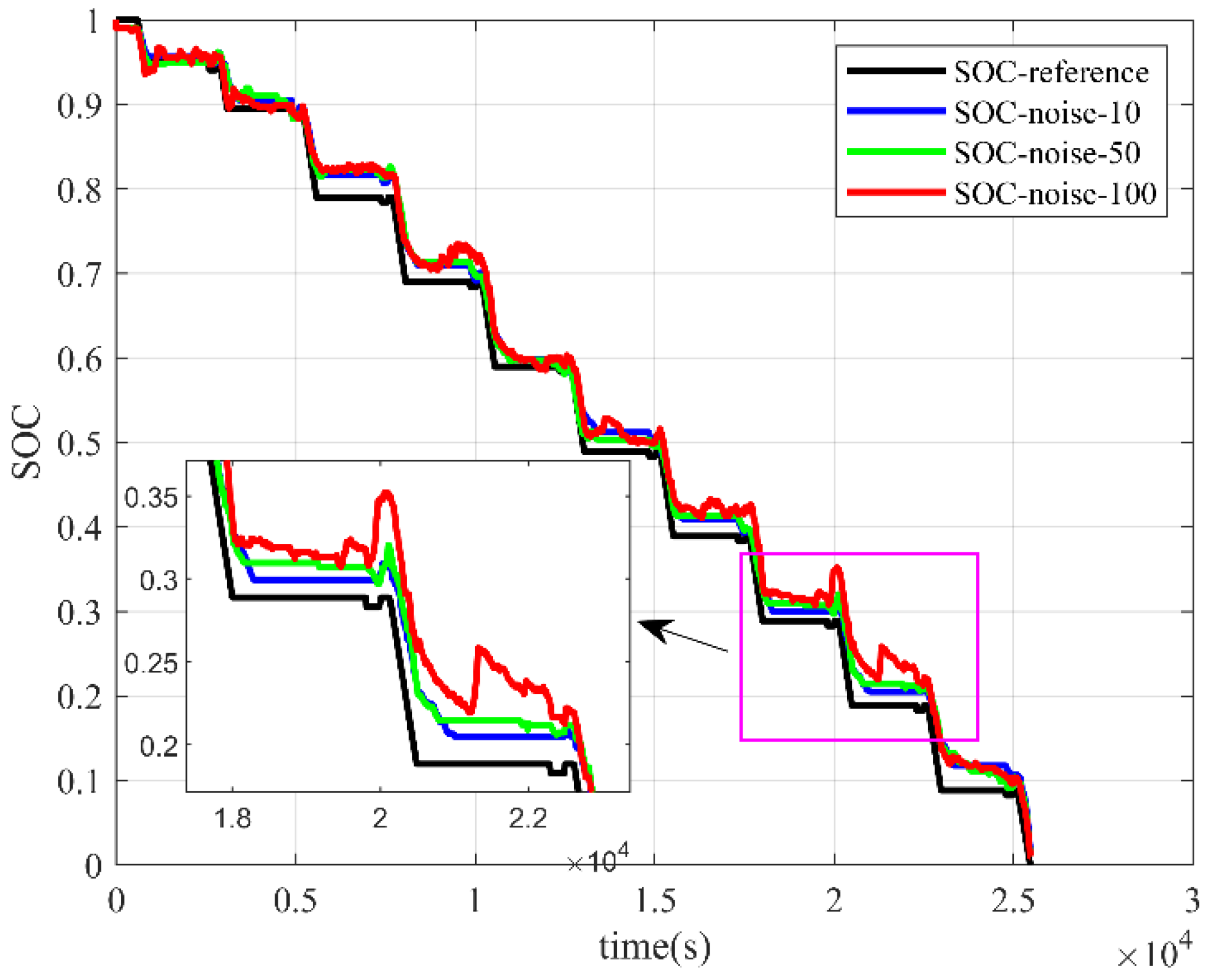
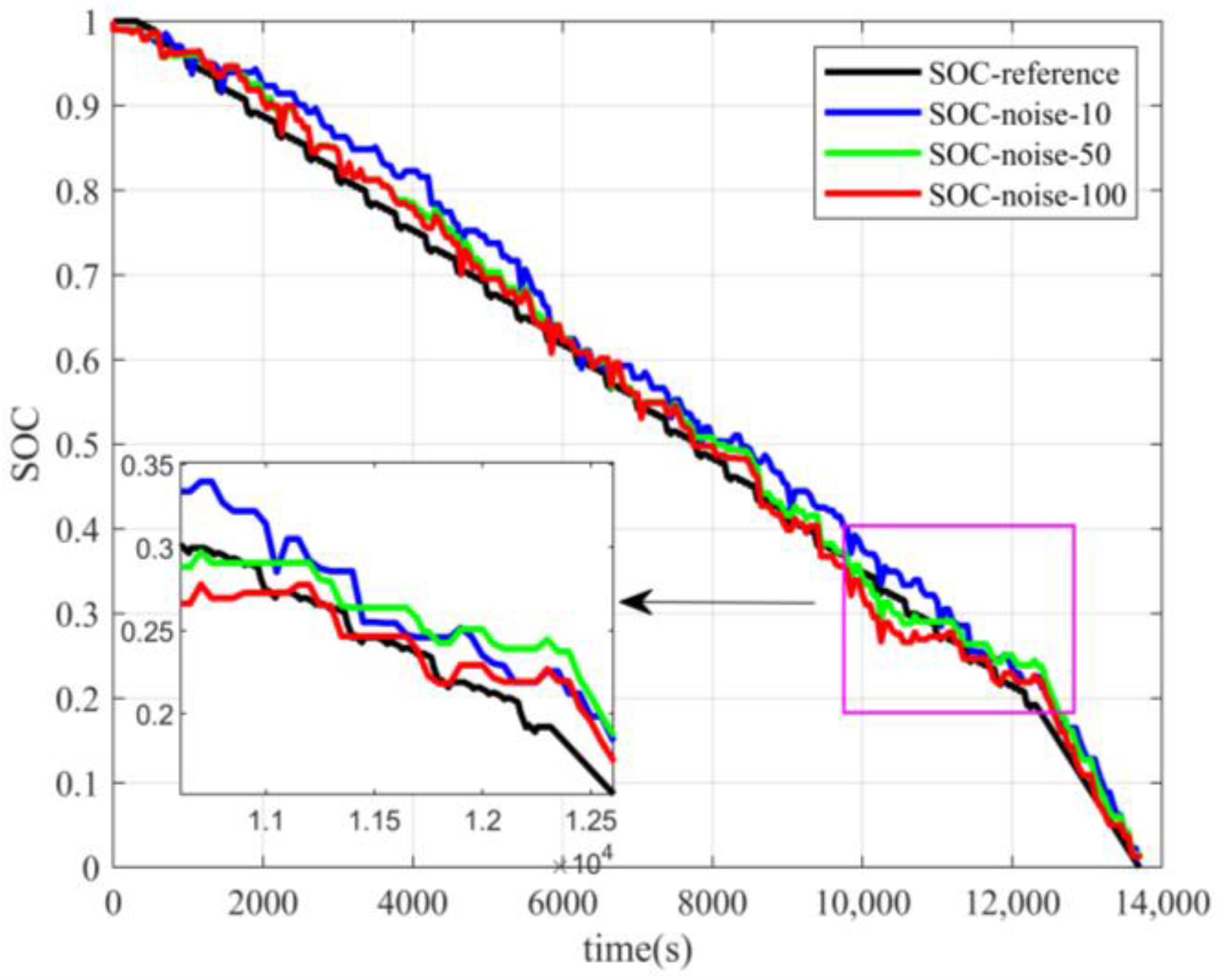
4.2.1. Incremental Seeking Method

The SOC estimation results under different voltage noise using the incremental seeking method are shown in Figure 11 and Figure 12.

When applying the incremental seeking method under voltage noise, the estimation trend was consistent with the actual reference value, and the estimation results reflected the same changes as the battery charging and discharging states.

However, the presence of voltage noise caused more irregular fluctuations in the algorithm’s estimation accuracy, resulting in large errors. This suggests that the incremental seeking method is susceptible to noise.

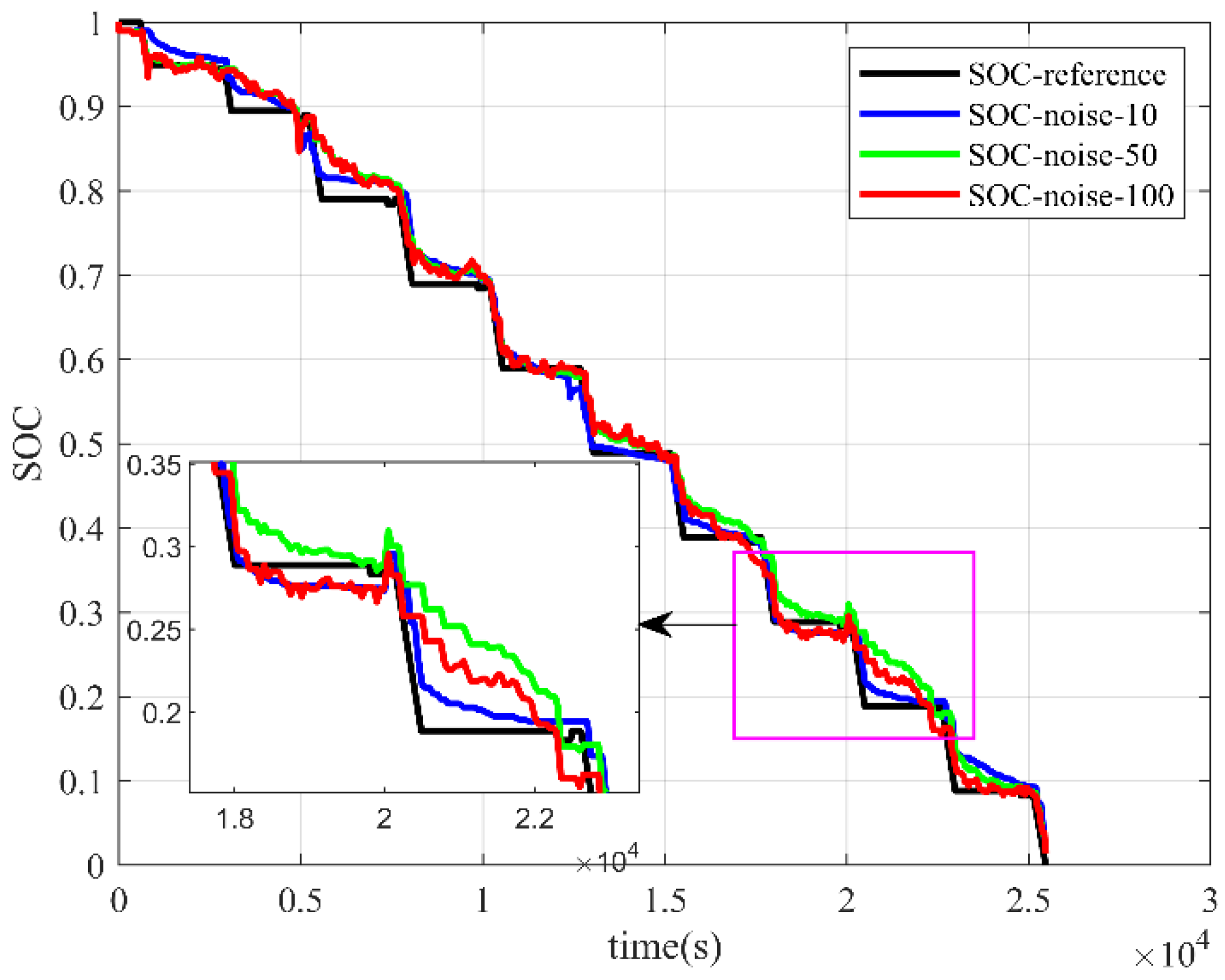
4.2.2. Dichotomous Method

The SOC estimation results using the dichotomous method with different voltage noises are shown in Figure 13 and Figure 14.

When using the dichotomous method under voltage noise, the estimation trend was consistent with the actual reference value, and the estimation result reflected the same changes as the battery charging and discharging states.

The mean error of SOC estimation is small when using the dichotomous method. However, appropriate voltage noise could improve the estimation accuracy of the algorithm, while excessive noise led to significant deviations in the results under the DST condition. This shows the poor stability of the dichotomous method.

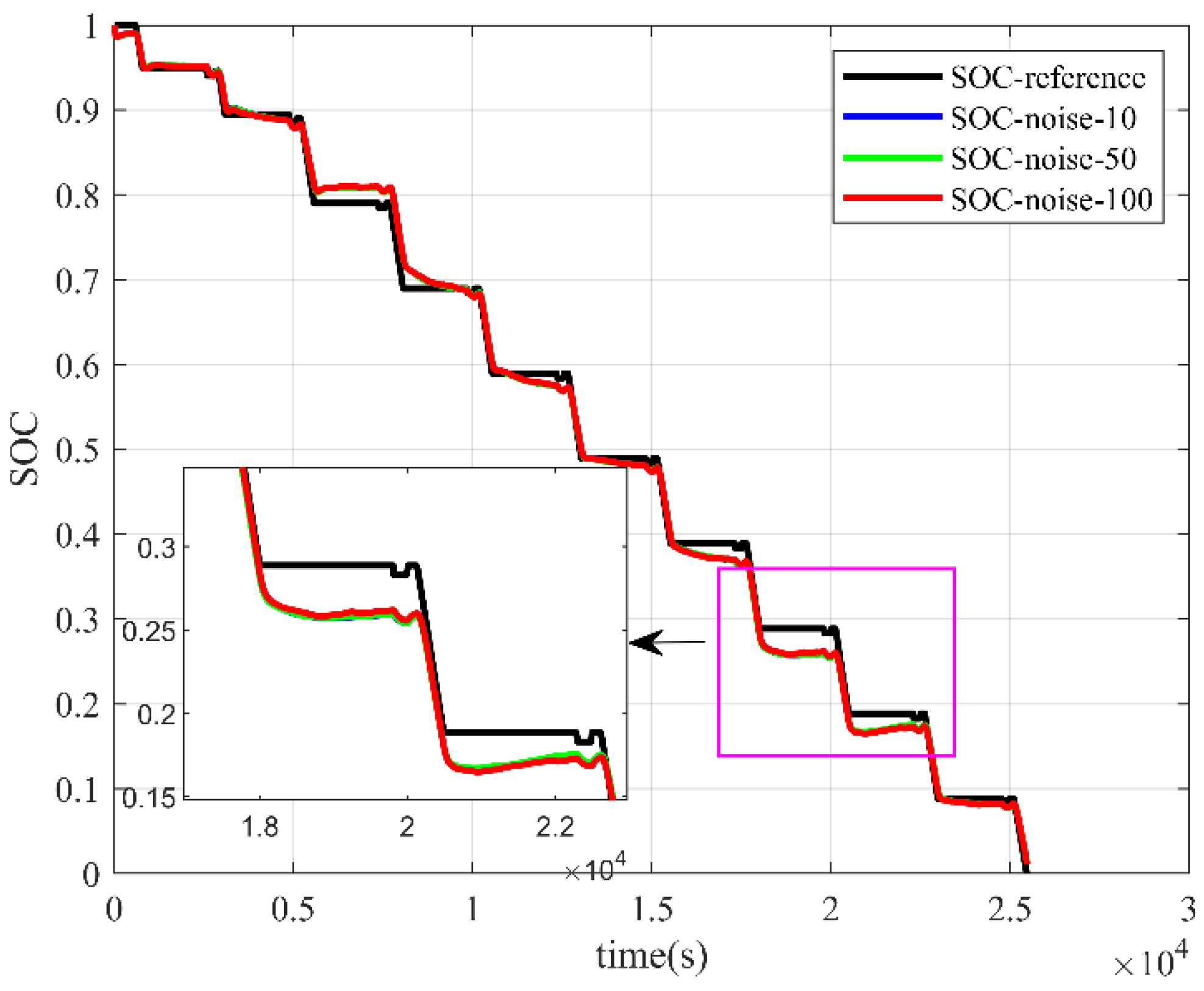
4.2.3. EKF

The SOC estimation results using the EKF algorithm with different voltage noise are shown in Figure 15 and Figure 16.

When using the EKF method under voltage noise, the estimation trend remained consistent with the actual reference value, and the estimation results could keep the same change when the charge and discharge state of the battery changed.

Overall, the EKF algorithm demonstrated a high estimation accuracy even under voltage noise, and the SOC estimation results were consistently reliable despite the presence of different levels of voltage noise.

The estimation errors of the three methods under different voltage noise are shown in

Table 5. Estimation error under different voltage noise.

		No Noise		10 mV Noise		50 mV Noise		100 mV Noise
Incremental seeking method		soc	Voltage	soc	Voltage	soc	Voltage	soc	Voltage
DST	Average value	3.58%	0.042 V	5.92%	0.044 V	5.81%	0.051 V	5.01%	0.060 V
	Maximum value	12.76%	0.300 V	11.99%	0.422 V	11.31%	0.342 V	11.14%	0.418 V
HPPC	Average value	7.62%	0.025 V	6.63%	0.026 V	6.63%	0.033 V	7.27%	0.056 V
	Maximum value	15.13%	0.373 V	14.78%	0.411 V	14.86%	0.374 V	15.58%	0.406 V
Dichotomous method		soc	Voltage	soc	Voltage	soc	Voltage	soc	Voltage
DST	Average value	1.87%	0.014 V	3.66%	0.077 V	1.83%	0.074 V	1.56%	0.082 V
	Maximum value	5.02%	0.416 V	7.34%	1.020 V	5.09%	0.685 V	7.19%	0.732 V
HPPC	Average value	4.51%	0.028 V	1.38%	0.024 V	1.54%	0.040 V	1.58%	0.057 V
	Maximum value	8.82%	0.352 V	5.74%	0.937 V	7.18%	0.520 V	6.96%	0.539 V
EKF		soc	Voltage	soc	Voltage	soc	Voltage	soc	Voltage
DST	Average value	1.94%	0.034 V	1.94%	0.034 V	1.96%	0.037 V	1.90%	0.045 V
	Maximum value	5.27%	0.414 V	5.30%	0.420 V	5.42%	0.448 V	4.98%	0.415 V
HPPC	Average value	1.13%	0.0098 V	1.13%	0.011 V	1.11%	0.020 V	1.11%	0.032 V
	Maximum value	3.69%	0.3872 V	3.67%	0.384 V	3.69%	0.375 V	3.76%	0.359 V

.

From the experimental results, we can see that the error of the EKF algorithm under different noises was within 2%, which would meet the practical requirements. The dichotomous method was the second-best and had a certain ability to fight against noise. However, the incremental seeking method exhibited the poorest performance, with the highest error, failing to meet practical requirements and requiring further improvements.

With regard to the impact of voltage noise on the algorithm’s estimation performance, the EKF algorithm effectively filtered out the noise and was almost unaffected. In contrast, both the incremental seeking and dichotomous methods were more susceptible to voltage noise, resulting in lower stability and accuracy.

4.3. Algorithm Computational Efficiency

Because the process of completing the overall battery SOC estimation was long, the computational efficiency of the three algorithms was considered by comparing the time required to perform a single SOC estimation among them.

The algorithms were run in the following environment: under PC conditions using processor: Intel (R) Core (TM) i5-10200H CPU @ 2.40 GHz, RAM configuration:16.00 GB, and MATLAB software.

The time consumption of all algorithms is shown in

Table 6. Algorithm operation schedule.

	Algorithm	Incremental Seeking Method	Dichotomous Method	EKF
Work Conditions
DST	Total time	331 s	250 s	171 s
	Average data estimation time per frame	0.024 s	0.018 s	0.012 s
HPPC	Total time	636 s	498 s	191.0 s
	Average data estimation time per frame	0.025 s	0.020 s	0.007 s

. The incremental pathfinding method took 0.024 s and 0.025 s to complete a single SOC estimation without a current sensor under the two operating conditions. The dichotomous method took 0.018 s and 0.02 s. The EKF algorithm took 0.012 s and 0.007 s. The ratio of the calculated efficiencies of the three methods at DST conditions is about 2:3:4.

4.4. Repeatability Verification

In order to avoid the chance of single battery data, more test data of LCO lithium-ion batteries were used to verify the reliability of the algorithm. The HPPC operation data of more batches of batteries were used to verify the algorithm. The average error is shown in

Table 7. Estimation error at different initial SOC states in HPPC conditions.

	Accurate Initial SOC		Initial SOC 0.9		Initial SOC 0.7
Incremental seeking method	soc	Voltage	soc	Voltage	soc	Voltage
Average value	7.59%	0.026 V	7.74%	0.030 V	9.16%	0.041 V
Maximum value	15.72%	0.336 V	15.21%	0.339 V	30%	0.697 V
Dichotomous method	soc	Voltage	soc	Voltage	soc	Voltage
Average value	3.23%	0.026 V	3.41%	0.029 V	5.42%	0.037 V
Maximum value	7.73%	0.336 V	10.00%	0.287 V	30%	0.276 V
EKF	soc	Voltage	soc	Voltage	soc	Voltage
Average value	3.06%	0.010 V	3.67%	0.010 V	4.73%	0.011 V
Maximum value	9.07%	0.308 V	11.22%	0.4003 V	30.16%	0.4003 V

.

In order to ensure the reliability of the algorithm, the simulation results of constant current charge-discharge test data of the LFP lithium-ion battery are also presented. When the initial SOC is accurate, the average error results of the EKF algorithm are shown in

Table 8. Average error of EKF algorithm for eight batteries.

Battery Number	A	B	C	D	E	F	G	H
SOC	1.99%	1.67%	1.08%	1.76%	1.73%	1.52%	1.46%	1.56%
Voltage	0.0185 V	0.0168 V	0.0203 V	0.0189 V	0.0177 V	0.173 V	0.0180 V	0.0180 V

.

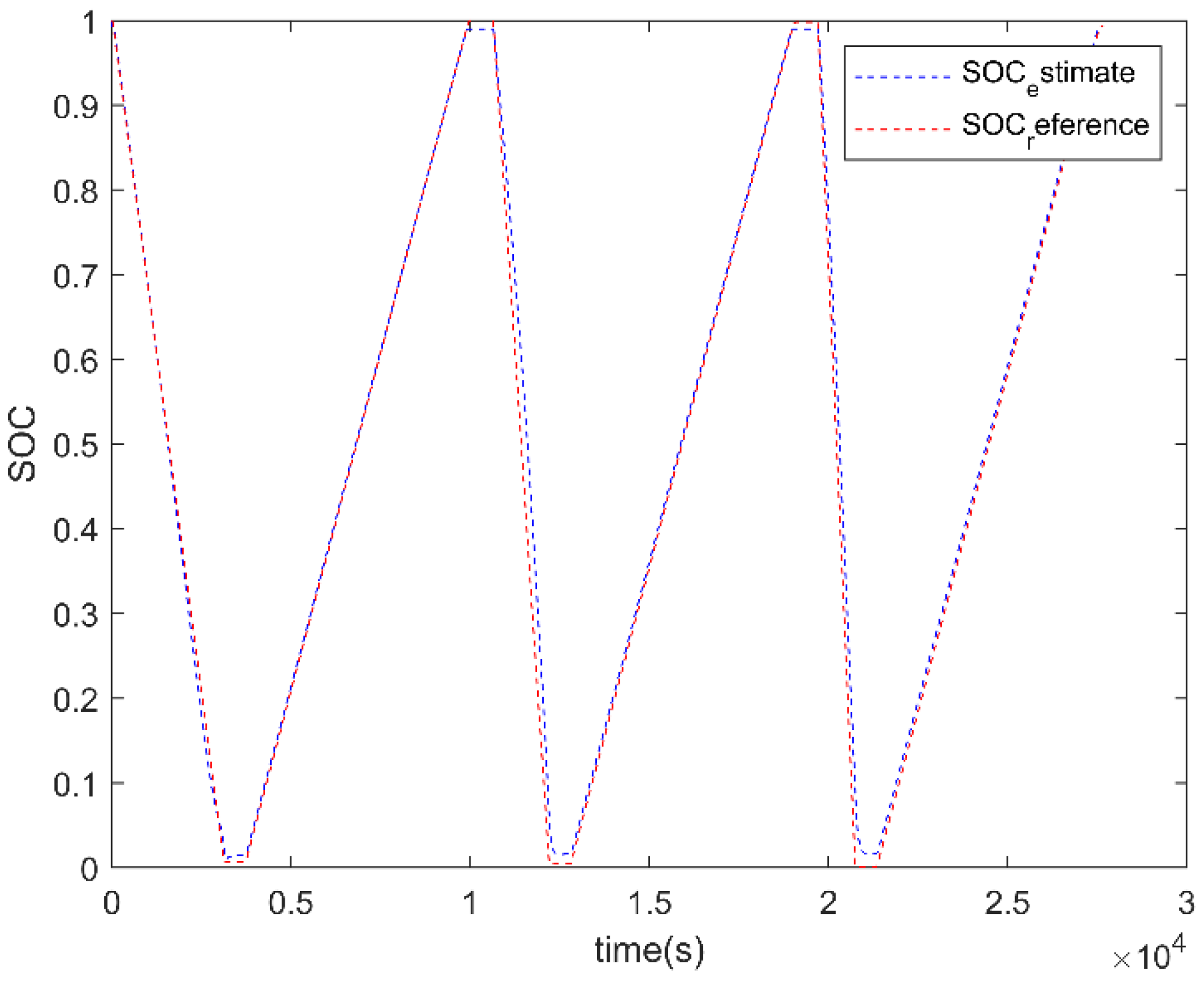
The SOC estimation results of the battery numbered A are shown in Figure 17.

When using different battery test data, the EKF algorithm can still maintain a good estimation effect.

5. Conclusions

It is important to obtain current information for accurate SOC estimation of lithium-ion batteries. However, due to concerns about cost, size, and power consumption, current sensors are sometimes not equipped in portable devices.

In this work, three methods were developed for lithium battery SOC estimation that provide new solutions for SOC estimation for small portable devices in the absence of current monitoring and fill the gap in existing studies. The dichotomous and incremental seeking methods were found to be sensitive to initial SOC accuracy, and estimation errors exceeded the allowed range. For instance, using the dichotomous method led to a 6.37% error at an initial SOC of 70% under HPPC conditions. The incremental seeking method was also more susceptible to voltage noise than the other two methods, with a 10 mV noise causing an estimation error of 5.92% in DST conditions.

The dichotomous method and the extended Kalman filter method demonstrated superior accuracy in the presence of certain measurement noises, with estimation errors under 100 mV noise controlled within ±2%. The extended Kalman filter algorithm was particularly effective in filtering out the noise, with error variation following noise addition not exceeding 0.04%. Additionally, the extended Kalman filter method outperformed the other two methods in terms of estimation speed, with an average time of 0.01 s per frame of data estimated.

In addition, it is worth noting that the estimation error of SOC will be larger when the initial SOC error is large due to the absence of current input. However, measures can be taken to avoid excessive errors. For example, the battery is left for a period of time, and the battery is calibrated by OCV after it is fully charged. In that case, this weakness does not affect the usefulness and sophistication of the algorithms used.

Considering the aging process of the battery, the battery model parameters will change, leading to an increase in SOC estimation error. In order to solve this problem, a possible approach is to use an improved extended Kalman filter (IEKF) algorithm [32] or a model adaptive EKF (MAEKF) [33] algorithm. The general idea is to select the parameters of the electrical model with high sensitivity. In view of the fact that the battery voltage derivative changes abruptly twice with time when the discharge current is constant, the parameters are updated using IEKF or MAEKF. Thus, the excellent accuracy of the model is maintained during the aging process of the battery.