Determination of the Contact Resistance of Planar Contacts: Electrically Conductive Adhesives in Battery Cell Connections
Abstract
:1. Introduction
- How does the setup influence the contact resistance measurement accuracy?
- How can the contact resistance be determined as a function of the contact area?
Electrical Joining Techniques
2. Basics of Electrically Conductive Adhesives
3. Experimental
3.1. Measurement of Electrical Contact Resistance
3.1.1. Phenomena at the Current Injection
3.1.2. Method to Calculate the Electrical Connection Resistance within Planar Contacts
3.1.3. Performing the Measurement
4. Results
4.1. Comparison of Joining Techniques in Terms of Electrical Connection Resistance and Ultimate Tensile Force
4.2. Discussion
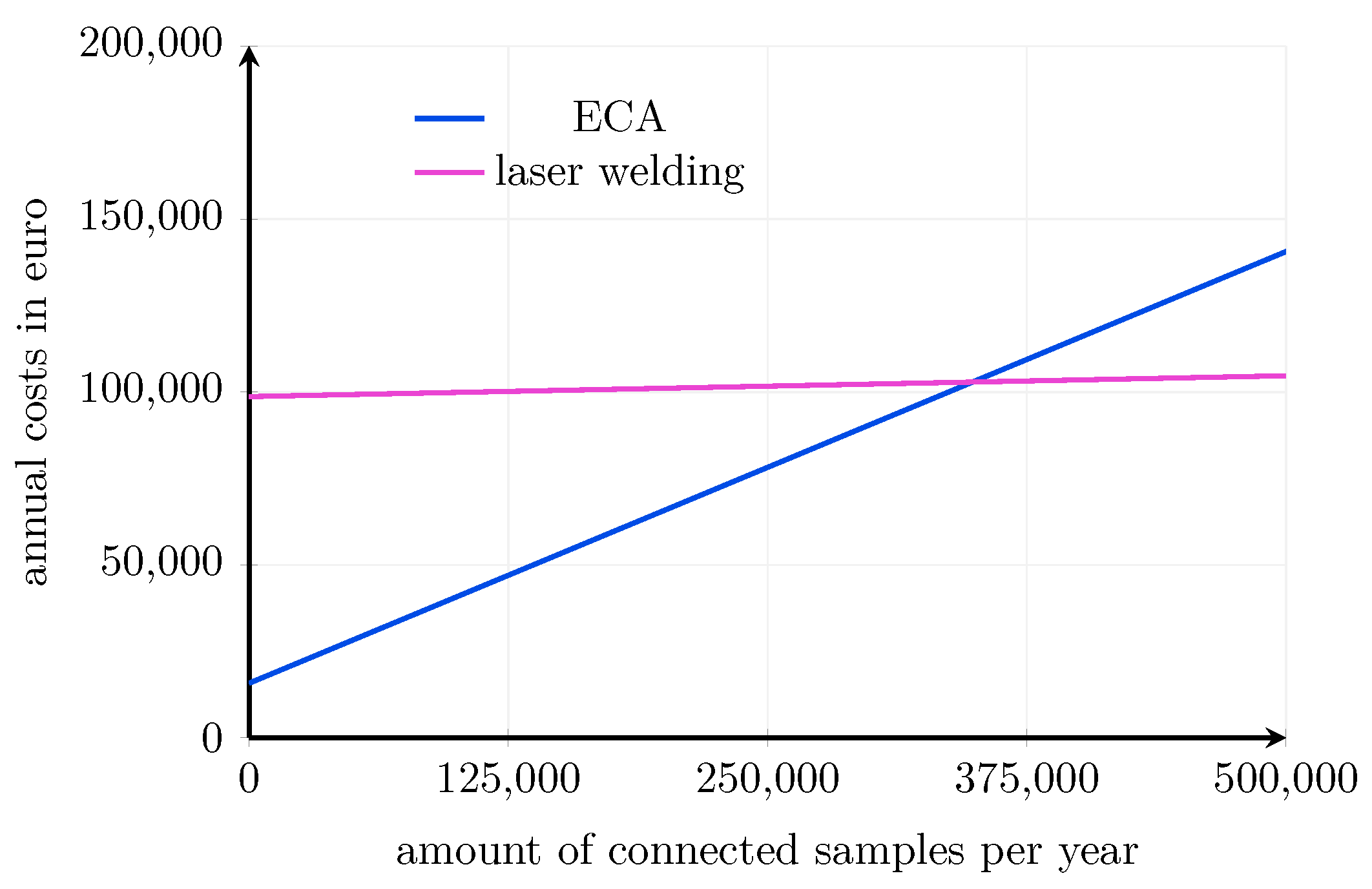
4.3. Economic Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A | adhesive |
| ACA | anisotropically conductive adhesive |
| CI | confidence interval |
| C | cohesive |
| ECD | Equivalent Circuit Diagram |
| ECM | electrical circuit model |
| contact resistance | |
| ECA | electrically conductive adhesives |
| EV | electric vehicle |
| μ | expected value |
| FEM | finite element method |
| ICA | isotropically conductive adhesive |
| UTF | ultimate tensile force |
| MUX | multiplexer |
| NCA | non-conductive adhesive |
| UTF | ultimate tensile force |
| UTM | universal testing machine |
| TCA | thermally conductive adhesives |
| VDA | German Association of the Automotive Industry |
Appendix A. Test Bench

Appendix B. Force–Displacement Curve
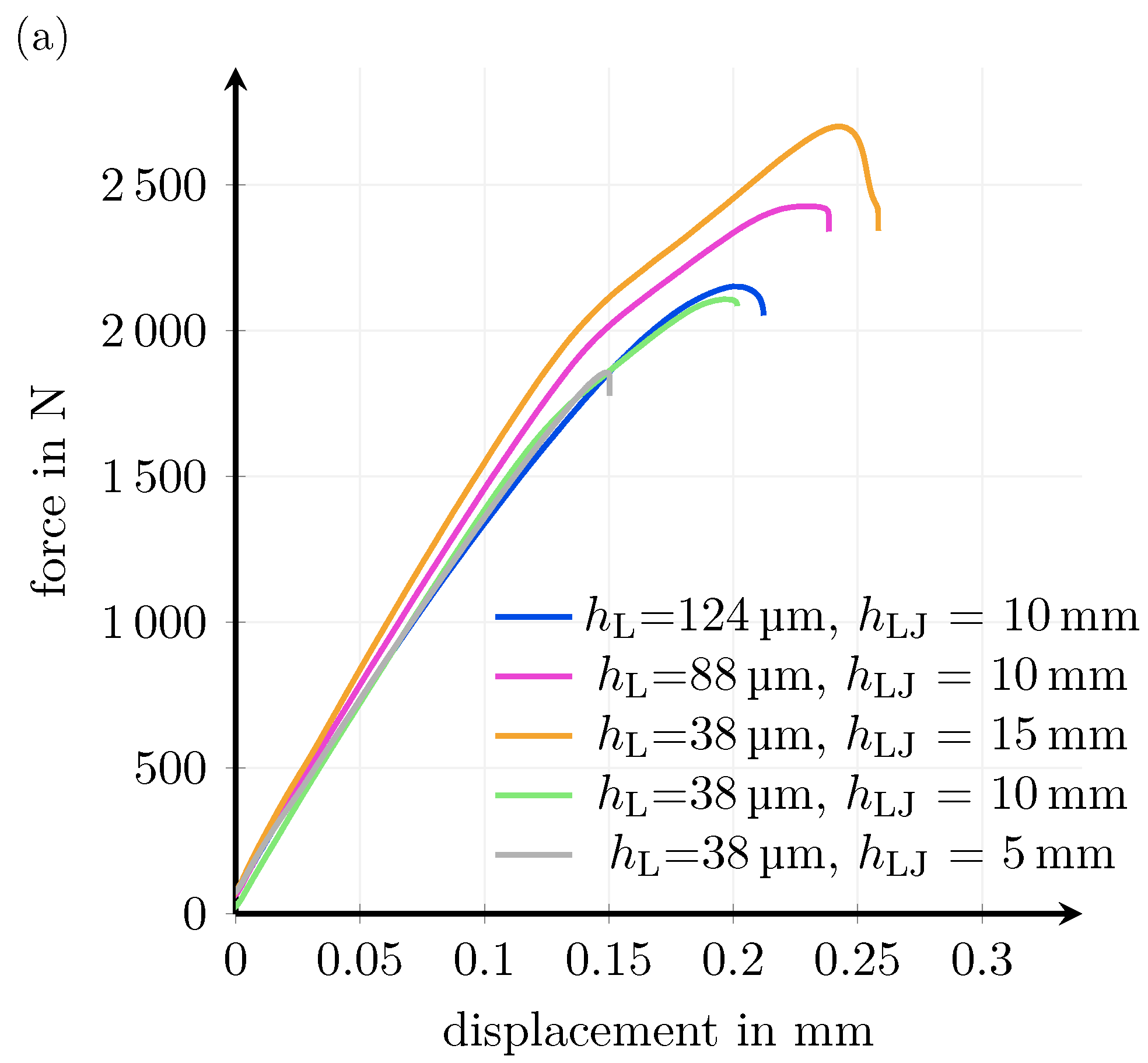
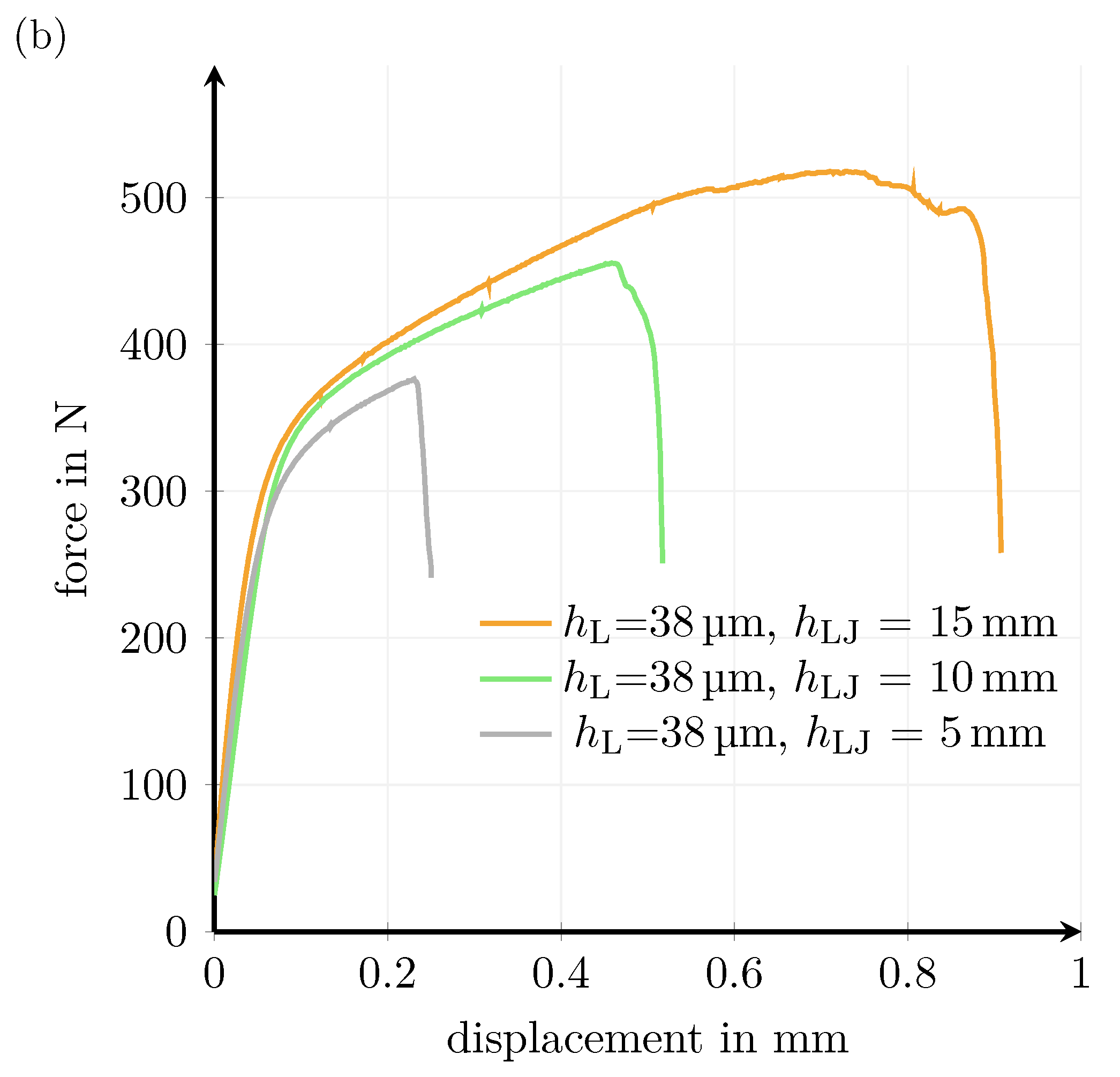
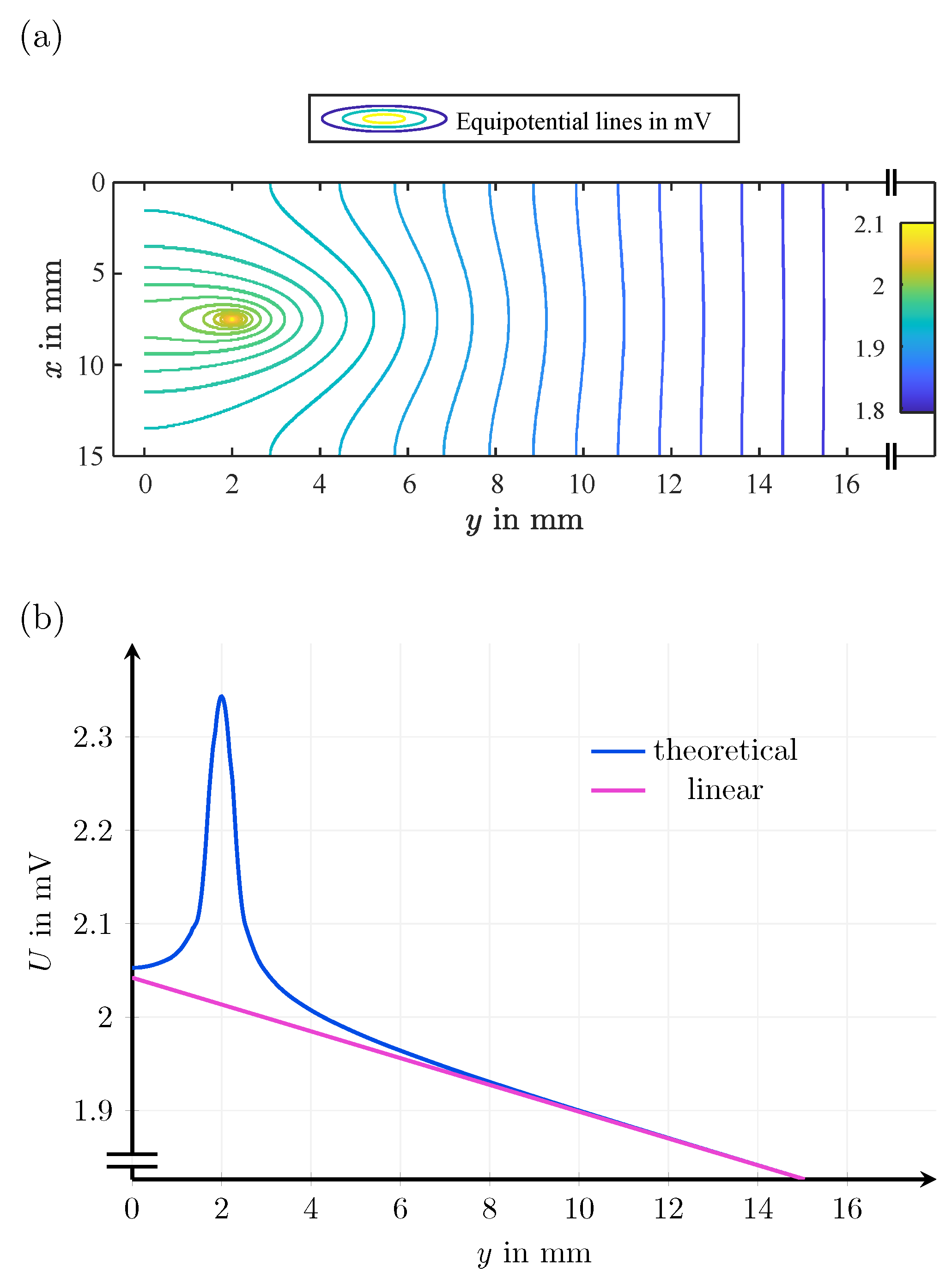
Appendix C. Theoretical Consideration of the Influence of Current Injection on the Voltage Measurement
Appendix C.1. Formulation of the Problem
Appendix C.2. Governing Equations and the Infinite Plate Problem
Appendix C.3. The Finite Plate Problem
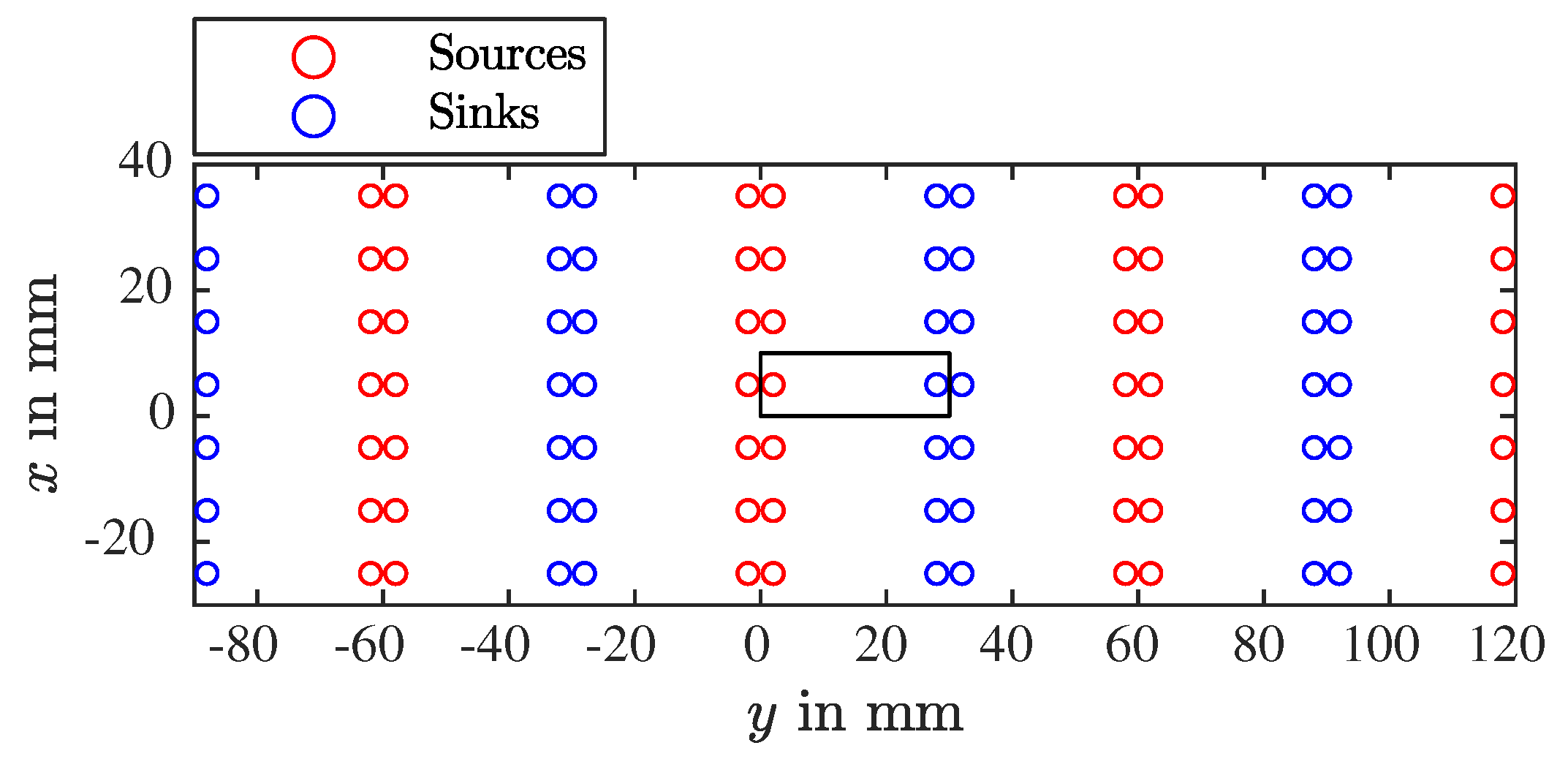
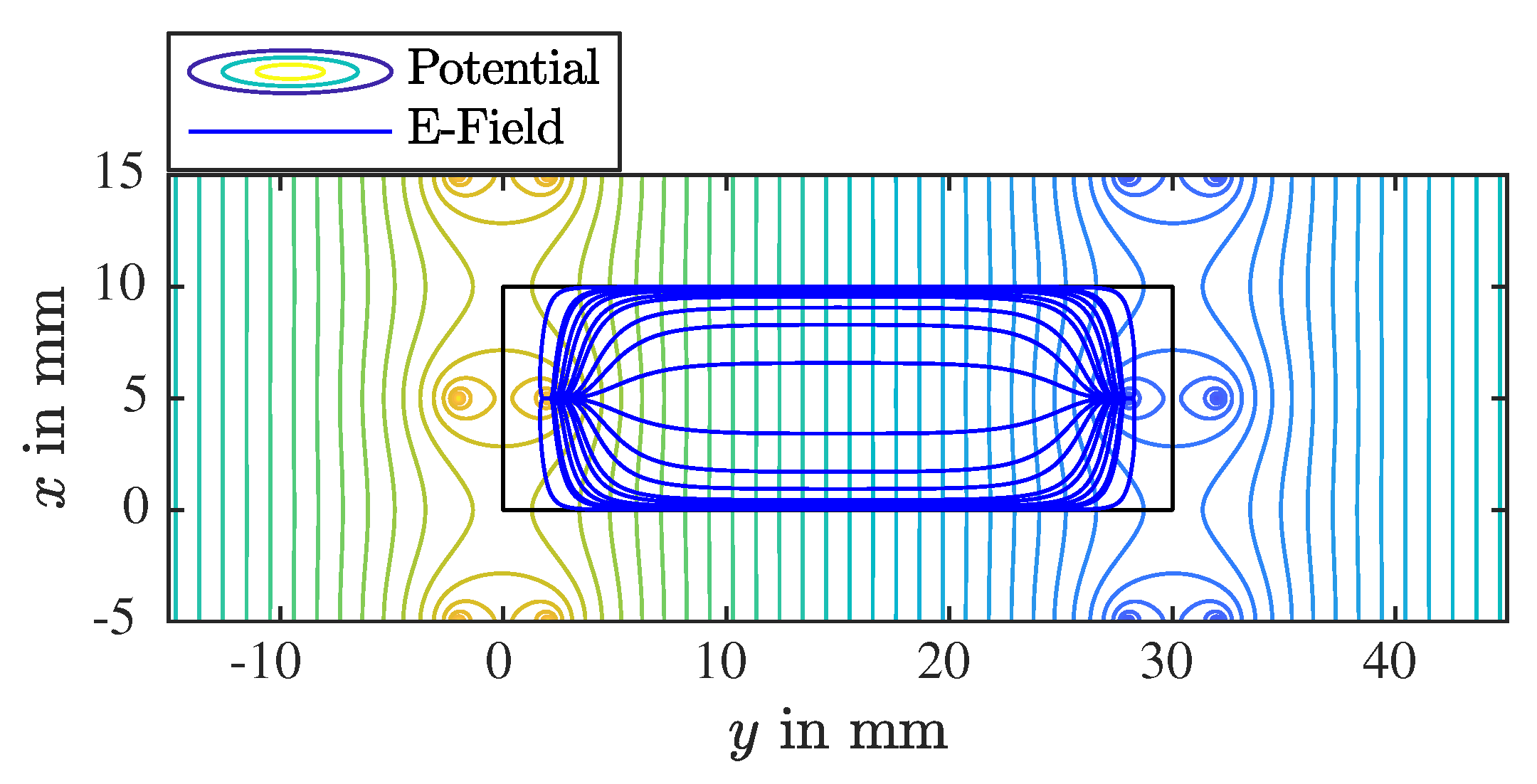
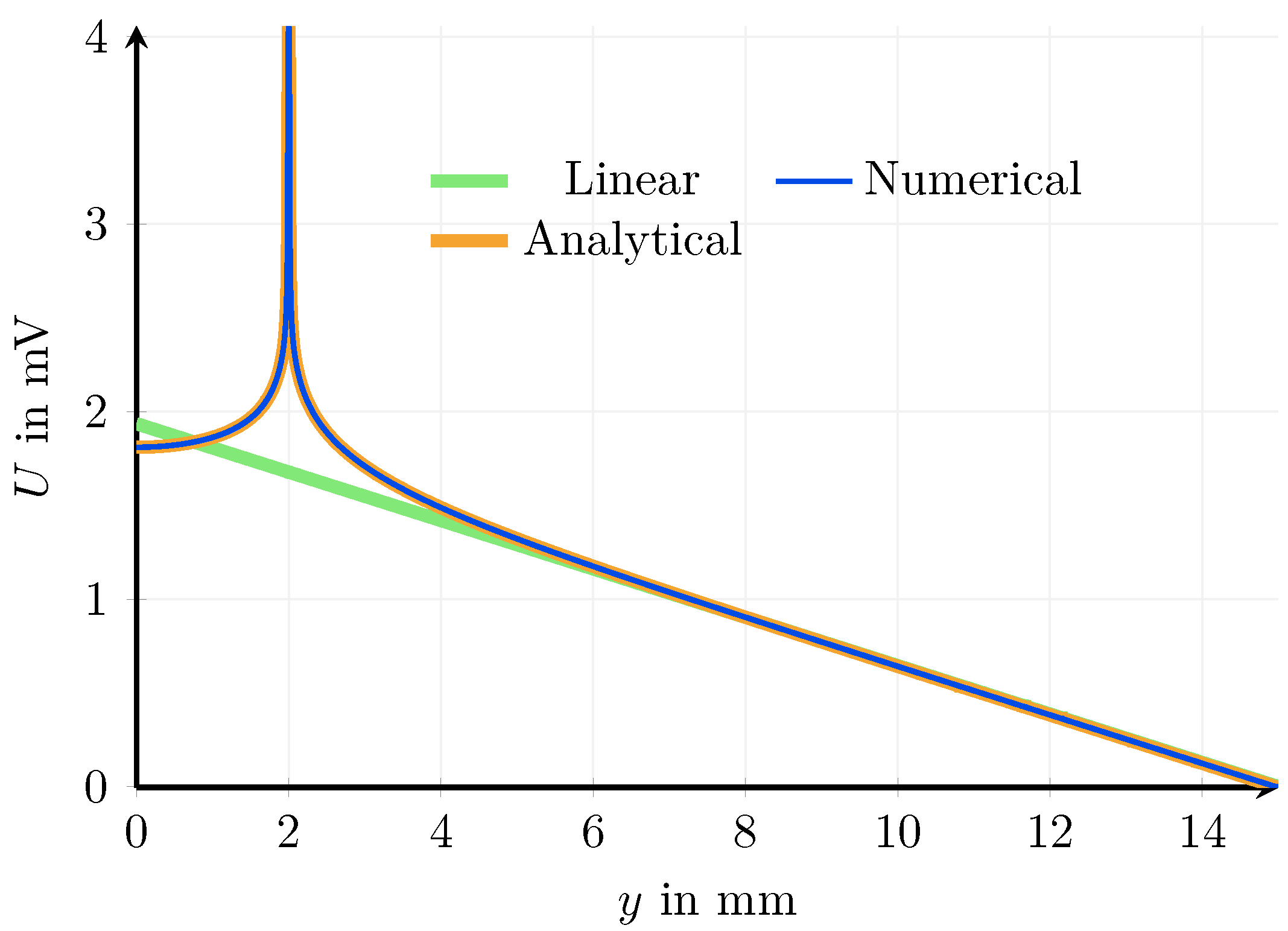
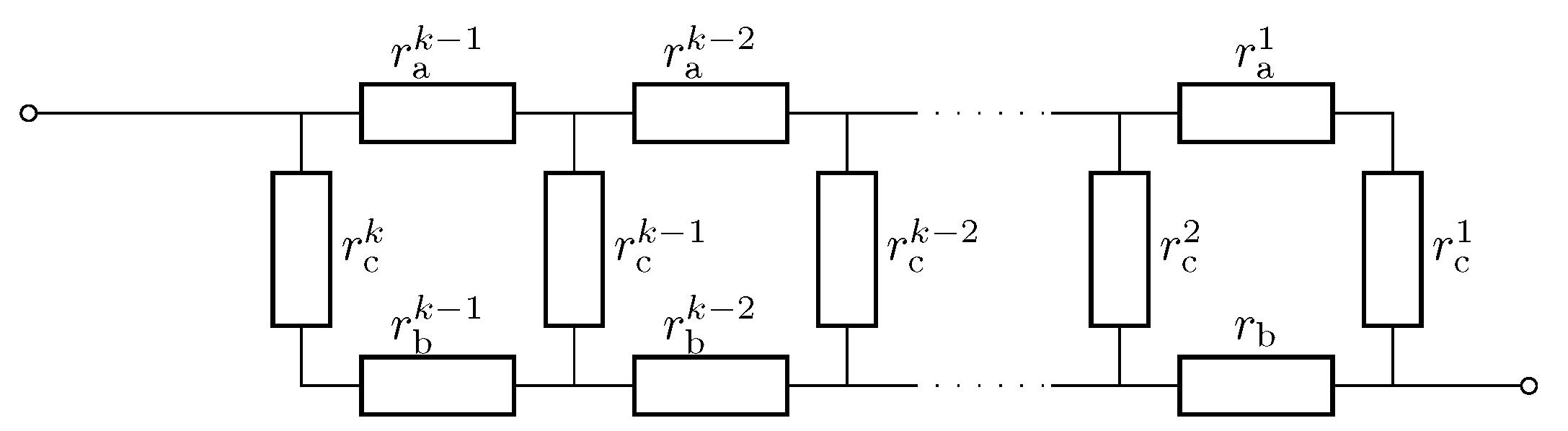
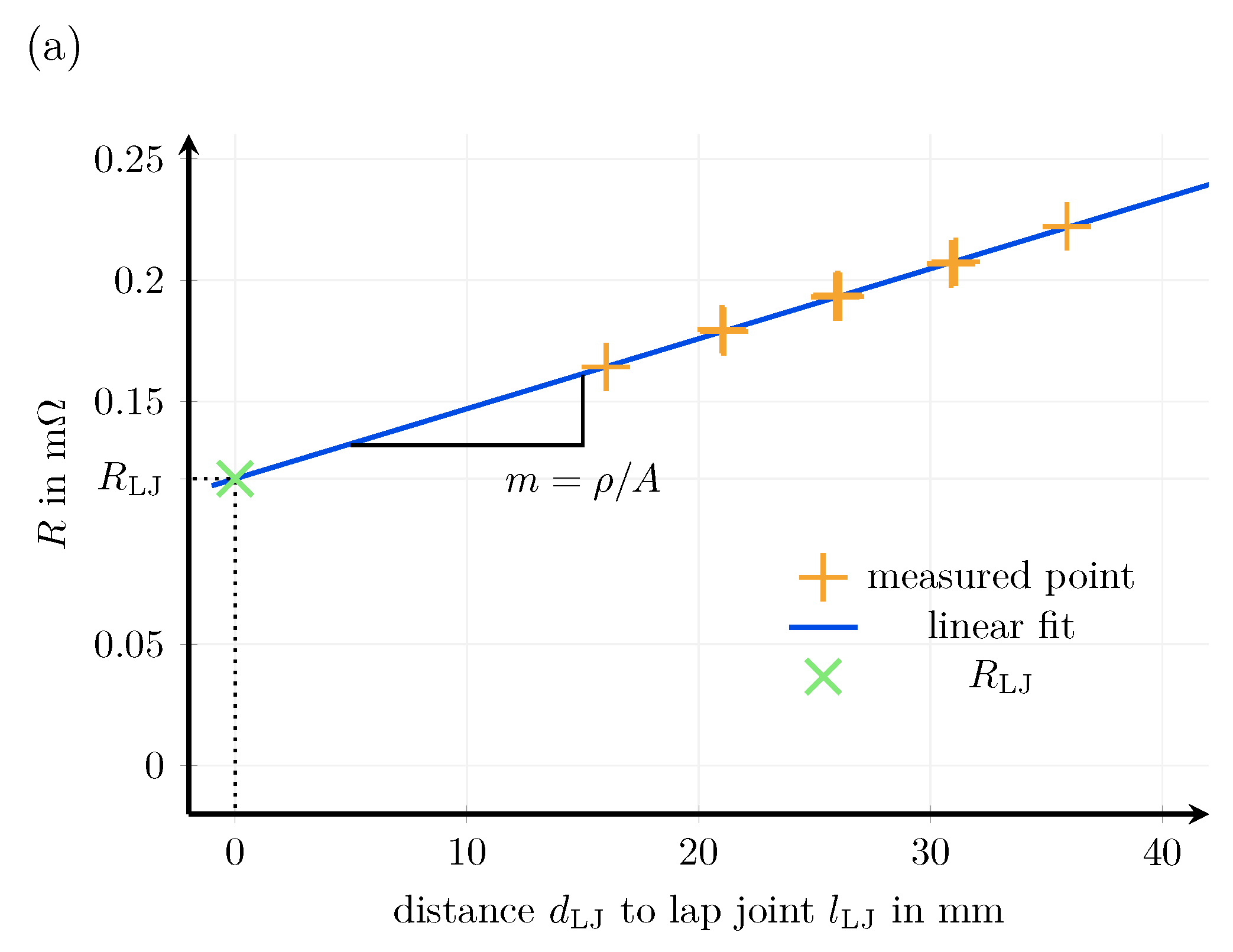
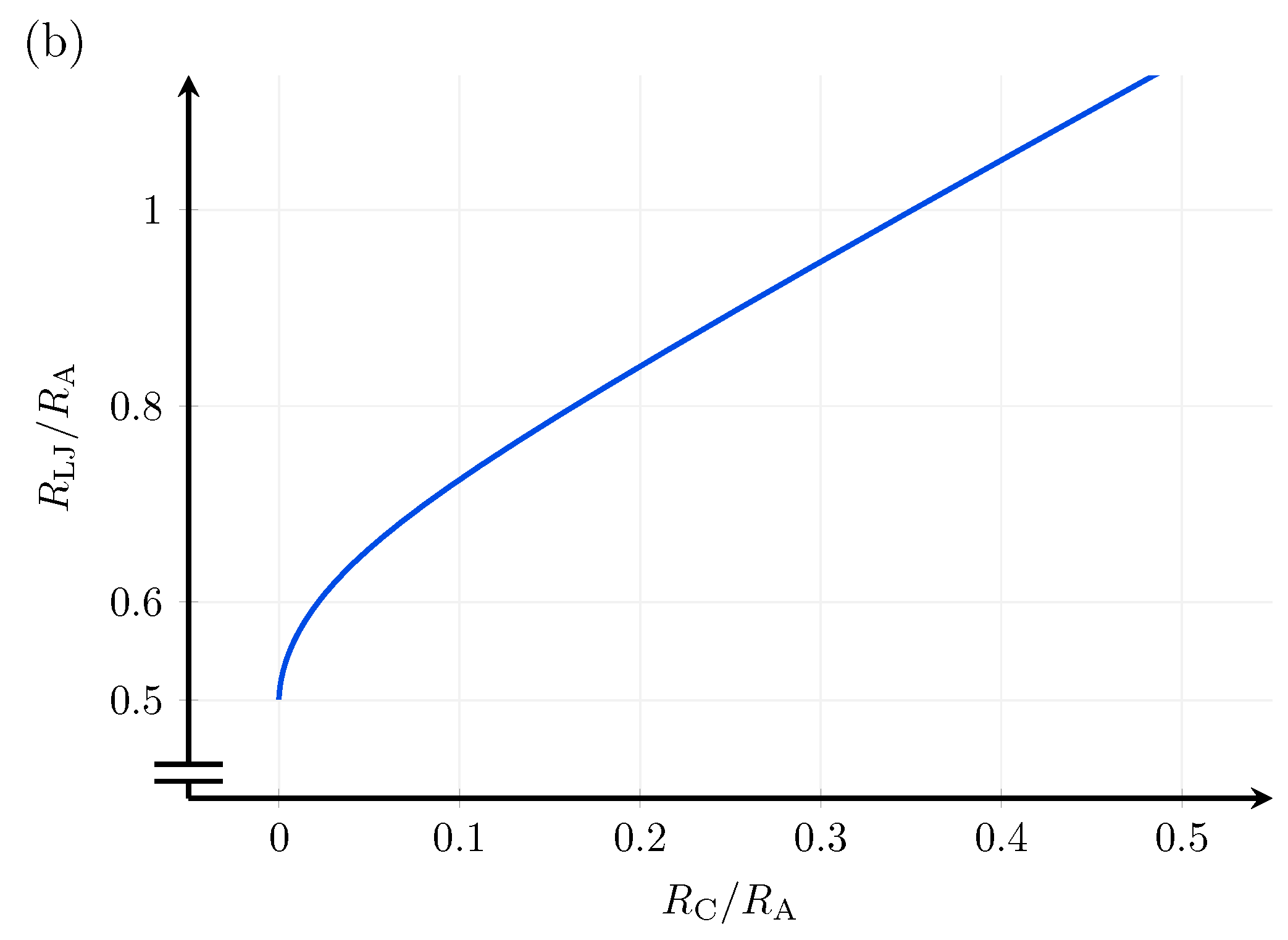
Appendix D. Resistance of An Adhesive Joining
Appendix D.1. Derivation of the Recursive Formula
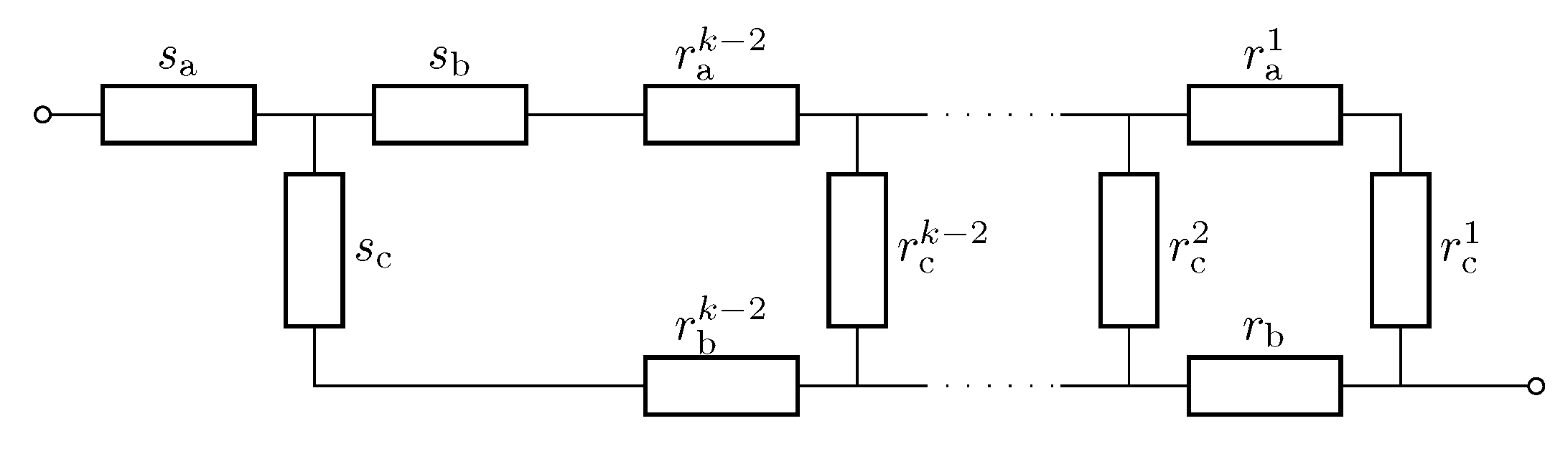
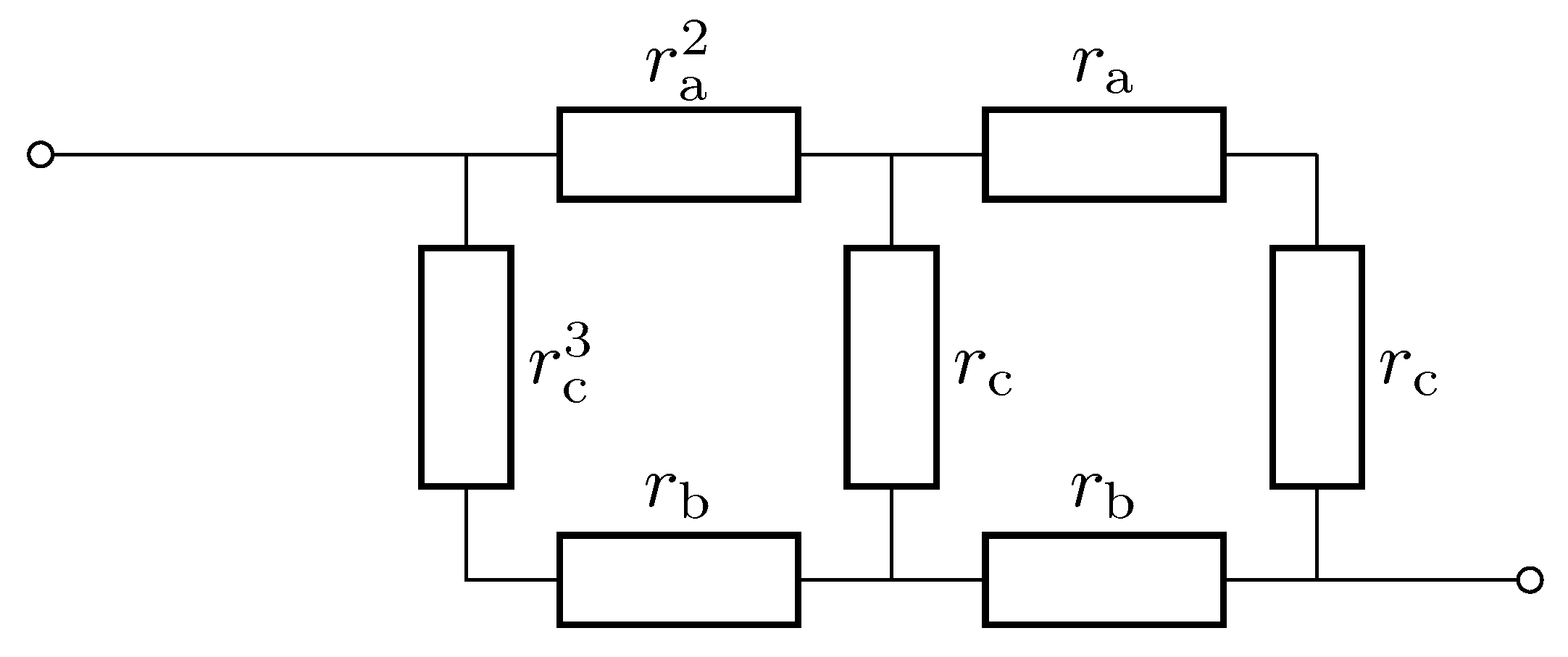

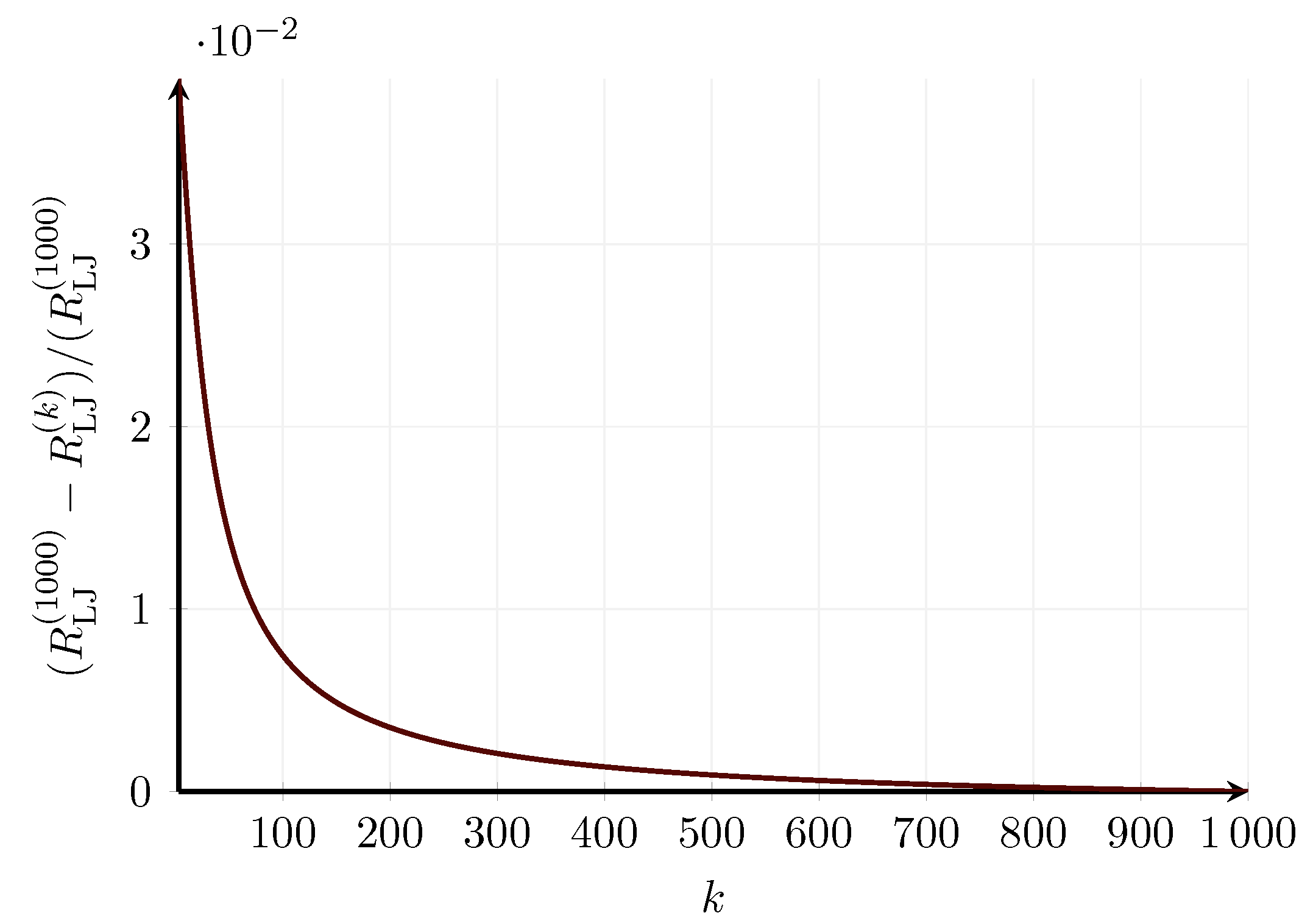
Appendix D.2. Convergence
Appendix E. Economical Evaluation
| Costs | Data | ECA | Laser Beam Welding |
|---|---|---|---|
| Machine | |||
| (1) | Acquisition | EUR 50,000 | EUR 453,000 |
| (2) | Useful life | 5 y | 5 y |
| (3) | Working hours | 3392 /y | 3392 /y |
| (4) | Plant availability | 90% | 90% |
| Fixed | |||
| (5) | Interest rate | 1.14% | 1.14% |
| (6) | Space requirement | 10 | 10 |
| (7) | Operating cost rate | 550 euro/ | 550 euro/ |
| (8) | Nominal power | 10 W | 8 W |
| (9) | Utilization rate | 100% | 100% |
| (10) | Electricity price | 0.225/kWh | 0.225/kWh |
| (11) | Maintenance cost rate | 7% | 7% |
| Variable | |||
| (12) | Labor costs | euro/ | euro/ |
| (13) | Total cycle time | 20 /sample | 1 /sample |
| (14) | Adhesive | euro/ | 0 |
| (15) | Spacer | euro/ | 0 |
| (16) | Adhesive per sample | 0.0045 g/sample | 0 |
| (17) | Spacer per sample | 0.000025 g/sample | 0 |
| Costs | Formula | ECA | Laser Beam Welding | |
|---|---|---|---|---|
| fixed | acc. Table A1 | |||
| (18) | Depreciation | |||
| (19) | Interest cost per hour | |||
| (20) | Room cost per hour | |||
| (21) | ∑ of fixed costs—machine hours | |||
| (22) | ∑ of fixed costs | 15,785 euro/y | 98,682.1 euro/y | |
| variable | ||||
| (23) | Energy | |||
| (24) | Maintenance | |||
| (25) | Labor | |||
| (26) | Material | |||
| (27) | Material | (26)(3600)/(13) | ||
| (28) | ∑ of variable costs | |||
| (29) | ∑ of variable costs | |||
| (30) | Max. number of samples per year | samples/y | 10,990,080 samples/y |
| Cell | Diameter or Lengths of Edges | 90% Area | Adhesive Thickness | Adhesive Volume |
|---|---|---|---|---|
| At the positive pole in cm | In cm | In µm | In | |
| 18650 | 0.8 | 0.4072 | 38 | 0.001547 |
| 21700 | 1 | 0.6362 | 38 | 0.002417 |
| 4680 | 1.5 | 1.431 | 38 | 0.005439 |
| BEV2 | 5.832 | 38 | 0.02216 |
References
- Das, A.; Li, D.; Williams, D.; Greenwood, D. Joining Technologies for Automotive Battery Systems Manufacturing. World Electr. Veh. J. 2018, 9, 22. [Google Scholar] [CrossRef]
- Brand, M.J.; Schmidt, P.A.; Zaeh, M.F.; Jossen, A. Welding techniques for battery cells and resulting electrical contact resistances. J. Energy Storage 2015, 1, 7–14. [Google Scholar] [CrossRef]
- Brand, M.J.; Berg, P.; Kolp, E.I.; Bach, T.; Schmidt, P.; Jossen, A. Detachable electrical connection of battery cells by press contacts. J. Energy Storage 2016, 8, 69–77. [Google Scholar] [CrossRef]
- Brand, M.J.; Kolp, E.I.; Berg, P.; Bach, T.; Schmidt, P.; Jossen, A. Electrical resistances of soldered battery cell connections. J. Energy Storage 2017, 12, 45–54. [Google Scholar] [CrossRef]
- Reichel, A.; Sampaio, R.F.; Pragana, J.P.; Bragança, I.M.; Silva, C.M.; Martins, P.A. RForm-fit joining of hybrid busbars using a flexible tool demonstrator. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2022, 236, 1164–1175. [Google Scholar] [CrossRef]
- Bolsinger, C.; Zorn, M.; Birke, K.P. Electrical contact resistance measurements of clamped battery cell connectors for cylindrical 18650 battery cells. J. Energy Storage 2017, 12, 29–36. [Google Scholar] [CrossRef]
- Wassiliadis, N.; Ank, M.; Wildfeuer, L.; Kick, M.K.; Lienkamp, M. Experimental investigation of the influence of electrical contact resistance on lithium-ion battery testing for fast-charge applications. Appl. Energy 2021, 295, 117064. [Google Scholar] [CrossRef]
- Aradhana, R.; Mohanty, S.; Nayak, S.K. A review on epoxy-based electrically conductive adhesives. Int. J. Adhes. Adhes. 2020, 99, 102596. [Google Scholar] [CrossRef]
- Mostafavi, S.; Hesser, D.F.; Markert, B. Effect of process parameters on the interface temperature in ultrasonic aluminum wire bonding. J. Manuf. Process. 2018, 36, 104–114. [Google Scholar] [CrossRef]
- Kim, T.H.; Yum, J.; Hu, S.J.; Spicer, J.P.; Abell, J.A. Process robustness of single lap ultrasonic welding of thin, dissimilar materials. CIRP Ann. 2011, 60, 17–20. [Google Scholar] [CrossRef]
- Siddiq, A.; Ghassemieh, E. Thermomechanical analyses of ultrasonic welding process using thermal and acoustic softening effects. Mech. Mater. 2008, 40, 982–1000. [Google Scholar] [CrossRef]
- Choi, S.; Fuhlbrigge, T.; Nidamarthi, S. Vibration analysis in robotic ultrasonic welding for battery assembly. In Proceedings of the 2012 IEEE International Conference on Automation Science and Engineering (CASE), Seoul, South Korea, 20–24 August 2012; pp. 550–554. [Google Scholar] [CrossRef]
- Katayama, S. Fundamentals and Details of Laser Welding; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Kick, M.K.; Kuermeier, A.; Stadter, C.; Zaeh, M.F. Weld Seam Trajectory Planning Using Generative Adversarial Networks. In Towards Sustainable Customization: Bridging Smart Products and Manufacturing Systems; Lecture Notes in Mechanical, Engineering; Andersen, A.L., Andersen, R., Brunoe, T.D., Larsen, M.S.S., Nielsen, K., Napoleone, A., Kjeldgaard, S., Eds.; Springer International Publishing: Cham, Switzerland, 2022; Volume 248, pp. 407–414. [Google Scholar] [CrossRef]
- Grabmann, S.; Mayr, L.; Kick, M.K.; Zaeh, M.F. Enhancing laser-based contacting of aluminum current collector foils for the production of lithium-ion batteries using a nanosecond pulsed fiber laser. Procedia CIRP 2022, 111, 778–783. [Google Scholar] [CrossRef]
- Grabmann, S.; Kick, M.K.; Geiger, C.; Harst, F.; Bachmann, A.; Zaeh, M.F. Toward the flexible production of large-format lithium-ion batteries using laser-based cell-internal contacting. J. Laser Appl. 2022, 34, 042017. [Google Scholar] [CrossRef]
- Kick, M.K.; Habedank, J.B.; Heilmeier, J.; Zaeh, M.F. Contacting of 18650 lithium-ion batteries and copper bus bars using pulsed green laser radiation. Procedia CIRP 2020, 94, 577–581. [Google Scholar] [CrossRef]
- Lee, S.S.; Kim, T.H.; Hu, S.J.; Cai, W.W.; Abell, J.A. Joining Technologies for Automotive Lithium-Ion Battery Manufacturing: A Review. In Proceedings of the ASME 2010 International Manufacturing Science and Engineering, Erie, PA, USA, 12–15 October 2010; Volume 1, pp. 541–549. [Google Scholar] [CrossRef]
- Humpston, G.; Jacobson, D.M. Principles of Soldering; ASM International: Materials Park, OH, USA, 2004. [Google Scholar]
- Schwartz, M. Soldering: Understanding the Basics; ASM International: Materials Park, OH, USA, 2014. [Google Scholar]
- DIN Deutsches Institut für Normung e.V. Adhesives—Terms and Definitions, German version EN 923:2015; Beuth Verlag GmbH: Berlin, Germany, 2016. [Google Scholar] [CrossRef]
- Holm, R. Electric Contacts: Theory and Application, 4th ed.; Springer: Berlin/Heidelberg, Germany, 1967. [Google Scholar] [CrossRef]
- Li, Y.; Lu, D.; Wong, C.P. Electrical Conductive Adhesives with Nanotechnologies; Springer: Boston, MA, USA, 2010. [Google Scholar] [CrossRef]
- Lu, D.; Wong, C.P. Materials for Advanced Packaging; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Li, Y.; Wong, C.P. Recent advances of conductive adhesives as a lead-free alternative in electronic packaging: Materials, processing, reliability and applications. Mater. Sci. Eng. R Rep. 2006, 51, 1–35. [Google Scholar] [CrossRef]
- Gaynes, M.A.; Lewis, R.H.; Saraf, R.F.; Roldan, J.M. Evaluation of contact resistance for isotropic electrically conductive adhesives. IEEE Trans. Compon. Packag. Manuf. Technol. Part B 1995, 18, 299–304. [Google Scholar] [CrossRef]
- Yim, M.J.; Li, Y.; Moon, K.S.; Paik, K.W.; Wong, C.P. Review of Recent Advances in Electrically Conductive Adhesive Materials and Technologies in Electronic Packaging. J. Adhes. Sci. Technol. 2008, 22, 1593–1630. [Google Scholar] [CrossRef]
- Lee, J.; Cho, C.S.; Morris, J.E. Electrical and reliability properties of isotropic conductive adhesives on immersion silver printed-circuit boards. Microsyst. Technol. 2009, 15, 145–149. [Google Scholar] [CrossRef]
- Maurer, A. Power-Module kleben statt löten. Adhäsion Kleben Dichten 2016, 60, 18–23. [Google Scholar] [CrossRef]
- Sancaktar, E.; Bai, L. Electrically Conductive Epoxy Adhesives. Polymers 2011, 3, 427–466. [Google Scholar] [CrossRef]
- Prechtl, A. Vorlesungen über die Grundlagen der Elektrotechnik: Band 1; Springer: Vienna, Austria, 1994. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Toupin, R.A. Saint-Venant’s Principle. Arch. Ration. Mech. Anal. 1965, 18, 83–96. [Google Scholar] [CrossRef]
- Murrmann, H.; Widmann, D. Current crowding on metal contacts to planar devices. IEEE Trans. Electron Devices 1969, 16, 1022–1024. [Google Scholar] [CrossRef]
- Berger, H.H. Models for contacts to planar devices. Solid-State Electron. 1972, 15, 145–158. [Google Scholar] [CrossRef]
- Schmidt, P.A. Laserstrahlschweißen elektrischer Kontakte von Lithium-Ionen-Batterien in Elektro- und Hybridfahrzeugen. Ph.D. Thesis, Herbert Utz Verlag, München, Germany, 2015. [Google Scholar]
- Lin, H.; Smith, S.; Stevenson, J.T.M.; Gundlach, A.M.; Dunare, C.C.; Walton, A.J. An evaluation of test structures for measuring the contact resistance of 3-D bonded interconnects. In Proceedings of the 2008 IEEE International Conference on Microelectronic Test Structures, Edinburgh, UK, 24–27 March 2008; pp. 123–127. [Google Scholar] [CrossRef]
- Euler, J.; Nonnenmacher, W. Stromverteilung in porösen elektroden. Electrochim. Acta 1960, 2, 268–286. [Google Scholar] [CrossRef]
- Habenicht, G. Kleben—Erfolgreich und Fehlerfrei; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2016. [Google Scholar] [CrossRef]
- Habenicht, G. Kleben; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics, 4th ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA; Melbourne, Australia; New Delhi, India; Singapore, 2017. [Google Scholar]
- Choi, Y.; Humphrey, J.A. Analytical prediction of two-dimensional potential flow due to fixed vortices in a rectangular domain. J. Comput. Phys. 1984, 56, 15–27. [Google Scholar] [CrossRef]





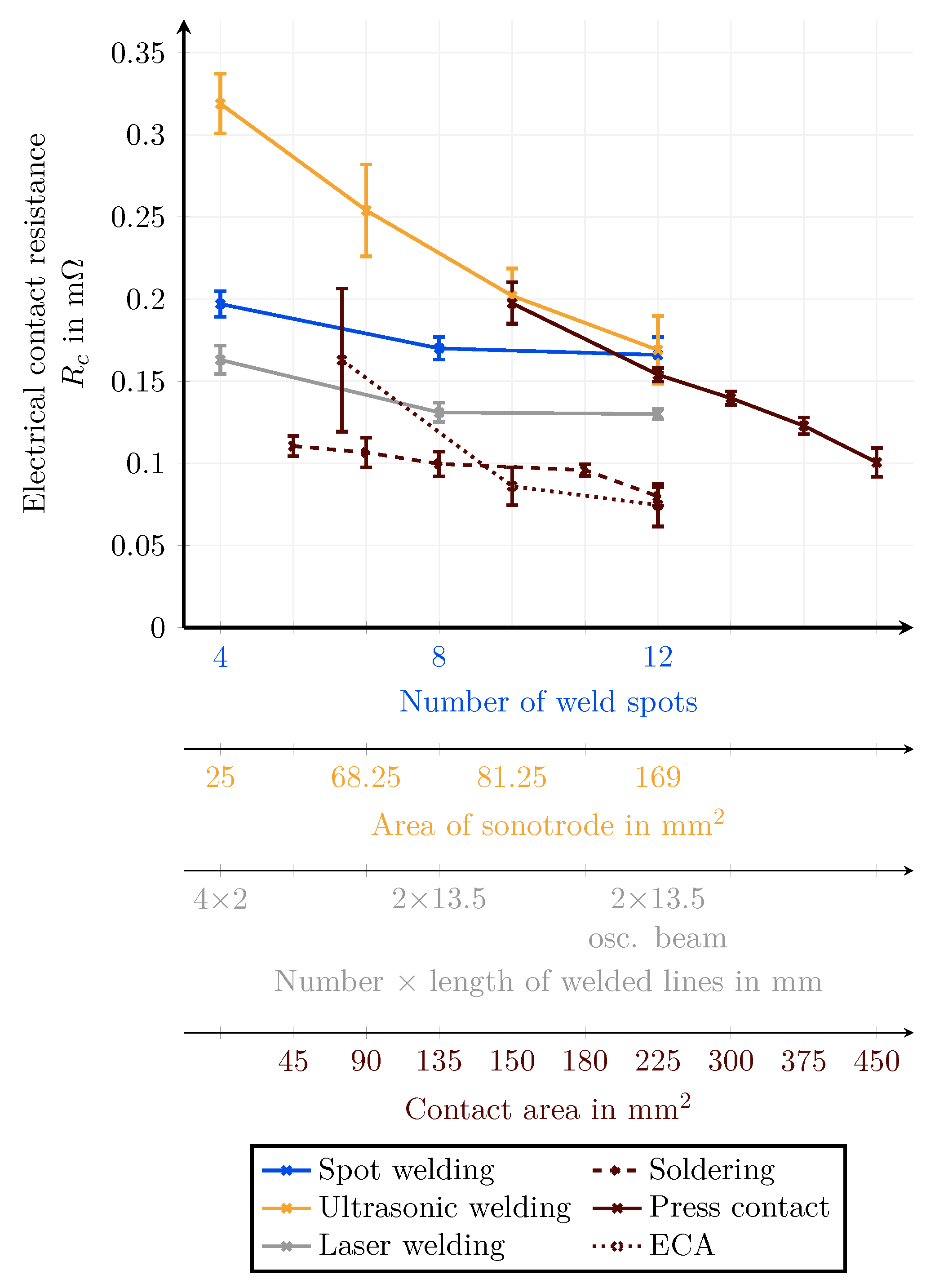


| UTF | Fracture | |||||||
| Specimen | μ | CI | μ | CI | μ | |||
| Material | in | in | in | in | in | in | ||
| µ | µ | µ | N | N | ||||
| Copper | 5 | 38 | 42.78 | 29.55 | 283.6 | 114.7 | A | 2.428 |
| 10 | 38 | 19.74 | 12.61 | 417.0 | 20.93 | A | 1.080 | |
| 15 | 38 | 10.53 | 3.478 | 515.7 | 271.1 | A | 0.7872 | |
| Brass | 5 | 38 | 162.8 | 87.09 | 1862 | 145.6 | C | 15.32 |
| 10 | 38 | 86.02 | 22.94 | 2165 | 279.0 | C | 4.536 | |
| 15 | 38 | 74.62 | 26.16 | 2519 | 252.4 | C | 2.902 | |
| Brass | 10 | 38 | 86.02 | 22.94 | 2165 | 279.0 | C | 4.536 |
| 10 | 88 | 109.5 | 58.36 | 2400 | 87.54 | C | 5.591 | |
| 10 | 124 | 306.5 | 57.65 | 2112 | 165.7 | A | 14.46 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jocher, P.; Kick, M.K.; Rubio Gomez, M.; Himmelreich, A.V.; Gruendl, A.; Hoover, E.; Zaeh, M.F.; Jossen, A. Determination of the Contact Resistance of Planar Contacts: Electrically Conductive Adhesives in Battery Cell Connections. Batteries 2023, 9, 443. https://doi.org/10.3390/batteries9090443
Jocher P, Kick MK, Rubio Gomez M, Himmelreich AV, Gruendl A, Hoover E, Zaeh MF, Jossen A. Determination of the Contact Resistance of Planar Contacts: Electrically Conductive Adhesives in Battery Cell Connections. Batteries. 2023; 9(9):443. https://doi.org/10.3390/batteries9090443
Chicago/Turabian StyleJocher, Philipp, Michael K. Kick, Manuel Rubio Gomez, Adrian V. Himmelreich, Alena Gruendl, Edgar Hoover, Michael F. Zaeh, and Andreas Jossen. 2023. "Determination of the Contact Resistance of Planar Contacts: Electrically Conductive Adhesives in Battery Cell Connections" Batteries 9, no. 9: 443. https://doi.org/10.3390/batteries9090443
APA StyleJocher, P., Kick, M. K., Rubio Gomez, M., Himmelreich, A. V., Gruendl, A., Hoover, E., Zaeh, M. F., & Jossen, A. (2023). Determination of the Contact Resistance of Planar Contacts: Electrically Conductive Adhesives in Battery Cell Connections. Batteries, 9(9), 443. https://doi.org/10.3390/batteries9090443







