Abstract
Because the new energy is intermittent and uncertain, it has an influence on the system’s output power stability. A hydrogen energy storage system is added to the system to create a wind, light, and hydrogen integrated energy system, which increases the utilization rate of renewable energy while encouraging the consumption of renewable energy and lowering the rate of abandoning wind and light. Considering the system’s comprehensive operation cost economy, power fluctuation, and power shortage as the goal, considering the relationship between power generation and load, assigning charging and discharging commands to storage batteries and hydrogen energy storage, and constructing a model for optimal capacity allocation of wind–hydrogen microgrid system. The optimal configuration model of the wind, solar, and hydrogen microgrid system capacity is constructed. A particle swarm optimization with dynamic adjustment of inertial weight (IDW-PSO) is proposed to solve the optimal allocation scheme of the model in order to achieve the optimal allocation of energy storage capacity in a wind–hydrogen storage microgrid. Finally, a microgrid system in Beijing is taken as an example for simulation and solution, and the results demonstrate that the proposed approach has the characteristics to optimize the economy and improve the capacity of renewable energy consumption, realize the inhibition of the fluctuations of power, reduce system power shortage, and accelerate the convergence speed.
1. Introduction
In recent years, wind and photovoltaic power generation have been essential for new power systems mainly based on new energy sources. With the promotion of carbon neutrality and the increasingly prominent problem of energy shortage, the large-scale application of new energy generation has become the trend of power system development. Because wind and sunlight are the primary energy sources of new energy generation, they are randomly influenced by the environment, temperature, geographical location, and other aspects, quickly leading to the imbalance of power conversion and the instability of power generation time, affecting the system’s stability. Given the intermittent and uncertain influence of new energy, with the popularization of new energy, the proportion is increasing, which will significantly impact the stability, safety, and system operating rate for new energy sources [1]. The application of energy storage technology in new energy systems helps to improve the utilization rate of power generation in new energy power systems, keep the system stable in power supply during peak power generation and low power generation due to external influence, and improve the utilization efficiency of power generation systems [2]. Aiming at the intermittency and instability nature of new energy power generation, the energy storage is utilized in order to store and release the electric energy, and power supplementation is carried out so as to improve the energy utilization rate and the stability of the power supply of the power system.
Because of the uncertainty and fluctuation of scenery, large-scale access to clean energy will also contain more uncertain factors, which will cause the phenomenon of abandoning wind and light and affect power stability [3]. The incorporation of hydrogen energy storage in the system has the advantages of being pollution-free, sustainable, and energy-saving, and is a green and clean energy storage system. The use of a hydrogen energy storage system allows for the storage of excess electricity from wind and solar energy abandonment, realizing the use of clean energy in the form of integrated energy of electricity–hydrogen–electricity, and improving the efficiency of the available renewable energy sources. Hydrogen energy storage has high energy density, a low cost of running and sustaining compared with other energy storage, long-term storage and non-pollution, applicable to both instantaneous power supply and long time power supply, applicable to different situations. Compared with the traditional battery, the fuel cell in hydrogen energy storage can be between the hydrogen chemical energy converted to electrical energy without the mutual conversion of other energy forms, which significantly reduces the loss and increases the power generation efficiency, and has the advantage of high energy conversion, environmental protection and the like.
With the gradual increase in the occupation of new energy sources, the percentage of wind and solar farms has been increasing, and consequently the research on power fluctuation problems has been gradually deepened. There have been many studies at home and abroad on the problem of optimal allocation of integrated energy system capacity. Literature [4] uses variational mode decomposition (VMD) to analyze the unbalanced power in a wind–solar hybrid microgrid. It establishes a model for the optimal allocation of hybrid energy capacity for the storage of batteries and supercapacitors. Literature [5] established a capacity optimization allocation method to reduce grid-connected photovoltaic power for photovoltaic power plants as well as hybrid energy storage systems. According to [6], the megawatt isolated microgrid consisting of photovoltaic/wind turbines, energy storage, diesel, and gas turbines is optimized in capacity allocation to solve electricity supply problems for powerless remote locations. Literature [7] proposes a quantitative optimal configuration method for a wind and solar complementary power supply system. Literature [8] puts forward an optimization strategy of double-layer hybrid energy storage capacity for a distribution grid by accounting for the distribution network loss and the total cost of the stored capacity system. In literature [9], a configuration model of a multi-source microgrid is constructed considering three aspects: installation location, unit arrangement and combination, extraordinary load of electric vehicles, and the dynamic matching problem between power generation and power consumption is analyzed. In reference [10], a multi-objective optimal allocation method of energy storage systems is proposed to deal with the issue of energy storage allocation under one-party investment and multiple benefits. These studies all show that the adoption with hybrid energy storage is crucial in rational distribution of microgrids, both consider the issues of reducing power loss and system investment cost or maximum economy, but do not consider the utilization of clean energy. In literature [11], the coupling of renewable energy power generation and hydrogen energy storage is shown to be a powerful means of achieving clean and carbon-neutral energy consumption, which has excellent potential for development. Literature [12] explains the application value system of hydrogen energy storage in the “source-network load” of the new power system. Hydrogen energy storage has the advantages of cross-season, cross-regional and large-scale storage. It has a specific rapid response ability, which has substantial application value in all aspects of the “source-network load” of new power systems. Literature [13] mainly considers how to construct a multi-energy combined storage and supply model in the integrated energy system with hydrogen storage as the conversion hub of multiple energy forms in low carbon parks, so as to achieve the optimized allocation method with low carbon emission and low cost; literature [14] uses the hydrogen produced by the hydrogen storage system to work together with a heat storage system and air source heat pump to reduce the use cost of electricity, heat and cold energy in the park, and establishes a capacity optimal allocation model taking integrated energy cost minimization as the optimization target. The research on hydrogen energy storage systems mainly focuses on using hydrogen without considering the conversion of hydrogen energy storage as electric energy. Literature [15] builds a typical wind and solar hydrogen storage capacity configuration model based on wind energy, solar photovoltaic, electric energy storage, and hydrogen production equipment, Then establishes a demand response model of day-ahead segmented electricity price load to reduce the total cost of running the system. The application of hydrogen energy storage focuses on the recycling of hydrogen. Increasing hydrogen energy conversion into electric energy is conducive to improving the rate of abandoning wind and light and transforming into a green and low-carbon environment [16].
Based on the issues described above, a wind–solar hydrogen storage microgrid system with a wind turbine, photovoltaic generator, hydrogen storage system, and battery system as subsystems is constructed in the paper, and the particle swarm algorithm for improving the dynamic adjustment of inertia weights is applied to the system’s capacity configuration, and the optimal configuration proposal on system capacity is obtained, which makes the highest system economy, achieves power stabilization, reduces the rate of abandoning wind and solar power, as well as the reduction of the system’s shortage of power.
2. Wind–Solar Hydrogen Microgrid System
The distributed new energy system has wind power, photovoltaic, geothermal, tidal, and other subsystems with random output. The integrated development of a comprehensive energy system enhances the combined application of energy [17]. This paper’s wind, light, and hydrogen microgrid system consists of wind turbines, photovoltaic generators, hydrogen production units, hydrogen storage units, fuel cells, and other auxiliary equipment. Hydrogen energy storage is used to realize the interconnection of electricity–hydrogen–electricity, to suppress the power fluctuation of distributed new power sources, which can contribute to the sustainability of energy [18]. The electricity–hydrogen system architecture of the park is schematically displayed in Figure 1. By matching and coupling various forms of energy storage, the energy utilization rate can be improved, achieving peak shaving and valley filling, stabilizing power fluctuation, and leading to certain economic benefits.
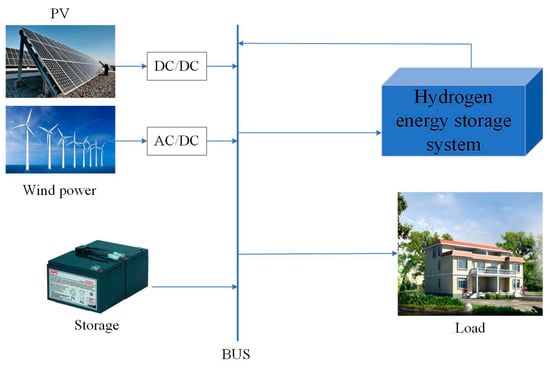
Figure 1.
Schematic diagram of electric–hydrogen integrated energy structure.
Figure 1 is a schematic structural diagram of an electric–hydrogen system, mainly consisting of a generation unit, a capacity storage unit and load. The electricity generation unit comprises of wind power generation and photovoltaic power generation, which takes renewable energy as the main energy source of the system, while the energy storage unit comprises a storage battery and hydrogen storage system, which has a role of balancing the load of the system, and absorbs excess energy through the energy storage system when there is sufficient wind and light energy; and supplements it through the energy storage system when there is insufficient wind and light energy.
2.1. Modeling of Generator Set
2.1.1. Photovoltaic Generation System
Physical photovoltaic (PV) power generation is the direct transformation of solar energy through PV panels into electrical energy. Photovoltaic power generation is affected by solar radiation, the radiation angle, sunshine hours, and environmental temperature. The specific photovoltaic power generation output model is shown in Formula (1) [19]:
where: Ppv(t) represents the actual electricity generation power of the photovoltaic panel; PpvN is the nominal capacity of the photovoltaic panel to generate electricity; fpv is the operation efficiency of photovoltaic system; G(t) is the actual light intensity at time t; Gref is the reference standard light intensity; α is the temperature coefficient; Tc(t) is the operating temperature of the photovoltaic panel at time t; Tref is the reference standard ambient temperature.
Photovoltaic panel operation temperature transformation is caused by the ambient temperature, and solar light intensity is caused by many aspects of the influence of the relationship shown in Formula (2):
where: T(t) is the actual ambient temperature; and Trated is the standard reference temperature of a photovoltaic panel.
2.1.2. Wind Power Generation Model
Wind turbine power output is affected by various aspects such as the speed of wind, blades, ambient temperature, air pressure, etc. [20]. Wind power generation means to convert the kinetic energy to mechanical energy and utilize a turbine to convert the mechanical energy into electrical power. The wind speed changes randomly due to external factors, leading to intermittent and fluctuating wind power generation. The power delivery by wind turbine is most affected by the wind speed, and approximated relationship with the wind speed is shown in Formula (3):
where: Pwt(t) is the active output power of the wind farm in time t, Pr is the rated output power of the wind turbine, v(t) is the actual wind speed of the wind turbine in time t, vr is the rated wind speed, vin is the cut-in wind speed, and vo is the cut-out wind speed.
2.2. Modeling of Hydrogen Energy Storage System
The hydrogen energy storage system is an integral part for the energy storage system in an independent microgrid system. The hydrogen energy storage system mainly comprises electrolytic cells, fuel cells, and hydrogen storage equipment. Its structural schematic diagram is shown in Figure 2.
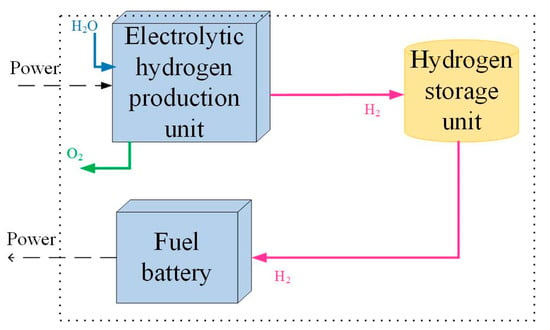
Figure 2.
Structure diagram of hydrogen energy storage system.
2.2.1. Mathematical Modeling of Electrolytic Cell
Electrolyzed water is a widely used primary hydrogen production method in industrial hydrogen production [21]. The electrolyzer electrolyzes water into hydrogen and oxygen. There are alkaline electrolyzers, proton exchange membrane electrolyzers, and solid oxide electrolyzers. Compared with other electrolyzers, alkaline electrolyzers have higher efficiency and the best hydrogen production capacity. The system life is twice as long as that of proton exchange membrane electrolyzers, and the cold start-up time is shorter than that of solid oxide electrolyzers. An alkaline electrolyzer is the safest, most mature, and most widely used. The hydrogen production rate of an alkaline electrolyzer is [22]
where: VH2 is the hydrogen production rate; ηF is Faraday efficiency; NC is the number of electrolyzers; F is Faraday constant (C/mol); I is the current in the electrolytic cell.
In practice, the electrolytic cell cannot be electrolyzed entirely, and its conversion efficiency is represented by
where: PH2(t) is the power generated by hydrogen production in the electrolytic cell; Pe(t) is the electricity consumption of the electrolytic cell; and ηEL is the conversion efficiency of electricity and hydrogen in the electrolyzer.
2.2.2. Mathematical Modeling of Fuel Cell
A mathematical example is provided for the fuel cell:
where: QH2fc is the hydrogen consumption of the fuel cell; NS is the number of batteries connected in series; Pfc is the output power of the fuel cell; Ufc is the battery voltage; and F is the Faraday constant (C/mol).
2.2.3. Mathematical Modeling of Hydrogen Storage Device
Most hydrogen storage devices use hydrogen storage tanks, which can store the hydrogen produced by electrolytic cells and provide hydrogen for fuel cells. The hydrogen storage tank device has the characteristics of low cost, high safety, and fast charging and discharging speed. A hydrogen storage tank is characterized by a mathematical model:
where: PaH2 is the pressure of the hydrogen storage tank; R is a gas constant; Ta is the thermodynamic temperature of the gas; V is the total capacity of the hydrogen storage tank; t1 and t2 are the start time for starting hydrogen production and the end time for stopping hydrogen production, respectively.
2.3. Battery Modeling
A storage battery is a kind of galvanic energy storage, while chemical energy storage is a relatively stable and high-grade energy storage method. This article selected a lithium battery as a storage battery, and the running state of the storage system is marked by the state of charge (SOC) of the lithium battery. When SOC = 1, the battery capacity reaches a maximum value [23]. The battery output model is
Charging status:
Discharge state:
where: σ is the charge and discharge rate of the storage battery; Pc and Pf are the charging and discharging power of the battery in t time; ηc and ηf are charge and discharge efficiency; and Emax is the maximum capacity of the battery.
3. Capacity Optimal Allocation Model
Based on the microgrid system of wind–solar hydrogen storage, this paper not only considers the economy of the independent microgrid of wind–solar hydrogen storage; but also to consider the power fluctuations on the wind generated by the wind and light abandonment, so as to make the wind utilization rate to reach the highest, and put forward the corresponding optimization scheme.
3.1. Objective Function
In this paper, the most economical price is used as the objective function in the independent wind, solar, and hydrogen storage microgrid.
Objective function 1 includes: In the hydrogen-containing composite energy storage system, investment and recovery costs are considered to achieve the best economic benefits. In this paper, the objective function of minimizing the integrated operating cost of the system can be expressed as:
CT is the system’s total operation cost, composed of each piece of equipment’s investment and operation cost. Each piece of equipment is comprised of wind turbines, photovoltaics, batteries, and hydrogen storage, and their installation cost, replacement cost, in addition to operation and maintenance cost together constitute the operating cost of the investment [24].
where: CT is the total operating cost of the system; CIN is the installed cost of the equipment; CRE is the replacement cost of the equipment; and COM is the operation and maintenance cost of the equipment.
CIN represents the installed cost for the equipment, which can be expressed as
where: CIN is the installed cost of the equipment; Q is the rated capacity of the equipment; PIN is the unit installed cost of the equipment; r is the discount rate of equipment; and m is the service life of the equipment.
CRE as replacement cost for devices, which can be expressed as
where: CRE is the replacement cost of the equipment; Q is the rated capacity of the equipment; PRE is the unit replacement cost of equipment; r is the discount rate of equipment; and m is the service life of the equipment.
COM is the operation and maintenance cost for equipment, which can be expressed as
where: COM is the operation and maintenance cost of the equipment; Q is the rated capacity of the equipment; P is the unit cost of equipment; and λ is the ratio of the operation and maintenance cost of each equipment to the total cost of each equipment.
Objective function 2 can restrain the power fluctuation and build an optimal configuration model of a microgrid, including the wind–hydrogen storage as well as the energy storage system formed by the battery, which can be expressed as follows:
where: EA is the sum capacity for energy storage of wind and solar batteries. Because the battery has the function of charging and discharging, EA has a maximum and minimum value.
Hydrogen storage system discharge:
Charging (hydrogen storage) of hydrogen energy storage system:
where: EH2 is the energy storage capacity of the hydrogen energy storage system; and EL is the total capacity of the load.
Objective function 3 for the wind–solar hydrogen storage-independent microgrid, due to many external influences, after increasing the energy storage system, cannot completely guarantee the reliability of the system power supply [25]. The critical index of load shortage can refer to the power fluctuation problem. When the load is short of electricity, the system is more stable and reliable, and vice versa. Figure 3 shows the load power shortage operation flow in the wind–solar hydrogen storage microgrid system. Elps shows a power shortage of the load, which can be expressed as
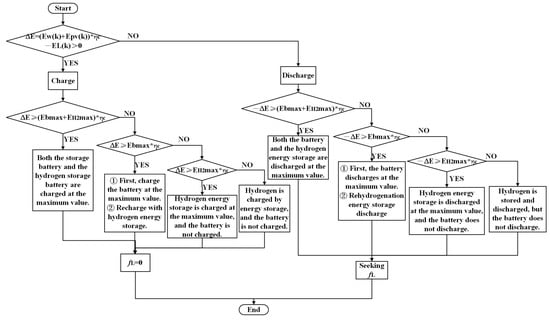
Figure 3.
Operation flow chart of load power shortage.
When power generation from wind and solar meets the load requirements, when ΔE > 0, power shortage Elps = 0, and the ΔE is judged, and different charging combination devices are selected. When ΔE is greater than or equal to the max range between the battery and hydrogen storage capacity, the maximum value of the battery and hydrogen storage is used for charging; When ΔE is greater than the maximum range of the battery capacity, the maximum value of the battery is used to charge, and the remaining electricity is used to charge the hydrogen storage. When ΔE exceeds the upper range of the hydrogen storage capacity, the maximum amount in hydrogen storage is used for charging. When ΔE becomes less than the maximum range of capacity of hydrogen storage, hydrogen storage is used for charging.
When the amount of wind–solar power generation satisfies the load requirement, that is, ΔE < 0, the wind–solar power generation is insufficient, so it is necessary to discharge the stored power to supplement the shortage of the system, judge ΔE, and choose different discharge combination distribution methods. When −ΔE is greater than or equal to the maximum range of the storage battery and hydrogen storage capacity, the maximum value of storage battery and hydrogen storage capacity is used for discharge. When −ΔE is greater than the maximum range of the battery capacity, the maximum value of the battery is employed for discharge, and the balance of the power is used to discharge on hydrogen energy storage. When −ΔE is greater than the maximum range of the hydrogen storage capacity, the maximum value of hydrogen storage is used for discharge. When −ΔE is less than the maximum range of hydrogen storage capacity, hydrogen storage is used for discharge.
3.2. Constraints
(1) Capacity constraints of hydrogen storage equipment:
where: Vmin and Vmax are the minimum and maximum capacities of the hydrogen storage tank.
(2) Capacity constraints of hydrogen storage equipment:
where: SOC is the operating state of charge in the energy storage system.
(3) Power load constraint:
where: PL is the power load of the system, kW.
(4) Energy waste rate constraint:
Excess power is generated in the system when the power generated in the system is greater than the load demand in the system and the maximum energy stored in the system, resulting in wasted energy. This is because the capacity allocation is unreasonable, and the power generation unit is configured with excessive output. When the system energy waste rate is less, the system capacity allocation is more reasonable, which can significantly reduce the waste of resources.
where: fset is the control range of the energy waste efficiency of the system for a setting of 0.5.
To solve the multi-objective function problem, fuzzy mathematics is used in this paper. In most cases, the objective functions may affect each other, so it is not easy to achieve simultaneous optimization. The sub-objective optimization and multi-objective are solved by fuzzy mathematics. Under the condition of satisfying all constraints, each objective function is fuzzified, and the objective function is solved based on fuzzy statistics by taking the maximum value according to the affiliation function, and the optimal solution is obtained.
In this paper, the membership function of the distributed function of half Γ decline is
where: Fkmin(t) is the minimum value of the single objective function Fk(t) under the constraint conditions.
Under the principle of maximum affiliation, the fuzzy multi-objective optimization problem is converted into a nonlinear but targeted optimization issue, and the multi-objective function solving model becomes
where: u(t), u1(t), u2(t), and u3(t) are, respectively, the satisfaction of fuzzy optimization, the satisfaction of system total operation cost, the satisfaction of power fluctuation, and the satisfaction of load power shortage.
4. Improved Particle Swarm Optimization Algorithm
4.1. Particle Swarm Optimization
The particle swarm optimization (PSO) algorithm was inspired by the study of artificial life and was proposed as a global stochastic search algorithm in the simulation of bird flock foraging [26]. The particle swarm optimization algorithm has strong anti-interference ability, good results, fast speed, and memory function, and is also a multi-agent optimization system. Each particle can dynamically adjust according to the surrounding state to find its optimal and overall solution [27].
In the optimization process, after initializing the target population in N-dimensional space, the particles constantly update their positions and velocities, generating a new position each time and solving the next time to attain the optimal result. The iterative expression for the update rate as well as the position in the process of particle solution is
where: k is the number of iterations; ω is the inertia weight coefficient; vik and xik are the velocity and position of particles; c1 and c2 are acceleration factors; r1 and r2 are random numbers between [0,1]; PM is the particle individual extreme value; and GM is the extreme value of the population.
4.2. Improved Particle Swarm Optimization
For the particle swarm optimization algorithm, it is susceptible to problems such as falling into the local extremum and poor local search ability. To solve these problems, the particle swarm optimization algorithm is improved. A particle swarm optimization with dynamic adjustment of intrinsic weight is used, and exponential function and random function of beta distribution [28] are used to improve it, achieve the algorithm’s global search ability, and reduce the possibility of falling into local extremum.
The inertia weight ω is an essential variable among the particle swarm, determining influence degree of particle velocity on the velocity in the next iteration. The capability of global search is strong when ω is large, the capability of local search is weak, and it can easily fall into the local optimization state. With the increase in iteration times, the exponential function is adopted to increase the global search ability and the later search accuracy.
The improved expression for the inertia weights is
where: kmax is the maximum number of iterations; σ is the inertia adjustment factor; ωmax is the initial inertia weight; ωmin is the inertia weight of the maximum number of iterations.
In particle swarm optimization, the acceleration factor determines the influence of individual particle experience information and other particle experience information on the optimization trajectory. For the acceleration factor, c1 is the global acceleration factor and c2 is the local acceleration factor [29]. To converge faster, the acceleration factor is improved so that c1 gradually increases and c2 gradually decreases, thus strengthening the convergence ability of particles to the global optimum.
where: c0 is the initial value.
4.3. Solution Steps
In solving the problem of optimal system capacity configuration, the paper applies the improved IDW-PSO problem solving and the flow is shown in Figure 4.

Figure 4.
Solution flow.
5. Model Solving
This paper uses the improved particle swarm optimization algorithm with dynamically adjusted inertia weight to optimize the configuration of each device’s hydrogen-containing hybrid energy storage microgrid capacity. Firstly, the fundamental parameter models of each device unit, including illumination intensity and load parameters, are determined—secondly, input parameters, including capacity range, conversion rate, etc. Then, the system’s capacity is optimized according to the system’s total operating cost. The core of the system optimal analysis method based on IDW-PSO is to determine the optimal capacity allocation under the condition of minimum total system cost, to reduce the loss of power supply probability, reduce the fluctuation of power, preventing instability of the microgrid. A flow diagram of the operation strategy is illustrated in Figure 5:
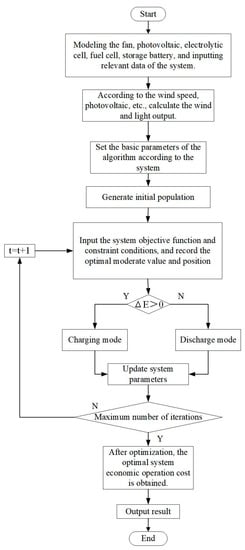
Figure 5.
Operation strategy flow chart.
- Step (1):
- Modeling each unit of the microgrid, inputting data such as wind speed and load, and inputting relevant parameters;
- Step (2):
- Initialize the calculated output of photovoltaic and wind power generation;
- Step (3):
- Input system constraints and objective functions;
- Step (4):
- Calculate whether the wind and solar power generation meet the load demand ΔE, execute an objective function, and select different operation processes;
- Step (5):
- After executing the objective function, check whether the microgrid is within the constraint range and update the relevant parameters of the system;
- Step (6):
- Whether the maximum number of iterations has been reached. Without satisfying the condition, the program will continue to run;
- Step (7):
- Obtain optimal economic operating cost and related data.
6. Example Analysis
Taking a wind, solar, and hydrogen microgrid system in Beijing as an example, the capacity of centralized photovoltaic units is 200 KW, and that of centralized wind turbines is 350 KW. Figure 6 shows the data on wind power, photovoltaic power generation, and load consumption on a specific day in this area. Relevant parameters of battery and hydrogen storage of the system are presented in Table 1. The optimization model of the capacity optimization of wind and hydrogen storage system constructed in this paper is solved by MATLAB.
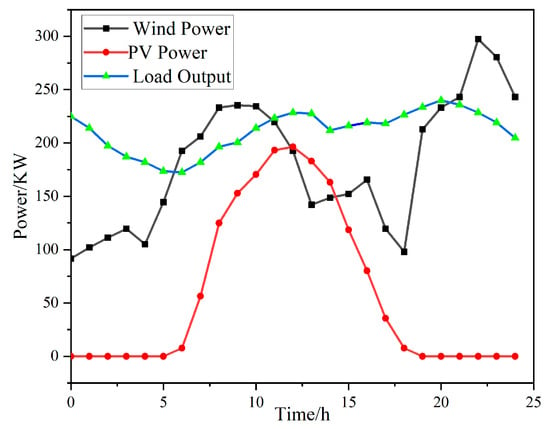
Figure 6.
Wind–solar load curve.

Table 1.
Example parameters.
In the whole microgrid system, the equipment at the power generation end includes a wind turbine, photovoltaic equipment, storage battery, and hydrogen energy storage system. According to a defined objective value function and various parameters, wind turbine, photovoltaic unit, and hydrogen energy storage jointly bear the load consumption of the system and keep the power balance in real time. At 5~18 h, due to the sun’s rising, the light amplitude appeared and reached the maximum peak at 12 h at noon, when the light incident angle reached the maximum. Because wind turbines are built in places with abundant wind resources, they can generate electricity 24 h a day.
Simulation Results Analysis
To comprehensively analyze the economic advantages of the energy storage operation of the system according to the improved IDW-PSO algorithm, the effects of system load shortage and power balance on the configuration results are considered, this paper sets the following four schemes for comparative analysis. Scheme 1: Choose the energy storage configuration scheme that is currently widely used. Scheme 2: The battery and hydrogen energy storage is selected as the energy storage schemes of the system for optimal configuration, and the compression factor particle swarm optimization algorithm is used. Scheme 3: Select battery and hydrogen energy storage as the system energy storage scheme for optimal configuration, and use the IDW-PSO algorithm. Scheme 4: Select battery and hydrogen energy storage as the system energy storage scheme to optimize the structure and use the improved IDW-PSO algorithm. The simulation establishes the population scale of 200, and iteration number of 200, acceleration factor initial value is set to 1.65, the battery SOC lower limit is 0.1, the SOC upper limit is 0.9, while a battery SOC initial value is set to 0.5, and a simulation results are as follows:
Upon calculation, the results of the optimized configuration under each scenario are obtained as shown in Figure 7 and Table 2. Scheme 2, Scheme 3, and Scheme 4, respectively, show the differences in iteration times, average time, and total cost caused by different operation results. The above three schemes can all be applied to the capacity optimization arrangement of hydrogen-containing composite power storage system. From a comparative analysis of Figure 7, the improved IDW-PSO algorithm can reduce the number of iterations, speed up the calculation time, and calculate the optimal system operating cost more effectively. The convergence speed and accuracy of the improved IDW-PSO are different from those of IDW-PSO and compressed factor particle swarm optimization, which reduces the local optimal solution, slow divergence speed and efficiency. The algorithms in the present paper have fewer iteration times and operation times. Compared with other algorithms, this algorithm is superior to different algorithms with the capacity optimization configuration scheme, which improves the system economy.
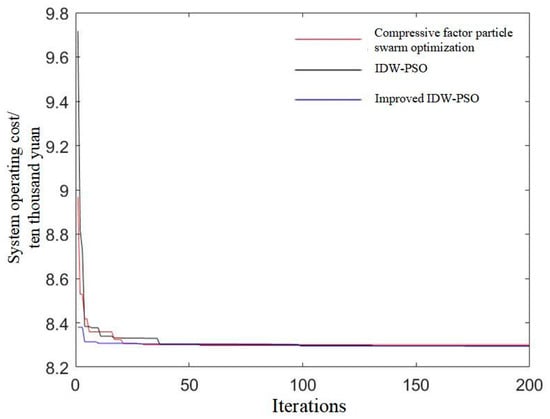
Figure 7.
Comparison of convergence curves of various algorithms.

Table 2.
Comparison of economic results of each algorithm.
At this time, see Table 3 for the system capacity optimization configuration scheme through Scheme 1, Scheme 3, and Scheme 4.

Table 3.
Optimization result.
Table 3 shows that the optimal configuration for the microgrid system in the hybrid energy storage of supercapacitors and storage batteries in Scheme 1 is 2034 storage batteries and 28,956 supercapacitors. In this case, the system loss of power supply probability is 0.0321, and the system’s total operating cost is 83,210 yuan. The optimal configuration of the Scheme 3 microgrid system before improvement is 1975 batteries and 127 hydrogen storage batteries; now the system loss of power supply probability is 0.0297, and the comprehensive operating of the system costs 83,590 yuan. The optimal configuration of the improved Scheme 4 microgrid system is 1989 batteries and 106 hydrogen storage batteries. Currently, the system loss of power supply probability is 0.014, and the system’s total operating cost is 83,230 yuan. From the comparative analysis of Table 3, in the hybrid energy storage of battery and supercapacitor, the minimum price for Scheme 3 is higher than that of Scheme 1 because the cost of hydrogen energy storage is much higher than that of the supercapacitor, and the operating cost of Scheme 4 is unchanged. The scheme proposed in this paper (Scheme 4) reduces the power shortage by 56.4% in Scheme 1 and 52.9% in Scheme 3 while maintaining the running cost unchanged. Therefore, the scheme used in this paper is superior to other projects, which improves the power shortage problem caused by the system’s unbalanced configuration.
From the perspective of solving the problem of the power shortage rate, the scheme in this paper has increased by 1.81% and 1.57%, respectively, compared with Scheme 1 and 3. In this paper, Beijing’s average daily electricity consumption in 2022 is 210 degrees. According to this ratio, the scheme in this paper can solve the power shortage of about 3.5 degrees by storing energy. Thermal power plants need about 320 g standard coal for the first generation of electricity, saving 1 kg of typical coal = reducing emissions by 2.493 kg “carbon dioxide” = reducing emission by 0.68 kg “carbon.” Then, this scheme can reduce carbon dioxide and carbon emissions by about 1019.13 kg a year in this area. Therefore, the scheme proposed in this paper has great practical significance for promoting carbon neutrality.
For wind–solar hybrid electricity generation, both wind turbines and photovoltaic units have limited capacities, and the adjustment range is relatively small. Hydrogen storage has excellent advantages for power generation because hydrogen storage can perform charging and discharging functions and has a wide range of power adjustments. As can be seen from Figure 8, from 0:00 to 6:00, since the load output is higher than the wind and light energy export power, batteries and hydrogen energy storage are discharged; At 6:00–16:00, because the load output is less than the wind and light output power, the battery and hydrogen energy storage are charged. From 16:00 to 22:00, the battery and hydrogen energy storage discharge because the load output is greater than the wind and light output power. From 22:00 to 24:00, the battery and hydrogen energy storage charge because the load output is less than the wind and light output power.
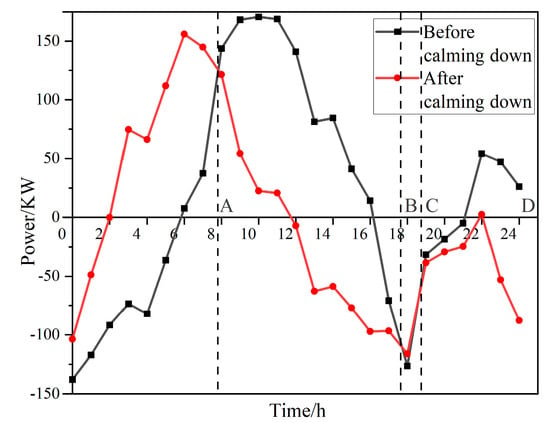
Figure 8.
Power comparison diagram before and after optimization.
Based on the economic and system loss of power supply probability, the system optimizes the capacity allocation scheme for wind, light, and hydrogen storage systems, thus achieving the purpose of shaving peaks and filling valleys and restraining power fluctuation. When the generating power of wind and light is greater than the load output, the hydrogen storage is optimized by the algorithm to realize “peak clipping”. When the generating power of wind and light is less than the load output, the hydrogen storage system is discharged through algorithm optimization to realize “valley filling” of the system power.
Figure 8 is a power comparison chart before and after system optimization, which is, respectively, the power comparison in the whole system before and after the optimization of the hydrogen energy storage system. Before the optimal configuration of the hydrogen energy storage system, a variance of the output power of the whole system was 9171.78 kW2. After the optimal configuration, the variance of the whole system’s output power is 6582.22 kW2, with an obvious decrease in the fluctuation of the output power. The 0-A region represents the supplementary power region where the fuel cell of the hydrogen energy storage system discharges to supplement wind power and photovoltaic power, thus achieving the function of “valley filling” for the system power. The area A-B region represents the electrolyze in the hydrogen storage system for hydrogen storage, to absorb the force of wind power and photovoltaic, and thus achieve the “peak clipping” effect on the system power. The B—C region is the same as the 0—A region, and the C—D region is the same as the A—B region. Meanwhile, the waste power of the hydrogen energy storage system before configuration is 3.7435 kW, while after configuration, it is 1.8263 kW, which significantly reduces the waste air volume.
7. Conclusions
In this paper, the influence of wind turbines, photovoltaic systems, hydrogen storage systems, and battery output ratios on the operation of independent microgrid systems is considered, which is experimentally verified to improve the degree of renewable energy consumption.
In this paper, a particle swarm algorithm is proposed to improve the particle swarm algorithm for dynamically adjusting the inertia weights, establish a capacity optimization model, and obtain a capacity optimization scheme with the optimal system operating cost, system loss of power supply probability and system power. The integrated operation cost of the wind–solar hydrogen storage microgrid system is reduced by 0.431%, and the variance of the whole system after hydrogen storage configuration is 28.23% of that before configuration. The power fluctuation and the rate of abandoning wind and light are reduced.
The improved IDW-PSO algorithm will improve the optimization accuracy, reduce the risk of falling into the optimal local solution, and accelerate the iteration speed so that the system can get the optimal solution faster and better. The improved algorithm is improved from 142 to 124 iterations, and the accuracy of the results is improved by 0.024%.
This scheme can reduce carbon dioxide and carbon emissions by about 1019.13 km annually in this area. When building the optimal configuration of wind and solar hydrogen storage systems, considering the economic indicators and power shortage load, the complementary relationship between hydrogen energy storage and storage battery is used to combine them and realize the suppression of power fluctuations, to achieve the purpose of peak shaving peaks and filling in valleys, to eliminate the wind and light rejection rate better, increase system economic efficiency, to reduce the amount of power shortage in the system, and strive to make the system more environmentally friendly by realizing carbon neutrality.
This paper in the microgrid capacity optimization configuration model allows for a wind-optical-hydrogen-storage microgrid system to provide some support. Starting from the energy demand side, this model can not only configure the capacity of wind, light, storage battery, and hydrogen storage, but also add more forms of energy—for example, flywheel energy storage, biological energy storage, pumped storage, and so on. The system is more environmentally friendly for the application of hydrogen energy storage, and the interconnection of electricity and hydrogen is used to realize carbon emission reduction. With the development of time and the application of hydrogen energy, the cost of hydrogen production is reduced, the difficulty of hydrogen production is reduced, and the efficiency of hydrogen production is improved. Hydrogen energy storage can optimize power and energy simultaneously in electricity storage and power generation and will be further studied. High-density, pollution-free, and sustainable utilization of hydrogen is a significant trend and the significance of efficient production. In future research, the load-side model or the model of demand-side response and load-side interaction will be further considered when optimizing the system to be closer to the actual demand.
Author Contributions
Conceptualization, G.H. and Z.W.; methodology, G.H.; software, G.H.; H.M.; validation, G.H.; formal analysis, G.H.; investigation, G.H.; H.M.; X.Z.; resources, G.H.; H.M.; data curation, G.H.; Z.W.; writing—original draft preparation, G.H.; writing—review and editing, G.H.; Z.W.; visualization, G.H.; Z.W.; supervision, Z.W.; project administration, G.H.; Z.W.; funding acquisition, none. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xia, D. Overview of new energy power system stability. Sci. Technol. Innov. Appl. 2021, 331, 69–72. [Google Scholar]
- Lian, Z. Research on Capacity Allocation Optimization of Hybrid Energy Storage System of Wind Power Heat Pump Based on Particle Swarm Optimization. Master’s Thesis, Shenyang University of Technology, Shenyang, China, 2021. [Google Scholar]
- Xiong, Y.; Chen, L.; Zheng, T.; Si, Y.; Mei, S. Optimal configuration of hydrogen energy storage in low-carbon park integrated energy system considering electricity-heat-gas coupling characteristics. Electr. Power Autom. Equip. 2021, 41, 31–38. [Google Scholar]
- Lei, S.; He, Y.; Zhang, J.; Deng, K. Optimal Configuration of Hybrid Energy Storage Capacity in a Microgrid Based on Variational Mode Decomposition. Energies 2023, 16, 4307. [Google Scholar] [CrossRef]
- Li, W.; Jin, R.; Ma, X.; Zhang, G. Capacity Optimal Allocation Method and Frequency Division Energy Management for Hybrid Energy Storage System Considering Grid-Connected Requirements in Photovoltaic System. Energies 2023, 16, 4154. [Google Scholar] [CrossRef]
- Xie, H.; Zheng, S.; Ni, M. Microgrid Development in China: A method for renewable energy and energy storage capacity configuration in a megawatt-level isolated microgrid. IEEE Electrif. Mag. 2017, 5, 28–35. [Google Scholar] [CrossRef]
- Xiu, X. Research on Optimal Allocation of Energy Storage System Capacity and Life Cycle Economic Evaluation Method. Master’s Thesis, China Agricultural University, Beijing, China, 2018. [Google Scholar]
- Sun, H.; Jie, C.; Liang, S.; Hu, J.; Zang, J.; Li, Y. Optimization of double-layer energy storage capacity of wind, solar and electricity grid-connected based on improved slime mold algorithm. Power Grid Clean Energy 2023, 39, 128–136. [Google Scholar]
- Sun, S. Study on Optimal Allocation and Economic Operation Model of Multi-Energy Microgrid. Master’s Thesis, Hefei University of Technology, Hefei, China, 2012. [Google Scholar]
- Ye, C.; Huang, M.; Wang, Y.; Sun, F.; Zhong, Y. Optimal configuration of wind-solar hybrid power supply system based on discrete probability model. Power Syst. Autom. 2013, 37, 48–54. [Google Scholar]
- Zhou, J.L.; Wu, Y.N.; Zhong, Z.M. Modeling and configuration optimization of the natural gas-wind-photovoltaic-hydrogen integrated energy system: A novel deviation satisfaction strategy. Energy Convers. Manag. 2021, 243, 114340. [Google Scholar] [CrossRef]
- Xu, C.; Liu, J. Application value, challenge and prospect of hydrogen energy storage in China’s new power system. China Eng. Sci. 2022, 24, 89–99. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, H.; Hu, Z.; Ma, Z.; Zhang, J.; Yao, L. Power System Probabilistic Production Simulation Including Wind Farms. Proc. CSEE 2009, 29, 34–39. [Google Scholar]
- Yu, X. Study on Optimal Allocation and Operation of Comprehensive Energy System in the Park with Hydrogen Storage and Heat Storage. Master’s Thesis, North China Electric Power University, Beijing, China, 2020. [Google Scholar]
- Hong, F.; Xu, F.; Liu, G. Optimal capacity allocation of photovoltaic hydrogen storage system considering load demand response. Power Supply 2023, 40, 45–51. [Google Scholar] [CrossRef]
- Zhao, B.; Zhao, P.; Hu, J.; Niu, M.; Xiao, Y.; Liu, F. Overview of Hydrogen Energy Storage Technology in Large Scale Intermittent Renewable Energy Integration Application. Dianqi Yu Nengxiao Guanli Jishu 2018, 16, 1–7. [Google Scholar]
- Peng, S.; Zhu, L.; Dou, Z.; Liu, D.; Yang, R.; Pecht, M. Method of Site Selection and Capacity Setting for Battery Energy Storage System in Distribution Networks with Renewable Energy Sources. Energies 2023, 16, 3899. [Google Scholar] [CrossRef]
- Liu, H.; Wang, S.; Liu, G.; Zhang, J.; Wen, S. SARAP Algorithm of Multi-Objective Optimal Capacity Configuration for WT-PV-DE-BES Stand-Alone Microgrid. IEEE Access 2020, 8, 126825–126838. [Google Scholar] [CrossRef]
- Zhu, Z.; Guo, J.; Yu, G.; Xu, M.; Hu, Z. Bi-Layer Optimization Model for Energy Storage Systems Under Wind and PV Access. Acta Energiae Solaris Sin. 2022, 43, 443–451. [Google Scholar]
- Du, G.; Zhao, D.; Liu, X. Research review on optimal scheduling considering wind power uncertainty. Proc. CSEE 2022, 10, 1–21. [Google Scholar]
- Xie, X.; Wang, H.; Tian, S.; Liu, Y. Optimal capacity configuration of hybrid energy storage for an isolated microgrid based on QPSO algorithm. In Proceedings of the International Conference on Electric Utility Deregulation & Restructuring & Power Technologies, Changsha, China, 26–29 November 2015. [Google Scholar] [CrossRef]
- Li, Q.; Zhao, S.; Pu, Y.; Chen, W.; Yu, J. Capacity Optimization of Hybrid Energy Storage Microgrid Considering Electricity-Hydrogen Coupling. Trans. China Electrotech. Soc. 2021, 36, 486–495. [Google Scholar]
- Wang, C.; Meng, J.; Wang, Y.; Li, C. Multi-source Coordinated Control Strategy Considering Battery’s SOC for Islanded DC Microgrid. High Volt. Eng. 2018, 44, 160–168. [Google Scholar]
- Pan, X.; Liu, K.; Wang, J.; Hu, Y.; Zhao, J. Capacity Allocation Method Based on Historical Data-Driven Search Algorithm for Integrated PV and Energy Storage Charging Station. Sustainability 2023, 15, 5480. [Google Scholar] [CrossRef]
- Xu, L.; Ruan, X.; Zhang, B.; Mao, C. Improved optimal allocation method of wind-solar hybrid power generation system capacity. J. China Electr. Eng. 2012, 32, 11. [Google Scholar]
- Dang, X.; He, B.; Sun, J.; Kong, L.; Meng, F. Photovoltaic maximum power point tracking based on improved particle swarm optimization. Shandong Electr. Power Technol. 2022, 49, 36–43. [Google Scholar]
- Shi, Y.H.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999. [Google Scholar] [CrossRef]
- Dong, H.; Li, D.; Zhang, X. A Particle Swarm Optimization Algorithm with Dynamic Adjustment of Inertia Weight. Comput. Sci. 2018, 45, 98–102+139. [Google Scholar]
- Mao, K.F.; Bao, G.Q.; Xu, C. Particle Swarm Optimization Algorithm Based on Non-symmetric Learning Factor Adjusting. Comput. Eng. 2010, 36, 182–184. [Google Scholar]
- Li, Y.; Guo, X.; Dong, H.; Gao, Z. Optimal Capacity Configuration of Wind/PV/Storage Hybrid EnergyStorage System in Microgrid. Power Syst. Its Acta Autom. Sin. 2020, 32, 6. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).