Abstract
The state of charge (SOC) of a battery is a key parameter of electrical vehicles (EVs). However, limited by the lack of computing resources, the SOC estimation strategy used in vehicle-mounted battery management systems (V-BMS) is usually simplified. With the development of the new energy vehicle big data platforms, it is possible to obtain the battery SOC through cloud-based BMS (C-BMS). In this paper, a battery SOC estimation method based on common feature extraction and transfer learning is proposed for C-BMS applications. Considering the diversity of driving cycles, a common feature extraction method combining empirical mode decomposition (EMD) and a compensation strategy for C-BMS is designed. The selected features are treated as the new inputs of the SOC estimation model to improve the generalization ability. Subsequently, a long short-term memory (LSTM) recurrent neural network is used to construct a basic model for battery SOC estimation. A parameter-based transfer learning method and an adaptive weighting strategy are used to obtain the C-BMS battery SOC estimation model. Finally, the SOC estimation method is validated on laboratory datasets and cloud platform datasets. The maximum root-mean-square error (RMSE) of battery SOC estimation with the laboratory dataset is 2.2%. The maximum RMSE of battery pack SOC estimation on two different electric vehicles is 1.3%.
1. Introduction
Due to the shortage of resources and environmental pollution, the energy supply for transportation is constantly changing. As electric power resources can be obtained with a variety of energy sources, electrification has become an important direction for the development of automotive technology. Many types of batteries are used in electric vehicles (EVs) for energy storage. Considering the performance of batteries, it is necessary to obtain battery state information to ensure the safety of the energy storage system [1,2]. In a vehicle battery management system (V-BMS), various hardware resources are used to measure the battery voltage, current, temperature, insulation, and other states to ensure the safety of the battery system [3,4,5]. With the establishment of new energy vehicle cloud data platforms, it is feasible to use cloud platform data to evaluate the states of battery packs. The concept of a cloud-based battery management system (C-BMS) is proposed [6]. A cloud platform has advantages in data quantity and computing ability, which provides favorable conditions for battery state estimation.
Among the states of batteries, the battery state of charge (SOC) is an important and basic parameter. SOC is important not only for safety but also for an estimation of the remaining available energy, which is needed for range estimation. SOC allows us to evaluate performance with discharge and recharge power. Additionally, to more effectively utilize the energy storage resources of electric vehicles, an accurate estimation of the battery state is essential [7]. It has been widely studied by scholars in recent years. Many battery SOC estimation methods have been proposed. The methods can be roughly divided into three categories. The first category is single-factor SOC estimation methods, such as the ampere-hour (Ah) counting method [8], the open circuit voltage (OCV) method [9], and the internal resistance method [10,11]. Battery SOC estimation algorithms have low complexity and are easy to apply in V-BMSs. The second category is multifactor fusion methods mainly based on Kalman filters [1,12]. The methods are combined with battery model techniques, such as battery physical models [13] and equivalent circuit models [14] to solve the battery SOC estimation problem with high accuracy and robustness. The third category is battery SOC estimation methods based on multiple factors and machine learning [15,16]. In recent years, with the development of artificial intelligence technologies, the third category has been increasingly developed. Based on the review of the application of machine learning technologies in lithium-ion battery fault diagnosis and state estimation, methods such as logic regression, random forest, support vector machine, neural network, and Bayesian process regression have been applied in battery state estimation and fault diagnosis. With the accumulation of lithium-ion battery data and the development of computing chip technology, machine learning technology will play a greater role in battery state assessment [16].
To build the relationships of the voltage, current, temperature and the state of the battery, Liu et al. [17] adopted a back-propagation neural network (BPNN) model. The model achieved good accuracy without a large computational cost. However, BPNN cannot easily capture temporal information. To process time series and avoid gradient vanishing, a long short-term memory (LSTM) network [18] and a gated recurrent unit (GRU) network [19] were employed for battery SOC estimation. Generally, there was a positive correlation between the complexity and accuracy of the model. However, the more complex the model, the harder it is to converge. To solve this problem, Tian et al. [20] and Yang et al. [21] introduced the adaptive cubature Kalman filter (ACKF) and unscented Kalman filter (UKF) on the basis of LSTM. The proposed methods were verified by dynamic tests at various temperatures. Good feature extraction is beneficial for the training of the battery SOC estimation model. In the method, the voltage and current data of the battery are not directly used as inputs for the state estimation model. Instead, an automatic encoder is used to extract new features of the input quantity. Considering the close correspondence between battery OCV and SOC, Li et al. [22] combined recursive least squares (RLS) with an LSTM recurrent neural network model for the multi-state estimation of lithium-ion supercapacitors. In the method, new feature parameters are generated using RLS and LSTM. The SOC of the energy storage device is obtained through the constructed energy storage device status lookup table. It can be seen that reasonable processing of the input parameters of the model helps to improve the training effectiveness of the neural network model. To capture the information in both forward and reverse directions, Bian et al. [23] introduced a bidirectional mechanism on the basis of LSTM. The bidirectional LSTMs were stacked to enhance the precision of SOC estimation. Later, Bian et al. [24] employed a bidirectional LSTM encoder–decoder architecture for the estimation of the SOC sequence. With a more complex structure, it had a stronger sequence expression ability than their former work. To simplify the process of model training, Bhattacharjee et al. used parameter-transfer learning for the development of SOC estimation models with different battery types and working conditions [25]. To make full use of the cloud platform, Li et al. adopted stacked denoising autoencoders (SDAE) and an extreme learning machine (ELM) to realize EV battery pack SOC estimation for C-BMS applications [1]. A joint operation mode of C-BMS and V-BMS was presented. In this research, the battery pack SOC estimated by the C-BMS was used to update the equivalent circuit model parameters and the hyperparameters of the Kalman filter in the V-BMS.
Based on the investigation of the SOC estimation methods, the results of the research have proven the effectiveness of machine learning for battery state estimation. However, most of the existing technical solutions cannot be directly applied to C-BMS applications. The particularity of battery state estimation based on C-BMS is mainly reflected in the following aspects:
- Large data recording interval.
With the increase in the number of new energy vehicles, the cloud data platform needs to manage a large amount of vehicle data. The data logging interval on the data platform is large. In China, the data recording interval is within 30 s according to the requirements of national standards. A large recording interval makes the data unable to meet the sampling theorem. It is difficult to adapt to the phenomenon. Estimating the battery SOC with a large data recording interval is a difficult problem.
- 2.
- Various driving conditions.
Due to the variety of driving periods and working conditions, the accuracy of the state estimation with machine learning methods is reduced due to the poor generalization ability of the method. How to construct the common features among various working conditions from the original voltage, current, and temperature, and improve the correlation between features and SOC need to be studied.
- 3.
- Differences between laboratory and vehicle batteries.
Due to the differences between the laboratory and vehicle battery samples, such as the battery types, capacities, scales, working conditions, etc., the SOC estimation model obtained based on the laboratory training data cannot be used in the cloud data platform directly. How to revise the model and training method so that the model can be applied to each vehicle in the cloud platform and can be applied to different operating conditions and battery aging states is a problem to be solved.
With unresolved problems, a battery SOC estimation method based on common feature extraction and transfer learning for C-BMS applications is proposed in this paper. The empirical mode decomposition (EMD) method and a compensation strategy based on the internal resistance model are used to extract the common features. An analysis of correlation is conducted to select the appropriate features for SOC estimation. In terms of battery SOC estimation, an LSTM neural network is used to build the cell-level battery SOC estimation model with laboratory data. Subsequently, in view of the inconsistency of the laboratory battery data and the cloud platform data, the cell-level battery SOC estimation model for the C-BMS application is obtained through parameter-based transfer learning. With the adaptive weighting strategy, the battery pack SOC estimation model for C-BMS application is obtained.
The remainder of this paper is organized as follows. In Section 2, the definitions of the cell-level battery SOC and the battery pack SOC are given. In Section 3, a common feature extraction method based on EMD and the internal resistance model is introduced. In Section 4, a battery SOC estimation model for a C-BMS application is presented. Discussions of the experimental results are shown in Section 5. Some conclusions are given in Section 6.
2. The Definition of Battery SOC
2.1. The Definition of Cell-Level Battery SOC
The definition of battery SOC is usually to charge and discharge the battery in a constant temperature environment using a small C-rate constant current–constant voltage (CC-CV) charging method. After resting for 1~2 h, the battery is subjected to a constant current discharge mode. After charging and resting for 1~2 h, the battery is repeatedly subjected to 3 charging and discharging cycles, and the average value is taken to obtain the battery capacity value. Taking the fully charged state of the battery as SOC = 100%, we further calculate the changes in SOC during the charging and discharging process of the battery. In this paper, the cell-level battery SOC can be defined as the ratio of the residual available battery capacity to the nominal capacity [26]. If the SOC at time k − 1 is known, the SOC at time k can be calculated using
where SOCk is the battery SOC at time k. Δt represents the sample interval. ηc represents the Coulombic efficiency. Ik−1 is the battery load current at time k − 1, which is negative during the discharging process and positive during the charging process. Q is the nominal capacity of the battery cell. The value of Q is influenced by the operating temperature and the number of driving cycles [27].
2.2. The Definition of Battery Pack SOC
To meet the demands of EV powertrain systems, batteries need to be connected in series and parallel to form a battery pack [28]. In practice, the performances of battery cells are sorted to guarantee the safety and performance of EVs [29,30]. Additionally, the definition of battery pack SOC should also consider safety. To prevent the battery from being overcharged or overdischarged, the battery pack should stop discharging when one battery cell arrives at the low cutoff voltage, and the battery pack SOC is defined as 0%. Charging should be stopped when one battery cell arrives at the high cutoff voltage with a low current rate, and the battery pack SOC is defined as 100%. When the SOC is between 0% and 100%, it can be calculated using Equation (1). It should be noted that current Ik−1 and capacity Q in the equation represent the current and capacity of the battery pack.
3. Feature Extraction for Battery SOC Estimation
Due to the influence of driving habits, battery current distribution has great randomness and fluctuation. Battery terminal voltage also fluctuates greatly with the dynamic current. In the process of battery SOC estimation, conventional methods mainly rely on the terminal voltage, load current, and environmental temperature time series data of the battery. The initial feature pool is battery voltage, current, and temperature data. The battery terminal voltage is related to the battery open circuit voltage. It is generally believed that there is a one-to-one correspondence between the two parameters. The integral result of the battery current with time reflects the amount of charge capacity discharged or charged into the battery. Due to the large fluctuation of the battery operating current and the large sampling interval, directly using battery voltage and current timing data cannot accurately calculate the battery SOC. The inputs of the machine learning model parameters such as the battery terminal voltage and current is not optimal. Herein, a common feature extraction method for EV working condition data on the cloud platform is proposed. EMD is used to extract the tendency features from the original voltage and current to reduce the fluctuation of the original data. The voltage residue is compensated for by the average voltage on the internal resistance of the battery. Subsequently, according to the correlation analysis result, the common features for battery SOC estimation are selected.
3.1. Empirical Mode Decomposition
Compared with the original voltage, the change trend of the battery terminal voltage is more stable during the driving process of the vehicle. To obtain the change trend information, EMD is adopted for battery feature extraction. By giving an original time series signal Xk (k = 1, 2, …, N), the process of EMD can be described by Algorithm 1.
| Algorithm 1: Empirical mode decomposition |
| Step 1: Initialize: |
| Step 2: Acquire the i th intrinsic mode function (IMF): |
| (a): Initialize: |
| (b): Identify all the extreme points of hj−1,k and then adopt the three-order Hermite interpolation function to obtain the upper envelope uk and the lower envelope lk of hj−1,k. Later, the average envelope mlk of uk and lk can be computed using Equation (2).
|
| (c): Subtract the average envelope mlk from the signal hj−1,k. The new signal hj,k can be obtained, as shown in Equation (3).
|
| (d): Judge whether hj,k meets the two characteristics of IMF. If hj,k satisfies the above characteristics, it will be defined as the ith IMF named by IMFi,k and step 3 will be executed. If hj,k does not satisfy the above characteristics, j = j + 1 and step (b) to (d) will be executed until hj,k satisfies the above characteristics. The Cauchy convergence criterion is adopted for the termination condition of screening IMF. It is shown in Equation (4).
|
| Step 3: Equation (5) is used to extract residue ri,k. If the extreme points’ number of residue ri,k is greater than 2, i = i + 1 and Step 2 is executed. Otherwise, the decomposition is stopped and the current ri,k is the original signal Xk’ s residue named by Rk.
|
Finally, the original time series signal Xk can be reconstructed by IMFi,k and Rk:
where m is the number of IMFs of the original time series signal.
Substitute voltage Uk for Xk and conduct the process of the EMD algorithm. The IMFi,k (i = 1, 2, …, m) of voltage and voltage residue Uresidue,k can be obtained (k = 1, 2, …, N). In this paper, the IMFi,k of the terminal voltage are added, and the sum is regarded as voltage IMFs UIMFs,k. It can reflect the local change in the battery parameters. Uresidue,k can reflect the variation trend of the voltage. In addition, for the acquirement of a stable variate, current Ik is processed similarly. Current IMFs IIMFs,k and current residue Iresidue,k are obtained. As temperature values are relatively stable compared with voltage and current, they are not decomposed through EMD.
3.2. Online Parameter Identification and the Compensation Strategy
In the case of a large sampling interval among the battery data on the cloud platform, using complicated models to simulate batteries will introduce a systematic error during the course of discretization. Hence, a simplified internal resistance model [13] shown in Figure 1 was adopted to model batteries in this paper.
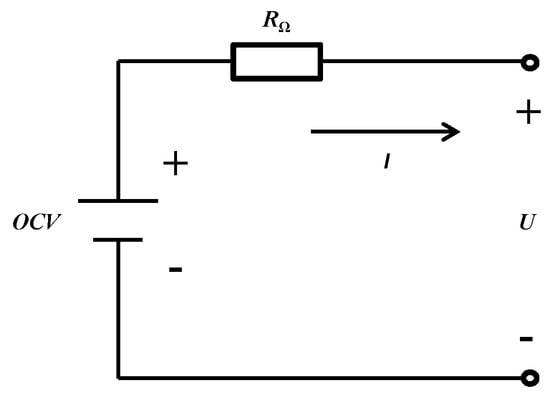
Figure 1.
The internal resistance model.
In Figure 1, U and I are the terminal voltage and current of the internal resistance model, respectively. OCV represents the open-circuit voltage. RΩ is the internal resistance of the battery.
The terminal voltage of the battery can be expressed as follows:
It is assumed that there is little difference between the OCV and OCV tendency in the local range. In view of the average voltage deviation on the internal resistance between the OCV tendency and voltage residue, the following relationship is established:
where is the mean current in a period of time.
The linear regression equation for the internal resistance parameter identification is shown in Equation (9). The least-squares (LS) method is used to obtain the optimal solution through Equation (11).
where and .
To further improve the dependency between the voltage residue and SOC, the voltage residue is compensated for through Equation (11).
where Uc,residue,k is the compensated voltage residue at time k.
3.3. Feature Selection Based on Correlation Analysis
For the training of an artificial neural network model, too many input features with high or low correlation will lead to overfitting [31]. As a result, correlation analysis should be executed to select the appropriate features as the inputs of the model. Herein, the selectable features are mainly about voltage, voltage residue, compensated voltage residue, current, current residue, and temperature. Figure 2 shows the Pearson correlation coefficients (PCCs) between features and SOC. To simplify the analysis, the calculation results of PCCs were taken as absolute values.
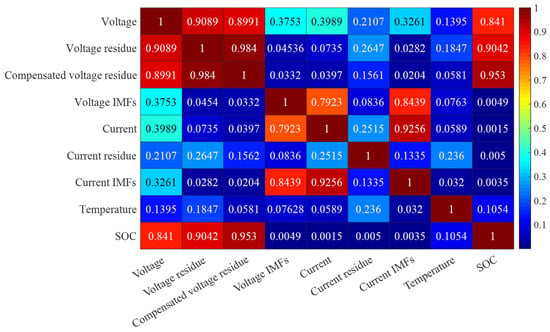
Figure 2.
The PCCs between all considered parameters and SOC.
In Figure 2, it can be seen that features such as voltage, voltage residue, and compensated voltage residue have high PCCs with SOC. Among them, the compensated voltage residue has the highest value of 0.953. Among the three features, to avoid overfitting, only the compensated voltage residue was selected. Considering that voltage IMFs represent the local variation in voltage, which contains detailed information on the SOC, voltage IMFs that have a low PCC with the SOC should also be selected. In addition, as the current residue can reflect the average change rate of SOC, it was also regarded as one of the input features. Combined with the current residue, the current IMFs can represent the instantaneous change direction of SOC, so it should also be chosen. As the batteries release different capacities at diverse temperatures, temperature should also be chosen. In conclusion, the final input features of the model were the compensated voltage residue, voltage IMFs, current residue, current IMFs, and temperature.
4. Battery SOC Estimation for C-BMS
The battery cell SOC estimation model for C-BMS application in this paper was built using common feature extraction and the transfer learning method. To shorten the development period of battery SOC estimation models with different types and working conditions, the battery cell SOC estimation model for C-BMS was transferred from the laboratory battery cell SOC estimation model. The transferring process includes data range matching and parameter-transfer learning. In addition, a battery SOC calibration method based on a cloud platform was designed to provide training samples for model training.
4.1. Battery SOC Estimation with Laboratory Data
In recent years, with the development of data-driven technology, machine learning has become increasingly popular with researchers. As the battery SOC estimation task refers to time series data, recurrent neural networks (RNNs) can be adopted. However, the classical RNN suffers from vanishing gradients and exploding gradients. In 1997, Sepp Hochreiter proposed the LSTM network, which consists of input gate i, forgetting gate f, output gate o, hidden layer h, and cell state c, to solve the problems [32]. The model is very suitable for addressing time series data modeling problems. As a result, it is used for laboratory battery SOC estimation. The structure of the LSTM cell is shown in Figure 3.
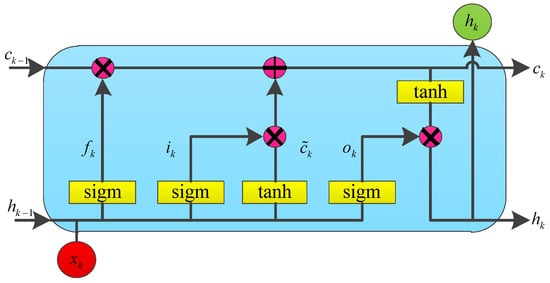
Figure 3.
The structure of the LSTM cell.
In Figure 3, x is the model input. The range of the three gate units is from 0 to 1, which determines how much information is stored. Hidden layer h is used for storing short memory, while the cell state is used for storing long memory. The forget gate f determines the forgetfulness level of the last cell state c, while the input gate i determines the absorption level of the current input information . Both of them determine the current cell state c. Later, the current hidden layer h is obtained through the current state cell c and the output gate o. The above mechanism of LSTM can be described by Equations (12)–(17):
where W and U represent weight matrices, and b represents the corresponding bias. sigm is the sigmoid function, which scales the output value into the range of 0 to 1, and tanh is the hyperbolic tangent function, which scales the output value into the range of 0 to 1. is the operator of a dot product.
Figure 4 shows the laboratory battery SOC estimation model in this paper. The experimental data are processed by the common feature extraction method. The new series of battery feature data, including the compensated voltage residue, voltage IMFs, current residue, current IMFs and temperature, are obtained. h0 and c0 are the initial values of hidden layer h and cell state c, respectively. Based on the long- and short-term memory function of hidden layer h and cell state c, the model can learn the internal characteristics of the batteries from the series data. Three layers of the fully connected (FC) neural network are connected to the hidden layer hk for dimension conversion. Finally, with the numerical conversion through the sigm(·) activation function, the battery SOC at time k is obtained.
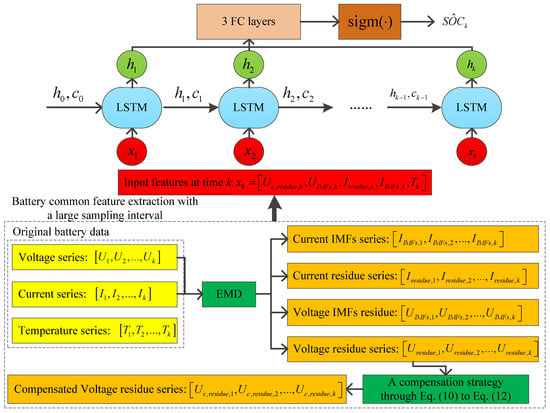
Figure 4.
The laboratory battery SOC estimation model.
4.2. Model Transferring for C-BMS Applications
Compared with laboratory battery cells, a vehicle battery has a complex structure, which is composed of multiple battery cells in series and parallel. There are significant differences between vehicle battery data and the laboratory battery cell data in terms of battery model, data magnitude, and operating conditions. As a result, the battery cell SOC estimation model obtained from laboratory data cannot be directly used for C-BMS battery SOC estimation. Existing studies have shown that transfer learning has the ability to capture model differences and usage condition differences between batteries [32,33]. Model transfer is implemented to solve the problem.
4.2.1. Data Range Matching
Before model transfer, data range matching is used to reduce model differences and operating condition differences. The main purpose of battery data range matching is to improve the consistency between the input parameters during model usage and the input parameters during model training, which is beneficial for enhancing the model’s generalization ability. In this process, it is necessary to consider the characteristics of the battery to scale the battery voltage and voltage data reasonably to avoid losing physical meaning after scaling. Therefore, the cloud platform battery cell data and the input volume of the laboratory battery cell SOC estimation model are consistent in the data range.
In terms of battery voltage, the cloud platform battery cell voltage is processed using Equation (18) to match the voltage range of the laboratory battery cell:
where and are the voltages before and after the data matching of the actual vehicle battery cells, respectively. and are the upper cutoff voltage and lower cutoff voltage of the actual vehicle battery cells, respectively. and are the upper cutoff voltage and lower cutoff voltage of the laboratory battery cells, respectively.
Since the actual vehicle current data are much larger than the current data of the laboratory battery cell, the load current of the vehicle needs to be scaled using Equation (19):
where and are the currents before and after data matching, respectively. and are the cell capacities of the vehicle battery and the laboratory battery, respectively. Figure 5 shows the data range matching result of the battery load current. In Figure 5a, the statistical results of the battery load current values under laboratory and driving conditions are shown. The discharge current is set to a negative value, and the energy feedback current is set to a positive value. The load current fluctuates under both laboratory and driving conditions. In the statistical result, the horizontal axis represents the range of numerical changes in the load current, and the vertical axis represents the proportion of the load current value that appears under two battery operating conditions. The current distributions are significantly different without data range matching. In Figure 5b, after data range matching, the current distribution is relatively consistent.
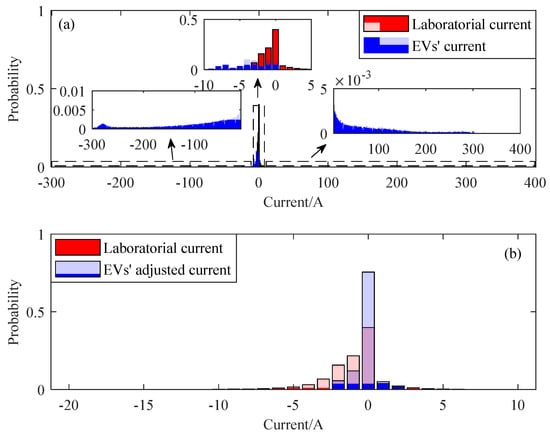
Figure 5.
Data range matching results of the battery load current. (a) Without and (b) with data matching.
4.2.2. Parameter-Transfer Learning
Due to the large recording interval of cloud platform data, the amount of data that can be used as battery SOC samples is small. Considering that transfer learning technologies are suitable for few-shot learning tasks, transfer learning was selected to solve the problem of battery SOC estimation on the cloud platform. In a transfer learning task, given a source domain DS and learning task TS, a target domain DT and learning task TT, transfer learning is devoted to using the knowledge of the source domain DS and the source domain learning task TS to help improve the estimation result of the target domain DT. In the process, DS ≠ DT or TS ≠ TT [34]. In general, the source domain DS is rich in a large amount of labeled data, while the target domain DT has little labeled data. As the target domain data distribution is not the same as the source domain data distribution, the model obtained by the source domain data cannot be applied to the target task. However, transfer learning can solve the problem well [35]. According to the classification of the transferred contents, transfer learning methods can be classified into four cases, including sample-based transfer learning, feature-based transfer learning, relation-based transfer learning, and parameter-based transfer learning. In this paper, parameter-based transfer learning was used to solve the SOC estimation task of the C-BMS. The method shares prior knowledge and some parameters between the source domain model and the target domain model to reduce the complexity of the transfer learning training process.
In this paper, the transfer of the laboratory battery cell SOC estimation model to the cloud platform battery cell SOC estimation model was implemented. The source domain DS is the laboratory battery cell dataset, and the target domain DT is the cloud platform battery cell dataset, which is derived from a real vehicle. Both the source task TS and the target task TT are battery cell SOC estimations.
The cloud platform battery cell SOC estimation model shares the initial weight parameters of the laboratory battery cell SOC estimation model. During the model transfer process, the LSTM network parameters of the time series feature extraction layer are frozen. Only the output layer FC network parameters with nonlinear mapping relationships are adjusted to capture the model difference and working condition difference between the laboratory battery cell and the real vehicle battery cell to obtain the cloud platform battery cell SOC estimation model. The transfer learning process is shown in Figure 6.
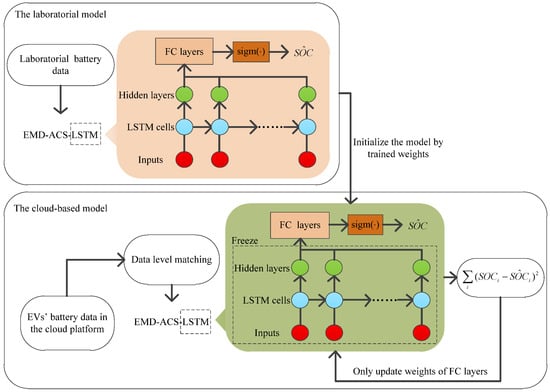
Figure 6.
The process of transfer learning of the battery cell SOC estimation model.
4.3. Battery Pack SOC Estimation
Battery pack SOC is associated with the remaining driving range of EVs and needs to be estimated accurately. For the battery pack, when the first battery cell reaches the charging cutoff voltage with a low current rate, it should stop charging, and its SOC is 100%. When the first battery cell reaches the discharging cutoff voltage, it should stop discharging, and its SOC is 0%. The definition can avoid the abuse of the battery pack. These two representative battery cells are of great significance to the battery pack.
The initial terminal voltage reflects the order of the battery cells reaching the charging or discharging cutoff voltages. With it, the representative battery cells mentioned above can be selected. The battery cell with the highest initial voltage is called the strongest battery cell, and it reaches the charging cutoff voltage fastest during the charging process. The battery cell with the lowest initial voltage is called the weakest battery cell, and it reaches the discharging cutoff voltage fastest [36]. When estimating the battery pack SOC with representative battery cells, these four guidelines should be followed [37].
When the battery pack nears full charging, the battery pack SOC should converge to the SOC of the strongest battery cell quickly. When the battery pack nears full discharging, the battery pack SOC should converge to the SOC of the weakest battery cell quickly. When the battery pack is between full charging and full discharging, the battery pack SOC should transition smoothly between the SOCs of the representative battery cells.
In view of the above criteria, the battery pack SOC can be weighted by the SOCs of the strongest battery cell and the weakest battery cell. The weighted strategy is shown in Equation (20).
where SOCstrongest,k and SOCweakest,k are the SOCs of the strongest battery cell and the weakest battery cell at time k, respectively. wstrongest,k and wweakest,k are the weighted coefficients of the strongest battery cell and the weakest battery cell at time k, respectively. SOCpack,k is the battery pack SOC at time k.
The weighted coefficients of a charging process are shown in Equation (21), and the weighted coefficients of a discharging process are shown in Equation (22). They can satisfy the above four criteria.
where and are the charging cutoff voltage and the discharging cutoff voltage, respectively. Ustrongest,k and Uweakest,k are the voltages of the strongest battery cell and the weakest battery cell at time k, respectively.
At the start or end of charging and at the start or end of discharging, the battery terminal voltage changes rapidly. At the end of charging, wstrongest and wweakest converge to 1 and 0, respectively. This makes the battery pack SOC converge to the SOC of the strongest battery cell rapidly. At the end of the discharging, wstrongest and wweakest converge to 0 and 1, respectively. This makes the battery pack SOC converge to the SOC of the weakest battery cell. At the mid period of charging or discharging, the battery terminal voltage changes gently, so wstrongest and wweakest change slowly. This makes the battery pack SOC transition smoothly between the SOCs of the strongest battery cell and the weakest battery cell.
The data transmitted from the EV to the cloud platform contain the battery cell data with the highest and lowest voltages. It can ensure the smooth SOC estimation of the EV’s battery pack on the cloud platform. The battery pack SOC estimation model based on the cloud platform is shown in Figure 7.
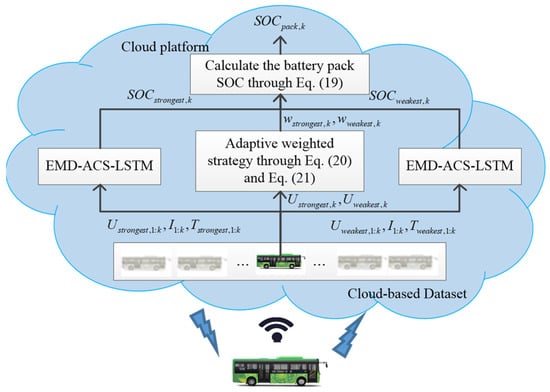
Figure 7.
Cloud-based battery pack SOC estimation model.
The current EV data are uploaded to the cloud platform in real time, and the established battery cell SOC estimation model is used to obtain the SOCs of the strongest battery cell and weakest battery cell. Finally, with Equation (20) to Equation (22), the EV’s battery pack SOC is acquired on the cloud platform.
4.4. Battery SOC Calibration with C-BMS
For the cloud platform battery cell SOC estimation model, both its acquisition and online update process depend on real vehicle battery measurement data. The key issue of model transfer is how to calibrate the SOC of a real vehicle battery based on cloud platform data and build a real vehicle battery training dataset. Due to dynamic and changeable driving conditions, the on-board BMS cannot guarantee the long-term stable operation of the battery SOC estimation strategy. Therefore, the battery module SOC uploaded by the on-board BMS cannot be used as the real SOC value for model training. In response to this problem, two cloud-based SOC calibration methods are presented as follows:
(1) The cloud platform requires the real vehicle to upload battery data with a sampling interval of 1 s in a certain period. Battery capacity values and SOC-tagged datasets are obtained through data analysis. In terms of battery capacity calculation, a long continuous full charge segment can be selected, and the ampere-hour integration method can be used to obtain the charging capacity of the battery cell in this interval. The battery cell capacity is updated by scaling the voltage interval. In addition, the cell capacity can also be obtained using a voltage reconstruction model based on partial charge data [38]. In this paper, the former is used to obtain the battery cell capacity. In the production of datasets with SOC labels, the ampere-hour integration method is used to calibrate the SOC of the discharge segment, which provides a training sample set for the cloud platform battery SOC estimation.
(2) When the cloud data platform cannot regularly obtain battery data with a 1 s sampling interval, the discharge segment data before and after long-term rest can be selected. Battery SOC can be obtained by using the OCV-SOC curve. For a qualified discharge segment of a vehicle, only one training sample can be provided. The cloud data platform monitors a large number of electric vehicles, which can provide rich training samples with different aging states, driving conditions, and a wide range of battery SOCs. The data can be used for model transfer learning. It should be noted that, considering the battery aging problem, the cloud platform needs to correct the OCV-SOC curve to ensure SOC calibration accuracy [39].
In this paper, method (1) was used to build the battery SOC dataset on the cloud data platform. The data of two different types of electric buses were calibrated and could be used for model transfer learning and method validation.
5. Experiments
The lithium-ion battery (LIB) experimental datasets in the laboratory originate from the University of Wisconsin–Madison. The experiments were carried out on the same type of battery, a Panasonic NCR18650PF LiNiCoAlO2. Its main parameters are shown in Table 1. Among the datasets, there were nine dynamic driving cycles, which consisted of Cycle1–4, neural network (NN), urban dynamometer driving schedule (UDDS), unified driving schedule (LA92), HWFET and US06. The driving cycles were repeated at four ambient temperatures: 25 °C, 10 °C, 0 °C, and −10 °C. During the test, the battery was charged to 4.2 V with a constant current–constant voltage (CC-CV) test whose charge rate and cutoff current were 1 C and 50 mA, respectively. After charging, the battery rested for enough time to ensure stability. Cycles 1–4 were the random combinations of NN, UDDS, LA92, HWFET and US06. NN consisted of LA92, US06, and some additional dynamic conditions, which was useful for the convergence of the network models. HWFET and US06 were used to test the performance of the battery cell SOC estimation model named EMD-ACS-LSTM, while the other driving cycle data were regarded as training datasets. The laboratory battery data were processed using downsampling to simulate the data storage interval of the cloud platform before training and testing.

Table 1.
The specifications of the NCR18650PF battery.
Two different types of electric buses monitored by the cloud platform were used to verify the battery SOC estimation method for C-BMS application in this paper. Both of them were from YIXING ELECTRIC AUTO limited company in China’s Shandong province. The battery pack of electrical bus 1 came from Boston Power Battery company, and the battery pack of electrical bus 2 came from Shandong Weihai Dongsheng Energy Technology company. Both of them were lithium-ion batteries. Their specifications are shown in Table 2. The modeling data used for battery state estimation (battery voltage, current, temperature) and actual vehicle operating conditions data were all measurement data.

Table 2.
The battery pack specifications of two electrical buses.
Due to the different battery manufacturers, the model transferring processes of the two electric buses were separate. Discharging fragments were selected from the two electric buses’ battery data. They were be divided into respective training sets during the model transfer. Then, two discharging fragments were selected from the two electric buses’ battery data to verify the battery SOC estimation method for C-BMS application in this paper.
Figure 8 shows the main process for implementing and verifying the proposed battery SOC estimation method. It will be described in detail as follows:
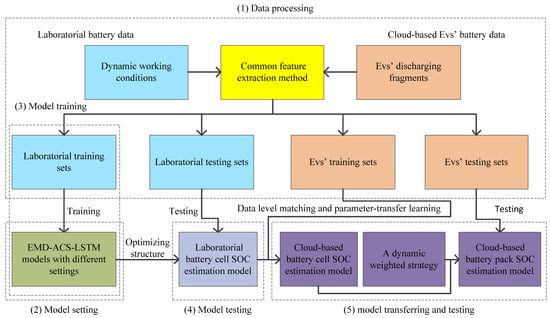
Figure 8.
The main procedure of the training and testing of models.
(1) Data processing: The EV battery data were matched and calibrated based on Section 4.2.1 and Section 4.4, and the laboratory battery data were calibrated by the Ah counting method. Subsequently, the sampling frequencies of both were reduced to 0.1 Hz to simulate the sparsity of the platform data. A sliding window with size N was set to determine series data of voltage U1:N, current I1:N, and temperature T1:N. To reduce the fluctuations of U1:N and I1:N, EMD was used to decompose them into the voltage IMFs UIMFs,1:N, voltage residue Uresidue,1:N, current IMFs IIMFs,1:N, and current residue Iresidue,1:N. The stable component, Uresidue,1:N,, was compensated for through the average voltage of the internal resistance identified online, further improving the correlation with SOC. xk = [Uc,residue,k, UIMFs,k, Iresidue,k, IIMFs,k, Tk] (k = 1, 2, 3, ……, N) was the input vector of the LSTM network, and it was normalized to a range [0, 1] to accelerate the convergence of training. Uc,residue,k was the compensated voltage residue. SOCN represented the true SOC at time step N, which was also the true value of the model’s output. With the sliding window, the above course was repeated, and many sample points could be acquired for training and testing.
(2) Model setting: Experiments were conducted to explore the influence of various lengths of the input sequence and different numbers of hidden layers on the battery cell SOC estimation model. A suitable setting could effectively guarantee the accuracy of the model. The model structure was optimized.
(3) Model training: Stratified sampling was used to divide the laboratory training sets into 10 disjoint subsets with the same size. One of them was selected as the laboratory validation set, and the other was regarded as the laboratory training set. This process was repeated 10 times. Each model was trained 10 times, and the results were averaged to provide a more valid estimation result. The laboratory training sets were used to adjust the model parameters. The laboratory validation sets were used to select the model during training to prevent the model from overfitting. The training process consisted of forward propagation and back propagation based on the Adam algorithm.
(4) Model testing: The test sets were used to obtain the performance of the trained models with different settings, and the best model was chosen. Laboratory test sets, including HWFET and US06, were used to test the battery SOC estimation model EMD-ACS-LSTM under different model settings, and the optimal structure of the battery cell SOC estimation model was confirmed.
(5) Model transferring and testing: Through data level matching and parameter-transfer learning, the laboratorial battery cell SOC estimation model was fine-tuned to obtain the battery cell SOC estimation model for C-BMS application. With the battery pack SOC estimation model, battery pack SOC estimation for C-BMS applications was realized. It was tested using two electric buses monitored by the cloud platform.
6. Results and Discussion
6.1. Comparison of Different Model Structures
Due to the differences in battery scales and working conditions, laboratory battery data were not completely consistent with the EV battery data on the cloud platform. However, it was modeled after the real operating conditions of EVs. Therefore, it could be used for the structure optimization of the battery cell SOC estimation model and the laboratory verification of the battery SOC estimation method in this paper. To select a suitable neural network model structure, experiments with various lengths of the input sequence and numbers of hidden layers were conducted to explore their impact on the SOC estimation results. With different model settings, models were trained with training sets, and their SOC estimation performances were evaluated using test sets. The evaluation indexes were RMSE and maximum absolute error (MaxAE). The number of hidden layers was first fixed at 32 before exploring the impact of different lengths of the input sequence on the SOC estimation model. Generally, the longer the input sequence is, the more available information the model can learn, which improves the SOC estimation accuracy. However, when the input sequence is too long, it will cause the common problems of gradient disappearance or gradient explosion in model training. In addition, the increasing length of the input sequence will also cause a decline in the model computation speed. Table 3 compares the performance of SOC estimation under various lengths of the input sequence among [30, 60, 90, 120]. The corresponding average RMSEs of the HWFET and US06 driving cycles are 2.4%, 1.7%, 1.3%, and 1.2%, respectively. The corresponding average MaxAEs of HWFET and US06 are 6.2%, 4.2%, 3.3%, and 3.1%, respectively. As the length of the input sequence increases, the model performance improves greatly at first and then slows down. Hence, to balance the computation speed and accuracy, the length of the input sequence was set as 90. Table 4 compares the performance of SOC estimation under various numbers of hidden layers among [8, 16, 32, 64]. The corresponding average RMSEs of the HWFET and US06 driving cycles are 1.4%, 1.3%, 1.3%, and 1.4%, respectively, and the corresponding average MaxAEs of the HWFET and US06 driving cycles are 3.5%, 3.4%, 3.3%, and 3.4%, respectively. The SOC estimation model with 32 hidden layers has the best performance.

Table 3.
SOC estimation error with different sequence lengths.

Table 4.
SOC estimation error with different hidden sizes.
To balance the computation speed and the SOC estimation accuracy, the model trained under the length of the input sequence and number of hidden layers fixed as 90 and 32 is regarded as the best model.
6.2. Comparison with the Standard LSTM Method
In this section, the performance of battery cell SOC estimation models constructed using EMD-ACS-LSTM and standard LSTM will be compared through laboratory battery data. Their model structures and training mode were consistent. The difference is that the input features of the former were obtained using the common feature extraction method in this paper, while the latter was the original voltage, current, and temperature. In Figure 9, there are not only estimated results of battery SOC but also reference true values of battery SOC. The results in the figure were all calculated based on experimental data. These results are battery state information calculated based on measured values (battery terminal voltage, load current, temperature). They were not obtained through simulation. Figure 9a,c shows the results of SOC estimation under the HWFET driving cycle at 25 °C and −10 °C ambient temperatures, obtained using the above two models, respectively. Figure 9b,d shows the corresponding state estimation errors. Figure 10a,c shows the results of SOC estimation under the US06 driving cycle at 25 °C and −10 °C ambient temperatures obtained by the above two models. Figure 10b,d shows the corresponding errors. As shown in Figure 9 and Figure 10, both standard LSTM and EMD-ACS-LSTM reach a high accuracy under the HWFET and US06 driving cycles at 25 °C. However, in regard to the HWFET driving cycle at −10 °C, the performance of the standard LSTM method declines obviously, while EMD-ACS-LSTM still has a good performance, which effectively verifies that the extracted feature in this paper is greatly beneficial for models to learn the general characteristics of different driving cycles.
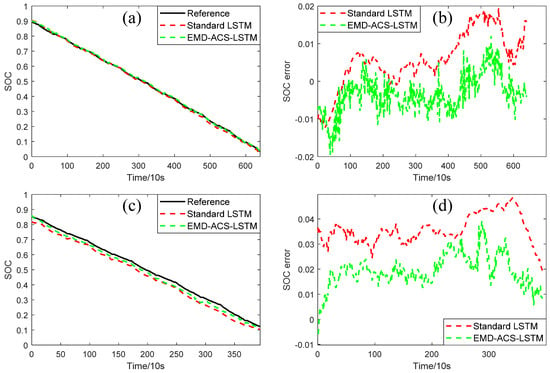
Figure 9.
Comparison of SOC results with different methods under HWFET at 25 °C and −10 °C ambient temperatures. (a) SOC and (b) error at 25 °C. (c) SOC and (d) error at −10 °C.
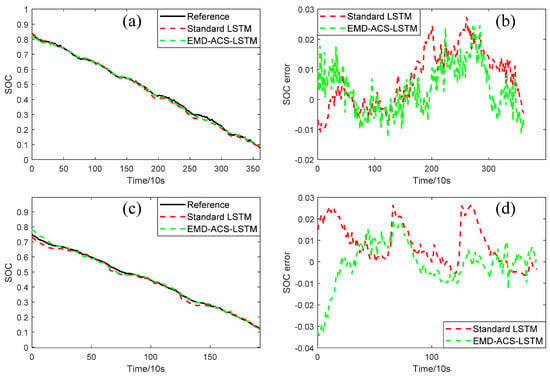
Figure 10.
Comparison of SOC results with different methods under US06 at 25 °C and −10 °C ambient temperatures. (a) SOC and (b) error at 25 °C. (c) SOC and (d) error at −10 °C.
Table 5 summarizes the SOC estimation performance of the two models under the HWFET and US06 driving cycles at four ambient temperatures. The RMSEs of SOC estimation under HWFET at 25 °C, 10 °C, 0 °C, and −10 °C obtained using standard LSTM are 1.0%, 1.1%, 1.9%, and 3.8%, respectively. The RMSEs of SOC estimation under HWFET at 25 °C, 10 °C, 0 °C, and −10 °C obtained using EMD-ACS-LSTM are 0.8%, 0.9%, 1.4%, and 2.2%, respectively. The RMSEs of SOC estimation under US06 at 25 °C, 10 °C, 0 °C, and −10 °C obtained using standard LSTM are 1.1%, 1.7%, 2.2%, and 1.2%, respectively. The RMSEs of SOC estimation under US06 at 25 °C, 10 °C, 0 °C, and −10 °C obtained using EMD-ACS-LSTM are 1.0%, 1.4%, 1.7%, and 1.3%, respectively. According to the RMSE results, EMD-ACS-LSTM can reach a better accuracy than the standard LSTM at 25 °C, 10 °C, and 0 °C. As the temperature decreases, EMD-ACS-LSTM can still behave well, while the standard LSTM cannot guarantee the accuracy of HWFET at −10 °C. In summary, the accuracies of SOC estimation obtained using EMD-ACS-LSTM are superior to the accuracies of SOC estimation obtained using the standard LSTM. The result strongly indicates that the input features extracted in this paper can enhance the reliability of SOC estimation.

Table 5.
SOC estimation error obtained using standard LSTM and EMD-ACS-LSTM.
6.3. Comparison of the Methods with Different Sampling Intervals
This section analyzes the impact of different sampling intervals (sampling rates) on battery SOC estimation algorithms, such as the Ah counting method, the OCV method, and the model-based method. Figure 11a shows the SOC estimation results of different sampling intervals under the US06 driving cycle at 25 °C, obtained using the Ah counting method without the initial error and measuring error. Figure 11b shows the corresponding error results. As the sampling interval increases, the accuracy of SOC estimation declines gradually. When the sampling interval is 1 s, the estimated SOC can be regarded as the true value. The RMSEs of SOC estimation under sampling intervals of 5 s and 10 s are 0.8% and 2.3%, respectively. Although the SOC estimation accuracy under the sampling interval of 10 s is acceptable, the Ah counting method is not suitable for C-BMS SOC estimation due to the usual existence of the initial error and measuring error. Figure 11c shows the SOC estimation results of different sampling intervals under the US06 driving cycle at 25 °C, obtained using the OCV method. Figure 11d shows the estimation error results. The accuracy of SOC estimation drops sharply with increasing sampling intervals. The RMSEs of SOC estimation under sampling intervals of 1 s, 5 s, and 10 s are 1.6%, 10.3%, and 16.0%, respectively. The battery OCV identification result is largely influenced by the sampling intervals. It is not suitable for C-BMS SOC estimation.
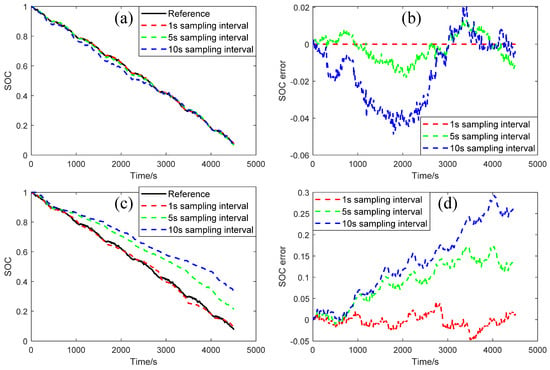
Figure 11.
Comparison of SOC results with different sampling intervals obtained using the Ah counting method and OCV method. (a) SOC and (b) error obtained using the Ah counting method. (c) SOC and (d) error obtained using the OCV method.
Figure 12a shows the SOC estimation results of different sampling intervals under the US06 driving cycle at 25 °C, obtained using the model-based method. Figure 12b shows the corresponding error results. Herein, the first-order RC model was selected, and the cubature Kalman filter (CKF) was used to estimate SOC. It can be seen that as the sampling interval rises, the SOC estimation accuracy changes slightly. The RMSEs of SOC estimation under sampling intervals of 1 s, 5 s, and 10 s are 1.6%, 1.6%, and 1.8%, respectively. The main factor influencing the exactness of the model-based method is the battery model, which can be explained using Figure 12c,d. Figure 12c shows the SOC estimation results of different biases on the OCV-SOC curve under the US06 driving cycle at 25 °C, obtained using the model-based method. Figure 12d shows the corresponding error results. When there is no bias in the OCV-SOC curve, the model-based method can reach an acceptable accuracy. However, in regard to the ±0.05 V bias in the OCV-SOC curve, the RMSEs of SOC estimation are 5.7% and 7.0%, respectively. Considering the limited transmission bandwidth and the large numbers of EVs, the OCV-SOC curves of EVs cannot be accurately obtained or obtained in a timely manner by the cloud platform, which makes the model-based method difficult to carry out on the cloud platform.
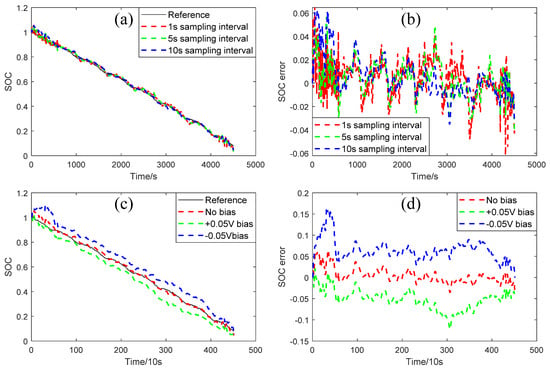
Figure 12.
Comparison of SOC results with different sampling intervals. (a) SOC and (b) error. SOC results with different biases on the OCV-SOC curve. (c) SOC and (d) error.
Table 6 summarizes the SOC estimation results of different methods under US06 at 25 °C with a 10 s sampling interval. The RMSEs of SOC estimation obtained using the Ah counting method, the OCV method, the model-based method, and the LSTM are 2.3%, 16.0%, 1.8%, and 1.1%, respectively. The data-based LSTM methods are more suitable for C-BMS SOC estimation than the three traditional methods.

Table 6.
SOC estimation error obtained using different methods.
6.4. Comparison of the Results between C-BMS and V-BMS
In the previous section, the battery cell SOC estimation model was fully validated on laboratory battery measurement data. This section will verify the battery pack SOC estimation model for C-BMS applications with the EV battery data on the cloud platform. Combining data level matching and parameter-transfer learning, the battery cell SOC estimation model for C-BMS applications was transferred from the laboratory battery cell SOC estimation model. Later, the SOC estimation result of the battery pack for C-BMS application was calculated. Figure 13a,c shows the results of SOC estimation under two discharging fragments of electrical bus 1 data, obtained using V-BMS and C-BMS, respectively. Figure 13b,d show the corresponding errors. For discharging fragment 1 of the electrical bus 1 data, the SOC estimation results of both the V-BMS and C-BMS behave well in most cases. However, the SOC estimation results of V-BMS are not stable during the discharge process. In regard to discharging fragment 2 of the electrical bus 1 data, there exists not only a sudden change but also a bias in the SOC estimation result of V-BMS, which is greatly harmful to EV driving. In fragment 2, there is a certain deviation between the results of the method proposed in this paper and the results of V-BMS, mainly due to the possible use of the Ah counting method in V-BMS, which does not have the ability to correct cumulative errors. In both discharging fragments 1 and 2 of the electrical bus 1 data, the EVs’ battery pack SOC estimation model for C-BMS applications exhibits better accuracy and stability.
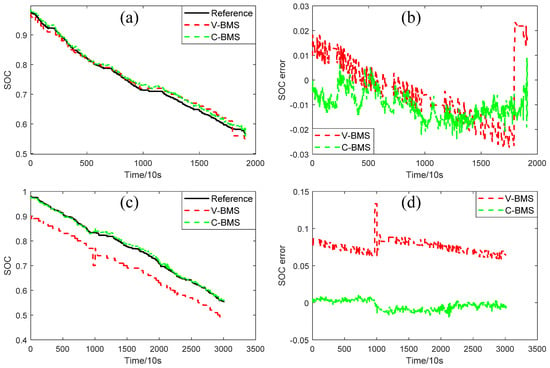
Figure 13.
Comparison of SOC results of V-BMS and C-BMS under two discharging fragments of electrical bus 1. (a) SOC and (b) error of discharging fragment 1. (c) SOC and (d) error of discharging fragment 2.
Figure 14a,c shows the results of SOC estimation under two discharging fragments of electrical bus 2 obtained using V-BMS and C-BMS, respectively. Figure 14b,d shows the corresponding errors. For discharging fragment 1 of the electrical bus 2 data, the SOC estimation result of the C-BMS is better than that of the V-BMS. For discharging fragment 2 of the electrical bus 2 data, the SOC estimation result of V-BMS deviates from the SOC reference gradually during the discharging process, but that of C-BMS tightly follows the SOC reference all the time. The main reason for the difference in slope is that the V-BMS does not update the battery capacity information in a timely manner. However, the method in this paper can recalibrate the relevant parameters through the transfer learning method, which can be applied to the change in battery capacity.
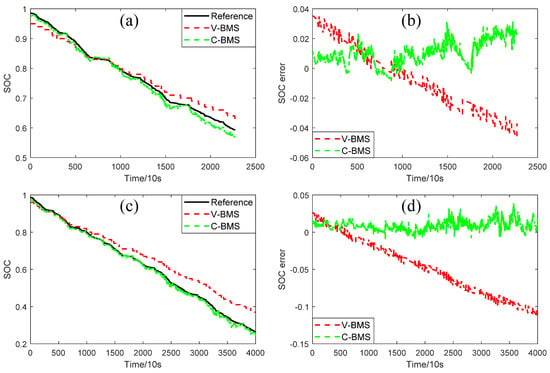
Figure 14.
Comparison of SOC results of V-BMS and C-BMS under two discharging fragments of electrical bus 2. (a) SOC and (b) error of discharging fragment 1. (c) SOC and (d) error of discharging fragment 2.
Based on the above analysis, the battery pack SOC estimation models for C-BMS applications behave well on both electrical buses. The result effectively proves the operability of the battery pack SOC estimation method on the cloud platform.
Table 7 summarizes the SOC estimation performance of the V-BMS and C-BMS with two electrical buses. The RMSEs of SOC estimation under two discharging fragments of electrical bus 1, obtained using the V-BMS, are 1.3% and 8.0%. The corresponding MaxAEs are 2.7% and 13.3%, respectively. The RMSEs of SOC estimation under two discharging fragments of electrical bus 1, obtained using the C-BMS, are 1.2% and 0.7%, respectively. The corresponding MaxAEs are 2.4% and 2.1%, respectively. The RMSEs of SOC estimation under two discharging fragments of electrical bus 2, obtained using the V-BMS, are 2.3% and 6.1%. The corresponding MaxAEs are 4.6% and 11.4%, respectively. The RMSEs of SOC estimation under two discharging fragments of electrical bus 2, obtained using the C-BMS, are 1.3% and 1.1%, respectively. The corresponding MaxAEs are 3.2% and 3.9%, respectively. Based on the data listed in Table 7, it can be concluded that the battery pack SOC estimation models for C-BMS applications have a high accuracy and a great stability, which can be proposed as a solid reference and correction for V-BMS.

Table 7.
SOC estimation error obtained using V-BMS and C-BMS.
7. Conclusions
In this paper, a battery pack SOC estimation method for C-BMS applications is proposed. The contributions of this paper can be summarized in three parts:
(1) In terms of extracting common features of batteries’ working conditions, this paper studies a common feature extraction method for C-BMS applications to reduce the volatility of working conditions. It includes EMD, an internal resistance model, online parameter identification, and a compensation strategy. The PCC between the compensated voltage residue and SOC reaches a maximum value of 0.953. Based on the correlation analysis and SOC influencing factors, the compensated voltage residue, voltage IMF, current residue, current IMF, and temperature are treated as the new model inputs.
(2) In terms of constructing the battery pack SOC estimation method for C-BMS applications, the battery cell SOC estimation model is built by combining the common feature extraction method and LSTM network first. Later, with the weighted strategy, the battery pack SOC estimation model is obtained. To shorten the development cycle of the model, the laboratory battery cell SOC estimation model is fine-tuned to obtain the battery cell SOC estimation model for C-BMS applications. Before transferring, data level matching reduces the difference between EV battery data and laboratory battery data and improves the stability of the transferred model. A battery SOC calibration method with C-BMS is designed to provide training samples for model transfer.
(3) In terms of the verification of the proposed battery SOC estimation method, verifications of the laboratory and cloud platform have been carried out. On the laboratory battery cell data, the maximum RMSE of battery cell SOC estimation obtained using the proposed EMD-ACS-LSTM is only 2.2%. Its overall performance is better than that of the standard LSTM. On the battery pack data of two electric buses monitored by the cloud platform, the maximum RMSE of battery pack SOC estimation is only 1.3%, showing good performance.
The method proposed in this paper can be used on the new energy vehicle big data platforms. The state estimation result can provide a unified basis for the calibration of the vehicle SOC estimation value and vehicle state evaluation. In future work, we will focus on the application of machine learning methods to the battery state of energy, state of power estimation, and battery safety assessment.
Author Contributions
Conceptualization, X.L. and J.X.; methodology, X.L.; software, J.X.; validation, J.X. and X.L.; formal analysis, X.L. and J.X.; investigation, J.X. and X.D.; resources, X.L. and X.D.; data curation, H.L.; writing—original draft preparation, X.L. and J.X.; writing—review and editing, X.L., X.D. and H.L.; visualization, J.X. and H.L.; supervision, X.L. and X.D.; project administration, X.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of Guangdong Province (2021A1515010525), the National Natural Science Foundation of China (No. 52177219) and the Natural Science Foundation of Shenzhen (University Stability Support Program No. 20220807222119001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
https://data.mendeley.com/datasets/wykht8y7tg/1, accessed on 1 January 2021.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Ko, Y.; Choi, W. A New SOC Estimation for LFP Batteries: Application in a 10 Ah Cell (HW 38120 L/S) as a Hysteresis Case Study. Electronics 2021, 10, 705. [Google Scholar] [CrossRef]
- Gabbar, H.; Othman, A.; Abdussami, M. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Lelie, M.; Braun, T.; Knips, M.; Nordmann, H.; Ringbeck, F.; Zappen, H.; Sauer, D. Battery Management System Hardware Concepts: An Overview. Appl. Sci. 2018, 8, 534. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.S.; Fiori, F. Susceptibility to EMI of a Battery Management System IC for electric vehicles. In Proceedings of the 2015 IEEE International Symposium on Electromagnetic Compatibility (EMC), Dresden, Germany, 16–22 August 2015; pp. 749–754. [Google Scholar]
- Aiello, O. Electromagnetic Susceptibility of Battery Management Systems’ ICs for Electric Vehicles: Experimental Study. Electronics 2020, 9, 510. [Google Scholar] [CrossRef]
- Li, S.; He, H.; Li, J. Big data driven lithium-ion battery modeling method based on SDAE-ELM algorithm and data pre-processing technology. Appl. Energy 2019, 242, 1259–1273. [Google Scholar] [CrossRef]
- Doridant, A.; Abouda, K.; Givelin, P.; Thibaud, B. Battery Management System Demonstrator Board design using EMC System simulation. In Proceedings of the 2019 International Symposium on Electromagnetic Compatibility—EMC EUROPE, Barcelona, Spain, 2–6 September 2019. [Google Scholar]
- Ng, K.S.; Moo, C.; Chen, Y.; Hsieh, Y. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Lee, J.; Cho, B.H. State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge. J. Power Sources 2008, 185, 1367–1373. [Google Scholar] [CrossRef]
- Hung, M.; Lin, C.; Lee, L.; Wang, C. State-of-charge and state-of-health estimation for lithium-ion batteries based on dynamic impedance technique. J. Power Sources 2014, 268, 861–873. [Google Scholar] [CrossRef]
- Coleman, M.; Lee, C.K.; Zhu, C.; Hurley, W.G. State-of-Charge Determination From EMF Voltage Estimation: Using Impedance, Terminal Voltage, and Current for Lead-Acid and Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2007, 54, 2550–2557. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, H.; Feng, F.; Liu, B. An enhanced multi-state estimation hierarchy for advanced lithium-ion battery management. Appl. Energy 2020, 257, 114019. [Google Scholar] [CrossRef]
- Li, X.; Fan, G.; Pan, K.; Wei, G.; Zhu, C.; Rizzoni, G.; Canova, M. A physics-based fractional order model and state of energy estimation for lithium ion batteries. Part I: Model development and observability analysis. J. Power Sources 2017, 367, 187–201. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Chang, W. Estimation of the state of charge for a LFP battery using a hybrid method that combines a RBF neural network, an OLS algorithm and AGA. Int. J. Electr. Power Energy Syst. 2013, 53, 603–611. [Google Scholar] [CrossRef]
- Samanta, A.; Chowdhuri, S.; Williamson, S.S. Machine Learning-Based Data-Driven Fault Detection/Diagnosis of Lithium-Ion Battery: A Critical Review. Electronics 2021, 10, 1309. [Google Scholar] [CrossRef]
- Liu, X.; Wu, J.; Zhang, C.; Chen, Z. A method for state of energy estimation of lithium-ion batteries at dynamic currents and temperatures. J. Power Sources 2014, 270, 151–157. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long Short-Term Memory Networks for Accurate State-of-Charge Estimation of Li-ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6730–6739. [Google Scholar] [CrossRef]
- Jiao, M.; Wang, D.; Qiu, J. A GRU-RNN based momentum optimized algorithm for SOC estimation. J. Power Sources 2020, 459, 228051. [Google Scholar] [CrossRef]
- Tian, Y.; Lai, R.; Li, X.; Xiang, L.; Tian, J. A combined method for state-of-charge estimation for lithium-ion batteries using a long short-term memory network and an adaptive cubature Kalman filter. Appl. Energy 2020, 265, 114789. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, S.; Li, W.; Miao, Q. State-of-charge estimation of lithium-ion batteries using LSTM and UKF. Energy 2020, 201, 117664. [Google Scholar] [CrossRef]
- Li, X.; Long, T.; Tian, J.; Tian, Y. Multi-state joint estimation for a lithium-ion hybrid capacitor over a wide temperature range. J. Power Sources 2020, 479, 228677. [Google Scholar] [CrossRef]
- Bian, C.; He, H.; Yang, S.; Huang, T. State-of-charge sequence estimation of lithium-ion battery based on bidirectional long short-term memory encoder-decoder architecture. J. Power Sources 2020, 449, 227558. [Google Scholar] [CrossRef]
- Bian, C.; He, H.; Yang, S. Stacked bidirectional long short-term memory networks for state-of-charge estimation of lithium-ion batteries. Energy 2020, 191, 116538. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Verma, A.; Mishra, S.; Saha, T.K. Estimating State of Charge for xEV Batteries Using 1D Convolutional Neural Networks and Transfer Learning. IEEE Trans. Veh. Technol. 2021, 70, 3123–3135. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhang, L. Co-estimation of capacity and state-of-charge for lithium-ion batteries in electric vehicles. Energy 2019, 174, 33–44. [Google Scholar] [CrossRef]
- Luo, X.; Kang, L.; Lu, C.; Linghu, J.; Lin, H.; Hu, B. An Enhanced Multicell-to-Multicell Battery Equalizer Based on Bipolar-Resonant LC Converter. Electronics 2021, 10, 293. [Google Scholar] [CrossRef]
- Kim, J.; Cho, B.H. Screening process-based modeling of the multi-cell battery string in series and parallel connections for high accuracy state-of-charge estimation. Energy 2013, 57, 581–599. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Gong, X.; He, H. Adaptive state of charge estimator for lithium-ion cells series battery pack in electric vehicles. J. Power Sources 2013, 242, 699–713. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Chen, W.; Wang, L.; Qu, C. Online joint-prediction of multi-forward-step battery SOC using LSTM neural networks and multiple linear regression for real-world electric vehicles. J. Energy Storage 2020, 30, 101459. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Fang, X.; Gong, G.; Li, G.; Chun, L.; Li, W.; Peng, P. A hybrid deep transfer learning strategy for short term cross-building energy prediction. Energy 2021, 215, 119208. [Google Scholar] [CrossRef]
- Li, X.; Xu, J.; Hong, J.; Tian, J.; Tian, Y. State of energy estimation for a series-connected lithium-ion battery pack based on an adaptive weighted strategy. Energy 2021, 214, 118858. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Shen, J.; Yan, W.; Xiao, R. A Novel State of Charge Estimation Algorithm for Lithium-Ion Battery Packs of Electric Vehicles. Energies 2016, 9, 710. [Google Scholar] [CrossRef]
- Tan, Y.; Zhao, G. Transfer Learning with Long Short-Term Memory Network for State-of-Health Prediction of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2020, 67, 8723–8731. [Google Scholar] [CrossRef]
- Pan, S.J.; Qiang, Y. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, C.; Jiang, J.; Zhang, W.; Gao, Y.; Zhang, L. A voltage reconstruction model based on partial charging curve for state-of-health estimation of lithium-ion batteries. J. Energy Storage 2021, 35, 102271. [Google Scholar] [CrossRef]
- Chen, X.; Lei, H.; Xiong, R.; Shen, W.; Yang, R. A novel approach to reconstruct open circuit voltage for state of charge estimation of lithium ion batteries in electric vehicles. Appl. Energy 2019, 255, 113758. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).