An Efficient EMS for BESS in Monopolar DC Networks with High Penetration of Renewable Generation: A Convex Approximation

Abstract

This research presents an efficient energy management system (EMS) for battery energy storage systems (BESS) connected to monopolar DC distribution networks which considers a high penetration of photovoltaic generation. The optimization model that expresses the EMS system with the BESS and renewable generation can be classified as a nonlinear programming (NLP) model. This study reformulates the NLP model as a recursive convex approximation (RCA) model. The proposed RCA model is developed by applying a linear approximation for the voltage magnitudes only at nodes that include constant power loads. The nodes with BESS and renewables are approximated through the relaxation of their voltage magnitude. Numerical results obtained in the monopolar version of a 33-bus system, which included three generators and three BESS, demonstrate the effectiveness of the RCA reformulation when compared to the solution of the exact NLP model via combinatorial optimization techniques. Additional simulations considering wind power and diesel generators allow one to verify the effectiveness of the proposed RCA in dealing with the efficient operation of distributed energy resources in monopolar DC networks via recursive convex programming.

1. Introduction

Monopolar DC networks are efficient electrical systems that utilize DC technology at all voltage levels [1,2]. These grids can be constructed for high voltage levels, i.e., transmission lines to interconnect large-scale power systems with different frequencies, as well as extra-large transmission lines to transfer thousands of megawatts for distances larger than 1000 km [3,4]. In addition, DC networks can also be constructed for medium- and low-voltage levels to distribute energy to all end users while improving voltage quality and reducing the total grid energy losses [5,6]. The main advantage of using DC instead of AC technology to provide the electrical service at medium- and low-voltage levels is the fact that there is no reactive power and frequency in these systems [7], which makes these grids efficient in terms of energy losses, as well as easy to control, because power flows and voltages are the only variables of interest in these grids [8,9].

One of the greatest challenges in the operation of monopolar DC networks is the efficient integration of distributed energy resources, given that, as in the case of AC networks, these devices must be effectively coordinated in order to extract their greatest benefit [10]. This research aims to propose an efficient energy management system (EMS) for batteries interconnected in monopolar DC networks with a high penetration of renewable energy resources based on photovoltaic (PV) generation technology. The main goal to obtain the best generation outputs and energy-storage profiles to minimize the expected grid energy losses. Note that, even though the daily energy losses can be a secondary optimization objective in electrical networks with multiple distributed energy resources, the nonlinear structure of this optimization problem can be used to propose new solution methodologies that include economic and environmental analyses, in which PV plants and battery energy storage systems (BESS) can play an essential role in their efficient operation. In the current literature, there are many studies on the optimal integration and operation of dispersed generation units in monopolar DC networks [11], some of which are presented below.

The authors of [12] proposed a mixed-integer quadratic convex formulation to locate dispersed generation sources and select BESS systems in monopolar DC distribution networks. The nonconvex equations regarding power balance were relaxed by using the McCormick approximation of the product of two variables. Numerical results in the 21-bus grid demonstrated the effectiveness of the proposed mixed-integer convex model to locate distributed energy resources in comparison with the exact mixed-integer nonlinear programming model solved in the GAMS software. However, the authors did not propose any alternative to minimize the errors introduced by the McCormick approximation in the final calculation of the objective function. The study by [11] provided a detailed analysis of the possibility of supplying a part of the electrical energy consumption of residential users in Bogotá, Colombia based on the benefits granted by Law 1715 of 2014. It studied two different residential consumers (strata 2 and 3 of the Colombian socioeconomic scale, with 1 being the lowest level), considering a PV penetration between 10 and 100% of their self-consumption. Numerical results demonstrated positive profits perceived by the users during the first year of operating their PV residential systems. In [13], the authors presented a semidefinite programming model by which to operate distributed energy resources in monopolar DC networks. The main advantage of semi-definite programming is that it belongs to the family of the convex optimization techniques, which ensures that the optimum global for the studied problem is found. Numerical results in the 21-node grid demonstrated the effectiveness of the proposed convex formulation in comparison with the solution of the exact NLP model in the GAMS software. However, the main flaw of semidefinite programming corresponds to the quadratic increment of the model variables, as it works in the space of the semidefinite matrices. The authors of [14] proposed a convex approximation methodology to operate wind power and PV generation in medium-voltage DC distribution grids. Numerical results in two test feeders composed of 10 and 39 buses confirmed the effectiveness of the proposed convex model in comparison with their solution via specialized commercial tools. However, the authors focused on the stability analysis of the system while considering uncertainties in renewable energy resources. They did not resolve an optimization problem for an operation horizon because their interest was in observing the stability of the distribution network when it undergoes sudden variations in renewable generation.

In light of the reviewed state of the art, the main contributions of this research are as follows:

i.

The reformulation of the NLP model that describes the EMS system for PV generation units and BESS in monopolar DC networks as a quadratic convex approximation by using the McCormick approximation of the product of two variables.

ii.

The application of an iterative solution of the proposed convex model to minimize/eliminate the error induced by the McCormick approximation by using a recursive solution approach.

Note that the scope of this research does not include the possible uncertainties in PV generation and demand, which are considered to be well-known inputs for the NLP model that represents the EMS system. Nevertheless, more research is required regarding the stochastic nature of the demand profile and generation input as a function of the weather conditions and the type of the day under analysis (working day or weekend). In addition, the main difference of the current proposal with respect to the convex approximation proposed by the authors of [12] is that, in this research, the McCormick approximation is recursively evaluated to minimize the error induced by the approximation of the product of two variables while using a linear equivalent approximation, which was not implemented by the mixed-integer quadratic approximation employed in [12] for the efficient integration of dispersed generation sources and BESS systems in monopolar DC networks.

The rest of this paper is organized as follows. Section 2 presents the exact nonlinear programming (NLP) model to represent the optimal dispatch of PV generation units and BESS in monopolar distribution systems with the purpose of minimizing daily energy losses. Section 3 describes the proposed McCormick approximation to transform the product of two variables into an affine plane that allows one to turn the exact NLP model into a convex approximated one. In addition, a recursive procedure is implemented to minimize/eliminate the estimation errors introduced by the linear approximation. 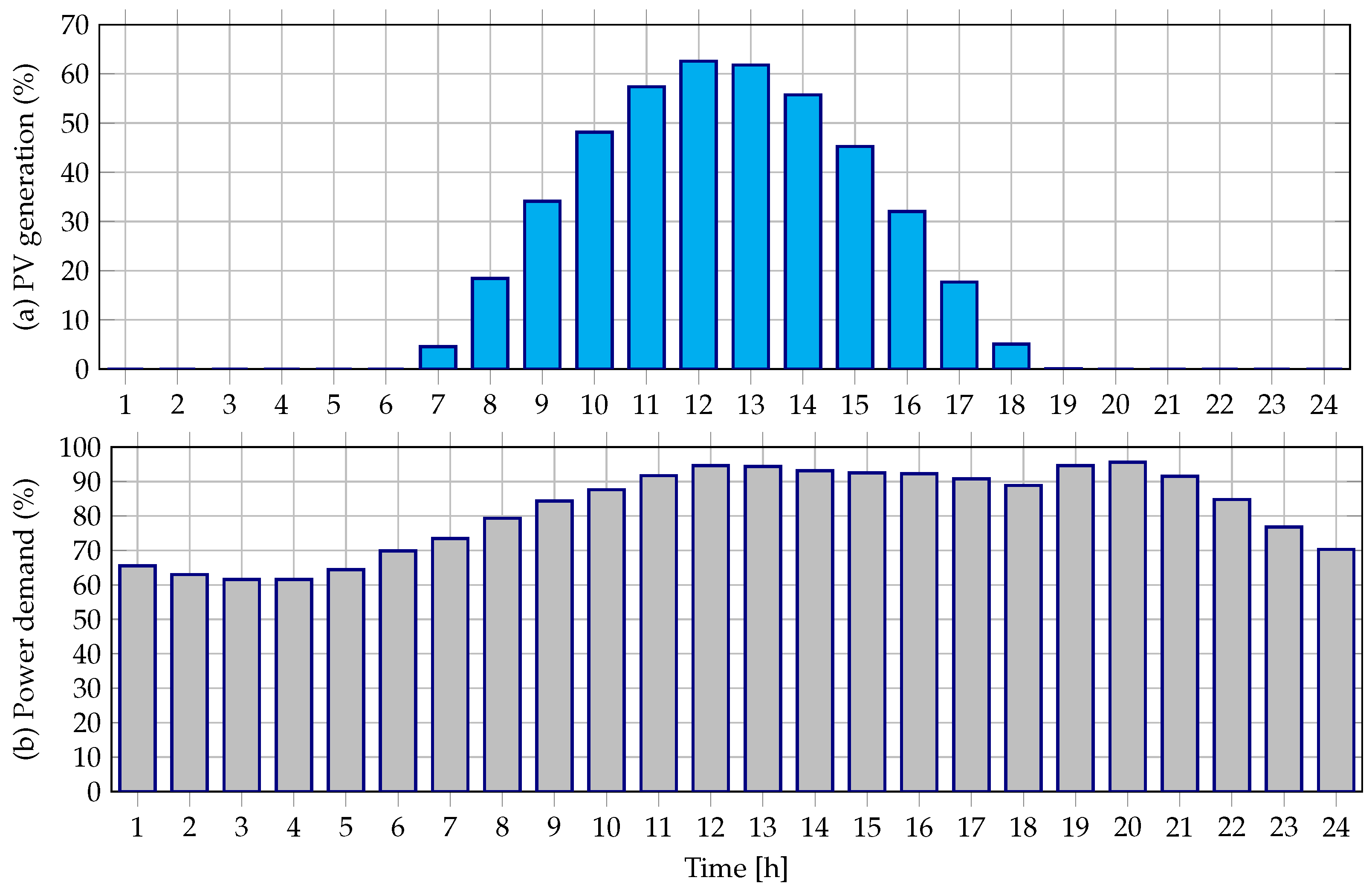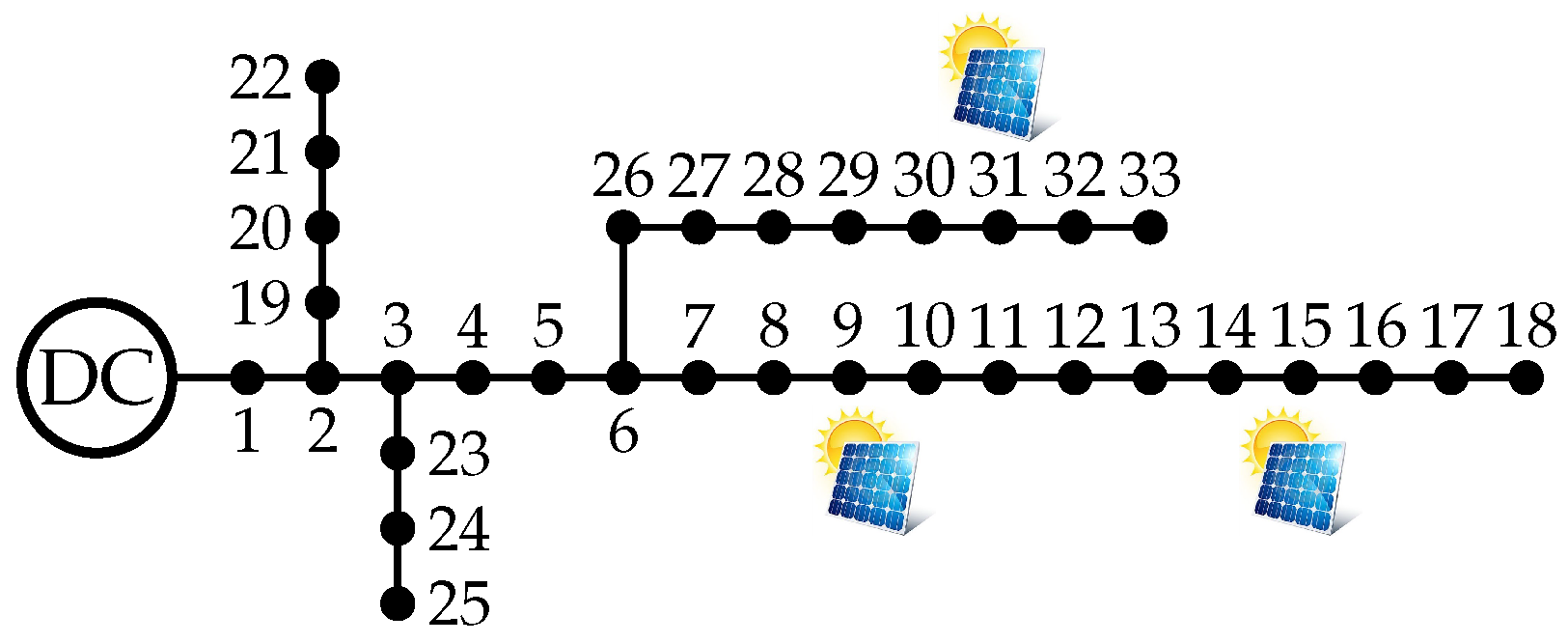Section 4 presents the general characterization of the test feeder, which corresponds to the DC version of the IEEE 33-node grid adapted for operating with information regarding PV generation and demand consumption in the city of Medellín (Colombia). Section 5 describes all the numerical validations, including four different simulation scenarios and some comparative analyses with combinatorial optimization methods. Finally, Section 6 presents the main conclusions from this research and possible future developments.

2. Exact NLP Formulation

The problem regarding the optimal operation of BESS in monopolar DC distribution networks with a high presence of renewable generation systems can be represented as an NLP formulation, in which the objective function corresponds to the minimization of the expected costs of the daily energy losses, and the main constraints (i.e., the nonlinear constraints) include the power balance equation at each node of the grid. The complete mathematical formulation of the studied problem is presented from (1) to (10):

$$\begin{array}{cc}\hfill \mathrm{Obj}.\mathrm{func}.:& \hfill \\ \hfill & min{E}_{\mathrm{costs}}=\sum _{t\in \mathcal{H}}Co{E}_t\left(\sum _{i\in \mathcal{B}}{v}_{i,t}\left(\sum _{j\in \mathcal{B}}{G}_{ij}{v}_{j,t}\right)\right){\Delta }_t\hfill & \hfill \\ \hfill \mathrm{Const}.:& \hfill & \hfill \\ \hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill & p_{i,t}+p_{i,t}^{dg}+\sum _{b\in \mathcal{E}}{p}_{i,t}^b-p_{i,t}^d=v_{i,t}\sum _{j\in \mathcal{B}}{G}_{ij}{v}_{j,t},\hfill & \hfill \left\{\forall i\in \mathcal{B},\forall t\in \mathcal{H}\right\}\end{array}$$

(2)

$$\begin{array}{ccc}\hfill & So{C}_{i,t}^b=So{C}_{i,t-1}^b-{\phi }_i^b{p}_{i,t}^b{\Delta }_t,\hfill & \hfill \left\{\begin{array}{c}\forall b\in \mathcal{E},\forall i\in \mathcal{B}\\ \forall t\in \mathcal{H}\end{array}\right\}\end{array}$$

(3)

$$\begin{array}{ccc}\hfill & So{C}_{i,t_0}^b=So{C}_i^{b,\mathrm{ini}},\hfill & \hfill \left\{\forall b\in \mathcal{E},\forall i\in \mathcal{B}\right\}\end{array}$$

(4)

$$\begin{array}{ccc}\hfill & So{C}_{i,t_f}^b=So{C}_i^{b,\mathrm{fin}},\hfill & \hfill \left\{\forall b\in \mathcal{E},\forall i\in \mathcal{B}\right\}\end{array}$$

(5)

$$\begin{array}{ccc}\hfill & p_{i,t}^{min}\le p_{i,t}\le p_{i,t}^{max},\hfill & \hfill \left\{\forall i\in \mathcal{B},\forall t\in \mathcal{H}\right\}\end{array}$$

(6)

$$\begin{array}{ccc}\hfill & p_{i,t}^{dg,min}\le p_{i,t}^{dg}\le p_{i,t}^{dg,max},\hfill & \hfill \left\{\forall i\in \mathcal{B},\forall t\in \mathcal{H}\right\}\end{array}$$

(7)

$$\begin{array}{ccc}\hfill & p_i^{b,min}\le p_{i,t}^b\le p_i^{b,max},\hfill & \hfill \left\{\begin{array}{c}\forall b\in \mathcal{E},\forall i\in \mathcal{B}\\ \forall t\in \mathcal{H}\end{array}\right\}\end{array}$$

(8)

$$\begin{array}{ccc}\hfill & v_i^{min}\le v_{i,t}\le v_i^{max},\hfill & \hfill \left\{\forall i\in \mathcal{B},\forall t\in \mathcal{H}\right\}\end{array}$$

(9)

$$\begin{array}{ccc}\hfill & So{C}_i^{b,min}\le So{C}_{i,t}^b\le So{C}_i^{b,max},\hfill & \hfill \left\{\begin{array}{c}\forall b\in \mathcal{E},\forall i\in \mathcal{B}\\ \forall t\in \mathcal{H}\end{array}\right\}.\end{array}$$

(10)

This NLP model has the following interpretation. The objective function in (1) corresponds to the expected energy loss costs caused by all the resistive effects of the distribution lines that compose the monopolar DC network. The equality constraint (2) is the application of Tellegen’s second theorem to each node of the grid. This constraint corresponds to the power equilibrium at each node of the network (a combination of Kirchhoff’s first and second laws) [15,16]. Equality constraint (3) corresponds to the relationship between the state of charge in a battery and its power consumption/generation, which is modeled linearly, as proposed by the authors of [17] through a charge/discharge coefficient. Equality constraints (4) and (5) refer to the initial and final states of charge assigned to the batteries by the distribution company at the beginning and end of the operation horizon. Box-type constraints (6)–(8) are associated with the minimum and maximum operation bounds regarding power injection in the slack node, dispersed generators, and batteries, respectively. Inequality constraint (9) is related to the voltage regulation bounds assigned by the regulating bodies in order to ensure that the energy service received by the end users is adequate in terms of quality and waveform. Finally, box-type constraint (10) is associated with the energy-storage capabilities of the BESS systems, which are defined as a function of the state-of-charge indicator.

The main characteristics of the geometrical structure of the NLP model (1)–(10), which represents the EMS for operating BESS and renewable energy resources in distribution systems, are the following:

i.

The objective function in (1) corresponds to a nonlinear function belonging to the family of convex functions, given the properties of the conductance matrix G, which is a semidefinite matrix [7]. Note that this matrix fulfills the semidefinite condition if and only if all the nodes are connected at least in radial form, i.e., if the distribution system has no isolated nodes or areas [7].

ii.

The set of constraints (3)–(10) corresponds to affine and box-type constraints that pertain to the family of convex constraints.

iii.

The power balance constraint in (2) is a set of nonlinear equations that are nonconvex given the product between voltage variables. This nonlinearity turns the optimization model (1)–(10) into a nonconvex optimization problem.

Remark 1.

To address the nonconvex structure of the problem pertaining the optimal of PV generation and BESS in monopolar DC networks, this work proposes a recursive approximation model that employs the McCormick approximation of the product of two positive variables, as presented in the next section.

3. Proposed Convex Approximation

As mentioned in the previous section, the set of constraints (2) is the only set of nonconvex constraints in the NLP model (1)–(10), which implies that, if it is convexified, the entirety of the NLP model will become a convex optimization problem, whose advantages are well-known, i.e., the possibility of finding the global optimum via interior-point methods.

3.1. McCormick Approximation

In order to obtain a convex approximation for the set of power balances, the approximation regarding the product of two variables, i.e., $f\left(x,y\right)=xy$ around the operation point $\left(x_0,y_0\right)$ by using McCormick envelopes is used [18]:

$$\begin{array}{c}\hfill f\left(x,y\right)=xy\leftrightarrow f\left(x,y\right)\approx y_{0}x+x_{0}y-x_0{y}_0,\end{array}$$

(11)

which clearly turns the product of two variables (i.e., a nonconvex constraint) into an affine expression, which is indeed a convex constraint [12].

Now, considering that $v_{i,t}^0=x_0$, $v_{j,t}^0=y_0$ and the variables x and y are defined as $v_{i,t}$ and $v_{j,t}$, Equation (2) takes the following convex approximation:

$$\begin{array}{cc}\hfill p_{i,t}+p_{i,t}^{dg}+\sum _{b\in \mathcal{E}}{p}_{i,t}^b-p_{i,t}^d=\sum _{j\in \mathcal{B}}{G}_{ij}\left(v_{j,t}^0{v}_{i,t}+v_{i,t}^0{v}_{j,t}-v_{i,t}^0{v}_{j,t}^0\right),& \left\{\forall i\in \mathcal{B},\forall t\in \mathcal{H}\right\}\hfill \end{array}$$

(12)

with $v_{i,t}^0$ and $v_{j,t}^0$ being the linearizing points used in the McCormick approximation, which correspond to the initial voltage values associated with nodes i and i at each period of time.

Remark 2.

The convex approximation of the power balance equation defined in (12) allows transforming the NLP model (1)–(10) into a convex optimization model. However, the inclusion of the linearizing point $\left(v_{i,t}^0,v_{j,t}^0\right)$ introduces an estimation error between the exact solution of the NLP model and the proposed convex approximation, although this error can be reduced/eliminated by using a recursive solution methodology [19].

3.2. Recursive Optimization Model

To minimize the error induced by the McCormick approximation into the solution of the NLP model that represents the problem concerning the efficient operation of PV sources and BESS systems in monopolar DC networks, a recursive solution methodology is introduced as proposed by Ocampo et al., in the case of the optimal power flow problem [19].

The main idea of the recursive solution methodology is solving the convex developed optimization model in a sequential way, i.e., by updating the linearizing point via an iterative counter m. The addition of the iterative procedure allows it to have a recursive convex approximation with the mathematical structure defined in (13):

$$\begin{array}{cc}\hfill \mathrm{Obj}.\mathrm{func}.:& \hfill \\ \hfill & min{E}_{\mathrm{costs}}=\sum _{t\in \mathcal{H}}Co{E}_t\left(\sum _{i\in \mathcal{B}}{v}_{i,t}^{m+1}\left(\sum _{j\in \mathcal{B}}{G}_{ij}{v}_{j,t}^{m+1}\right)\right){\Delta }_t\hfill & \hfill \\ \hfill \mathrm{Const}.:& \hfill & \hfill \\ \hfill & p_{i,t}+p_{i,t}^{dg}+\sum _{b\in \mathcal{E}}{p}_{i,t}^b-p_{i,t}^d=\sum _{j\in \mathcal{B}}{G}_{ij}\left(\begin{array}{c}{v}_{j,t}^m{v}_{i,t}^{m+1}+v_{i,t}^m{v}_{j,t}^{m+1}\\ -v_{i,t}^m{v}_{j,t}^m\end{array}\right),\hfill & \hfill \left\{\forall i\in \mathcal{B},\forall t\in \mathcal{H}\right\}\\ \hfill & So{C}_{i,t}^b=So{C}_{i,t-1}^b-{\phi }_i^b{p}_{i,t}^b{\Delta }_t,\hfill & \hfill \left\{\begin{array}{c}\forall b\in \mathcal{E},\forall i\in \mathcal{B}\\ \forall t\in \mathcal{H}\end{array}\right\}\\ \hfill & So{C}_{i,t_0}^b=So{C}_i^{b,\mathrm{ini}},\hfill & \hfill \left\{\forall b\in \mathcal{E},\forall i\in \mathcal{B}\right\}\\ \hfill & So{C}_{i,t_f}^b=So{C}_i^{b,\mathrm{fin}},\hfill & \hfill \left\{\forall b\in \mathcal{E},\forall i\in \mathcal{B}\right\}\\ \hfill & p_{i,t}^{min}\le p_{i,t}\le p_{i,t}^{max},\hfill & \hfill \left\{\forall i\in \mathcal{B},\forall t\in \mathcal{H}\right\}\\ \hfill & p_{i,t}^{dg,min}\le p_{i,t}^{dg}\le p_{i,t}^{dg,max},\hfill & \hfill \left\{\forall i\in \mathcal{B},\forall t\in \mathcal{H}\right\}\\ \hfill & p_i^{b,min}\le p_{i,t}^b\le p_i^{b,max},\hfill & \hfill \left\{\begin{array}{c}\forall b\in \mathcal{E},\forall i\in \mathcal{B}\\ \forall t\in \mathcal{H}\end{array}\right\}\\ \hfill & v_i^{min}\le v_{i,t}^{m+1}\le v_i^{max},\hfill & \hfill \left\{\forall i\in \mathcal{B},\forall t\in \mathcal{H}\right\}\\ \hfill & So{C}_i^{b,min}\le So{C}_{i,t}^b\le So{C}_i^{b,max},\hfill & \hfill \left\{\begin{array}{c}\forall b\in \mathcal{E},\forall i\in \mathcal{B}\\ \forall t\in \mathcal{H}\end{array}\right\},\end{array}$$

(13)

where $v_{i,t}^m$ and $v_{i,t}^{m+1}$ are the voltage values in two consecutive iterations.

Remark 3.

Note that the recursive convex optimization model (13) is iteratively solved by using a convex optimization tool until the desired convergence is obtained, which is defined as the difference in voltage magnitudes between two consecutive iterations that fulfills the expected convergence error. The convergence criterion is presented below:

$$\begin{array}{c}\hfill \underset{i\in \mathcal{B},t\in \mathcal{T}}{max}\left|v_{i,t}^{m+1}-v_{i,t}^m\right|\le \epsilon ,\end{array}$$

(14)

where ε is the maximum convergence error, which is defined as $1\times {10}^{-10}$.

To illustrate the application of the proposed recursive convex approximation applied to the EMS for BESS and PV sources in monopolar DC distribution systems, a flowchart is presented in Figure 1.

The recursive properties in Figure 1 associated with the iterative solution of the approximated convex model (13) are as follows. (i) The solution algorithm initializes all the voltage values in all the buses of the network as equal to the substation’s nominal voltage $v_{i,t}^m=V_{nom}$ for each period. Then, the new voltage profiles $v_{i,t}^{m+1}$ are obtained with these parameters by solving the model (13) via the SDPT3 solver with the CVX tool in the MATLAB programming environment. (ii) The convergence criterion is evaluated, and the final solution for the voltage profiles is reported when the convergence error is met; otherwise, $v_{i,t}^m=v_{i,t}^{m+1}$, and the convex model (13) is again solved until the desired convergence is met.

4. Test Feeder Characterization

This section presents the main aspects of the test feeder under analysis.

4.1. PV Generation Modeling and Demand Curve

To determine the power production of a PV generation source, Equations (15) and (16) are widely employed in the current literature [20]. These equations model the hourly effect of environmental temperature and solar radiation on total power production. We have

$$p_{i,t}^{pv}=P_i^{pv}{f}_{pv}\left(\frac{G_t^T}{G_i^{T,STC}}\right)\left[1+{\alpha }_p\left(T_{i,t}^c-T_i^{c,STC}\right)\right],$$

(15)

where $P_i^{pv}$ is the nominal capacity of the PV DG located at bus i, $f_{pv}$ denotes an efficiency factor that takes into account the external variation related to the panel’s material and mismatching, among other aspects, $G_h^T$ and $G_i^{T,STC}$ correspond to the solar radiation of the PV systems in hour h and under standard test conditions (STC), ${\alpha }_p$ denotes the power coefficient related to the temperature, and $T_{i,h}^c$ and $T_i^{c,STC}$ represent the surface temperature of the PV system installed at bus i in period h and under STC, respectively.

Note that Equation (15) allows one to determine the total power generation output for a PV source connected at bus i in the period of time t.

For calculating $T_{i,h}^c$ regarding each hour of operation, Equation (16) is employed,

$$T_{i,h}^c=T_h^a+G_h^T\left(\frac{T_i^{c,NOCT}-T_i^{a,NOCT}}{G_i^{T,NOCT}}\right)\left(1-\frac{{\eta }_i^c}{\tau \alpha }\right),$$

(16)

where $T_h^a$ represents the environmental temperature in hour h, $T_i^{c,NOCT}$$G_i^{T,NOCT}$, and $T_i^{a,NOCT}$ correspond to the surface temperature, the solar radiance, and the environmental temperature of the PV system at bus i under nominal operating conditions, respectively, ${\eta }_i^c$ denotes the efficiency, $\tau$ represents the solar transmittance, and $\alpha$ corresponds to the solar absorption of the PV systems at bus i.

Figure 2a depicts the power generation of an average day for a distribution network located in the metropolitan area of Medellín. To obtain these PV power generation data, a PV polycrystalline silicon panel was taken into account. This type of panel is very common around the world [21,22], and, in this case, it was especially adapted for Colombia. The PV parameters reported for these PV panels are the following: $P_i^{pv}$ (1 W), $f_{pv}$ (95%), $G_i^{T,STC}$ (1000 W/m${}^2$), ${\alpha }_p$ ($0.00451{/}^{\circ }$C), d $T_i^{c,STC}$ (25 °C), $T_i^{c,NOCT}$ (46 °C), $G_i^{T,NOCT}$ (800 W/m${}^2$, $T_i^{a,NOCT}$ (20 °C), ${\eta }_i^c$, and $\tau$$\alpha$ (0.9). Furthermore, in this work, the average solar radiation and environmental temperature values were considered as reported in [23]. These values, in addition to the power generation behavior of this PV system in Medellín, are outlined in

Table 1. Parametric information on PV generation: solar radiation (W/m${}^2$), environmental temperature (°C), and PV power generation in (pu).

Hour	${\mathit{G}}_{\mathit{T}}$	${\mathit{T}}_{\mathit{a}}$	${\mathit{C}}_{\mathit{p}\mathit{v}}$
1	0	16.14132	0
2	0	15.90636	0
3	0	15.68132	0
4	0	15.46022	0
5	0	15.27545	0
6	0	15.10329	0
7	46.02425	15.15718	0.04541
8	190.83559	16.15636	0.18424
9	362.83753	17.43868	0.34100
10	526.64647	18.87312	0.48161
11	640.99058	20.27438	0.57375
12	709.05312	21.36342	0.62572
13	701.86370	21.98721	0.61809
14	626.82690	22.12107	0.55716
15	499.86074	21.83071	0.45236
16	346.26581	21.20351	0.32052
17	186.66671	20.38668	0.17693
18	52.334030	19.35951	0.05066
19	0.509860	18.32258	0.00050
20	0	17.72414	0
21	0	17.29586	0
22	0	16.96148	0
23	0	16.67395	0
24	0	16.40545	0

: the hour under analysis, the average daily solar radiation $G_T$, the environmental temperature $T_a$, and the power generation $C_{pv}$ in p.u., which was obtained via Equation (15).

Figure 2b depicts the average daily power demand for an electrical distribution grid located in the metropolitan area of Medellín [20].

Finally, Table 1 reports the main parameters of the PV characterization, which can be used in future works for comparative purposes in studies on the optimal operation of renewables and batteries in electrical distribution grids.

4.2. IEEE 33-Bus Grid

In this research, to validate the proposed convex modeling used to operate BESS and PV sources in monopolar distribution grids, the IEEE 33-bus grid configuration was considered. It was adapted for a monopolar DC operation with a voltage value of 12.66 kV at the terminals of the substation. The electrical configuration of this test feeder is depicted in Figure 3.

For this test system, three PV generation sources were installed at nodes 12, 15, and 31, all of which have an installed capacity of about 2400 kW. Note that these dispersed generation sources were previously located in these nodes by the distribution company after implementing a planning optimization approach; in addition to a comparative simulation scenario, the location of these PV plants has been taken from [24].

The electrical parameters regarding distribution lines, peak demand values, and maximum current allowed per distribution branch are listed in

Table 2. Electrical parameters of the IEEE 33-bus network.

Branch	Node i	Node j	R ($\mathbf{\Omega }$)	Pj (kW)	Imax (A)
1	1	2	0.0922	100	320
2	2	3	0.4930	90	280
3	3	4	0.3660	120	195
4	4	5	0.3811	60	195
5	5	6	0.8190	60	195
6	6	7	0.1872	200	95
7	7	8	17114	200	85
8	8	9	10300	60	70
9	9	10	10400	60	55
10	10	11	0.1966	45	55
11	11	12	0.3744	60	55
12	12	13	14.680	60	40
13	13	14	0.5416	120	40
14	14	15	0.5910	60	25
15	15	16	0.7463	60	20
16	16	17	12890	60	20
17	17	18	0.7320	90	20
18	2	19	0.1640	90	30
19	19	20	15042	90	25
20	20	21	0.4095	90	20
21	21	22	0.7089	90	20
22	3	23	0.4512	90	85
23	23	24	0.8980	420	70
24	24	25	0.8900	420	40
25	6	26	0.2030	60	85
26	26	27	0.2842	60	85
27	27	28	10590	60	70
28	28	29	0.8042	120	70
29	29	30	0.5075	200	55
30	30	31	0.9744	150	40
31	31	32	0.3105	210	25
32	32	33	0.3410	60	20

.

Three batteries were considered, which were located along the IEEE 33-bus grid. The first battery was installed at node 6 with a rated capacity of 2000 kWh and charge/discharge times of 5 h. The second battery can store about 1500 kWh with charge/discharge times of 4 h at node 14. The third battery was located at node 31, with a rated capacity of 1000 kWh and charge/discharge times of 4 h. As mentioned earlier, the distribution company previously defined the location of these batteries, and this research only focuses on proposing an efficient operation strategy for these BESS while considering their current locations [24]. Nevertheless, more research is required on planning monopolar DC networks regarding the optimal location and size of the distributed energy resources that can be connected to them to improve their technical, economic, and/or environmental indices.

To illustrate the aggregate penetration level of PV generation in the monopolar DC distribution grid under analysis, Figure 4 presents the aggregate demand value at terminals of the substation, as well as the total expected generation availability in the PV sources.

In Figure 4, it is evidenced that, from hours 10 to 15, the expected generation availability in the PV plants exceeds the aggregate demand behavior, which allows storing this energy in the BESS for use in periods with high demand and low generation availability.

5. Computational Validation

This section presents all the computation validations of the proposed convex model for operating BESS and PV sources in monopolar DC networks, as well as some numerical comparisons with combinatorial optimization methods.

5.1. Software and Simulation Scenarios

For the computational validation, the MATLAB software (version $2021b$) was used on a PC with an AMD Ryzen 7 3700 $2.3$ GHz processor and 16.0 GB RAM running a 64-bit version of Microsoft Windows 10 Single Language. The solution of the recursive convex approximation (13) was obtained via the convex disciplined tool environment (CVX) of MATLAB, using the SEDUMI and SDPT3 solvers. Note that, in these simulation scenarios, the value of the energy losses was evaluated, i.e., $E_{\mathrm{loss}}=E_{\mathrm{costs}}/Co{E}_t$, in order to make comparisons with some literature reports that use energy losses instead of their costs as a performance indicator.

Different scenarios were considered for operating BESS and PV generation units in monopolar DC networks, as shown below:

i.

S1: The operation of the monopolar DC network, considering that the PV sources and the BESS are not connected to the grid.

ii.

S2: The operation of the monopolar DC network, only considering the optimal dispatch of the BESS.

iii.

S3: The operation of the monopolar DC network, only considering that the PV generation units are dispatched.

iv.

S4: The operation of the monopolar DC network, considering that the PV generation units and the BESS are simultaneously dispatched.

5.2. Evaluation of the Proposed Simulation Scenarios

Table 3. Numerical results with the proposed recursive convex formulation in all the simulated scenarios.

Scenario	${\mathit{E}}_{\mathbf{loss}}$ (kWh/day)	Reduction (%)	Avg. Time (s)
S1	2186.2799	—	10.5630
S2	2100.4280	3.9268	23.8403
S3	1224.8548	43.9754	21.8805
S4	952.2670	56.4435	30.7007

presents the comparative analysis of all the proposed simulation scenarios.

From these results, the following remarks can be made. (i) When the batteries are dispatched without considering the injection of power by dispersed sources, the energy loss reduction is about $3.9268\%$, which is a small value. However, this implies that these batteries store energy for the slack source when the demand curve is low, and they return this energy when the demand is high in order to help the slack source to compensate the total grid energy losses. (ii) When the PV sources are dispatched in S3, an important reduction in the total grid energy losses can be noted (about $43.9754\%$, i.e., 961.4251 kWh/day). This is an expected result, as the PV sources are dispatched under the optimal power flow concept, i.e., the definition of the power outputs in all the generation systems with the aim to minimize the total grid power losses of each period [25]. (iii) When the PV generation sources and the BESS have been simultaneously dispatched in S4, there is a positive effect of using batteries for storing the energy surplus of PV generation, to later inject this energy in the grid when the demand is high and the renewable generation is null. When comparing S3 and S4, an additional reduction in the energy losses can be noted (about $12.4681\%$, i.e., $272.5878$ kWh/day). (iv) Regarding processing times, as expected, S4 spends significant processing time resources (about $30.7007$ s), as it combines the highest number of variables in the studied problem by defining the PV generation output in each of the generation sources and the batteries’ power injection with its corresponding state-of-charge variables. Nevertheless, this time is minimal when it comes to defining the expected day-ahead operation of the monopolar DC grid (i.e., 24 h), which implies that multiple simulations can be done prior to the utility company’s definition of the final operation plan.

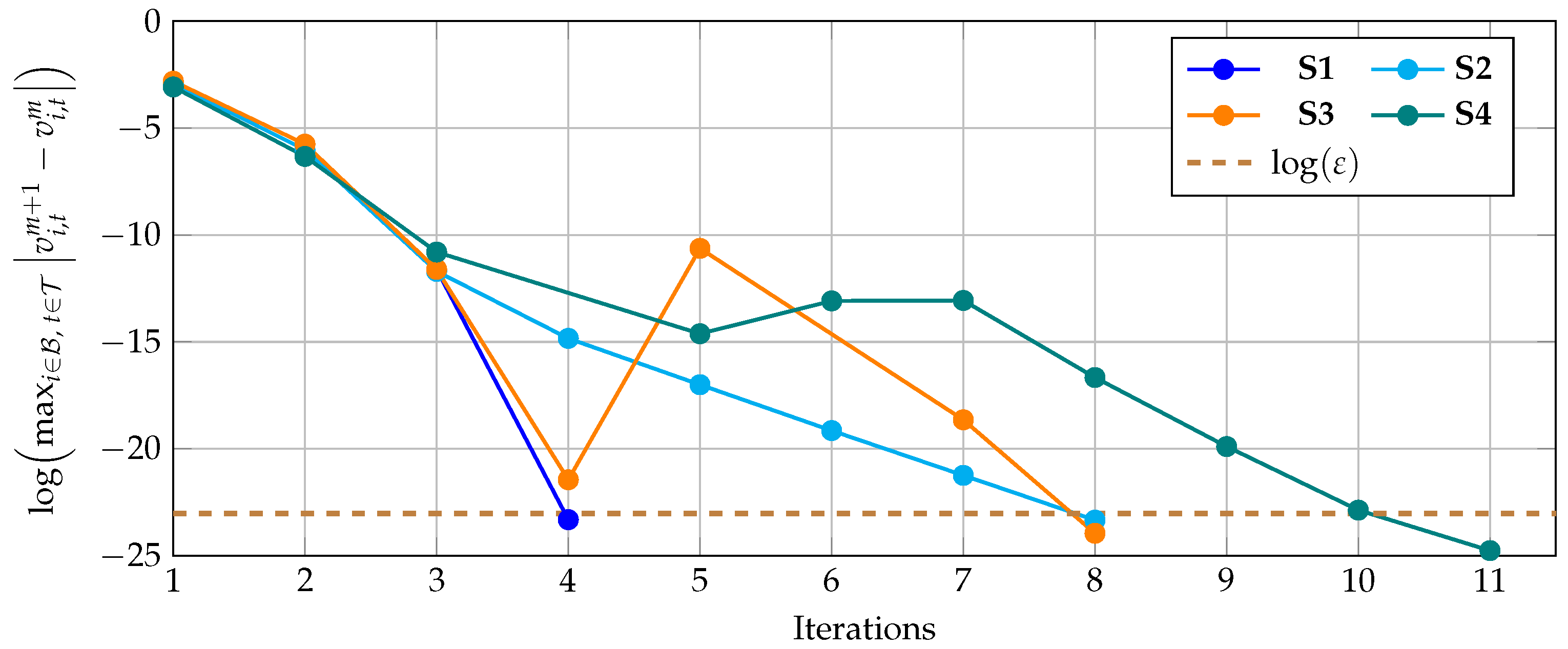
Now, to illustrate the effect of the recursive approximation on the minimization of the error induced by the McCormick approximation in the power balance constraints, as presented in Figure 1, the logarithmic value of the error in (14) is presented in Figure 5.

The behavior of the convergence error in Figure 5 allows one to note that (i) in S1 the convergence is quadratic, which is expected behavior, as this simulation scenario solves the classical power flow problem by using the McCormick approximation, a Taylor-based numerical method from the family of the Newton–Raphson approaches [26]; (ii) in S2, a linear convergence behavior is observed, which can be attributed to the fact that the optimal dispatch of the BESS without dispersed generation has small effects on the final objective function value, i.e., small variations in the grid voltage profiles, which allows the proposed recursive convex approximation to deal with the solution in a linear way; and (iii) in S3 and S4, the behaviors of the convergence error do not evidence a clear tendency, which is due to their variations. In some interactions, it increases with respect to the value of the previous iteration, but these oscillations in the convergence error can be attributed to the higher degrees of freedom when the PV sources and batteries are dispatched, given that the number of variables increase considerably with respect to S1 and S2. However, more research is required regarding the convergence properties of recursive optimization models. To confirm that all the numerical results reached in each one of the proposed simulation scenarios, the NLP model of the problem under study was implemented with the GAMS software with its BONMIN solver (see [17]), and these evaluations confirm the effectiveness of the proposed RCA model by reaching the same results reported in Table 3.

5.3. Comparative Analysis with EMS for PV Sources

To validate the effectiveness of the recursive convex formulation to dispatch PV generators and batteries, this section presents the comparative results of S3 against multiple combinatorial optimizers reported in [20]. These combinatorial optimizers are the multiverse optimization (MVO) approach, the particle swarm optimizer (PSO), the crow search algorithm (CSA), and the salp swarm algorithm (SSA). This comparative analysis is reported in

Table 4. Comparison of the proposed recursive convex approximation with combinatorial optimization methods.

Method	${\mathit{E}}_{\mathbf{loss}}$ (kWh/day)	Reduction (%)	Avg. Time (s)
SSA	1225.3323	43.9536	20.8476
MVO	1231.2531	43.6827	2.4479
PSO	1268.5973	41.9746	5.9597
CSA	1270.1562	41.9033	36.3663
Proposed	1224.8548	43.9946	21.8805

. Note that the metric associated with the average processing time corresponds to the mean time obtained after 100 consecutive evaluations of all the solution methodologies, including the proposed iterative convex approximation method.

The results in Table 4 show the following.

i.

The best combinatorial optimization methodology to define the optimal dispatch of the PV generation sources in the DC monopolar network is the SSA approach, which allowed for a reduction of about $43.9536\%$ concerning the benchmark case.

ii.

The remaining metaheuristic optimizers are stuck in local optima, with the CSA and PSO approaches being the worst (with reductions of $41.9033\%$ and $41.9746\%$ regarding to the benchmark case). The MVO approach found a near-optimal solution compared to the SSA approach, with a difference of about $5.9208$ kWh/day.

iii.

Even though the SSA approach is the best combinatorial optimization method, it is also stuck in a local optimum when compared to the proposed recursive convex approximation, as the best possible solution regarding the energy losses value at the end of the day is $1224.8548$ kWh/day, which implies that the SSA approach has a small difference in favor of the proposed approach (about $0.4775$ kWh/day).

Regarding processing times, it was observed that the proposed approach requires about $21.8805$ s to find the optimal global solution, while the time spent by the combinatorial optimizers oscillates between $2.4479$ s and $36.3663$ s. These simulation times confirm that the best optimization method is indeed the proposed convex approximation, as it finds the global optimum in a time similar to that of the SSA approach, which is the best combinatorial optimizer.

Remark 4.

The main advantage of the proposed recursive convex approximation is that, due to the convex nature of the solution space (see the mathematical model (13)), each solution via interior-point methods with a logarithmic barrier always reaches the same numerical solution (global optimum). In contrast, the combinatorial optimization methods require statistical evaluations in order to ensure their average behavior [20].

5.4. Complementary Analysis

This subsection presents two complementary analyses to confirm the effectiveness and robustness of the convex optimization model for designing efficient EMS while including renewables, conventional sources, and BESS. The first analysis compares the proposed convex model with three combinatorial optimization methods, and the second one includes modifying the DC version of the IEEE 33-node grid, including a diesel generator and a wind power source.

5.4.1. Comparative Results with Combinatorial Optimization Methods

Three combinatorial optimization methods with paralleled processes were implemented in order to demonstrate the effectiveness of the convex approximation method based on the McCormick approximation: the parallel antlion optimizer (PALO), the parallel vortex search algorithm (PVSA), and the parallel particle swarm optimizer (PPSO). In addition, this analysis considered that the PV generation units were reallocated at nodes 13, 25, and 30, with nominal power rates of 1125, 1320, and 999 kW, respectively. The main characteristic of this comparative analysis is that all the PV plants were dispatched by using maximum power point tracking (MPPT), i.e., they perfectly follow the expected generation curve in Figure 2.

Table 5. Comparison of the proposed recursive convex approximation with combinatorial optimization methods considering MPPT in PV plants.

Method	${\mathit{E}}_{\mathbf{loss}}$ (kWh/day)	Reduction (%)	Avg. Time (s)
Ben. case	1357.8724	—	—
PPSO	1255.2538	7.5573	58.6334
PVSA	1254.0538	7.6457	87.0673
PALO	1251.9038	7.8040	110.2476
Proposed	1203.5710	11.3635	45.6878

shows the comparative analysis between the combinatorial optimizers and the proposed convex recursive formulation.

The results in Table 5 allow one to state the following.

i.

All the combinatorial optimization methods with paralleled processes are stuck in local optima solutions. The PALO approach is the best option, with an expected reduction of $7.8040\%$, followed by the PVSA approach, with an expected reduction of 7.6457%. In the case of the PPSO approach, the difference with respect to the PALO approach is only $0.2467\%$, i.e., 3.50 kWh per day of operation. These results confirm that, in general, the three combinatorial optimizers have a good performance and a small number of differences. However, no one of them ensures that the global optimum is found.

ii.

The proposed recursive convex approximation finds a reduction concerning the benchmark case of about $11.3635\%$, which is at least $3.5595\%$ better than the PALO approach, which implies that the proposed approach allows for the reaching of an additional daily reduction of 48.3328 kWh/day in comparison with the PALO approach (the best combinatorial optimizer). In addition, the most important characteristic of the proposed convex approximation is that its solution is the global optimum. This was corroborated by the global nonlinear programming solvers available in the GAMS software.

iii.

The proposed optimization approach reaches the optimal solution, with a processing time of about 45.6878 s, whereas the best combinatorial optimizer (i.e., the PALO approach) requires approximately 110.2476 s to solve the studied problem. However, due to the random nature of the PALO approach, it is not possible to ensure that the same solution is reached in every execution, which implies that, although the processing time can be considered low for daily economic dispatch studies, the main complication is that the solution reported by this approach can vary for each evaluation, which implies that it is not reproducible. At the same time, the proposed convex approach will always find the exact solution for the same input parameters.

5.4.2. Analysis with Wind and Diesel Generation Sources

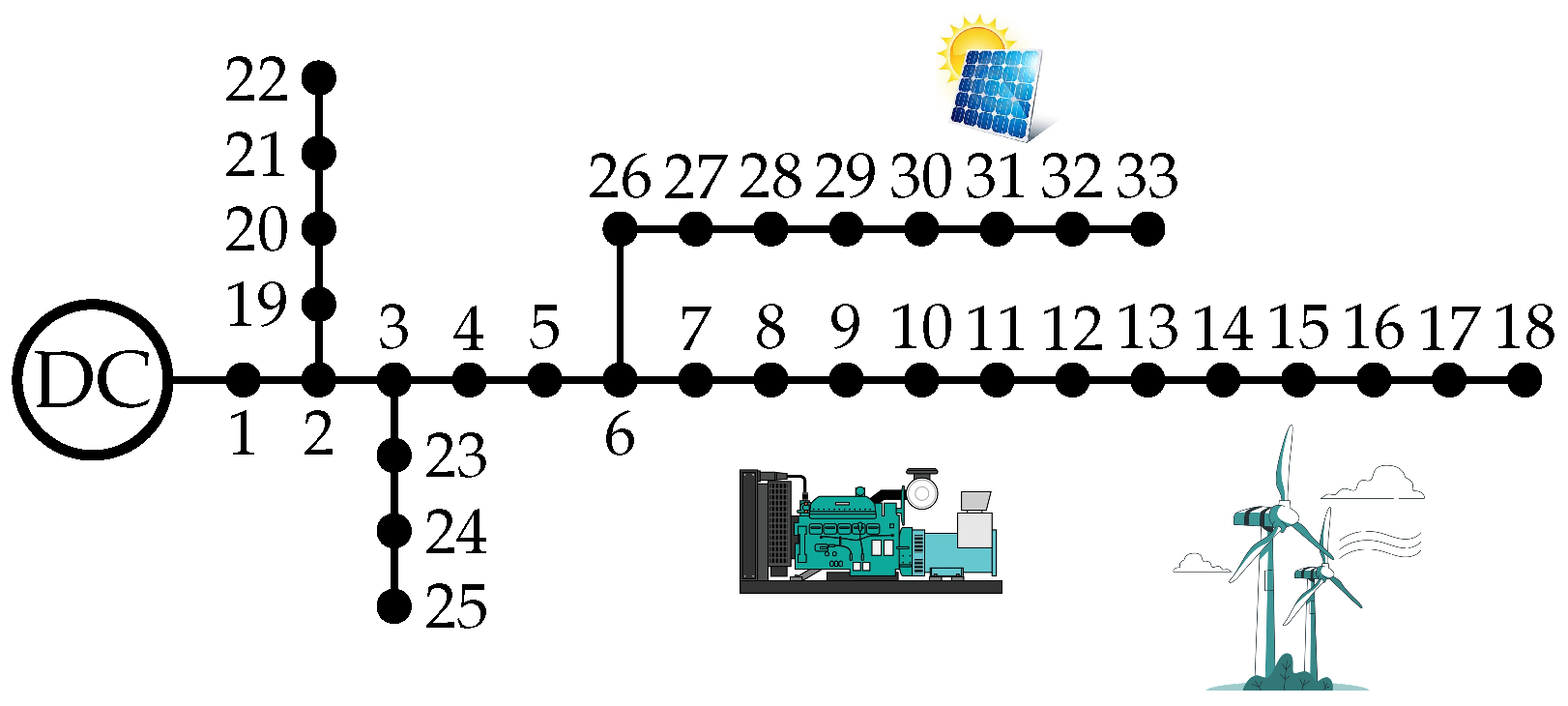
To validate the effectiveness and robustness of the proposed optimization methodology for operating BESS in the presence of renewable and conventional energy sources, a modification of the DC version of the IEEE 33-bus system was proposed, including a wind turbine and a diesel generator, as depicted in Figure 6. For this test system, the PV generators at nodes 12 and 15 have been substituted by a diesel source with a generation capacity of 800 kW and a wind power source with 1750 kW of generation capacity. The remaining PV generator has a nominal generation capacity of 2400 kW. To guarantee that future works can validate the numerical results reported in this proposed simulation,

Table 6. Renewable and demand generation curves.

Hour	Wind Power (pu)	Solar Power (pu)	Demand (pu)
1	0.7275	0	0.655092250
2	0.7151	0	0.630152498
3	0.7078	0	0.615569653
4	0.7079	0	0.615829592
5	0.7223	0	0.644566657
6	0.7495	0	0.698937446
7	0.7676	0.045411451	0.734229507
8	0.7986	0.184241504	0.793483486
9	0.8279	0.340998605	0.843313061
10	0.8953	0.481610242	0.876224102
11	0.8862	0.573748577	0.917021370
12	0.9783	0.625715388	0.945950545
13	0.9779	0.618090573	0.943876054
14	0.9730	0.557162448	0.931269100
15	0.9069	0.452363827	0.925405805
16	0.8754	0.320523656	0.922597520
17	0.8620	0.176932056	0.908069636
18	0.8497	0.050658349	0.888587275
19	0.8732	0.000498894	0.946218065
20	0.8781	0	0.956175455
21	0.8578	0	0.915546278
22	0.8239	0	0.847794326
23	0.7842	0	0.768310994
24	0.7515	0	0.702968456

presents the daily demand and renewable generation curves.

In this numerical evaluation, two cases of analysis were considered.

i.

C1: The evaluation of the proposed convex model, including all the renewable generation sources and a continuous generation of the 600 kW diesel source, i.e., 75% of its nominal capacity for all 24 h of the day.

ii.

C2: The possibility of dispatching the dispersed generation source between 0 and its nominal capacity at any hour of the day.

Note that, for both simulation cases, the renewable generation sources are optimally dispatched as a function of the grid requirements. Moreover, all the numerical results reported were validated in the GAMS software, and no comparison with metaheuristics was included, because the previous subsection demonstrated that the proposed recursive convex model is the only methodology with the ability to reach the optimal global solution.

Table 7. Analysis of the simulation cases C1 and C2.

Method	${\mathit{E}}_{\mathbf{loss}}$ (kWh/day)	Reduction (%)
Ben. case (C1)	623.3192	—
Ben. case (C2)	620.5141	—
C1	554.8556	10.9837
C2	553.7511	10.7593

shows the numerical results for both proposed simulation cases. The benchmark cases correspond to the optimal dispatch of renewables under the conditions imposed for diesel generation without connecting batteries.

The results in Table 7 allow us to state that (i) the proposed convex optimization methodology can work with multiple generation sources (renewables and diesel) while ensuring that the global optimal solution is found (these results were validated in the GAMS software). In the case of fixed generation in the diesel source, the daily energy losses are approximately $623.3192$ kWh/day, which are reduced by about $2.8051$ kWh/day when this source is optimally dispatched during the day without any generation restriction. Moreover, (ii) batteries allow for additional reductions in the objective functions under analysis (between $10.9837$ and $10.7593\%$) when they are optimally dispatched considering fixed and free generation scenarios in the diesel source.

The main result in Table 7 is that it validates the proposed convex approximation methodology based on a recursive solution approach, which can analyze multiple distributed energy resources in monopolar DC grids with small computational effort (less than 40 s for all the C1 and C2 simulations) in order to ensure their optimal operation while considering different operating conditions, with the main advantage that the convex nature of the solution space allows ensuring that the final solution reported for each case is indeed the global optimum.

6. Conclusions and Future Works

The problem regarding an efficient EMS design for distributed energy resources in monopolar DC distribution grids was solved in this research by transforming the exact NLP model that represents it into a convex approximated model by using the McCormick approximation for the product of two variables. To reduce/eliminate the estimation error in the final objective function value (i.e., the daily energy losses), a recursive solution methodology was introduced, which iteratively updated the value of the voltage profiles until the desired convergence was reached. To confirm the effectiveness of the proposed recursive convex approximation, the DC version of the IEEE 33-bus grid was adapted with information regarding PV generation and demand in the city of Medellín, Antioquia, Colombia. Numerical results considering four simulation scenarios confirmed that (i) when the BESS are operated without considering renewable generation, their effect on the total grid power losses reduction is minimal (reductions of less than $5\%$), which is an expected result because these systems must be charged from the substation in periods with low demand, in order to inject power when demand increases, and (ii) when they are optimally dispatched while considering PV generation, the expected reductions in the total energy losses were higher than 50%, thus confirming that the efficient coordination between energy-storage systems and renewable energy resources is a perfect combination to improve the electrical grid performance with regard to the minimization of the total grid energy losses during the operation horizon.

A comparative analysis with different combinatorial optimizers for the optimal operation of PV generation units demonstrated that the proposed recursive convex model could indeed find the global optimum. In contrast, all the combinatorial optimization methods (i.e., MVO, PSO, CSA, and SSA) were stuck in local optima. Regarding the objective function value, the proposed recursive convex approximation found a reduction of approximately $43.9754\%$ with respect to the benchmark case (optimal solution), only followed by the SSA approach with a similar reduction of approximately $43.9536\%$. Nevertheless, the main advantage of our proposal is that, due to the convex nature of the solution space, every time that the optimization model (13) is solved by using convex tools, the optimal solution will be the same, which is not possible to ensure with combinatorial optimization methods, given their random nature.

Numerical results considering wind-based renewable generation and diesel-based conventional generation confirmed that the proposed RCA allows finding better generation outputs and energy storage profiles as a function of the desired grid operating conditions while considering fixed and variable power generation. The system’s operation, which included batteries, allowed for reductions in the daily energy losses higher than 10% for both simulation cases with respect to the benchmark, confirming that these devices are optimally managed as a function of the grid operating consigns.

In future works, it will be possible to conduct the following studies: (i) extending the proposed recursive convex model to the problem regarding the optimal integration of distributed energy resources, i.e., developing a mixed-integer convex formulation to locate and size PV sources and BESS in monopolar DC networks; (ii) evaluating additional recursive convex models to operate PV generation units and batteries in DC networks, considering generation and demand uncertainties and different kinds of users (i.e., residential, industrial, and commercial); and (iii) including uncertainties in PV generation and demand profiles into the exact NLP model to make the proposed EMS system more realistic in monopolar DC networks by considering the stochastic nature of these parameters.