Research on Bionic Fish Scale Channel for Optimizing Thermal Performance of Liquid Cooling Battery Thermal Management System
Abstract
:1. Introduction
2. Model Description
3. Results
3.1. Bionic Model Design Parameters
3.2. Boundary Conditions
3.3. Control Equations
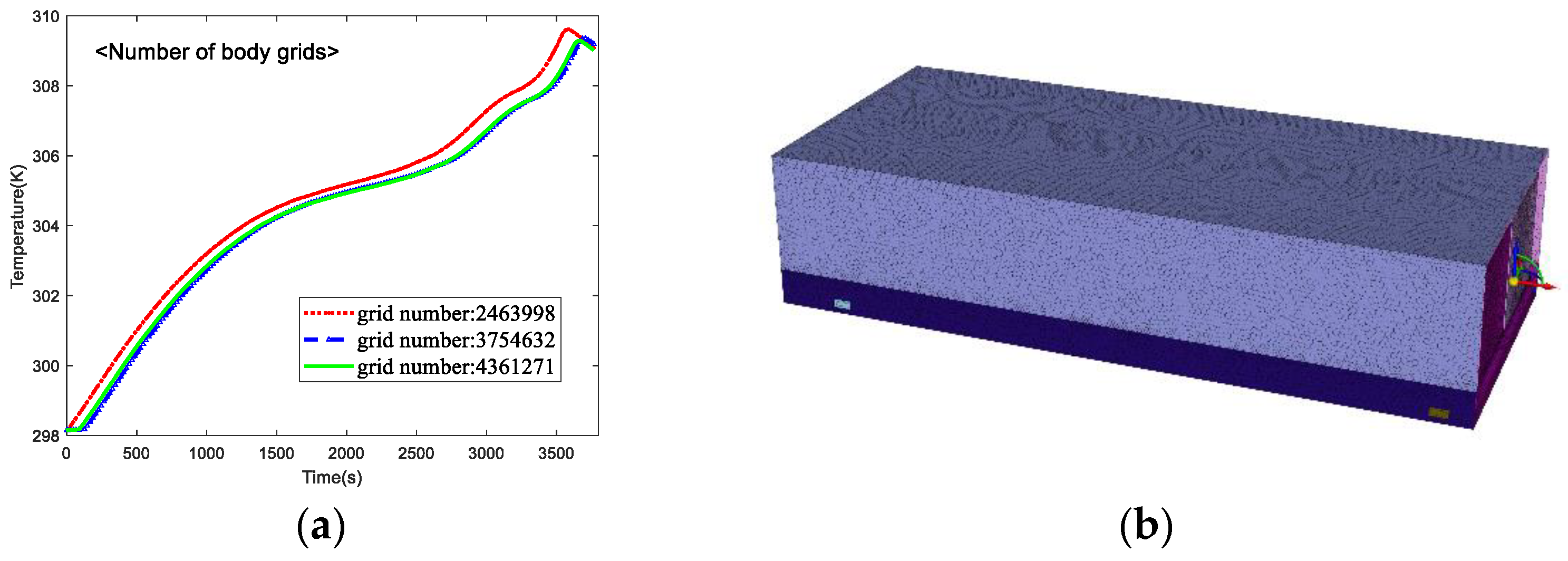
3.4. Grid Independence Analysis
4. Experimental Setup and Thermal Model Validation
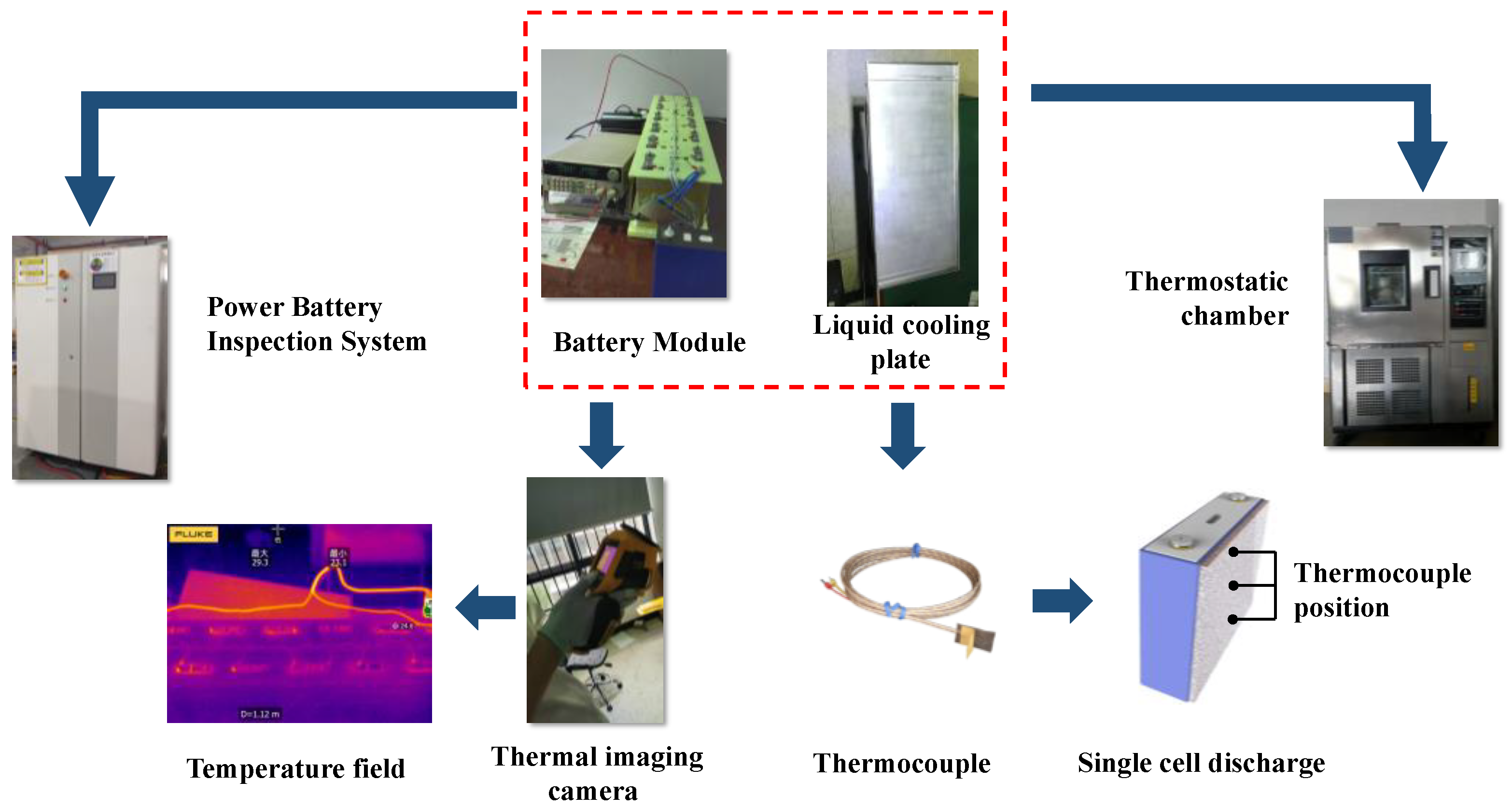
4.1. Experimental Setup
4.2. Thermal Model Validation
5. Results and Discussion
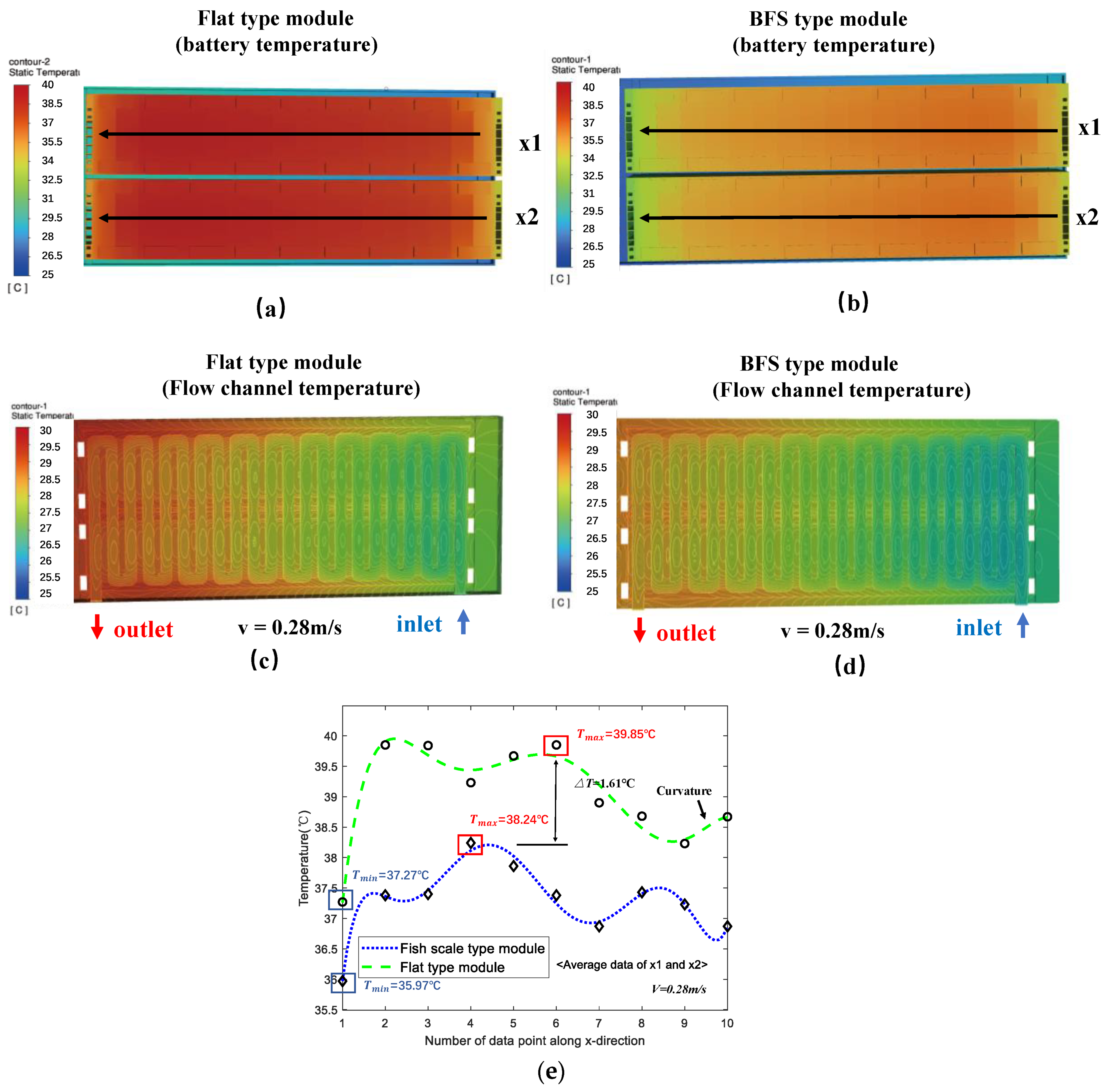
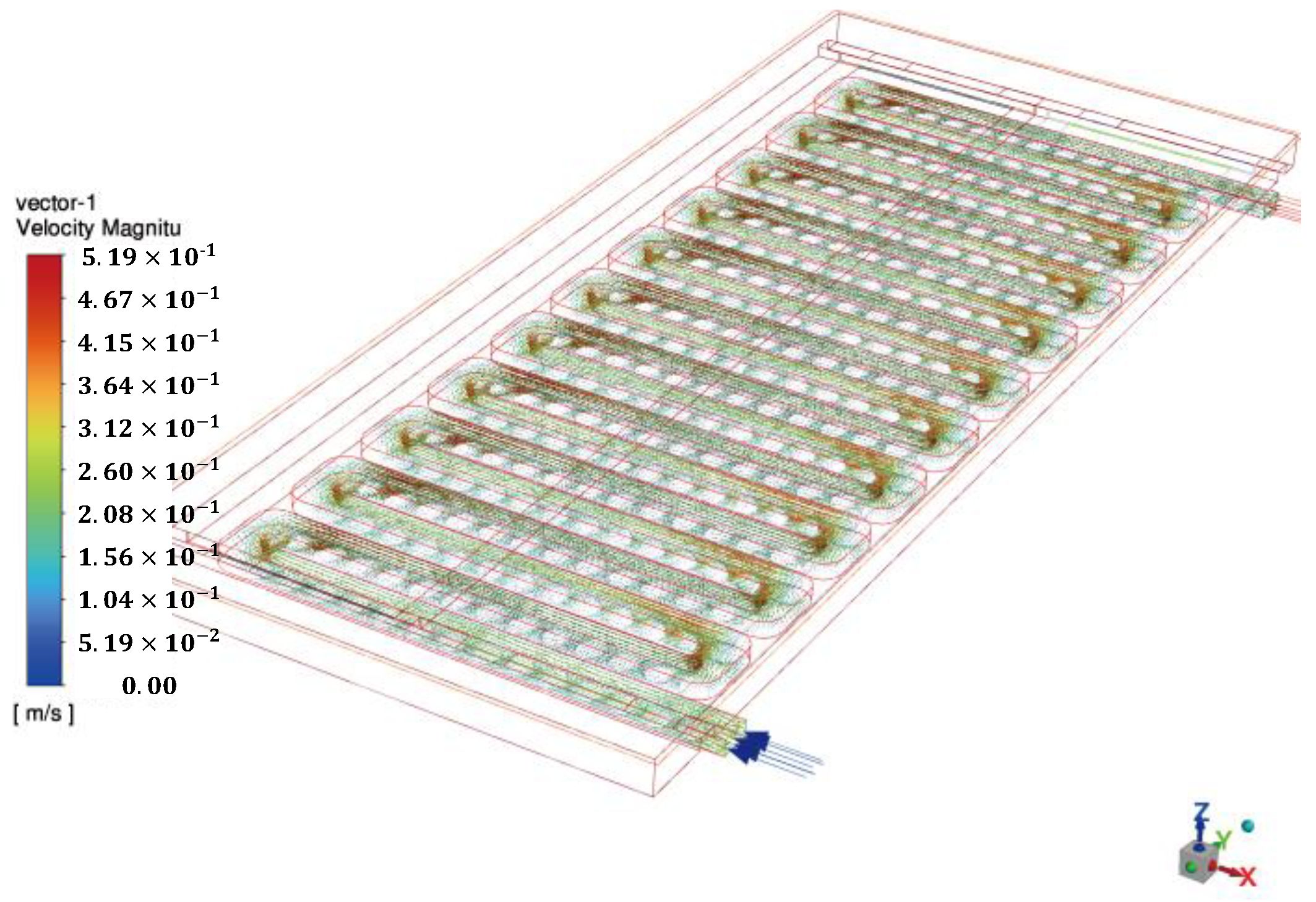
5.1. Performance Comparison of BFS Channel and Flat Type Channel
5.2. Orthogonal Experiments
5.3. Analysis of Experimental Results
5.4. Analysis of BFS Structure Design Principles
5.5. Heat Transfer Rate Analysis between Cell and Liquid Cooling Plate
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, L.; Tian, Q.; Zou, C.; Huang, J.; Ye, Y.; Wu, X. A study on energy distribution strategy of electric vehicle hybrid energy storage system considering driving style based on real urban driving data. J. Renew. Sustain. Energy Rev. 2022, 162, 112416. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, Z.; Zheng, Y.; Liu, Y.; Li, H.; Che, Y.; Peng, J.; Teodorescu, R. Spatial–temporal data-driven full driving cycle prediction for optimal energy management of battery/supercapacitor electric vehicles. J. Energy Convers. Manag. 2023, 277, 116619. [Google Scholar] [CrossRef]
- Fuhao, M.O.; Tian, Y.; Zhao, S.; Xiao, Z.; Zhiling, M.A. Working Temperature Effects on Mechanical Integrity of Cylindrical Lithium-ion Batteries. Eng. Fail. Anal. 2022, 137, 106399. [Google Scholar]
- Mali, V.; Saxena, R.; Kumar, K.; Kalam, A.; Tripathi, B. Review on battery thermal management systems for energy-efficient electric vehicles. Renew. Sustain. Energy Rev. 2021, 151, 111611. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, X.; Negnevitsky, M.; Zhang, H. A review of air-cooling battery thermal management systems for electric and hybrid electric vehicles. J. Power Sources 2021, 501, 230001. [Google Scholar] [CrossRef]
- Lee, J.; Abidi, A.; Sajadi, S.M.; El-Shafay, A.S.; Degani, M.; Sharifpur, M. Study of the effect of the aspect ratio of a cylindrical lithium-ion battery enclosure in an air-cooled thermal management system. J. Energy Storage 2022, 45, 103684. [Google Scholar] [CrossRef]
- Chung, Y.; Kim, M.S. Thermal analysis and pack level design of battery thermal management system with liquid cooling for electric vehicles. Energy Convers. Manag. 2019, 196, 105–116. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.; Wu, W.; Chen, K.; Hong, S.; Lai, Y. A critical review of battery thermal performance and liquid based battery thermal management. Energy Convers. Manag. 2019, 182, 262–281. [Google Scholar] [CrossRef]
- Wu, W.; Liu, J.; Liu, M.; Rao, Z.; Deng, H.; Wang, Q.; Wang, S. An innovative battery thermal management with thermally induced flexible phase change material. Energy Convers. Manag. 2020, 221, 113145. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Zhang, G.; Wang, Y.; Guo, J.; Wang, Y.; Zhong, Z. Characterization and experimental investigation of aluminum nitride-based composite phase change materials for battery thermal management. Energy Convers. Manag. 2020, 204, 112319. [Google Scholar] [CrossRef]
- Liang, J.; Gan, Y.; Li, Y. Investigation on the thermal performance of a battery thermal management system using heat pipe under different ambient temperatures. Energy Convers. Manag. 2018, 155, 1–9. [Google Scholar] [CrossRef]
- Ren, R.; Zhao, Y.; Diao, Y.; Liang, L. Experimental study on preheating thermal management system for lithium-ion battery based on U-shaped micro heat pipe array. Energy 2022, 253, 124178. [Google Scholar] [CrossRef]
- Murali, G.; Sravya, G.S.N.; Jaya, J.; Vamsi, V.N. A review on hybrid thermal management of battery packs and it’s cooling performance by enhanced PCM. Renew. Sustain. Energy Rev. 2021, 150, 111513. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, X.; Feng, C. Heat transfer performances of the capillary loop pulsating heat pipes with spring-loaded check valve. Appl. Therm. Eng. 2020, 167, 114803. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, P.; He, Y.; Li, S. Cooling performance optimization of air cooling lithium-ion battery thermal management system based on multiple secondary outlets and baffle. J. Energy Storage 2022, 52, 104678. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Kalogiannis, T.; Jaguemont, J.; Jin, L.; Behi, H.; Karimi, D.; Berecibar, M. A comparative study between air cooling and liquid cooling thermal management systems for a high-energy lithium-ion battery module. Appl. Therm. Eng. 2021, 198, 117503. [Google Scholar] [CrossRef]
- Olabi, A.G.; Maghrabie, H.M.; Adhari, O.H.K.; Sayed, E.T.; Yousef, B.A.; Salamah, T.; Abdelkareem, M.A. Battery thermal management systems: Recent progress and challenges. Int. J. Thermofluids 2022, 15, 100171. [Google Scholar] [CrossRef]
- Kong, D.; Peng, R.; Ping, P.; Du, J.; Chen, G.; Wen, J. A novel battery thermal management system coupling with PCM and optimized controllable liquid cooling for different ambient temperatures. Energy Convers. Manag. 2020, 204, 112280. [Google Scholar] [CrossRef]
- Gao, R.; Fan, Z.; Liu, S. A gradient channel-based novel design of liquid cooling battery thermal management system for thermal uniformity improvement. J. Energy Storage 2022, 48, 104014. [Google Scholar] [CrossRef]
- Wang, N.; Li, C.; Li, W.; Chen, X.; Li, Y.; Qi, D. Heat dissipation optimization for a serpentine liquid cooling battery thermal management system: An application of surrogate assisted approach. J. Energy Storage 2021, 40, 102771. [Google Scholar] [CrossRef]
- Tang, Z.; Liu, Z.; Li, J.; Cheng, J. A lightweight liquid cooling thermal management structure for prismatic batteries. J. Energy Storage 2021, 42, 103078. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, F.; Chen, X.; Li, K.; Shen, J. Thermal performance of honeycomb-type cylindrical lithium-ion battery pack with air distribution plate and bionic heat sinks. Appl. Therm. Eng. 2023, 218, 119299. [Google Scholar] [CrossRef]
- Liu, F.; Chen, Y.; Qin, W.; Li, J. Optimal design of liquid cooling structure with bionic leaf vein branch channel for power battery. Appl. Therm. Eng. 2023, 218, 119283. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, F.; Liu, Y.; Xu, S.; Chen, X. Thermal performance of honeycomb-like battery thermal management system with bionic liquid mini-channel and phase change materials for cylindrical lithium-ion battery. Appl. Therm. Eng. 2021, 188, 116649. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.; Liu, F.; Liu, Y.; Wang, F.; Yang, N. Numerical optimization of the cooling effect of the bionic spider-web channel cold plate on a pouch lithium-ion battery. Case Stud. Therm. Eng. 2021, 26, 101124. [Google Scholar] [CrossRef]
- An, Z.; Zhang, C.; Gao, Z.; Luo, Y.; Dong, Y. Heat dissipation performance of hybrid lithium battery thermal management system using bionic nephrolepis micro-channel. Appl. Therm. Eng. 2022, 217, 119127. [Google Scholar] [CrossRef]
- Liu, H.; Gao, X.; Zhao, J.; Yu, M.; Niu, D.; Ji, Y. Liquid-based battery thermal management system performance improvement with intersected serpentine channels. Renew. Energy 2022, 199, 640–652. [Google Scholar] [CrossRef]
- Yin, B.; Zuo, S.; Xu, Y.; Chen, S. Performance of liquid cooling battery thermal management system in vibration environment. J. Energy Storage 2022, 53, 105232. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Frazzica, A.; Chàfer, M.; Vérez, D.; Palomba, V. Research trends and perspectives of thermal management of electric batteries: Bibliometric analysis. J. Energy Storage 2020, 32, 101976. [Google Scholar] [CrossRef]
- Zichen, W.; Changqing, D. A comprehensive review on thermal management systems for power lithium-ion batteries. Renew. Sustain. Energy Rev. 2021, 139, 110685. [Google Scholar] [CrossRef]
- Jithin, K.V.; Rajesh, P.K. Numerical analysis of single-phase liquid immersion cooling for lithium-ion battery thermal management using different dielectric fluids. Int. J. Heat Mass Transf. 2022, 188, 122608. [Google Scholar] [CrossRef]
- You, Y.; Wang, S.; Lv, W.; Chen, Y.; Gross, U. A CFD model of frost formation based on dynamic meshes technique via secondary development of ANSYS fluent. Int. J. Heat Fluid Flow 2021, 89, 108807. [Google Scholar] [CrossRef]
- Bellwald, B.; Planke, S.; Lebedeva-Ivanova, N.; Piasecka, E.D.; Andreassen, K. High-resolution landform assemblage along a buried glacio-erosive surface in the SW Barents Sea revealed by P-Cable 3D seismic data. Geomorphology 2019, 332, 33–50. [Google Scholar] [CrossRef]
- Dai, W.; Zhang, W.; Zheng, Z.; Li, J. Investigation of micron-sized fish-scale surface structures on tool steel surfaces using laser galvanometer scanning. Appl. Surf. Sci. 2019, 470, 1111–1121. [Google Scholar] [CrossRef]
- Park, S.; Jang, D.S.; Lee, D.; Hong, S.H.; Kim, Y. Simulation on cooling performance characteristics of a refrigerant-cooled active thermal management system for lithium ion batteries. Int. J. Heat Mass Transf. 2019, 135, 131–141. [Google Scholar] [CrossRef]
- Wu, W.; Wu, W.; Wang, S. Thermal management optimization of a prismatic battery with shape-stabilized phase change material. Int. J. Heat Mass Transf. 2018, 121, 967–977. [Google Scholar] [CrossRef]
- Yun, S.; Kwon, J.; Cho, W.; Lee, D.; Kim, Y. Performance improvement of hot stamping die for patchwork blank using mixed cooling channel designs with straight and conformal channels. Appl. Therm. Eng. 2020, 165, 114562. [Google Scholar] [CrossRef]
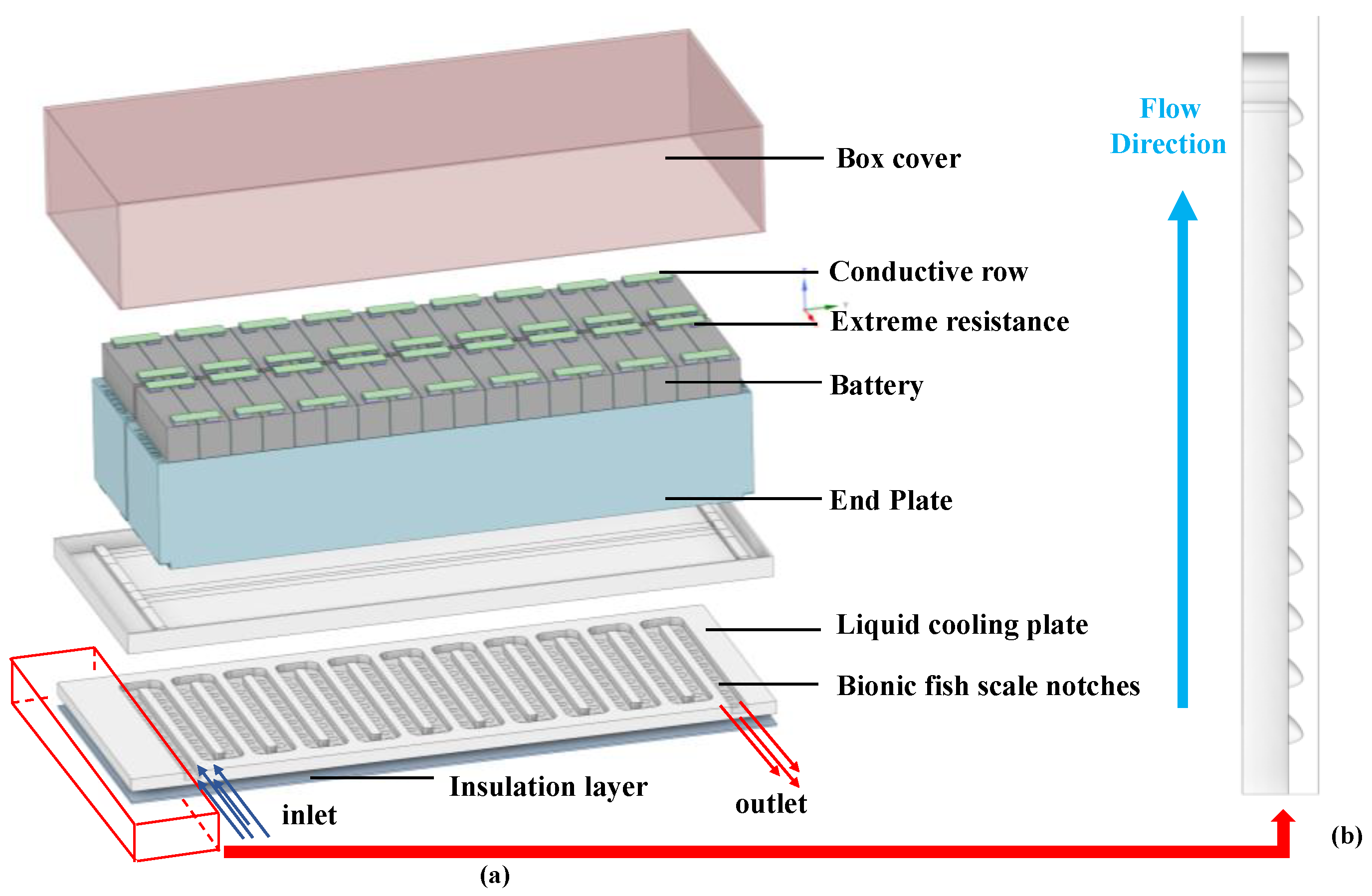



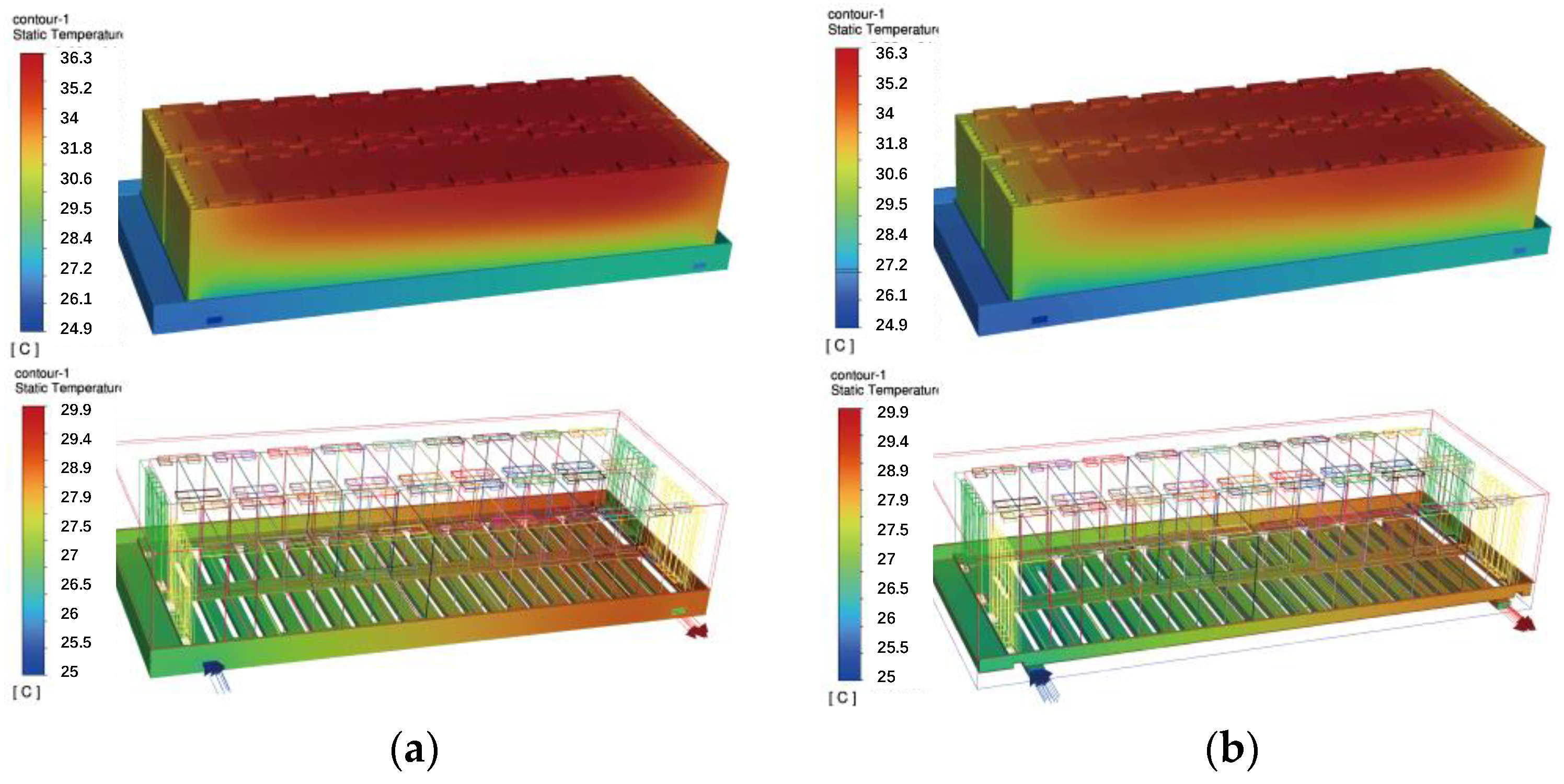

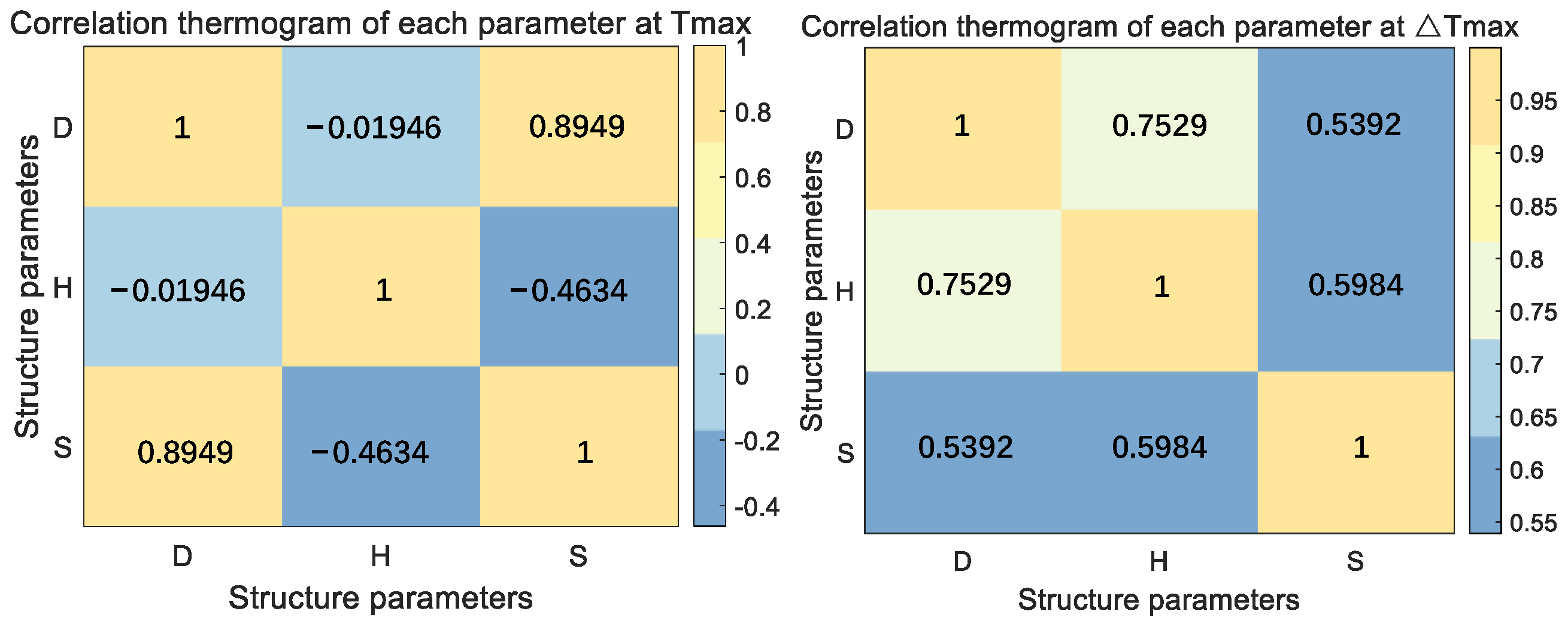

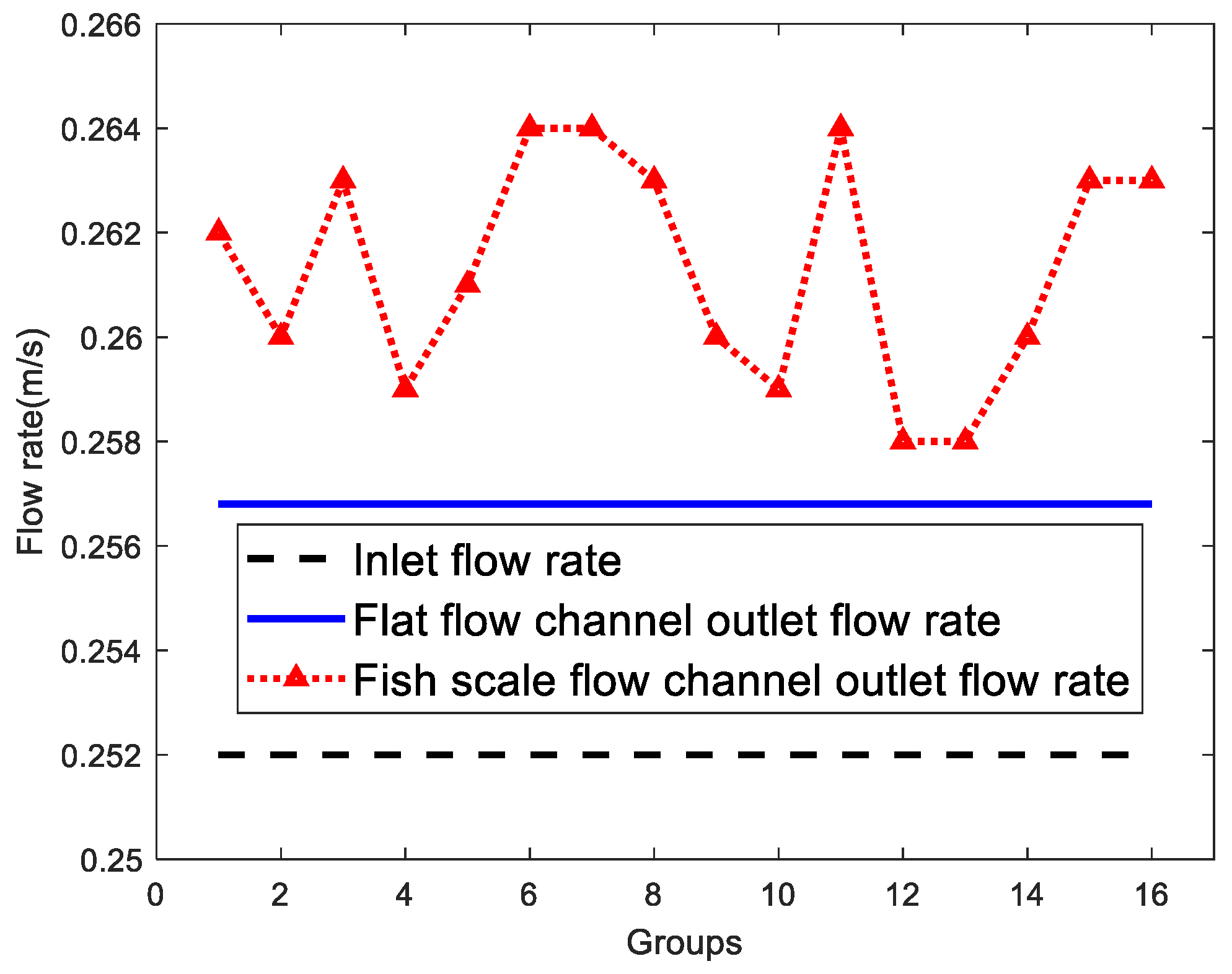
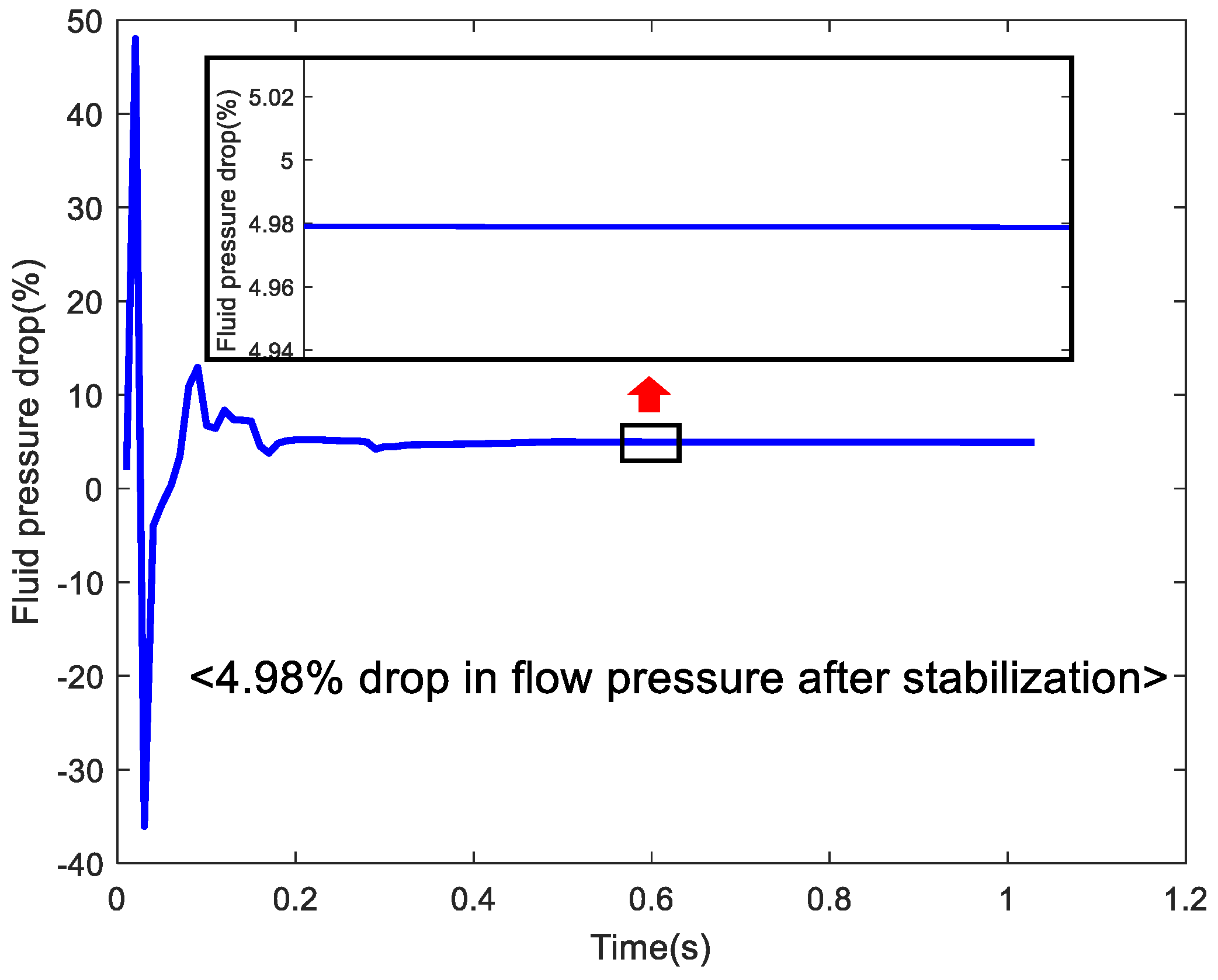


| Specifications | Value |
|---|---|
| Battery pack | 864 × 174 × 159 mm |
| Insulation layer | 1 × 174 × 168 mm |
| Liquid cooling plate | 991 × 411 × 51 mm |
| End plate | 912 × 177 × 159 mm |
| Box cover | 991 × 411 × 169 mm |
| Conductive row | 72 × 26 × 2 mm |
| Nominal voltage | 133.2 V |
| Energy (Cell measurement value calculation) | 18 kWh |
| Specifications | Value |
|---|---|
| Cell Length | 148 mm |
| Cell width | 27 mm |
| Cell height | 97 mm |
| Weight | 0.88 kg |
| AC internal resistance | ≤0.1 mΩ |
| Nominal capacity | 50 Ah |
| Nominal Voltage | 3.7 V |
| Life cycle | ≥2000 |
| Maximum allowable charging temperature range | 0–55 °C |
| Specific Heat (J/kg·K) | Density (kg/m3) | Thermal Conductivity (W/m·K) | Dynamic Density (Pa·s) | |
|---|---|---|---|---|
| Battery pack | 1033 | 2218 | 17.4, 5.3, 23 | |
| Thermal pad | 1800 | 2000 | 1.8 | |
| Epoxy plate | 1581 | 1800 | 0.2 | |
| Insulated board | 1260 | 1150 | 0.2 | |
| Aerogel | 1180 | 230 | 0.025 | |
| Conductive row | 900 | 2700 | 243 | |
| Cabinet | 900 | 2700 | 209 | |
| Coolant (25/30/35/40 °C) | 3281 | 1073 | 0.38 | 0.00394 |
| 3300 | 1071 | 0.384 | 0.00339 | |
| 3399 | 1066 | 0.391 | 0.00256 | |
| 3358 | 1063 | 0.394 | 0.00226 | |
| Insulation layer | 1700 | 65 | 0.034 | |
| Heating film | 1130 | 1840 | 1.2 |
| Level | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| D | 10 | 12.5 | 15 | 17.5 |
| H | 1.75 | 2.5 | 3.25 | 4 |
| S | 7 | 9 | 11 | 13 |
| Groups | Caliber (mm) | Breadth (mm) | Density (mm) | |||
|---|---|---|---|---|---|---|
| 1 | 10 | 1.75 | 7 | 0.94 | 38.91 | 2.37 |
| 2 | 10 | 2.5 | 9 | 1.1 | 38.75 | 2.15 |
| 3 | 10 | 3.25 | 11 | 1.04 | 38.81 | 2.28 |
| 4 | 10 | 4 | 13 | 1.05 | 38.80 | 2.33 |
| 5 | 12.5 | 1.75 | 9 | 1.61 | 38.24 | 2.27 |
| 6 | 12.5 | 2.5 | 7 | 1.07 | 38.78 | 2.24 |
| 7 | 12.5 | 3.25 | 13 | 1.09 | 38.76 | 2.19 |
| 8 | 12.5 | 4 | 11 | 1.08 | 38.77 | 2.24 |
| 9 | 15 | 1.75 | 11 | 1 | 38.85 | 2.25 |
| 10 | 15 | 2.5 | 13 | 1.03 | 38.82 | 2.23 |
| 11 | 15 | 3.25 | 7 | 1.05 | 38.80 | 2.28 |
| 12 | 15 | 4 | 9 | 1.03 | 38.82 | 2.27 |
| 13 | 17.5 | 1.75 | 13 | 0.96 | 38.89 | 2.27 |
| 14 | 17.5 | 2.5 | 11 | 1.1 | 38.75 | 2.18 |
| 15 | 17.5 | 3.25 | 9 | 1.16 | 38.69 | 2.29 |
| 16 | 17.5 | 4 | 7 | 1.15 | 38.70 | 2.19 |
| Indicators | Parameters | |||
|---|---|---|---|---|
| D | H | S | ||
| 38.8175 | 38.7225 | 38.7975 | ||
| 38.6375 | 38.775 | 38.625 | ||
| 38.8225 | 38.765 | 38.795 | ||
| 38.7575 | 37.7725 | 38.8175 | ||
| Q | 0.1850 | 0.0525 | 0.1925 | |
| 2.2825 | 2.29 | 2.27 | ||
| 2.235 | 2.2 | 2.245 | ||
| 2.2575 | 2.26 | 2.2375 | ||
| 2.2325 | 2.2575 | 2.255 | ||
| Q | 0.05 | 0.09 | 0.0325 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, Y.; Gao, K.; Luo, P.; Ma, D.; Chang, H.; Du, R. Research on Bionic Fish Scale Channel for Optimizing Thermal Performance of Liquid Cooling Battery Thermal Management System. Batteries 2023, 9, 134. https://doi.org/10.3390/batteries9020134
Mu Y, Gao K, Luo P, Ma D, Chang H, Du R. Research on Bionic Fish Scale Channel for Optimizing Thermal Performance of Liquid Cooling Battery Thermal Management System. Batteries. 2023; 9(2):134. https://doi.org/10.3390/batteries9020134
Chicago/Turabian StyleMu, Yutao, Kai Gao, Pan Luo, Deng Ma, Haoran Chang, and Ronghua Du. 2023. "Research on Bionic Fish Scale Channel for Optimizing Thermal Performance of Liquid Cooling Battery Thermal Management System" Batteries 9, no. 2: 134. https://doi.org/10.3390/batteries9020134
APA StyleMu, Y., Gao, K., Luo, P., Ma, D., Chang, H., & Du, R. (2023). Research on Bionic Fish Scale Channel for Optimizing Thermal Performance of Liquid Cooling Battery Thermal Management System. Batteries, 9(2), 134. https://doi.org/10.3390/batteries9020134








