Next Article in Journal
A Two-State-Based Hybrid Model for Degradation and Capacity Prediction of Lithium-Ion Batteries with Capacity Recovery
Previous Article in Journal
Rational Design of a Cost-Effective Biomass Carbon Framework for High-Performance Lithium Sulfur Batteries
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Batteries
Volume 9
Issue 12
10.3390/batteries9120595
batteries-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Percolation Behavior of a Sulfide Electrolyte–Carbon Additive Matrix for Composite Cathodes in All-Solid-State Batteries

by
Elias Reisacher
*,
Pinar Kaya
and
Volker Knoblauch
Materials Research Institute Aalen (IMFAA), Aalen University of Applied Sciences, Beethovenstraße 1, 73430 Aalen, Germany
*
Author to whom correspondence should be addressed.
Batteries 2023, 9(12), 595; https://doi.org/10.3390/batteries9120595
Submission received: 9 November 2023 / Revised: 9 December 2023 / Accepted: 13 December 2023 / Published: 15 December 2023
(This article belongs to the Topic Advances in Energy Storage Materials/Devices and Solid-State Batteries)
Browse Figures
Versions Notes

Abstract

:
To achieve high energy densities with sufficient cycling performance in all-solid-state batteries, the fraction of active material has to be maximized while maintaining ionic and electronic conduction throughout the composite cathode. It is well known that low-surface-area carbon additives added to the composite cathode enhance the rate capability; however, at the same time, they can lead to rapid decomposition of the solid electrolyte in thiophosphate-based cells. Thus, the fraction of such conductive additives has to be well balanced. Within this study we determined the electronic percolation threshold of a conducting matrix consisting of Li6PS5Cl and C65. Furthermore, we systematically investigated the microstructure and effective conductivity (σeff) of the conducting matrix. The percolation threshold pc was determined as ~4 wt.-% C65, and it is suggested that below pc, the ionic contribution is dominant, which can be seen in temperature-dependent σeff and blocked charge transport at low frequencies. Above pc, the impedance of the conducting matrix becomes frequency-independent, and the ohmic law applies. Thus, the conducting matrix in ASSB can be regarded as an electronic and ionic conducting phase between active material particles. Additionally, guidelines are provided to enable electronic conduction in the conducting matrix with minimal C65 content.

1. Introduction

The electrification of mobility is one key aspect in reducing greenhouse gas emissions [1]. For this reason, the demand for electrochemical storage systems is increasing. All-solid-state batteries (ASSBs) are considered a possible candidate for next-generation battery systems [2]. ASSBs do not only exhibit the potential to increase safety by superseding flammable organic liquids but can also increase energy density by employing lithium metal anodes with a theoretical capacity of 3860 mAh g−1 [3,4,5,6]. In the past decade, substantial progress has been made in the development of highly conductive solid electrolytes (SEs) [7,8,9], which are essential for high power densities in ASSBs [10,11]. Within the class of lithium thiophosphates, Li-argyrodites are SEs of particular interest because they not only offer high ionic conductivity but can be readily densified at room temperature [12], and expensive raw materials such as Ge can be discarded for their synthesis [13]. Despite these potentials and advancements in SEs, sulfide-based ASSBs have not been brought to market due to several challenges. In addition to the complexity of upscaled production [14], one of the main reasons is the degradation of the composite cathode and the formation of a conductivity-impeding solid-electrolyte interface (SEI) between layered-oxide cathode active materials (CAMs) and thiophosphate SEs upon cycling [15,16]. It is known that degradation is accelerated by introducing conductive carbons into the composite [17], even if a passivation coating is applied to the layered-oxide CAMs [18,19]. However, to utilize a 3D network with high fractions of active material particles, percolating ionic and electronic pathways must be provided in the form of a conducting matrix within the composite cathode [20,21,22,23]. This is especially valid for thick electrodes and coated active materials where the passivation layer impedes the electronic conductivity [24,25].
Regarding electronic conduction, Strauss et al. compared different carbon additives and reported that low active surface carbons such as C65 improve the rate capability of thiophosphate-based ASSBs without deterioration in capacity retention within 50 cycles, in contrast to electrodes without additives [26]. Furthermore, Park et al. presented the advantageous effect of graphitic hollow nanotubes with fewer functional surface groups compared to Ketjen black carbon on electrochemical performance [27]. In addition to different additives, Neumann et al. simulated the 3D microstructures of composite cathodes and showed the inhomogeneous lithium distribution attributed to the limited electronic conduction of NMC at higher SOC, resulting in capacity losses [25,28]. These findings prove that extensive electronic interconnection is crucial, not only to utilize active material particles but also to enhance the rate capability.
On the other hand, it is also known that ion transport can be the bottleneck in cathode kinetics [29]. To ensure sufficient Li+ mobility, characteristically, an SE fraction of ≥30 wt.-% is required, especially when competitive power densities are desired, and thus C-rates have to be increased [30,31,32]. Increasing the SE fraction in the composite cathode reduces its active material loading, resulting in a trade-off between energy and power density [33]. Here, the percolation theory is a useful and well-established concept that describes the connectivity of occupied and unoccupied sites in a lattice [34]. In this study, it is used to describe the electronic conductivity within the conducting matrix in which the C65 particles are randomly distributed and form clusters if they are interconnected, in other words, percolating when reaching throughout a finite space [35,36].
We aim to contribute to the discussion on whether conductive additives are needed in composite cathodes and how they affect the cathode performance and aging. For example, Minnmann et al. argue that the electronic conductivity of the active material NCM 622 they use is sufficient (10−2 S cm−1 fully lithiated) to provide homogeneous electronic conduction throughout the electrode [37]. However, others report a much lower electronic conductivity for NMC 622 of 1.6 · 10−6 S cm−1 [38], and Amin et al. point out the decrease in the electronic conductivity of NMC 523 upon lithiation from around 10−2 to 10−6 S cm−1 [28]. Also, one has to keep in mind that a passivation layer of the active material is needed in a thiophosphate-based electrode to prevent active material degradation. This layer might even decrease the electronic conductivity of the material, which highlights the need for electronic additives in composite cathodes.
Based on the necessities in the composite cathode and percolation theory, this study aims to minimize the carbon additive content in the conducting matrix mixtures consisting of Li-argyrodite and C65 to alleviate degradation and enable higher CAM and SE-fractions, respectively. This is carried out by systematically examining the effective conductivity as a function of additive content and thereby defining the electronic percolation threshold. The presented results provide (i) guidelines to enable electronic percolation in the conducting matrix with minimal conductive additive required and (ii) a practical contribution to improve the energy and power density of ASSBs.

2. Materials and Methods

2.1. Preparation of Li6PS5Cl Powder and Separator

Stoichiometric mixtures of lithium sulfide (Li2S, 99.9%, Alfa Aesar, Haverhill, MA, USA), phosphorus pentasulfide (P2S5, 99%, Sigma Aldrich, St. Louis, MO, USA) and lithium chloride (LiCl, 99.995%, Alfa Aesar) were prepared by ball milling (Fritsch, Idar-Oberstein, Germany, Pulverisette 7) for 1 h with 100 rpm and a ball-to-powder weight ratio of 30:1. The powder mixtures were pelletized and vacuum-sealed in quartz tubes. The thermal treatment was carried out at 550 °C for 6 h with a ramp rate of 1.5 °C min−1. Subsequently, the synthesis product was ground by hand in an agate mortar. Separators were produced by uniaxial densification of 100 mg of SE powder with 375 MPa.

2.2. Preparation of the Conducting Matrix

To prepare the conducting matrix mixture, the synthesized Li6PS5Cl solid electrolyte powder was mixed with the super C65 conductive additive (MTI, Imerys, Bironico, Switzerland) in different ratios. The weight fraction of C65 was between 1.00 and 10.00 wt.-%. The proportions of the individual samples are listed in Table 1. The mixture was ground by hand in an agate mortar for 30 min. Then, 40 mg of the powder mixture was evenly distributed on a 10 mm diameter indium blocking electrode in a symmetric cell setup. Subsequently, the measuring cell (TSC, rhd instruments, Darmstadt, Germany) was sealed with a force of 163.2 N (=2.07 MPa). By applying this force, the powder is compacted directly within the measurement cell. To be precisely comparable, pure SE powder was compacted directly in the measurement cell, as well as for the preparation of the solid separator. This ‘in situ’ preparation procedure was necessary because it was not possible to obtain a mechanically stable and handleable pellet of the powder mixture of the conducting matrix by uniaxial pressing. The geometry of the densified samples was determined after the measurement cell opening on the indium electrode with a caliper. The average diameter and the thickness of the samples were approximately 10.12 mm and 400 µm, respectively. With this value, the conductivity of the samples was calculated.

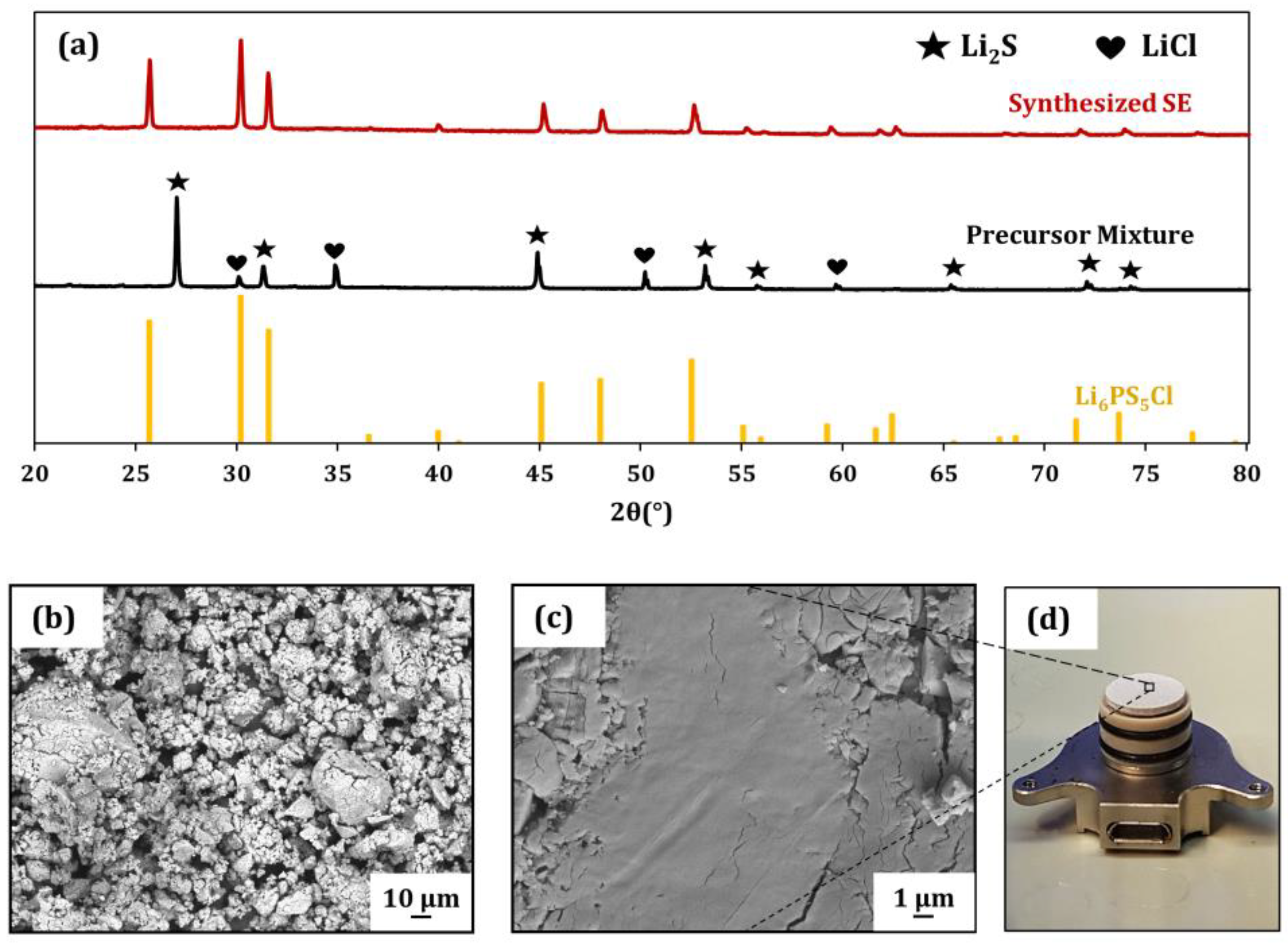
2.3. Phase and Microstructural Analysis

The phases of the synthesized SE were analyzed with an X-ray diffraction (XRD) device Seifert Sun X-ray diffractometer (XRD) 3003 by using Cu-Kα radiation (15–80° 2θ, scan rate of 0.026°/min). Scanning electron microscopy (SEM) investigations of the microstructures were performed in a Zeiss Sigma 300VP. To protect the samples from the ambient atmosphere, they were transferred from the glovebox to XRD and SEM with transport shuttles from Kammrath & Weiss (Schwerte, Germany).

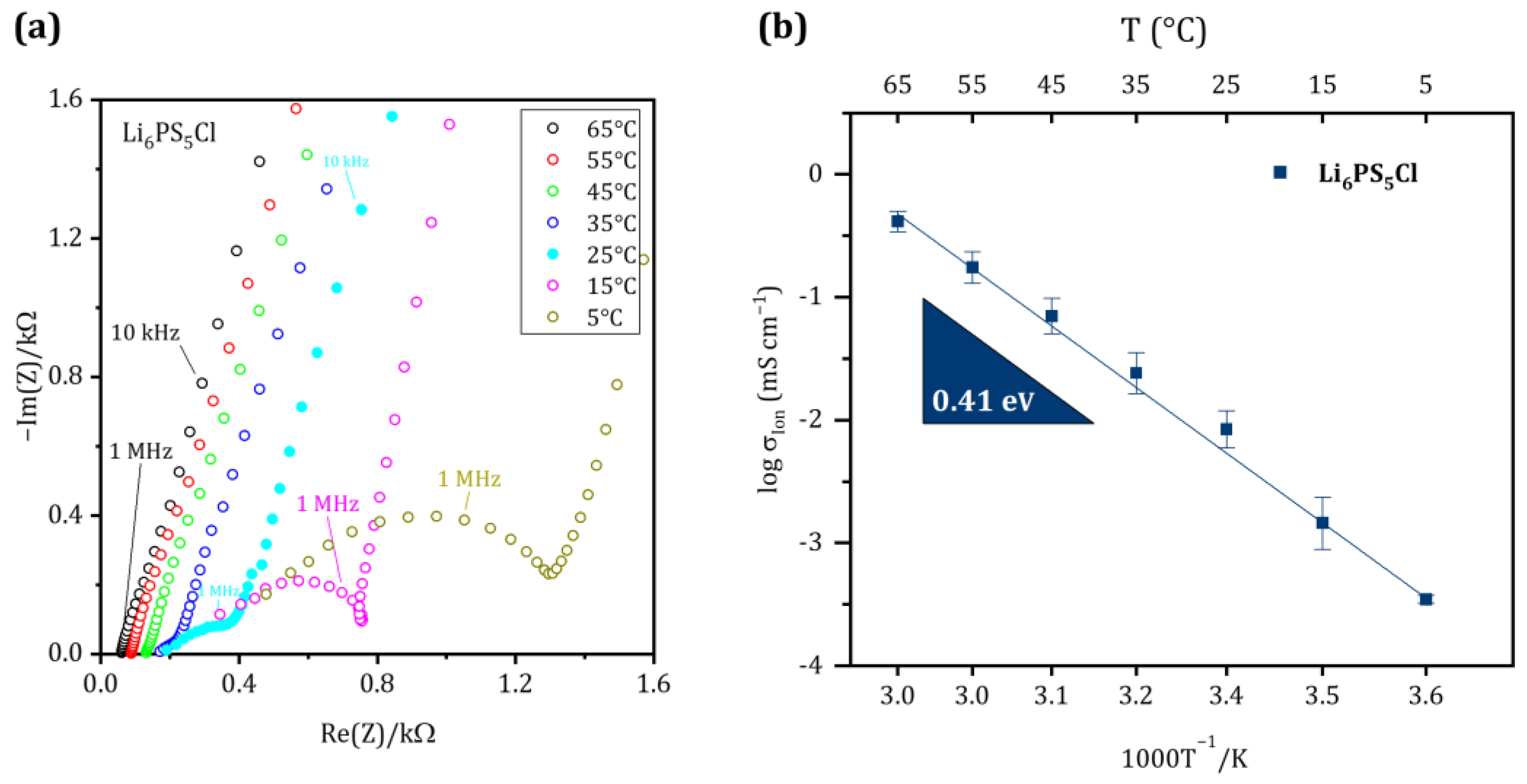
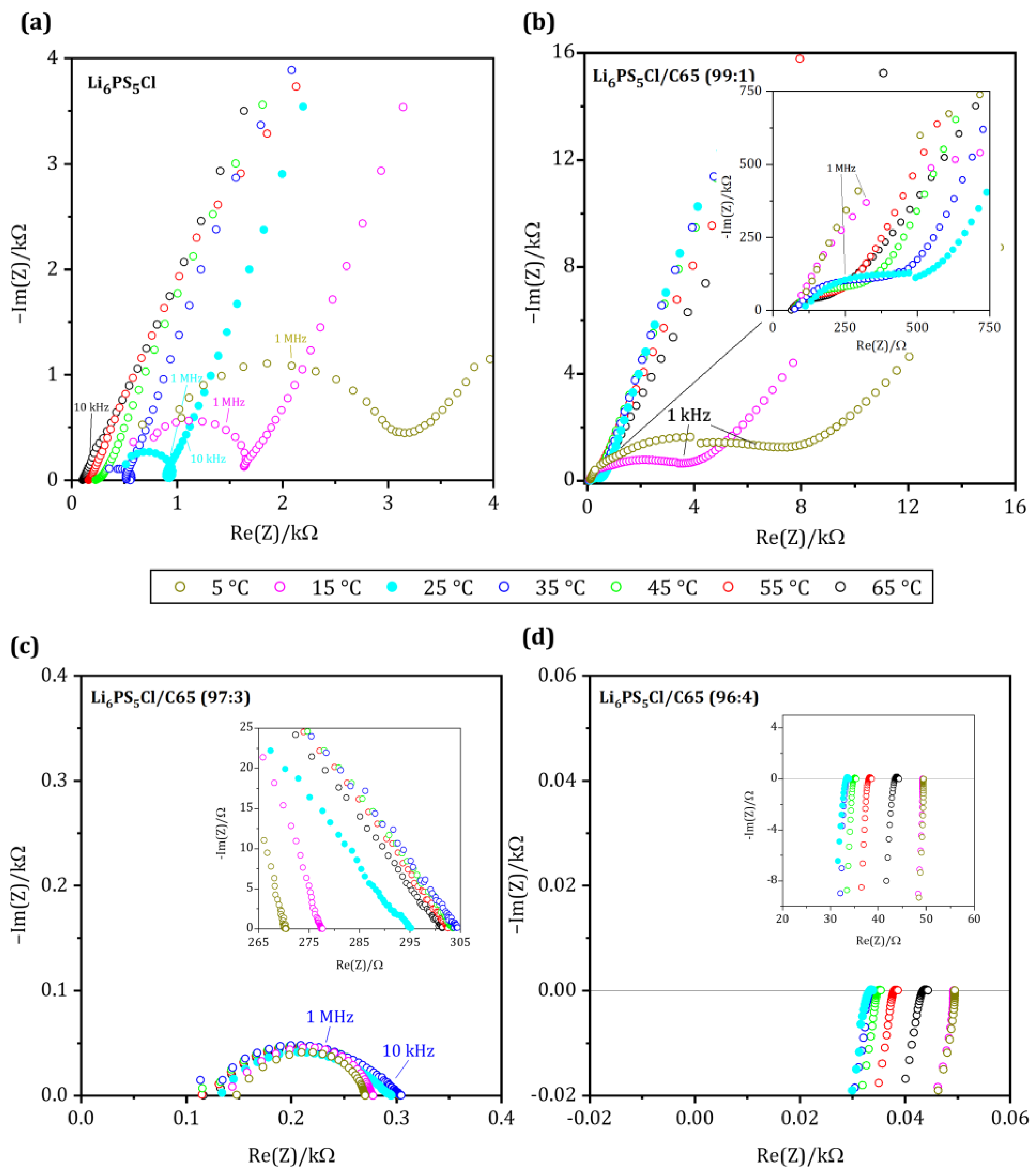
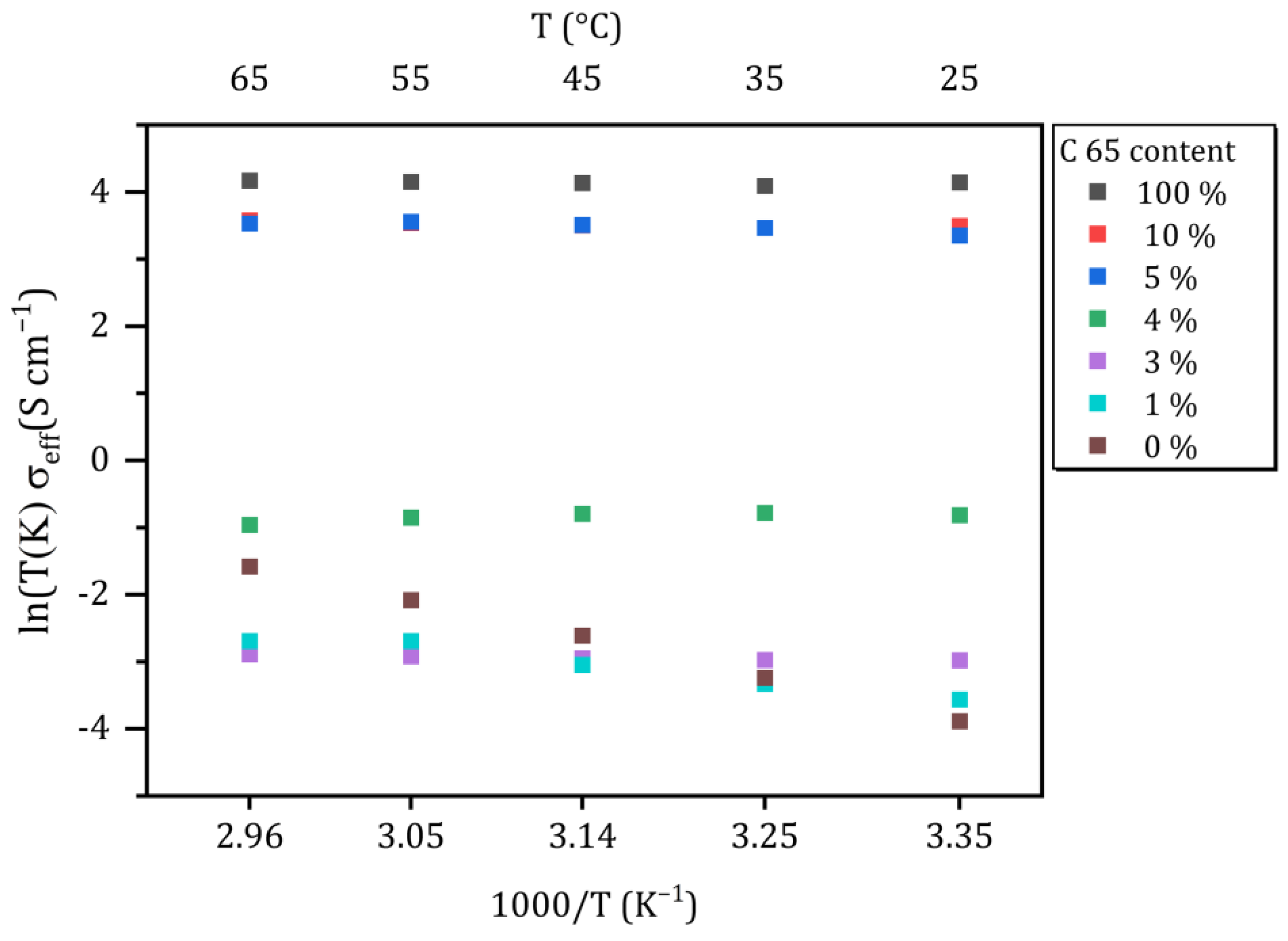
2.4. Electrochemical Impedance Measurement

The effective conductivities of the samples were measured using electrochemical impedance spectroscopy (EIS) in a climate chamber (CTS Clima Temperatur Systeme type T-40/200, Hechingen, Germany) as a function of temperature. An alternating voltage with an amplitude of 10 mV in a wide frequency range from 7 MHz to 1 Hz was applied using a potentiostat (VSP-300, Bio-Logic, Seyssinet-Pariset, France). The EIS measurements of the individual samples were performed at different temperatures to determine the activation energy (Ea) for Li-ion transport using the Arrhenius equation. The temperature-dependent measurement protocols for the conducting matrix and the separator are shown in Table 2. To ensure stabilization of the system after heating (or cooling) to the desired measurement temperature step, the temperature was held for 120 min before starting the measurement. Measurements were carried out in a range from 5 °C to 65 °C in 10 °C steps. Curve fitting of the impedance spectra was performed using Z-View software (version 4.0d). Different equivalent circuits were used to determine the resistance values. At room temperature (RT) and above, the linear intercept of the tail of the blocking electrodes was used to determine the resistance. Below RT and for the 1 wt.-% mixture, a serial connection of a resistor (R0), a parallel arrangement of a resistor (R1) with CPE element and an additional CPE element were used to fit the spectra. The 3 wt.-% mixture was fitted to a serial connection of a resistor and two Randles circuits. When the percolation threshold was reached for the samples at 4 wt.-% and above, a single resistor was used to extract the resistance value R. The conductivity was calculated with the total resistance according to Equation (1), where A is the sample area and d is the thickness of the sample. DC measurements are used to confirm the behavior of the electronic conductivity.
σ i o n = d A R − 1

3. Results and Discussion

The XRD patterns of the synthesized Li6PS5Cl and precursor mixture are illustrated in Figure 1a. After the homogenization of the raw materials, the crystallinity and purity were preserved in the precursor mixture (black). In the diffractogram, the peaks of P2S5 are not visible in the plot. This can be attributed to the triclinic space group, which has a complex structure and no symmetry planes, which leads to peaks of low intensity compared to Li2S and LiCl (the unprocessed XRD plot of the precursor mixture can be found in Figure S1 in the Supplementary Information). The diffractogram of the heat-treated sample unveils the pure and crystalline phase Li6PS5Cl (red). Figure 1b–d show the secondary electron (SE) SEM images of the ground solid electrolyte powder after heat treatment (Figure 1b), the densified separator pellet surface (Figure 1c) and the separator (Figure 1d), which was used to determine the conductivity values of the material, placed on the bottom current collector of the measurement cell. The ground SE shows spherical submicrometer-sized grains, which tend to agglomerate to secondary particles with sizes of >10 µm. After densification to separator pellets at 375 MPa, the microstructure displays the plastic compaction behavior of the SE, which is known for its soft nature in Figure 1c.
Figure 2 shows the EIS spectra and the Arrhenius plot of the ionic conductivity of the Li6PS5Cl separator in the temperature range of 5 °C to 65 °C. Semicircles were observed at mid-high frequencies of impedance spectra and gradually disappeared with increasing temperature, indicating that bulk contribution is dominated at high temperatures. Therefore, the bulk and grain boundary contributions cannot be deconvoluted at room temperature. The ionic conductivity of synthesized Li6PS5Cl is 0.12 mS cm−1 at 5 °C and increases to 2.02 mS cm−1 at 65 °C, while it is 0.43 mS cm−1 at room temperature. The total ohmic resistance decreases continuously with increasing temperature from 354.40 Ω at 25 °C to 58.79 Ω at 65 °C. These data are in good agreement with studies such as those by Yu et al. and Zhang et al., published previously [39,40]. The calculated activation energy for Li-ion transport in Li6PS5Cl from the slope of the linear Arrhenius plot (Figure 2b) is 0.41 eV, which is in accordance with the reported results [40]. The linear behavior also indicates the thermal stability of the Li6PS5Cl within the temperature range that was investigated in our study.
Figure 3 shows the impedance spectra of the conducting matrix with increasing fractions of C65 in the temperature range 5 °C to 65 °C. For comparison, the impedance spectra of the pure solid electrolyte (from Figure 2a) are added. A linear behavior can be assessed (Figure 3a) for the measurements at room temperature up to 65 °C for pure solid electrolyte that was compacted in the measurement cell, comparable to the conducting matrix (unlike SE in Figure 2, which was pre-densified (see Section 2)). The determined total ohmic resistance decreases continuously with increasing temperature from 903.50 Ω at 25 °C to 102.10 Ω at 65 °C. At 15 °C and below, the formation of an evolved semicircle can be observed. Along with the decrease in temperature, the ohmic resistance increases from 1628.50 Ω at 15 °C to 3098.60 Ω at 5 °C. In all measurements, there is a high impedance of the imaginary part in the low-frequency range, triggered by the blocked charge transport at the SE/In electrode interface. Note that the resistance values are slightly higher than those of the pre-pressed pellet, mainly due to the densification difference.
For simplicity, in the following sections, we will use the sample notation “CM-A”, where CM stands for conducting matrix, and A gives the amount of C65 (in wt.-%) that is added to the SE.
The impedance spectrum of the sample CM-1 is shown in Figure 3b. Although the temperature dependence of the Nyquist plots for CM-1 is similar to the pure solid electrolyte, the total resistance values at 65 °C (RCM-1: 247.67 Ω; Rpure SE: 102.10 Ω) are higher, while it exhibits a lower total resistance of 522 Ω at room temperature. Below room temperature, the spectrum exhibits a stretched semicircle in the mid-frequency range, and in the low-frequency range, all spectra show a high impedance of the imaginary part representing the polarization at the blocking electrodes.
A change in conduction behavior can be observed in sample CM-3, the total resistance values decrease slightly from 302.43 Ω at 65 °C to 288.03 Ω at 15 °C, shown in Figure 3c. Unlike the sample with pure SE, no polarization can be observed in the low-frequency range, indicating that charge transport is not entirely blocked. At temperatures below 45 °C, the resistances are generally smaller than those of the pure solid electrolyte. Furthermore, at 5 °C, the resistance decreases significantly with a minimum value of 272.17 Ω. The impedance spectra of all samples show a stretched semicircle in the mid-frequency range.
The sample CM-4 behaves very differently from what was observed before: The ohmic resistance of the sample CM-4 (Figure 3d) remains almost identical throughout the entire temperature range, and no frequency dependence of the spectrum can be overserved. At high frequencies, however, an inductive behavior is present in all measurements and is more noticeable because of the smaller impedance range mapped. It can be considered as an artifact originating from the wires of the measurement cell. At lower frequencies, this inductance can no longer be detected, and we find an accumulation of all measured points on the axis of the real part. Resistance values are 33.50 Ω at 25 °C and 43.89 Ω at 65 °C. However, no clear correlation can be found between the temperature and the resistance. But we observe an increase of the ohmic resistance as a function of measurement time (please see Table 2 for the measurement protocol), which could potentially be a hint for interface reactions between the solid electrolyte and the carbon additive. In a similar system of LGPS and Acetylene Black, Oh et al. reported an interfacial reaction between the SE and additive after cycling [22]. The impedance spectra indicate no capacitance and behave like an ohmic resistor at low frequencies. This indicates that C65 builds an electronically conductive network that dominates the effective conductivity of the compound.
Similar behavior can be observed for mixtures with a fraction of C65 ≥ 5 wt.-% (Sample CM-5 and CM-10, Figure S2 in Supporting Information). The ohmic resistance is independent of the measurement frequency and no capacitance is built up. From 5 wt.-% C65 to the pure C65, the mean resistance values drop only from 0.50 to 0.24 Ω.
In Figure 4, the temperature-dependent effective conductivities of the different samples are plotted as a function of 1/T. Note that the pure electrolyte (SE; Li6PS5Cl) is assumed to be a pure ionic conductor and C65 as a pure electronic conductor for simplification.
According to the Arrhenius equation, the pure solid electrolyte shows a temperature-dependent increase in (ionic) conductivity. This formula does not apply to the conducting matrix, because it should be regarded as a mixed conductor. However, an increase in conductivity can be observed for the sample CM-1 with increasing temperature, too, indicating that ionic conductivity dominates the effective conductivity. In contrast, the conductivity of the samples with ≥3 wt.-% decreases with increasing temperature, which indicates that the electronic conduction is dominating the overall behavior of the samples.
At room temperature (25 °C), a systematic increase in the effective conductivity of the CM with increasing C65 content becomes obvious. While the total conductivities of pure SE, CM-1 and CM-3 are in the same order of magnitude, a remarkable change of about one order of magnitude can be overserved for 4 wt.-% of C65 (1.66 × 10−4 S cm−1 for 3 wt.-% vs. 1.36 × 10−3 S cm−1 for 4 wt.-%). The change in the spectra (Figure 3c) comparing CM-1 to CM-3 corresponds to an increase in the conductivity of 1.20 × 10−4 S cm−1 at room temperature. An even more distinct increase of three orders of magnitude in conductivity to 1.02 × 10−1 S cm−1 is observed for the sample CM-5 compared to CM-3. A further increase of the amount of C65 up to 10 wt.-% only marginally increases the conductivity of the mixture, since the conductivity of CM-5 is already close to that of pure C65. Neglecting cell and cable resistances, the conductivity of the pure conductive additive can be determined to be approximately 0.2 S cm−1, corresponding to an absolute resistance of about 0.25 Ω. These findings are accompanied by the fact that the real part of the impedance spectra no longer shows any frequency dependence from a proportion of 4 wt.-% (Figure 3d). Furthermore, at low frequencies, there is no phase shift of voltage and current since there is no capacitance, and the conducting matrix behaves like an ohmic resistor, which was confirmed by DC measurements (Figures S3 and S4 in Supporting Information).
The effective conductivity of the conducting matrix at 25 °C as a function of the C65 content is plotted in Figure 5. As described before, a distinct increase in the conductivity can be observed between 3 and 5 wt.-% of C65, and the curve shows a step-like progression. This is a typical phenomenon when reaching the percolation threshold and can also be observed in different systems, such as sintering ceramics, conduction in fuel cells or carbon-nanotube-reinforced polymers, just to name a few [41,42,43]. For the interpretation of the diagram, it can be divided into two areas. In the range below the percolation threshold p < pc, the effective conductivity is close to the conductivity of the pure solid electrolyte. Above the critical conductive additive fraction p > pc, the C65 forms a percolating network that allows electronic conduction. It can be assumed that for a C65 fraction ≥ 4 wt.-%, the charge transport in the chosen experimental set-up proceeds almost exclusively by an electronic current across the network of C65 nanoparticles, as the effective conductivity is orders of magnitude higher than the ionic conductivity of the pure solid electrolyte.
Although carbon additives have already been shown to increase the rate performance of thiophosphate-based composite cathodes [26], they have detrimental effects on the battery performance mainly due to forming side reactions [18]. When defining a conducting matrix based on percolation theory and describing the formation of interconnected regions of randomly distributed particles in this structure, the so-called percolating clusters could provide a minimized conductive additive/cathode active material ratio [44]. The conductive matrix prepared in this study can be considered as such a structure in which the C65 nanoparticles are randomly distributed and form a percolating cluster above a critical content that allows electronic conduction through the matrix.
The fact that percolation occurs at a fraction as low as 3 < pc < 5 wt.-% (Figure 6), even though both materials have similar densities of 1.83 (Li6PS5Cl) and 1.60 g cm−3 (C65), can be attributed to the extremely high specific surface area of the nanoparticles of 62 m2 g−1, which easily form a 3D network throughout the matrix (as shown in Figure 6). Here, Bielefeld et al. modeled the microstructure of a composite cathode and its percolation behavior; the authors concluded that the critical threshold occurs earlier for smaller active material particles due to their higher surface area [45]. This behavior has already been described for other material compositions. For example, Guzman et al. show that for a material system of LiFePO4 and C65, the percolation threshold is about 7 wt.-% [46].
A schema of the conducting matrix’ microstructure is shown in Figure 6a. Illustrated on the left is the subcritical percolation phase, where the C65 nanoparticles are distributed within the solid electrolyte as isolated islands (the SEM image of the C65 particles can be found in Supporting Information Figure S5). At the percolation threshold pc, the amount of C65 is sufficient to form a network and electronic conduction can occur via the network. A further increase in C65 in the supercritical percolation phase will inevitably reduce the ionic conduction of the CM. SEM backscattered electron (BSE) images of the powder mixtures with increasing amounts of the conductive additive of 1, 2, 5 and 10 wt.-%, are shown in Figure 6b–e, respectively. In Figure 6b to 1 wt.-% C65, an almost-complete exposure of the SE grains becomes visible. The isolated C65 particles are distributed within the composite and do not form any network. Isolated agglomerates of C65 particles which show only slight crosslinking can be observed in sample CM-2 (see Figure 6c). The increase in the C65 content from 2 to 5 wt.-% (Figure 6d) changes the microstructure significantly, as almost the entire surface of the SE grains is covered with C65. Although the proportion of C65 in Figure 6e is only 10 wt.-%, the C65 particles cover the surface of the SE phase almost completely.

4. Conclusions

Through systematic investigation of different mixtures of synthesized Li6PS5Cl and C65 as a conductive additive, we found the electronic percolation threshold of this matrix at about 4 wt.-%. Considering a typical composite cathode mixture for sulfide-based solid-state batteries of 70 wt.-% of active material, this equals a total C65 fraction of 1.2 wt.-% in the conducting matrix. Therefore, this work provides a guideline for the effective design of a conducting matrix for thiophosphate-based composite cathodes for ASSBs. Furthermore, we proposed a conducting matrix in sulfide-based ASSBs that provides ionic and electronic conduction in the composite cathode, whereby a C65 fraction of 4 wt.-% might be considered as an optimized composition combining high electronic conductivity at a low amount of C65. Improving the electronic conductivity within the composite cathode becomes especially important as protective coatings of CAMs lead to a decreased partial electronic conductivity. A natural progression of this work is to analyze the cycling performance of full cells using different active materials with different fractions of C65 and Li6PS5Cl. Furthermore, EIS measurements under electronic blocking conditions could help to better understand the interplay between ionic and electronic conductivity of the conductive matrix with different composition, i.e., with different C65 content.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/batteries9120595/s1, Figure S1: Unprocessed XRD Pattern of the precursor mixture; Figure S2: Nyquist plots of the conducting matrix with 5 wt.-% C65 and pure C65 measured between 5 and 65 °C; Figure S3: DC measurement of the conducting matrix with 4 wt.-% C65 at temperatures between 5 and 65 °C; Figure S4: Additional EIS measurements at RT with C65 fractions above the percolation threshold; Figure S5: SE image of the conducting matrix highlighting the C65 nanoparticles.

Author Contributions

Conceptualization, E.R. and P.K.; methodology, E.R.; formal analysis, E.R.; investigation, E.R.; data curation, E.R.; writing—original draft preparation, E.R.; writing—review and editing, P.K. and V.K.; visualization, E.R.; supervision, P.K. and V.K.; project administration, V.K.; funding acquisition, V.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the German Federal Ministry of Education and Research within the program “FH-Impuls” (Project SmartPro, Subproject Smart-BAT, Grant no. 13FH4I07IA). Publication funded by Aalen University of Applied Sciences and Deutsche Forschungsgemeinschaft (DFG, German Research Foundation).

Data Availability Statement

The data presented in this study are available in the article and the Supplementary Materials.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rüdisüli, M.; Bach, C.; Bauer, C.; Beloin-Saint-Pierre, D.; Elber, U.; Georges, G.; Limpach, R.; Pareschi, G.; Kannan, R.; Teske, S.L. Prospective life-cycle assessment of greenhouse gas emissions of electricity-based mobility options. Appl. Energy 2022, 306, 118065. [Google Scholar] [CrossRef]
  2. Kato, Y.; Hori, S.; Saito, T.; Suzuki, K.; Hirayama, M.; Mitsui, A.; Yonemura, M.; Iba, H.; Kanno, R. High-power all-solid-state batteries using sulfide superionic conductors. Nat. Energy 2016, 1, 652. [Google Scholar] [CrossRef]
  3. Krauskopf, T.; Mogwitz, B.; Hartmann, H.; Singh, D.K.; Zeier, W.G.; Janek, J. The Fast Charge Transfer Kinetics of the Lithium Metal Anode on the Garnet-Type Solid Electrolyte Li6.25Al0.25La3Zr2O12. Adv. Energy Mater. 2020, 10, 2000945. [Google Scholar] [CrossRef]
  4. Liu, J.; Bao, Z.; Cui, Y.; Dufek, E.J.; Goodenough, J.B.; Khalifah, P.; Li, Q.; Liaw, B.Y.; Liu, P.; Manthiram, A.; et al. Pathways for practical high-energy long-cycling lithium metal batteries. Nat. Energy 2019, 4, 180–186. [Google Scholar] [CrossRef]
  5. Gao, Z.; Sun, H.; Fu, L.; Ye, F.; Zhang, Y.; Luo, W.; Huang, Y. Promises, Challenges, and Recent Progress of Inorganic Solid-State Electrolytes for All-Solid-State Lithium Batteries. Adv. Mater. 2018, 30, e1705702. [Google Scholar] [CrossRef] [PubMed]
  6. Xu, W.; Wang, J.; Ding, F.; Chen, X.; Nasybulin, E.; Zhang, Y.; Zhang, J.-G. Lithium metal anodes for rechargeable batteries. Energy Environ. Sci. 2014, 7, 513–537. [Google Scholar] [CrossRef]
  7. Adeli, P.; Bazak, J.D.; Huq, A.; Goward, G.R.; Nazar, L.F. Influence of Aliovalent Cation Substitution and Mechanical Compression on Li-Ion Conductivity and Diffusivity in Argyrodite Solid Electrolytes. Chem. Mater. 2021, 33, 146–157. [Google Scholar] [CrossRef]
  8. Li, Y.; Xu, B.; Xu, H.; Duan, H.; Lü, X.; Xin, S.; Zhou, W.; Xue, L.; Fu, G.; Manthiram, A.; et al. Hybrid Polymer/Garnet Electrolyte with a Small Interfacial Resistance for Lithium-Ion Batteries. Angew. Chem. Int. Ed. Engl. 2017, 56, 753–756. [Google Scholar] [CrossRef]
  9. Kamaya, N.; Homma, K.; Yamakawa, Y.; Hirayama, M.; Kanno, R.; Yonemura, M.; Kamiyama, T.; Kato, Y.; Hama, S.; Kawamoto, K.; et al. A lithium superionic conductor. Nat. Mater. 2011, 10, 682–686. [Google Scholar] [CrossRef]
  10. Bielefeld, A.; Weber, D.A.; Janek, J. Modeling Effective Ionic Conductivity and Binder Influence in Composite Cathodes for All-Solid-State Batteries. ACS Appl. Mater. Interfaces 2020, 12, 12821–12833. [Google Scholar] [CrossRef]
  11. Bielefeld, A.; Weber, D.A.; Rueß, R.; Glavas, V.; Janek, J. Influence of Lithium Ion Kinetics, Particle Morphology and Voids on the Electrochemical Performance of Composite Cathodes for All-Solid-State Batteries. J. Electrochem. Soc. 2022, 169, 20539. [Google Scholar] [CrossRef]
  12. Doux, J.-M.; Yang, Y.; Tan, D.H.S.; Nguyen, H.; Wu, E.A.; Wang, X.; Banerjee, A.; Meng, Y.S. Pressure effects on sulfide electrolytes for all solid-state batteries. J. Mater. Chem. A 2020, 8, 5049–5055. [Google Scholar] [CrossRef]
  13. Ruiz, A.G.; Sola, P.C.; Palmerola, N.M. Germanium: Current and Novel Recovery Processes. In Advanced Material and Device Applications with Germanium; Lee, S., Ed.; InTech: London, UK, 2018; ISBN 978-1-78984-031-5. [Google Scholar]
  14. Lee, J.; Lee, T.; Char, K.; Kim, K.J.; Choi, J.W. Issues and Advances in Scaling up Sulfide-Based All-Solid-State Batteries. Acc. Chem. Res. 2021, 54, 3390–3402. [Google Scholar] [CrossRef] [PubMed]
  15. Walther, F.; Koerver, R.; Fuchs, T.; Ohno, S.; Sann, J.; Rohnke, M.; Zeier, W.G.; Janek, J. Visualization of the Interfacial Decomposition of Composite Cathodes in Argyrodite-Based All-Solid-State Batteries Using Time-of-Flight Secondary-Ion Mass Spectrometry. Chem. Mater. 2019, 31, 3745–3755. [Google Scholar] [CrossRef]
  16. Jung, S.-K.; Gwon, H.; Lee, S.-S.; Kim, H.; Lee, J.C.; Chung, J.G.; Park, S.Y.; Aihara, Y.; Im, D. Understanding the effects of chemical reactions at the cathode–electrolyte interface in sulfide based all-solid-state batteries. J. Mater. Chem. A 2019, 7, 22967–22976. [Google Scholar] [CrossRef]
  17. Walther, F.; Randau, S.; Schneider, Y.; Sann, J.; Rohnke, M.; Richter, F.H.; Zeier, W.G.; Janek, J. Influence of Carbon Additives on the Decomposition Pathways in Cathodes of Lithium Thiophosphate-Based All-Solid-State Batteries. Chem. Mater. 2020, 32, 6123–6136. [Google Scholar] [CrossRef]
  18. Zhang, W.; Leichtweiß, T.; Culver, S.P.; Koerver, R.; Das, D.; Weber, D.A.; Zeier, W.G.; Janek, J. The Detrimental Effects of Carbon Additives in Li10GeP2S12-Based Solid-State Batteries. ACS Appl. Mater. Interfaces 2017, 9, 35888–35896. [Google Scholar] [CrossRef] [PubMed]
  19. Yoon, K.; Kim, J.-J.; Seong, W.M.; Lee, M.H.; Kang, K. Investigation on the interface between Li10GeP2S12 electrolyte and carbon conductive agents in all-solid-state lithium battery. Sci. Rep. 2018, 8, 8066. [Google Scholar] [CrossRef] [PubMed]
  20. Noh, S.; Nichols, W.T.; Park, C.; Shin, D. Enhanced energy density and electrochemical performance of all-solid-state lithium batteries through microstructural distribution of solid electrolyte. Ceram. Int. 2017, 43, 15952–15958. [Google Scholar] [CrossRef]
  21. Ann, J.; Choi, S.; Do, J.; Lim, S.; Shin, D. Effects of binary conductive additives on electrochemical performance of a sheettype composite cathode with different weight ratios of LiNi0.6Co0.2Mn0.2O2 in allsolid-state lithium batteries. Ceram. Process. Res. 2018, 19, 413–418. [Google Scholar]
  22. Oh, G.; Hirayama, M.; Kwon, O.; Suzuki, K.; Kanno, R. Bulk-Type All Solid-State Batteries with 5 V Class LiNi0.5Mn1.5O4 Cathode and Li10GeP2S12 Solid Electrolyte. Chem. Mater. 2016, 28, 2634–2640. [Google Scholar] [CrossRef]
  23. Al-Salih, H.; Houache, M.S.E.; Baranova, E.A.; Abu-Lebdeh, Y. Composite Cathodes for Solid-State Lithium Batteries: “Catholytes” the Underrated Giants. Adv. Energy Sustain. Res. 2022, 3, 2200032. [Google Scholar] [CrossRef]
  24. Kato, Y.; Shiotani, S.; Morita, K.; Suzuki, K.; Hirayama, M.; Kanno, R. All-Solid-State Batteries with Thick Electrode Configurations. J. Phys. Chem. Lett. 2018, 9, 607–613. [Google Scholar] [CrossRef] [PubMed]
  25. Neumann, A.; Randau, S.; Becker-Steinberger, K.; Danner, T.; Hein, S.; Ning, Z.; Marrow, J.; Richter, F.H.; Janek, J.; Latz, A. Analysis of Interfacial Effects in All-Solid-State Batteries with Thiophosphate Solid Electrolytes. ACS Appl. Mater. Interfaces 2020, 12, 9277–9291. [Google Scholar] [CrossRef] [PubMed]
  26. Strauss, F.; Stepien, D.; Maibach, J.; Pfaffmann, L.; Indris, S.; Hartmann, P.; Brezesinski, T. Influence of electronically conductive additives on the cycling performance of argyrodite-based all-solid-state batteries. RSC Adv. 2020, 10, 1114–1119. [Google Scholar] [CrossRef] [PubMed]
  27. Park, S.W.; Oh, G.; Park, J.-W.; Ha, Y.-C.; Lee, S.-M.; Yoon, S.Y.; Kim, B.G. Graphitic Hollow Nanocarbon as a Promising Conducting Agent for Solid-State Lithium Batteries. Small 2019, 15, e1900235. [Google Scholar] [CrossRef]
  28. Amin, R.; Chiang, Y.-M. Characterization of Electronic and Ionic Transport in Li1−xNi0.33Mn0.33Co0.33O2 (NMC333) and Li1−xNi0.50Mn0.20Co0.30O2 (NMC523) as a Function of Li Content. J. Electrochem. Soc. 2016, 163, A1512–A1517. [Google Scholar] [CrossRef]
  29. Asano, T.; Yubuchi, S.; Sakuda, A.; Hayashi, A.; Tatsumisago, M. Electronic and Ionic Conductivities of LiNi1/3Mn1/3Co1/3O2-Li3PS4 Positive Composite Electrodes for All-Solid-State Lithium Batteries. J. Electrochem. Soc. 2017, 164, A3960–A3963. [Google Scholar] [CrossRef]
  30. Conforto, G.; Ruess, R.; Schröder, D.; Trevisanello, E.; Fantin, R.; Richter, F.H.; Janek, J. Editors’ Choice—Quantification of the Impact of Chemo-Mechanical Degradation on the Performance and Cycling Stability of NCM-Based Cathodes in Solid-State Li-Ion Batteries. J. Electrochem. Soc. 2021, 168, 70546. [Google Scholar] [CrossRef]
  31. Han, Y.; Jung, S.H.; Kwak, H.; Jun, S.; Kwak, H.H.; Lee, J.H.; Hong, S.-T.; Jung, Y.S. Single- or Poly-Crystalline Ni-Rich Layered Cathode, Sulfide or Halide Solid Electrolyte: Which Will be the Winners for All-Solid-State Batteries? Adv. Energy Mater. 2021, 11, 2100126. [Google Scholar] [CrossRef]
  32. Nam, Y.J.; Oh, D.Y.; Jung, S.H.; Jung, Y.S. Toward practical all-solid-state lithium-ion batteries with high energy density and safety: Comparative study for electrodes fabricated by dry- and slurry-mixing processes. J. Power Sources 2018, 375, 93–101. [Google Scholar] [CrossRef]
  33. Froboese, L.; van der Sichel, J.F.; Loellhoeffel, T.; Helmers, L.; Kwade, A. Effect of Microstructure on the Ionic Conductivity of an All Solid-State Battery Electrode. J. Electrochem. Soc. 2019, 166, A318–A328. [Google Scholar] [CrossRef]
  34. Newman, M.E.; Ziff, R.M. Efficient Monte Carlo algorithm and high-precision results for percolation. Phys. Rev. Lett. 2000, 85, 4104–4107. [Google Scholar] [CrossRef] [PubMed]
  35. Xu, W.; Su, X.; Jiao, Y. Continuum percolation of congruent overlapping spherocylinders. Phys. Rev. E 2016, 94, 32122. [Google Scholar] [CrossRef] [PubMed]
  36. McLachlan, D.S.; Blaszkiewicz, M.; Newnham, R.E. Electrical Resistivity of Composites. J. Am. Ceram. Soc. 1990, 73, 2187–2203. [Google Scholar] [CrossRef]
  37. Minnmann, P.; Quillman, L.; Burkhardt, S.; Richter, F.H.; Janek, J. Editors’ Choice—Quantifying the Impact of Charge Transport Bottlenecks in Composite Cathodes of All-Solid-State Batteries. J. Electrochem. Soc. 2021, 168, 40537. [Google Scholar] [CrossRef]
  38. Noh, H.-J.; Youn, S.; Yoon, C.S.; Sun, Y.-K. Comparison of the structural and electrochemical properties of layered Li[NixCoyMnz]O2 (x = 1/3, 0.5, 0.6, 0.7, 0.8 and 0.85) cathode material for lithium-ion batteries. J. Power Sources 2013, 233, 121–130. [Google Scholar] [CrossRef]
  39. Yu, C.; Ganapathy, S.; Hageman, J.; van Eijck, L.; van Eck, E.R.H.; Zhang, L.; Schwietert, T.; Basak, S.; Kelder, E.M.; Wagemaker, M. Facile Synthesis toward the Optimal Structure-Conductivity Characteristics of the Argyrodite Li6PS5Cl Solid-State Electrolyte. ACS Appl. Mater. Interfaces 2018, 10, 33296–33306. [Google Scholar] [CrossRef]
  40. Zhang, Z.; Zhang, L.; Liu, Y.; Yu, C.; Yan, X.; Xu, B.; Wang, L. Synthesis and characterization of argyrodite solid electrolytes for all-solid-state Li-ion batteries. J. Alloys Compd. 2018, 747, 227–235. [Google Scholar] [CrossRef]
  41. Kuo, C.-H.; Gupta, P.K. Rigidity and conductivity percolation thresholds in particulate composites. Acta Metall. Mater. 1995, 43, 397–403. [Google Scholar] [CrossRef]
  42. Chen, D.; He, H.; Zhang, D.; Wang, H.; Ni, M. Percolation Theory in Solid Oxide Fuel Cell Composite Electrodes with a Mixed Electronic and Ionic Conductor. Energies 2013, 6, 1632–1656. [Google Scholar] [CrossRef]
  43. Li, J.; Ma, P.C.; Chow, W.S.; To, C.K.; Tang, B.Z.; Kim, J.-K. Correlations between Percolation Threshold, Dispersion State, and Aspect Ratio of Carbon Nanotubes. Adv. Funct. Mater. 2007, 17, 3207–3215. [Google Scholar] [CrossRef]
  44. Park, J.; Kim, J.Y.; Shin, D.O.; Oh, J.; Kim, J.; Lee, M.J.; Lee, Y.-G.; Ryou, M.-H.; Lee, Y.M. Dimension-controlled solid oxide electrolytes for all-solid-state electrodes: Percolation pathways, specific contact area, and effective ionic conductivity. Chem. Eng. J. 2020, 391, 123528. [Google Scholar] [CrossRef]
  45. Bielefeld, A.; Weber, D.A.; Janek, J. Microstructural Modeling of Composite Cathodes for All-Solid-State Batteries. J. Phys. Chem. C 2019, 123, 1626–1634. [Google Scholar] [CrossRef]
  46. Guzmán, G.; Vazquez-Arenas, J.; Ramos-Sánchez, G.; Bautista-Ramírez, M.; González, I. Improved performance of LiFePO4 cathode for Li-ion batteries through percolation studies. Electrochim. Acta 2017, 247, 451–459. [Google Scholar] [CrossRef]
Batteries 09 00595 g001
Figure 1. (a) XRD patterns of the precursor mixture after ball milling (black) and the corresponding pattern after reaction induced by heat treatment at 550 °C (red). Additionally, the reference pattern (ICSD: 418490) of Li-argyrodite is plotted. (b) SEM image of the synthesized solid electrolyte after heat treatment. (c) Surface of a pelletized separator. (d) Fabricated separator on the bottom current collector of the measurement cell.
Figure 1. (a) XRD patterns of the precursor mixture after ball milling (black) and the corresponding pattern after reaction induced by heat treatment at 550 °C (red). Additionally, the reference pattern (ICSD: 418490) of Li-argyrodite is plotted. (b) SEM image of the synthesized solid electrolyte after heat treatment. (c) Surface of a pelletized separator. (d) Fabricated separator on the bottom current collector of the measurement cell.
Batteries 09 00595 g001
Batteries 09 00595 g002
Figure 2. (a) Nyquist plot of the synthesized SE in blocking condition at temperatures between 65 °C and 5 °C. (b) Arrhenius plot of Li6PS5Cl to determine the activation energy for Li-ion transport.
Figure 2. (a) Nyquist plot of the synthesized SE in blocking condition at temperatures between 65 °C and 5 °C. (b) Arrhenius plot of Li6PS5Cl to determine the activation energy for Li-ion transport.
Batteries 09 00595 g002
Batteries 09 00595 g003
Figure 3. Nyquist plot of the conducting matrix with (a) pure SE, (b) CM-1: 1 wt.-% C65, (c) CM-3: 3 wt.-% C65 and (d) CM-4: 4 wt.-% C65 measured between 5 and 65 °C with temperatures steps of 10 °C (7.0 MHz–1.0 Hz).
Figure 3. Nyquist plot of the conducting matrix with (a) pure SE, (b) CM-1: 1 wt.-% C65, (c) CM-3: 3 wt.-% C65 and (d) CM-4: 4 wt.-% C65 measured between 5 and 65 °C with temperatures steps of 10 °C (7.0 MHz–1.0 Hz).
Batteries 09 00595 g003
Batteries 09 00595 g004
Figure 4. Effective conductivities of the conducting matrix as a function of the temperature. Different colors represent the weight fraction of C65 in the powder mixture.
Figure 4. Effective conductivities of the conducting matrix as a function of the temperature. Different colors represent the weight fraction of C65 in the powder mixture.
Batteries 09 00595 g004
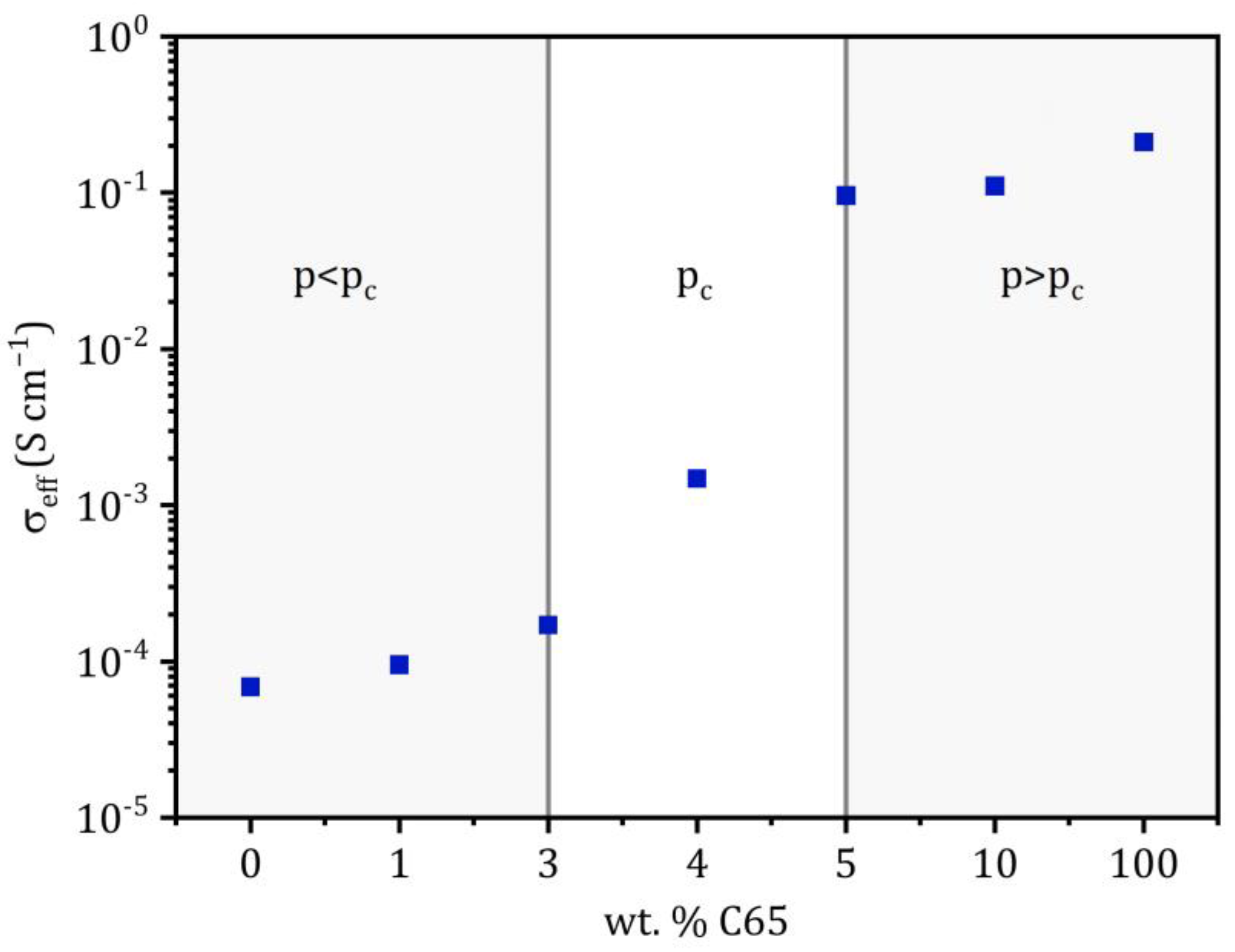
Batteries 09 00595 g005
Figure 5. Effective conductivities of the conducting matrix as a function of the C65 weight and volume fraction at 25 °C. The approximate range of the percolation threshold pc is highlighted. The X-axes are not scaled and display tested C65 fractions.
Figure 5. Effective conductivities of the conducting matrix as a function of the C65 weight and volume fraction at 25 °C. The approximate range of the percolation threshold pc is highlighted. The X-axes are not scaled and display tested C65 fractions.
Batteries 09 00595 g005
Batteries 09 00595 g006
Figure 6. (a) Schema of the conducting matrix microstructure with different weight fractions of C65; (b–e) correlated top-view images of the conducting matrix with increasing C65 content (yellow arrows indicate solid electrolyte particles and dark blue arrows indicate C65 nanoparticles): (b) CM-1, (c) CM-2, (d) CM-5 and (e) CM-10.
Figure 6. (a) Schema of the conducting matrix microstructure with different weight fractions of C65; (b–e) correlated top-view images of the conducting matrix with increasing C65 content (yellow arrows indicate solid electrolyte particles and dark blue arrows indicate C65 nanoparticles): (b) CM-1, (c) CM-2, (d) CM-5 and (e) CM-10.
Batteries 09 00595 g006
Table 1. Prepared powder mixtures of the conducting matrix with weight (wt.) and volume (vol.) fractions.
Table 1. Prepared powder mixtures of the conducting matrix with weight (wt.) and volume (vol.) fractions.
Wt.-ratio [Li6PS5Cl:C65]100:090:1095:596:497:399:10:100
Fraction C65 [vol.]0.00%11.44%5.77%4.62%3.47%1.16%100.00%
Fraction C65 [wt.]0.00%10.00%5.00%4.00%3.00%1.00%100.00%
Li6PS5Cl [mg]/Pellet40.0036.0038.0038.4038.8039.600.00
C65 [mg]/Pellet0.004.002.001.601.200.4040.00
Table 2. Temperature protocol of the EIS measurements for the separator and the conducting matrix.
Table 2. Temperature protocol of the EIS measurements for the separator and the conducting matrix.
Measurement step1234567
Separator
Temperature [°C]2565554535155
Conducting matrix
Temperature [°C]2535455565155
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Reisacher, E.; Kaya, P.; Knoblauch, V. Percolation Behavior of a Sulfide Electrolyte–Carbon Additive Matrix for Composite Cathodes in All-Solid-State Batteries. Batteries 2023, 9, 595. https://doi.org/10.3390/batteries9120595

AMA Style

Reisacher E, Kaya P, Knoblauch V. Percolation Behavior of a Sulfide Electrolyte–Carbon Additive Matrix for Composite Cathodes in All-Solid-State Batteries. Batteries. 2023; 9(12):595. https://doi.org/10.3390/batteries9120595

Chicago/Turabian Style

Reisacher, Elias, Pinar Kaya, and Volker Knoblauch. 2023. "Percolation Behavior of a Sulfide Electrolyte–Carbon Additive Matrix for Composite Cathodes in All-Solid-State Batteries" Batteries 9, no. 12: 595. https://doi.org/10.3390/batteries9120595

APA Style

Reisacher, E., Kaya, P., & Knoblauch, V. (2023). Percolation Behavior of a Sulfide Electrolyte–Carbon Additive Matrix for Composite Cathodes in All-Solid-State Batteries. Batteries, 9(12), 595. https://doi.org/10.3390/batteries9120595

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop