Online Fast Charging Model without Lithium Plating for Long-Dimensional Cells in Automotive Applications
Abstract
:1. Introduction
2. Methodology
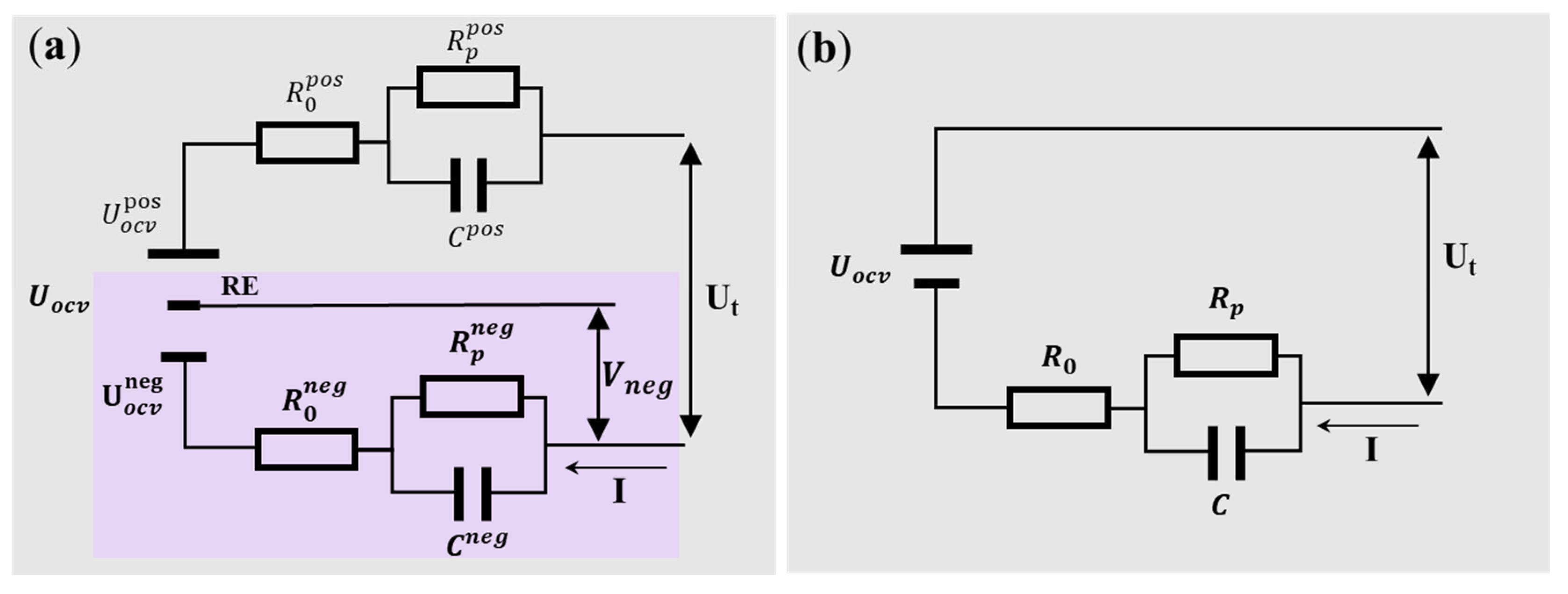
2.1. Theory of Negative Electrode Potential Closed-Loop Estimation
2.2. Current Control Theory
3. Experiment
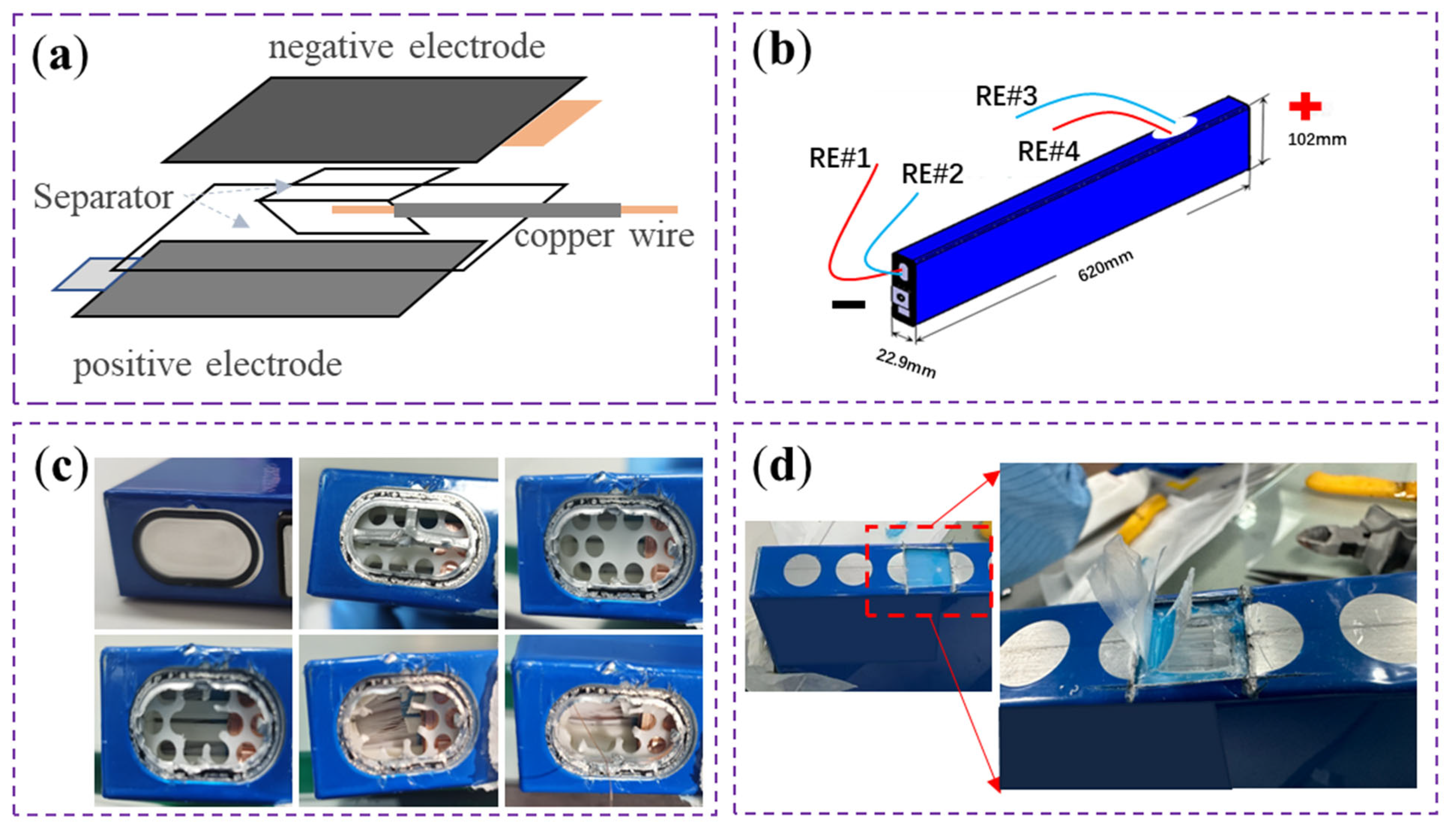
3.1. Reference Electrode Implantation, Activation, and Stability Testing
3.2. OLFEM Parameter Calibration and Validation
4. Results and Discussions
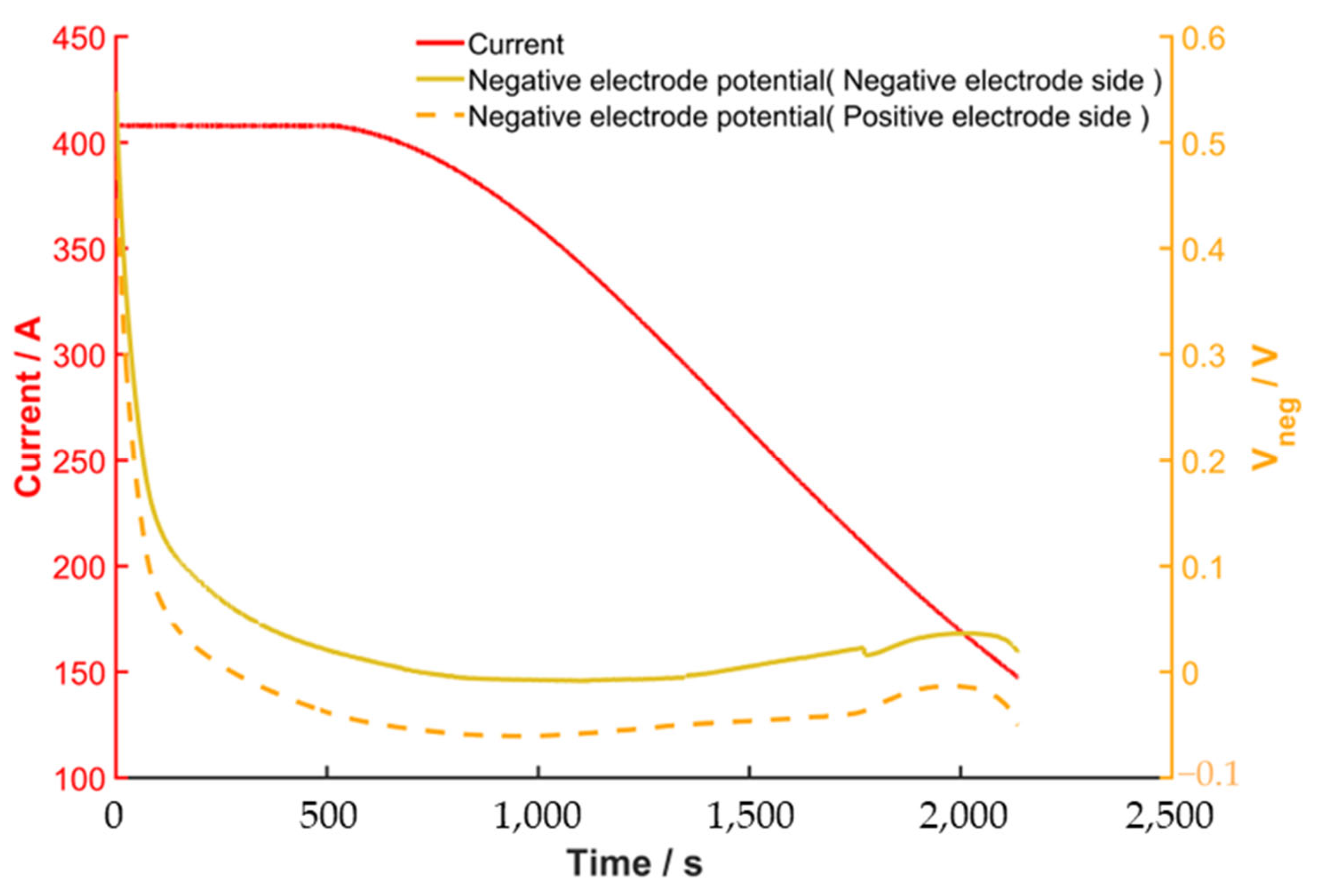
4.1. Stability and Comparison of Negative Electrode Potential Results on the Positive and Negative Sides
4.2. Validation of OLFEM
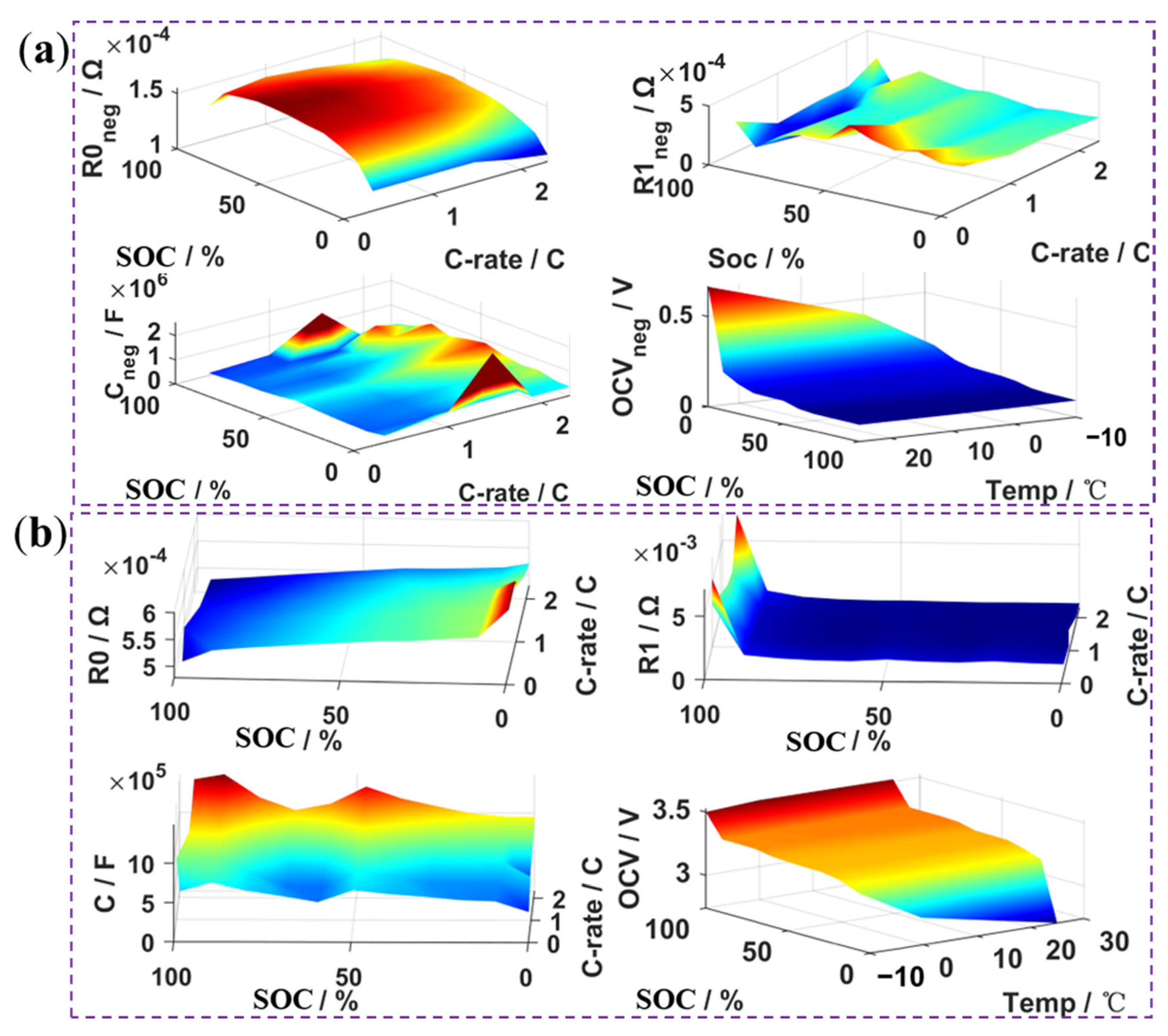
4.2.1. Results of Parameter Identification
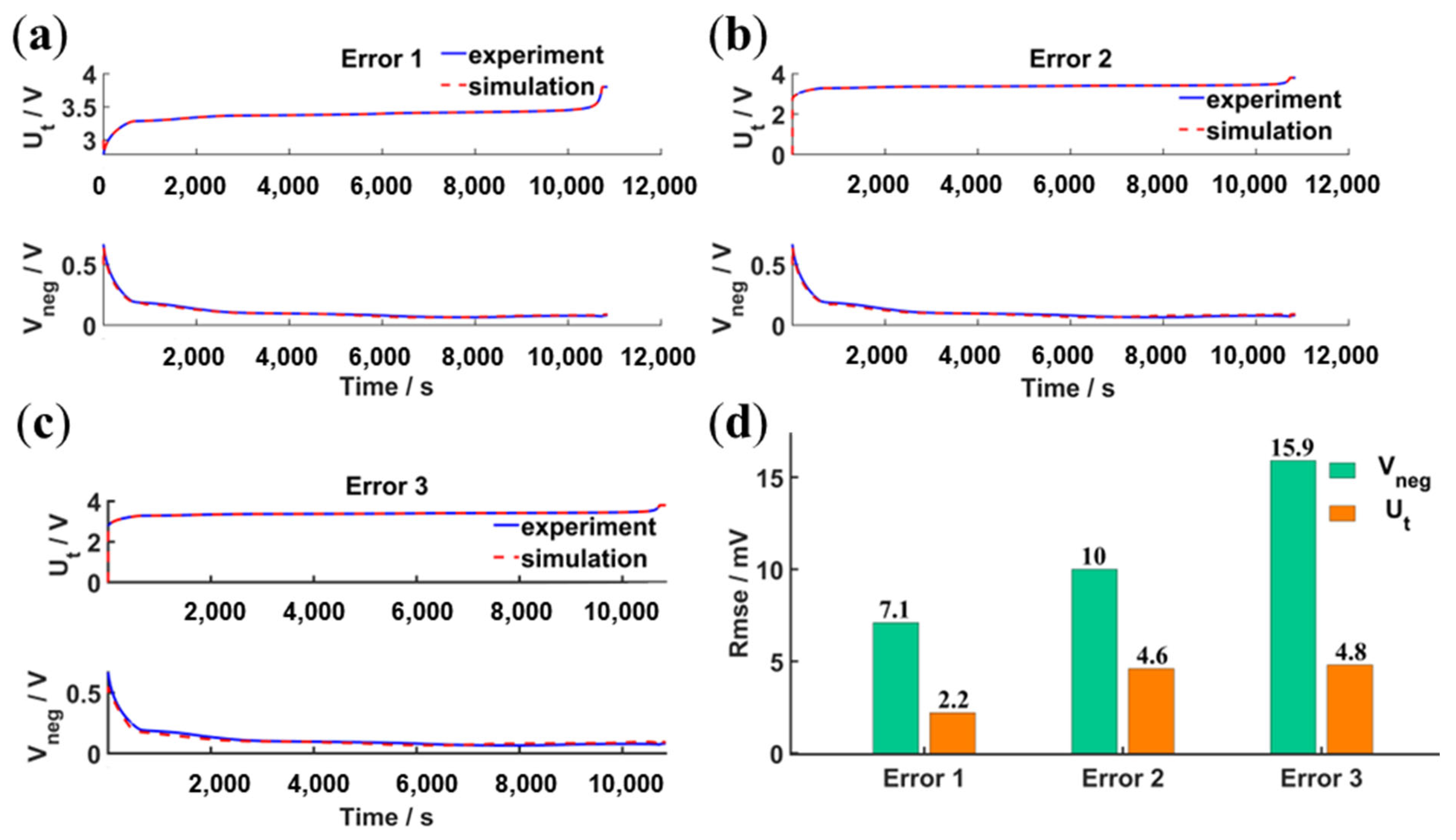
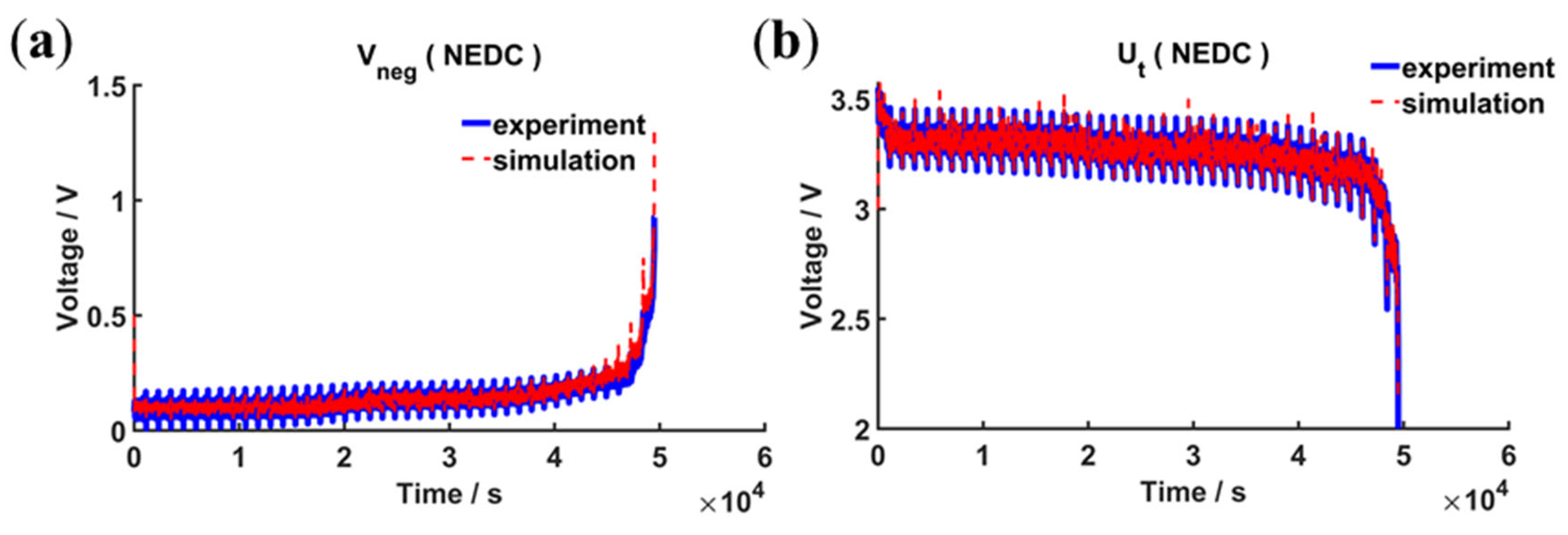
4.2.2. Validation under Static and Dynamic Operating Conditions
4.2.3. Model Analysis
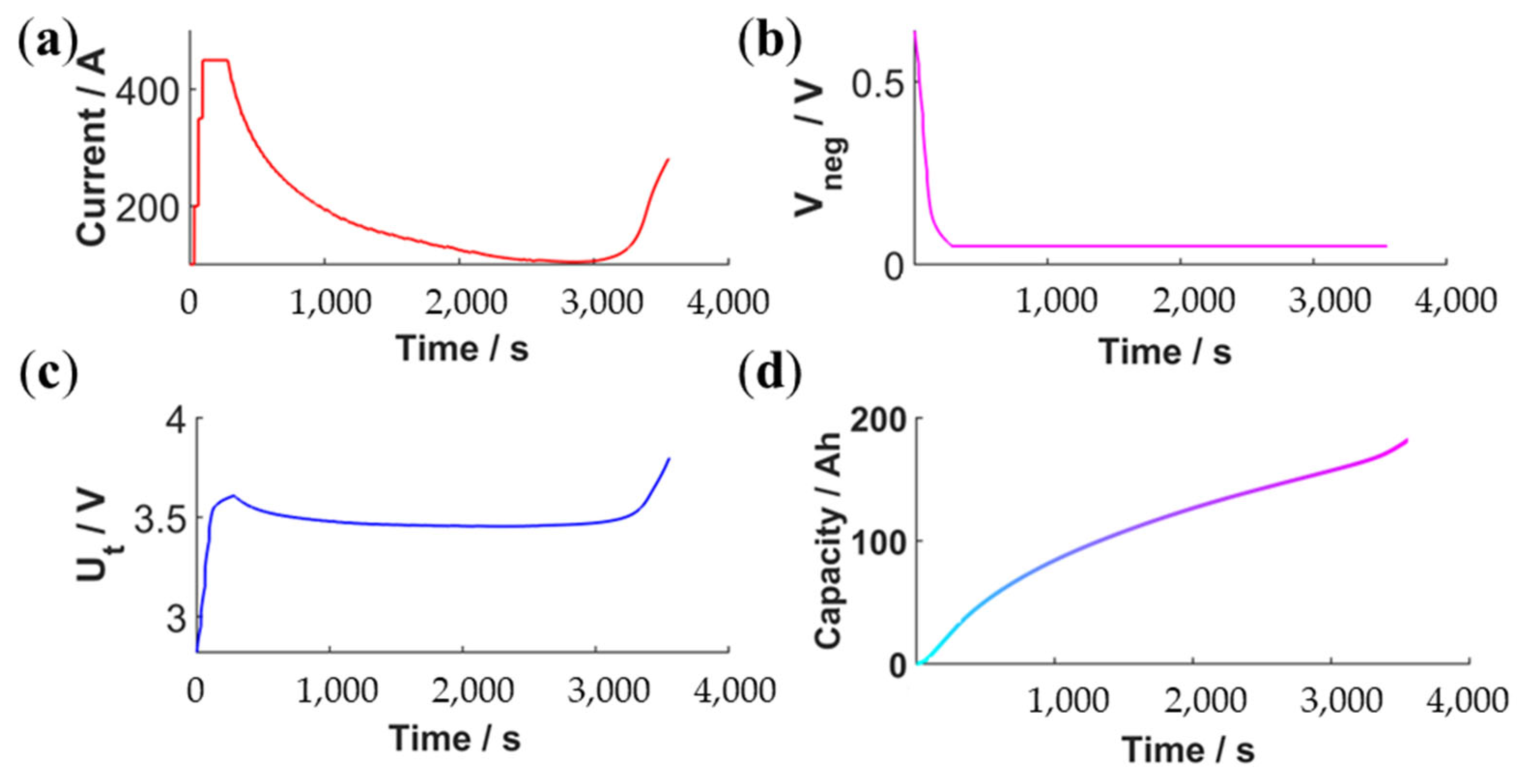
4.3. OLFEM-Based Fast-Charging Calibration and Cycle Verification
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harichandan, S.; Kar, S.K.; Bansal, R.; Mishra, S.K.; Balathanigaimani, M.S.; Dash, M. Energy transition research: A bibliometric mapping of current findings and direction for future research. Clean. Prod. Lett. 2022, 3, 100026. [Google Scholar] [CrossRef]
- Wang, G.; Chen, C.; Beshiwork, B.A.; Lin, B. Developing a low-carbon hybrid of ammonia fuel cell and internal combustion engine for carbon neutrality. Appl. Energy Combust. Sci. 2023, 16, 100214. [Google Scholar] [CrossRef]
- Cai, T.; Valecha, P.; Tran, V.; Engle, B.; Stefanopoulou, A.; Siegel, J. Detection of Li-ion battery failure and venting with Carbon Dioxide sensors. eTransportation 2021, 7, 100100. [Google Scholar] [CrossRef]
- Waseem, M.; Amir, M.; Lakshmi, G.S.; Harivardhagini, S.; Ahmad, M. Fuel Cell-based Hybrid Electric Vehicles: An Integrated Review of Current Status, Key Challenges, Recommended Policies, and Future Prospects. Green Energy Intell. Transp. 2023, 100121. [Google Scholar] [CrossRef]
- Wu, L.; Lyu, Z.; Huang, Z.; Zhang, C.; Wei, C. Physics-based battery SOC estimation methods: Recent advances and future perspectives. J. Energy Chem. 2023, 89, 27–40. [Google Scholar] [CrossRef]
- Liu, T.; Yang, X.-G.; Ge, S.; Leng, Y.; Wang, C.-Y. Ultrafast charging of energy-dense lithium-ion batteries for urban air mobility. eTransportation 2021, 7, 100103. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, B. Multi-objective optimization for fast charging design of lithium-ion batteries using constrained Bayesian optimization. J. Power Sources 2023, 584, 233602. [Google Scholar] [CrossRef]
- Zhong, C.; Weng, S.; Wang, Z.; Zhan, C.; Wang, X. Kinetic limits and enhancement of graphite anode for fast-charging lithium-ion batteries. Nano Energy 2023, 117, 108894. [Google Scholar] [CrossRef]
- Piao, N.; Gao, X.; Yang, H.; Guo, Z.; Hu, G.; Cheng, H.-M.; Li, F. Challenges and development of lithium-ion batteries for low temperature environments. eTransportation 2022, 11, 100145. [Google Scholar] [CrossRef]
- Tian, Y.; Lin, C.; Chen, X.; Yu, X.; Xiong, R.; Zhang, Q. Reversible lithium plating on working anodes enhances fast charging capability in low-temperature lithium-ion batteries. Energy Storage Mater. 2023, 56, 412–423. [Google Scholar] [CrossRef]
- Yang, Z.; Charalambous, H.; Lin, Y.; Trask, S.E.; Yu, L.; Wen, J.; Jansen, A.; Tsai, Y.; Wiaderek, K.M.; Ren, Y.; et al. Extreme fast charge aging: Correlation between electrode scale and heterogeneous degradation in Ni-rich layered cathodes. J. Power Sources 2022, 521, 230961. [Google Scholar] [CrossRef]
- Chinnam, P.R.; Tanim, T.R.; Dufek, E.J.; Dickerson, C.C.; Li, M. Sensitivity and reliability of key electrochemical markers for detecting lithium plating during extreme fast charging. J. Energy Storage 2022, 46, 103782. [Google Scholar] [CrossRef]
- Mei, W.; Zhang, L.; Sun, J.; Wang, Q. Experimental and numerical methods to investigate the overcharge caused lithium plating for lithium ion battery. Energy Storage Mater. 2020, 32, 91–104. [Google Scholar] [CrossRef]
- Liu, J.; Peng, W.; Yang, M.; Jin, K.; Liu, P.; Sun, J.; Wang, Q. Quantitative analysis of aging and detection of commercial 18650 lithium-ion battery under slight overcharging cycling. J. Clean. Prod. 2022, 340, 130756. [Google Scholar] [CrossRef]
- Gao, Z.H.; Xie, H.C.; Yu, H.Q.; Ma, B.; Liu, X.H.; Chen, S.Y. Study on Lithium-Ion Battery Degradation Caused by Side Reactions in Fast-Charging Process. Front. Energy Res. 2022, 10, 905710. [Google Scholar] [CrossRef]
- Hein, S.; Danner, T.; Latz, A. An Electrochemical Model of Lithium Plating and Stripping in Lithium Ion Batteries. ACS Appl. Energy Mater. 2020, 3, 8519–8531. [Google Scholar] [CrossRef]
- You, H.; Jiang, B.; Zhu, J.; Wang, X.; Shi, G.; Han, G.; Wei, X.; Dai, H. In-situ quantitative detection of irreversible lithium plating within full-lifespan of lithium-ion batteries. J. Power Sources 2023, 564, 232892. [Google Scholar] [CrossRef]
- Liu, Z.; Li, K.; Zhang, W.; Xie, Y.; Liu, J.; Sun, L.; Zan, J. Research on safe charging strategy of lithium-ion battery based on three-electrode equivalent circuit model. J. Energy Storage 2023, 72, 108563. [Google Scholar] [CrossRef]
- Gao, X.-L.; Liu, X.-H.; Xie, W.-L.; Zhang, L.-S.; Yang, S.-C. Multiscale observation of Li plating for lithium-ion batteries. Rare Met. 2021, 40, 3038–3048. [Google Scholar] [CrossRef]
- Al-Haj Hussein, A.; Batarseh, I. A Review of Charging Algorithms for Nickel and Lithium Battery Chargers. IEEE Trans. Veh. Technol. 2011, 60, 830–838. [Google Scholar] [CrossRef]
- Liu, Y.H.; Teng, J.H.; Lin, Y.C. Search for an Optimal Rapid Charging Pattern for Lithium–Ion Batteries Using Ant Colony System Algorithm. IEEE Trans. Ind. Electron. 2005, 52, 1328–1336. [Google Scholar] [CrossRef]
- Rangarajan, S.P.; Barsukov, Y.; Mukherjee, P.P. Anode potential controlled charging prevents lithium plating. J. Mater. Chem. A 2020, 8, 13077–13085. [Google Scholar] [CrossRef]
- Epding, B.; Rumberg, B.; Mense, M.; Jahnke, H.; Kwade, A. Aging-Optimized Fast Charging of Lithium Ion Cells Based on Three-Electrode Cell Measurements. Energy Technol. 2020, 8, 2000457. [Google Scholar] [CrossRef]
- Liu, J.; Chu, Z.; Li, H.; Ren, D.; Zheng, Y.; Lu, L.; Han, X.; Ouyang, M. Lithium-plating-free fast charging of large-format lithium-ion batteries with reference electrodes. Int. J. Energy Res. 2021, 45, 7918–7932. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z.; He, J.; Yu, S. Lithium battery state-of-health estimation and remaining useful lifetime prediction based on non-parametric aging model and particle filter algorithm. eTransportation 2022, 11, 100156. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Jokar, A.; Rajabloo, B.; Désilets, M.; Lacroix, M. Review of simplified Pseudo-two-Dimensional models of lithium-ion batteries. J. Power Sources 2016, 327, 44–55. [Google Scholar] [CrossRef]
- Li, J.; Adewuyi, K.; Lotfi, N.; Landers, R.G.; Park, J. A single particle model with chemical/mechanical degradation physics for lithium ion battery State of Health (SOH) estimation. Appl. Energy 2018, 212, 1178–1190. [Google Scholar] [CrossRef]
- Wu, M.Y.; Qin, L.L.; Wu, G. State of power estimation of power lithium-ion battery based on an equivalent circuit model. J. Energy Storage 2022, 51, 104538. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, D.; Cheng, J.; Wang, B.; Luk, P.C.K. An improved Thevenin model of lithium-ion battery with high accuracy for electric vehicles. Appl. Energy 2019, 254, 113615. [Google Scholar] [CrossRef]
- Zhang, C.; Allafi, W.; Dinh, Q.; Ascencio, P.; Marco, J. Online estimation of battery equivalent circuit model parameters and state of charge using decoupled least squares technique. Energy 2018, 142, 678–688. [Google Scholar] [CrossRef]
- Zhao, T.Z.; Zheng, Y.J.; Liu, J.H.; Zhou, X.; Chu, Z.Y.; Han, X.B. A study on half-cell equivalent circuit model of lithium-ion battery based on reference electrode. Int. J. Energy Res. 2021, 45, 4155–4169. [Google Scholar] [CrossRef]
- Lu, Y.; Han, X.; Chu, Z.; Feng, X.; Qin, Y.; Ouyang, M.; Lu, L. A decomposed electrode model for real-time anode potential observation of lithium-ion batteries. J. Power Sources 2021, 513, 230529. [Google Scholar] [CrossRef]
- Chen, D.; Gao, W.; Zhang, C.; Chen, L. SOC estimation of lithium battery based on double modified ampere-hour integral method. In Proceedings of the 2022 37th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Beijing, China, 19–20 November 2022; pp. 1093–1098. [Google Scholar]
- Mao, S.; Han, X.; Lu, Y.; Wang, D.; Su, A.; Lu, L.; Feng, X.; Ouyang, M. Multi sensor fusion methods for state of charge estimation of smart lithium-ion batteries. J. Energy Storage 2023, 72, 108736. [Google Scholar] [CrossRef]
- Drees, R.; Lienesch, F.; Kurrat, M. Fast Charging Formation of Lithium-Ion Batteries Based on Real-Time Negative Electrode Voltage Control. Energy Technol. 2022, 11, 2200868. [Google Scholar] [CrossRef]
- Rahman, A.; Lin, X. Li-ion battery individual electrode state of charge and degradation monitoring using battery casing through auto curve matching for standard CCCV charging profile. Appl. Energy 2022, 321, 119367. [Google Scholar] [CrossRef]
- Bohinsky, A.; Rangarajan, S.P.; Barsukov, Y.; Mukherjee, P. Preventing lithium plating under extremes: An untold tale of two electrodes. J. Mater. Chem. A 2021, 9, 17249–17260. [Google Scholar] [CrossRef]
- Zou, B.; Xiong, M.; Wang, H.; Ding, W.; Jiang, P.; Hua, W.; Zhang, Y.; Zhang, L.; Wang, W.; Tan, R. A Deep Learning Approach for State-of-Health Estimation of Lithium-Ion Batteries Based on a Multi-Feature and Attention Mechanism Collaboration. Batteries 2023, 9, 329. [Google Scholar] [CrossRef]
- Chen, Y.; Xiong, H.; Guo, Y. SOC Estimation of Lithium-ion Batteries at Different Temperatures. J. Phys. Conf. Ser. 2022, 2401, 012055. [Google Scholar] [CrossRef]



| Test | Temperature/°C | Details |
|---|---|---|
| Capacity | 25 | 1/3 C CC-CV charge, 1/3 C discharge |
| HPPC | 25 | Pulse rates include 0.33 C, 1 C, 1.5 C, 1.9 C and 2.3 C |
| HPPC | 0 | Pulse rates include 0.1 C, 0.3 C and 0.55 C |
| HPPC | −10 | Pulse rates include 0.05 C, 0.1 C and 0.22 C |
| MRCC | 25 | 0.167 C, 0.33 C, 0.5 C, 1 C, 1.5 C, 1.9 C and 2.3 C CC charge |
| MRCC | 0 | 0.1 C, 0.3 C and 0.55 C CC charge |
| MRCC | −10 | 0.05 C, 0.1 C and 0.22 C CC charge |
| NEDC | 25 | Maximum charge rate 1.23 C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Mao, S.; Chen, Q.; Chen, F.; Zhang, X.; Ouyang, M.; Han, X.; Zheng, Y. Online Fast Charging Model without Lithium Plating for Long-Dimensional Cells in Automotive Applications. Batteries 2023, 9, 563. https://doi.org/10.3390/batteries9120563
Wang Y, Mao S, Chen Q, Chen F, Zhang X, Ouyang M, Han X, Zheng Y. Online Fast Charging Model without Lithium Plating for Long-Dimensional Cells in Automotive Applications. Batteries. 2023; 9(12):563. https://doi.org/10.3390/batteries9120563
Chicago/Turabian StyleWang, Yu, Shuoyuan Mao, Quanwei Chen, Fei Chen, Xue Zhang, Minggao Ouyang, Xuebing Han, and Yuejiu Zheng. 2023. "Online Fast Charging Model without Lithium Plating for Long-Dimensional Cells in Automotive Applications" Batteries 9, no. 12: 563. https://doi.org/10.3390/batteries9120563
APA StyleWang, Y., Mao, S., Chen, Q., Chen, F., Zhang, X., Ouyang, M., Han, X., & Zheng, Y. (2023). Online Fast Charging Model without Lithium Plating for Long-Dimensional Cells in Automotive Applications. Batteries, 9(12), 563. https://doi.org/10.3390/batteries9120563







