Hybrid Estimation Method for the State of Charge of Lithium Batteries Using a Temporal Convolutional Network and XGBoost
Abstract
:1. Introduction
- In the TCN part, the long-effective memory feature enables the learning of sequential battery parameters. Additionally, it facilitates the extraction of battery parameter features, enabling the model to learn the changing characteristics of batteries.
- An information layer is employed to interface the TCN part with the XGBoost part. The information layer determines how much past information from the output of the TCN part to incorporate and transforms the output values into a one-dimensional (1D) sequence data format.
- The output of the information layer is used as the input of XGBoost. XGBoost involves learning using a boosting algorithm, and it contributes to reducing errors in the SOC estimated through a strong generalization model. This is confirmed through the experimental results.
2. Proposed Lithium Battery SOC Estimation Algorithm Using the TCN-XGBoost Hybrid Model
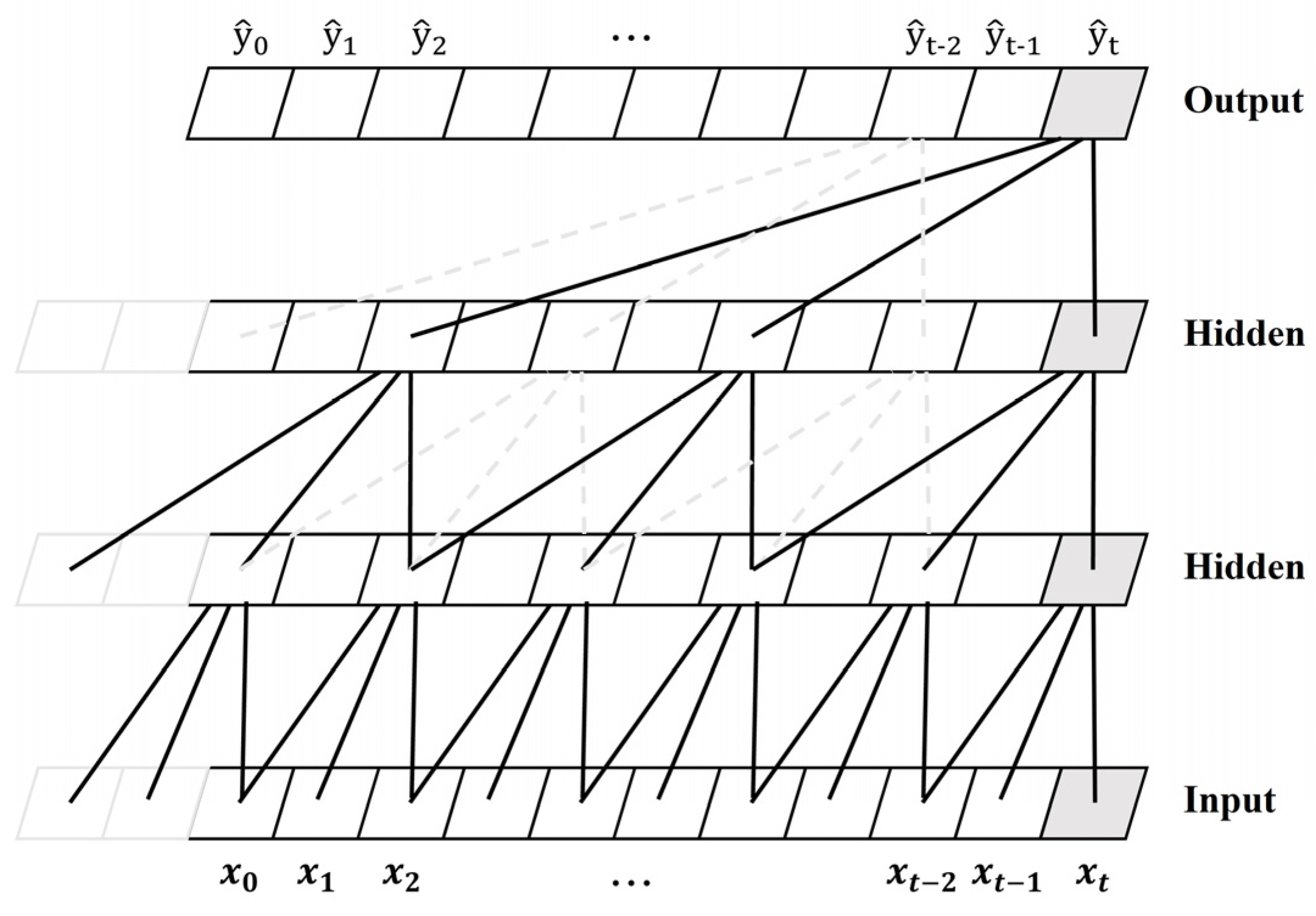
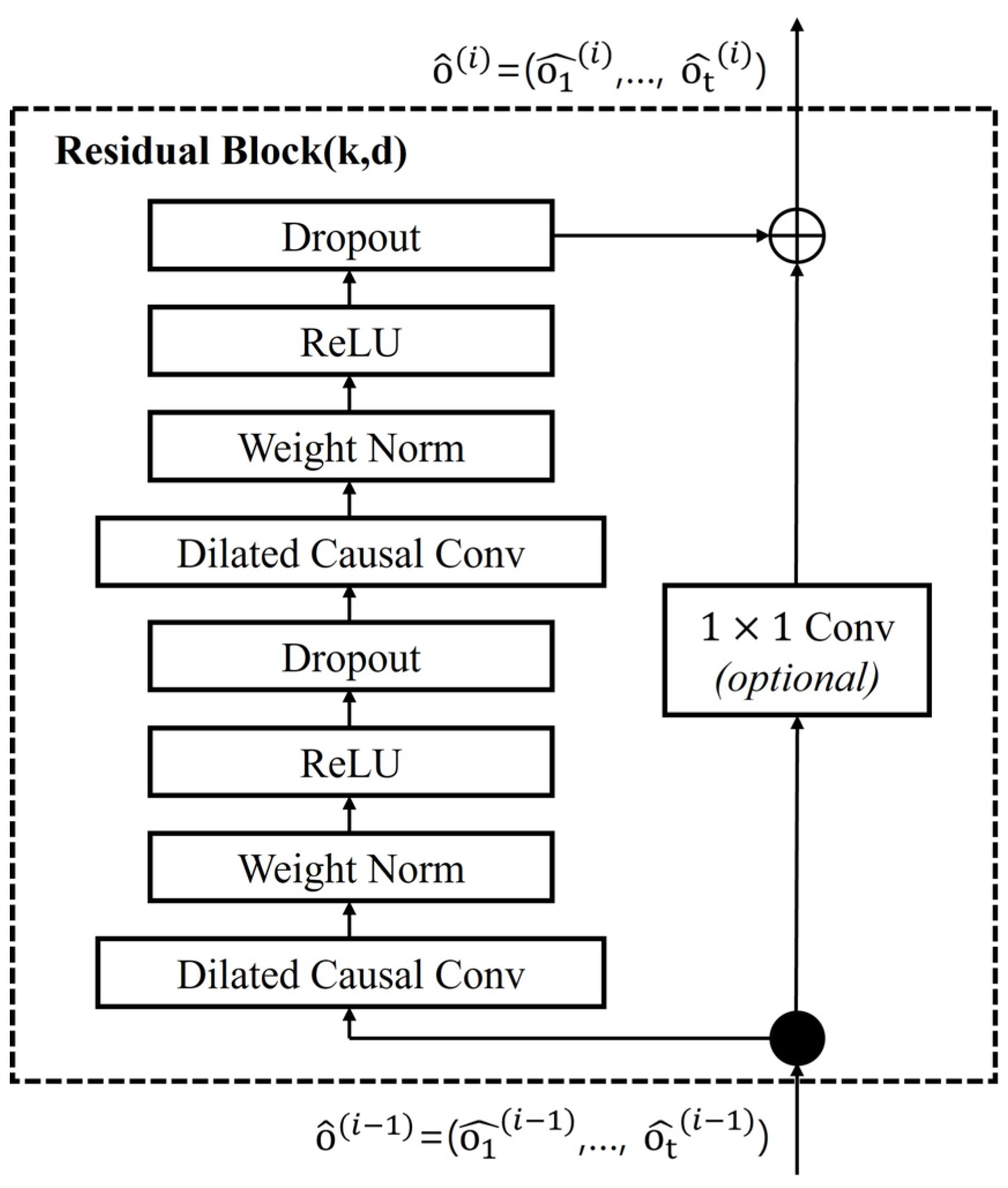
2.1. TCN
2.2. XGBoost
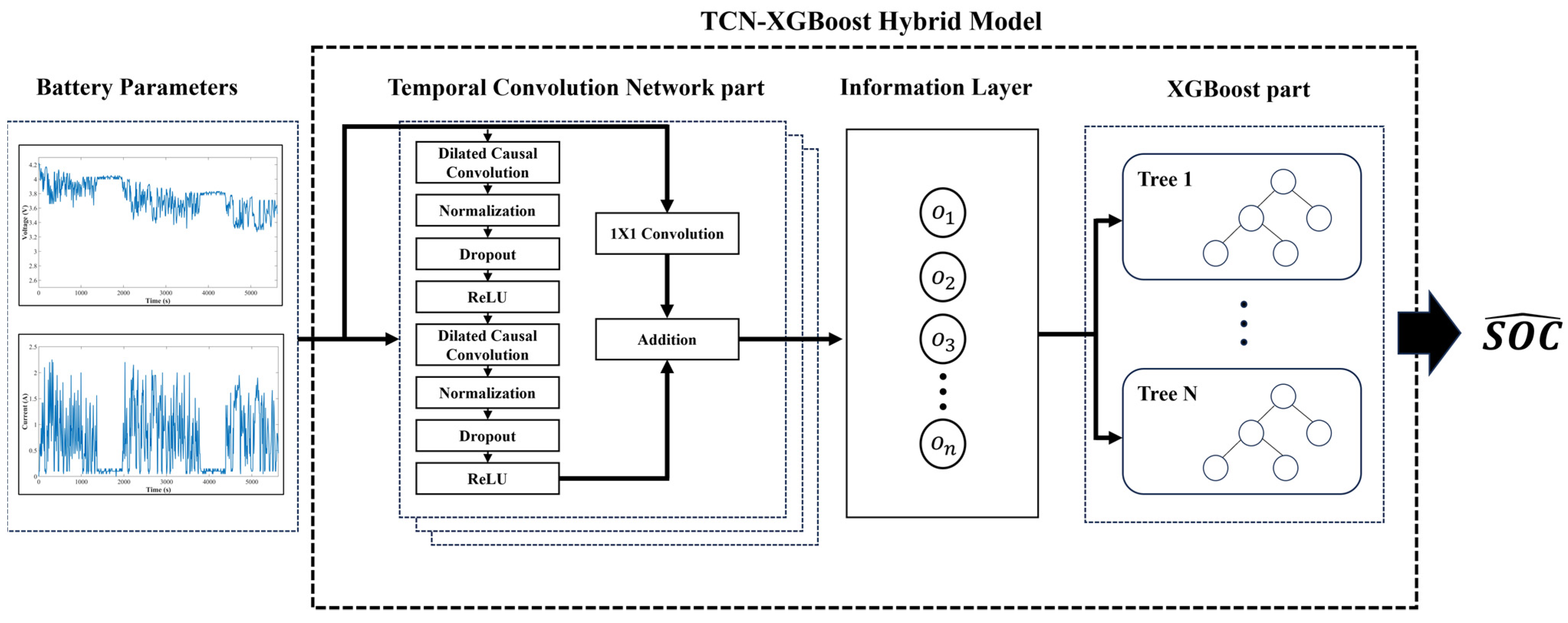
2.3. Proposed TCN-XGBoost Hybrid Model
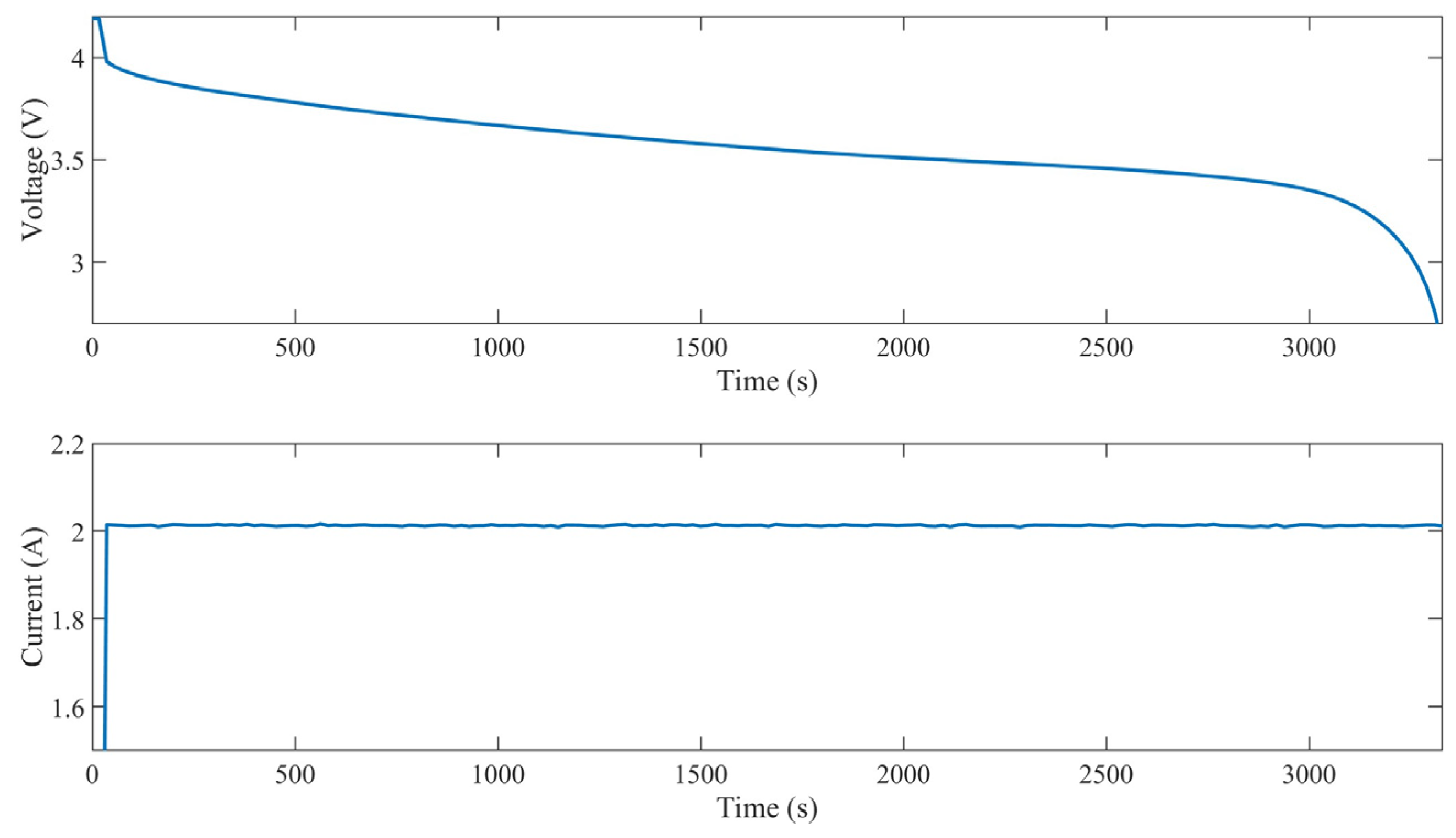
- To use the battery data as input to the proposed model, the data were set in sequence. Voltage, current, temperature, and operation time were used as input parameters.
- The input data were used as the input for TCN, and the output of TCN was obtained using the dilated convolution operation in Equation (2) and the activation function in Equation (3). Herein, the ReLU function was used as the activation function.
- The information layer determines how much past information from the output of TCN to use. For instance, if n pieces of past information are chosen, the sequential data , , …, , are used as inputs for the subsequent XGBoost model.
- The information layer transfers the data to XGBoost, and XGBoost ultimately estimates the SOC based on Equation (7).
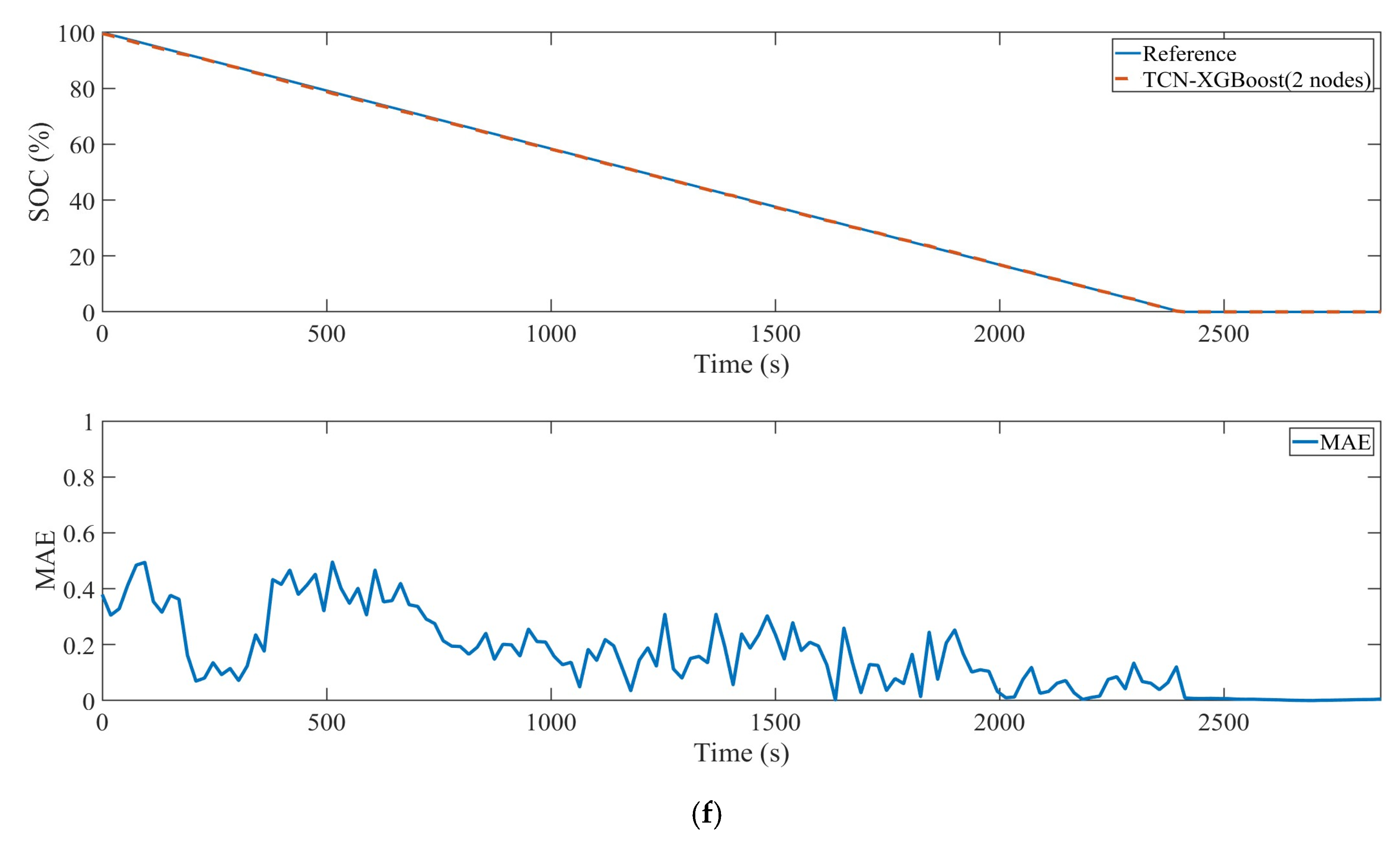
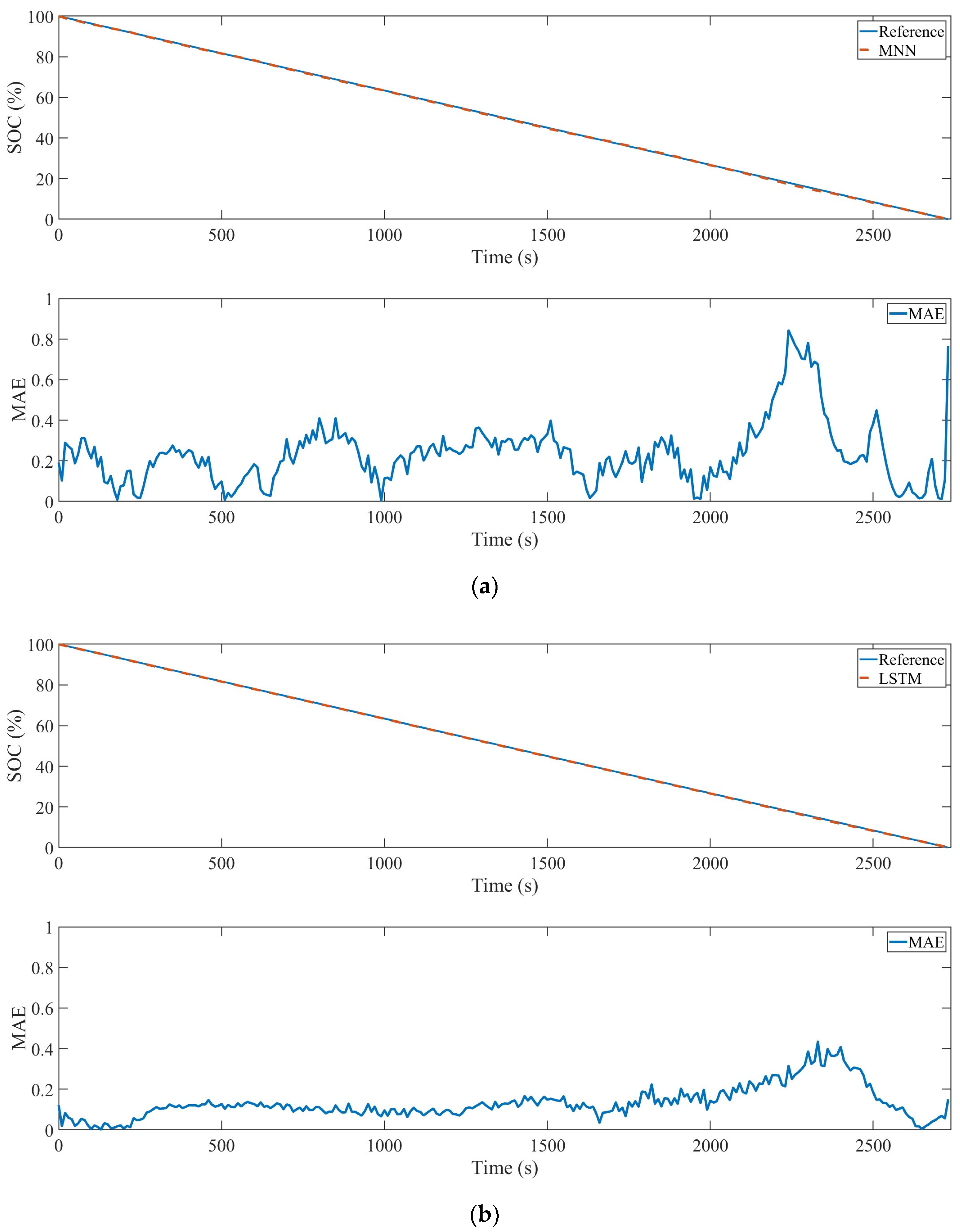
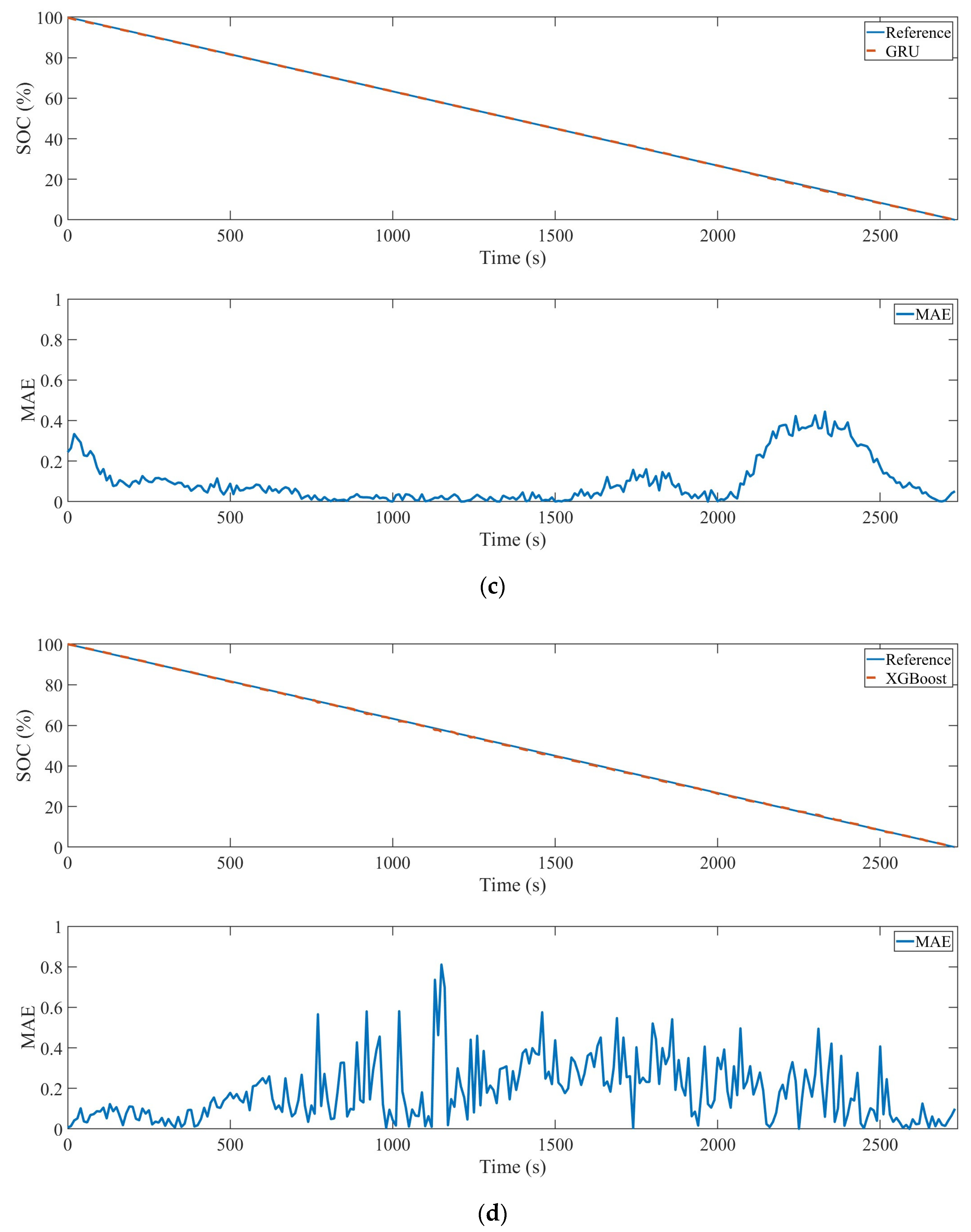
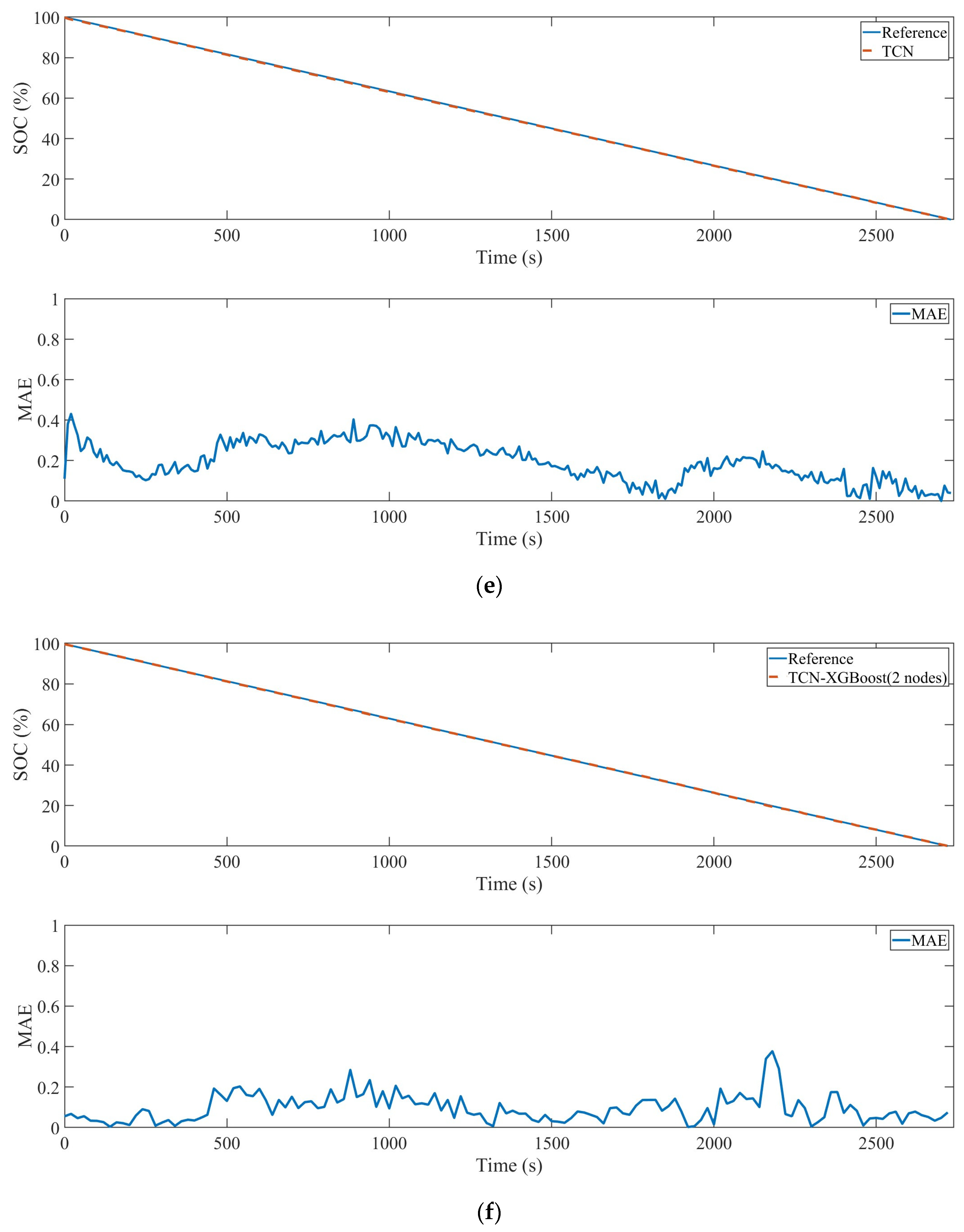
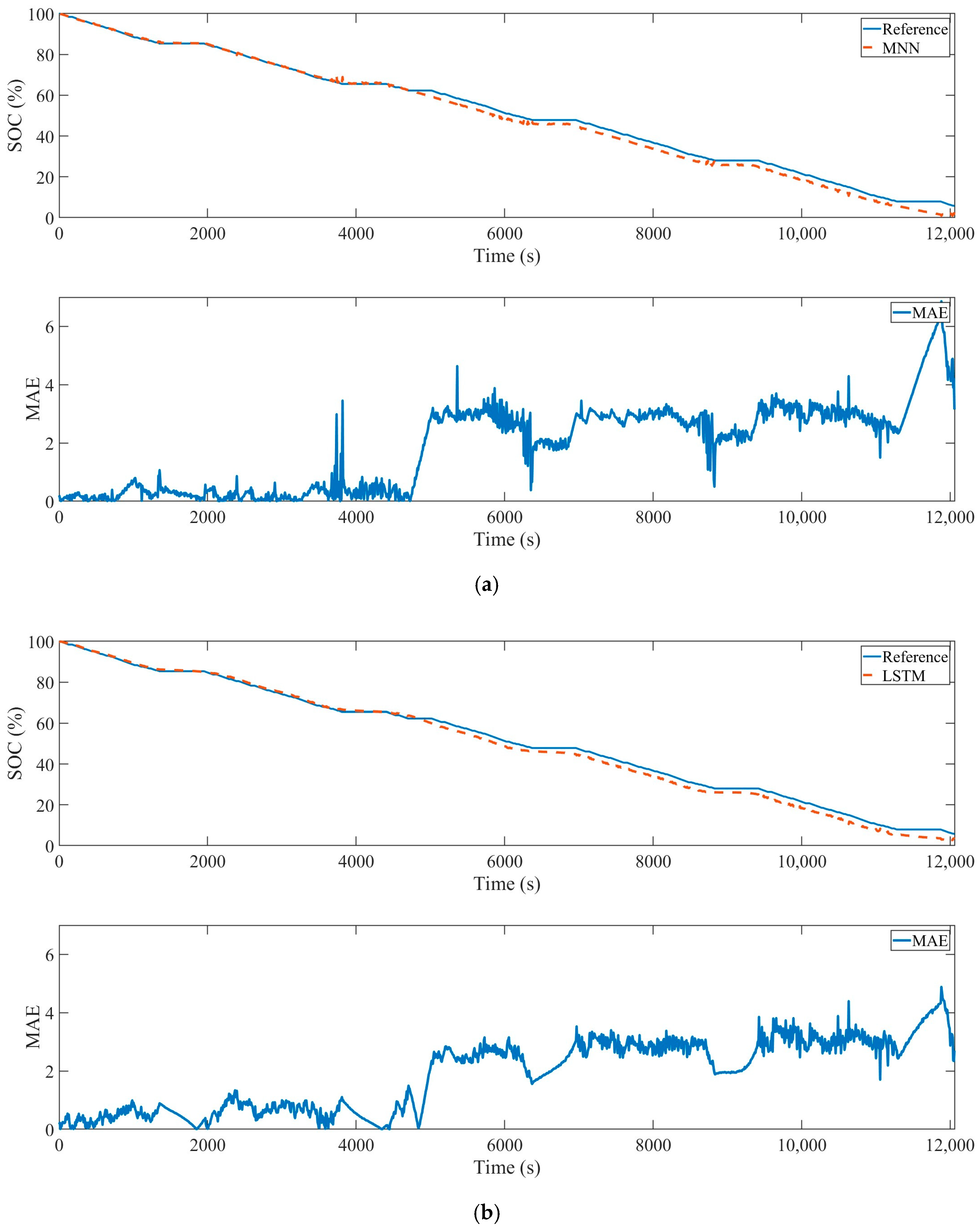
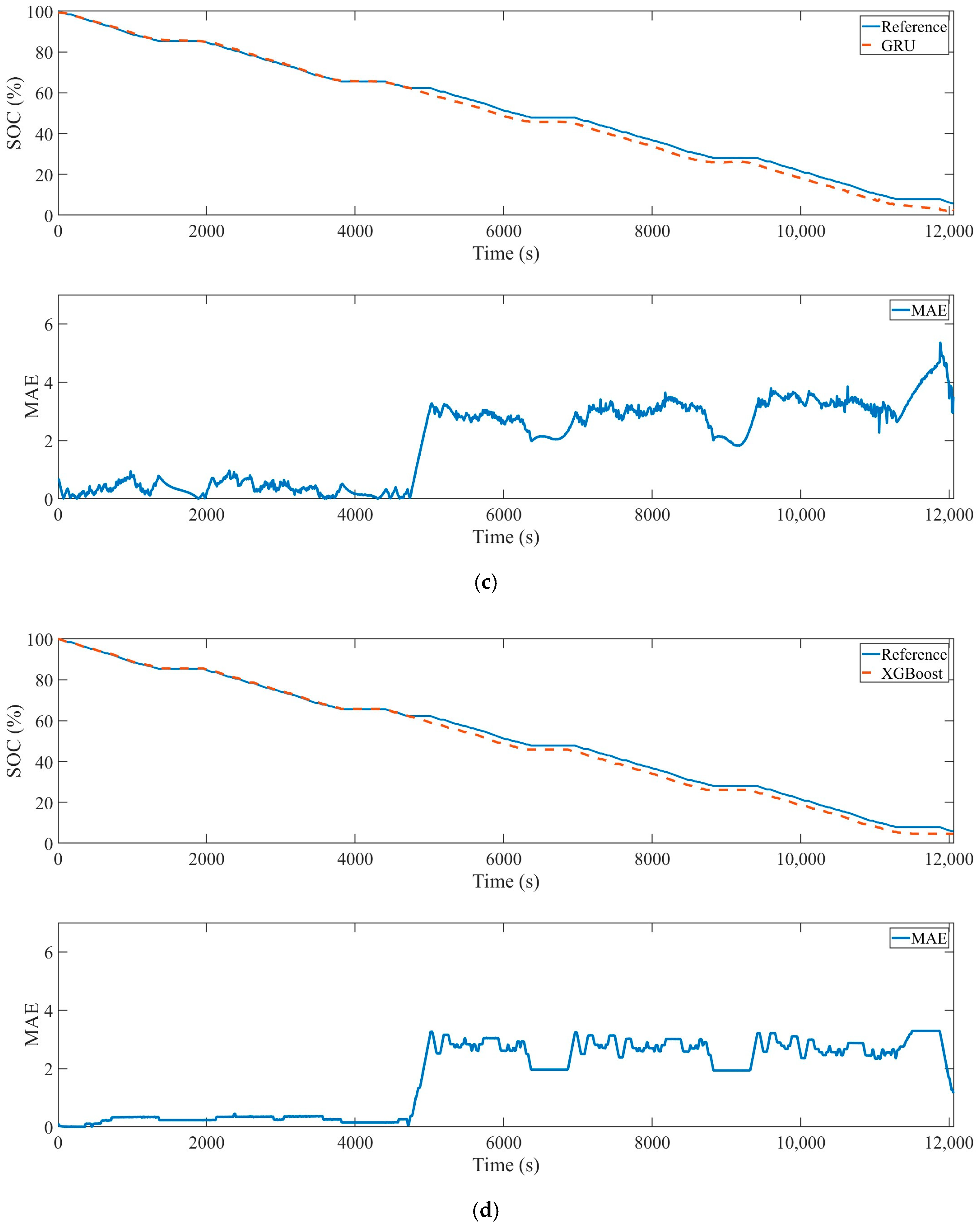
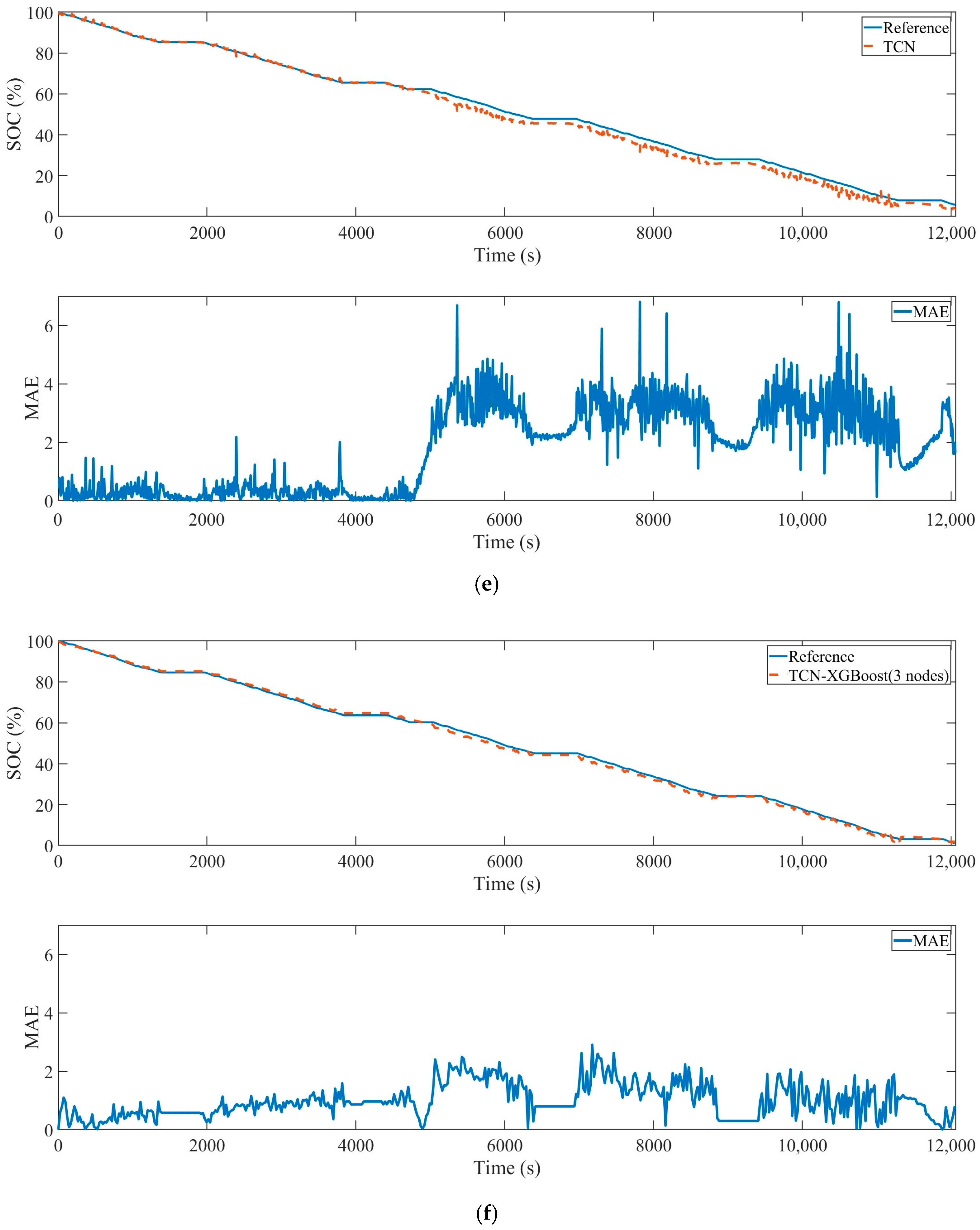
3. Experiments and Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, J.; Zhang, Y.; Wu, J.; Cheng, W.; Zhu, Q. SOC estimation for lithium-ion battery using the LSTM-RNN with extended input and constrained output. Energy 2023, 262, 125375. [Google Scholar] [CrossRef]
- Luo, K.; Chen, X.; Zheng, H.; Shi, Z. A review of deep learning approach to predicting the state of health and state of charge of lithium-ion batteries. J. Energy Chem. 2022, 74, 159–173. [Google Scholar] [CrossRef]
- Lai, X.; Yao, J.; Jin, C.; Feng, X.; Wang, H.; Xu, C.; Zheng, Y. A review of lithium-ion battery failure hazards: Test standards, accident analysis, and safety suggestions. Batteries 2022, 8, 248. [Google Scholar] [CrossRef]
- Wang, Q.; Mao, B.; Stoliarov, S.I.; Sun, J. A review of lithium ion battery failure mechanisms and fire prevention strategies. Prog. Energy Combust. Sci. 2019, 73, 95–131. [Google Scholar] [CrossRef]
- Park, J.H.; Lee, J.H.; Kim, S.J.; Lee, I.S. Real-time state of charge estimation for each cell of lithium battery pack using neural networks. Appl. Sci. 2020, 10, 8644. [Google Scholar] [CrossRef]
- Seh, Z.W.; Sun, Y.; Zhang, Q.; Cui, Y. Designing high-energy lithium–sulfur batteries. Chem. Soc. Rev. 2016, 45, 5605–5634. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Shen, M.; Gao, Q. A review on battery management system from the modeling efforts to its multiapplication and integration. Int. J. Energy Res. 2019, 43, 5042–5075. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Cao, P.; Zhu, T.; Shu, H.; Chen, J.; Zhang, J.; Zhu, J. Classification, summarization and perspectives on state-of-charge estimation of lithium-ion batteries used in electric vehicles: A critical comprehensive survey. J. Energy Storage 2021, 39, 102572. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- How, D.N.T.; Hannan, M.A.; Hossain Lipu, M.S.; Ker, P.J. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: A review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]
- Corno, M.; Bhatt, N.; Savaresi, S.M.; Verhaegen, M. Electrochemical model-based state of charge estimation for Li-ion cells. IEEE Trans. Control Syst. Technol. 2014, 23, 117–127. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Sun, F.; Hu, X.; Zou, Y.; Li, S. Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles. Energy 2011, 36, 3531–3540. [Google Scholar] [CrossRef]
- Wu, B.; Han, S.; Shin, K.G.; Lu, W. Application of artificial neural networks in design of lithium-ion batteries. J. Power Sources 2018, 395, 128–136. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long short-term memory networks for accurate state-of-charge estimation of Li-ion batteries. IEEE Trans. Ind. Electron. 2017, 65, 6730–6739. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The co-estimation of state of charge, state of health, and state of function for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2017, 67, 92–103. [Google Scholar] [CrossRef]
- Barai, A.; Widanage, W.D.; Marco, J.; McGordon, A.; Jennings, P. A study of the open circuit voltage characterization technique and hysteresis assessment of lithium-ion cells. J. Power Sources 2015, 295, 99–107. [Google Scholar] [CrossRef]
- Ng, M.F.; Zhao, J.; Yan, Q.; Conduit, G.J.; Seh, Z.W. Predicting the state of charge and health of batteries using data-driven machine learning. Nat. Mach. Intell. 2020, 2, 161–170. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef]
- Attia, P.M.; Grover, A.; Jin, N.; Severson, K.A.; Markov, T.M.; Liao, Y.H.; Chen, M.H.; Cheong, B.; Perkins, N.; Yang, Z.; et al. Closed-loop optimization of fast-charging protocols for batteries with machine learning. Nature 2020, 578, 397–402. [Google Scholar] [CrossRef] [PubMed]
- Ng, K.S.; Moo, C.S.; Chen, Y.P.; Hsieh, Y. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Truchot, C.; Dubarry, M.; Liaw, B.Y. State-of-charge estimation and uncertainty for lithium-ion battery strings. Appl. Energy 2014, 119, 218–227. [Google Scholar] [CrossRef]
- Jang, K.W.; Chung, G.B. A SOC estimation using Kalman filter for lithium-polymer battery. Trans. Korean Inst. Power Electron. 2012, 17, 222–229. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Chen, Z.; He, H. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles. Appl. Energy 2014, 113, 463–476. [Google Scholar] [CrossRef]
- Rzepka, B.; Bischof, S.; Blank, T. Implementing an extended Kalman filter for SoC estimation of a Li-ion battery with hysteresis: A step-by-step guide. Energies 2021, 14, 3733. [Google Scholar] [CrossRef]
- Li, J.; Ye, M.; Gao, K.; Xu, X.; Wei, M.; Jiao, S. Joint estimation of state of charge and state of health for lithium-ion battery based on dual adaptive extended Kalman filter. Int. J. Energy Res. 2021, 45, 13307–13322. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modelling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Li, L.; Li, Y.; Mao, R.; Li, L.; Hua, W.; Zhang, J. Remaining useful life prediction for lithium-ion batteries with a hybrid model based on TCN-GRU-DNN and dual attention mechanism. IEEE Trans. Transp. Electrif. 2023, 9, 4726–4740. [Google Scholar] [CrossRef]
- Tianqi, C.; Carlos, G. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- An, J.; Guo, W.; Lv, T.; Zhao, Z.; He, C.; Zhao, H. Joint prediction of the state of charge and the state of health of lithium-ion batteries based on the PSO-XGBoost algorithm. Energies 2023, 16, 4243. [Google Scholar] [CrossRef]
- Popescu, M.C.; Balas, V.E.; Perescu-Popescu, L.; Mastorakis, N. Multilayer Perceptron and neural networks. WSEAS Trans. Circuits Syst. 2009, 8, 579–588. [Google Scholar]
- Staudemeyer, R.C.; Morris, E.R. Understanding LSTM—A tutorial into long short-term memory recurrent neural networks. arXiv 2019, arXiv:1909.09586. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using rnn encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Zhang, X.; Hou, J.; Wang, Z.; Jiang, Y. Joint SOH-SOC estimation model for lithium-ion batteries based on GWO-BP neural network. Energies 2022, 16, 132. [Google Scholar] [CrossRef]
- Li, J.; Jiang, Z.; Jiang, Y.; Song, W.; Gu, J. The state of charge estimation of lithium-ion battery based on battery capacity. J. Electrochem. Soc. 2022, 169, 120539. [Google Scholar] [CrossRef]
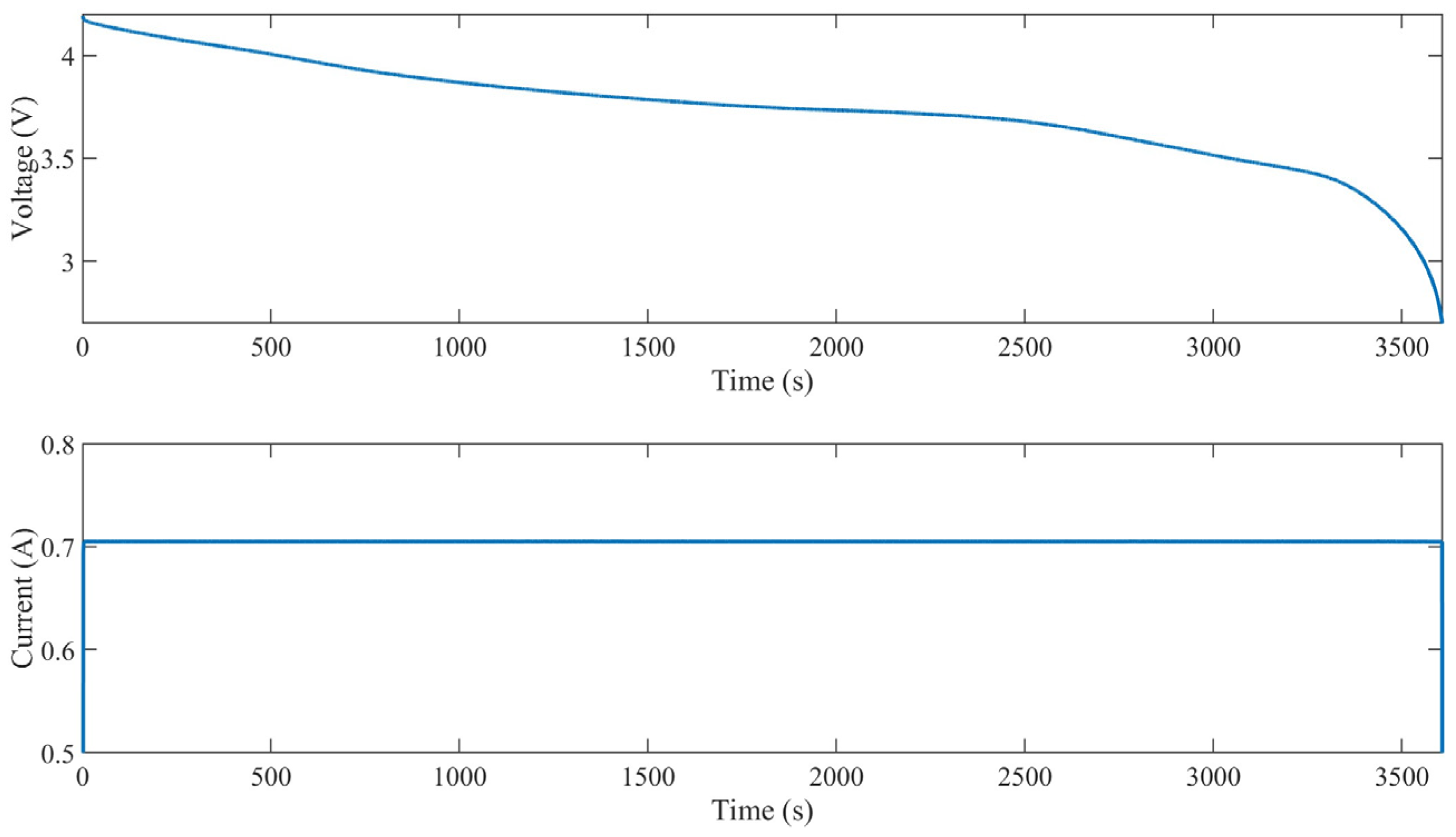
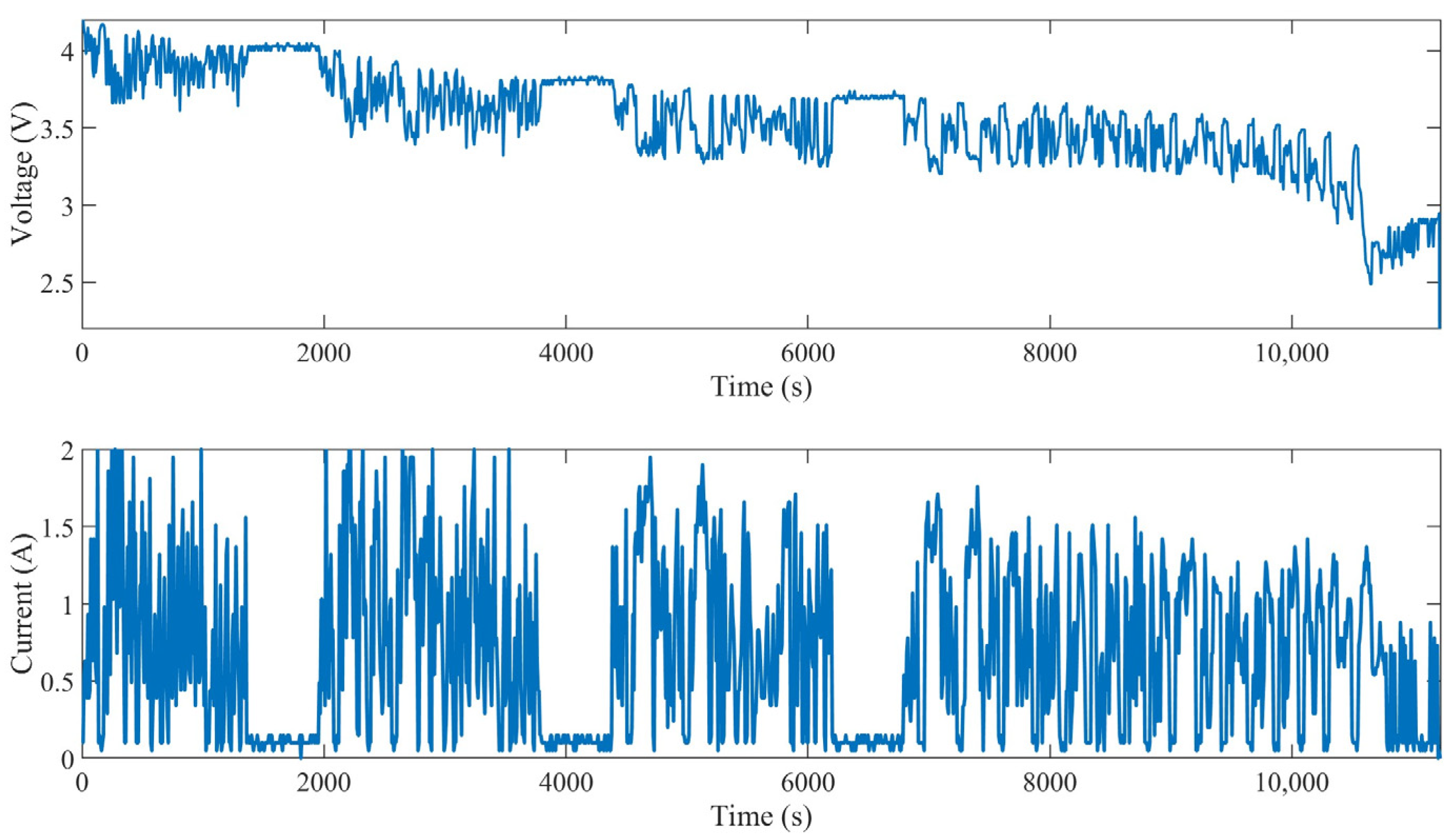
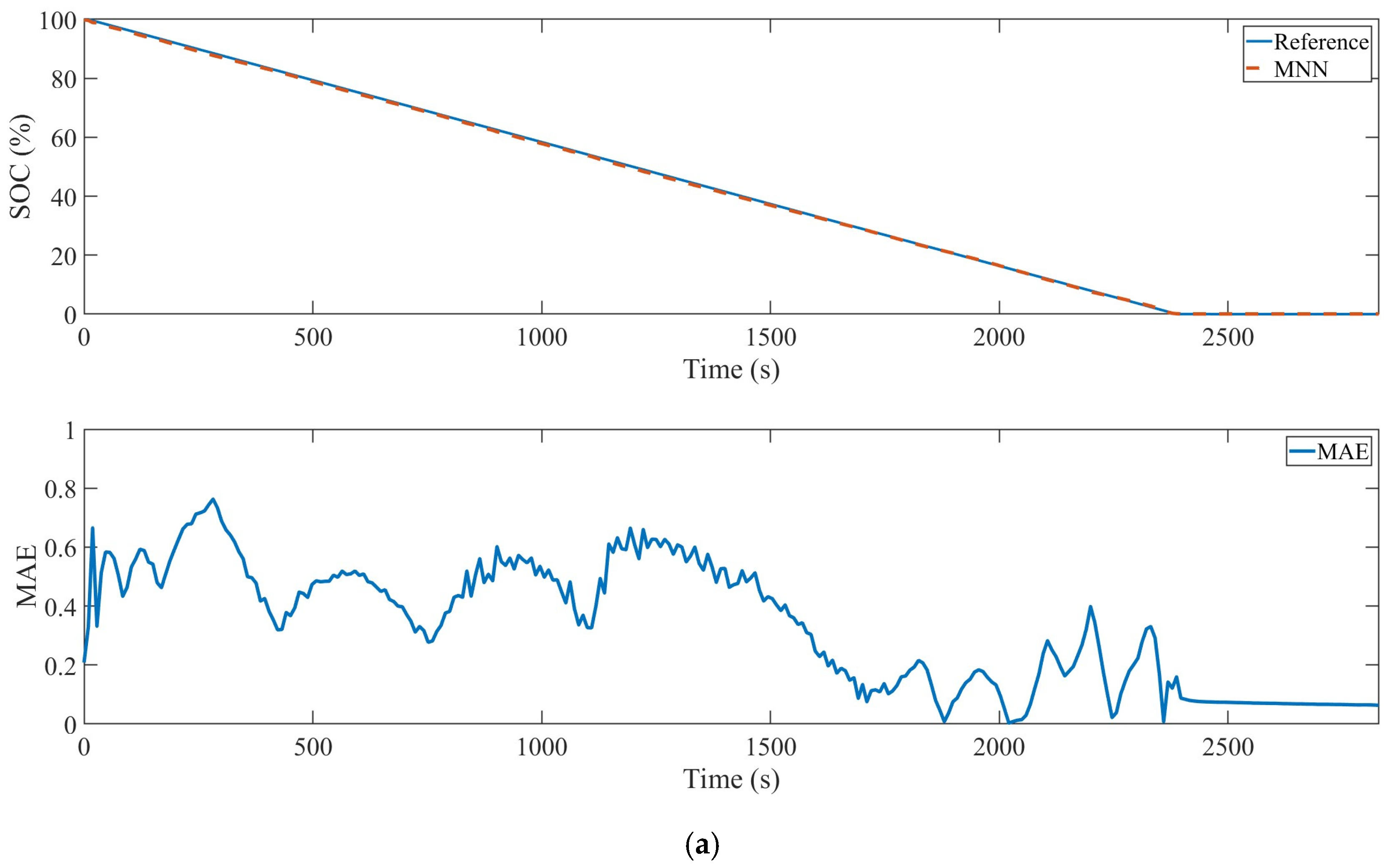
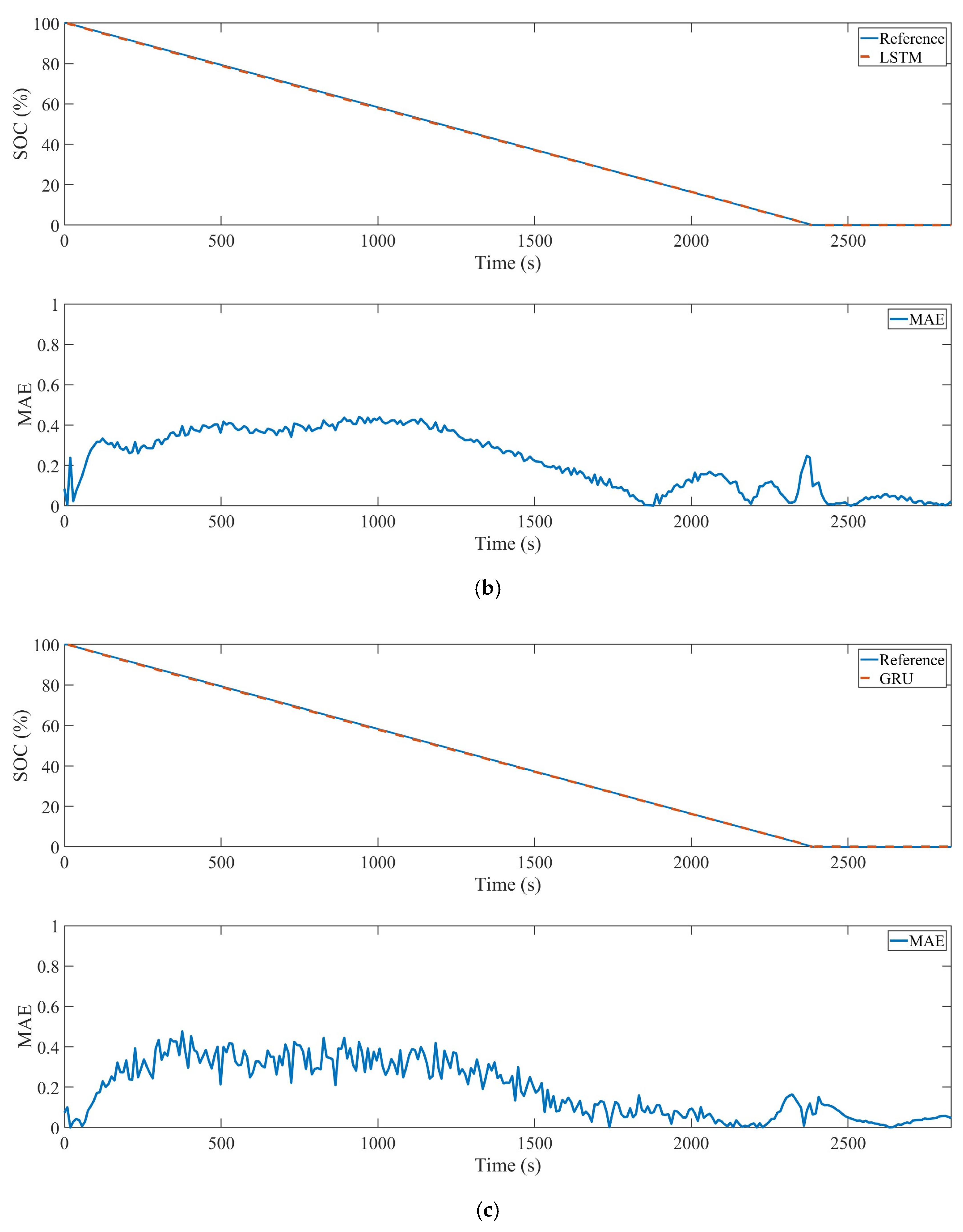

| Method | Advancements | Limitations | Exemplary Model |
|---|---|---|---|
| Model-based [12,13] | 1. Reliability and precision 2. Broad applicability | 1. Demands substantial domain expertise 2. Involves a protracted development period | 1. Equivalent circuit model 2. Electrochemical model 3. Kalman filter |
| Data-driven [14,15,16,17,18,19,20,21] | 1. Rapid development time 2. Minimal need for specialized knowledge | 1. Demands a significant volume of data | 1. Neural network 2. Deep learning 3. Look-up table |
| Coulomb counting [22,23] | Easy to implement | Accumulation of errors occurs over time | Coulomb counting |
| Model | Hyperparameter | Value |
|---|---|---|
| TCN | nb_filter | 128 |
| kernal_size | 3 | |
| nb_stack | 2 | |
| deliations | [1,2,4,8,16,32] | |
| padding | Causal | |
| use_skip_conections | Ture | |
| XGBoost | n_estimators | 1000 |
| max_depth | 5 | |
| gamma | 0 | |
| reg_alpha | 0 | |
| reg_lamda | 1 | |
| subsample | 0.75 | |
| learning rate | 0.001 | |
| MNN | hidden layer, one node | 64 |
| hidden layer, two nodes | 32 | |
| learning rate | 0.01 | |
| LSTM | LSTM layer, one node | 32 |
| LSTM layer, two nodes | 16 | |
| learning rate | 0.01 | |
| GRU | GRU layer, one node | 32 |
| GRU layer, two nodes | 16 | |
| learning rate | 0.01 |
| 41 Cycle | 63 Cycle | 78 Cycle | 100 Cycle | 125 Cycle | 150 Cycle | Average | |
|---|---|---|---|---|---|---|---|
| MNN | 0.076 | 0.101 | 0.083 | 0.136 | 0.115 | 0.334 | 0.1408 |
| LSTM | 0.09 | 0.141 | 0.096 | 0.103 | 0.126 | 0.222 | 0.1296 |
| GRU | 0.185 | 0.084 | 0.131 | 0.134 | 0.066 | 0.188 | 0.1313 |
| XGBoost | 0.176 | 0.097 | 0.083 | 0.093 | 0.088 | 0.228 | 0.1275 |
| TCN | 0.126 | 0.117 | 0.125 | 0.105 | 0.098 | 0.197 | 0.128 |
| TCN-XGBoost (one node) | 0.112 | 0.081 | 0.093 | 0.078 | 0.067 | 0.172 | 0.1005 |
| TCN-XGBoost (two nodes) | 0.093 | 0.080 | 0.094 | 0.081 | 0.063 | 0.162 | 0.0955 |
| 6 Cycle | 15 Cycle | 28 Cycle | 42 Cycle | 70 Cycle | 78 Cycle | Average | |
|---|---|---|---|---|---|---|---|
| MNN | 0.303 | 0.205 | 0.164 | 0.191 | 0.167 | 0.233 | 0.2105 |
| LSTM | 0.269 | 0.088 | 0.145 | 0.182 | 0.122 | 0.132 | 0.1563 |
| GRU | 0.21 | 0.103 | 0.115 | 0.132 | 0.095 | 0.097 | 0.1253 |
| XGBoost | 0.102 | 0.126 | 0.198 | 0.119 | 0.146 | 0.161 | 0.142 |
| TCN | 0.163 | 0.12 | 0.203 | 0.161 | 0.222 | 0.191 | 0.1767 |
| TCN-XGBoost (one node) | 0.116 | 0.045 | 0.135 | 0.092 | 0.123 | 0.091 | 0.1003 |
| TCN-XGBoost (two nodes) | 0.113 | 0.049 | 0.134 | 0.090 | 0.110 | 0.094 | 0.0983 |
| Cell 1 | Cell 2 | Cell 3 | Cell 4 | Cell 5 | Cell 6 | Cell 7 | Cell 8 | Average | |
|---|---|---|---|---|---|---|---|---|---|
| MNN | 3.173 | 1.36 | 1.154 | 2.772 | 1.989 | 1.008 | 1.862 | 1.545 | 1.857 |
| LSTM | 2.616 | 1.137 | 0.74 | 2.387 | 1.909 | 1.035 | 1.877 | 1.297 | 1.624 |
| GRU | 2.685 | 1.035 | 0.772 | 2.62 | 1.731 | 1.08 | 1.933 | 1.331 | 1.648 |
| XGBoost | 1.235 | 1.219 | 0.745 | 2.36 | 1.699 | 0.991 | 1.686 | 1.715 | 1.456 |
| TCN | 0.957 | 1.219 | 0.934 | 2.253 | 1.604 | 0.95 | 1.797 | 1.428 | 1.393 |
| TCN-XGBoost (one node) | 1.143 | 1.14 | 0.938 | 2.333 | 1.598 | 1.028 | 1.712 | 1.514 | 1.413 |
| TCN-XGBoost (two nodes) | 1.121 | 1.114 | 0.937 | 2.212 | 1.569 | 1.011 | 1.667 | 1.459 | 1.386 |
| TCN-XGBoost (three nodes) | 1.107 | 1.127 | 0.92 | 2.211 | 1.57 | 0.997 | 1.672 | 1.441 | 1.381 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-H.; Lee, I.-S. Hybrid Estimation Method for the State of Charge of Lithium Batteries Using a Temporal Convolutional Network and XGBoost. Batteries 2023, 9, 544. https://doi.org/10.3390/batteries9110544
Lee J-H, Lee I-S. Hybrid Estimation Method for the State of Charge of Lithium Batteries Using a Temporal Convolutional Network and XGBoost. Batteries. 2023; 9(11):544. https://doi.org/10.3390/batteries9110544
Chicago/Turabian StyleLee, Jong-Hyun, and In-Soo Lee. 2023. "Hybrid Estimation Method for the State of Charge of Lithium Batteries Using a Temporal Convolutional Network and XGBoost" Batteries 9, no. 11: 544. https://doi.org/10.3390/batteries9110544
APA StyleLee, J.-H., & Lee, I.-S. (2023). Hybrid Estimation Method for the State of Charge of Lithium Batteries Using a Temporal Convolutional Network and XGBoost. Batteries, 9(11), 544. https://doi.org/10.3390/batteries9110544






